Combined Multilateration with Machine Learning for Enhanced Aircraft Localization †
Abstract
:1. Introduction
2. The Aircraft Localization Competition
2.1. Competition Goal
2.2. Datasets
- A unique aircraft identifier
- The Unix timestamp indicated when the message was received by the OSN server
- Unique identifiers of all sensors that received the message
- Nanosecond timestamps at which each sensor received the message
- Signal strength measurements from each of the sensors
- The position of the aircraft (latitude, longitude, height); latitude and longitude is empty for the training rows
- The barometric altitude of the aircraft
- A unique sensor identifier
- The position of the sensor (latitude, longitude, height)
- The type of hardware and software
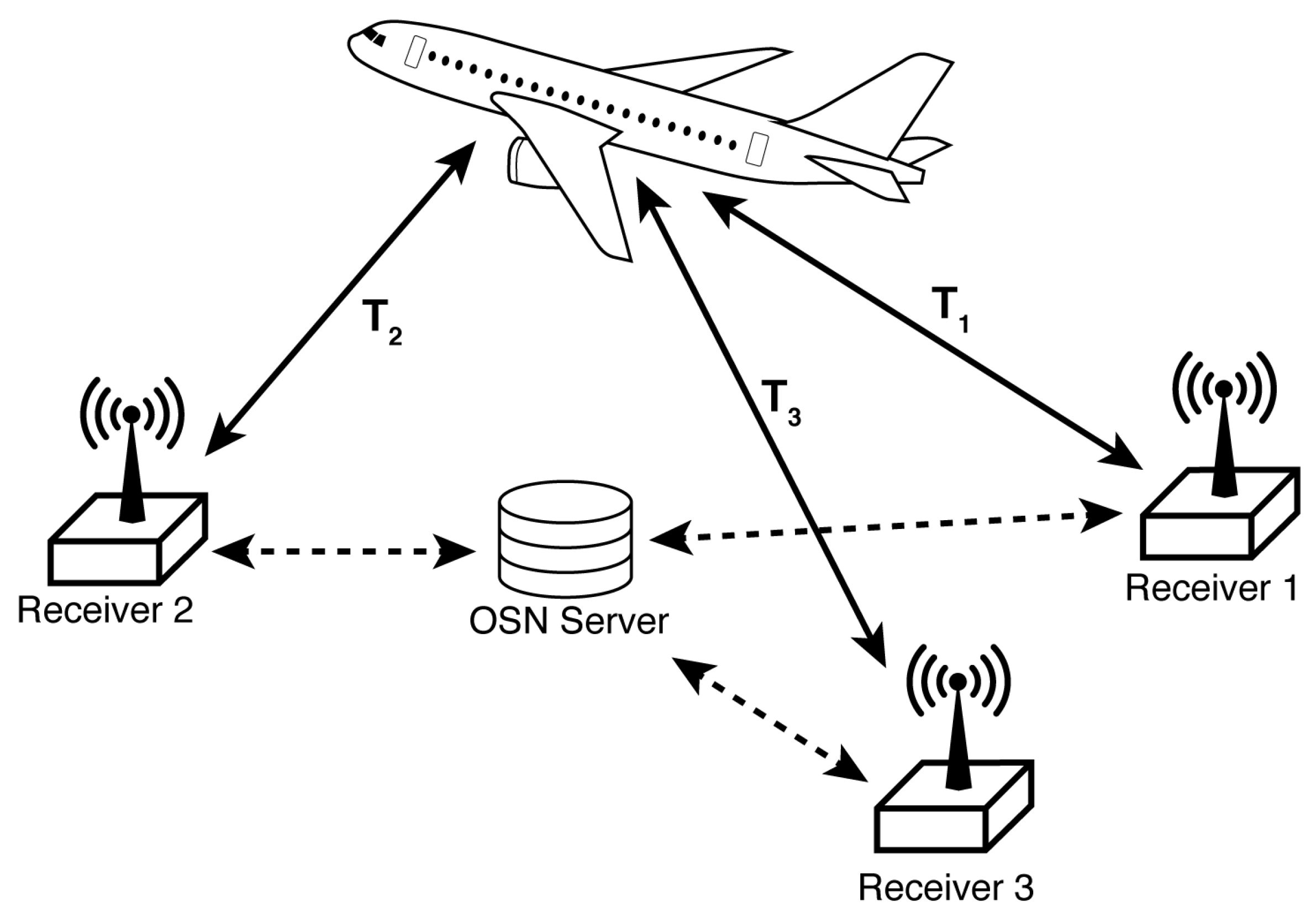
2.3. Time Difference of Arrival
2.3.1. Pairwise TDoA
2.3.2. Observation/Theoretical Comparison
3. The Localization Solution
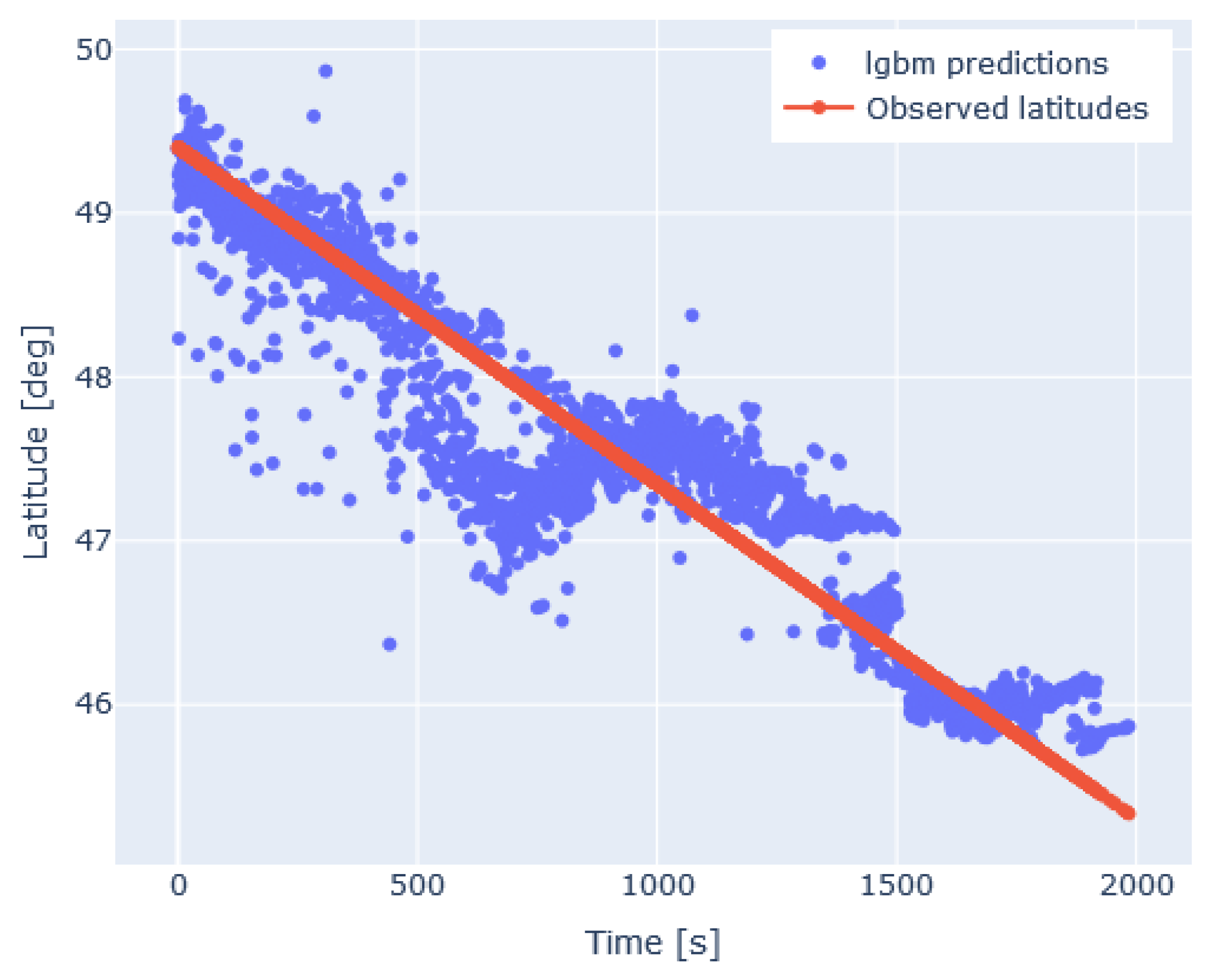
3.1. Machine Learning-Based Localization
3.2. Multilateration-Based Localization
3.2.1. Triplet-Wise Multilateration
3.2.2. All-in-View Multilateration
3.2.3. Combined Multilateration
- The triplet-wise multilateration is applied,
- the modified z-score [12] is computed for each triplet solution
- only the triplet of sensors with a z-score below 3.5 is labeled as “valid sensors”
- the all-in-view multilateration is solved for all the sensors that are in the list of valid sensors as defined in Step 3.
| Algorithm 1: Triplet-wise multilateration algorithm. |
 |
4. Results
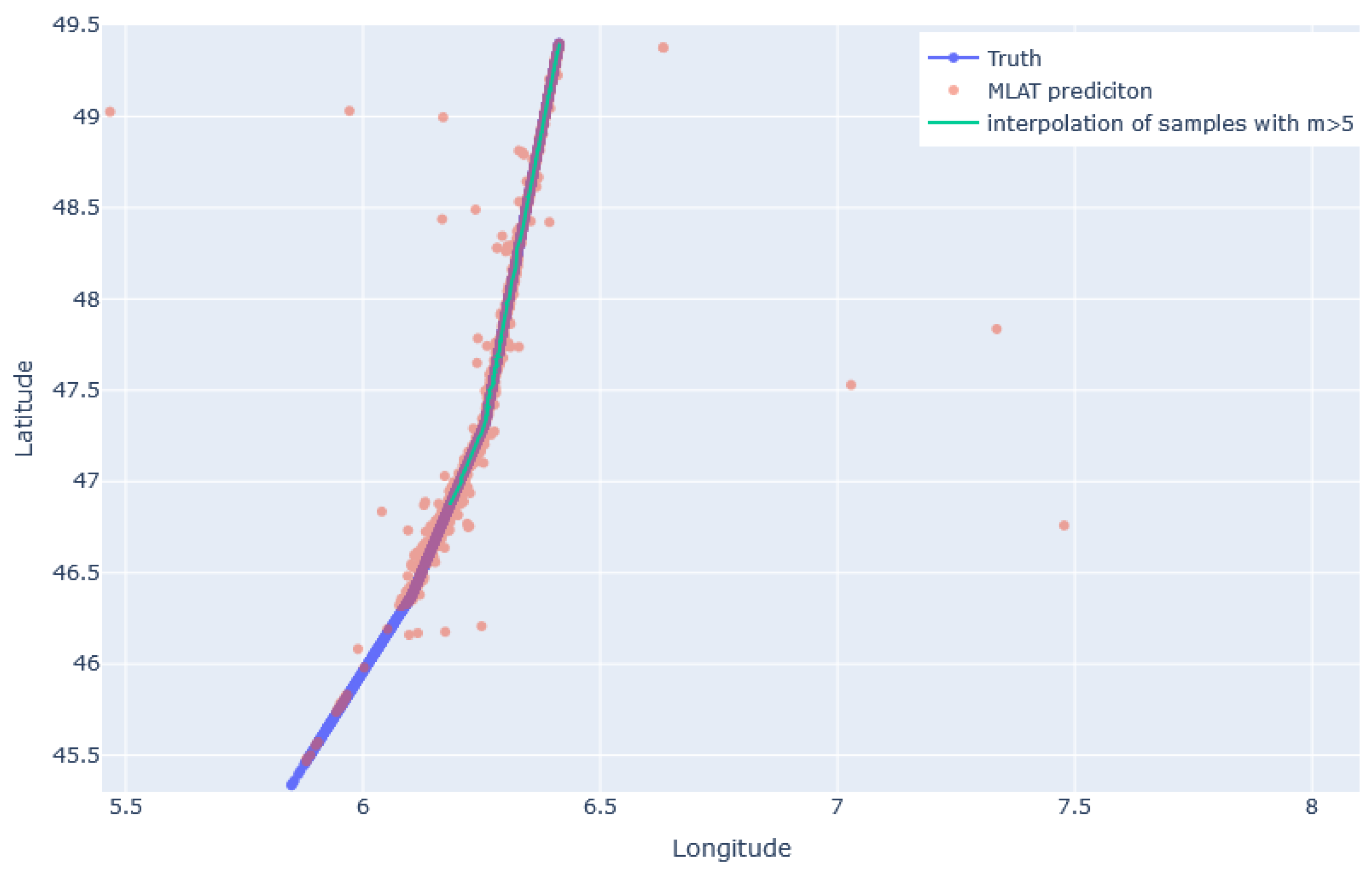
4.1. Triplet-Wise versus Combined Multilateration
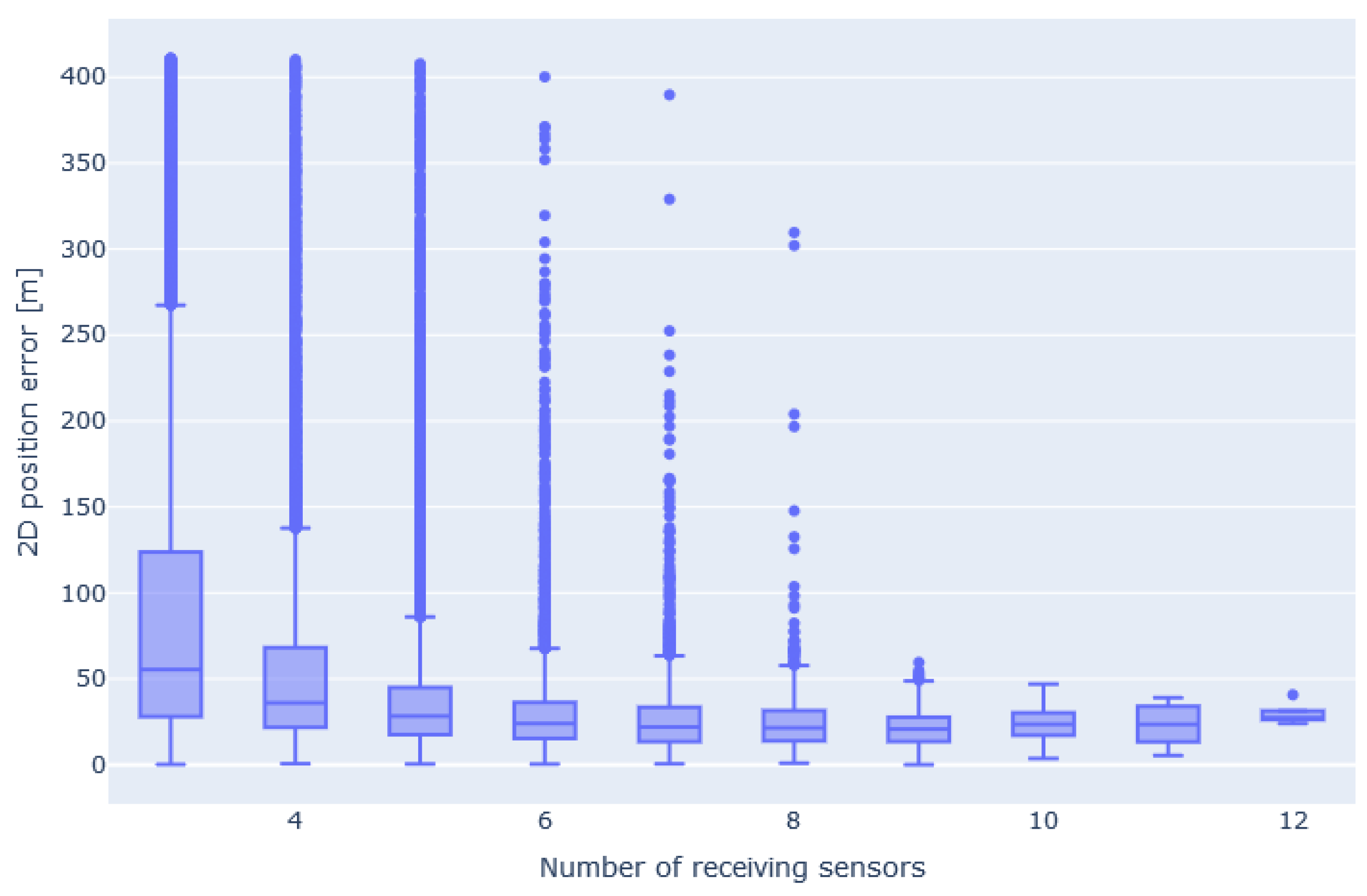
4.2. Accuracy as a Function of the Number of Receivers
4.3. Computational considerations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pérez Marcos, E.; Konovaltsev, A.; Caizzone, S.; Cuntz, M.; Yinusa, K.; Elmarissi, W.; Meurer, M. Interference and Spoofing Detection for GNSS Maritime Applications Using Direction of Arrival Measurements and a Conformal Antenna Array. In Proceedings of the 31st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24–28 September 2018. [Google Scholar]
- Psiaki, M.L.; Humphreys, T.E. GNSS spoofing and detection. Proc. IEEE 2016, 104, 1258–1270. [Google Scholar] [CrossRef]
- Schäfer, M.; Strohmeier, M.; Lenders, V.; Martinovic, I.; Wilhelm, M. Bringing up OpenSky: A large-scale ADS-B sensor network for research. In Proceedings of the 13th International Symposium on Information Processing in Sensor Networks (IPSN 2014), Berlin, Germany, 15–17 April 2014; pp. 83–94. [Google Scholar]
- Scaramuzza, M.; Loeser, M.; Früh, D. Mobile MLAT for PBN and ADS-B performance assessments. In Proceedings of the ENRI International Workshop on ATM/CNS (EIWAC2015), Tokyo, Japan, 17–19 November 2015. [Google Scholar]
- Strohmeier, M.; Martinovic, I.; Lenders, V. A k-NN-Based Localization Approach for Crowdsourced Air Traffic Communication Networks. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1519–1529. [Google Scholar] [CrossRef]
- CYD Campus Aircraft Localization Competition: Challenges. 2020. Available online: https://www.aicrowd.com/challenges/cyd-campus-aircraft-localization-competition (accessed on 2 November 2020).
- Aircraft Localization Competition: Documentation. 2020. Available online: https://competition.opensky-network.org/ (accessed on 2 November 2020).
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Advances in Neural Information Processing Systems 30; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 3146–3154. [Google Scholar]
- Yang, Y.; Miao, L. GDOP results in all-in-view positioning and in four optimum satellites positioning with GPS PRN codes ranging. In Proceedings of the PLANS 2004. Position Location and Navigation Symposium (IEEE Cat. No. 04CH37556), Monterey, CA, USA, 26–29 April 2004; pp. 723–727. [Google Scholar]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. [Google Scholar]
- Iglewicz, B.; Hoaglin, D. How to Detect and Handle Outliers; ASQC Basic References in Quality Control; ASQC Quality Press: Milwaukee, WI, USA, 1993. [Google Scholar]
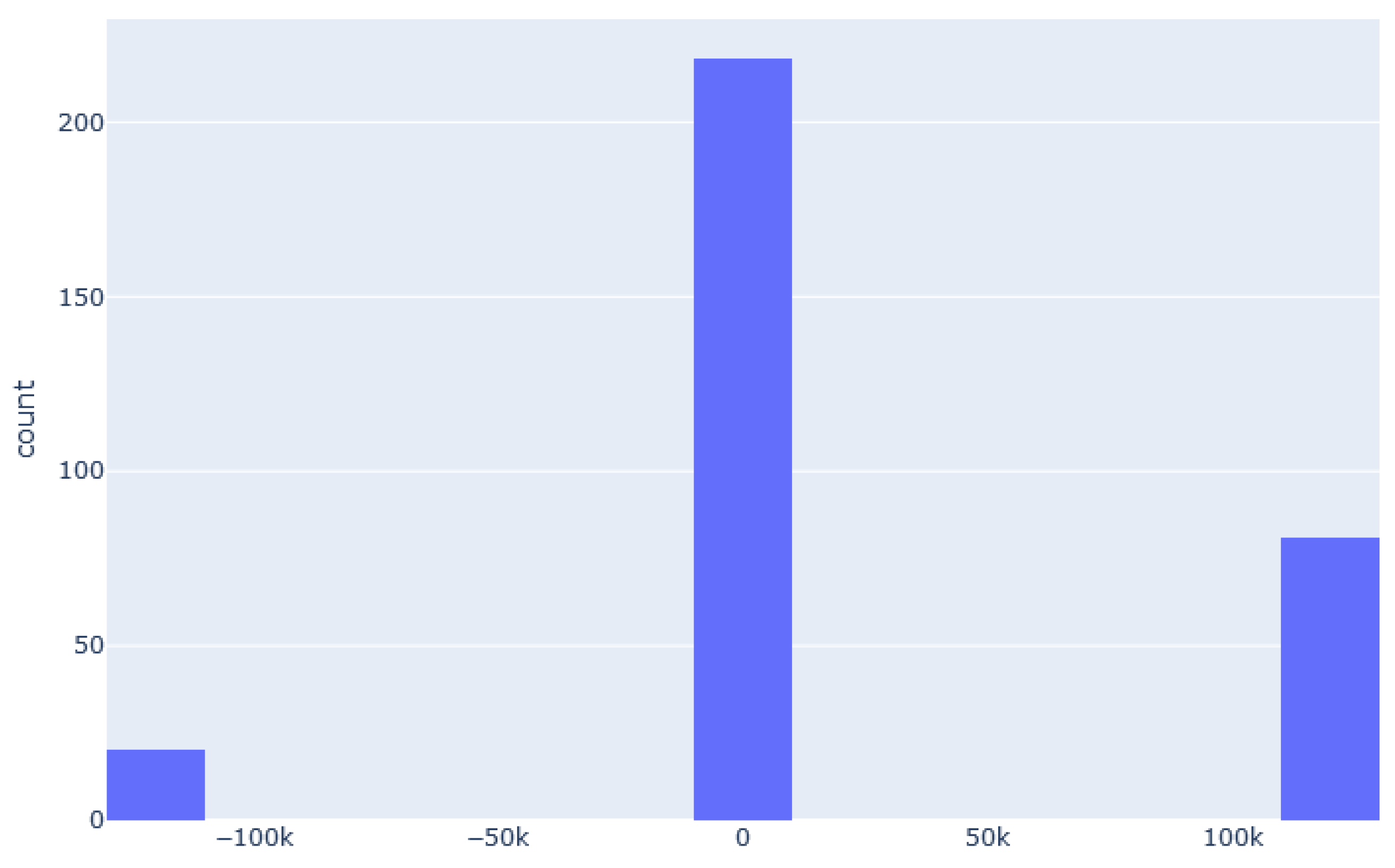



| Pairs | |||
|---|---|---|---|
| Observed errors (ns) | 103 | −120,785 | −120,888 |
| −131 | −120,509 | −120,409 | |
| −879 | −120,613 | −120,958 | |
| ⋯ | ⋯ | ⋯ | |
| Pairwise Median (ns) | 67 | −120,508 | −120,577 |
| Pairwise Interdecile Range (ns) | 444 | 419 | 840 |
| Metric | Triplet-Wise | Combined Multilateration |
|---|---|---|
| Coverage | 64.76% | 64.47% |
| 2D Error 1st quartile | 22.32 m | 20.18 m |
| 2D Error median | 39.19 m | 34.02 m |
| 2D Error 3rd quartile | 83.89 m | 67.53 m |
| Competition evaluation criteria | 155 m | 95.56 m |
| Localization Solution | ||||
|---|---|---|---|---|
| Triplet-wise | 0.15 s | 0.61 s | 1.53 s | 3.97 s |
| All-in-view | 0.12 s | 0.17 s | 0.23 s | 0.16 s |
| Combined | 0.27 s | 0.78 s | 1.76 s | 4.13 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Figuet, B.; Monstein, R.; Felux, M. Combined Multilateration with Machine Learning for Enhanced Aircraft Localization. Proceedings 2020, 59, 2. https://doi.org/10.3390/proceedings2020059002
Figuet B, Monstein R, Felux M. Combined Multilateration with Machine Learning for Enhanced Aircraft Localization. Proceedings. 2020; 59(1):2. https://doi.org/10.3390/proceedings2020059002
Chicago/Turabian StyleFiguet, Benoit, Raphael Monstein, and Michael Felux. 2020. "Combined Multilateration with Machine Learning for Enhanced Aircraft Localization" Proceedings 59, no. 1: 2. https://doi.org/10.3390/proceedings2020059002
APA StyleFiguet, B., Monstein, R., & Felux, M. (2020). Combined Multilateration with Machine Learning for Enhanced Aircraft Localization. Proceedings, 59(1), 2. https://doi.org/10.3390/proceedings2020059002





