Analysis of Radiation Propagation inside a Hierarchical Solar Volumetric Absorber †
Abstract
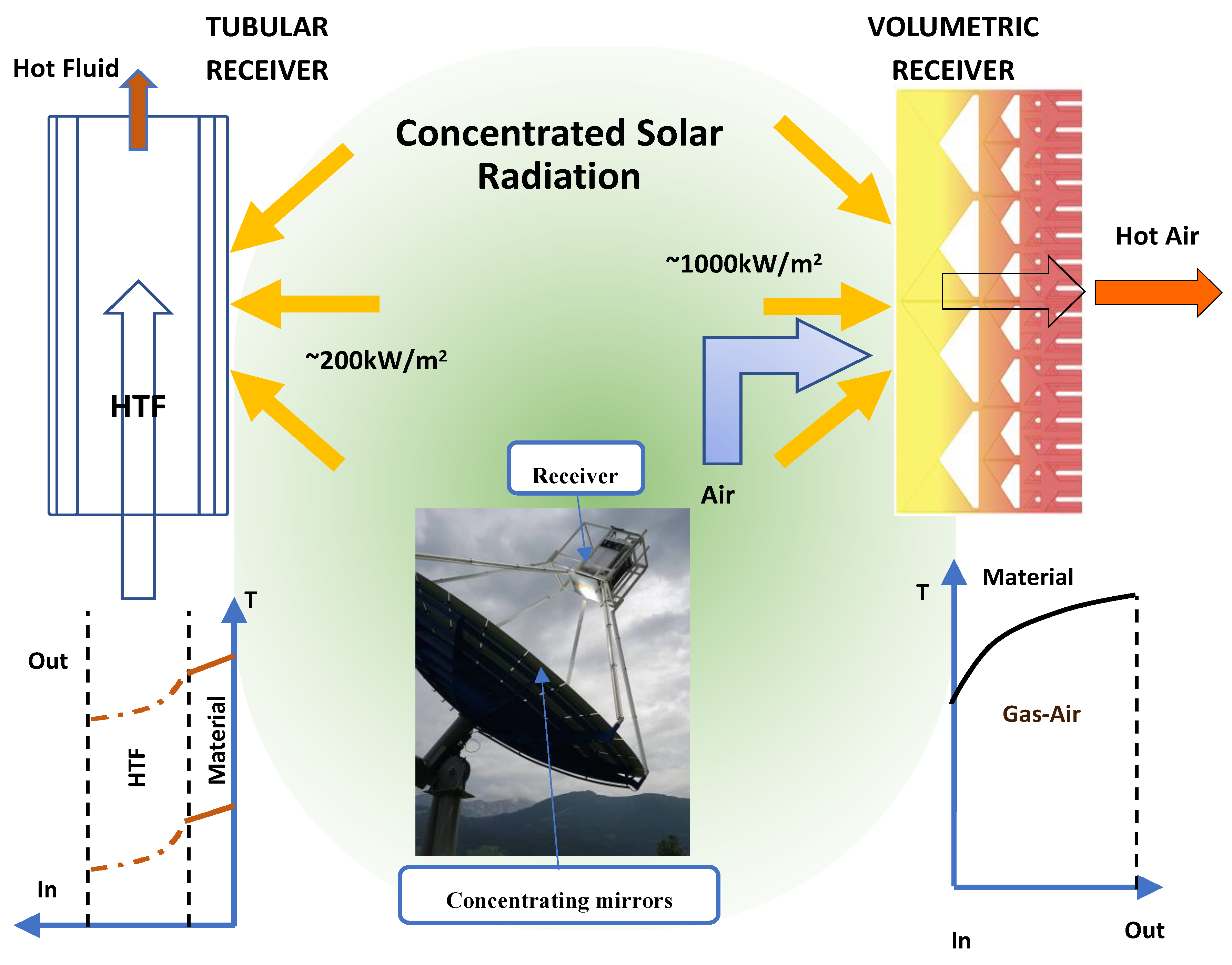
:1. Introduction
2. Methodology
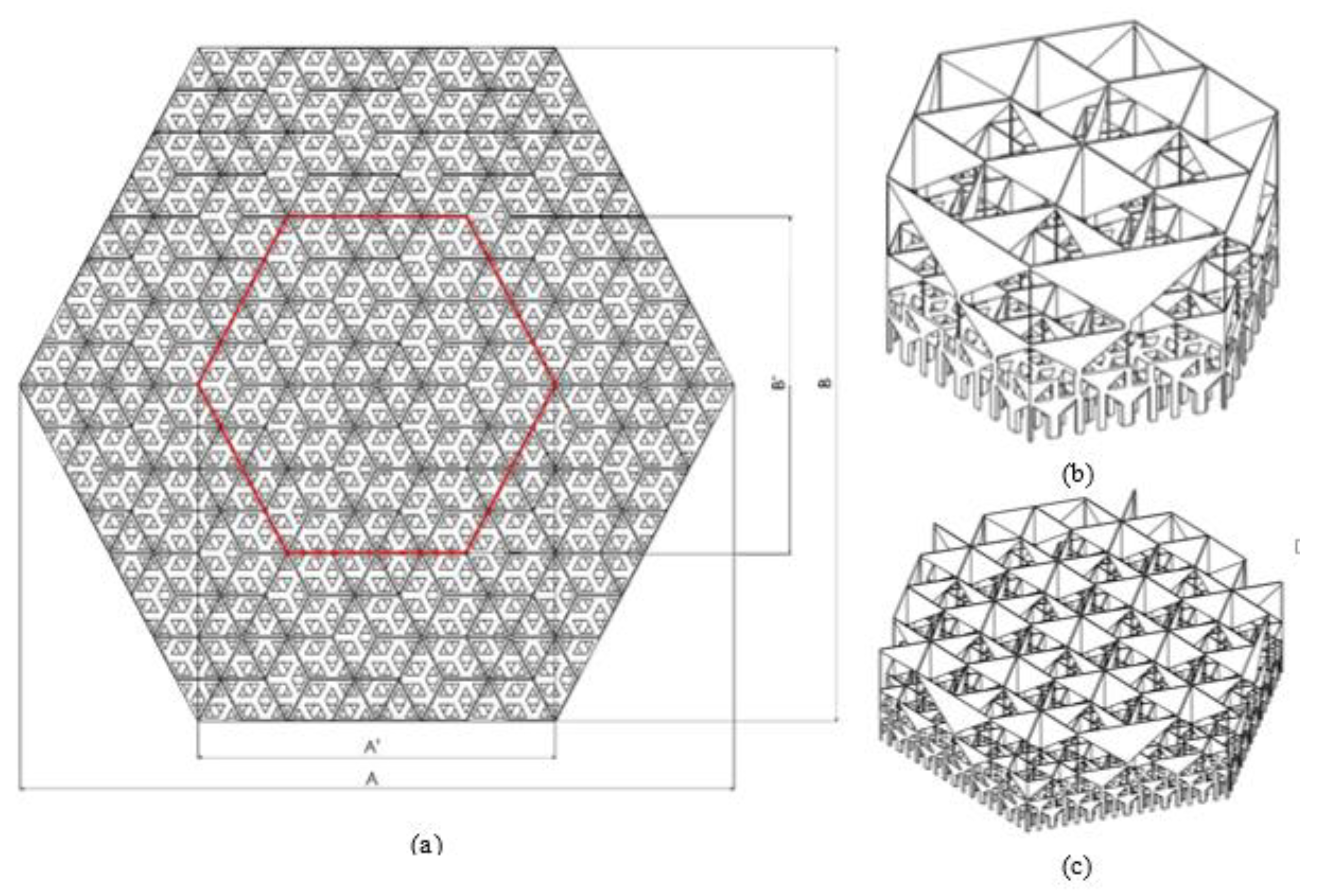
2.1. Numerical Methodology
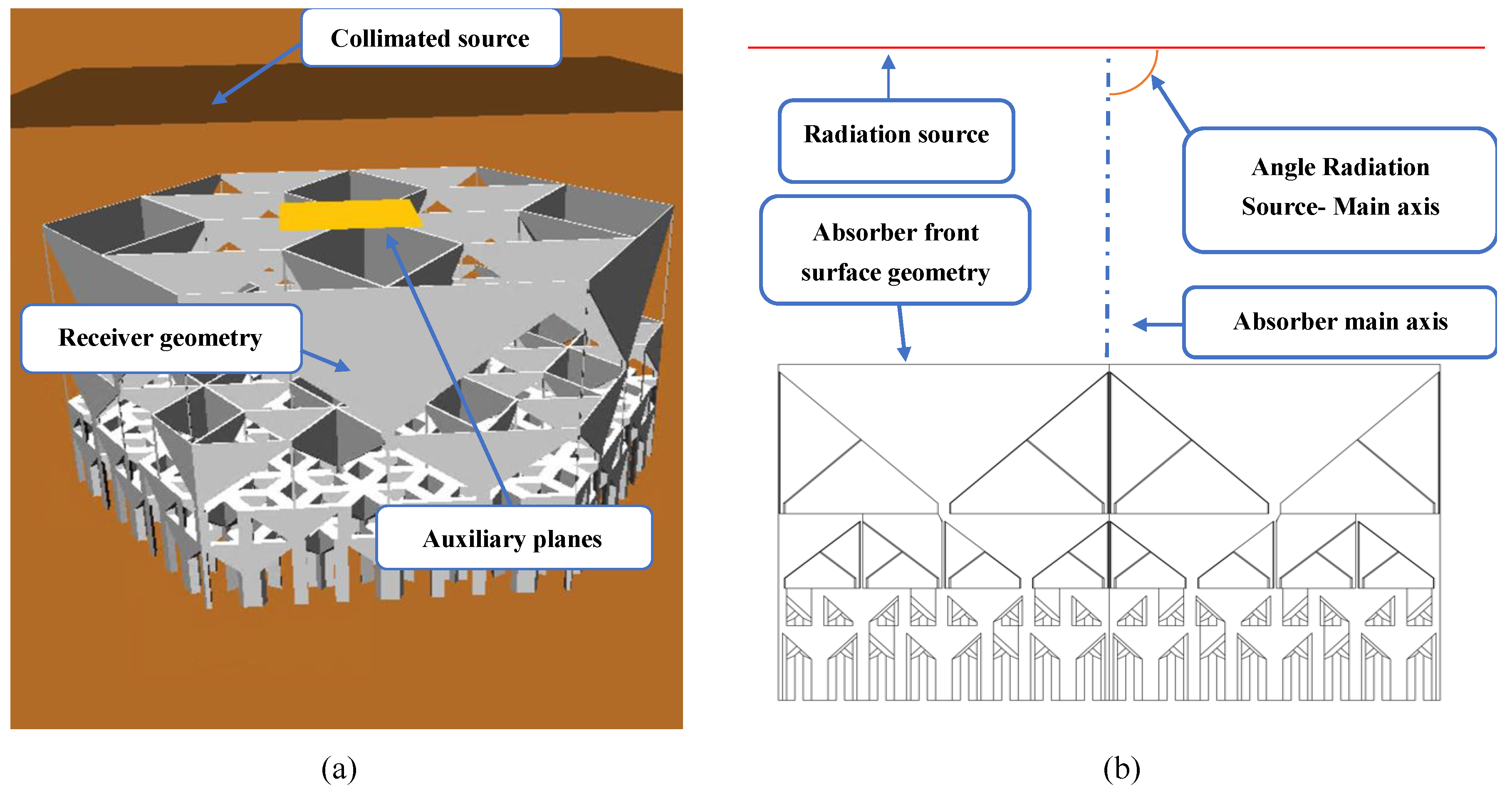
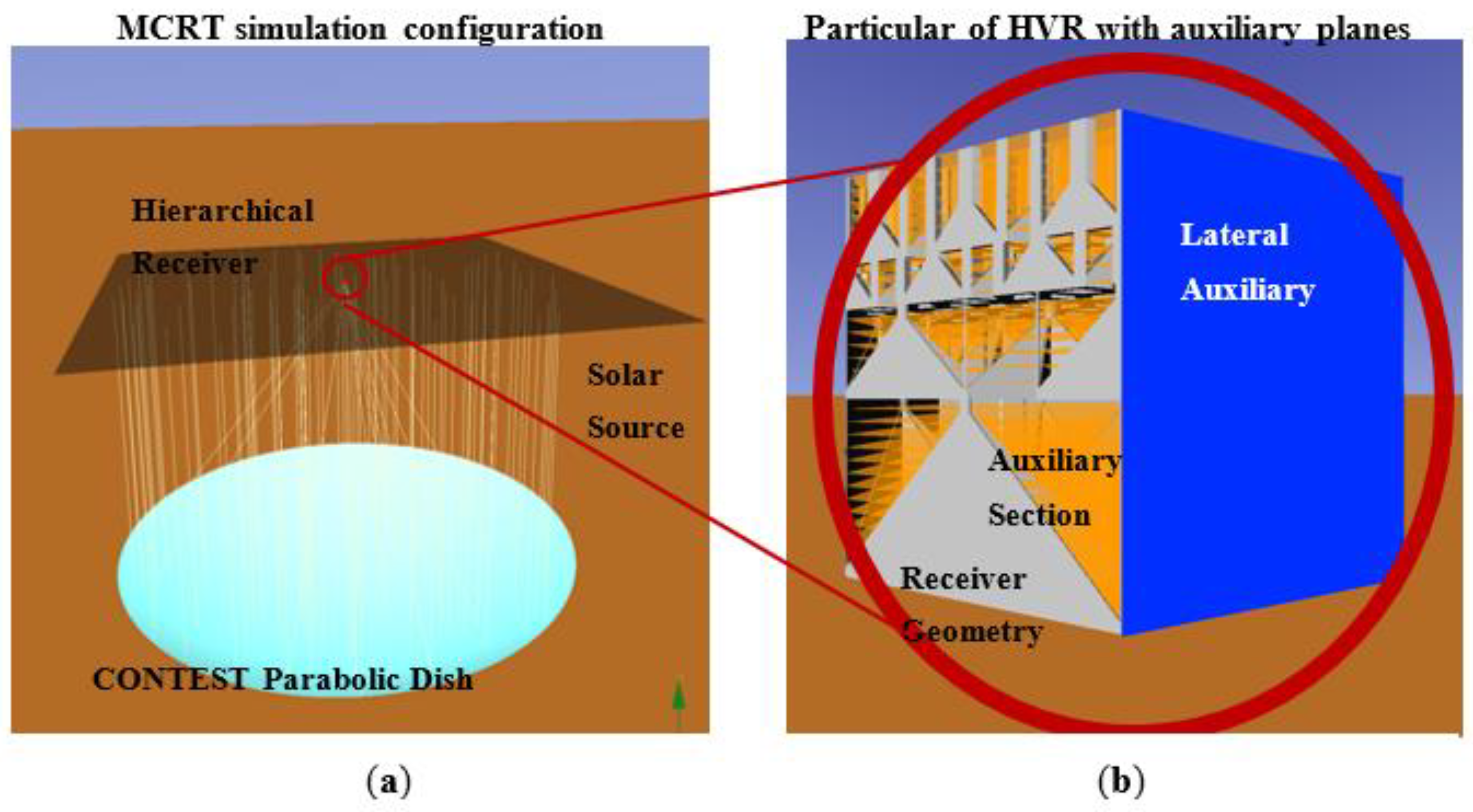
2.1.1. MCRT Collimated Source Simulations
2.1.2. MCRT Simulations Using Concentrated Radiative Source
2.2. Experimental Methodology
Experimental Measurements of Radiation Transmissivity
3. Results
3.1. Result of Transmissivity Experimental Setup
3.2. Result of Simulations
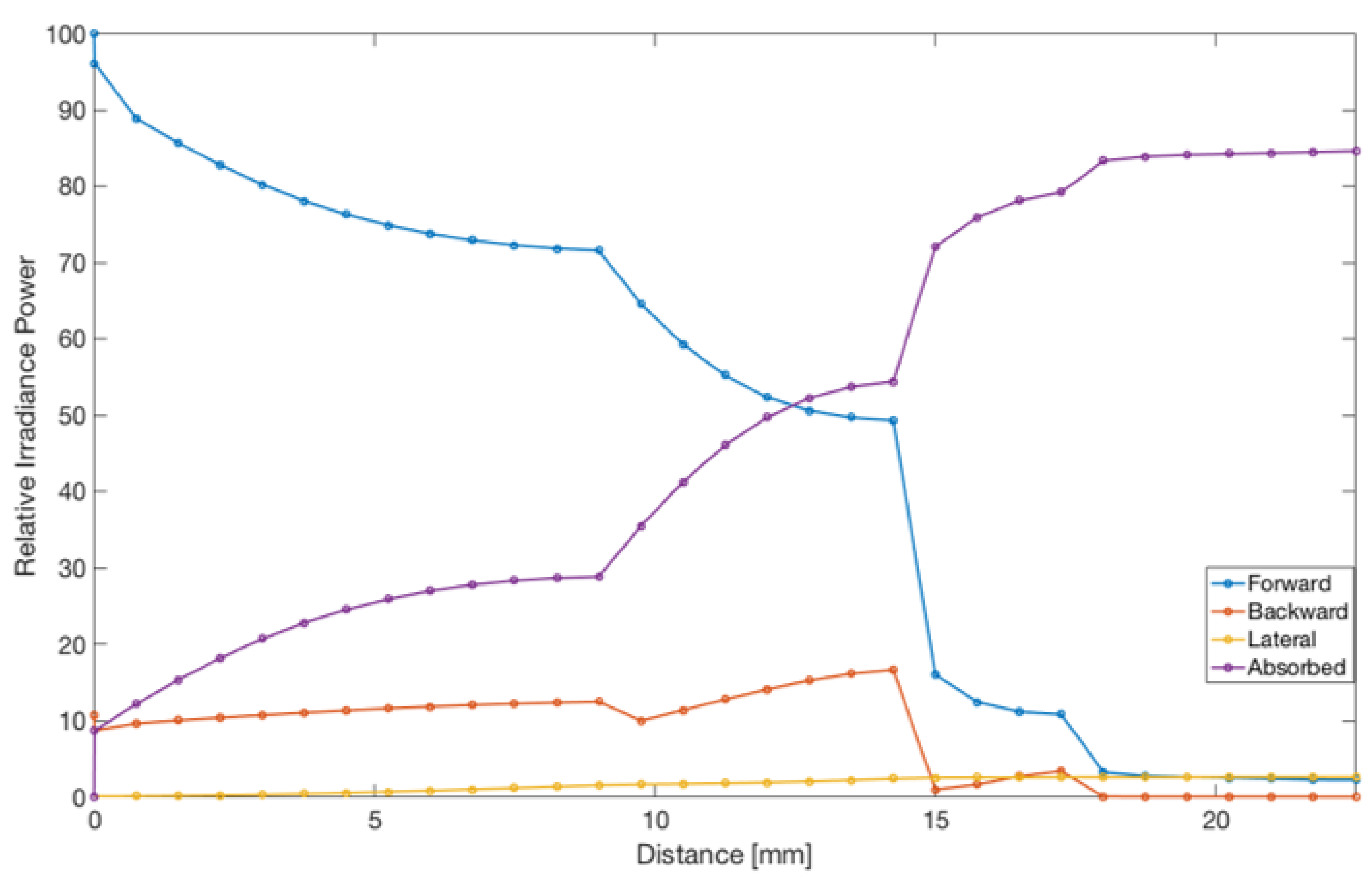
3.2.1. Collimated Source Simulations
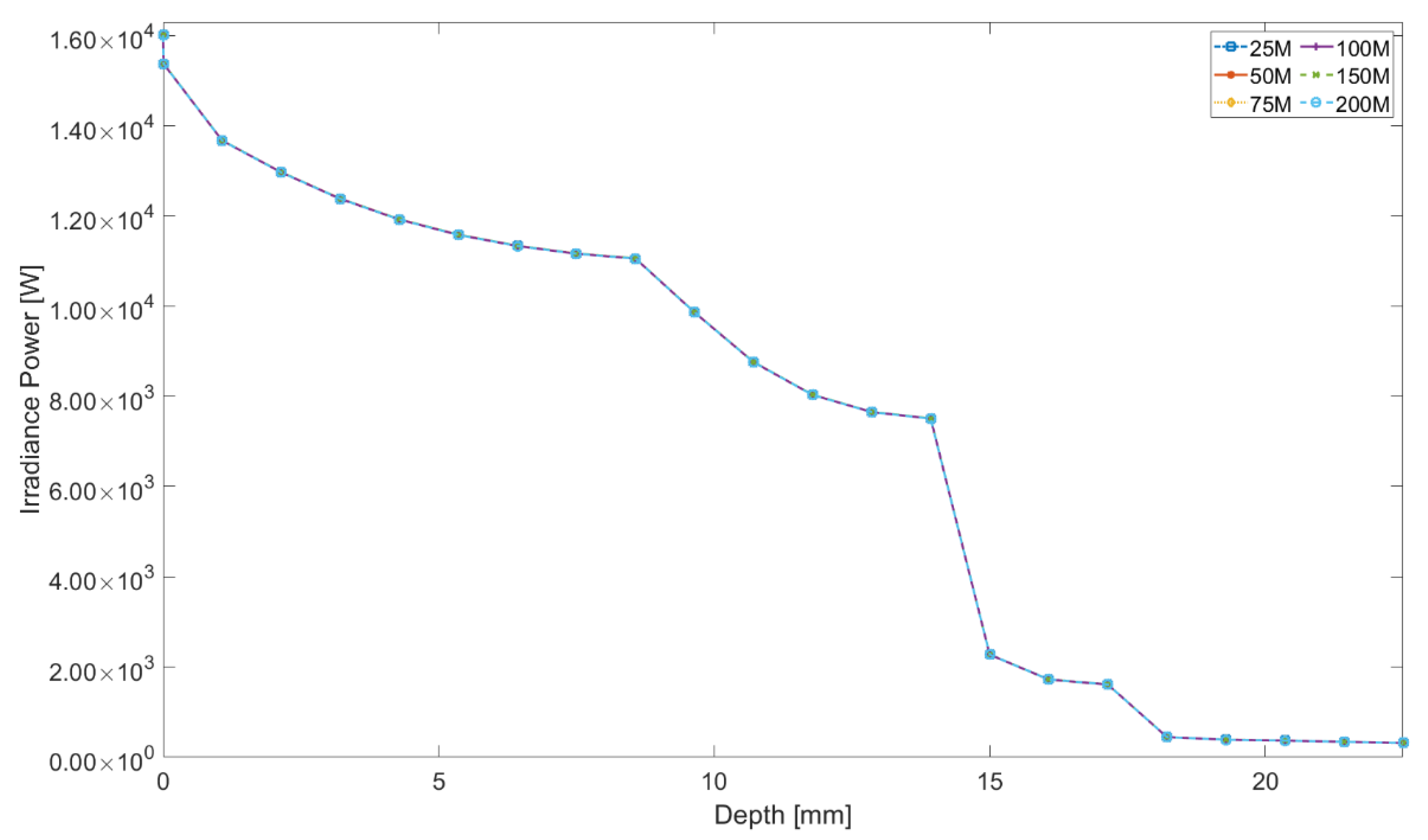
3.2.2. Photon Number Sensitivity Analysis
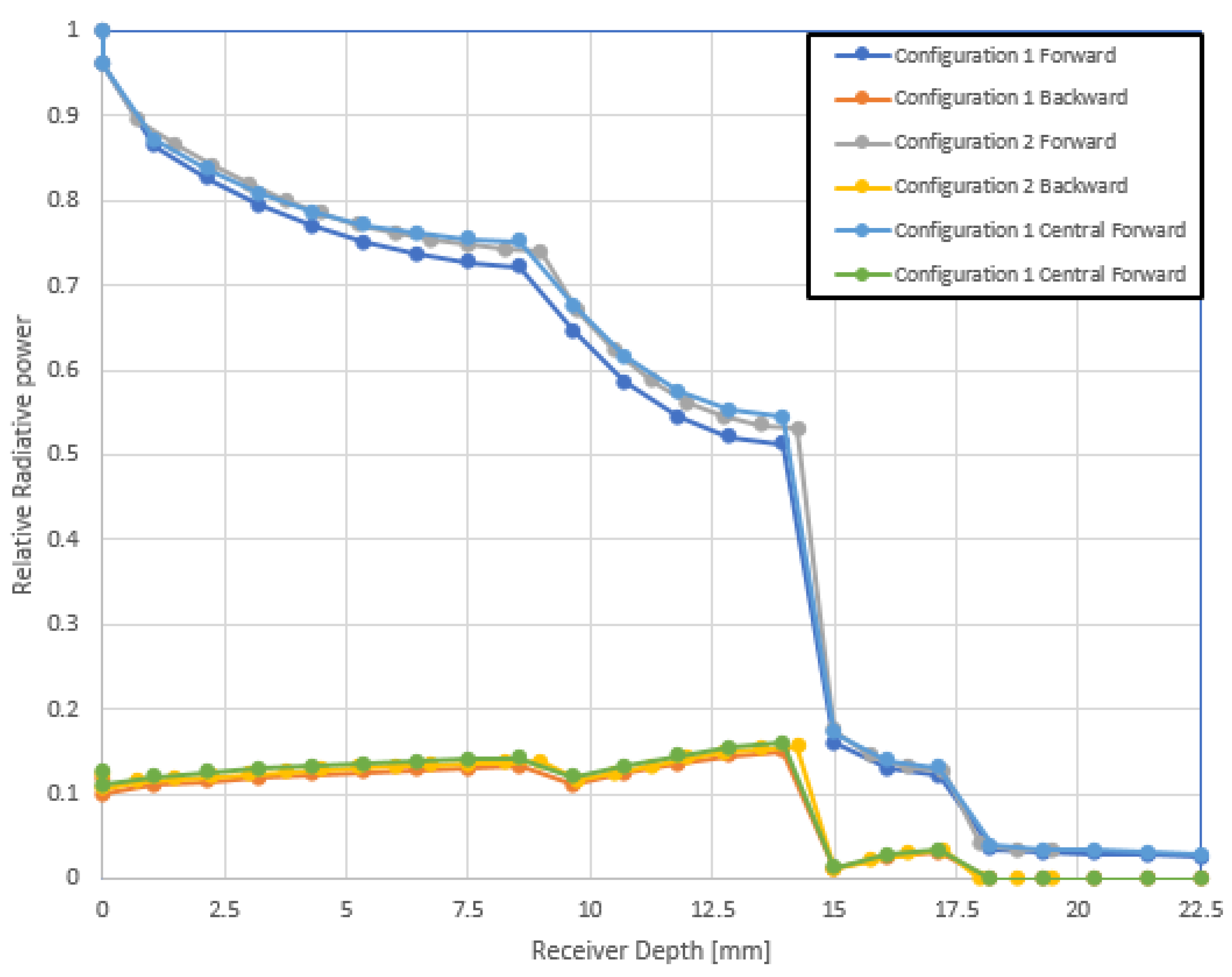
3.2.3. MCRT Simulation Results with Concentrated Source
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| CSP | concentrated solar power |
| HVR | hierarchical volumetric receiver |
| HTF | heat transfer fluid |
| MCRT | Monte Carlo ray tracing |
| STDEV | standard deviation |
| TR | Tubular receiver |
| VR | Volumetric receiver |
| List of Symbols | |
| α | angle between receiver main axis and radiative source |
| ρ | reflectivity |
References
- COP21. Available online: https://www.gouvernement.fr/en/cop21 (accessed on 2 April 2020).
- United States Environmental Protection Agency. Sources of Greenhouse Gas Emissions. Available online: https://www.epa.gov/ghgemissions/sources-greenhouse-gas-emissions (accessed on 2 April 2020).
- Avila-Marin, A.L.; Caliot, C.; Alvarez de Lara, M.; Fernandez-Reche, J.; Montes, M.J.; Martinez-Tarifa, A. Homogeneous equivalent model coupled with P1-approximation for dense wire meshes volumetric air receivers. Renew. Energy 2019, 135, 908–919. [Google Scholar] [CrossRef]
- Aichmayer, L.; Garrido, J.; Laumert, B. Thermo-mechanical solar receiver design and validation for a micro gas-turbine based solar dish system. Energy 2020, 196, 116929. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Solar Energy Engineering: Processes and Systems; Academic Press: Cambridge, MA, USA, 2013; ISBN 0-12-397256-6. [Google Scholar]
- Gigantino, M.; Kiwic, D.; Steinfeld, A. Thermochemical energy storage via isothermal carbonation-calcination cycles of MgO-stabilized SrO in the range of 1000–1100 °C. Sol. Energy 2019, 188, 720–729. [Google Scholar] [CrossRef]
- Romero, M.; Steinfeld, A. Concentrating solar thermal power and thermochemical fuels. Energy Environ. Sci. 2012, 5, 9234–9245. [Google Scholar] [CrossRef]
- Cagnoli, M.; Froio, A.; Savoldi, L.; Zanino, R. Multi-scale modular analysis of open volumetric receivers for central tower CSP systems. Sol. Energy 2019, 190, 195–211. [Google Scholar] [CrossRef]
- Ho, C.K.; Iverson, B.D. Review of high-temperature central receiver designs for concentrating solar power. Renew. Sustain. Energy Rev. 2014, 29, 835–846. [Google Scholar] [CrossRef]
- Avila-Marin, A.L.; Fernandez-Reche, J.; Martinez-Tarifa, A. Modelling strategies for porous structures as solar receivers in central receiver systems: A review. Renew. Sustain. Energy Rev. 2019, 111, 15–33. [Google Scholar] [CrossRef]
- Ávila-Marín, A.L. Volumetric receivers in Solar Thermal Power Plants with Central Receiver System technology: A review. Sol. Energy 2011, 85, 891–910. [Google Scholar] [CrossRef]
- Fend, T. High porosity materials as volumetric receivers for solar energetics. Opt. Appl. 2010, 40, 271–284. [Google Scholar]
- Kribus, A.; Gray, Y.; Grijnevich, M.; Mittelman, G.; Mey-Cloutier, S.; Caliot, C. The promise and challenge of solar volumetric absorbers. Sol. Energy 2014, 110, 463–481. [Google Scholar] [CrossRef]
- Luque, S.; Menéndez, G.; Roccabruna, M.; González-Aguilar, J.; Crema, L.; Romero, M. Exploiting volumetric effects in novel additively manufactured open solar receivers. Sol. Energy 2018, 174, 342–351. [Google Scholar] [CrossRef]
- Pitz-Paal, R.; Hoffschmidt, B.; Böhmer, M.; Becker, M. Experimental and numerical evaluation of the performance and flow stability of different types of open volumetric absorbers under non-homogeneous irradiation. Sol. Energy 1997, 60, 135–150. [Google Scholar] [CrossRef]
- Cagnoli, M.; Savoldi, L.; Zanino, R.; Zaversky, F. Coupled optical and CFD parametric analysis of an open volumetric air receiver of honeycomb type for central tower CSP plants. Sol. Energy 2017, 155, 523–536. [Google Scholar] [CrossRef]
- Nakakura, M.; Bellan, S.; Matsubara, K.; Kodama, T. Conjugate radiation-convection-conduction simulation of volumetric solar receivers with cut-back inlets. Sol. Energy 2018, 170, 606–617. [Google Scholar] [CrossRef]
- Capuano, R.; Fend, T.; Stadler, H.; Hoffschmidt, B.; Pitz-Paal, R. Optimized volumetric solar receiver: Thermal performance prediction and experimental validation. Renew. Energy 2017, 114, 556–566. [Google Scholar] [CrossRef]
- Sedighi, M.; Padilla, R.V.; Alamdari, P.; Lake, M.; Rose, A.; Izadgoshasb, I.; Taylor, R.A. A novel high-temperature (>700 °C), volumetric receiver with a packed bed of transparent and absorbing spheres. Appl. Energy 2020, 264, 114705. [Google Scholar] [CrossRef]
- Alberti, F.; Santiago, S.; Roccabruna, M.; Luque, S.; Gonzalez-Aguilar, J.; Crema, L.; Romero, M. Numerical analysis of radiation propagation in innovative volumetric receivers based on selective laser melting techniques. AIP Conf. Proc. 2016, 1734, 030001. [Google Scholar] [CrossRef]
- Roccabruna, M.; Fabio, M.; Fabio, R.; Crema, L. Solar Flux Map Distribution of a Parabolic-Spheric Dish Based on Photographic Method. In Proceedings of the 12th International Conference on Solar Energy for Buildings and Industry (ISES EuroSun 2018), Rapperswil, Switzerland, 10–13 September 2018. [Google Scholar] [CrossRef]
- Blanco, M.J.; Amieva, J.M.; Mancillas, A. The Tonatiuh Software Development Project: An Open Source Approach to the Simulation of Solar Concentrating Systems. In Proceedings of the ASME 2005 International Mechanical Engineering Congress and Exposition, Orlando, FL, USA, 5–11 November 2005; pp. 157–164. [Google Scholar] [CrossRef]
- Sun 2000 Class A. Available online: http://abet-technologies.com/solar-simulators/sun-2000-class-a/ (accessed on 28 May 2020).
- RS PRO Solar Power Meter ISM400, Solar Power|RS Components. Available online: https://uk.rs-online.com/web/p/solar-power-meter/1232218/ (accessed on 28 May 2020).

| Zone | Irradiance W/m2 | Transmissivity |
|---|---|---|
| Without Receiver + STDEV | 365 ± 2 | - |
| Average + STDEV | 33.8 ± 5.6 | 9.2% ± 1.6% |
| Source ConditionsAngle to Receiver Main Axis (Deg) | Average Irradiance Front Surface W/m2 | Average Irradiance Rear Surface (W/m2) | Transmissivity % | ||
|---|---|---|---|---|---|
| ρ = 53% | ρ = 30% | ρ = 53% | ρ = 30% | ||
| 90° | 367.2 | 46 | 45.9 | 12.5% | 12.5% |
| 89° | 365.9 | 44.2 | 43.4 | 12.1% | 11.9% |
| 88° | 365.7 | 37.9 | 39.1 | 10.4% | 10.7% |
| 87° | 364.6 | 33 | 32.5 | 9.2% | 8.9% |
| Average | 365.9 | 41.5 ± 5.7 | 40.2 ± 5.8 | 11.3% ± 1.5% | 10.9% ± 1.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pratticò, L.; Bartali, R.; Crema, L.; Sciubba, E. Analysis of Radiation Propagation inside a Hierarchical Solar Volumetric Absorber. Proceedings 2020, 58, 27. https://doi.org/10.3390/WEF-06932
Pratticò L, Bartali R, Crema L, Sciubba E. Analysis of Radiation Propagation inside a Hierarchical Solar Volumetric Absorber. Proceedings. 2020; 58(1):27. https://doi.org/10.3390/WEF-06932
Chicago/Turabian StylePratticò, Luca, Ruben Bartali, Luigi Crema, and Enrico Sciubba. 2020. "Analysis of Radiation Propagation inside a Hierarchical Solar Volumetric Absorber" Proceedings 58, no. 1: 27. https://doi.org/10.3390/WEF-06932
APA StylePratticò, L., Bartali, R., Crema, L., & Sciubba, E. (2020). Analysis of Radiation Propagation inside a Hierarchical Solar Volumetric Absorber. Proceedings, 58(1), 27. https://doi.org/10.3390/WEF-06932






