The Latest Method for Surface Tension Determination: Experimental Validation ^†

Abstract

The newest method for determining surface tension is being validated, which is done for the air–water interface. Since the relative differences between the benchmark values and the experimental results are very small, the newest method seems to be validated in a positive way.

1. Introduction

Technological progress in energy-saving causes heat transfer to be done during boiling more often [1]. Heat transfer investigation during combustion results in introducing surface tension into the calculation algorithms [2,3]. Forasmuch as new substances are coming into being, the surface tension values must be measured [4]. Surface tension is a factor which affects water injection in the engines [5].

Surface tension is mainly determined using the Young–Laplace equation:

$$\Delta \mathrm{p}=\mathsf{\gamma }\left(\frac{1}{{\mathrm{R}}_1}+\frac{1}{{\mathrm{R}}_2}\right)\left[\frac{\mathrm{N}}{\mathrm{m}{\mathrm{m}}^2}\right],$$

(1)

where:

Δp—pressure difference between two sides of the interface in the bulk phases [N/m²];

γ—surface tension [N/mm];

R₁, R₂—the main radii of curvature [mm].

The Young–Laplace Equation (1) is solved by applying Bushworth and Adams’ system of differential equations (cf. pp. 162–163 in Hartland and Hartley [6]), which was modified to the particular needs.

However, there is a failure of the algorithm in the case of the spherical drop or bubble, and there are no solutions near the poles. Hoorfar and Neumann [7] concluded that there is an inherent difficulty and no numerical change to improve the algorithm. It means that the algorithm is unable to solve the equation for the whole either drop or bubble. There is a moment when a bubble has just been created and has yet been motionless. At this particular moment, the forces’ origin is only from two fluids and the bubble is at rest, which is the closest approximation of the presumptions. Although the present cameras are able to make a still at this moment, the Young–Laplace equation cannot be applied because of the lack of the solutions at the poles.

Contemporary Interface Model

In contrast, a new analytical model fails neither at the poles nor for spherical drops or bubbles. In addition, it can be differentiated at the poles (cf. Gajewski [8,9]). In the case of the bubbles, the following system of equations is solved (cf. Gajewski [10]):

$${\mathrm{d}}_{\mathrm{m}\mathrm{a}\mathrm{x}}=\left(\mathrm{H}+{\left({\mathrm{H}}^2-8{\mathrm{a}}^2\cos {\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)}^{\frac{1}{2}}\right)\tan {\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left[\mathrm{m}\mathrm{m}\right],$$

(2)

$${\mathrm{h}}_{\mathrm{m}\mathrm{a}\mathrm{x}}=\frac{1}{2}\left(+{\left({\mathrm{H}}^2-8{\mathrm{a}}^2\cos {\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)}^{\frac{1}{2}}-{\left({\mathrm{H}}^2+8{\mathrm{a}}^2\right)}^{\frac{1}{2}}\right)\left[\mathrm{m}\mathrm{m}\right],$$

(3)

$$0={\mathrm{H}}^2+\mathrm{H}{\left({\mathrm{H}}^2-8{\mathrm{a}}^2\cos {\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)}^{\frac{1}{2}}-4{\mathrm{a}}^2\cos {\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(1+\cos {\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}^2\right)\left[\mathrm{m}\mathrm{m}\right],$$

(4)

where:

H—hydraulic head at the origin [mm];

d_max [mm], h_max [mm], and θ_max [rad] are the sizes at the widest diameter of the bubble and they are negative numbers in the case of the bubbles;

a—capillary constant is defined below [mm]:

$${\mathrm{a}}^2=\frac{\mathsf{\gamma }}{\left({\mathsf{\rho }}_{\mathrm{d}\mathrm{l}}-{\mathsf{\rho }}_{\mathrm{l}\mathrm{f}}\right)\mathrm{g}}\left[\mathrm{m}{\mathrm{m}}^2\right],$$

(5)

where:

g—gravitational acceleration [m/s²];

ρ_dl—density of denser liquid [kg/mm³];

ρ_lf—density of lighter fluid [kg/mm³].

There is a seeking of solutions of three variables—a², H, and cosθ_max—while the dimensions of d_max and h_max are taken from a still. In the case of the bubble, the radial distance r, polar angle θ, hydraulic head at the origin H, the widest diameter d_max, and one’s distance from the apex h_max are the negative numbers.

The system of the Equations (2)–(4) is solved in two systems of the equations,

$$\cos {\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}=-1-\frac{{\mathrm{h}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{2{\mathrm{a}}^2}\left[{\mathrm{h}}_{\mathrm{m}\mathrm{a}\mathrm{x}}+{\left({\mathrm{H}}^2+8{\mathrm{a}}^2\right)}^{\frac{1}{2}}\right][-],$$

(6)

$$\mathrm{H}={\mathrm{d}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\frac{\cos {\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{\left(1-{\cos }^2{\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)}^{\frac{1}{2}}}+\frac{4{\mathrm{a}}^2}{{\mathrm{d}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\left(1-{\cos }^2{\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)}^{\frac{3}{2}}\left[\mathrm{m}\mathrm{m}\right],$$

(7)

$${\mathrm{a}}^2=\frac{{\mathrm{d}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{8\left(1-{\cos }^2{\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)}\left[2\mathrm{H}{\left(1-{\cos }^2{\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)}^{\frac{1}{2}}-{\mathrm{d}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\cos {\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right]\left[\mathrm{m}{\mathrm{m}}^2\right],$$

(8)

or

$$4{\mathrm{h}}_{\max }^2\cos {\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(1-\cos {\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)+2{\mathrm{h}}_{\mathrm{m}\mathrm{a}\mathrm{x}}{\mathrm{d}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(1-\cos {\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right){\left(1-{\cos }^2{\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)}^{\frac{1}{2}}-{\mathrm{d}}_{\max }^2=0\left[\mathrm{m}{\mathrm{m}}^2\right],$$

(9)

$$\mathrm{a}=-\frac{{\mathrm{d}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{2{\left[2\cos {\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(1-{\cos }^2{\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)\right]}^{\frac{1}{2}}}\left[\mathrm{m}\mathrm{m}\right],$$

(10)

$$\mathrm{a}=-\frac{{\mathrm{h}}_{\mathrm{m}\mathrm{a}\mathrm{x}}{\left(2\cos {\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)}^{\frac{1}{2}}}{{\left[{\left(1+{\cos }^2{\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)}^2+4\cos {\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right]}^{\frac{1}{2}}-1+{\cos }^2{\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}}\left[\mathrm{m}\mathrm{m}\right],$$

(11)

$$\mathrm{H}=-\mathrm{a}\left(1+{\cos }^2{\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right){\left(2/\cos {\mathsf{\theta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)}^{\frac{1}{2}}\left[\mathrm{m}\mathrm{m}\right].$$

(12)

A validation of the newest method is the aim of the paper, which will be done using the values of surface tension for the interface of air and water.

2. The Experiment

An air bubble flowed out from the nozzle and was recorded by a high-speed camera. Its picture was observed in the monitor and recorded on a hard disc. An electric heater provided a desired water temperature, while an air temperature equalizer made the same temperature of air, which flowed from a compressor through the plenum tank. The proper probes provided measurement of the thermodynamic parameters, which were necessary to determine the fluids’ properties.

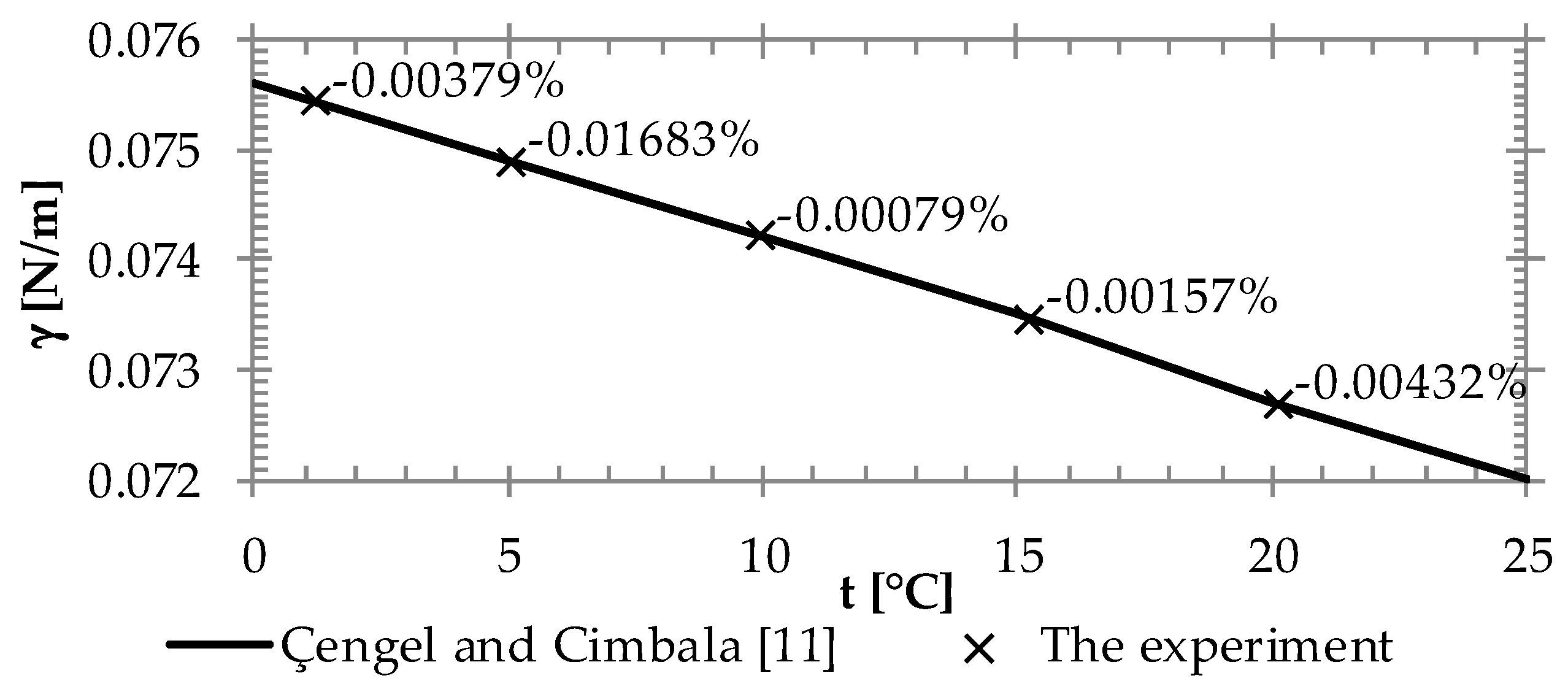
3. Determining Specific Gravity of the Fluids

Gravitational acceleration was determined for the geographic data in the location. Density of water was taken from a table, while density of moist air is as follows:

$${\mathsf{\rho }}_{\mathrm{a}\mathrm{i}\mathrm{r}}=\frac{{\mathrm{p}}_{\mathrm{a}\mathrm{i}\mathrm{r}}+\mathrm{\phi }{\mathrm{p}}_{\mathrm{s}\mathrm{a}\mathrm{t}}\left(\frac{{\mathrm{R}}_{\mathrm{a}\mathrm{i}\mathrm{r}}}{{\mathrm{R}}_{\mathrm{v}}}-1\right)}{\mathrm{T}{\mathrm{R}}_{\mathrm{a}\mathrm{i}\mathrm{r}}}\left[\frac{\mathrm{k}\mathrm{g}}{\mathrm{m}{\mathrm{m}}^3}\right],$$

(13)

where:

p_air—absolute pressure [N/mm²];

ϕ—relative humidity [-];

R_air—specific gas constant for air [mJ/(kg·K)];

R_v—specific gas constant for water vapor [mJ/(kg·K)];

T—absolute temperature [K].

Since capillary constant, gravitational acceleration, and density of the fluids were determined, surface tension was calculated from Equation (5), as shown in Figure 1.

4. Discussion

Since the relative errors between Çengel and Cimbala’s [11] data and the experimental results are extremely small, it is justified to say that the validation of the newest method for surface tension determination has been successful.