Abstract
Sunlight is converted into electrical energy due to the photovoltaic effect in photovoltaic arrays. The energy yield of photovoltaic systems depends on the solar array location, orientation, tilt, tracking and local weather conditions. Currently, simulation software is most often used to analyze the operation of photovoltaic (PV) systems and to estimate the energy yield. In this article, the differences in energy yield calculations given by the simulation software and the measured data are determined. The analysis was carried out based on mathematical models and real measurement data, regarding the dependence of the average temperature of PV arrays on variable and difficult to predict ambient conditions. For the purpose of this analysis, thermal models for flat-plate photovoltaic arrays were used. The photovoltaic installations PV1, PV2a and PV2b, belonging to the hybrid power plant of the Bialystok University of Technology in Poland, were indicated as the data source. There is no universal mathematical model to determine the average temperature of the PV modules for every type of the installation with a small normalized root-mean-squared error. The Skoplaki model proved to be the best method in the case of a free-standing solar system. On the other hand, the data values obtained from building integrated installations were better modeled by a method which used parameters under NOCT (Normal Operating Cell Temperature) conditions.
1. Introduction
The purpose of the article is to analyze the efficiency of small-scale photovoltaic energy systems that are part of the hybrid power plant of the Faculty of Electrical Engineering of the Bialystok University of Technology and assess the impact of environmental factors on the energy yield of the installation. The measurement data from 2016 to 2019 were obtained from the hybrid power plant data acquisition system and the results of simulation calculations are the basis of the conducted research. The literature used information on the impact of changes in external conditions (irradiance, temperature and wind speed) on the parameters of the solar panels. The basic concepts of the operation of photovoltaic systems can be found in books [1,2,3]. In the description of the dependence of the photovoltaic panels and arrays efficiency on the external conditions of their work, mainly scientific articles such as [4,5,6] were used. Mathematical models and values necessary to conduct the analysis are described in [7,8].
The statistical analysis was developed in accordance with the relationships described in articles [9,10]. The comparison of the applied mathematical models for three small-scale energy systems was carried out by means of normalized root-mean-squared error (NRMSE), normalized mean-bias error (NMBE) of determining the temperature of photovoltaic modules and Pearson’s correlation coefficient. The models include the influence of ambient temperature, irradiance and wind speed.
2. Materials
The object of research are three photovoltaic installations that are part of the hybrid power plant of the Faculty of Electrical Engineering of the Bialystok University of Technology, established in 2015:
- PV1—photovoltaic installation with a rated peak power of 3 kWp; the PV generator is located on the roof of a building. It consists of 12 modules arranged in two rows and optimally mounted, i.e., the object facing south (azimuth 180°), the tilt angle is 38°. The modules are connected to the SMA SUNNY BOY 3000 HF inverter with a maximum power of 3.15 kWp DC;
- PV2a—photovoltaic installation with a rated peak power of 1.5 kWp. It is located on the south-eastern facade of the building. It consists of six modules. Their azimuth is 160°, the tilt angle is 90°. The modules are connected to the GoodWe NS-1500 inverter with a maximum power of 1.8 kWp DC.
- PV2b—photovoltaic installation with a peak power rating of 1.5 kWp, which, like the PV2a installation, consists of 6 modules connected to the GoodWe NS-1500 inverter with a maximum power of 1.8 kWp DC. However, its location is different, as the PV generator is mounted on the south-west facade of the building. The azimuth is 250°, the tilt angle is 90°.
The PB hybrid power plant is also equipped with a specially developed measuring system that records all relevant operating parameters of solar panels and inverters, as well as ambient conditions. The measurement acquisition, archiving and visualization system collects and processes information about weather conditions, including solar radiation parameters, wind direction and speed, ambient temperature, as well as the temperature of individual photovoltaic modules (polycrystalline Europe Solar Production type ESP 250 6P) belonging to the analyzed PV installations.
3. Methods
The actual module temperature depends on the material properties of the applied semiconductor, the foil and the enclosure ensuring hermetic protection as well as the surrounding environment and weather conditions. The following mathematical models were used for the analysis:
- NOCT (standard) model–formula which uses NOCT parameters: irradiance on the cell surface is 800 W/m2, air temperature is 20 °C, wind velocity equals 1 m/s [1,2,3];
- King model—developed at Sandia National Laboratory [11], taking into account the coefficients associated with the thermal radiation of the module and its cooling by wind measured at a height of 10 m;
- Skoplaki models—two formulas for estimating the module operating temperature [12]. In addition to the atmospheric conditions, the first model (called as Skoplaki) includes various types of solar panel systems assembly, while the second model (Skoplaki 1, Skoplaki 2, Skoplaki 3) contains specific solar cell properties, such as efficiency, temperature power factor as well as transmission and absorption coefficients. The following wind parameters are used: wind speed at a height of 10 m (Skoplaki 1); the local wind speed close to the PV module (Skoplaki, Skoplaki 2); wind speed in directions that are perpendicular and parallel to the module’s surface (Skoplaki 3).
- Faiman model—it contains coefficients, proposed by Koehl, describing the effect of the radiation on the module temperature and the effect of cooling by the wind [13];
- Mattei models—two formulas depending on the method of determining the heat exchange coefficient. Wind speed measured close to the module is a parameter [7].
4. Results
Charts showing the variability of average temperature values of photovoltaic modules of PV1, PV2a and PV2b installations were determined. Figure 1 shows the effect of average monthly temperature values of the PV1 installation modules in individual months of 2019, determined based on mathematical models.
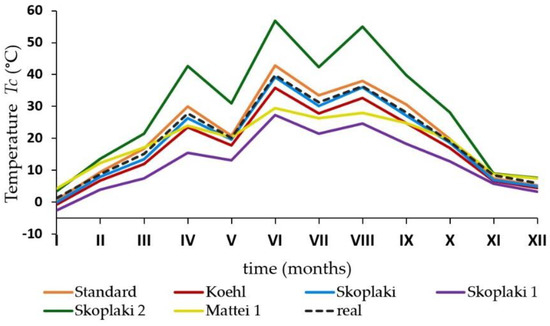
Figure 1.
The curves illustrating variability of average monthly temperature values of PV1 array in 2019. They were determined on the basis of mathematical models.
The calculated average values were the monthly average operating temperatures of the modules in 2019 obtained using mathematical models: standard, Skoplaki, Skoplaki 1, Skoplaki 2, Faiman (Koehl), Mattei 1. The real average measured monthly operating temperature values of the modules of individual installations were determined basing on the data acquisition system. Due to the one-year analysis period, the sample size n was 12, while the summation index i values were consistent with the numbers of the months examined. Table 1 presents the values of normalized root-mean-squared error (NRMSE), normalized mean bias error (NMBE) and Pearson’s correlation coefficient determined on the basis of monthly average operating temperature values of the PV modules.

Table 1.
NRMSE, NMBE values and Pearson’s correlation coefficient for monthly temperatures mean values of PV1, PV2 and PV2b installations modules calculated with the use of mathematical models for 2019.
5. Conclusions
The results of the presented analysis confirm the significant impact of wind speed, which naturally reduces the operating temperature of photovoltaic modules and improves the adverse effect of increasing ambient temperature on their operating parameters. Good compliance of the results of calculations carried out based on the Skoplaki model with the real measurement data proves the need to take into account the impact of wind speed when determining the temperature of photovoltaic modules of free-standing installations. As shown in Table 1, the NRMSE was 5.29% and the NMBE was −4.87%. Whereas for the installations mounted on a facade (PV2b), the values obtained from the data storage system were better expressed by the standard model (NOCT). The error values were slightly higher (NRMSE was 16.93% maximum and NMBE −10.49% maximum).
At the stage of designing a solar installation, external conditions prevailing in a given location should be taken into account in order to determine their possible impact on the functioning of the entire PV installation, as well as to increase the obtained energy yields. The presented temperature analysis was performed for three small-scale installations with polycrystalline PV modules. This is a preliminary research to find the simple correlations for PV operating temperature, efficiency and electrical power output [14].
Author Contributions
A.I. and K.K. conceived and designed the experiments; A.I. and K.K. analyzed the data; W.W. contributed reagents/materials/analysis tools; A.I. and W.W. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been supported by project WZ/WE-IA/2/2020 of the Bialystok University of Technology and financed from a subsidy provided by the Ministry of Science and Higher Education.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Markvart, T. Solar Electricity, 2nd ed.; Wiley: Chichester, UK, 2000. [Google Scholar]
- Petrone, G.; Ramos-Paja, C.A.; Spagnuolo, G. Photovoltaic Sources Modeling; Wiley-IEEE Press: Chichester, UK, 2017. [Google Scholar]
- Xiao, W. Photovoltaic Power System: Modeling, Design, and Control; Wiley: Chichester, UK, 2017. [Google Scholar]
- Gokmen, N.; Hu, W.H.; Hou, P.; Chen, Z.; Sera, D.; Spataru, S. Investigation of wind speed cooling effect on PV panels in windy locations. Renew. Energy 2016, 90, 283–290. [Google Scholar] [CrossRef]
- Nkurikiyimfura, I.; Safari, B.; Nshingabigwi, E. A Simulink Model of Photovoltaic Modules under Varying Environmental Conditions. IOP Conf. Ser. Earth Environ. Sci. 2018, 159, 012024. [Google Scholar] [CrossRef]
- Perovic, B.; Klimenta, D.; Jevtic, M.; Milovanovic, M.A. Transient Thermal Model for Flat-Plate Photovoltaic Systems and Its Experimental Validation. Elektron. Elektrotechnika 2019, 25, 40–46. [Google Scholar] [CrossRef]
- Schwingshackl, C.; Petitta, M.; Wagner, J.E.; Belluardo, G.; Moser, D.; Castelli, M.; Zebisch, M.; Tetzlaff, A. Wind Effect on PV Module Temperature: Analysis of Different Techniques for an Accurate Estimation. Energy Procedia 2013, 40, 77–86. [Google Scholar] [CrossRef]
- Veldhuis, A.J.; Nobre, A.; Reindl, T.; Ruther, R.; Reinders, A.H.M.E. The influence of wind on the temperature of PV modules in tropical environments, evaluated on an hourly basis. In Proceedings of the 39th IEEE Photovoltaic Specialists Conference (PVSC), Tampa, FL, USA, 16–21 June 2013; pp. 824–829. [Google Scholar]
- Frydrychowicz-Jastrzebska, G.; Bugala, A. Modeling the distribution of solar radiation on a two-axis tracking plane for photovoltaic conversion. Energies 2015, 8, 1025–1041. [Google Scholar] [CrossRef]
- Ruiz, G.R.; Bandera, C.F. Validation of Calibrated Energy Models: Common Errors. Energies 2017, 10, 1587. [Google Scholar] [CrossRef]
- King, D.L.; Boyson, W.E.; Kratochvill, J.A. Photovoltaic Array Performance Model, Sandia National Laboratories. Available online: https://prod-ng.sandia.gov/techlib-noauth/access-control.cgi/2004/043535.pdf (accessed on 1 August 2004).
- Skoplaki, E.; Boudouvis, A.G.; Palyvos, J.A. A simple correlation for the operating temperature of photovoltaic modules of arbitrary mounting. Sol. Energy Mater. Sol. Cells 2008, 92, 1393–1402. [Google Scholar] [CrossRef]
- Koehl, M.; Heck, M.; Wiesmeier, S.; Wirth, J. Modeling of the nominal operating cell temperature based on outdoor weathering. Sol. Energy Mater. Sol. Cells 2011, 95, 1638–1646. [Google Scholar] [CrossRef]
- Sohani, A.; Sayyaadi, H. Providing an accurate method for obtaining the efficiency of a photovoltaic solar module. Renew. Energy 2020, 156, 395–406. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).