A New Perspective on the Kauzmann Entropy Paradox: A Crystal/Glass Critical Point in Four- and Three-Dimensions ^†

Abstract

In this article, a new perspective on the Kauzmann point is presented. The “ideal glass transition” that occurs at the Kauzmann temperature is the point at which the configurational entropy of an undercooled metastable liquid equals that of its crystalline counterpart. We model solidifying liquids by using a quaternion orientational order parameter and find that the Kauzmann point is a critical point that exists to separate crystalline and non-crystalline solid states. We identify the Kauzmann point as a first-order critical point, and suggest that it belongs to quaternion ordered systems that exist in four- or three-dimensions. This “Kauzmann critical point” can be considered to be a higher-dimensional analogue to the superfluid-to-Mott insulator quantum phase transition that occurs in two- and one-dimensional complex ordered systems. Such critical points are driven by tuning a non-thermal frustration parameter, and result due to characteristic softening of a ‘Higgs’ type mode that corresponds to amplitude fluctuations of the order parameter. The first-order nature of the finite temperature Kauzmann critical point is a consequence of the discrete change of the topology of the ground state manifold of the quaternion order parameter field that applies to crystalline and non-crystalline solids.

1. Introduction

The nature of the glass transition is widely thought to be one of the most challenging open problems in condensed matter physics [1,2,3,4]. Despite their ubiquity, a fundamental understanding of amorphous solids and the glass transition has yet to be obtained. This is in stark contrast to our understanding of crystalline solids, which form by first-order phase transitions and in which phonons (collective Nambu–Goldstone modes) transport thermal energy. Unlike crystallization, glass formation is non-equilibrium and results as an undercooled liquid breaks ergodicity to become a rigid solid.

Glass transitions are highly dependent on cooling rate; with slower cooling rates, undercooled liquids may remain ergodic to lower temperatures. As the temperature of an undercooled liquid decreases, the difference in entropy between the liquid and crystalline solid phase decreases. Because the entropy of undercooled fluids declines faster with temperature than does crystal entropy, this results in an entropy paradox at a certain finite temperature (the Kauzmann temperature $T_K$) that may be achieved in the limit of an infinitely slow cooling rate [5,6,7]. An “ideal glass”, i.e., one that forms at the Kauzmann temperature, has a configurational entropy that matches its crystalline counterpart. This is known in the literature as the Kauzmann entropy paradox [5,6,7]. “Ideal glass transitions” have never been obtained in the laboratory, as any real glass transition occurs at a temperature higher than $T_K$ due to kinetic constraints that are responsible for a loss of ergodicity [8]. Yet, the underlying physics that gives rise to the Kauzmann entropy paradox presents an interesting open problem.

The objective of this article is to describe the origins of the Kauzmann entropy paradox, in light of the application of a quaternion orientational order parameter. This approach makes use of principles of spontaneous symmetry breaking, and of topological-ordering, that are known to play key roles in understanding condensed matter. Analogies between solidification and the formation of complex ordered states of matter, in two- and one-dimensions, are developed in order to frame the Kauzmann point as a critical point that exists to separate crystalline and glassy solid states.

Topological properties of the free energy functions that apply to crystalline and glassy solids are compared, and the roles of the two types of fundamental excitations: massless phase modes (Nambu–Goldstone) and a massive amplitude mode (‘Higgs’) are discussed. These considerations enable the characterization of the “ideal glass transition," at the finite Kauzmann temperature, as a first-order critical point similar to the second-order superfluid/Mott-insulator quantum phase transition (QPT) that occurs in two- and one-dimensions [9].

2. Crystalline-to-Glass First-Order Critical Point and the Kauzmann Entropy Paradox

Quantum phase transitions [10] exist for $O\left(N\right)$ quantum rotor models of N-vector ordered systems, that exist in N or $N-1$ dimensions, which are constructed by taking into account both potential and kinetic energy terms. Such QPTs [10] are driven by tuning a dimensionless frustration parameter (g), that is a measure of the ratio of kinetic energy to potential energy. In complex ordered systems, an order parameter with $N=2$ components develops, and $O\left(2\right)$ quantum rotor models have been applied extensively to understand the nature of the superfluid/Mott-insulator QPT in two- and one-dimensions [9]. That is, in two- and one-dimensions, such $O\left(2\right)$ quantum rotor models give the dynamics of the complex order parameter ($\mathrm{\Psi }=\left|\mathrm{\Psi }\right|e^{\widehat{i}\theta }$) near a QPT between phase-coherent superfluid ($\left|\mathrm{\Psi }\right|>0$) and phase-incoherent Mott-insulator ($\left|\mathrm{\Psi }\right|=0$) states.

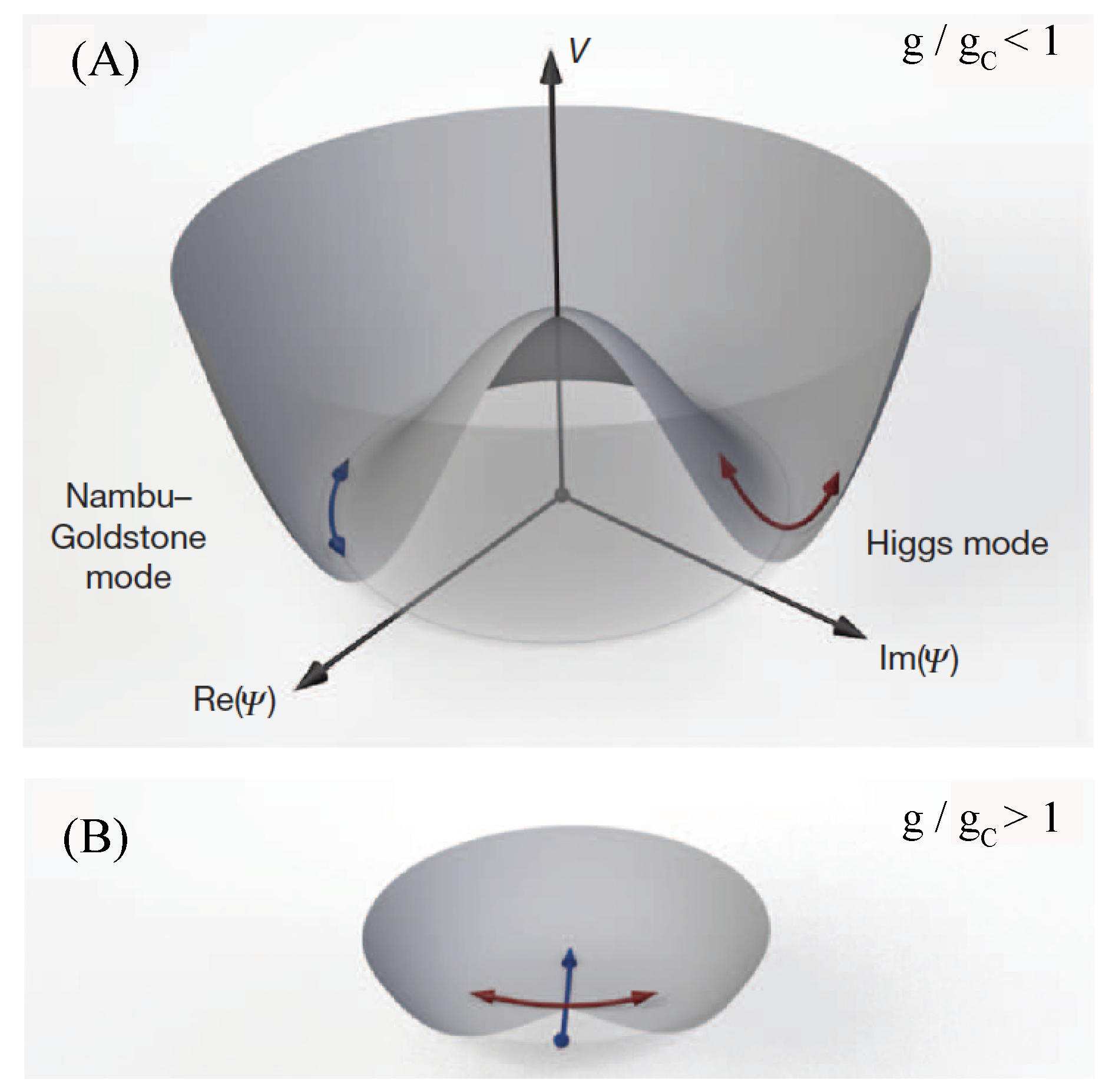
In complex ordered systems, the free energy function has the form of a conventional ‘Mexican hat’ (Figure 1A) where the amplitude degree of freedom of the order parameter takes on a constant non-zero value at its basin. Around the symmetry-broken ground state, two mode types exist: a single massless Nambu–Goldstone mode that is related to fluctuations in the scalar phase angle $\theta$, and a massive ‘Higgs’ mode that is related to amplitude variations in $\mathrm{\Psi }$. 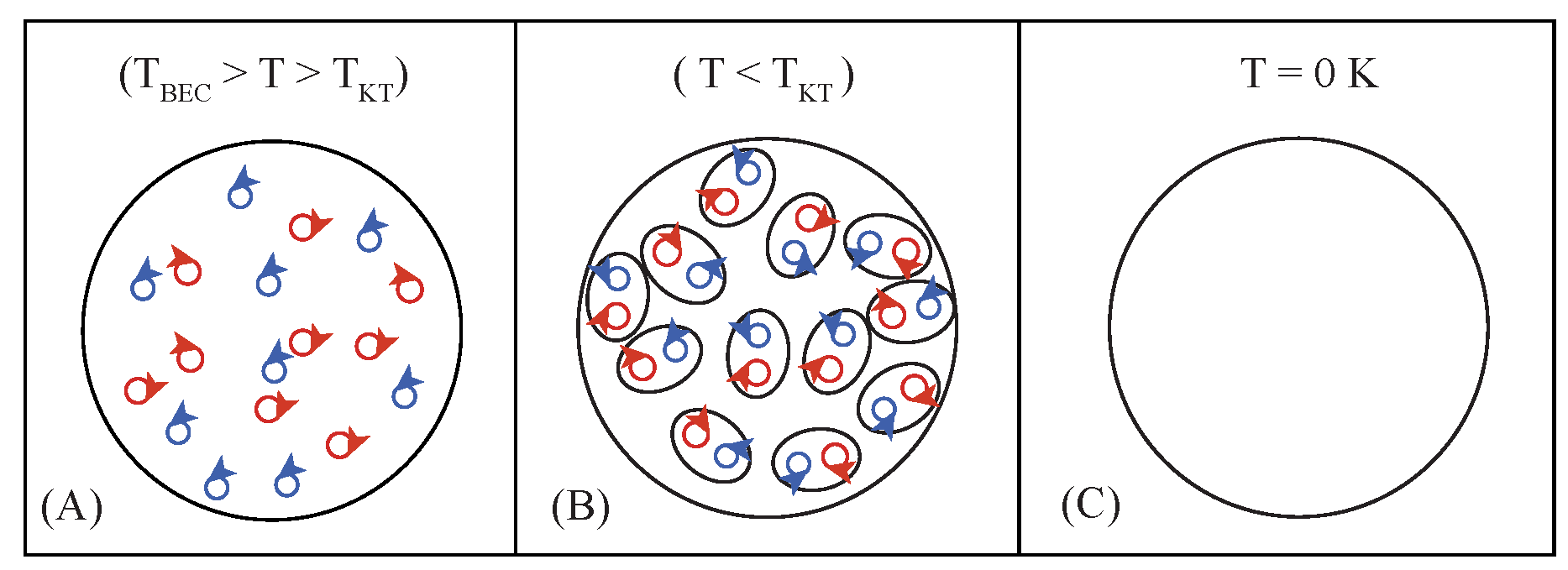For complex ordered systems that exist in two- or one-dimensions, as opposed to 3D complex ordered systems, phase-coherent superfluid ground states are achieved via a Kosterlitz–Thouless topological-ordering transition in which vortex defects and anti-defects form bound states (Figure 2). In the classical limit, i.e., in absence of kinetic energy effects, the scalar phase angle $\theta$ acquires a definite value below the Kosterlitz–Thouless transition—through breaking of rotational symmetry—resulting in a perfectly phase-coherent superfluid ground state. As the amount of frustration reaches a critical value, in the vicinity of the QPT to the phase-incoherent Mott-insulator, there is a characteristic softening of the excitation gap (or mass) of the ‘Higgs’ amplitude mode [9]. This softening transforms the free energy into a function with a minimum at $\left|\mathrm{\Psi }\right|=0$ in the phase-incoherent Mott-insulating state [9] (Figure 1B).

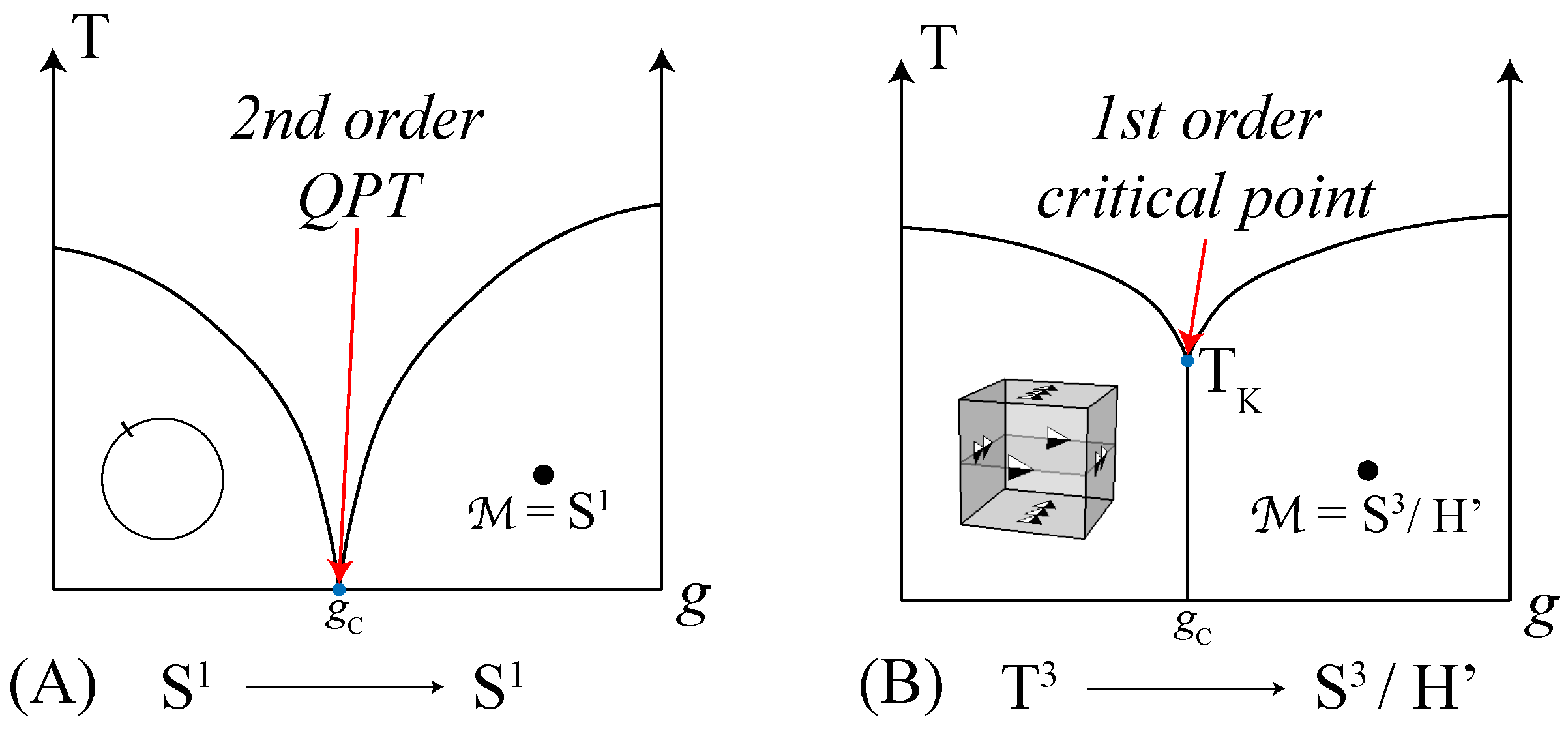
The order of the quantum phase transition, that belongs to an $O\left(N\right)$ quantum rotor model, in N or $N-1$ dimensions, can be discerned by taking note of changes in the topological properties of the free energy function in its vicinity. In the case of the superfluid/Mott-insulator QPT, the ‘Mexican hat’ free energy function that applies to superfluids is circular and the free energy of the Mott-insulator retains $U\left(1\right)\cong S^1$ symmetry at the origin. Thus, the superfluid/Mott-insulator QPT is a continuous transition and is therefore of second-order. Such a second-order QPT may occur at zero Kelvin (Figure 3A), and describes a change in the ground state as a result of quantum fluctuations arising from the Heisenberg uncertainty principle [10].

Along similar lines of reasoning, it has recently been proposed by the authors that orientational-order in crystalline solids may be described by a quaternion order parameter [11,12] alike phase-coherence in complex ordered superfluids. The quaternion orientational order parameter that is adopted has the form: $\mathrm{\Psi }=\left|\mathrm{\Psi }\right|e^{\widehat{n}\theta }$ where $\theta \in [0,\pi ]$ is a rotation angle and $\widehat{n}$ is a unit-length vector quaternion (${\widehat{n}}^2=-1$) that acts as an axis of rotation. This quaternion orientational order parameter depends upon three scalar phase angle parameters ($\theta ,{\theta }_1\in [0,\pi ]$ and ${\theta }_2\in [0,2\pi ]$) and a single amplitude degree of freedom ($\left|\psi \right|$). In four- and three-dimensions, $O\left(4\right)$ quantum rotor models apply to mathematically model quaternion ordered systems—as these may be considered to be “restricted dimensions” for quaternionic order parameters in the Hohenberg–Mermin–Wagner sense [13,14,15]. When applied to the solidification problem, the critical point that belongs to $O\left(4\right)$ quantum rotor models is anticipated to separate crystalline (i.e., orientationally-ordered) and non-crystalline (i.e., orientationally-disordered) solids.

Figure 3. (A) Complex ordered systems ($N=2$) that exist in 2D/1D are mathematically described using O(2) quantum rotor models, and admit a second-order quantum critical point at absolute zero temperature [16] that is known as the superfluid/Mott-insulator QPT [9]. (B) Solidification in four- and three-dimensions, as characterized by a quaternion orientational order parameter ($N=4$), may be described using $O\left(4\right)$ quantum rotor models. Such $O\left(4\right)$ quantum rotor models admit a critical point that is first-order which may be identified with the “ideal glass transition”, that occurs at a finite Kauzmann [5] temperature.

Figure 3. (A) Complex ordered systems ($N=2$) that exist in 2D/1D are mathematically described using O(2) quantum rotor models, and admit a second-order quantum critical point at absolute zero temperature [16] that is known as the superfluid/Mott-insulator QPT [9]. (B) Solidification in four- and three-dimensions, as characterized by a quaternion orientational order parameter ($N=4$), may be described using $O\left(4\right)$ quantum rotor models. Such $O\left(4\right)$ quantum rotor models admit a critical point that is first-order which may be identified with the “ideal glass transition”, that occurs at a finite Kauzmann [5] temperature.

Physical crystalline solids are anticipated to develop via a defect-driven topological-ordering transition [12,17], in analogue to the Kosterlitz–Thouless mechanism [18,19] that allows for the realization of phase-coherent superfluids in two- and one-dimensions. While vortices are available to complex ordered systems (i.e., ${\pi }_1\left(S^1\right)$ first homotopy group defects), third homotopy group defects are available to quaternion ordered systems (${\pi }_3\left(S^3\right)$). Just as vortices are points in the two-dimensional complex plane, third homotopy group defects are points in the four-dimensional quaternion plane. In “restricted dimensions” (Hohenberg–Mermin–Wagner theorem [13,14,15]), defect binding via a Kosterlitz–Thouless mechanism is considered necessary to prevent the mobility defects and their misorientational fluctuations such that phase-coherency or orientational-order may be obtained.

In addition to third homotopy group defects that belong to quaternion ordered systems, as a consequence of the discrete orientational-order in clustered undercooled fluids, closed-loop (fundamental group) defects [20,21,22] known as disclinations exist in solidifying atomic systems just below the melting temperature. Just as complementary third homotopy group point defects form bound pairs on crystallization, disclinations of equal and opposite sign come together to form dislocations [23,24,25,26]. At absolute zero temperature in perfect crystals, i.e., those with defect-free ground states, definite values for the scalar phase angle parameters of the quaternion orientational order parameter are obtained as all bound pair excitations come together and annihilate.

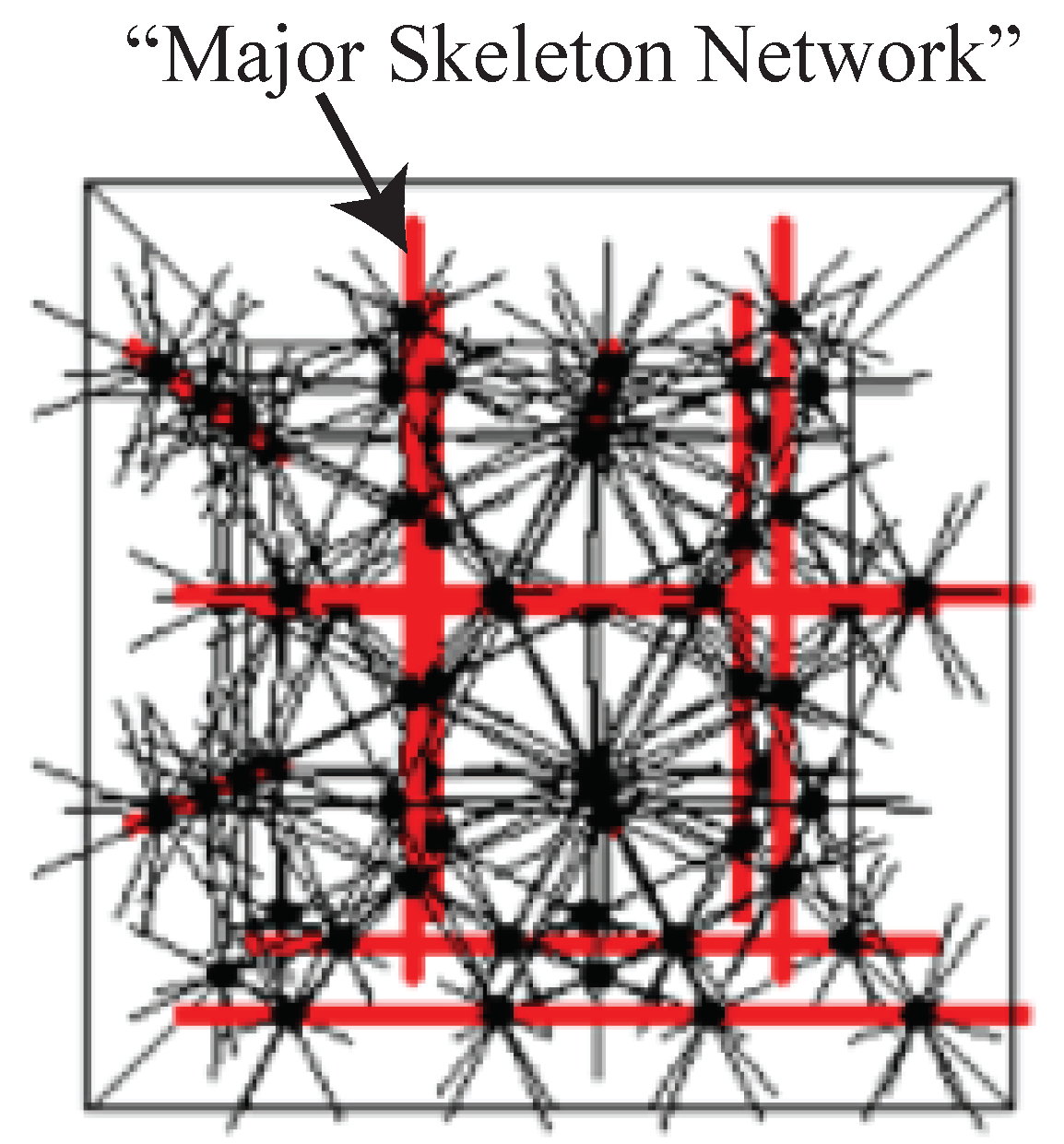
In the presence of finite geometrical frustration effects, on approaching the Kauzmann critical point from the limit of a perfect crystal, crystalline solid states may form in which the local orientational-order is incompatible with long-range crystallographic packing. Examples of such structures are topologically close-packed Frank–Kasper crystalline solids [27,28], in which geometric frustration [29,30] prevents the development of long-range icosahedral orientational-order. Such geometrically frustrated crystalline structures (e.g., Frank–Kasper) are stabilized in the ground state by the inclusion of a periodic arrangement of signed topological defects. In particular, frustration-induced signed disclination lines that are present carry negative curvature and form what is known as a “major skeleton network” (Figure 4). An entangled array of negative disclination lines is an attractive model for the structure of glasses [22,29,31], that form in the limit of geometrical frustration above a critical value. Thus, topologically close-packed crystalline solids are similar to 2D/1D superfluids in the limit of finite frustration effects (e.g., superconducting Josephson junction arrays in transverse magnetic field [32]) and orientational-disorder in glassy solids is akin to phase-incoherence in Mott-insulators [9].

In crystalline solids, the ground state manifold of the quaternion order parameter field has the topology of a three-dimensional torus ($T^3\cong S^1\times S^1\times S^1$) that accommodates periodic boundary conditions. This can be viewed as a higher-dimensional version of the conventional ‘Mexican hat’ free energy function that applies to complex ordered superfluids (Figure 1A). Around the symmetry-broken crystalline ground state, there are: three massless phonon modes (Nambu–Goldstone), and a massive mode (‘Higgs’) that is related to amplitude variations in $\mathrm{\Psi }$. Softening of the excitation gap of the amplitude mode is anticipated as frustration is increased to approach the critical point that belongs to $O\left(4\right)$ quantum rotor models that exist in 4D/3D, in line with the behavior of the ‘Higgs’ mode in the vicinity of the 2D/1D superfluid/Mott-insulator transition [9]. This softening transforms the ground state manifold into a function with a minimum located at $\left|\mathrm{\Psi }\right|=0$, at the critical point, which retains $SU\left(2\right)/H^{\prime }$ symmetry at the origin (where $H^{\prime }$ is the binary polyhedral group of preferred local orientational order $H\in SO\left(3\right)$, and $SU\left(2\right)\cong S^3$).

Owing to the discontinuous change in the genus topological invariant of the ground state manifold that applies to crystalline and glassy solids, the frustration-induced critical point is of first-order and thereby must occur at a finite temperature (Figure 3B). This first-order critical point may be identified as the Kauzmann point [5], that occurs at the finite Kauzmann temperature (i.e., the “ideal glass transition”). The Kauzmann entropy paradox, where the configurational entropy of an undercooled liquid and its crystalline counterpart are equal, is physically acceptable at such a finite temperatures but would not be so at the absolute zero of temperature. While the finite temperature nature of the “ideal glass transition” is well-understood based upon thermodynamic principles, the topological interpretation of its first-order nature presented herein is novel.

3. Conclusions and Outlook

The abundance of literature that exists on the nature of both real and “ideal” glass transitions clearly reflects the importance of the free energy landscape in providing a qualitative explanation of the phenomenon. In this article, we have suggested that crystallization and glass formation can be understood within a unified framework by the application of a four-dimensional quaternion orientational order parameter. As a generalization of the superfluid/Mott-insulator quantum phase transition (QPT) in two- and one-dimensions, a critical point is anticipated for quaternion ordered systems that exist in four- or three-dimensions which has been identified with the “ideal glass transition” that occurs at the finite Kauzmann temperature. The first-order nature of the Kauzmann critical point, at which the Kauzmann entropy paradox may be realized, has been identified as a result of the discrete change in the topology of the ground state manifold that applies to crystalline and non-crystalline solid states. Just as in the case of the superfluid/Mott-insulator QPT, it is anticipated that the ground state manifold becomes modified due to characteristic softening of the amplitude mode (‘Higgs’) on approaching the Kauzmann critical point from the limit of a perfect crystal.