New Explanation for the Mpemba Effect †
Abstract
1. Introduction
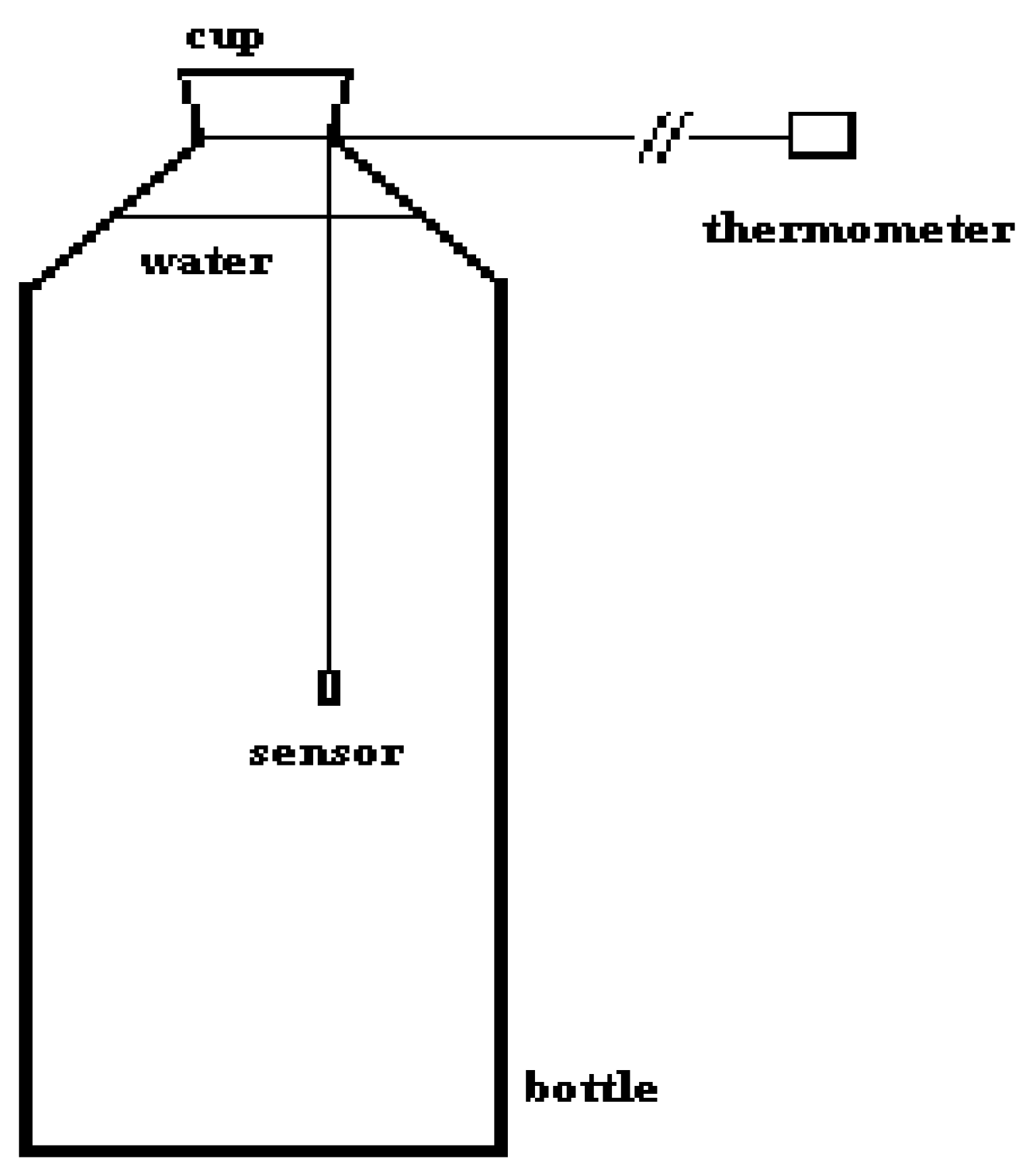
2. Materials and Methods
3. Results
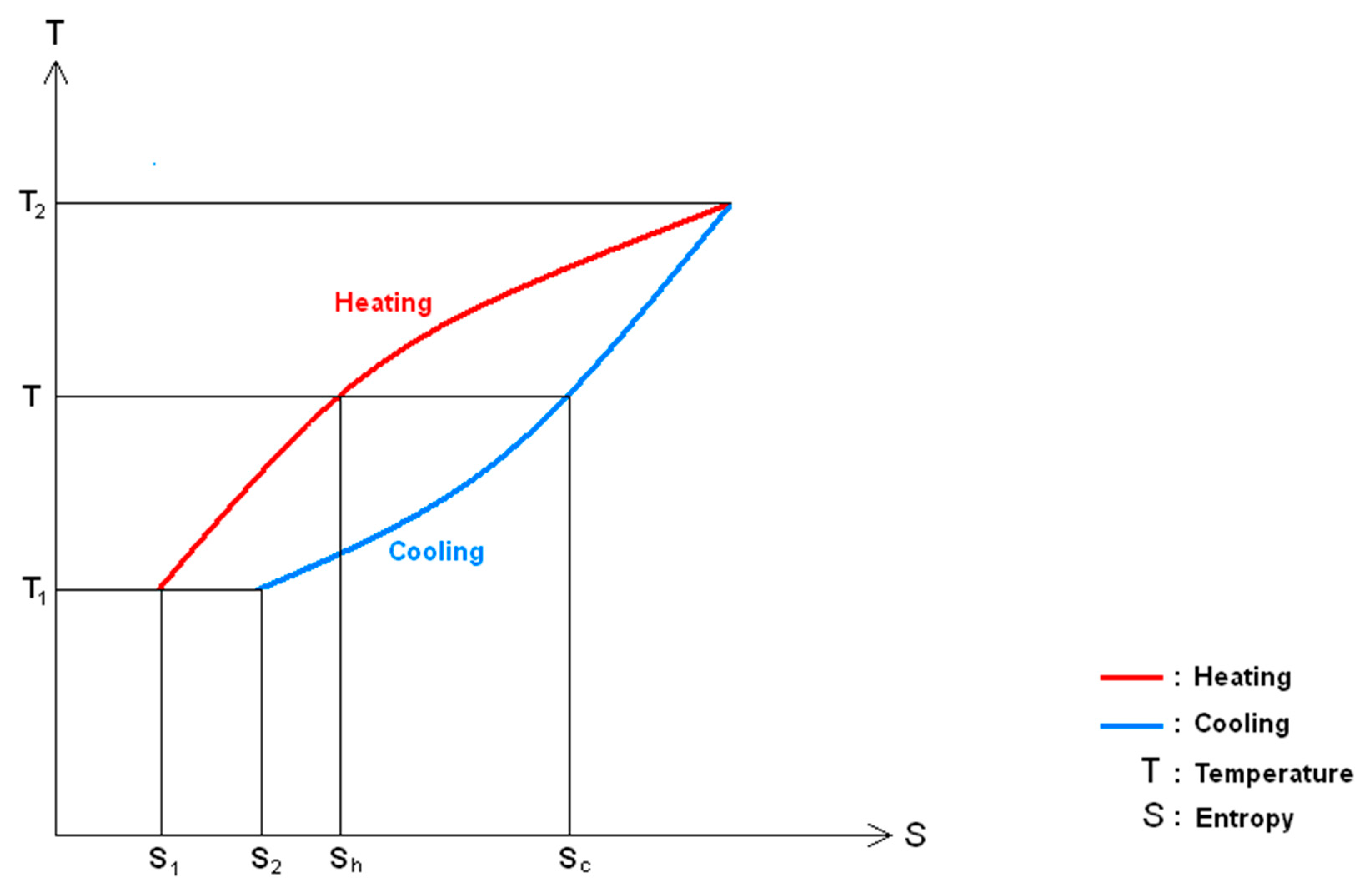
4. Discussion
- If dSh = dSc the Mpemba effect does not happen (slow process – low HTC)
- If dSh > dSc the Mpemba effect occurs (fast process – high HTC)
5. Conclusions
Conflicts of Interest
Appendix A




References
- Mpemba, E.; Osborne, D. Cool? Phys. Educ. 1979, 14, 410. [Google Scholar] [CrossRef]
- Auerbach, D. Supercooling and the Mpemba effect: When hot water freezes quicker than cold. Am. J. Phys. 1995, 63, 882. [Google Scholar] [CrossRef]
- Brownridge, J. Physics. A search for the Mpemba effect: When hot water freezes faster than cold. Physics. Pop-ph. 2010. Available online: https://arxiv.org/abs/1003.3185.
- Burridge, H.C.; Linden, P.F. Questioning the Mpemba effect: Hot water does not cool more quickly than cold. Sci. Rep. 2016, 6, 37665. [Google Scholar] [CrossRef] [PubMed]
- Lasanta, A.; Vega Reyes, F.; Prados, A.; Santos, A. When the hotter cools more quickly: Mpemba effect in granular fluids. Phys. Rev. Lett. 2017, 119, 148001. [Google Scholar] [CrossRef]
- Lu, Z.; Raz, O. Nonequilibrium thermodynamics of the Markovian Mpemba effect and its inverse. Proc. Natl. Acad. Sci. USA 2017, 114, 5083–5088. [Google Scholar] [CrossRef]
- Kell, G.S. The freezing of hot and cold water. Am. J. Phys. 1969, 37, 564–565. [Google Scholar] [CrossRef]
- Jeng, M. Hot water can freeze faster than cold? Am. J. Phys. 2006, 74, 514. [Google Scholar] [CrossRef]
- Kowalewski, T. Experimental Methods for Quantitative analysis of thermally driven flows, Phase Change with Convection, Modeling and Validation. In International Centre for Mechanical Sciences (Courses and Lectures); Kowalewski, T.A., Gobin, D., Eds.; Springer-Verlag Wien: New York, NY, USA, 2004; Volume 449, pp. 171–218. [Google Scholar]
- Katz, J.I. When hot water freezes before cold. Am. J. Phys. 2009, 77, 27–29. [Google Scholar] [CrossRef]
- Vynnycky, M.; Kimura, S. Can natural convection alone explain the Mpemba effect? Int. J. Heat Mass Transf. 2015, 80, 243–255. [Google Scholar] [CrossRef]
- Jin, J.; Goddard, W.A. Mechanisms Underlying the Mpemba Effect in Water from Molecular Dynamics Simulations. J. Phys. Chem. C 2015, 119, 2622–2629. [Google Scholar] [CrossRef]
- Tao, Y.; Zou, W.; Jia, J.; Li, W.; Cremer, D. Different Ways of Hydrogen Bonding in Water-Why Does Warm Water Freeze Faster than Cold Water? J. Chem. Theory Comput. 2017, 13, 55. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Huang, Y.; Ma, Z.; Zhou, Y.; Zhou, J.; Zheng, W.; Jiang, Q.; Sun, C.Q. Hydrogen-bond memory and water-skin supersolidity resolving the Mpemba paradox. Phys. Chem. Chem. Phys. 2014, 16, 22995–23002. [Google Scholar] [CrossRef] [PubMed][Green Version]
- O’ Sullivan, C. Newton’s law of cooling—A critical assessment. Am. J. Phys. 1990, 58, 956–960. [Google Scholar] [CrossRef]
- Liga, A.; Montesanto, S.; Mannella, G.; La Carrubba, V.; Brucato, V.; Cammalleri, M. Study on heat transfer coefficients during cooling of PET bottles for food beverages. Heat Mass Transf. 2016, 52, 1479–1488. [Google Scholar] [CrossRef]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures; Wiley: Chichester, UK, 2002; pp. 54–82. [Google Scholar]
- Ignatov, I.; Mosin, O.V. Structural Mathematical Models Describing Water Clusters. Nanotechnol. Res. Pract. 2014, 3, 141. [Google Scholar] [CrossRef]
- Chaplin, M.F. Structure and Properties of Water in its Various States. In Encyclopedia of Water; P.Maurice, Wiley, 2019; pp. 1–19. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, X.; Ma, Z.; Zhou, Y.; Zheng, W.; Zhu, J.; Sun, C. Hydrogen-bond relaxation dynamics: Resolving mysteries of water ice. Coord. Chem. Rev. 2015, 285, 109–165. [Google Scholar] [CrossRef]
- Martelli, F. Unravelling the contribution of local structures to the anomalies of water: The synergistic action of several factors. J. Chem. Phys. 2019, 150. [Google Scholar] [CrossRef]
- Mallamace, F.; Corsaroa, C.; Stanley, H. Possible relation of water structural relaxation to water anomalies. Proc. Natl. Acad. Sci. USA 2013, 110, 4899–4904. [Google Scholar] [CrossRef]
- Pramuditya, S. Water Thermodynamic Properties. ITB Physics Department–Technical Document. Available online: https://syeilendrapramuditya.wordpress.com/2011/08/20/water-thermodynamic-properties.
- Temperature Entropy Diagram-Thermodynamics. Engineers Edge. Available online: http://www.engineersedge.com/thermodynamics/temp_enthalpy_th_diagram.htm.
- Pang, X.; Deng, B. Infrared absorption spectra of pure and magnetized water at elevated temperatures. Europhys. Lett. 2010, 92, 65001. [Google Scholar] [CrossRef]
- Hribar, B.; Southall, N.; Vlachy, V.; Dill, K. How Ions Affect the Structure of Water. J. Am. Chem. Soc. 2002, 124, 12302–12311. [Google Scholar] [CrossRef]
- Ahmed, M.; Namboodiri, V.; Singh, A.; Mondal, J.; Sarkar, S. How Ions Affect the Structure of Water: A Combined Raman Spectroscopy and Multivariate Curve Resolution Study. J. Phys. Chem. B 2013, 117, 16479–16485. [Google Scholar] [CrossRef] [PubMed]
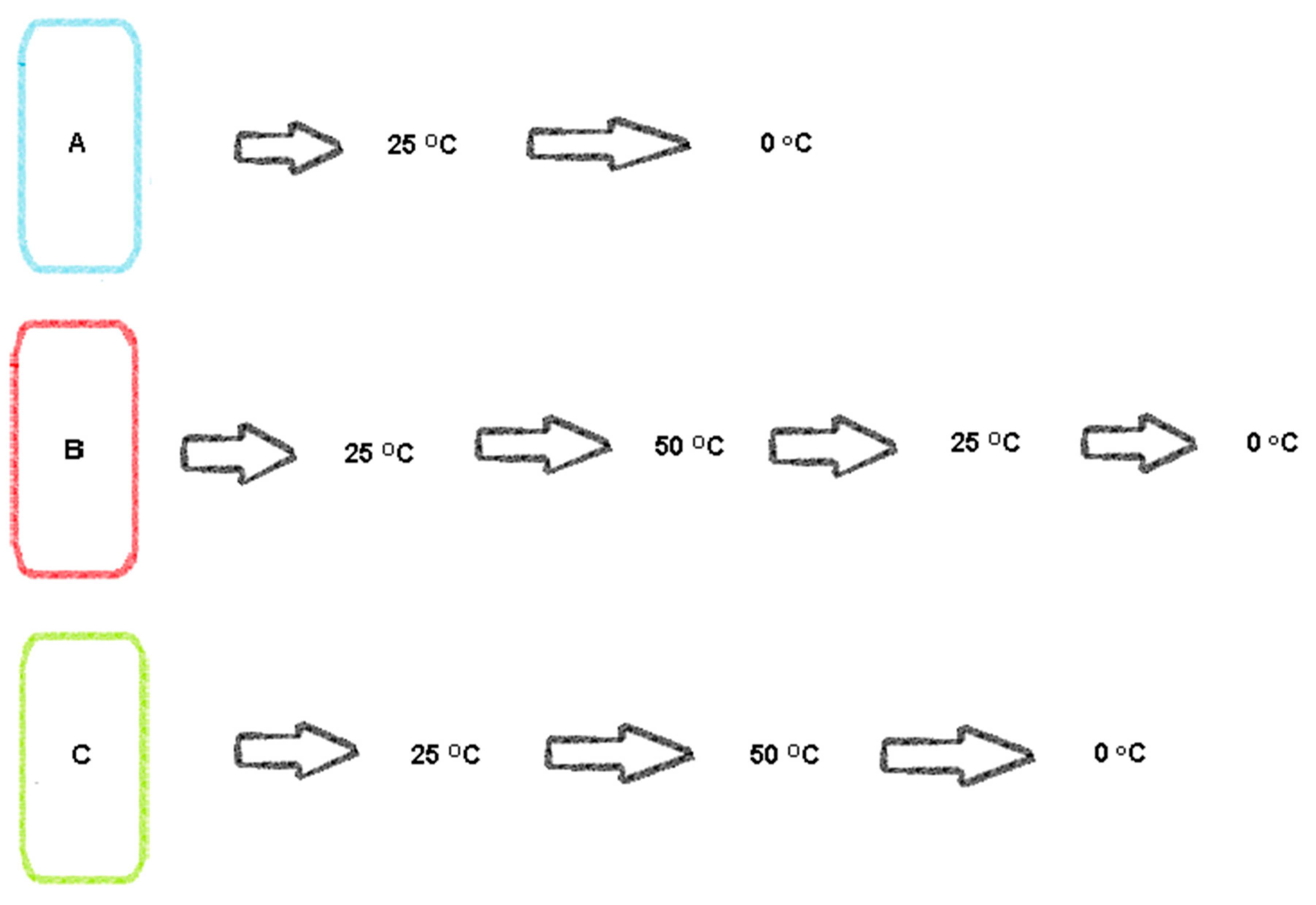
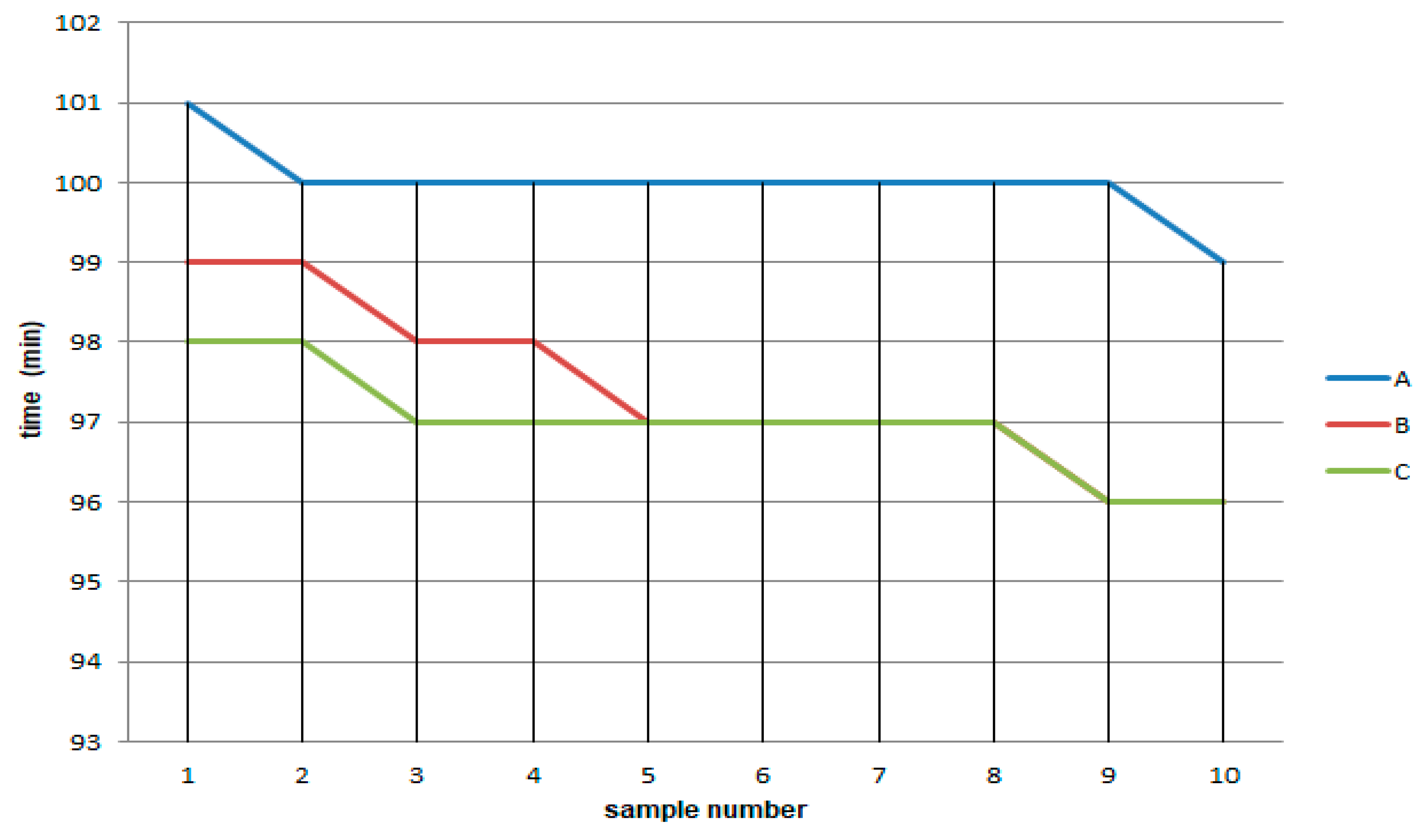
| Process | Time (min) | Average | S.D. | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 101 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 99 | 100 | 0.5 |
| Β | 99 | 99 | 98 | 98 | 97 | 97 | 97 | 97 | 96 | 96 | 97.4 | 1.1 |
| C | 98 | 98 | 97 | 97 | 97 | 97 | 97 | 97 | 96 | 96 | 97 | 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tyrovolas, I.J. New Explanation for the Mpemba Effect. Proceedings 2020, 46, 2. https://doi.org/10.3390/ecea-5-06658
Tyrovolas IJ. New Explanation for the Mpemba Effect. Proceedings. 2020; 46(1):2. https://doi.org/10.3390/ecea-5-06658
Chicago/Turabian StyleTyrovolas, Ilias J. 2020. "New Explanation for the Mpemba Effect" Proceedings 46, no. 1: 2. https://doi.org/10.3390/ecea-5-06658
APA StyleTyrovolas, I. J. (2020). New Explanation for the Mpemba Effect. Proceedings, 46(1), 2. https://doi.org/10.3390/ecea-5-06658





