Entropy Production and the Maximum Entropy of the Universe †
Abstract
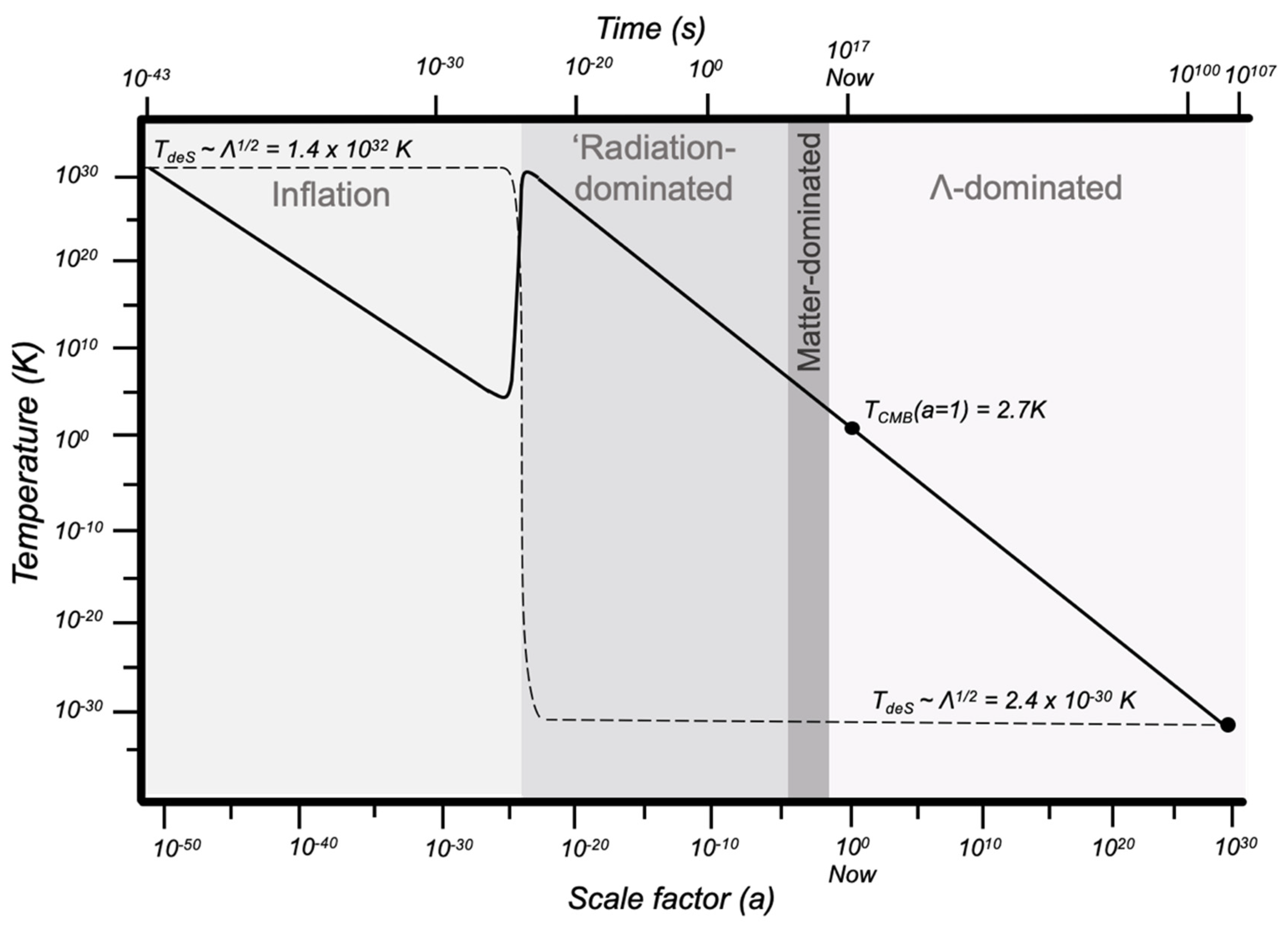
:1. The Entropy Gap and the Approach to ‘Heat Death’
1.1. Estimating the Entropy Gap and Free Energy
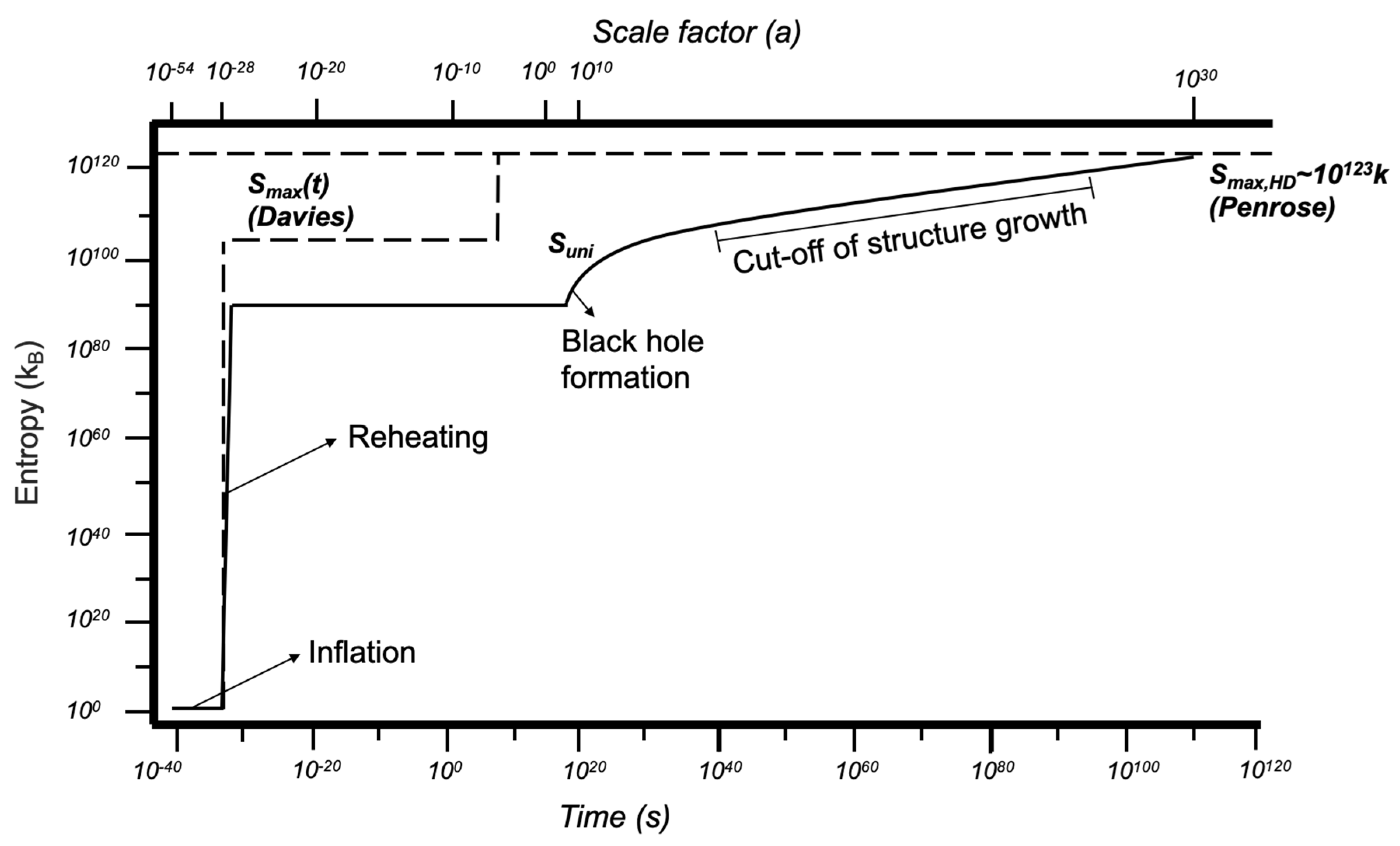
1.2. The Maximum Entropy at Heat Death—A Time-Independent Definition
2. A Time-Dependent Definition of Maximum Entropy
2.1. The Availability of Free Energy and Dyson’s Hang-Ups
2.2. Davies’
2.3. Time-Dependent Maximum Entropy vs. Time-Dependent Entropy Production Rate
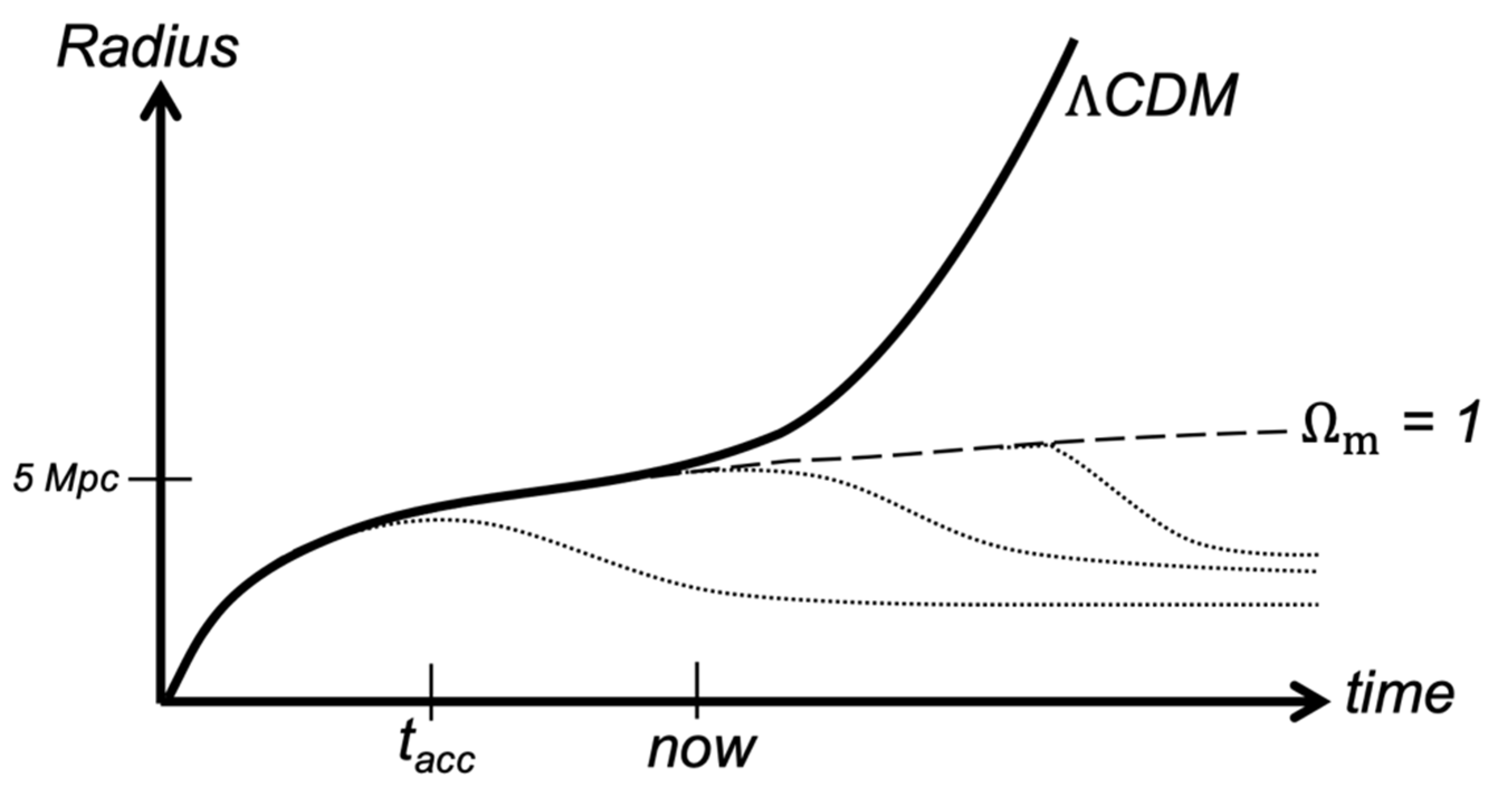
3. Cut-Off of Structure Growth Constrains the Rate of Entropy Production
3.1. Decoupled Evolution of Gravitationally-Dominated Systems
3.2. Limits on Structure Growth as a Constraint on
4. Conclusions
References
- Egan, C.A.; Lineweaver, C.H. A larger estimate of the entropy of the universe. Astrophys. J. 2010, 710, 1825–1834. [Google Scholar] [CrossRef]
- Lineweaver, C.H.; Egan, C. Life, Gravity and the Second Law of Thermodynamics. Phys. Life Rev. 2008, 5, 225–242. [Google Scholar] [CrossRef]
- Patel, V.; Lineweaver, C. Solutions to the Cosmic Initial Entropy Problem without Equilibrium Initial Conditions. Entropy 2017, 19, 411. [Google Scholar] [CrossRef]
- Lineweaver, C.H. A Simple Treatment of Complexity: Cosmological Entropic Boundary Conditions on Increasing Complexity; Lineweaver, C.H., Davies, P.C.W., Ruse, M., Eds.; Cambridge University Press: Cambridge, UK, 2013; Chapter 3 of Complexity and the Arrow of Time; pp. 42–67. [Google Scholar]
- Adams, F.C.; Laughlin, G. A dying universe: The long-term fate and evolution of astrophysical objects. Rev. Mod. Phys. 1997, 69, 337–372. [Google Scholar] [CrossRef]
- Dyson, F.J. Time without end: Physics and biology in an open universe. Rev. Mod. Phys. 1979, 51, 447. [Google Scholar] [CrossRef]
- Lineweaver, C.H.; Davis, T.; Patel, V. Using the Maximum Entropy Production Principle to Constrain the Value of the Cosmological Constant. In Proceedings of the 2nd International Electronic Conference Entropy and Its Applications, 15–30 November 2015. [Google Scholar]
- Peacock, J.A. Cosmological Physics, 1st ed.; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Krauss, L.M.; Starkman, G.D. The fate of life in the universe. Sci. Am. 1999, 281, 58–65. [Google Scholar] [CrossRef] [PubMed]
- Krauss, L.M.; Starkman, G.D. Life, the Universe, and Nothing: Life and Death in an ever-expanding Universe. Astrophys. J. 2000, 531, 22–30. [Google Scholar] [CrossRef]
- Penrose, R. The Big Bang and its Thermodynamic Legacy. In Road to Reality: A Complete Guide to the Laws of the Universe, 1st ed.; Jonathan Cape: London, UK, 2004; pp. 686–734. [Google Scholar]
- Frautschi, S. Entropy in an expanding universe. Science 1982, 217, 593–599. [Google Scholar] [CrossRef] [PubMed]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures; John Wiley and Sons: New York, NY, USA, 1998. [Google Scholar]
- Zemansky, M.W.; Dittman, R.H. Heat and Thermodynamics, 1st ed.; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Kolb, E.W.; Turner, M.S. The Early Universe; Avalon Publishing: New York, NY, USA, 1994. [Google Scholar]
- Davis, T.; Davies, P.C.W.; Lineweaver, C.H. Black hole versus cosmological horizon entropy. Class. Quant. Grav. 2003, 20, 2752–2764. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W. Cosmological event horizons, thermodynamics, and particle creation. Phys. Rev. D 1977, 15, 2738. [Google Scholar] [CrossRef]
- Bejan, A.; Jones, J.A. Advanced Engineering Thermodynamics, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Kestin, J. Availability: The concept and associated terminology. Energy 1980, 5, 679–692. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Universal upper bound on the entropy-to-energy ratio for bounded systems. Phys. Rev. D 1981, 21, 287. [Google Scholar] [CrossRef]
- Davies, P.C.W. Inflation and time asymmetry of the universe. Nature 1983, 301, 398–400. [Google Scholar] [CrossRef]
- Hooft, G.T. Dimensional reduction in quantum gravity. arXiv 1993, arXiv:gr-qc/9310026. [Google Scholar]
- Susskind, L. The world as a hologram. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar] [CrossRef]
- Page, D.N. Entropy Evaporated by a Black Hole. Phys. Rev. Lett. 1982, 49, 1683. [Google Scholar]
- Dyson, F.J. Energy in the universe. Sci. Am. 1971, 225, 50–59. [Google Scholar] [CrossRef]
- Albrecht, A. Cosmic Inflation and the Arrow of Time. In Science and Ultimate Reality: Quantum Theory, Cosmology and Complexity, 1st ed.; Cambridge University Press: Cambridge, UK, 2002; pp. 363–401. [Google Scholar]
- Penrose, R. Singularities and Time Asymmetry. In General Relativity: An Einstein Centenary Volume; Hawking, S.W., Israel, W., Eds.; University Press: Cambridge, UK, 1979; pp. 581–638. [Google Scholar]
- Page, D.N. Comment on a universal upper bound on the entropy-to-energy ratio for bounded systems. Phys. Rev. D 1982, 26.4, 946. [Google Scholar] [CrossRef]
- Bejan, A. Advanced Engineering Thermodynamics, 3rd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Birkhoff, G.D. Relativity and Modern Physics; Harvard University Press: Cambridge, MA, USA, 1923. [Google Scholar]
- Barrow, J.D.; Saich, P. Growth of large-scale structure with a cosmology constant. Mon. Not. R. Astron. Soc. 1993, 262, 717–725. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patel, V.M.; Lineweaver, C. Entropy Production and the Maximum Entropy of the Universe. Proceedings 2020, 46, 11. https://doi.org/10.3390/ecea-5-06672
Patel VM, Lineweaver C. Entropy Production and the Maximum Entropy of the Universe. Proceedings. 2020; 46(1):11. https://doi.org/10.3390/ecea-5-06672
Chicago/Turabian StylePatel, Vihan M., and Charles Lineweaver. 2020. "Entropy Production and the Maximum Entropy of the Universe" Proceedings 46, no. 1: 11. https://doi.org/10.3390/ecea-5-06672
APA StylePatel, V. M., & Lineweaver, C. (2020). Entropy Production and the Maximum Entropy of the Universe. Proceedings, 46(1), 11. https://doi.org/10.3390/ecea-5-06672




