Abstract
In recent years, the advancement of the microelectronics industry has allowed for a major expansion in the development of sensor-based equipment and applications, driven primarily by the cost reduction of micro-electro-mechanical systems (MEMS) devices. Currently, using this type of component, it is feasible to develop cost-effective systems aimed at early detection of failures in electrical machines and, in special cases, three-phase induction motors (TIM). These devices, coupled with predictive maintenance records, can prevent unexpected shutdowns due to malfunctions and signal the need for actions to extend the life cycle of the equipment. This is a relevant topic considering that the industrial sector is increasingly seeking for solutions based on non-destructive techniques (NDT) for preventive and predictive fault diagnosis. In this scenario, the objective of this work is to evaluate the application of a low-cost MEMS accelerometer to identify insulation failures in stator windings through vibration analysis. For this purpose, two MEMS accelerometers were coupled on either side of the frame of a TIM. Then, vibration signals were acquired for different types and levels of insulation failures. The data obtained were processed using different metrics such as root mean square (RMS), kurtosis, and skewness. The results allowed us to identify the insulation faults applied to the TIM, confirming the feasibility of applying the low-cost MEMS accelerometer in the vibration analysis for fault diagnosis.
1. Introduction
Nowadays, there is a growing demand for sensor-based fault detection techniques. In the industrial sector, there is an effort to develop reliable solutions for failure detection in three-phase induction motors (TIMs), since this equipment corresponds to the main applications and consume approximately 60% of all energy produced [1]. Among the known alternatives, the use of micro-electro-mechanical systems (MEMS) sensors stands out as a low-cost application that has improved in recent years. The combination of this type of sensor with non-destructive techniques (NDT) such as vibration analysis, has already demonstrated satisfactory results for TIM diagnosis [2,3,4,5].
Moreover, the early fault diagnosis is an ideal application for the industry. It allows the creation of predictive maintenance plans to avoid unwanted shutdowns as well as irreversible damage to the motors. As TIMs are typically involved in the main production line steps, these shutdowns have an extremely high operational cost [1]. Consequently, the application of low-cost MEMS-based sensors enhances the financial aspect of this approach. In the three-phase motor stators, winding insulation faults are one of the most commonly observed. Inter-turn failures cause current rise and reduce the lifespan of the electric machine. If these faults occur without being detected, it can lead to a phase to phase short-circuit and to permanent damage to the coils [6].
Based on the evidences, the main goal of this paper is to evaluate the performance of a MEMS accelerometer to identify insulation faults in the stator windings by vibration analysis. To achieve this scope, two MEMS accelerometers were attached on both sides of a 1.5 hp TIM that has external electrical access to segments of the stator windings. Different levels of insulation faults were emulated by resistors applied in parallel to the windings segments and the vibration signals were acquired. Finally, the collected data were processed using different metrics, such as root mean square (RMS), kurtosis, and skewness to estimate a correspondence between vibrations and fault level.
This paper is divided in six sections. Section 2 and Section 3 present, respectively, the MEMS-based accelerometer and the signal processing techniques based on RMS, kurtosis, and skewness measures. The experimental setup is described in Section 4. In Section 5, the results are discussed. Then, the article is finalized in Section 6.
2. MEMS Accelerometer
There are two main types of MEMS accelerometers: piezo resistive and capacitive [7]. In this work, the focus will be on capacitive-based MEMS accelerometer. The sensor operation is based on the test mass movement, which causes a change in capacitance between the mass and a fixed conductive electrode. This acceleration unbalances the differential capacitor used for measurement. The sensor output is proportional to the acceleration applied to the test mass [6,7,8]. The typical construction of a capacitive-based MEMS accelerometer is shown in Figure 1a. Accelerometers can be approximated to a mass-spring-damper system as seen in [8]:
where is the movement of test mass, is an external input acceleration, is the suspension stiffness, and is the damping coefficient. Assuming natural resonance frequency and the quality factor , Equation 1 can be expressed in Laplace domain as:
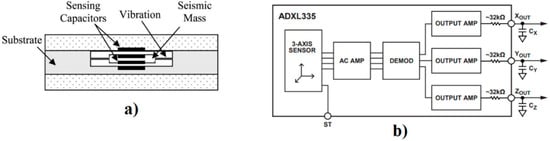
Figure 1.
(a) A typical capacitive-based micro-electro-mechanical systems (MEMS) accelerometer construction [7]; (b) basic block diagram of ADXL335 [9].
For this work, the accelerometer used was the ADXL335 from Analog Devices. ADXL335 is a three-axis accelerometer and minimum full-scale range of ±3 g. The bandwidth for the X and Y axes is between 0.5 Hz and 1600 Hz, while for the Z axis it is 0.5 Hz to 500 Hz [9]. The basic block diagram of ADXL335 is shown in Figure 1b.
Understanding the operating principle allows us to evaluate the potential of this sensor for a wide range of applications, such as earthquake early warning systems [10], to detect peak particle velocity in explosions [11], motion monitoring [12], and finally, the use for fault diagnosis by means of vibration analysis in TIMs [2,3,4].
3. Signal Processing Analysis Applied to Vibration Signals
The following section will present and formulate the techniques used to process the acquired data. Beyond the traditional root mean square (RMS) analysis, two statistical analyses were also applied: kurtosis and skewness.
3.1. RMS Measure
The RMS technique is a method that has been proven successful when applied for vibration analysis. Previous work has shown that this technique is effective not only in characterization and diagnosis, but also in monitoring and estimating indicators of TIM faults [13]. Furthermore, the Equation:
is described for discrete sampling, with being the number of samples collected and the value for the nth sample of the signal [13].
3.2. Kurtosis Measure
Kurtosis is a dimensionless measure that describes the deviation of a signal from the probability density function (PDF). When the signal approaches the Gaussian distribution, its value tends to 3. In previous works, this parameter was applied and proved to be a very sensitive tool to study the characteristics of the vibration signal [14,15]. The kurtosis can be expressed as:
where, in the Equation (4), is the kurtosis, is the expected value of the signal , m, and are, respectively the mean and standard deviation of the signal [15].
3.3. Skewness Measure
Skewness is a statistical measure that evaluates the asymmetry of the signal distribution. It can be negative, positive, or zero, indicating, respectively, an asymmetry to the left, right, or a symmetrical distribution [16]. Previous work has shown that this measure is extremely useful in identifying statistical patterns or filtering [17]. Skewness is computed through the equation following:
where, in the Equation 5, is the skewness factor and , m, and s are, respectively, the expected value, the mean, and standard deviation of the signal [16].
4. Methods
In this section, the steps adopted for signal acquisition and the assembly of electrical machines will be detailed.
4.1. Machines Setup
First, the 1.5 hp TIM was coupled to a DC machine and both of them were aligned and firmly bolted to the test bench. The induction motor was powered at its nominal voltage using a software-controlled AC power source. Additionally, the DC machine was set up as a generator and connected to a resistor bank in order to request the nominal mechanical power from the motor, simulating real operational conditions. The TIM was especially modified to allow electrical access to sections of its windings Figure 2a. The winding of each phase consists of six coils. One of these coils was divided into two sections Figure 2b, equivalent to 5.5% and 11% of the winding. Aiming to reproduce the insulation faults effects on the TIM, five different resistors (2.5, 5, 10, 12.5, 15 Ω) were connected, one at a time, to one of the two sections, representing different levels of fault. This procedure was repeated for each of the three phases, resulting in thirty different experiments. A baseline experiment was also performed without any resistors connected to the windings.
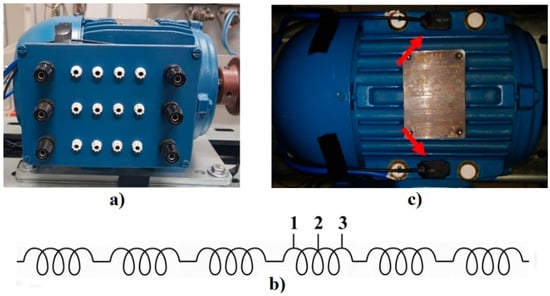
Figure 2.
(a) Three-phase induction motor (TIM) external connections; (b) winding sections; and (c) MEMS sensors attached to the TIM.
4.2. Data Acquisition
The signal acquisition was performed by two ADXL335 3-axis accelerometers attached to the left and right side of the TIM using cyanoacrylate adhesive (Figure 2c). Its outputs bandwidths were limited to 500 Hz by CX, CY, and CZ capacitors. To avoid the effects of aliasing, the signals were sampled at 25 kS/s by a 16-channel Yokogawa DL850 DSO. Shielded cables were used to connect the sensors to the oscilloscope probes in order to prevent unwanted noise. Moreover, the test bench and the voltage sources were grounded with the same purpose. Thus, the acquired signals were transferred from the oscilloscope memory to a personal computer where the signal processing was accomplished. Furthermore, an additional 2 kHz digital low-pass filter was applied aiming to limit the frequencies to a range that is usually observed in vibration analysis [1]. The values of RMS, kurtosis, and skewness measures were achieved using MATLAB® software.
5. Results and Discussion
Aiming to correlate the RMS, kurtosis, and skewness measures to the insulation failures, its values were plotted as a function of the fault current. Figure 3 presents the values of the three measures for the Y-axis of the right sensor, as well as their coefficients of determination . The RMS values are represented by the “circle” marks, the kurtosis values are represented by the “asterisk” marks, and the skewness values are represented by the “cross” marks. The Y-axis was chosen due its better performance, although the X-axis and Z-axis also presented satisfactory results. The graphs in the same column refer to the experiments with the same percentage of winding on failure, while the graphs in the same row refer to the experiments along the same phase. Moreover, the values were normalized between 0 and 1 for better data visualization.
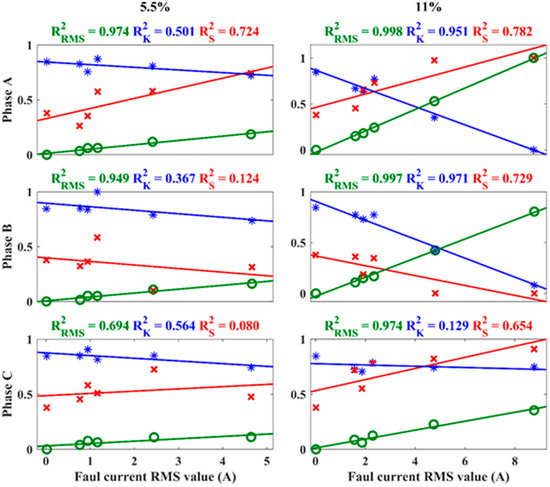
Figure 3.
RMS, kurtosis, and skewness and their R2 values.
Figure 3 shows that the RMS measure presented R2 coefficients very close to 1 for all the experiments, pointing to a directly proportional linear behavior between the RMS value and the fault current. The increase in RMS values denotes that insulation faults can cause an intensification of vibration activity in the induction motor.
Figure 3 also indicates that kurtosis values did not present R2 values as close to 1 as RMS for 5.5% faults. However, they were satisfactory for phases A and B for 11% of winding failure. Skewness values also showed unsatisfactory values for 5.5% failures. Nevertheless, they presented acceptable values for all the three phases in a failure situation of 11%. The experiments with winding failure of 11% presented higher values of fault currents. This explains the best performances of all techniques for this case.
Finally, the three techniques demonstrated some degree of sensitivity for identifying insulation failures in the stator winding. However, it is important to emphasize that the measure that showed the best results was the RMS. In addition, the RMS value is the measure that requires the least computational effort to be achieved.
6. Conclusions
The operational relevance and massive implementation of TIM justify the development of reliable systems for early fault identification. Low-cost sensors and non-destructive techniques ensure the feasibility of these systems and stand out as alternatives for the high-cost commercial products. Given the context, this work presented an approach based on low cost MEMS sensors and vibration analysis to identify insulation faults in the TIM.
Based on the results, it is possible to confirm the success of the proposed signal processing techniques in the identification of the different levels of insulation failures. The RMS, kurtosis, and skewness measures were capable to identify the faults. However, the RMS presented the best results for all scenarios. Future work should use more advanced signal processing techniques. Further, new approaches may cover the classification of failure levels in the insulation of stator windings.
Author Contributions
All authors contributed in writing, proofreading, and providing suggestions for the improvement of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cusidó, J.; Romeral, L.; Ortega, J.A.; Rosero, J.A.; García Espinosa, A. Fault Detection in Induction Machines Using Power Spectral Density in Wavelet Decomposition. IEEE Trans. Ind. Electron. 2008, 55, 633–643. [Google Scholar] [CrossRef]
- Pedotti, L.A.D.S.; Zago, R.M.; Fruett, F. Fault diagnostics in rotary machines through spectral vibration analysis using low-cost MEMS devices. IEEE Instrum. Meas. Mag. 2017, 20, 39–44. [Google Scholar] [CrossRef]
- Koene, I.; Viitala, R.; Kuosmanen, P. Internet of Things Based Monitoring of Large Rotor Vibration With a Microelectromechanical Systems Accelerometer. IEEE Access 2019, 7, 92210–92219. [Google Scholar] [CrossRef]
- Maruthi, G.S.; Hegde, V. Application of MEMS Accelerometer for Detection and Diagnosis of Multiple Faults in the Roller Element Bearings of Three Phase Induction Motor. IEEE Sensors J. 2016, 16, 145–152. [Google Scholar] [CrossRef]
- Mohd Ismail, M.I.; Dziyauddin, R.A.; Ahmad Salleh, N.A.; Muhammad-Sukki, F.; Aini Bani, N.; Mohd Izhar, M.A.; Latiff, L.A. A Review of Vibration Detection Methods Using Accelerometer Sensors for Water Pipeline Leakage. IEEE Access 2019, 7, 51965–51981. [Google Scholar] [CrossRef]
- Drif, M.; Cardoso, A.J.M. Stator Fault Diagnostics in Squirrel Cage Three-Phase Induction Motor Drives Using the Instantaneous Active and Reactive Power Signature Analyses. IEEE Trans. Ind. Inf. 2014, 10, 1348–1360. [Google Scholar] [CrossRef]
- Albarbar, A.; Mekid, S.; Starr, A.; Pietruszkiewicz, R. Suitability of MEMS Accelerometers for Condition Monitoring: An experimental study. Sensors 2008, 8, 784–799. [Google Scholar] [CrossRef] [PubMed]
- Acar, C.; Shkel, A.M. Experimental evaluation and comparative analysis of commercial variable-capacitance MEMS accelerometers. J. Micromech. Microeng. 2003, 13, 634–645. [Google Scholar] [CrossRef]
- Analog Devices ADXL335. Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/ADXL335.pdf (accessed on 24 September 2019).
- Husni, E.; Laumal, F. The Development of an Earthquake Early Warning System Using an ADXL335 Accelerometer. In Proceedings of the 2018 21st Saudi Computer Society National Computer Conference (NCC), Riyadh, Saudi Arabia, 25–26 April 2018; IEEE: Riyadh, Saudi Arabia, 2018; pp. 1–5. [Google Scholar]
- Ragam, P.; Nimaje, D.S. Selection and Evolution of MEMS Accelerometer Sensor for Measurement of Blast-Induced Peak Particle Velocity. IEEE Sens. Lett. 2018, 2, 1–4. [Google Scholar] [CrossRef]
- Manjiyani, Z.A.A.; Jacob, R.T. Development of MEMS Based 3-Axis Accelerometer for Hand Movement Monitoring. Int. J. Comput. Sci. Eng. Commun. 2014, 4, 4. [Google Scholar]
- Lucas, G.B.; de Castro, B.A.; Rocha, M.A.; Andreoli, A.L. Study of a Low-Cost Piezoelectric Sensor for Three Phase Induction Motor Load Estimation. Proceedings 2019, 4, 46. [Google Scholar]
- Wang, C.; Li, H.; Huang, G.; Ou, J. Early Fault Diagnosis for Planetary Gearbox Based on Adaptive Parameter Optimized VMD and Singular Kurtosis Difference Spectrum. IEEE Access 2019, 7, 31501–31516. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, E. Fault Diagnosis of Circuit Breaker Energy Storage Mechanism Based on Current-Vibration Entropy Weight Characteristic and Grey Wolf Optimization–Support Vector Machine. IEEE Access 2019, 7, 86798–86809. [Google Scholar] [CrossRef]
- Khorasani, A.M.; Littlefair, G.; Goldberg, M. Time Domain Vibration Signal Processing on Milling Process for Chatter Detection. J. Mach. Form. Technol. 2014, 6, 21. [Google Scholar]
- Stepanic, P.; Latinovic, I.V.; Djurovic, Z. A new approach to detection of defects in rolling element bearings based on statistical pattern recognition. Int. J. Adv. Manuf. Technol. 2009, 45, 91–100. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).