Abstract
Within a Bayesian framework we propose a non-intrusive reduced-order spectral approach (polynomial chaos expansion) to assess the uncertainty of ion-solid interaction simulations. The method not only reduces the number of function evaluations but provides simultaneously a quantitative measure for which combinations of inputs have the most important impact on the result. It is applied to the ion-solid simulation program SDTrimSP with several uncertain and Gaussian distributed input parameters, i.e., angle , projectile energy and surface binding energy . In combination with recently acquired experimental data the otherwise hardly accessible model parameter can now be estimated.
1. Introduction
Plasma-wall interactions are of crucial importance in the design of future fusion reactors, since they determine the replacement cycle for the plasma exposed components of the wall. In order to estimate the life-time of those wall components atomistic simulations are essential. Almost all computer codes for the simulation of ion-solid interactions [1] rely on a large number of input parameters, e.g., surface binding energies, composition, energy distribution etc. However, many of these parameters are uncertain and a proper comparison with experimental data or other models requires the quantification of the uncertainty of the result. Unfortunately, the computational demand of single simulation runs often severely restricts the quantification of output uncertainties by full-grid or simple sampling (e.g., Monte Carlo sampling) based approaches due to the curse of dimensionality for more than a very limited number of uncertain input parameters. Therefore, to reduce the computational effort we propose a non-intrusive reduced-order model approach (polynomial chaos expansion), which not only reduces the number of function evaluations but provides simultaneously a quantitative measure of which combinations of inputs have the most important impact on the result, i.e., it yields a sensitivity analysis and the associated Sobol coefficients.
2. Bayesian Uncertainty Quantification
Based on the Bayesian framework we employ a spectral expansion to quantify the propagation of uncertainty through the model. First introduced by Wiener [2] in the context of Hermite basis functions it was termed ‘polynomial chaos expansion’ at his time. Nowadays the notion of ‘chaos’ has shifted and the use of the term ‘spectral expansion’ is more appropriate. Once successfully achieved, the spectral representation is capable of quantifying the uncertainty for any point in model space or to serve as a surrogate model.
Since we calculate the sought-for spectral coefficients from a discrete set of collocation points in the space of the random variable, our approach is non-intrusive, but approximate. The emerging integrals in the calculation of the coefficients are evaluated by Gaussian quadrature which identifies the collocation points with those of the quadrature. Moreover, we assume mutually independent normally distributed random variables. The adjunctive set of orthonormal basis functions in such a case are Hermite polynomials.
To quantify the uncertainty of a result R we seek the appropriate function , such that R will have the required distribution of the model response, . As for all random variables with finite variance it is possible to find an infinite expansion
which we limit to polynomial order P since the contributions of higher orders become numerically insignificant. The coefficients are given by
We assume Gaussian character for the random variable, so the density is distributed according to the normal (probability) distribution
The adjunctive set of orthonormal basis functions is given by the so-called probabilist Hermite functions, which read up to fourth order
It turns out that for the model simulations under consideration this polynomial order is sufficient since contributions from higher orders become numerically insignificant for the result. With these definitions the normalization constants in Equation (2) are readily
Due to the Gaussian nature of the probability function omnipresent in the integrals above, it is beneficial to use Gauss-Hermite quadrature for the evaluation
where the weights and the abscissas are for instance provided by Numerical Recipes [3]. Eventually, by exploiting the properties of the orthogonal Hermite polynomials the expectation value of the model outcome and its variance can be assigned to the spectral coefficients in Equation (2)
In order to provide a measure for the influence of the uncertainty of input variables on the above variance we employ Sobol coefficients [4]. They are defined by
where the evaluation of the integrals
results in combinations of the coefficients of Equation (2) (the index of the function relates to the specific variable(s) which are omitted in the integral ). The higher the value of a Sobol coefficient with respect to the others is, the more it is advantageous to reduce the uncertainty of its associated variable in order reduce the uncertainty of the quantity of interest.
3. Ion-Solid Interaction Program SDTrimSP
SDTrimSP [5,6] is a parallelized Monte-Carlo code which simulates transport of energetic particles through a target by employing sequentially two-body collision approximation to compute collision-cascades in three dimensions. This approximation has been shown to be valid (i.e., the stochastic fluctuations of the collision processes exceed the approximation error) for impact energies larger than about 50 eV [7]. Versions of the SDTrimSP-code differ in the description of the target composition, e.g., as one-dimensional (c(x) [6]), two-dimensional (c(x,y) [8]) or three-dimensional (c(x,y,z) [9]). Common to all versions (and key to the high code efficiency) is the assumption of amorphous targets, which circumvents the storage of sample atom coordinates. The simulations were performed with standard settings, i.e., considering a static one-dimensional target (the concentral profile c(x) was kept constant) and the scattering integral was computed using the Gauss-Mehler quadrature scheme with eight pivots. The varied parameters were the projectile energy and the impact angle (with zero degrees corresponding to a perpendicular impact, parallel to the surface normal).
4. Results and Discussion
The above program is applied to simulate ion-solid interactions for the case of incident deuterium ions with an energy of eV at an impact angle of degrees to a surface consisting of iron with a commonly used surface binding energy of eV. We assume the parameters to be normally distributed within a standard deviation of roughly 10%, i.e., eV, degrees and eV.
First, in order to have a calibration standard to compare with we employ random sampling of the model response. For each realization of the random variable there exists a model response constituting the sample solution set from which moments can be computed. The expected mean is and its variance read
In Figure 1 the results of = 8000 samples are shown for the above parameter settings. The mean value for the sputter yield is with a standard deviation of = 0.013. Even more, the full uncertainty distribution may be established with help of a histogram if the sample solution set is sufficiently large (1000). But, although this procedure is straightforward and automatically contains the full model answer with all correlations, it has the vital drawback of a comparatively low convergence rate. If the computation time of a single model output is not in the order of seconds or becomes more sophisticated with a higher number of variables (curse of dimension), the mere accumulation of sample point densities to infer the complete distribution is futile. Much more promising in this respect is the spectral approach of Section 2 which results will be discussed next.
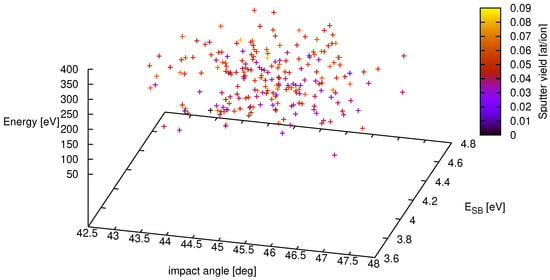
Figure 1.
Sputter yield for deuterium on iron from SDTrimSP-simulations with energy, angle and surface binding energy distribution for 203 samples. The respective input variables are E0 = 200 ± 20 eV, ESB = 4.28 ± 0.4 eV and an incident angle of 45 ±4 degrees, The resulting sputter yield is plotted with a color scheme ranging from dark blue at zero up to light yellow at 0.09 sputtered atoms per incoming ion. The mean value of the sputter yield is YMC = 0.052 with a standard deviation of σMC = 0.013.
Extending the formulas of Section 2 to three random variables with , and , the summation of the terms in Equation (6) runs over three indices , and with an upper boundary of in the present setup of fourth order polynomials (for numerical accuracy of the Gaussian quadrature it is expedient to be one order higher than the polynomial order of the spectral expansion). This results in a total of 216 terms (three nested summations, each running from = 0 to 5 with i = 1, 2, 3) over the collocation points composed of 6 Gaussian quadrature abscissas assigned to and 6 weights . The value for the function is obtained from a SDTrimSP run, which takes roughly 3 min on a modern CPU. However, the complete run for the 216 terms can be speeded up enormously since the calculations are independent and can be done in parallel. Once calculated, the 35 coefficients of Equation (6) establish a fast surrogate model, which is simply the evaluation of a polynomial. This is shown in Figure 2 as the red mesh. The respective sputter yield, for which the uncertainty quantification was performed, is depicted in the center as the green sphere with at/ion and its standard deviation of as the green perpendicular line. The comparison with the result of the sampling approach above () shows excellent agreement.
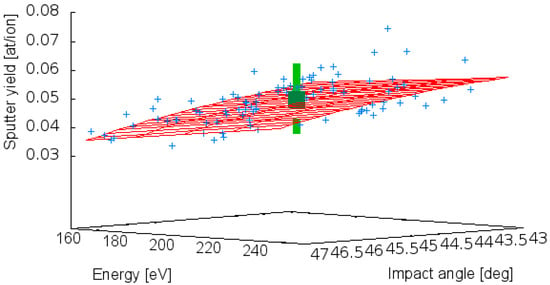
Figure 2.
Sputter yield reproduced by the surrogate model from the uncertainty quantification of SDTrimSP calculations for eV, eV and an incident angle of 45 degrees. The filled circle in dark green shows a yield of 0.050 for these settings with a standard deviation of 0.011 (light green line). For reason of portrayal the surrogate model (red mesh) was varied in two dimensions only for and , while was kept fixed at 4.28 eV. In addition, the blue plus signs show the scatter data from the sampling approach already shown in Figure 1.
Without the need to do any further simulations, various quantities may be inferred from the coefficients, e.g., the variance as in Equation (2), or the Sobol coefficients, which allow to investigate the sensitivity of the result on the uncertainty of the input variables. For the above variables , and we get a relationship of 10:20:70 in the Sobol coefficients (only first order is numerically significant) for , indicating that the improvement of the knowledge of is most rewarding if one wants to reduce the uncertainty of the sputter yield.
Following this trail, we performed a series of experimental measurements of the sputter yield for different impact angles with = 0, 45, 60 and 75 degrees at = 2 keV. Then we applied the uncertainty quantification method discussed above in order to provide quantitative estimates of the sputter yields at a variety of settings for the surface binding energy . It turned out that the most probable value for the surface binding energy is eV, one and a half standard deviations larger than the value commonly used up to now [1], i.e., eV. With the revised setting of we compared (see Figure 3) simulations of the sputter yield for different incident energies of deuterium with results from Rutherford backscattering (RBS) and weight loss (WL) experiments and got an improved agreement (except for = 1 keV). With these results the Bayes factor rules out another competitor to SDTrimSP (i.e., Monte Carlo decision for the occurrences of collisions of incident ions with atoms in the target) being the SRIM-model, which employs a quantum mechanical treatment of ion-atom collisions and seems not to comprise all important effects present..
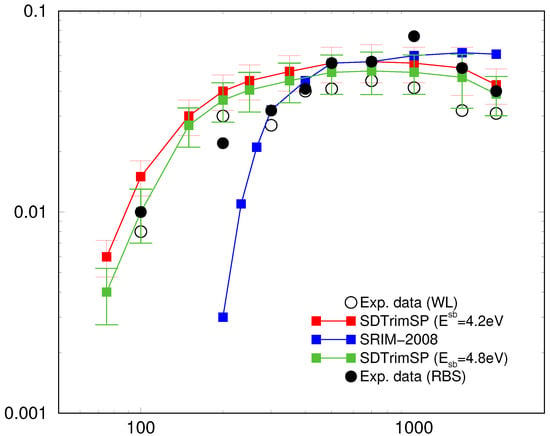
Figure 3.
Comparison of the sputter yield for the previously set surface binding energy eV (red squares) and the newly acquired setting of energy eV (green squares) with data from experiments done in a Rutherford backscattering setup (RBS, filled circles) and a weight loss setup (WL, open circles). A further model, SRIM (blue squares), can almost certainly be ruled out. All lines shown are guide to the eye.
5. Summary and Conclusions
The non-intrusive polynomial chaos expansion for quantifying the propagation of uncertainty through the model has been proven to be a valuable tool in describing the reliability of a model outcome. The experience with the employed algorithm revealed that the spectral expansion with moderate settings of employing only up to 4th order polynomials and six Gaussian quadrature abscissa, which requires less than 1000 simulation runs, is well suited for the determination of a medium number of uncertain parameters. We applied the method to SDTrimSP simulations in determining the sputtering yield and its standard deviation for the example of incident deuterium ions on an iron target. Residing on both quantities we could rule out the existing parameter setting for the surface binding energy and assigned a new much more accurate one. With this newly set input parameter it was possible to get a better agreement with available experimental data and eventually put us in the position to rule out another physical model.
Author Contributions
R.A. performed the experiments and provided the data; R.P. and U.v.T. analyzed the data, contributed analysis tools and wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eckstein, W. Computer Simulation of Ion-Solid Interactions; Springer Series in Materials Science; Springer-Verlag: Berlin, Heidelberg; New York, NY, USA, 1991; Volume 10. [Google Scholar]
- Wiener, N. The homogeneous chaos. Am. J. Math. 1938, 60, 897–936. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, 2007. [Google Scholar]
- Smith, R.C. Uncertainty Quantification: Theory, Implementation, and Applications; SIAM: Philadelphia, PA, USA, 2014. [Google Scholar]
- Möller, W.; Eckstein, W.; Biersack, J. Tridyn-binary collision simulation of atomic collisions and dynamic composition changes in solids. Comput. Phys. Commun. 1988, 51, 355–368. [Google Scholar] [CrossRef]
- Eckstein, W.; Dohmen, R.; Mutzke, A.; Schneider, R. SDTrimSP: Ein Monte-Carlo Code zur Berechnung von Stossereignissen in Ungeordneten Targets (SDTrimSP: A Monte-Carlo Code for Calculating Collision Phenomena in Randomized Targets); Technical Report IPP 12/3; Max-Planck-Institut für Plasmaphysik: Garching, Germany, 2007. [Google Scholar]
- Behrisch, R.; Eckstein, W. Sputtering by Particle Bombardment; Springer: Berlin/Heidelberg, 2007. [Google Scholar]
- Mutzke, A.; Schneider, R. SDTrimSP-2D: Simulation of Particles Bombarding on a Two Dimensional Target Version 1.0; Technical Report IPP 12/4; Max-Planck-Institut für Plasmaphysik: Garching, Germany, 2009. [Google Scholar]
- von Toussaint, U.; Mutzke, A.; Manhard, A. Sputtering of rough surfaces: A 3D simulation study. Phys. Scr. 2017, T170, 014056. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).