Interaction between Model Based Signal and Image Processing, Machine Learning and Artificial Intelligence  ^†

Abstract

Signale and image processing has always been the main tools in many area and in particular in Medical and Biomedical applications. Nowadays, there are great number of toolboxes, general purpose and very specialized, in which classical techniques are implemented and can be used: all the transformation based methods (Fourier, Wavelets, …) as well as model based and iterative regularization methods. Statistical methods have also shown their success in some area when parametric models are available. Bayesian inference based methods had great success, in particular, when the data are noisy, uncertain, incomplete (missing values) or with outliers and where there is a need to quantify uncertainties. In some applications, nowadays, we have more and more data. To use these “Big Data” to extract more knowledge, the Machine Learning and Artificial Intelligence tools have shown success and became mandatory. However, even if in many domains of Machine Learning such as classification and clustering these methods have shown success, their use in real scientific problems are limited. The main reasons are twofold: First, the users of these tools cannot explain the reasons when the are successful and when they are not. The second is that, in general, these tools can not quantify the remaining uncertainties. Model based and Bayesian inference approach have been very successful in linear inverse problems. However, adjusting the hyper parameters is complex and the cost of the computation is high. The Convolutional Neural Networks (CNN) and Deep Learning (DL) tools can be useful for pushing farther these limits. At the other side, the Model based methods can be helpful for the selection of the structure of CNN and DL which are crucial in ML success. In this work, I first provide an overview and then a survey of the aforementioned methods and explore the possible interactions between them.

1. Introduction

Nowadays, there are great number of general purpose and very specialized toolboxes, in which, classical and advanced techniques of signal and image processing methods are implemented and can be used. Between them, we can mention all the transformation based methods (Fourier, Hilbert, Wavelets, Radon, Abel, … and much more) as well as all the Model Based and iterative regularization methods. Statistical methods have also shown their success in some areas when parametric models are available.

Bayesian inference based methods had great success, in particular, when the data are noisy, uncertain, some missing and some outliers and where there is a need to account and to quantify uncertainties.

Nowadays, we have more and more data. To use these “Big Data” to extract more knowledge, the Machine Learning and Artificial Intelligence tools have shown success and became mandatory. However, even if in many domains of Machine Learning such as classification and clustering these methods have shown success, their use in real scientific problems are limited. The main reasons are twofold: First, the users of these tools can not explain the reasons when they are successful and when they are not. The second is that, in general, these tools can not quantify the remaining uncertainties.

Model based and Bayesian inference approach have been very successful in linear inverse problems. However, adjusting the hyper parameters is complex and the cost of the computation is high. The Convolutional Neural Networks (CNN) and Deep Learning (DL) tools can be useful for pushing farther these limits. At the other side, the Model based methods can be helpful for the selection of the structure of CNN and DL which are crucial in ML success. In this work, first I give an overview and a survey of the aforementioned methods and explore the possible interactions between them.

The rest of the paper is organized as follows: First a classification of signal and image processing methods is proposed. Then, very briefly, the Machine Learning tools are introduced. Then, through the problem of Imaging inside the body, we see the different steps from acquisition of the data, reconstruction, post-processing such as segmentation and finally the decision and conclusion of the user are presented. After mentioning some successful case studies in which the ML tools have been successful, we arrive at the main part of this paper: Looking for the possible interactions between Model based and Machine Learning tools. Finally, we mention the Open problems and challenges in both classical, model based and the ML tool.

2. Classification of Signal and Image Processing Methods

Signal and image processing methods can be classified in the following categories:

• Transform based methods
• Model based and inverse problem approach
• Regularisation methods
• Bayesian inference methods

In the first category, the main idea is to use different ways the signal and images can be represented in time, frequency, space, spacial frequency, time-frequency, wavelets, etc.

3. Transform Domain Methods

Figure 1 shows the main idea behind the transform based methods. Mainly, first a linear transform (Fourier, Wavelet, Radon, etc.) is applied to the signal or the image, then some thresholding or windowing is applied in this transform domain and finally an inverse transform is applied to obtain the result. Appropriate choices of the transform and the threshold or the widow size and shape are important for the success of such methods [1,2].

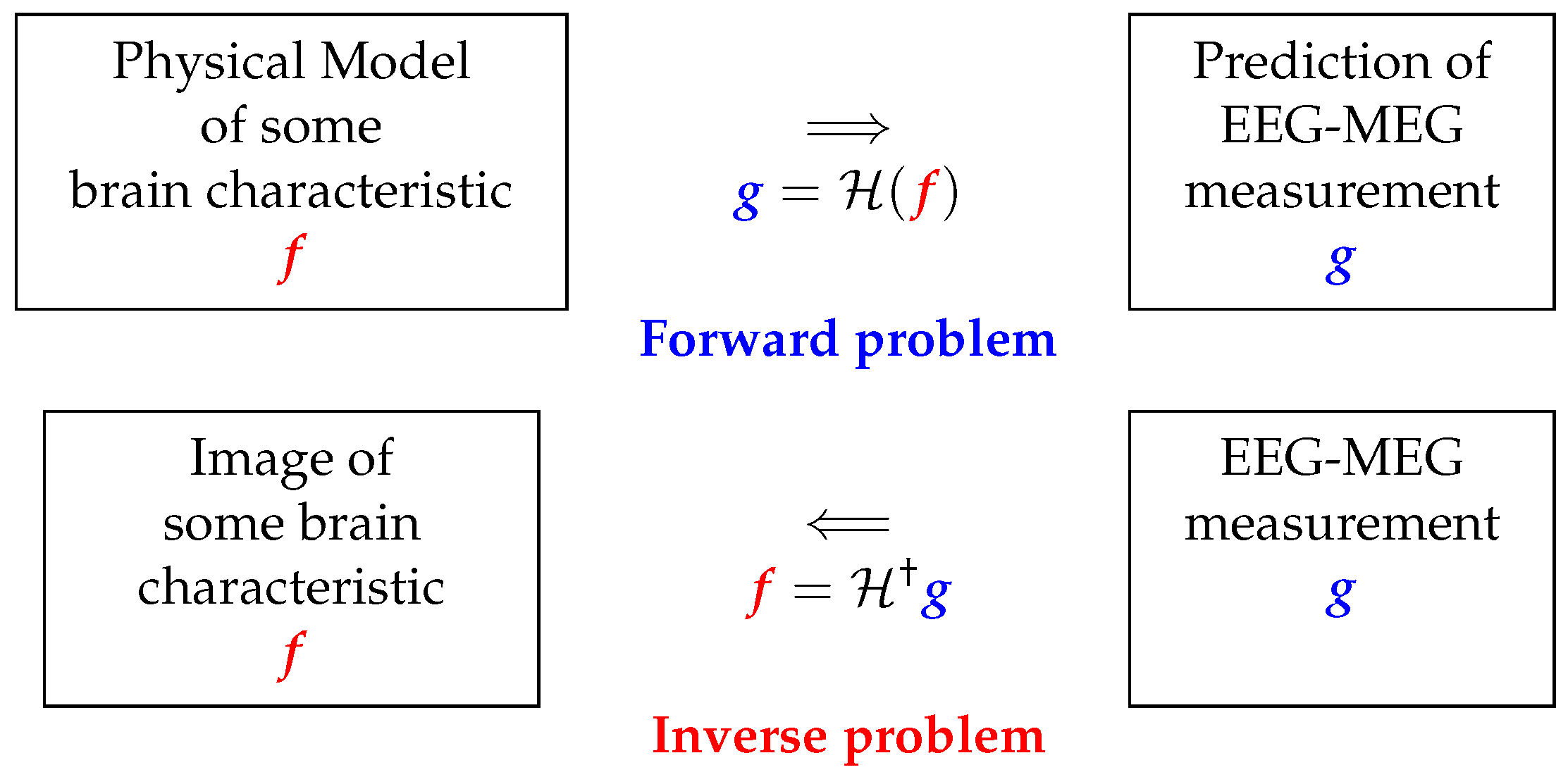
4. Model Based and Inverse Problem Approach

The model based methods are related to the notions of forward model and inverse problems approach. Figure 2 shows the main idea:

Given the forward model $\mathscr{H}$ and the sources $f$, the prediction of the data $g$ can be done, either in a deterministic way: $g=\mathsf{\mathscr{H}}\left(f\right)$ or via a probabilistic model: $p\left(g\right|f,\mathsf{\mathscr{H}})$.

In the same way, given the forward model $\mathscr{H}$ and the data $g$, the estimation of the unknown sources $f$ can be done either via a deterministic method or probabilistic one. One of the deterministic method is the Generalized inversion: $f={\mathsf{\mathscr{H}}}^{†}\left(g\right)$. A more general method is the regularization: $\hat{f}=\arg {\min }_f\left\{J\left(f\right)\right\}withJ\left(f\right)={\parallel g-\mathsf{\mathscr{H}}\left(f\right)\parallel }^2+\lambda \mathsf{ℛ}\left(f\right)$ [3].

As we will see later, the only probabilistic method which can be efficiently use for the inverse problems is the Bayesian approach.

5. Regularization Methods

Let consider the linear inverse problem:

$$g=\mathit{H}f+\mathit{ϵ},$$

(1)

Then the basic idea in regularization is to define a regularization criterion:

$$J\left(f\right)=\frac{1}{2}{\parallel g-\mathit{H}f\parallel }_2^2+\lambda R\left(f\right)$$

(2)

and optimize it to obtain the solution [4]. The first main issue in such regularization method is the choice of the regularizer. The most common examples are:

$$R\left(f\right)=\left\{{\parallel f\parallel }_2^2{,\parallel f\parallel }_{\beta }^{\beta }{,\parallel \mathit{D}f\parallel }_2^2,{\parallel \mathit{D}f\parallel }_{\beta }^{\beta },\sum _j\varphi \left({\left[\mathit{D}f\right]}_j\right)\right\},1\le \beta \le 2$$

(3)

The second main issue in regularization is the the choice of appropriate optimization algorithm. Mainly, depending on the type of the criterion, we have:

• $R\left(f\right)$ quadratic: Gradient based, Conjugate Gradient algorithms are appropriate.
• $R\left(f\right)$ non quadratic, but convex and differentiable: Here too the Gradient based and Conjugate Gradient (CG) methods can be used, but there are also great number of convex criterion optimization algorithms.
• $R\left(f\right)$ convex but non-differentiable: Here, the notion of sub-gradient is used.

Specific cases are:

• L2 or quadratic: $J\left(f\right)=\frac{1}{2}{\parallel g-\mathit{H}f\parallel }_2^2+\lambda {\parallel \mathit{D}f\parallel }_2^2$.
  In this case we have an analytic solution: $\hat{f}={({\mathit{H}}^{\prime }\mathit{H}+\lambda {\mathit{D}}^{\prime }\mathit{D})}^{-1}{\mathit{H}}^{\prime }g$. However, in practice this analytic solution is not usable in high dimensional problems. In general, as the gradient $\nabla J\left(f\right)=-{\mathit{H}}^{\prime }(g-\mathit{H}f)+2\lambda {\mathit{D}}^{\prime }\mathit{D}f$ can be evaluated analytically, gradient based algorithms are used.
• L1 (TV): convex but not differentiable at zero: $J\left(f\right)=\frac{1}{2}{\parallel g-\mathit{H}f\parallel }_2^2+\lambda {\parallel \mathit{D}f\parallel }_1$.
  The algorithms in this case use the notions of Fenchel conjugate, Dual problem, sub gradient, proximal operator, …
• Variable splitting and Augmented Lagrangian

  $$(f,\hat{z})=\underset{f,z}{\arg \min }\left\{\frac{1}{2}{\parallel g-\mathit{H}f\parallel }_2^2+{\lambda \parallel z\parallel }_1+q{\parallel z\parallel }_2^2\right\}\mathrm{s}.\mathrm{t}.z=\mathit{D}f$$

  (4)
  A great number of optimization algorithms have been proposed: ADMM, ISTA, FISTA, etc. [5,6,7].

Main limitations of deterministic regularization methods are:

• Limited choice of the regularization term. Mainly, we have: a) Smoothness (Tikhonov), b) Sparsity, Piecewise continuous (Total Variation).
• Determination of the regularization parameter. Even if there are some classical methods such as L-Curve and Cross validation, there are still controversial discussions about this.
• Quantification of the uncertainties: This is the main limitation of the deterministic methods, in particular in medical and biological applications where this point is important.

The best possible solution to push further all these limits is the Bayesian approach which has: (a) Many possibilities to choose prior models, (b) possibility of the estimation of the hyper-parameters, and most important (c) accounting for the uncertainties.

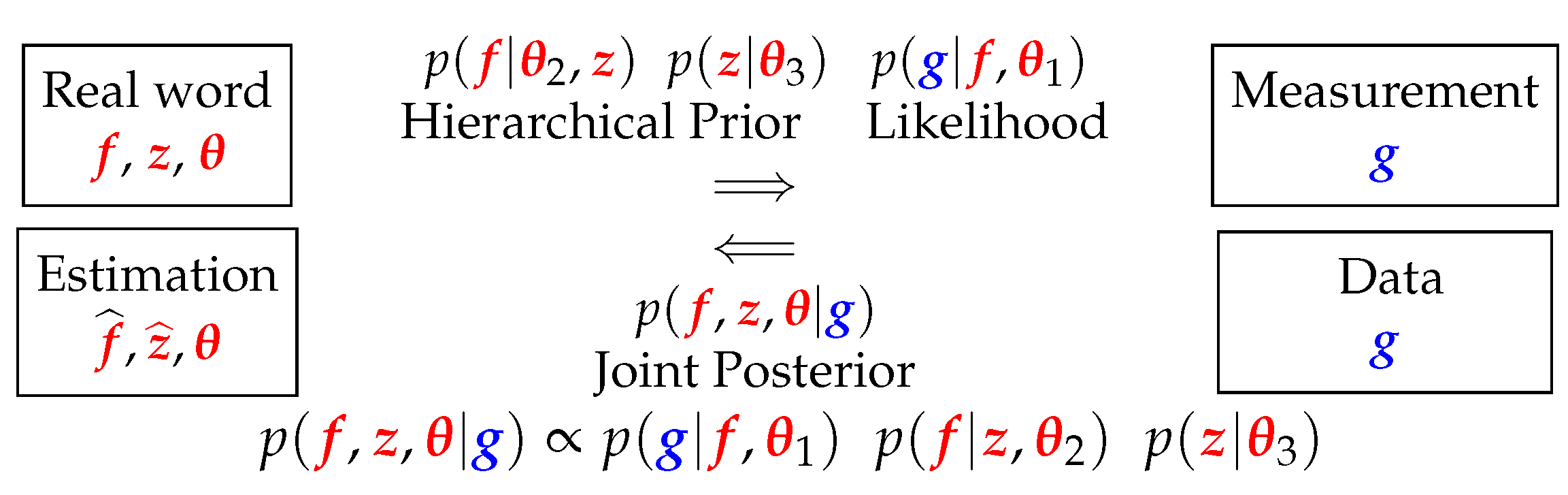
6. Bayesian Inference Methods

The simple case of the Bayes rule is:

$$p\left(f\right|g,\mathsf{ℳ})=\frac{p\left(g\right|f,\mathsf{ℳ}\left)p\right(f\left|\mathsf{ℳ}\right)}{p\left(g\right|\mathsf{ℳ})}\mathrm{where}p\left(g\right|\mathsf{ℳ})=\int p\left(g\right|f,\mathsf{ℳ})p\left(f\right|\mathsf{ℳ})df$$

(5)

When there are some hyper parameters which have also to be estimated, we have:

$$p(f,\theta |g,\mathsf{ℳ})=\frac{p\left(g\right|f,\theta ,\mathsf{ℳ}\left)p\right(f|\theta ,\mathsf{ℳ})p\left(\theta \right|\mathsf{ℳ})}{p\left(g\right|\mathsf{ℳ})}\mathrm{where}p\left(g\right|\mathsf{ℳ})=\int p\left(g\right|f,\theta ,\mathsf{ℳ})p\left(f\right|\theta ,\mathsf{ℳ})\mathrm{d}\theta \mathrm{d}f$$

(6)

From that joint posterior distribution, we may also obtain the marginals:

$$p\left(f\right|g,\mathsf{ℳ})=\int p(f,\theta |g,\mathsf{ℳ})\mathrm{d}f\mathrm{and}p(\theta |g\mathsf{ℳ},)=\int p(f,\theta |g,\mathsf{ℳ})\mathrm{d}f$$

(7)

To be more specific, let consider the case of linear inverse problems $g=\mathit{H}f+\mathit{ϵ},$. Then, assuming Gaussian noise, we have:

$$p\left(g\right|f)=\mathsf{𝒩}\left(g\right|\mathit{H}f,v_{\mathit{ϵ}}\mathit{I})\propto \exp \left[\frac{-1}{2v_{\mathit{ϵ}}}{\parallel g-\mathit{H}f\parallel }_2^2\right]$$

(8)

Assuming a Gaussian prior:

$$p\left(f\right)\propto \exp \left[\frac{-1}{2v_f}{\parallel f\parallel }_2^2\right]\mathrm{or}\exp \left[\frac{-1}{2v_f}{\parallel \mathit{D}f\parallel }_2^2\right],$$

(9)

Then, we see that the posterior is also Gaussian and the MAP and Posterior Mean (PM) estimates become the same and can be computed as the minimizer of : $J\left(f\right)={\parallel g-\mathit{H}f\parallel }_2^2+\lambda R\left(f\right)$:

$$p\left(f\right|g)\propto \exp \left[\frac{-1}{2v_{\mathit{ϵ}}}J\left(f\right)\right]\to {\hat{f}}_{MAP}=\underset{f}{\arg \max }\left\{p\left(f\right|g)\right\}=\underset{f}{\arg \min }\left\{J\left(f\right)\right\}$$

(10)

In summary, we have:

$$\left\{\begin{array}{c}p\left(g\right|f)=\mathrm{𝒩}\left(g\right|\mathit{H}f,v_{\mathit{ϵ}}\mathit{I})\hfill \\ p\left(f\right)=\mathrm{𝒩}\left(f\right|0,v_f\mathit{I})\hfill \end{array}\right.\to \left\{\begin{array}{c}p\left(f\right|g)=\mathsf{𝒩}\left(f\right|\hat{f},\hat{\Sigma })\hfill \\ \hat{f}={[{\mathit{H}}^{\prime }\mathit{H}+\lambda \mathit{I}]}^{-1}{\mathit{H}}^{\prime }g\hfill \\ \hat{\Sigma }=v_{\mathit{ϵ}}{[{\mathit{H}}^{\prime }\mathit{H}+\lambda \mathit{I}]}^{-1},\lambda =\frac{v_{\mathit{ϵ}}}{v_f}\hfill \end{array}\right.$$

(11)

For the case where the hyper parameters $v_{\mathit{ϵ}}$ and $v_f$ are unknown (Unsupervised case), we can derive the following:

$$\left\{\begin{array}{c}p\left(g\right|f,v_{\mathit{ϵ}})=\mathsf{𝒩}(g|\mathit{H}f,v_{\mathit{ϵ}}\mathit{I})\hfill \\ p\left(f\right|v_f)=\mathsf{𝒩}(f|0,v_f\mathit{I})\hfill \\ p\left(v_{\epsilon }\right)=\mathsf{ℐ}\mathsf{𝒢}\left(v_f\right|{\mathit{\alpha }}_{{\mathit{ϵ}}_0},{\mathit{\beta }}_{{\mathit{ϵ}}_0})\hfill \\ p\left(v_f\right)=\mathsf{ℐ}\mathsf{𝒢}\left(v_f\right|{\mathit{\alpha }}_{f_0},{\mathit{\beta }}_{f_0})\hfill \end{array}\right.\to \left\{\begin{array}{c}p\left(f\right|g,v_{\mathit{ϵ}},v_f)=\mathsf{𝒩}\left(f\right|\hat{f},\hat{\Sigma })\hfill \\ \hat{f}={[{\mathit{H}}^{\prime }\mathit{H}+\hat{\lambda }\mathit{I}]}^{-1}{\mathit{H}}^{\prime }g\hfill \\ \hat{\Sigma }={\hat{v}}_{\mathit{ϵ}}{[{\mathit{H}}^{\prime }\mathit{H}+\hat{\lambda }\mathit{I}]}^{-1},\hat{\lambda }=\frac{\hat{v}\mathit{ϵ}}{\hat{v}f}\hfill \\ p\left(v_{\mathit{ϵ}}\right|g,f)=\mathsf{ℐ}\mathsf{𝒢}\left(v_{\mathit{ϵ}}\right|{\tilde{\mathit{\alpha }}}_{\mathit{ϵ}},{\tilde{\mathit{\beta }}}_{\mathit{ϵ}})\hfill \\ p\left(v_f\right|g,f)=\mathsf{ℐ}\mathsf{𝒢}\left(v_f\right|{\tilde{\mathit{\alpha }}}_f,{\tilde{\mathit{\beta }}}_f)\hfill \\ {\tilde{\mathit{\alpha }}}_{\mathit{ϵ}},{\tilde{\mathit{\beta }}}_{\mathit{ϵ}},{\tilde{\mathit{\alpha }}}_f,{\tilde{\mathit{\beta }}}_f\hfill \end{array}\right.$$

(12)

where the expressions for ${\tilde{\mathit{\alpha }}}_{\mathit{ϵ}},{\tilde{\mathit{\beta }}}_{\mathit{ϵ}},{\tilde{\mathit{\alpha }}}_f,{\tilde{\mathit{\beta }}}_f$ can be found in [8].

The joint posterior can be written as:

$$p(f,v_{\mathit{ϵ}},v_{\mathit{\zeta }}|g)\propto \exp [-J(f,v_{\mathit{ϵ}},v_{\mathit{\zeta }})]$$

(13)

From this expression, we have different expansion possibilities:

• JMAP: Alternate optimization with respect to $f,v_{\mathit{ϵ}},v_f$:

  $$J\left(f,v_{\mathit{ϵ}},v_f\right)=\frac{1}{2v_{\mathit{ϵ}}}{\parallel g-\mathit{H}f\parallel }_2^2+\frac{1}{2v_f}{\parallel f\parallel }_2^2+({\mathit{\alpha }}_{{\mathit{ϵ}}_0}+1)ln{v}_{\mathit{ϵ}}+\frac{{\mathit{\beta }}_{{\mathit{ϵ}}_0}}{v_{\mathit{ϵ}}}+({\mathit{\alpha }}_{f_0}+1)ln{v}_f+\frac{{\mathit{\beta }}_{f_0}}{v_f}$$

  (14)
• Gibbs sampling MCMC:

  $$f\sim p(f,v_{\mathit{ϵ}},v_f|g)\to v_{\mathit{ϵ}}\sim p(v_{\mathit{ϵ}}|g,f)\to v_f\sim p\left(v_f\right|g,f)$$

  (15)
• Variational Bayesian Approximation: Approximate $p(f,v_{\mathit{ϵ}},v_f|g)$ by a separable one $q(f,v_{\mathit{ϵ}},v_f)=q_1\left(f\right)q_2\left(v_{\mathit{ϵ}}\right)q_3\left(v_f\right)$ minimizing KL$\left(q\right|p)$ [8].

7. Imaging inside the Body: From Acquisition to Decision

To introduce the link between the different model based methods and the Machine Learning tools, let consider the case of medical imaging, from the acquisition to the decision steps:

• Data acquisition:

  $$\mathrm{Object}f\to \begin{array}{|c|}\hline \mathrm{Scanner}\\ \hline\end{array}\to \mathrm{Data}g$$
• Reconstruction:

  $$\mathrm{Data}g\to \begin{array}{|c|}\hline \mathrm{Reconstruction}\\ \hline\end{array}\to \mathrm{Image}\hat{f}$$
• Post Processing (Segmentation):

  $$\mathrm{Image}\hat{f}\to \begin{array}{|c|}\hline \mathrm{Segmentation}\\ \hline\end{array}\to \hat{z}$$
• Understanding and Decision:

  $$\begin{array}{c}\mathrm{Image}\hat{f}\hfill \\ \mathrm{Segmentation}\hat{z}\hfill \end{array}\to \begin{array}{|c|}\hline \mathrm{Interpretation}\hfill \\ \mathrm{Decision}\hfill \\ \hline\end{array}\to \begin{array}{c}\mathrm{Tumor}\mathrm{or}\hfill \\ \mathrm{Not}\mathrm{Tumor}\hfill \end{array}$$

The questions now are: Can we join any of these steps? Can we go directly from the image to the decision? For the first one, the Bayesian approach can provide a solution:

$$\mathrm{Data}g\to \begin{array}{|c|}\hline \hfill \mathrm{Reconstruction}\hfill \\ \hfill \mathrm{Segmentation}\hfill \\ \hline\end{array}\begin{array}{c}\to \mathrm{Reconstruction}\hat{f}\hfill \\ \to \mathrm{Segmentation}\hat{z}\hfill \end{array}$$

The main tool here is to introduce a hidden variable which can represent the segmentation. A solution is to introduce a classification hidden variable $z$ with $z_j=\{1,2,\cdots ,K\}$. Then in Figure 3, we have in summary:

A few comments for these relations:

• $p\left(g\right|f,z)$ does not depend on $z$, so it can be written as $p\left(g\right|f)$.
• We may choose a Markovian Potts model for $p\left(z\right)$ to obtain more compact homogeneous regions [8,9].
• If we choose for $p\left(f\right|z)$ a Gaussian law, then $p(f,z|g)$ becomes a Gauss-Markov-Potts model [8].
• We can use the joint posterior $p(f,z|g)$ to infer on $(f,z)$: We may just do JMAP: $(\hat{f},\hat{z})=\arg \max \left\{p(f,z|g)\right\}$ or trying to access to the expected posterior values by using the Variational Bayesian Approximation (VBA) techniques [8,10,11,12,13].

This scheme can be extended to consider the estimation of the hyper parameters too. Figure 4 shows this.

Again, here, we can use the joint posterior $p(f,z,\mathit{\theta }|g)$ to infer on all the unknowns [12].

8. Advantages of the Bayesian Framework

• Large flexibility of Prior models prior

  -

  Smoothness (Gaussian, Gauss-Markov)

  -

  Direct Sparsity (Double Exp, Heavy-tailed distributions)

  -

  Sparsity in the Transform domain (Double Exp, Heavy-tailed distributions on the WT coefficients)

  -

  Piecewise continuous (DE or Student-t on the gradient)

  -

  Objects composed of only a few materials (Gauss-Markov-Potts), …

• Possibility of estimating hyper-parameters via JMAP or VBA
• Natural ways to take account for uncertainties and quantify the remaining uncertainties.

9. Imaging inside the Body for Tumor Detection

• Reconstruction and Segmentation

  $$\mathrm{Data}g\to \begin{array}{|c|}\hline \mathrm{Reconstruction}\\ \hline\end{array}\to \mathrm{Image}\hat{f}\to \begin{array}{|c|}\hline \mathrm{Segmentation}\\ \hline\end{array}\to \hat{z}$$
• Understanding and Decision

  $$\begin{array}{c}\mathrm{Image}\hat{f}\hfill \\ \mathrm{Segmentation}\hat{z}\hfill \end{array}\to \begin{array}{|c|}\hline \mathrm{Interpretation}\hfill \\ \mathrm{Decision}\hfill \\ \hline\end{array}\to \begin{array}{c}\mathrm{Tumor}\mathrm{or}\hfill \\ \mathrm{Not}\mathrm{Tumor}\hfill \end{array}$$
• Can we do all together in a more easily way?
• Machine Learning and Artificial Intelligence tools may propose solutions

  $$\mathrm{Data}g\to \begin{array}{|c|}\hline \mathrm{Machine}\mathrm{Learning}\mathrm{and}\hfill \\ \mathrm{Artificial}\mathrm{Intelligence}\hfill \\ \hline\end{array}\to \begin{array}{c}\mathrm{Tumor}\mathrm{or}\hfill \\ \mathrm{Not}\mathrm{Tumor}\hfill \end{array}$$
• Learning from a great number of data

From here, we may just do JMAP: $(\hat{f},\hat{z},\hat{\mathit{\theta }})=\arg \max \left\{p(f,z,\mathit{\theta }|g)\right)$, or better, use the Variational Bayesian Approximation (VBA) to do inference.

10. Machine Learning Basic Idea

The main idea in Machine Learning is to learn from a great number of data: $(g_i,d_i),i=1,\cdots N$:

$$\begin{array}{c}\hfill \mathrm{Data}\hfill \\ \hfill {(g_i,d_i)}_{i=1}^N\hfill \end{array}\to \begin{array}{|c|}\hline \mathrm{Machine}\mathrm{Learning}\mathrm{and}\hfill \\ \mathrm{Artificial}\mathrm{Intelligence}\hfill \\ \hline\end{array}\to \begin{array}{c}\mathrm{Tumor}\mathrm{or}\hfill \\ \mathrm{Not}\mathrm{Tumor}\hfill \end{array}$$

Between the basic tasks we can mention: (a) Classification (Tumor/Not Tumor), (b) Regression (Continuos parameter estimation) and (c) Clustering when the data have not yet labels.

Between the existing ML tools we may mention: Support Vector Machines (SVM), Decision-Tree learning (DT), Artificial Neural Networks (ANN), Bayesian Networks (BN), HMM and Random Forest (RF), Mixture Models (GMM, SMM, …), KNN, Kmeans,…

The frontiers between Image processing, Computer vision, Machine Learning & Artificial intelligence are not very precise as it is shown in Figure 5.

Between the Machine learning tools, we may mention Neural Networks (NN), Artificial NN (ANN), Convolutional NN (CNN), Recurrent NN (RNN), Deep Learning (DL). This last one had shown great success in Speech Recognition, Computer Vision and specifically in Segmentation, Classification and Clustering and in Multi-modality and cross-domain information fusion [14,15,16,17]. However, there are still many limitations: Lack of interpretability, reliability and uncertainty and No reasoning and explaining capabilities [18]. To overcome, there still much to do with the Fundamentals.

11. Interaction between Model Based and Machine Learning Tools

To show the possibilities of the interaction between classical and machine learning, let consider a few examples. The first one is the case of linear inverse problems and quadratic regularization or the Bayesian with Gaussian priors. The solution has an analytic expression:

$$g=\mathit{H}f+\mathit{ϵ}\to \hat{f}={(\mathit{H}{\mathit{H}}^t+\lambda \mathit{D}{\mathit{D}}^t)}^{-1}{\mathit{H}}^{t}g=\mathit{B}{\mathit{H}}^{t}g$$

which can be presented schematically as

$$g\to \begin{array}{|c|}\hline \hfill {\mathit{H}}^t\hfill \\ \hline\end{array}\to \begin{array}{|c|}\hline \hfill \mathit{B}\hfill \\ \hline\end{array}\to \hat{f}\mathrm{or}\mathrm{directly}g\to \begin{array}{|c|}\hline \hfill \mathrm{CNN}\mathrm{or}\mathrm{DL}\hfill \\ \hline\end{array}\to \hat{f}$$

As we can see, this induces directly a linear NN structure. In particular, if H represents a convolution operator, then ${\mathit{H}}^t$ and ${\mathit{H}}^t\mathit{H}$ are too and probably the operator B can also be well approximated by a convolution and the whole inversion can be modelled by a CNN [19].

The second example is the denoising $g=f+\mathit{ϵ}$ with L1 regularizer, or equivalently, the MAP estimator with a double exponential prior, where the solution can be obtained by a convolution followed by a thresholding [20,21].

$$g=f+\mathit{ϵ}\to \hat{f}=\frac{1}{\lambda }{\mathit{H}}^{t}g\mathrm{followed}\mathrm{by}\mathrm{Thresholding}$$

$$g\to \begin{array}{|c|}\hline \hfill {\mathit{H}}^t\hfill \\ \hline\end{array}\to \begin{array}{|c|}\hline \hfill \mathrm{Thresholding}\hfill \\ \hline\end{array}\to \hat{f}\mathrm{or}\mathrm{directly}g\to \begin{array}{|c|}\hline \hfill \mathrm{CNN}\mathrm{or}\mathrm{DL}\hfill \\ \hline\end{array}\to \hat{f}$$

The third example is the Joint Reconstruction and Segmentation that was presented in previous sections. If we present the different steps of reconstruction, segmentation and parameter estimation, we can also compare it with some kind of NN (combination of CNN, RNN and GAN) [22,23].

$$g\to \begin{array}{|c|}\hline \hfill \mathrm{Reconstruction}\hfill \\ \\ \hline\end{array}\to \hat{f}\to \begin{array}{|c|}\hline \hfill \mathrm{Segmentation}\hfill \\ \\ \hline\end{array}\to \hat{z}\to \begin{array}{|c|}\hline \hfill \mathrm{Parameter}\hfill \\ \mathrm{estimation}\\ \hline\end{array}\to \hat{\mathit{\theta }}$$

12. Conclusions and Challenges

Signal and image processing, imaging systems and computer vision have made great progress in the last forty years. The first category of the methods was based on linear transformation followed by a thresholding or windowing and coming back. The second generation was model based: forward modeling and inverse problems approach. The main successful approach was based on regularization methods using a combined criterion. The third generation was model based but probabilistic and using the Bayes rule, the so called Bayesian approach. Nowadays, Machine Learning (ML), Neural Networks (NN), Convolutional NN (CNN), Deep Learning (DL) and Artificial Intelligence (AI) methods have obtained great success in classification, clustering, object detection, speech and face recognition, etc. But, they need great number of training data and lack still explanation and they may fail very easily. For signal and image processing or inverse problems, they need still progress. This progress is coming via their interaction with the model based methods. In fact, the successful of CNN and DL methods greatly depends on the appropriate choice of the network structure. This choice can be guided by the model based methods. For inverse problems, when the forward models are not available or too complex, NN and DL may be helpfull. However, we may still need to choose the structure of the NN via approximate forward model and approximate Bayesian inversion.