Abstract
The effect of synchronization on the test results is explored by performing dynamic tensile tests on several continuous-fibre composite laminates. The results show that synchronization is key, because a delay of a single microsecond significantly affects the test outcome at high strain rates. Additionally, several upper limits on the maximum achievable strain rate of the experimental set-up are determined with the aid of a finite element model. These limits depend on the characteristics of the used equipment, the properties of the tested material and the chosen specimen dimensions.
1. Introduction
Car manufacturers are looking into the replacement of structural vehicle parts by composite alternatives. To ensure passenger safety during impact as well as a cost-effective design process, dynamic simulations of crashworthiness are a must to reduce the amount of testing. These simulations need to make use of rate-dependent composite material models, because the mechanical properties of composites vary with strain rate []. Still, testing is necessary to provide full stress-strain curves at strain rates from quasi-static up to about 200 s−1 [] for identification of the different parameters of these models.
Typically dynamic tension experiments are carried out using (i) a standard test bench close to its high velocity limit; (ii) a drop-weight tower with some mechanism to convert the impact load to tension; (iii) a hydraulic pulse machine; or (iv) a SHPB set-up with a special striker mechanism to produce a tensile strain wave []. In this work, a hydraulic pulse test bench is used to generate the required test data because it is currently the only equipment which allows testing in the full range of required strain rates without the need for a change in equipment or method.
Testing materials at high rates is challenging, especially for small strains to failure where the test duration can reduce to only tens of microseconds. The data acquisition becomes a critical factor in obtaining correct results. Synchronization of stress and strain should be achieved to only a fraction of the test duration if the resulting stress-strain curve is to be trusted. Additionally, the bandwidth and frame rate limits of the amplification and acquisition equipment can influence the results. Finally, the test duration can approach the period of the natural frequency of the load cell and/or the time needed for stress waves to progress through the specimen, in which case the curves can start to show oscillations unrelated to the material constitutive behaviour. It is of utmost importance to quantify the limits posed on the achievable strain rate by the experimental set-up to achieve reliable results which can be used with confidence as an input for predictive simulations.
2. Materials
Two composite material systems were subjected to dynamic tension in this re-search. The first is Pyrofil™ TR/360 carbon/epoxy, where the epoxy is curing modified to cure in under 5 min above 140 °C. Both a UD variant (TR 360E250S) and a plain weave variant (TR3110 360GMP) were used for the current research. The second material investigated is Cetex TC910 E-glass/polyamide-6 composite, also in two variants: a UD and a twill woven architecture. Both systems are relevant for the automotive industry. Laminates with maximum 50% fibres in the 0°-direction were tested using a dumbbell specimen shape which is a scaled version of De Baere et al. [] (Figure 1).
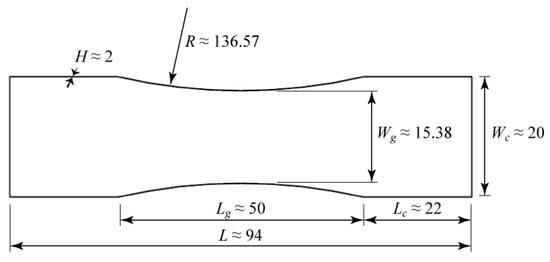
Figure 1.
Specimen shape and typical dimensions.
3. Experimental Method
An Instron VHS z25/20 test bench was used to for the experiments, which can generate a force of 25 kN at up to 20 ms−1. A slack rod connects the piston to the bottom grip to allow the piston to accelerate before pulling on the specimen. See also Figure 3 for the specimen gripping of the set-up on the left, where the top of the slack rod is shown on the bottom, connected to the bottom grip.
Force was measured using a Kistler 9061A 200 kN piezoelectric load cell (see also top left in Figure 3) and a Kistler 5011B Charge Amplifier with a bandwidth of 200 kHz. Strain was measured using strain gauges or digital image correlation (DIC), or both. General-purpose 350 Ω CEA-06-250UN-350 gauges by Vishay Precision Group were used to measure strain on the rear side of a specimen, the front was speckled black on a white background using a general-purpose matte spray paint.
The strain gauge was connected to a Vishay 2100 signal conditioning amplifier set at its maximum bandwidth of 35 kHz. A Photron SA-4 high-speed camera (HSC) was used to capture the strain optically using 2D-DIC. The camera recorded at its maximum of 500,000 frames per second for the shortest tests, reducing the image size to 128 × 16 pixels. This low resolution forced averaging of the data over a selected area. Slower tests were recorded at lower frame rates and increased image dimensions to reduce the noise on the DIC results.
Data was recorded using a 100 M Samples s−1 measurement card in a HBM GEN5i digital oscilloscope with a bandwidth of 26 MHz. The force measurement was used to trigger the HSC.
4. Results and Stress-Strain Synchronization
The output of multiple different measuring systems needs to be synchronised. For the current research, force is measured by a quartz transducer and strain using strain gauges and/or DIC. Typically, publications about dynamic tensile testing contain no information about data stream synchronisation, nor do the standards. Two minor exceptions are found. The first is the SAE J2749, in which it is stated that the data streams may need to be reconciled because of a measurable time lag [] but gives no mention about how this should be done or what is the origin of this lag. The second is a recent publication in which optical strain measurement was applied for dynamic tensile tests on a woven glass/vinylester composite where load and strain data were manually synchronized [].
The only option is to analyse the delay of each component in the chain of data acquisition to allow for an automatic synchronization []. Both the start or the end of the test are namely not discrete enough at high speed to be used to accurately align the data streams.
The difference is dramatic. The results for high-rate C/E 90° UD suggest a strong rate effect when synchronized on the start (Figure 2a), while the accurately synchronized results (Figure 2b) reveal that the high-rate results are actually no longer trustworthy. This is due to the surpassing of several upper limits on the strain rate, as explained in Section 6.
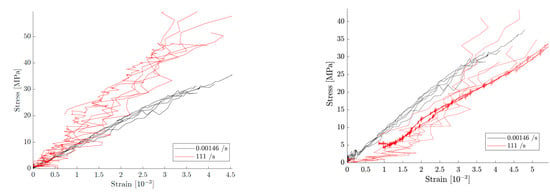
Figure 2.
Influence of synchronization on measured stress-strain response. Note that the incorrectly synchronized results (left) seem more logical than the correct synchronization (right) at first glance, though the suggested rate effect is caused by the surpassing of several upper limits in strain rate.
5. Finite-Element Modelling
To investigate how dynamic effects influence the results without uncertainty about the measurement delays, a 3D finite element (FE) analysis was carried out. The geometry of the model is shown to the right in Figure 3 and modelled after the dynamic tension set-up shown to the left in the figure. All parts except the specimen were given the linear elastic properties of steel. The specimen was given the linear elastic material properties to model a laminate by giving it the values of the MESI-model from reference []. All parts were connected by a tie condition on the mating surfaces. The top of the load cell was restricted in vertical motion. A smooth displacement ramp was applied to the bottom surface of the bottom grip support block using a sinusoidal formulation with different frequencies to match the different test speeds. The model was discretized into 34,952 reduced-integration hexahedral elements. An explicit solver was used to run the model, using the default values for bulk damping. Stress and strain were computed from the simulation results in a similar fashion as was done during the experiments.
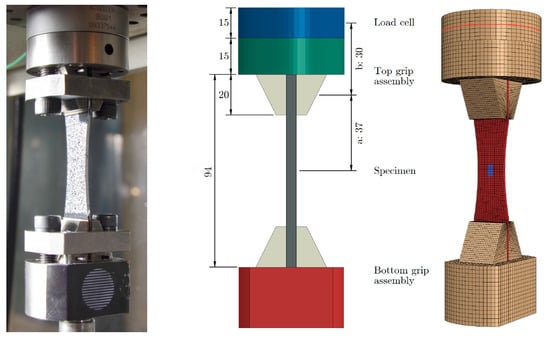
Figure 3.
A picture of the set-up (left), dimensions of the dynamic tensile test set-up in mm (middle), and the meshed FE model (right). The red line and blue area in the model show the force- and strain calculation surface areas, respectively.
Conclusions drawn from simulations at different speeds are given in the next sections.
6. Limits on Maximum Strain Rate
Five aspects were identified which limit the maximum strain rate at which a certain lay-up can be successfully tested using the current method []. Most depend on the test duration , which can be approximated by dividing the strain to failure by the strain rate. Given that the smallest failure strain in the current research is 0.6% (from the manufacturer’s data sheet for C/E 90° UD) and the highest requested rate 200 s−1, this gives the minimum test duration of .
6.1. Test Bench Capability
Perhaps the most obvious limit in strain rate stems from the maximum speed at which the test bench can be operated. The theoretical strain rate can be obtained by dividing the maximum speed of the test bench by the gauge length [], though it is known that this overestimates the obtained rate []. It was established that in the worst-case, the difference amounts to a factor for the current research, so this limit on strain rate can be written as:
6.2. Equipment Frequency Response
Any signal conditioning or amplifying device should be capable of handling sufficiently high frequencies. The SAE recommended practise for high strain rate tensile testing of polymers advises ten times the approximate maximum signal frequency, which is determined by assuming the shortest test resembles a quarter of a sine up to the yield point [], which is taken here as the failure point. The output of the FE-model described in Section 5 was filtered using various Butterworth filters at different strengths to mimic the effect of a limited bandwidth on the results. The SAE requirement was found to hold: only the results filtered with cut-off frequencies above the advised minimum bandwidth were equal to the unfiltered result. Hence, a limit on maximum strain rate can be formulated based on the bandwidth of amplifying equipment:
6.3. Maximum Frame- or Sample Rate
The oscilloscope poses no problem in terms of sample rate at the rates of interest, because it acquires data much faster than the advised lower limit []. The highest frame rate of 500,000 fps for the HSC, however, does approach the lower limit of what is still acceptable. The condition is posed here that a minimum of 50 data points are needed for the stress-strain curve, leading to an average error of 1% on the maximum strain for fully brittle materials tested at constant strain rate. This condition can be written as a limit for the maximum strain rate as:
6.4. Load Cell Ringing
The load measurement system has a natural frequency at which it ‘rings.’ For the current set-up, the post-failure response of a brittle showed that the load train rings at approximately 10.5 kHz. Below a certain test duration, the ringing starts to influence the results. Oscillations will appear, which do not represent actual material behaviour. The FE-model described in Section 5 shows the same behaviour. When the test duration remains larger than ten times the period of load cell ringing, the results are practically free of oscillations. This can be written as:
6.5. Approximate Equilibrium
At high speeds, the strain (or stress) no longer has the time to evenly distribute itself over the specimen. At some point, this invalidates the assumption of force equilibrium onto which the test relies, because the strain is measured in the middle of the specimen and the load in the load cell above the specimen. The FE-model shows that the effects become noticeable when the test duration drops below the time needed for a pulse to travel three times back and forth from end to end in the specimen. This also matches the condition posed by Xiao based on established research on SHPB testing []. This condition leads to the last upper bound in strain rate, which depends on the specimen length , the failure strain and the speed of sound in the tested material. Assuming a constant strain rate, the relationship becomes as follows:
If this limit would be surpassed, the stress will lag behind the strain. This is exactly what happens in Figure 2b, making the fast result appear below the quasi-static one.
6.6. Limits Quantified
Using the material, specimen and equipment properties given above, the equations in the previous subsections can be employed to provide numbers for the maximum strain rate for which reliable results can be obtained. The speeds of sound of the composites have been obtained with the use of contact ultrasonics on small blocks of material, leading to values of 2841 ms−1 for the C/E 90° UD, 6015 ms−1 for the C/E and 2821 ms−1 for the G/PA-6 90° UD. Table 1 summarizes the limits on strain rate due to the various described reasons. Clearly, the load cell ringing (column d) poses the most stringent limit on test speed. It needs to be noted, though, that surpassing this limit does not immediately render the results useless, though the oscillations should not be mistaken for material behaviour. Moreover, the limits for materials with a larger strain to failure (like quasi-isotropic or ±45 layups) are significantly higher.

Table 1.
Limits on strain rate. The numbers correspond to the subsections of Section 6.
7. Conclusions
A dynamic tensile test campaign has been carried out on various composite laminates. It was found that synchronization is key for high-rate testing, as a wrong synchronization method can lead to a false sense of rate-dependency. Finite-element modelling was used to quantify the limits of several aspects on the maximally attainable strain rate. It was found that the strain to failure is present in most conditions, making that the brittlest materials are hardest to test at high rate. Ringing of the load cell poses the strongest limitation on high rate testing, and should thus be the first candidate to improve if one intends to push the boundaries of this test method.
Author Contributions
S.W.F.S., F.A.G., R.D.B.S., D.G. and W.V.P. designed the experimental set-up and outlined the necessary actions and analyses. S.W.F.S. carried out the experiments and simulations under the supervision of F.A.G. and W.V.P., E.V. and M.K. designed the set-up for ultrasonic characterisation and applied it to the materials of this research. S.W.F.S. wrote the paper, F.A.G., R.D.B.S., D.G. and W.V.P. read and commented the work.
Acknowledgments
The work leading to this publication has been funded by the SBO project “M3Strength”, which fits in the MacroModelMat (M3) research program funded by SIM (Strategic Initiative Materials in Flanders) and VLAIO (Flemish government agency for Innovation & Entrepreneurship). E. Verboven acknowledges the financial support of the Fonds Wetenschappelijk Onderzoek (FWO) with project G0B9515N. The authors express their gratitude towards Honda R&D Co., Ltd., Mitsubishi Chemical Corporation, and Ten Cate Advanced Composites B.V. for their generousness in supplying materials for this research. They thank P. Baele, I. De Baere, M. Dolphen and N. Szymański for their support in the project.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Sierakowski, R.L. Strain Rate Effects in Composites. Appl. Mech. Rev. 1997, 50, 741–761. [Google Scholar] [CrossRef]
- Werner, H.; Gese, H. Zur Bedeutung Dehnratenabhängiger Werkstoffkennwerte in Der Crashsimulation. In Kennwertermittlung für die Praxis; WILEY-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2007; pp. 139–146. [Google Scholar]
- De Baere, I.; Van Paepegem, W.; Hochard, C.; Degrieck, J. On the Tension–tension Fatigue Behaviour of a Carbon Reinforced Thermoplastic Part II: Evaluation of a Dumbbell-Shaped Specimen. Polym. Test. 2011, 30, 663–672. [Google Scholar] [CrossRef]
- SAE International. SAE J2749, 2017, “Surface Vehicle Recommended Practise—High Strain Rate Testing of Polymers”; 400 Commonwealth Drive: Warrendale, PA, USA, 2017. [Google Scholar]
- Hufner, D.R.; Hill, S.I. High Strain Rate Testing and Modeling of a Woven E-Glass–vinylester Composite in Dry and Saturated Conditions. J. Compos. Mater. 2017, 51, 3017–3039. [Google Scholar] [CrossRef]
- Spronk, S.W.F.; Verboven, E.; Gilabert, F.A.; Sevenois, R.D.B.; Garoz, D.; Kersemans, M.; Van Paepegem, W. Stress-Strain Synchronization for High Strain Rate Tests on Brittle Composites. Polym. Test. 2018, 67, 477–486. [Google Scholar] [CrossRef]
- Sevenois, R.D.B.; Garoz, D.; Gilabert, F.A.; Spronk, S.W.F.; Fonteyn, S.; Heyndrickx, M.; Pyl, L.; Van Hemelrijck, D.; Degrieck, J.; Van Paepegem, W. Avoiding Interpenetrations and the Importance of Nesting in Analytic Geometry Construction for Representative Unit Cells of Woven Composite Laminates. Compos. Sci. Technol. 2016, 136, 119–132. [Google Scholar] [CrossRef]
- International Organization for Standardization. ISO 26203-2:2011. Metallic Materials—Tensile Testing at High Strain Rates—Part 2: Servo-Hydraulic and Other Test Systems. German Version DIN EN ISO 26203-2:2011; International Organization for Standardization: Geneva, Switzerland, 2011. [Google Scholar]
- Xiao, X. Dynamic Tensile Testing of Plastic Materials. Polym. Test. 2008, 27, 164–178. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).