Experimental and Numerical Investigation on the Impact Response of Elastomer-Coated Concrete ^†

Abstract

The use of a spray application elastomer coating as an effective retrofit strategy for blast and impact mitigation has gained increasing attention in recent years. Despite some encouraging studies in the literature, there remains a great deal yet to be understood, particularly regarding the coating’s impact mitigating capabilities when applied to structural elements. In this work, we consider the application of a spray-on elastomer coating to the impacted face of a concrete cube. High-speed, gas gun experiments are performed on concrete cubes in their uncoated and coated configurations and it is observed that the coating provides a significant protective benefit across the range of test velocities, 45–150 m/s. Quasi-static compression and indentation experimental tests are performed on uncoated and coated concrete cubes to inform the development of a numerical model. Despite a number of modelling challenges, we validate our model against experimental measurements and conclude it provides accurate predictions of behaviour at early time steps, before the concrete becomes severely damaged. Future work will focus on using this validated numerical model as an analysis tool for understanding the mechanism by which the elastomer alters the damage response of the underlying concrete substrate.

1. Introduction

Design against extreme load events continues to dominate both political and industrial agendas. With ever-increasing concerns related to global security and a growing proportion of vulnerable, ageing infrastructure, novel structural retrofit solutions are gaining attention. A number of design constraints arise as a result of the complexities of structural retrofit in the built environment. Offering a protective benefit is paramount but we must also consider cost, ease of installation, life-time maintenance and preservation of aesthetics. One solution that has gained attention in recent years is the application of a spray-on elastomer coating. Most literature studies have tended to explore this solution in terms of protection from blast pressure pulses when applied to masonry [1], steel [2] and reinforced concrete (RC) [3,4] substrates and promising results have been reported. By contrast, a limited number of studies have examined the elastomer coating’s ability to protect against projectile or fragmentation impact. Though some work has considered elastomer-metallic bilayer and laminate plates subjected to impact events [5,6], there still exists debate on the optimum coating location and the mechanism by which the elastomer achieves its effect.

In this work, we focus specifically on a spray-on elastomer coating applied to a concrete substrate. Concrete represents a significant proportion of today’s ageing infrastructure and given its tendency to emit secondary fragmentation upon impact (due to cracking and spallation), it appears a suitable candidate for this protective solution. Previous work [4,7] has focused on assessing the elastomer’s ability to protect RC from blast pressure pulse loading and it is found to be most effective in high blast intensity regimes when the concrete is severely damaged. Here, we turn our attention to its impact mitigating capabilities. We first perform an experimental investigation, using a gas gun apparatus to fire circular, cylindrical, steel projectiles at coated concrete cubes. A numerical model of the impact indentation is then developed, informed by quasi-static compression and indentation experiments, and validated against high-speed camera measurements. In future work, this numerical model will be employed to interrogate the mechanisms by which the elastomer coating achieves its impact mitigating effect.

2. Experimental Investigation

2.1. Methodology

Concrete cubes of side length 100 mm are mixed and cast to achieve a target mean compressive strength at 28 days of 47 MPa (typical of a normal to high strength concrete used in construction). The elastomer coating was chosen to be a commercially available spray application polyurea/polyurethane hybrid. A cylindrical, steel projectile, 28.5 mm in diameter and of mass 0.1 kg, is fired using a gas gun apparatus at the concrete cube, supported on its back face and resting atop a wooden block support. Two configurations are tested: the concrete in its uncoated configuration and the concrete coated with a 5 mm elastomer layer on its impacted face. The elastomer (which is prepared separately) is not bonded to the concrete but simply placed in frictional contact with the concrete. A range of projectile velocities are achieved between 45 and 150 m/s and the resulting damage experienced by the concrete cube is qualitatively assessed.

2.2. Results and Discussion

A qualitative assessment of the damage experienced by the concrete cubes in each configuration is described in

Table 1. Description of the damage observed in the dynamic impact tests.

Impact Velocity, m/s	Uncoated Concrete	5 mm Coated Concrete
50	Minor radial cracking.	No visible concrete or elastomer damage.
65	Extensive damage at impact site. Severe radial cracking.	No visible concrete or elastomer damage.
100	Concrete completely fragmented.	No visible concrete damage. Some evidence of elastomer tearing at impact site.
125	Concrete completely fragmented.	“Ballistic limit”. Projectile arrested by elastomer layer. Some radial concrete cracking but cube remains intact.
145	Concrete completely fragmented.	Concrete completely fragmented. Projectile penetrates elastomer forming a plug. Plug exhibits significant elastic contraction.

for the range of impact velocities tested.

An example of the recovered specimens after a projectile impact at 65 m/s are presented in Figure 1 to illustrate the marked protective benefit offered by the elastomer.

We observe a significant coating benefit across the range of velocities tested. For example, the uncoated concrete block completely fragments after it is subjected to impact velocities of 100 m/s and above, whereas the addition of a 5 mm elastomer layer results in an apparently undamaged concrete substrate for a 100 m/s impact.

3. Numerical Investigation

3.1. Numerical Model Development

A finite element (FE) model is developed in Abaqus/Explicit [8] to model the impact indentation of coated concrete cubes. To reduce computational time, an axisymmetric analysis is performed. The concrete constitutive model is chosen as the Concrete Damaged Plasticity model, scaled to match the uniaxial compressive response of the uncoated concrete cubes cast for the experimental study. The dimensions match those described in Section 2. The elastomer material model is based on a series of characteristion tests performed on samples of the same spray-on coating. We choose a hyperelastic relationship, based on the Yeoh strain energy potential and strain rate effects are accounted for by incorporating viscoelasticity using a Prony series. More details are described in [7].

3.2. Numerical Modelling Challenges

Before proceeding with the FE modelling of the dynamic tests, we first focus on the quasi-static indentation of coated and uncoated concrete cubes. The concrete, elastomer and indenter geometries match those described in Section 2. The results are presented in Figure 2 and they highlight a number of the modelling challenges encountered. These are described in more detail subsequently.

3.2.1. Mesh Sensitivity and Corner Radius

The cylindrical, steel projectile is modelled as an axisymmetric, rigid part with a small corner radius to reduce mesh sensitivity. A fine, 0.5 mm mesh is used for the concrete in the region directly under the indenter with ALE adaptive meshing employed. A 1.5 mm corner radius is chosen to ensure 3 elements span its width. The corner radius and mesh size were determined from a mesh sensitivity study.

3.2.2. Indentation Strength and Damage Response

We observe that the experimental curves exhibit post-peak catastrophic failure, in contrast to the more stable plateau observed in the numerical prediction. We believe that this is due to a limitation of the CDP model in Abaqus/Explicit [8]—severely damaged elements, which exhibit zero stiffness, cannot be deleted from the analysis. Their accumulation leads to an incorrect prediction of the post-peak, global failure response and thus, the validity of the model is questionable after the first significant load drop (plotted as a dotted line in Figure 2a).

Figure 2a also illustrates some of the challenges faced when working with a variable material such as concrete. All concrete cubes consisted of the same mix design, were cured for the same length of time, in the same conditions and were subjected to identical indentation tests. However, we observe some variability in the indentation response between specimens, particularly the indentation strength. This may be due to local effects, such as variations in the coarse aggregate distribution directly under the indentation site. Despite these challenges, the model achieves very good agreement for the indentation stiffness and a reasonable estimate for the indentation strength.

3.2.3. Contact Conditions

Details of the precise contact conditions during indentation are difficult to determine from the experiments. Good agreement with experimental data was achieved by assuming frictionless contact between steel/concrete interfaces but as Figure 2b illustrates, for elastomer/concrete interfaces, frictional effects appear to be more significant. A coefficient of friction, μ = 0.8 is implemented (a reasonable value for concrete/rubber interactions [9]) and shows excellent agreement with the experimental test.

3.2.4. Elastomer Hysteresis

The only method permitted in Abaqus/Explicit [8] for specifying elastomer hysteretic behaviour is through manipulation of the Prony parameters in the viscoelastic model definition. As has been reported in the literature [10], we find this method fails to capture the large hysteresis loop exhibited by our elastomer upon unloading. Thus, we must note this limitation on predicting the unloading response before examining the dynamic impact numerical results.

3.3. Numerical Modelling of Dynamic, Impact Indentation

The gas gun experiments, described in Section 2 are modelled in Abaqus/Explicit [8], employing the numerical model described in Section 3.2.

Figure 3 presents the numerical predictions for the projectile velocity-time histories in the 45 m/s impact tests. Comparing with the experimental measurements, obtained using the high-speed camera, we observe good agreement for the loading portion of the curve, until the time at which the projectile reaches its maximum penetration depth. As previously discussed, we fail to capture elastomer hysteresis and thus overestimate the projectile rebound velocity in the coated cases. Further, as described above, we remain cautious about interpreting our numerical results in regimes where the concrete experiences severe damage. Thus, in future work, we will use this numerical model as an analysis tool at early time steps only, to elucidate the mechanisms by which the elastomer achieves its significant impact mitigating effect.

4. Conclusions

Experimental and numerical studies are performed on the impact indentation of concrete cubes in two configurations: uncoated, and coated with a 5 mm thick, spray-on elastomer layer.

• The experimental investigation shows clearly that the presence of a thin elastomer coating can significantly reduce the damage experienced by a concrete cube subjected to projectile impact at velocities in the range 45–150 m/s.
• Quasi-static indentation experiments on coated and uncoated concrete cubes highlight some of the key challenges faced with numerical modelling of this complex problem. These include: material variability, predicting damage evolution and mesh sensitivity.
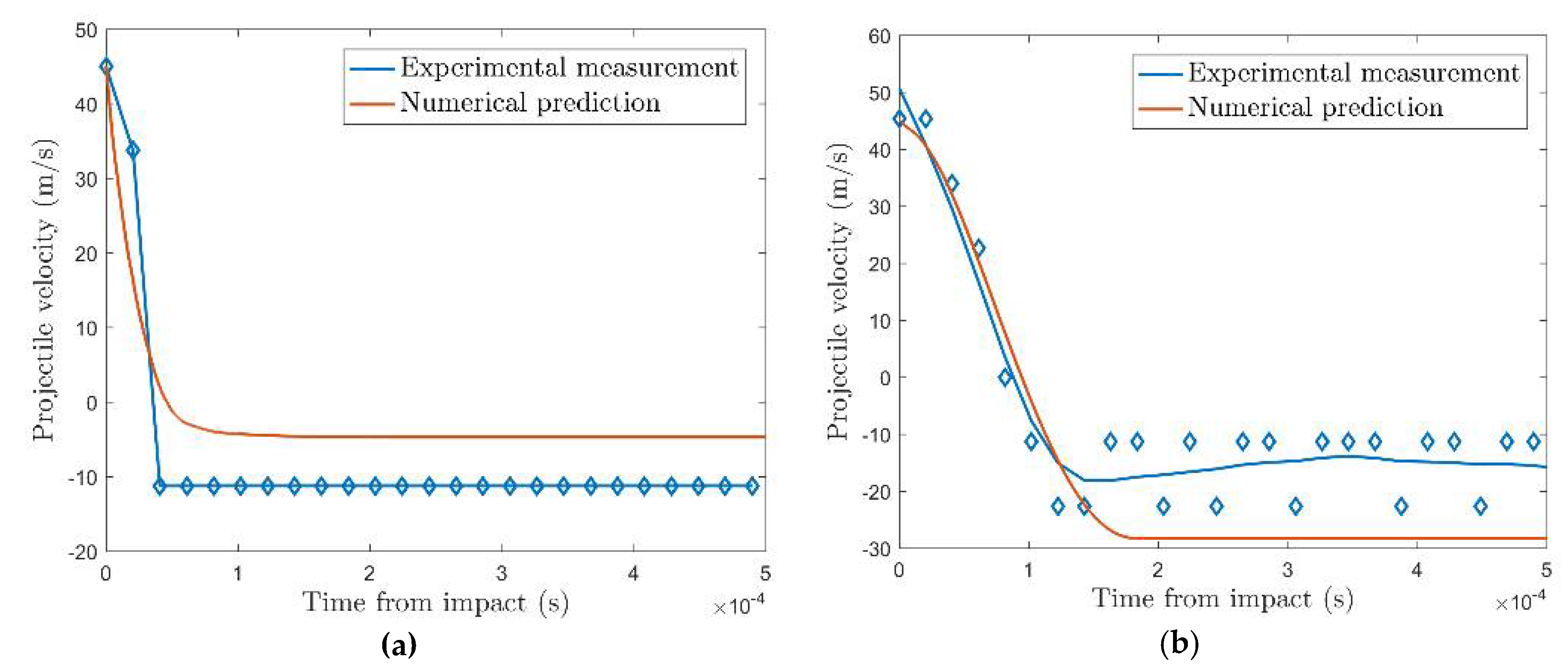
• A numerical model of the dynamic impact tests is validated against experimental measurements. Particularly good agreement is achieved for early time steps, before the concrete becomes severely damaged.
• This numerical modelling strategy provides an effective tool for studying the early stages of damage initiation and propagation. It will be employed in future work to better understand the mechanisms by which the elastomer coating achieves its mitigating effect.