Proposal to Standardize Fatigue Delamination Growth Tests Using Double Cantilever Beam Specimens without Fibre Bridging †
Abstract
:1. Introduction
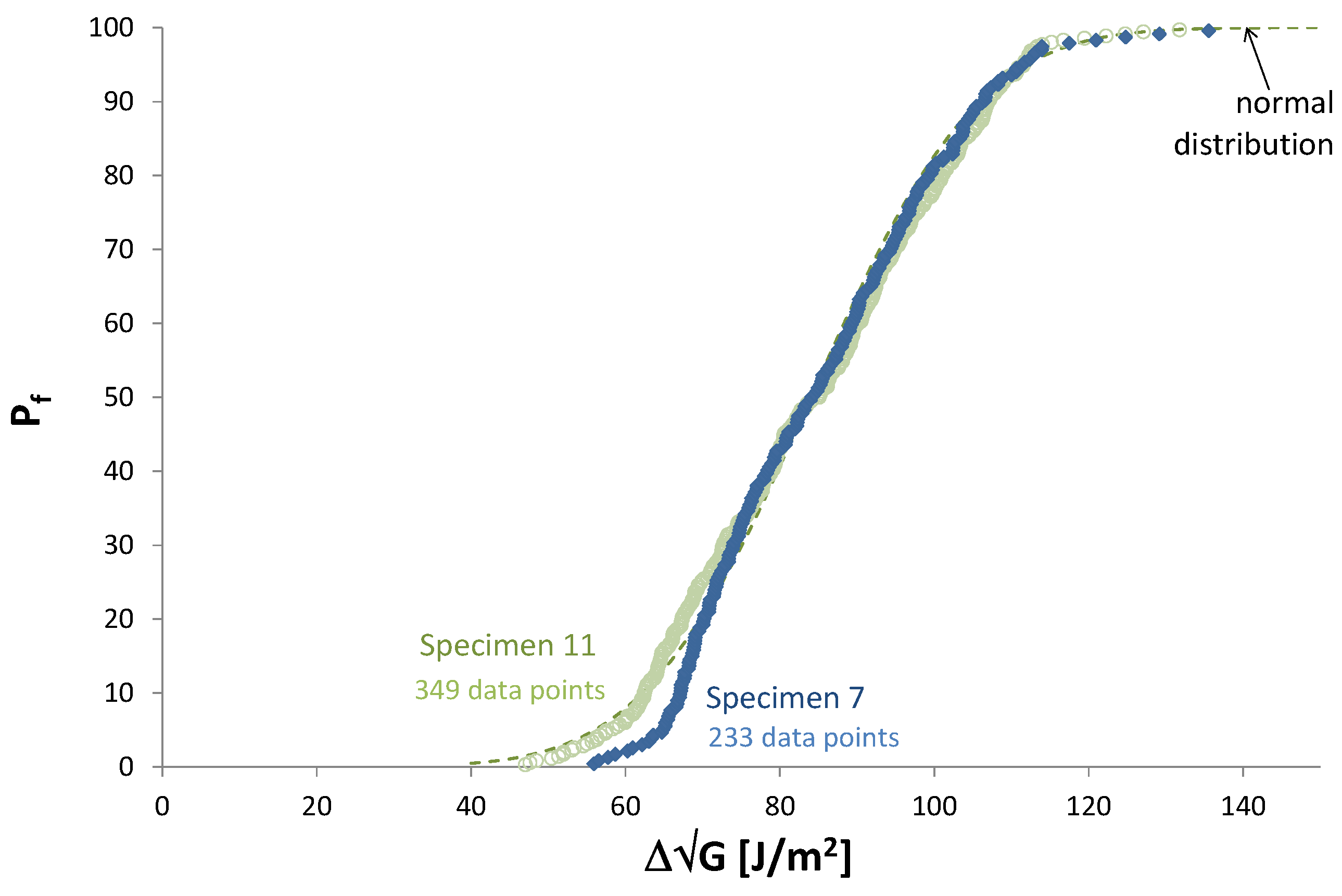
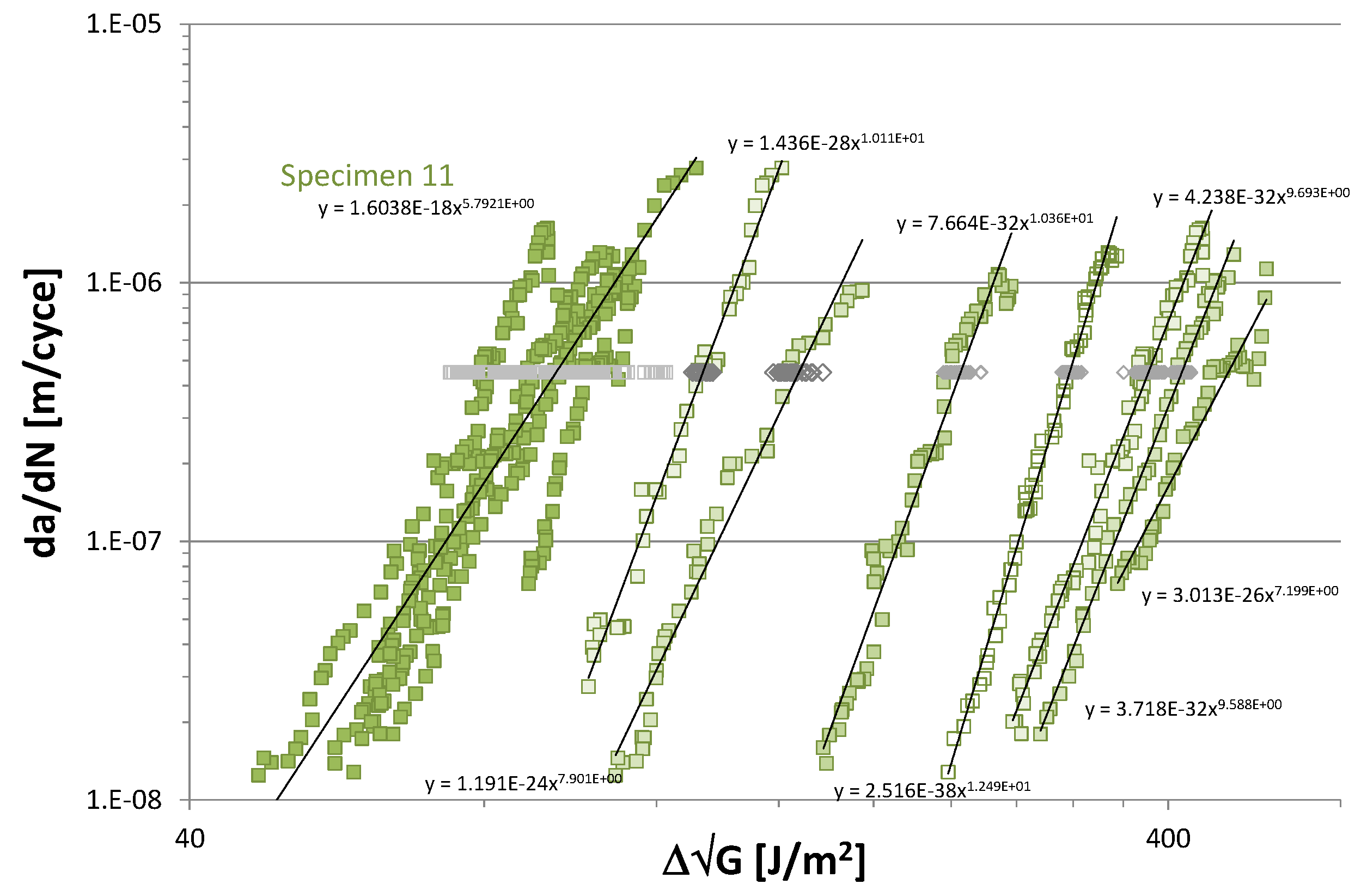
2. Problem Statement
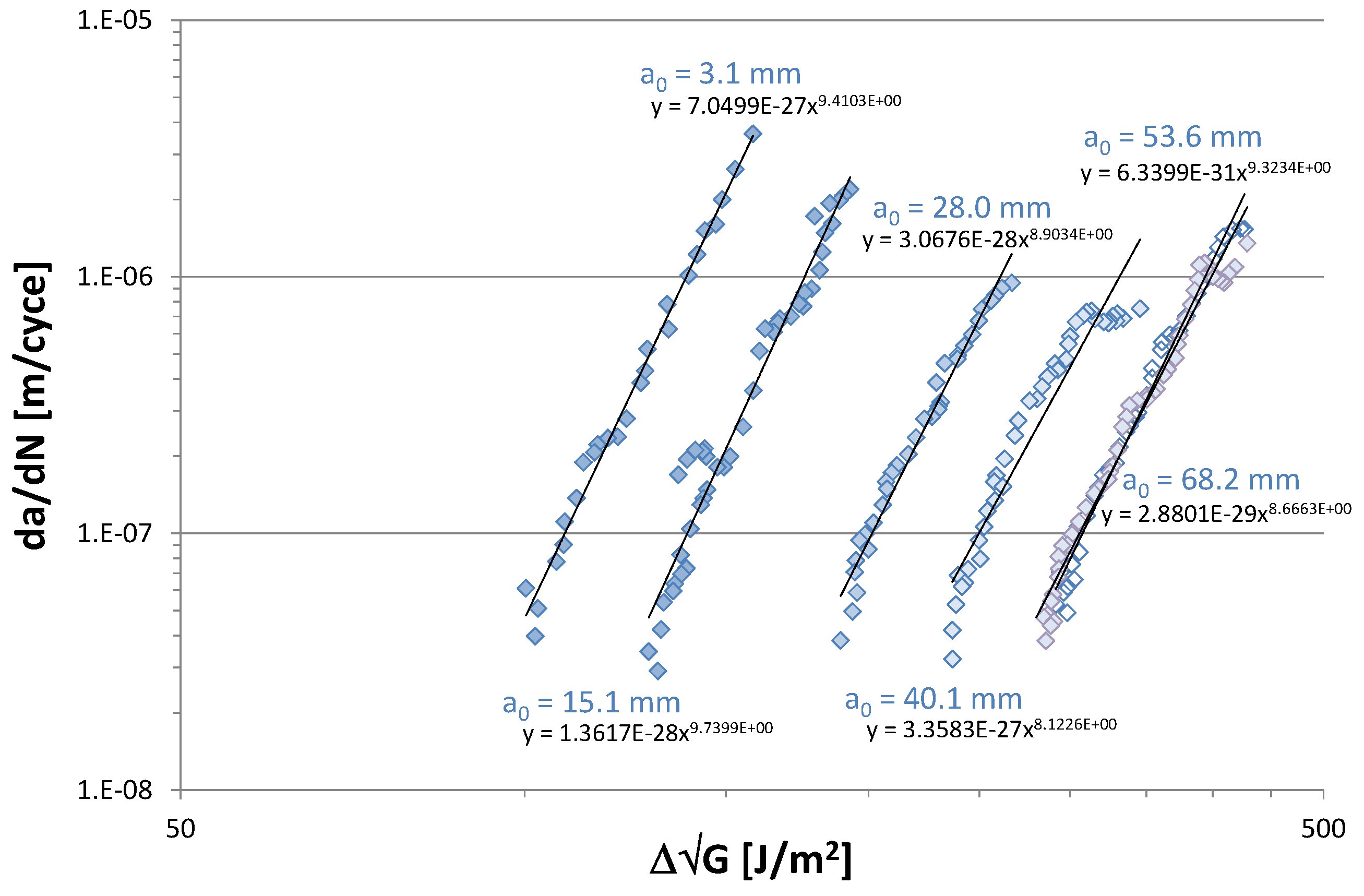
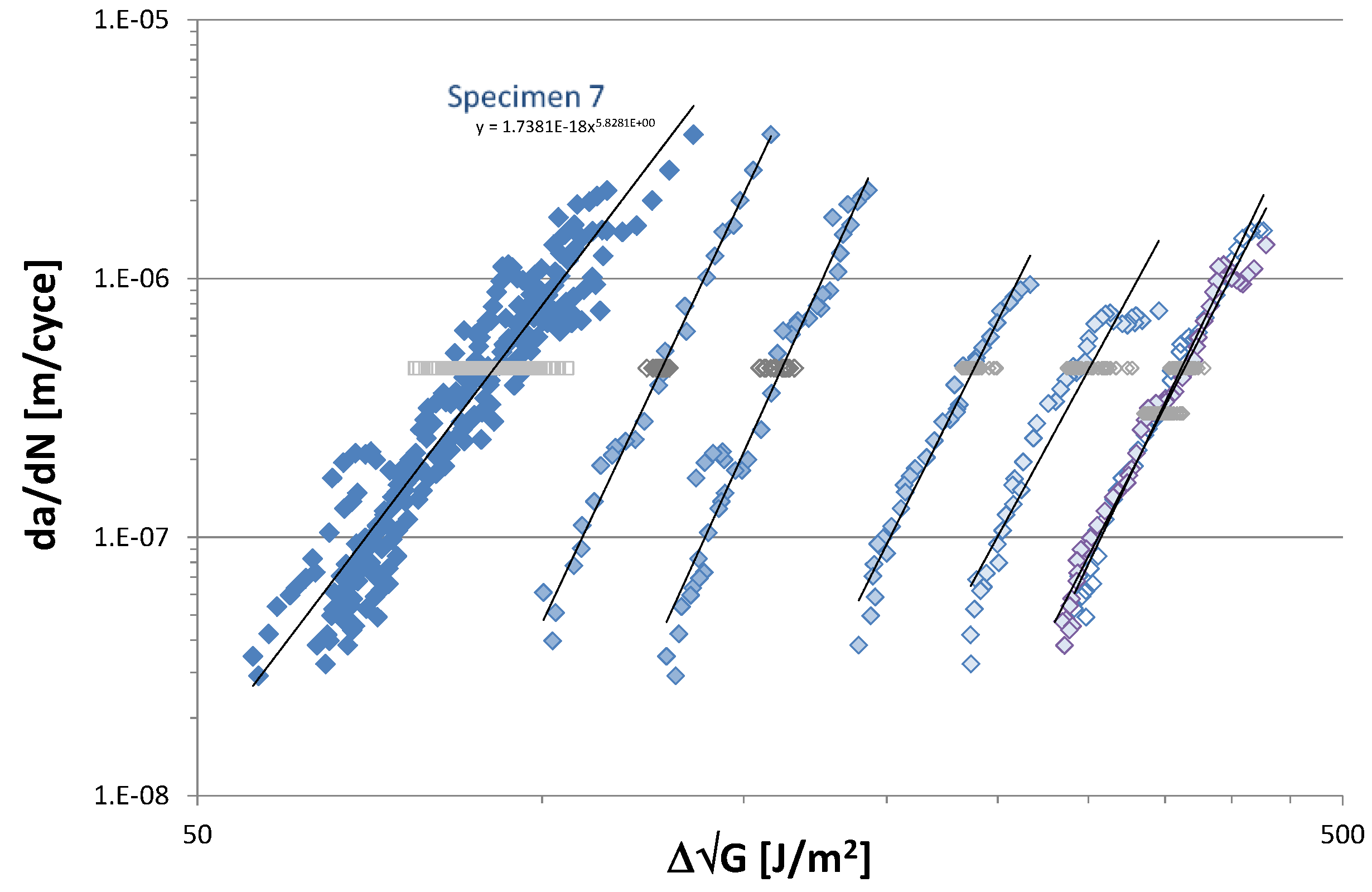
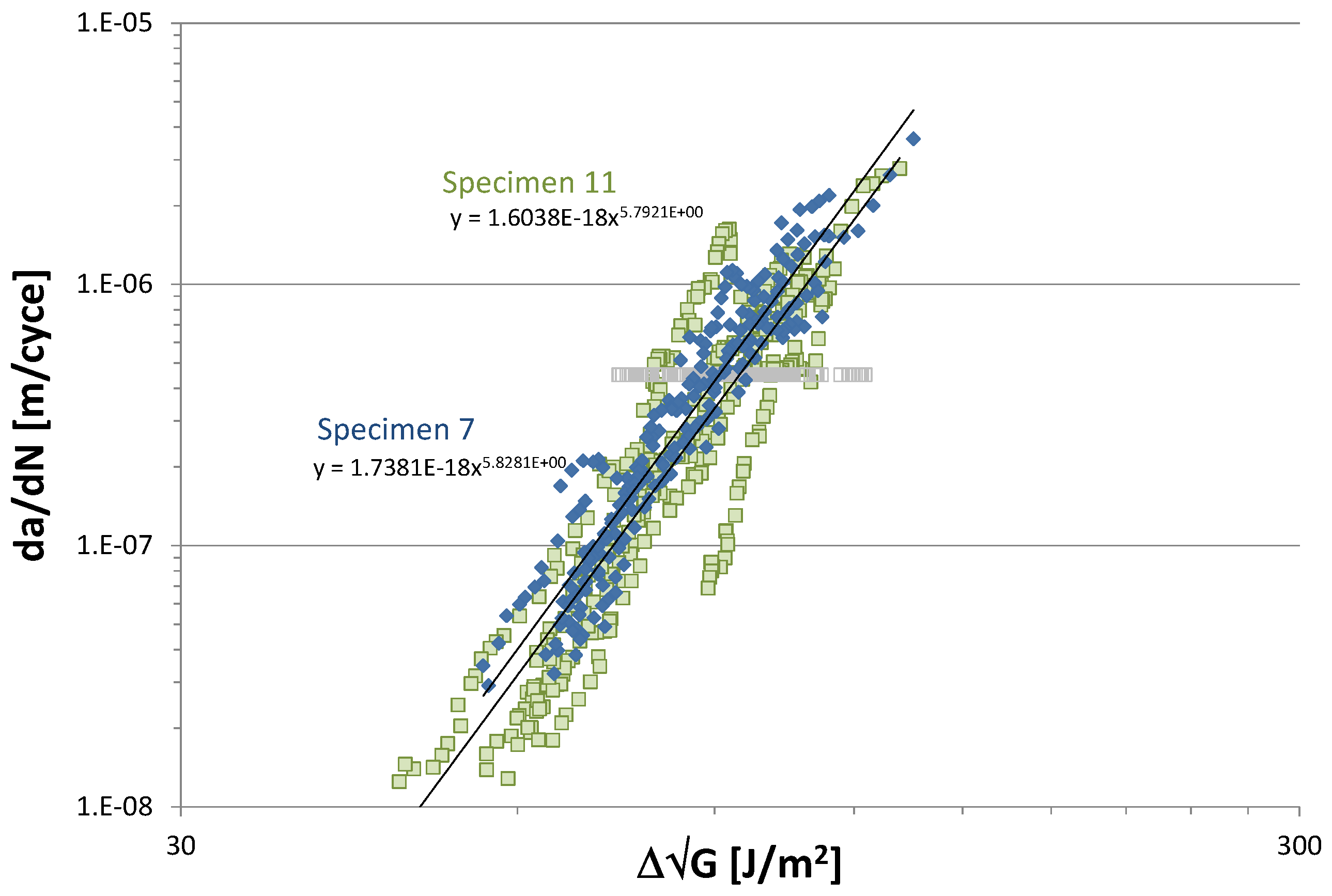
3. Proposed Experimental Procedure
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- American Society for Testing and Materials. Standard Test Method for Mode I Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites; ASTM D5528-01; ASTM: West Conshohocken, PA, USA, 1994. [Google Scholar]
- International Organization for Standardization. Fibre-Reinforced Plastic Composites—Determination of Mode I Interlaminar Fracture Toughness, GIC, for Unidirectionally Reinforced Materials; ISO 15024; ISO: Geneva, Switzerland, 2001. [Google Scholar]
- American Society for Testing and Materials. Standard Test Method for Determination of the Mode II Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites; ASTM D7905-14; ASTM: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Jones, R.; Kinloch, A.J.; Hu, W. Cyclic-fatigue crack growth in composite and adhesively-bonded structures: The FAA slow crack growth approach to certification and the problem of similitude. Int. J. Fatigue 2016, 88, 10–18. [Google Scholar] [CrossRef]
- Rans, C.D.; Alderliesten, R.C.; Benedictus, R. Misinterpreting the results: How similitude can improve our understanding of fatigue delamination growth. Compos. Sci. Technol. 2011, 71, 230–238. [Google Scholar]
- Alderliesten, R.C. How proper similitude can improve our understanding of crack closure and plasticity in fatigue. Int. J. Fatigue 2016, 82, 263–273. [Google Scholar] [CrossRef]
- Cano, A.J.; Salazar, J.A. Rodriguez, Evaluation of different crack driving forces for describing the fatigue crack growth behaviour of PET-G. Int. J. Fatigue 2018, 107, 27–32. [Google Scholar] [CrossRef]
- Jones, R.; Kinloch, A.J.; Yao, L.; Alderliesten, R.C. Delamination Fatigue Growth in Polymer-Matrix Fibre Composites: A Methodology for Determining the Design and Lifing Allowables. Compos. Struct. 2018. under review. [Google Scholar]
- Sørensen, B.F.; Jacobsen, T.K. Large-scale bridging in composite: R-curves and bridging laws. Compos. Part A 1998, 29, 1443–1451. [Google Scholar] [CrossRef]
- Jacobsen, T.K.; Sørensen, B.F. Mode I intra-laminar crack growth in composites-modelling of R-curves from measured bridging laws. Compos. Part A 2001, 32, 1–11. [Google Scholar] [CrossRef]
- Gregory, J.R.; Spearing, S.M. A fibre bridging model for fatigue delamination in composite materials. Acta Mater. 2004, 52, 5493–5502. [Google Scholar] [CrossRef]
- Yao, L.; Alderliesten, R.C.; Zhao, M.; Benedictus, R. Discussion on the use of the strain energy release rate for fatigue delamination characterization. Compos. Part A 2014, 66, 65–72. [Google Scholar] [CrossRef]
- Yao, L.; Alderliesten, R.C. Mode I Fatigue Delamination Growth in Composite Laminates with Fibre Bridging–Datasets, Collection of Datasets; TU Delft: Delft, The Netherlands, 2014. [Google Scholar]
- Van Lipzig, H. Spreiding bij Vermoeiing en Levensduur, Hoofdstuk 12 PAO cursus Vermoeiing van Constructies, PAO Techniek en Management, Delft. Available online: https://paotm.nl/nl/cursus/vermoeiing-van-constructies/?interest=431 (accessed on 24 May 2018). (in Dutch).
- Yao, L.; Alderliesten, R.C.; Zhao, M.; Benedictus, R. Bridging effect on mode I fatigue delamination behavior in composite laminates. Compos. Part A 2014 63, 101–109. [CrossRef]
- Yao, L.; Alderliesten, R.C.; Benedictus, R. The effect of fibre bridging on the Paris relation for mode I fatigue delamination growth in composites. Compos. Struct. 2016, 140, 125–135. [Google Scholar] [CrossRef]
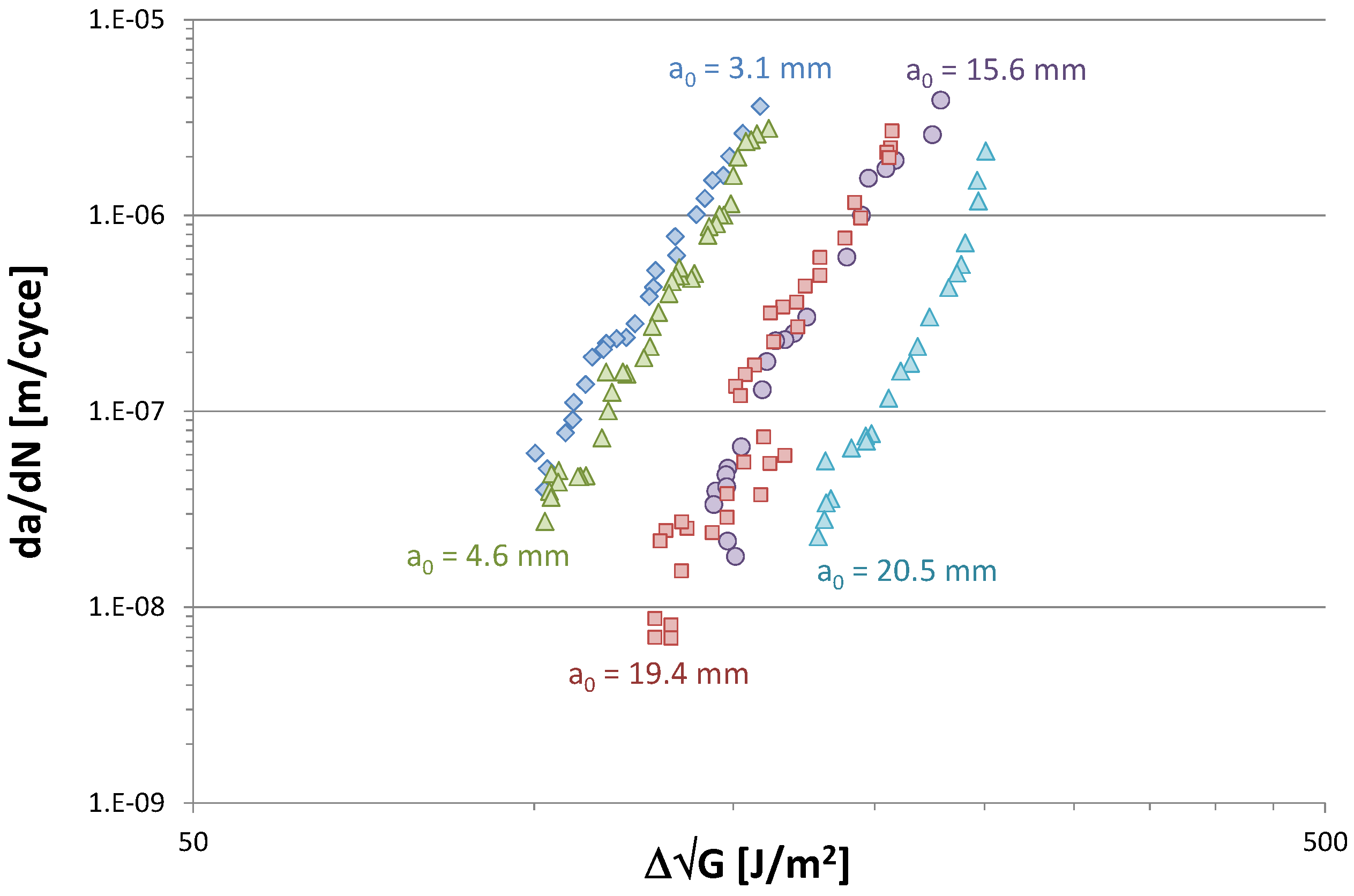

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alderliesten, R. Proposal to Standardize Fatigue Delamination Growth Tests Using Double Cantilever Beam Specimens without Fibre Bridging. Proceedings 2018, 2, 385. https://doi.org/10.3390/ICEM18-05194
Alderliesten R. Proposal to Standardize Fatigue Delamination Growth Tests Using Double Cantilever Beam Specimens without Fibre Bridging. Proceedings. 2018; 2(8):385. https://doi.org/10.3390/ICEM18-05194
Chicago/Turabian StyleAlderliesten, René. 2018. "Proposal to Standardize Fatigue Delamination Growth Tests Using Double Cantilever Beam Specimens without Fibre Bridging" Proceedings 2, no. 8: 385. https://doi.org/10.3390/ICEM18-05194
APA StyleAlderliesten, R. (2018). Proposal to Standardize Fatigue Delamination Growth Tests Using Double Cantilever Beam Specimens without Fibre Bridging. Proceedings, 2(8), 385. https://doi.org/10.3390/ICEM18-05194