Attitude Estimation of Skis in Ski Jumping Using Low-Cost Inertial Measurement Units ^†

Abstract

This paper presents an approach to estimate the attitude of skis for an entire ski jump using wearable, MEMS-based, low-cost Inertial Measurement Units (IMUs). First of all, a kinematic attitude model based on rigid-body dynamics and a sensor error model considering bias and scale factor error are established. Then, an extended Rauch-Tung-Striebel (RTS) smoother is used to combine measurement data provided by both gyroscope and magnetometer to achieve an attitude estimation. Moreover, parameters for the bias and scale factor error in the sensor error model and the initial attitude are determined via a maximum-likelihood principle based parameter estimation algorithm. By implementing this approach, an attitude estimation of skis is achieved without further sensor calibration. Finally, results based on both the simulated reference data and the real experimental measurement data are presented, which proves the practicability and the validity of the proposed approach.

1. Introduction

Nowadays, IMUs based on Micro-Electro-Mechanical Systems (MEMS) are becoming quite competitive solutions in sports applications for motion measurements. This is due to their relatively low price, wearability, and convenience to set up. In the ski jumping field, there are researchers who made big efforts in applying IMU measurements to ski jumping studies. Chardonnens et al. [1] built an IMU-based system to successfully measure the three-dimensional kinematics for ski jumpers. Logor et al. [2] attached 10 IMUs on different body segments and measured the ski jumpers’ movement. Moreover, they also calculated forces and moments acting on the joints. Brock et al. [3] developed an inertial motion capture system for ski jumpers, based on processing the IMU raw data using a complementary filter.

When using low-cost IMUs, it is common that sensors are affected by large sensor errors. Most obvious among them are bias and scale factor errors. In the previous mentioned studies, the experiments explicitly included calibration procedures so that sensor errors are already removed or minimized before data processing. However, in some cases, measurements are performed without knowing these effects in advance, resulting in raw data with significant errors. Also, the error in the measurements can adversely influence the initial attitude estimation. In addition, for low-cost IMUs, these sensor error parameters may be slowly time-varying and changed for another turn-on, which renders calibrations after the experiment meaningless.

In this paper, a method to post-processing the IMU raw data without calibration is proposed by estimating the gyroscope’s bias and the scale factor error and bias of the magnetometer through the filter error method for parameter estimation. The extended Rauch-Tung-Striebel (RTS) smoother, which is embedded in the method, is also able to estimate the attitude of the skis by combining gyroscope and magnetometer measurements.

2. Problem Formulation

2.1. Attitude Kinematic Equations

In this paper, we choose Euler angles in z-y-x rotation sequence from the local earth frame(I), fixed to the jumping hill, which is considered ‘inertial’ for our application, to the ski body fixed frame (B): the yaw angle $\psi$, the pitch angle $\theta$, and the roll angle $\varphi$ as our attitude parameters. The IMUs are mounted on both skis close to the bindings. Thus, the propagation equation of attitude kinematics for Euler angles is

$$\left[\begin{array}{c}\dot{\varphi }\\ \dot{\theta }\\ \dot{\psi }\end{array}\right]=\left[\begin{array}{ccc}1& \sin \left(\varphi \right)\tan \left(\theta \right)& \cos \left(\varphi \right)\tan \left(\theta \right)\\ 0& \cos \left(\varphi \right)& -\sin \left(\varphi \right)\\ 0& \sin \left(\varphi \right)/\cos \left(\theta \right)& \cos \left(\varphi \right)/\cos \left(\theta \right)\end{array}\right]{\left({\mathit{\omega }}_{\mathrm{K}}^{\mathrm{IB}}\right)}_{\mathrm{B}}.$$

(1)

where ${\left({\mathit{\omega }}_{\mathrm{K}}^{\mathrm{IB}}\right)}_{\mathrm{B}}={\left[\begin{array}{ccc}{\left({\omega }_{\mathrm{x},\mathrm{K}}^{\mathrm{IB}}\right)}_{\mathrm{B}}& {\left({\omega }_{\mathrm{y},\mathrm{K}}^{\mathrm{IB}}\right)}_{\mathrm{B}}& {\left({\omega }_{\mathrm{z},\mathrm{K}}^{\mathrm{IB}}\right)}_{\mathrm{B}}\end{array}\right]}^{\mathrm{T}}$ is the angular velocity denoted in the body frame.

2.2. Sensor Error Models

The inertial measurement data are considered to exhibit zero-mean, white, additive Gaussian noise. Also, when employing MEMS-based low-cost IMUs, a way to model sensors errors is to consider biases and sometimes also scale factor errors. Due to the short time span under our investigation, those are considered constant.

For gyroscope measurements ${\left({\tilde{\mathit{\omega }}}_{\mathrm{K}}^{\mathrm{IB}}\right)}_{\mathrm{B}}$, we consider measurement noise ${\mathit{w}}_{\mathrm{rot}}$ and a constant bias $\mathsf{\Delta }\mathit{\omega }={\left[\begin{array}{ccc}\mathsf{\Delta }{\omega }_x& \mathsf{\Delta }{\omega }_y& \mathsf{\Delta }{\omega }_z\end{array}\right]}^T$ involved in the measurements

$${\left({\tilde{\mathit{\omega }}}_{\mathrm{K}}^{\mathrm{IB}}\right)}_{\mathrm{B}}={\left({\mathit{\omega }}_{\mathrm{K}}^{\mathrm{IB}}\right)}_{\mathrm{B}}+\mathsf{\Delta }\mathit{\omega }+{\mathit{w}}_{\mathrm{rot}},$$

(2)

For the magnetometer measurement data ${\left(\tilde{\mathit{m}}\right)}_{\mathrm{B}}$, in addition to the measurement noise ${\mathit{v}}_{\mathrm{mag} }$ and the bias $\mathsf{\Delta }\mathit{m}$, we consider a magnetometer scale factor error

$${\left(\tilde{\mathit{m}}\right)}_{\mathrm{B}}=\left({\mathit{I}}_3+{\mathit{K}}_{\mathrm{m}}\right){\left(\mathit{m}\right)}_{\mathrm{B}}+\mathsf{\Delta }\mathit{m}+{\mathit{v}}_{\mathrm{mag}},$$

(3)

where ${\left(\mathit{m}\right)}_{\mathrm{B}}={\left[\begin{array}{ccc}{\left(m_x\right)}_B& {\left(m_y\right)}_B& {\left(m_z\right)}_B\end{array}\right]}^T$ is the actual magnetic strength vector denoted in the body frame; ${\mathit{I}}_3$ is a 3-by-3 identity matrix; and, ${\mathit{K}}_{\mathrm{m}}=diag\left(\left[\begin{array}{ccc}{K}_{\mathrm{m},\mathrm{x}}& K_{\mathrm{m},\mathrm{y}}& K_{\mathrm{m},\mathrm{z}}\end{array}\right]\right)$ is the magnetometer’s scale factor error matrix.

2.3. System Equations

In general, the nonlinear system equations with process noise $\mathit{w}$ and measurement noise $\mathit{v}$ are

$$\dot{\mathit{x}}\left(\mathit{t}\right)=\mathit{f}\left[\mathit{x}\left(\mathit{t}\right),\hspace{0.17em}\mathit{u}\left(\mathit{t}\right),\hspace{0.17em}\mathit{\Theta },\mathit{w}\left(\mathit{t}\right)\right],$$

(4)

$$\mathit{y}\left(t\right)=\mathit{g}\left[\mathit{x}\left(t\right),\hspace{0.17em}\mathit{u}\left(t\right),\hspace{0.17em}\mathit{\Theta }\right],$$

(5)

$$\mathit{z}\left({\mathit{t}}_{\mathit{k}}\right)=\mathit{y}\left({\mathit{t}}_{\mathit{k}}\right)+\mathit{v}\left({\mathit{t}}_{\mathit{k}}\right).$$

(6)

In our case, we choose system states as $\mathit{x}={\left[\begin{array}{ccc}\varphi & \theta & \psi \end{array}\right]}^T$. The gyroscope measurements serve as system inputs $\mathit{u}={\left[\begin{array}{ccc}{\left({\tilde{\omega }}_{\mathrm{x},\mathrm{K}}^{\mathrm{IB}}\right)}_{\mathrm{B}}& {\left({\tilde{\omega }}_{\mathrm{y},\mathrm{K}}^{\mathrm{IB}}\right)}_{\mathrm{B}}& {\left({\tilde{\omega }}_{z,\mathrm{K}}^{\mathrm{IB}}\right)}_{\mathrm{B}}\end{array}\right]}^T$, the gyroscope biases still need to be corrected for further calculation so that we rewrite Equation (2) as ${\left({\mathit{\omega }}_{\mathrm{K}}^{\mathrm{IB}}\right)}_{\mathrm{B}}={\left({\tilde{\mathit{\omega }}}_{\mathrm{K}}^{\mathrm{IB}}\right)}_{\mathrm{B}}-\mathsf{\Delta }\mathit{\omega }-{\mathit{w}}_{\mathrm{rot}}$. The parameters to be estimated are $\mathit{\Theta }={\left[\begin{array}{cc}\begin{array}{cc}\begin{array}{cc}\begin{array}{cc}{\varphi }_0& {\theta }_0\end{array}& \begin{array}{cc}{\psi }_0& \mathsf{\Delta }{\omega }_x\end{array}\end{array}& \begin{array}{cc}\begin{array}{cc}\mathsf{\Delta }{\omega }_y& \mathsf{\Delta }{\omega }_z\end{array}& \begin{array}{cc}\mathsf{\Delta }{m}_x& \mathsf{\Delta }{m}_y\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{cc}\mathsf{\Delta }{m}_z& K_{\mathrm{m},\mathrm{x}}\end{array}& \begin{array}{cc}{K}_{\mathrm{m},\mathrm{y}}& K_{\mathrm{m},\mathrm{z}}\end{array}\end{array}\end{array}\right]}^T$ where ${\varphi }_0$, ${\theta }_0$, and ${\psi }_0$ are the initial attitude. $\mathit{y}={\left[\begin{array}{ccc}\begin{array}{cc}\varphi & \theta \end{array}& \begin{array}{cc}\psi & {\left({\widehat{m}}_x\right)}_B\end{array}& \begin{array}{cc}{\left({\widehat{m}}_y\right)}_B& {\left({\widehat{m}}_z\right)}_B\end{array}\end{array}\right]}^T$are the system outputs, where ${\left(\widehat{\mathit{m}}\right)}_{\mathrm{B}}=\left({\mathit{I}}_3+{\mathit{K}}_{\mathrm{m}}\right){\left(\mathit{m}\right)}_{\mathrm{B}}+\mathsf{\Delta }\mathit{m}$. For a certain date and place, the magnetic strength vector in the local north-east-down frame ${\left(\mathit{m}\right)}_{\mathrm{N}}$ is a constant, which can be calculated by The World Magnetic Model 2015 [4]. Furthermore, we can link ${\left(\mathit{m}\right)}_{\mathrm{N}}$ with the outputs ${\left(\mathit{m}\right)}_B$ by the transformation matrices, as${\left(\mathit{m}\right)}_B={\left[\begin{array}{ccc}{\left({\widehat{m}}_x\right)}_B& {\left({\widehat{m}}_y\right)}_B& {\left({\widehat{m}}_z\right)}_B\end{array}\right]}^T={\mathit{M}}_{\mathit{B}\mathit{I}}\left(\varphi ,\theta ,\psi \right)·{\mathit{M}}_{\mathit{I}\mathit{N}}·{\left(\mathit{m}\right)}_{\mathrm{N}}$, where ${\mathit{M}}_{\mathit{I}\mathit{N}}$ is a constant transformation matrix from the local north-east-down frame to the inertial frame. Accordingly, the system measurements are $\mathit{z}={\left[\begin{array}{ccc}\begin{array}{cc}\tilde{\varphi }& \tilde{\theta }\end{array}& \begin{array}{cc}\tilde{\psi }& {\left({\tilde{m}}_x\right)}_B\end{array}& \begin{array}{cc}{\left({\tilde{m}}_y\right)}_B& {\left({\tilde{m}}_z\right)}_B\end{array}\end{array}\right]}^T$, where $\tilde{\varphi }$, $\tilde{\theta }$, and $\tilde{\psi }$ are the pseudo attitude measurements which will be introduced in Section 3.2.

3. Methods

3.1. Extended Rauch-Tung-Striebel Smoother

The Extended RTS smoother is a batch state estimation method for post-processing applications. It contains the Extended Kalman Filter (EKF) as a forward filter and combines it with a backward and smoothing pass to not only use the measurements before the current estimation point as EKF but also the measurements in the future to further improve the estimation quality. More detailed descriptions can be found in [5,6]. For the sake of brevity, the governing EKF equations for the forward pass are omitted. After executing the forward filtering, the smoother runs backward in time $k=N-1,\dots ,0$ with

$${\mathit{K}}_{\mathrm{k}}^{\mathrm{s}}={\mathit{P}}_{k|k}^f{\mathit{\Phi }}_k^{\mathrm{T}}{\left({\mathit{P}}_{k+1|k}^f\right)}^{-1},$$

(7)

$${\widehat{\mathit{x}}}_k^s={\widehat{\mathit{x}}}_{k|k}^f+{\mathit{K}}_{\mathrm{k}}^{\mathrm{s}}\left({\widehat{\mathit{x}}}_{k+1}^s+{\widehat{\mathit{x}}}_{k+1|k}^f\right) \mathrm{with} {\widehat{\mathit{x}}}_N^s={\widehat{\mathit{x}}}_{N|N}^f,$$

(8)

$${\mathit{P}}_k^s={\mathit{P}}_{k|k}^f-{\mathit{K}}_k^s\left({\mathit{P}}_{k+1|k}^f-{\mathit{P}}_{k+1}^s\right) \mathrm{with} {\mathit{P}}_N^s={\mathit{P}}_{N|N}^f,$$

(9)

where the superscript f denotes the variables, which were stored during the forward pass, the superscript s denotes the smoother variables. The subscript k indicates the time step, and the subscript with format $i|j$ is to be read as “the estimation at time i using information up to time j”. $\widehat{\mathit{x}}$ denotes the state estimate, and $\mathit{P}$ is the covariance matrix of the state estimation error. $N$stands for the total number of measurement time points.

3.2. Pseudo Attitude Measurements

When estimating the initial attitude by using magnetometer measurements with sensor errors involved, it will be difficult to distinguish the influence of the initial attitude and the magnetometer bias. To solve this problem, we propose to use also the geometrical shape information of the in-run as pseudo attitude measurements to improve the parameter estimation result.

The construction of the in-run is standardized and parameterized by [7]. Thus, we know that, from the starting point of the jump until the beginning of the in-run transition curve (the in-run ramp), the trajectory has to follow a straight line with a gradient angle $\gamma$; on the take-off table, there has to be a second straight part with a gradient angle $\alpha$. The value of $\gamma$ and $\alpha$ can be found out in the jumping hill certificate for each certified hill, such as in [8]. Also, for ski jumping in the in-run phase, the skis always move along the in-run track. Therefore, we can assume that the pseudo pitch angle during two straight part is around $\tilde{\mathsf{\theta }}=-\gamma \left(in-run ra\mathit{m}p\right)$ and $\tilde{\mathsf{\theta }}=-\alpha \left(take-off table\right)$ respectively, and both pseudo roll, and yaw angle are approximately $\tilde{\varphi }= \tilde{\mathsf{\psi }}=0^{\circ } \left(entire in-run\right)$.

3.3. Maximum-Likelihood Principle Based Parameter Estimation

With the system equations in Section 2.3, we can now formulate the original problem into a parameter estimation problem using the filter error method with internal RTS smoother. The filter error method is based on the maximum likelihood principle, which considers the probability of obtaining the measurements, given a set of parameters. The maximum likelihood parameter estimates are then those parameter values, which maximize this probability. Detailed descriptions of the classic maximum-likelihood parameter estimation methods can be found in [9].

After introducing pseudo attitude measurements, the cost function needs to be modified to adapt to the character of the attitude pseudo measurements, since they are only valid for parts of a jump and absent otherwise. Thus, at different time instants, the number of available measurements varies. To solve this problem, we propose to divide the entire time frame into different phases, where, within one phase the number of available measurements is constant; different phases still share the same parameters.

Then, we can treat each phase as a sub-problem that is optimized using a maximum likelihood-like principle. Therefore, we have the modified cost function to be minimized as

$$J=\sum _{i=1}^{N_{Phases}}{J}_i\left(\mathit{\Theta },\hspace{0.17em}{\mathit{R}}_i\right)=\sum _{i=1}^{N_{Phases}}\left\{\frac{1}{2}\sum _{k=1}^{N_i}\left[{\left({\mathit{z}}_{i,k}-{\widehat{\mathit{y}}}_{i,k}\right)}^{\mathrm{T}}{\mathit{R}}_i^{-1}\left({\mathit{z}}_{i,k}-{\widehat{\mathit{y}}}_{i,k}\right)\right]+\frac{N_i}{2}ln\left|{\mathit{R}}_i\right|+\frac{N_i{n}_{y,i} }{2}ln\left(2\pi \right)\right\}$$

(10)

where $N_{Phases}$ is the total number of the phases; $N_i$ is the total number of the time points in phase i; $n_{y,i}$ is the number of outputs for phase i; ${\widehat{\mathit{y}}}_{i,k}$ is the estimated system output by the extended RTS smoother; ${\mathit{R}}_i$is an estimate of the covariance matrix of the residual ${\mathit{r}}_{i,k}={\mathit{z}}_{i,k}-{\widehat{\mathit{y}}}_{i,k}$ for phase i, which is calculated separately as

$${\mathit{R}}_i=\frac{1}{N_i}\sum _{k=1}^{N_i}\left[{\mathit{z}}_{i,k}-{\widehat{\mathit{y}}}_{i,k}\left(\mathit{\Theta }\right)\right]{\left[{\mathit{z}}_{i,k}-{\widehat{\mathit{y}}}_{i,k}\left(\mathit{\Theta }\right)\right]}^{\mathrm{T}}$$

(11)

With cost function (10), the estimated parameters can be calculated iteratively by using numerical optimization methods, such as Gauss-Newton or Levenberg-Marquardt, with

$$\frac{\partial J}{\partial \mathit{\Theta }}=\sum _{i=1}^{N_{Phases}}\frac{\partial J_i\left(\mathit{\Theta },\hspace{0.17em}{\mathit{R}}_i\right)}{\partial \mathit{\Theta }}=\sum _{i=1}^{N_{Phases}}\left\{\sum _{k=1}^{N_i}{\left(\frac{\partial {\widehat{\mathit{y}}}_k}{\partial \mathit{\Theta }}\right)}^{\mathrm{T}}{\mathit{R}}_i^{-1}\left({\mathit{z}}_k-{\widehat{\mathit{y}}}_k\right)\right\}$$

(12)

$$\frac{{\partial }^{2}J}{\partial {\mathit{\Theta }}^2}=\sum _{i=1}^{N_{Phases}}\frac{{\partial }^2{J}_i\left(\mathit{\Theta },\hspace{0.17em}{\mathit{R}}_i\right)}{\partial {\mathit{\Theta }}^2}=\sum _{i=1}^{N_{Phases}}\left\{\sum _{k=1}^{N_i}{\left(\frac{\partial {\widehat{\mathit{y}}}_k}{\partial \mathit{\Theta }}\right)}^{\mathrm{T}}{\mathit{R}}_i^{-1}\left(\frac{\partial {\widehat{\mathit{y}}}_k}{\partial \mathit{\Theta }}\right)\right\}$$

(13)

3.4. Initial Guess for the Gyroscope Bias

During the implementation, we found that the algorithm is very sensitive to the initial guess of the gyroscope bias. Normally, ski jumpers will take off the ski after the jump and put them on the ground for few seconds. During this time, the skis can be considered in a static state. These parts of the time-series are easily identified in the data. Since the angular velocity should be zero in a steady state, we choose the mean value of the gyroscope in three axes as the initial guess for the gyroscope bias, which should be close to the true value.

4. Results and Discussion

4.1. Simulation-Based Result

To validate the algorithm, a set of simulated data was generated, based on the results using the real measurement data. Thus, the simulated date set share the typical angular movements of the skis as the real case. Sensor errors and zero-mean, normally distributed, white noise are added to the calculated reference angular velocity and magnetic data to generate artificial gyroscope and magnetometer measurements for estimation.

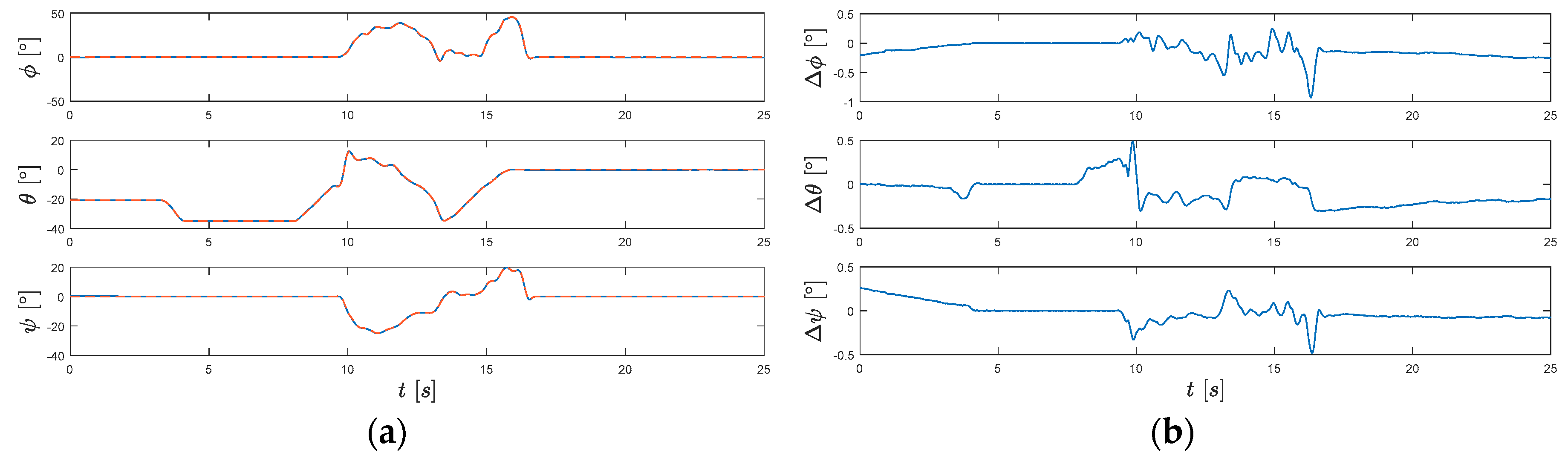
The estimation result for simulation data can be seen in Figure 1. In this case, the noise added to the gyroscope and magnetometer are with standard deviations of 0.05 rad/s and 1 microtesla (µT) respectively, and the noise matrices in the extended RTS smoother are set accordingly. The initial state error covariance matrix is set as $P_0={10}^{-9}·{\mathit{I}}_3$, since the initial value are already set to their estimated parameter values. The relative deviations of the estimated sensor error parameters are defined as $\left|\left({\widehat{\mathit{\Theta }}}_i-{\mathit{\Theta }}_i\right)/ {\mathit{\Theta }}_i\right|$, where ${\widehat{\mathit{\Theta }}}_i$ are the parameters’ estimation values, and ${\mathit{\Theta }}_i$ are the true values. The maximal relative deviation in this case is 5.21% in $\mathsf{\Delta }{m}_z$, and the relative deviation for the gyroscope biases are all less than 1%. In Figure 1a, the estimated attitude shows a nice fit with the created reference. Furthermore, from Figure 1b, we can see that the attitude estimation errors are all smaller than 1 degree in this case. This result indicates that the algorithm is valid for estimating the sensor error parameters and the attitude of the skis.

4.2. Real Measurement Based Result

The real measurement data is recorded during summer training season for young athletes on the Adlerschanze (HS108) [8] in Hinterzaten, Germany. The IMUs comprise of the following sensors: (1) gyroscope: InvenSense ITG-3200; (2) accelerometer: Analog Devices ADXL345; and (3) magneto-meter: Honeywell HMC5883L and record data at a frequency of 100 Hz. For each jumper, two IMUs are attached to the skis behind the bindings. The attitude estimation result based on the real measurement data can be found in Figure 2.

The extended RTS smoother noise covariance matrices, as well as initial conditions were turned to obtain a good fit. The initial guess for gyroscope bias is set as in Section 3.4, and the initial guesses for other sensor error parameters are all set to 0. The result fits nicely with both the pseudo attitude measurements and the magnetic field strength. Figure 2a shows the attitude estimation result of both skis, in which each phase of the jump, including the in-run, flying phase, landing, and outrun, can be clearly distinguished. Additionally, during flying phase, we can see slightly asymmetry movement of the skis. For brevity reasons, in Figure 2b,c only shows the result of the left ski. Comparing to the simulation-based case, there is more noise from the vibration of skis involved, which can be seen in both gyroscope and magnetometer measurements. The estimated relative standard deviation of the sensor error parameters, which is based on the Cramer Rao bounds [9], shows a good estimation quality. This result demonstrates the validity of the proposed method.

5. Conclusions

In this paper, an approach to post-processing raw IMU data is presented, which is able to achieve a solid attitude estimation of the skis even in the absence of calibration values. According to the result on the simulated reference data, the algorithm can successfully estimate the sensor error parameters as well as the initial attitude. Furthermore, it has been successfully applied to real measurement data.