Abstract
The objective of this study was to construct a finite element model for a carbon fiber reinforced plastic club shaft, and to investigate the effects of the torsional stiffness of the shaft on the dynamic behavior of a golf club during the swing. Mechanical properties of the shaft with orthotropic elasticity were determined using the rule of mixture which was defined by a volume fraction of fiber and resin. Swing simulations were conducted using club models with different torsional stiffness. The effect of the torsional stiffness on the clubhead alignment at impact tended to be stronger with the impact velocity of the clubhead due to the centrifugal force acting on the head. This indicates that the clubhead alignment at impact tends to be subject to effects of the timing of the impact, which depends on the relationship between the ball position and the impact velocity in addition to the mechanical properties of the shaft.
1. Introduction
For a design and development of club, a prediction and evaluation of club performance are in demand. Golf robots are widely used by manufacturers to evaluate golf equipment. One of the advantages of a robot is that it produces a repeatable swing. On the other hand, one of the disadvantages of robot tests is the need for the production of a prototype club for each test. If the evaluation of clubs in robot tests could be replaced by computer simulations, it is expected that the time and cost of preparing prototypes would be reduced, and to more efficient development of equipment would be led by easily varying the mechanical properties of the club or ball as well as swing profiles in simulation analysis. There have been many studies in the literature which have attempted to evaluate clubs during the swing both experimentally and computationally. With reference to research using computer simulations for example, the three-dimensional (3D) forward dynamics model of the swing was developed to represent the 3D motion of the golfer and club [1], and the effects of shaft stiffness and deflection on the clubhead orientation at impact were investigated using that model [2,3]. The 3D flexible shaft model based on the Rayleigh beam theory was constructed to represent the 3D nature of shaft dynamics during the swing [4]. The finite element (FE) method is widely utilized for various purposes, such as understanding the dynamic behavior of a ball and club during impact and swing and evaluating equipment. In a study on ball impact, there has been an attempt to use the impact model for the design of a clubhead by shape optimization of the clubface [5], and to develop a model for predicting the sound of a ball impacting the clubhead [6]. FE analysis for estimating the behavior of the club during the swing were conducted, but the 3D motion of the club could not be sufficiently analyzed due to the simple FE model for the club, which consisted of the beam elements for the shaft and the mass element for the clubhead [7,8,9].
A carbon fiber reinforced plastic (CFRP) club shaft with high-specific strength and rigidity has the qualities of more easily changing stiffness and its distribution of the shaft than that of a steel shaft with isotropic elasticity, through the combination of material properties of a fiber and matrix and a laminated constitution. It is, therefore, desirable to obtain FE modeling techniques which can express the behavior of a CFRP shaft. FE modeling for the composite structure of a shaft was attempted [10], but the previous work had insufficient information about how to construct the material model and the accuracy validation of the constructed model. Modeling for CFRP is also expected to be used as a predictable tool to efficiently develop high performing equipment using a wealth of information on the dynamic behavior, which is neither simply nor easily obtainable through experimental methods.
The objective of this study was to construct an FE model for a CFRP club shaft which was capable of representing the mechanical properties of a fiber and matrix, a laminated constitution and a fiber orientation angle, and to investigate the effects of the torsional stiffness of the shaft on the dynamic behavior of a golf club during the swing.
2. Modeling of CFRP Shafts with Different Torsional Stiffness
In this study, the commercial FE code LS-DYNA (ver. 971, Livermore Software Technology Corporation) was used for the simulations.
2.1. Geometry Model for Representing Laminated Structure of Cfrpshaft
The FE model of a CFRP shaft, which consisted of laminated unidirectional fiber reinforced composite materials, was constructed using four-node shell elements, as shown in Figure 1. The model was composed of 7 parts which were represented by the same type of laminated constitution.
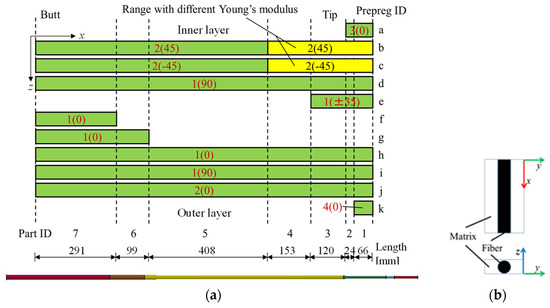
Figure 1.
These figures show (a) a laminated constitution of a CFRP shaft and a constructed FE model of the shaft, and (b) the definition of a local coordinate system in an element for representing the fiber orientation angle. The shaft consists of 11 types of unidirectional prepregs (ID: a-k). The numbers outside and inside the parentheses for each prepreg represent the number of lamination layers and the fiber orientation angle, respectively. The x and z axes are defined as the axis along the longitudinal and thickness directions of the shaft, respectively. The y-axis is determined by taking the cross product of the x and z-axes.
Each part was constructed based on the information about types of prepregs, the number of lamination layers and the fiber orientation angle. For example, Part ID 5 consisted of 6 types of prepregs (ID: b-d, h-i) and was composed of 9 layers. The fiber orientation angle for each prepreg was represented as the angle between the x-axis and the fiber direction of a unidirectional composite in the local coordinate system.
2.2. Definition of Mechanical Properties for Composite Materials
Each prepreg was expressed as an orthotropic elastic model. The mechanical properties of the prepreg were determined using the rule of mixture which was defined by the volume fraction and the mechanical properties of fiber and resin which were introduced in the prepreg [11], as shown in Table 1. In this study, the mechanical properties necessary for constructing the composite material model are the density, the Poisson’s ratio and the moduli of longitudinal and transverse elasticity, which are defined along the direction parallel and perpendicular to the fiber. These properties were obtained from publicly available sources of information by manufacturers of prepregs (e.g., [12,13]). Table 2 shows the information on the fiber and matrix used for prepreg ID: f (upper side) and results of composite materials (lower side) identified using each formula in Table 1, as a calculated example.

Table 1.
This table shows the formulae for determining mechanical properties of a composite material. The mechanical properties are calculated by applying the volume ratio, the density values, Young’s modulus and Poisson’s ratio for the fiber and resin to each formula.

Table 2.
This table shows the mechanical properties of the fiber and matrix for prepreg ID: f [13] (upper side) and identified composite material (lower side).
The torsional stiffness of the shaft was varied with the values of Ef in the range of a third part of shaft length from the tip end (Part ID: 1-4 in Figure 1) for 2 prepreg composites (ID: b, c in Figure 1). Three shaft models (shaft ID: A, B and C) with different torsional stiffness were constructed by changing the value of Ef (500, 450 and 400 GPa). All shafts were manufactured to validate the accuracy of the constructed shaft model.
2.3. Validation of Accuracy of Constructed Shaft Model
To confirm the accuracy of the shaft model, a static torsional test was conducted, and the model was compared to the result from the experiment. In the experiment, the torsional angle was measured by applying a constant torque around the longitudinal axis of the shaft to the tip of the shaft where the grip end was secured in a vice, as shown in Figure 2a. FE analyses using the implicit method were conducted with the constructed models under the same condition as those of the experiment.
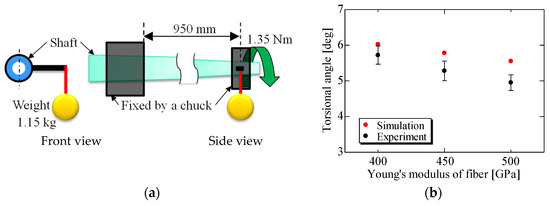
Figure 2.
These figures show (a) the experimental outline of the torsional test and (b) the result of the torsional angle for the experiment and the FE analyses.
The simulation results for all shafts are larger than that of the experiment, as shown in Figure 2b. The quantitative inaccuracy of the simulation result is thought to be due to a lack of accurate identification of Ey which is calculated using the formula in Table 1. It is generally known that the value of Ey estimated using the rule of mixture tends to be smaller than the real value [11]. This is considered to lead to the construction of a model with lower torsional stiffness. On the other hand, the results of both simulation and experiment of torsional angle tend to decrease as the value of Ef increases. From this result, the constructed model can qualitatively express the trend of the torsional stiffness with changes in the value of Ef.
3. Effects of Torsional Stiffness of the Shaft on the Dynamic Behavior of a Club
3.1. Simulation Analyses for Representing Swing Motion
A swing was modeled by prescribing the data on a swing motion, which was obtained from a robot test, in the club model which consisted of the CFRP shaft and a commercially available driver head with a rigid body. The swing motion was represented by prescribing the time histories of x, y and z positional coordinate of the grip end and the rotation angle (, and ) around 3 axes, that is, the arm and grip axes perpendicular to the swing plane and the longitudinal axis of the shaft, as shown in Figure 3a. Swing simulations were conducted using different types of swing profiles so that the head speed at impact was 30, 35 and 40 m/s. The clubhead behavior, as shown in Figure 3b,c, was calculated to compare with differences in the torsional stiffness of the shaft.
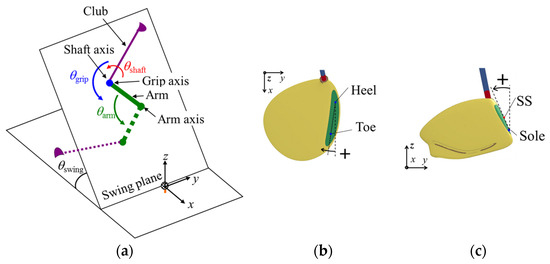
Figure 3.
These figures show (a) the motion for representing a swing by a robot and the definition of head behavior at impact: (b) the face angle, which is defined as the angle between the x-axis and face in the x-y plane; (c) the dynamic loft angle, which is defined as the angle between the z-axis and face in the y-z plane. The club model was swung by prescribing the time histories of x, y and z coordinate data of the grip end and of the rotation angle (, and ) around the 3 axes.
3.2. Simulation Results
Figure 4 shows the simulation results of the clubhead behavior at impact. The results for both face and dynamic loft angles of shaft A tend to be the smallest at speeds of 35 and 40 m/s. Little difference between all shafts for both results is found in the case of 30 m/s. On the other hand, the simulation results for shafts B and C tend to depend on swing profiles, in particular the magnitude relation of the face angle tends to be exchanged between 35 and 40 m/s.
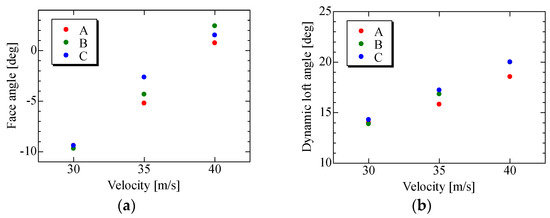
Figure 4.
These figures show the simulation results of the clubhead at impact: (a) the face angle; (b) the dynamic loft angle.
3.3. Discussion
Clubhead alignment varies by twisting the shaft due to the centrifugal force acting on the clubhead during the swing, on the grounds that the center of gravity for the clubhead is not an extension of the longitudinal axis of the shaft. The influence of the centrifugal force on the twist of the shaft increases with head speed at impact. However, shaft A with the highest torsional stiffness has a tendency to reduce a degree of torsional angle compared to shafts B and C. As a result, this is thought to lead to the tendency of shaft A, regardless of any range of impact speed.
To examine the causes of the tendency depending swing profiles for shafts B and C, the behavior of the head around the time of impact was analyzed, as shown in Figure 5. Time histories of the face angle for shafts A and B tend to be parallel, whereas the trend of shaft C tends to be different from that of shafts A and B. The clubhead alignment of shaft C with the lowest torsional stiffness has the tendency to be open to the influence of the magnitude and direction of the centrifugal force which changes with time. A similar trend in the results of the loft angle can also be observed. This is thought to be causally related to the tendency to vary according to the swing type. In a range of changes in this study, launch of a ball which collided with the club of shaft C is presumed to be open the influence of the timing of the impact, which has the tendency to easily change the dynamic loft angle of shaft C. This indicates that the alignment of the clubhead at impact tends to depend on the timing of the impact varying with the swing profile, as well as the stiffness of the shaft.
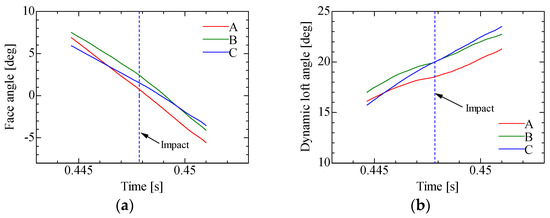
Figure 5.
These figures show the simulation results of the clubhead around the impact time at a speed of 40 m/s: (a) the face angle; (b) the dynamic loft angle. The broken line represents the time of impact.
4. Conclusions
An FE model for a CFRP club shaft, which was capable of representing the mechanical properties of a fiber and matrix, a laminated constitution and a fiber orientation angle was constructed using the rule of mixture and the coordinate systems in each element.
Swing simulation analyses were conducted using club models with varying torsional stiffness. The effect of the torsional stiffness on the clubhead alignment at impact tended to be stronger with the impact velocity of the clubhead due to the centrifugal force acting on the head. However, the simulation results of the alignment did not necessarily depend on the torsional stiffness. This indicates that the alignment of the clubhead at impact tends to be subject to the effects of the timing of the impact, which depends on the relationship between the ball position and the impact velocity in addition to the mechanical properties of the shaft.
Conflicts of Interest
The authors declare no conflict of interest.
References
- MacKenzie, S.J.; Sprigings, E.J. A three-dimensional forward dynamics model of the golf swing. Sports Eng. 2009, 11, 165–175. [Google Scholar] [CrossRef]
- MacKenzie, S.J.; Sprigings, E.J. Understanding the role of shaft stiffness in the golf swing. Sports Eng. 2009, 12, 13–19. [Google Scholar] [CrossRef][Green Version]
- MacKenzie, S.J.; Sprigings, E.J. Understanding the mechanisms of shaft deflection in the golf swing. Sports Eng. 2010, 12, 69–75. [Google Scholar] [CrossRef]
- Sandhu, S.; Millard, M.; McPhee, J.; Brekke, D. 3D dynamics modelling and simulation of a golf drive. Procedia Eng. 2010, 2, 3243–3248. [Google Scholar] [CrossRef]
- Petersen, W.; McPhee, J. Shape optimization of golf clubface using finite element impact models. Sports Eng. 2009, 12, 77–85. [Google Scholar] [CrossRef]
- Delaye, S.; Streeter, P.; Morales, E.; Wood, P.; Senior, T.; Hart, J.; Allen, T. Modelling the Sound of a Golf Ball Impacting a Titanium Plate. Procedia Eng. 2016, 147, 354–359. [Google Scholar] [CrossRef][Green Version]
- Suzuki, K.; Isobe, S.; Wang, C.; Kodama, H. Optimal design of golf club considering the body burdens. In Proceedings of the Conference on Computational Engineering and Science, Tokyo, Japan, 12–14 May 2009; The Japan Society for Computational Engineering and Science: Tokyo, Japan, 2009; Volume 14, pp. 103–104. (In Japanese). [Google Scholar]
- Oyashiki, Y.; Tominaga, J.; Hiromoto, S. Study on dynamics of golf swing. (1st report, Approach of 2-link multibody dynamics model). In Proceedings of the Japan Society of Mechanical Engineers, Tokyo, Japan, 3–6 November 2010; The Japan Society of Mechanical Engineers: Tokyo, Japan, 2010; Volume 10–53, pp. 325–328. (In Japanese). [Google Scholar]
- Matsumoto, K.; Tsujiuchi, N.; Koizumi, T.; Ito, A.; Ueda, M.; Okazaki, K. The Influence of a Golf Club’s Inertia on Shaft Movement during the Golfer’s Swing. In The engineering of Sport 11; Jansen, J.A., Ed.; Elsevier: Amsterdam, The Netherlands, 2016. Procedia Eng. 2016, 147, 360–365. [Google Scholar] [CrossRef][Green Version]
- Cheong, S.K.; Kang, K.W.; Jeong, S.K. Evaluation of the mechanical performance of golf shafts. Eng. Fail. Anal. 2006, 3, 464–473. [Google Scholar] [CrossRef]
- The Japan Society of Mechanical Engineers. JSME Mechanical Engineer’s Handbook a3: Materials and Mechanics; The Japan Society of Mechanical Engineers: Maruzen, Japan, 2005; pp. 156–158. (In Japanese) [Google Scholar]
- Torayca® Prepreg. Available online: http://www.torayca.com/en/download/pdf/prepreg.pdf (accessed on 15 December 2017).
- Nippon Graphite Fiber Corporation. Available online: http://www.ngfworld.com/en/en_skill.html (accessed on 15 December 2017).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).