The Influence of the Grip Acceleration on Club Head Rotation during a Golf Swing †
Abstract
:1. Introduction
2. Method
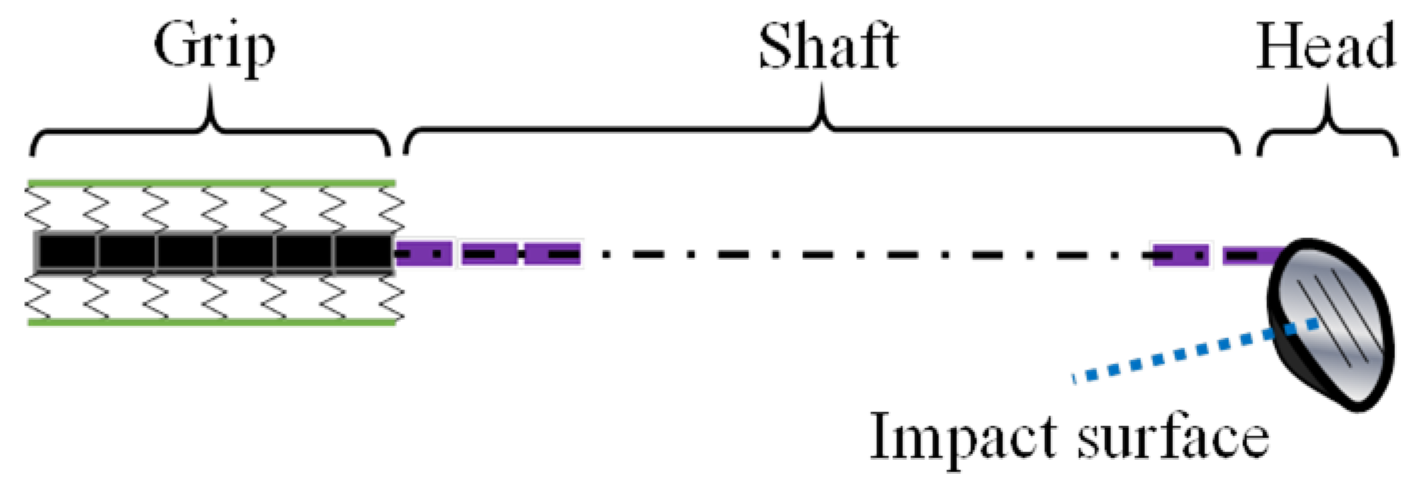
2.1. Model of Golf Club
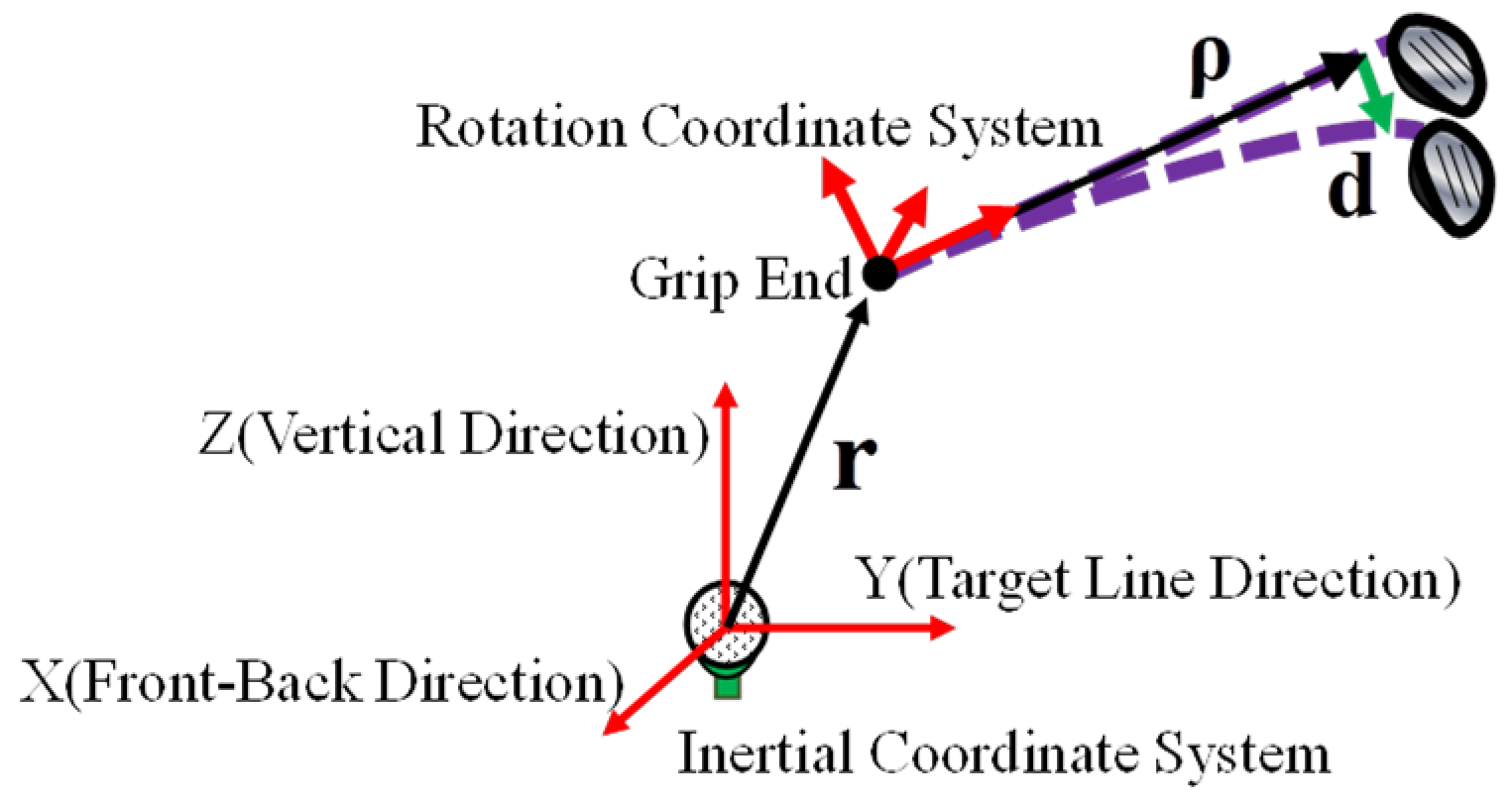
2.2. Motion Equation
2.3. Deflection Torque for Each Club Node
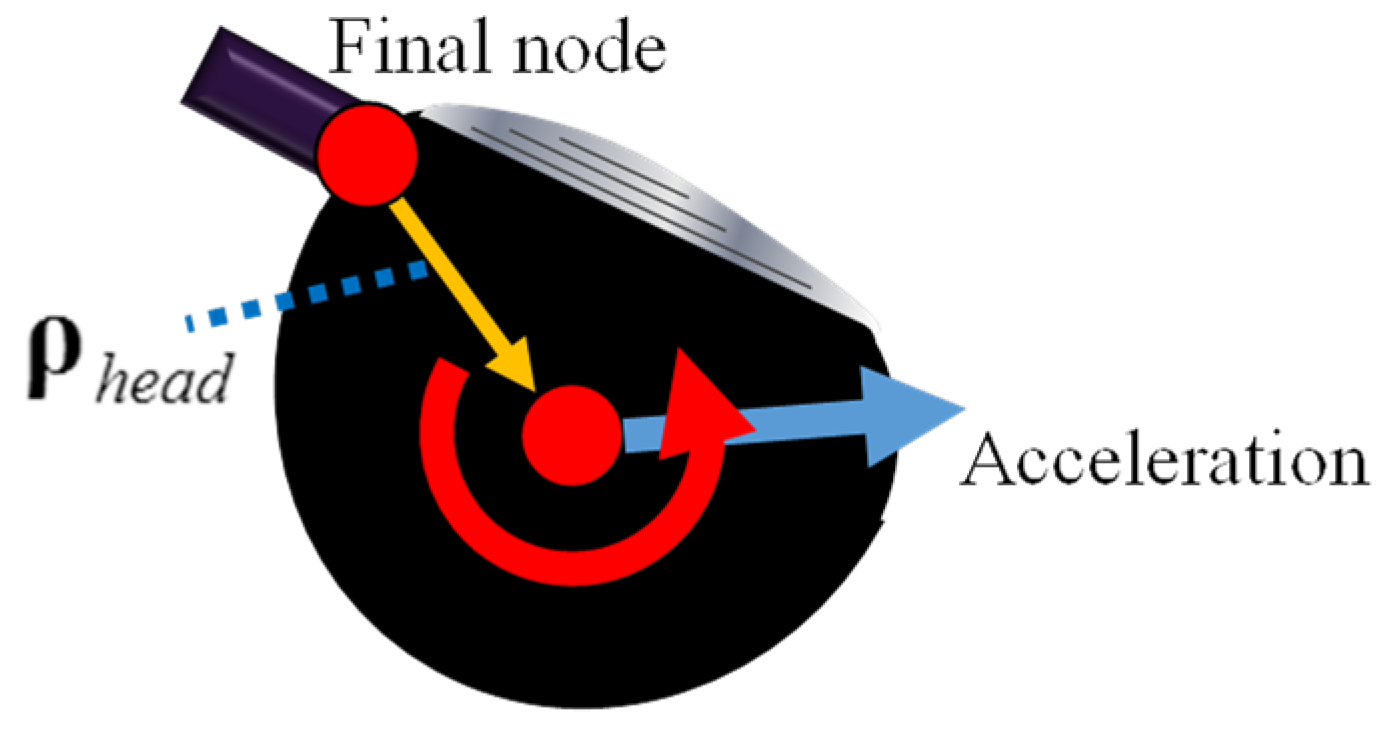
2.4. Head-Torque Caused by Grip Acceleration
3. Analysis Method
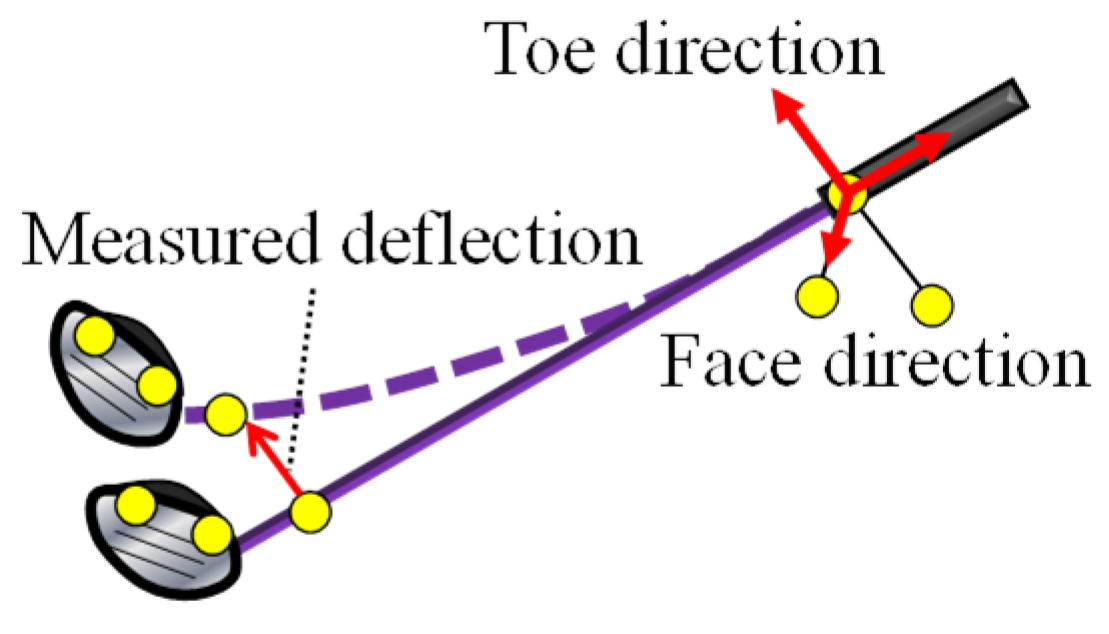
3.1. Experimental Measurements
3.2. Simulation
4. Results and Discussions
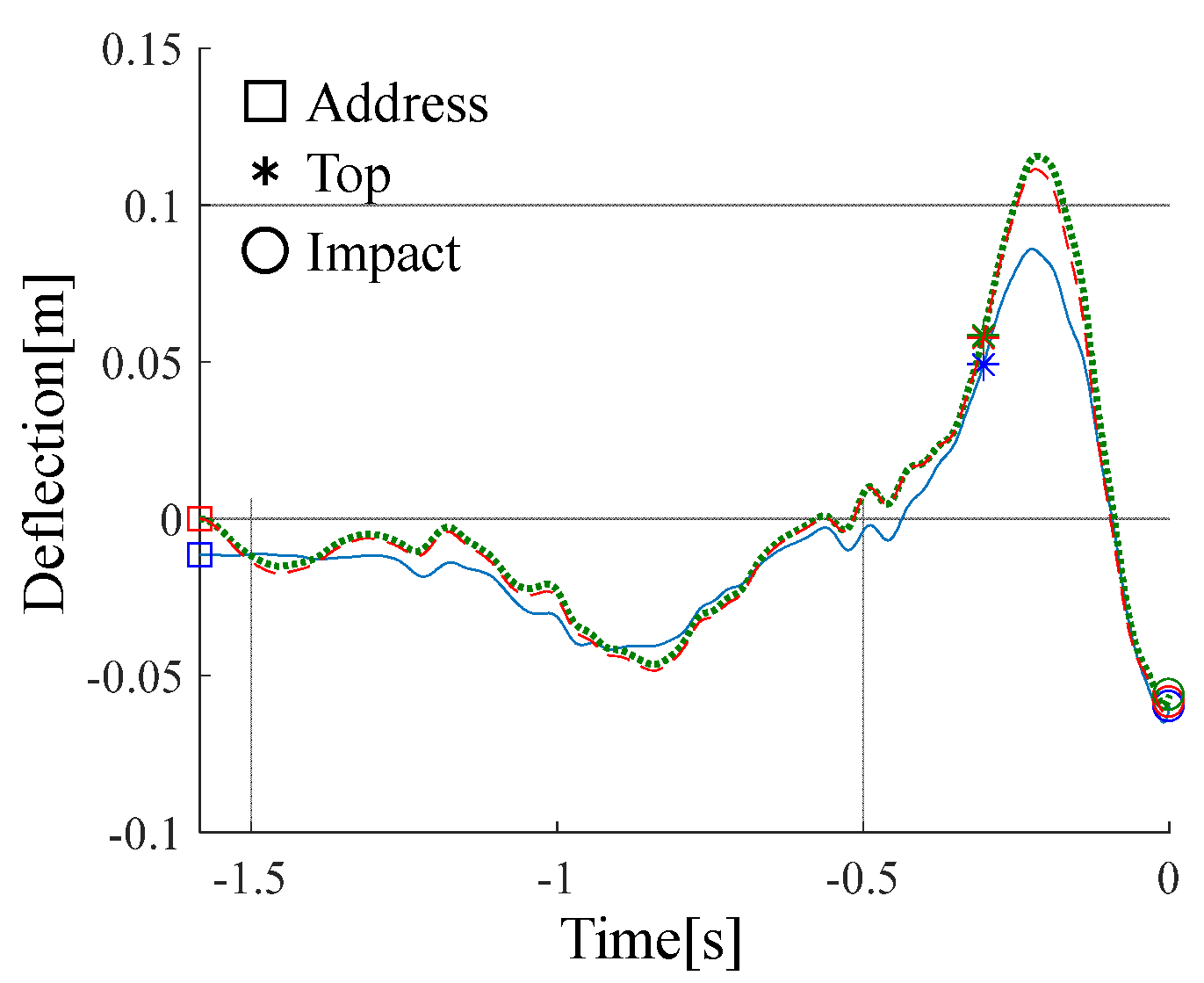
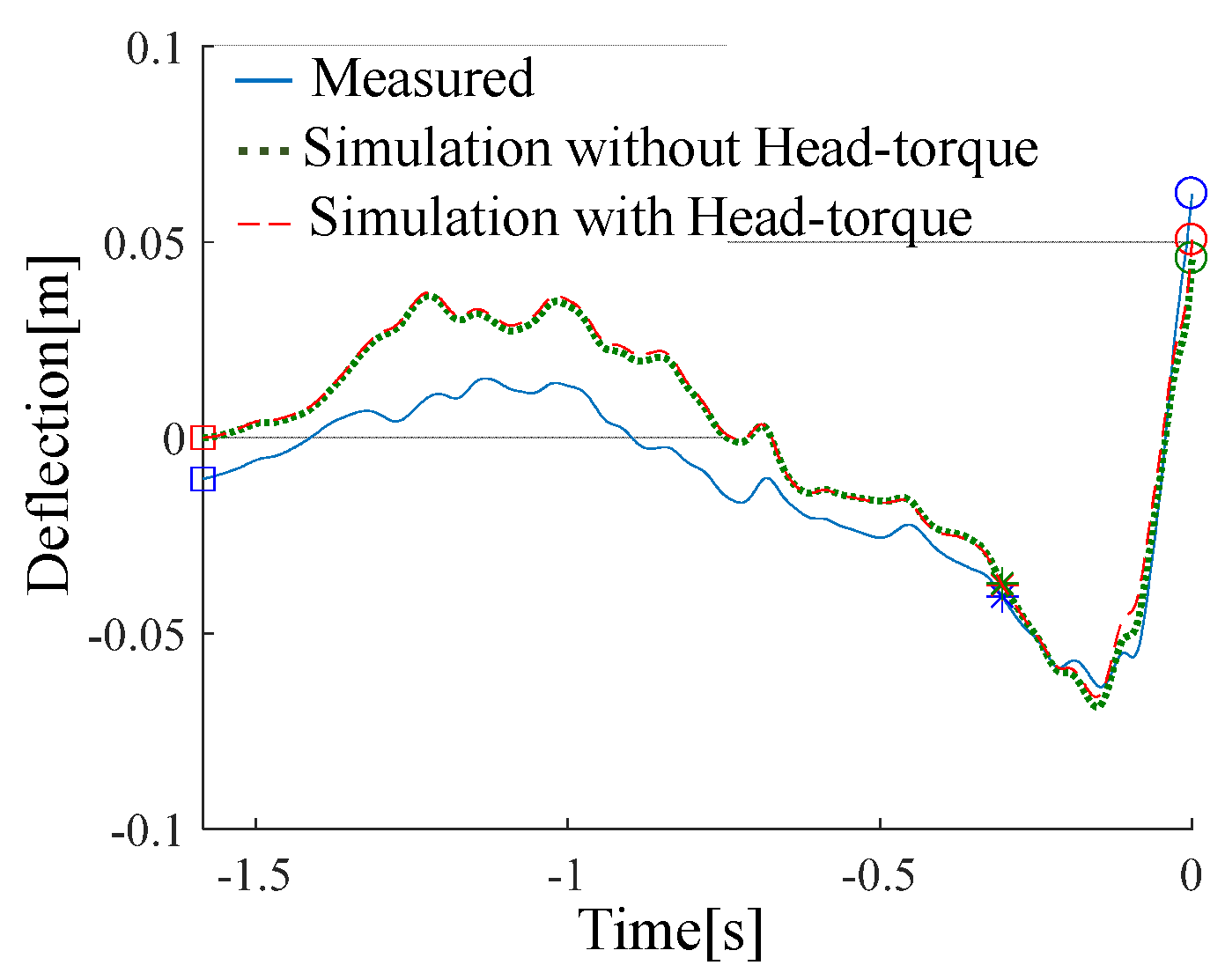
4.1. Comparison of Measured and Simulated Results of Club Shaft Deflection
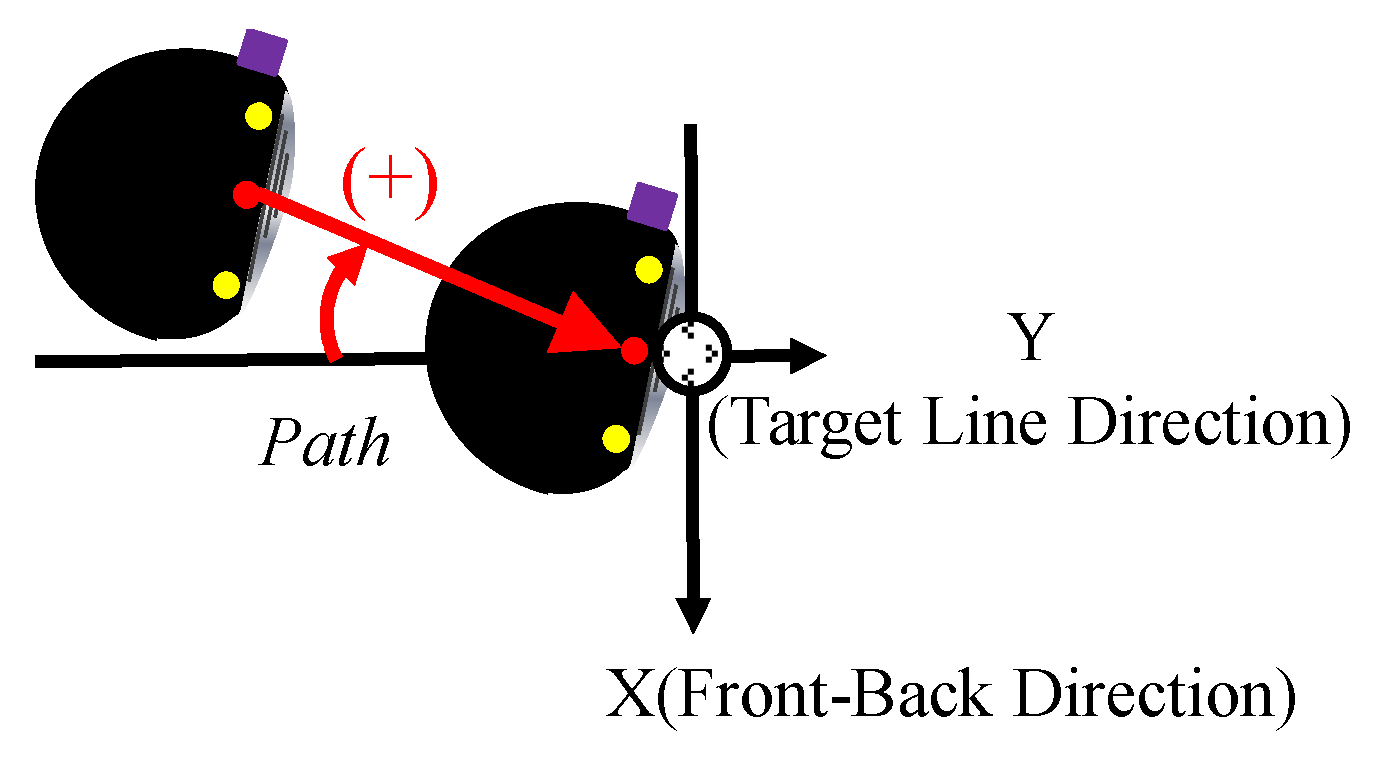
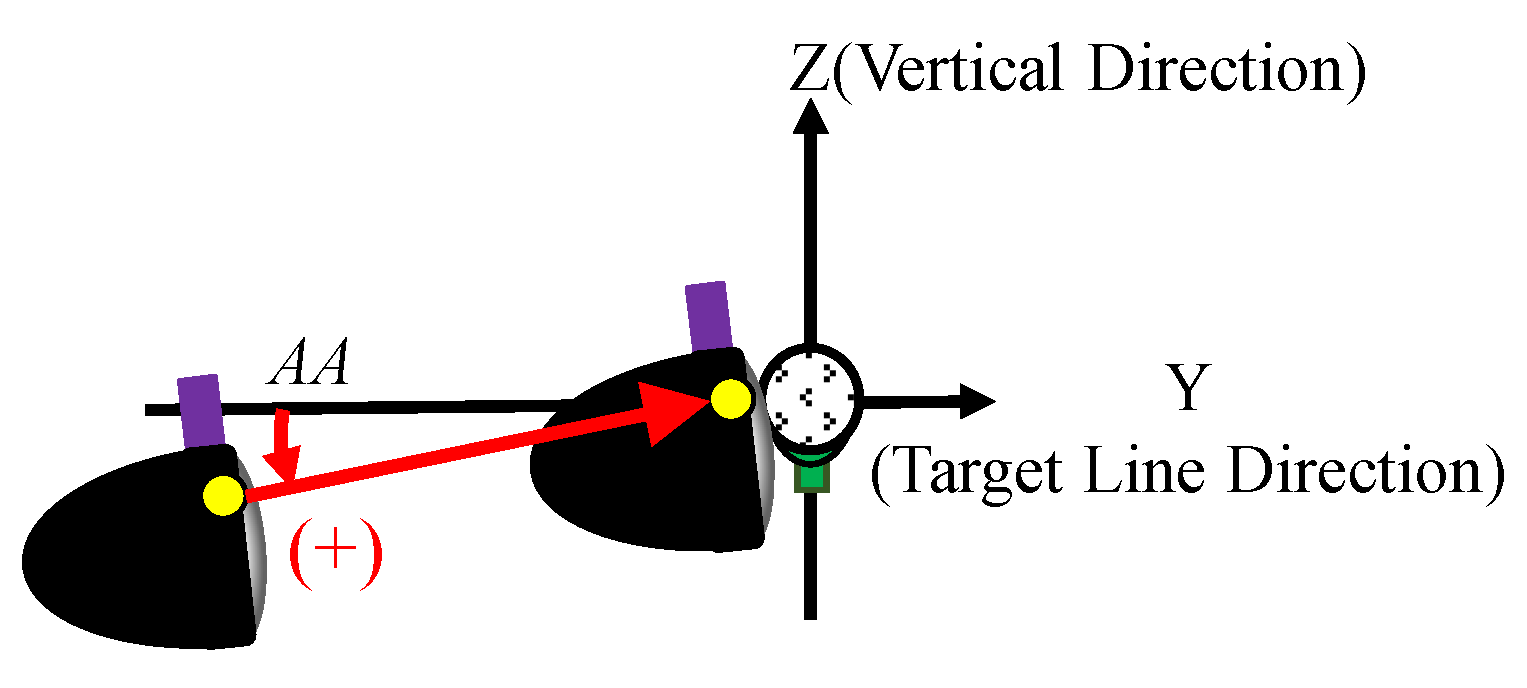
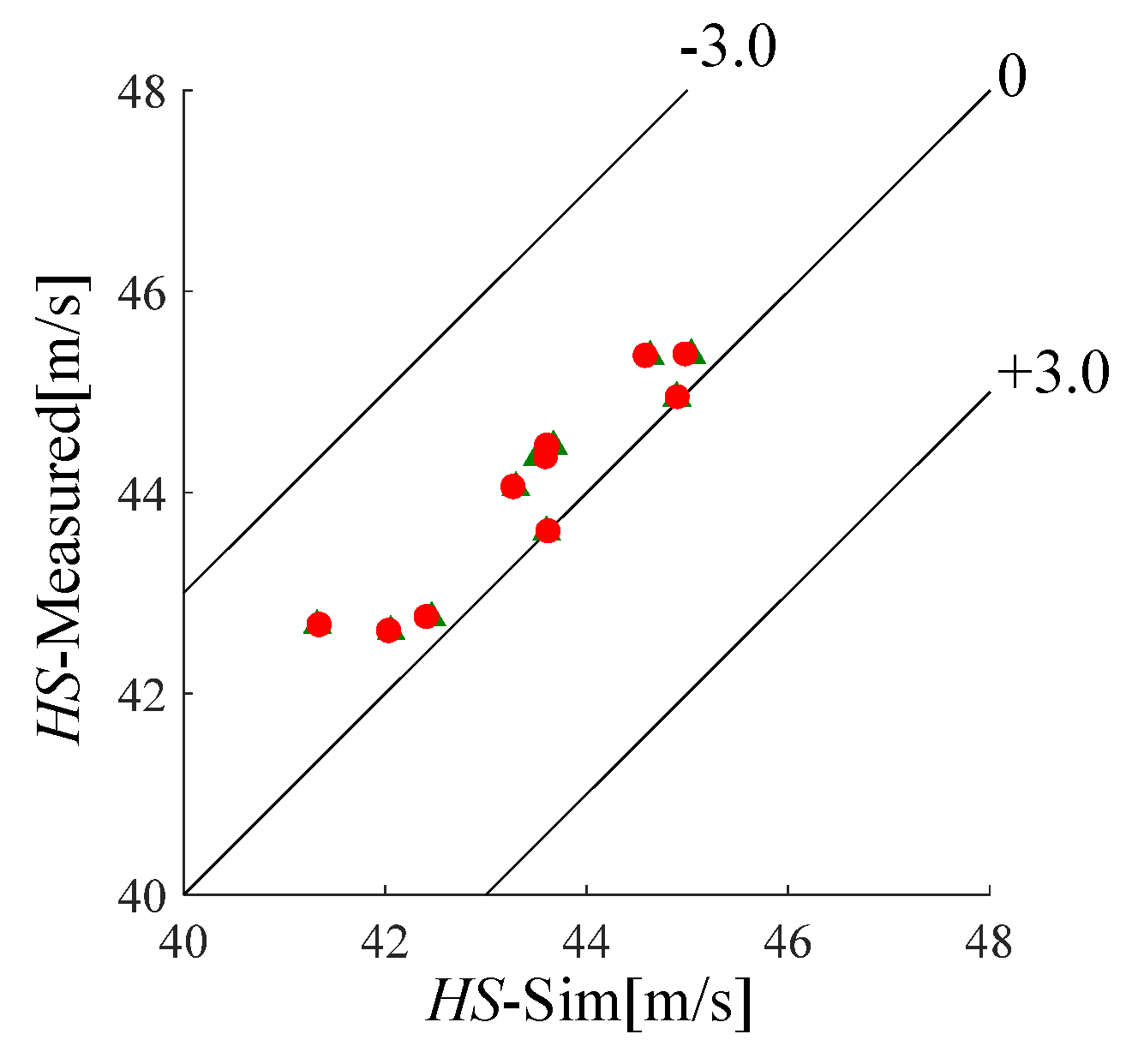
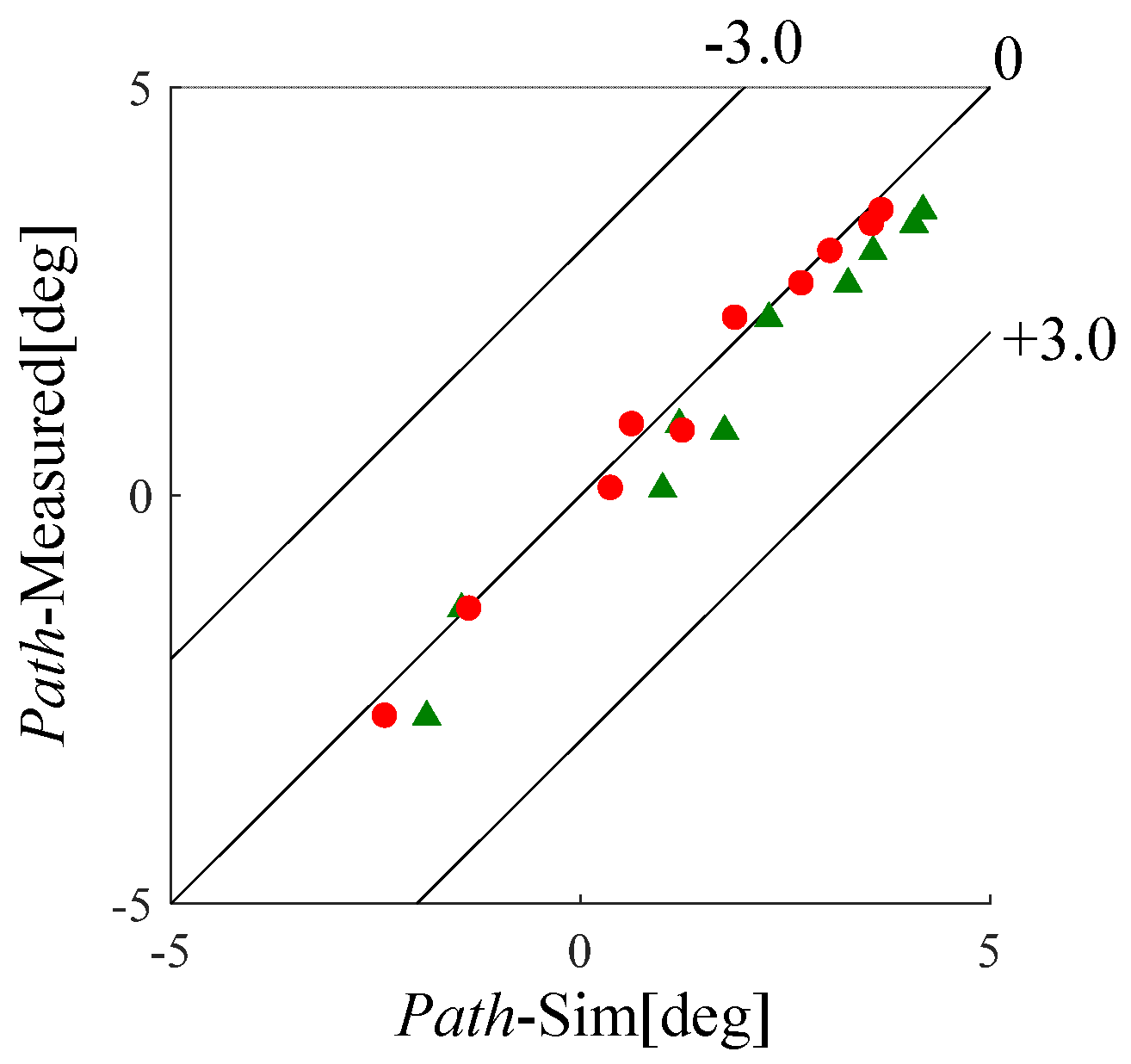
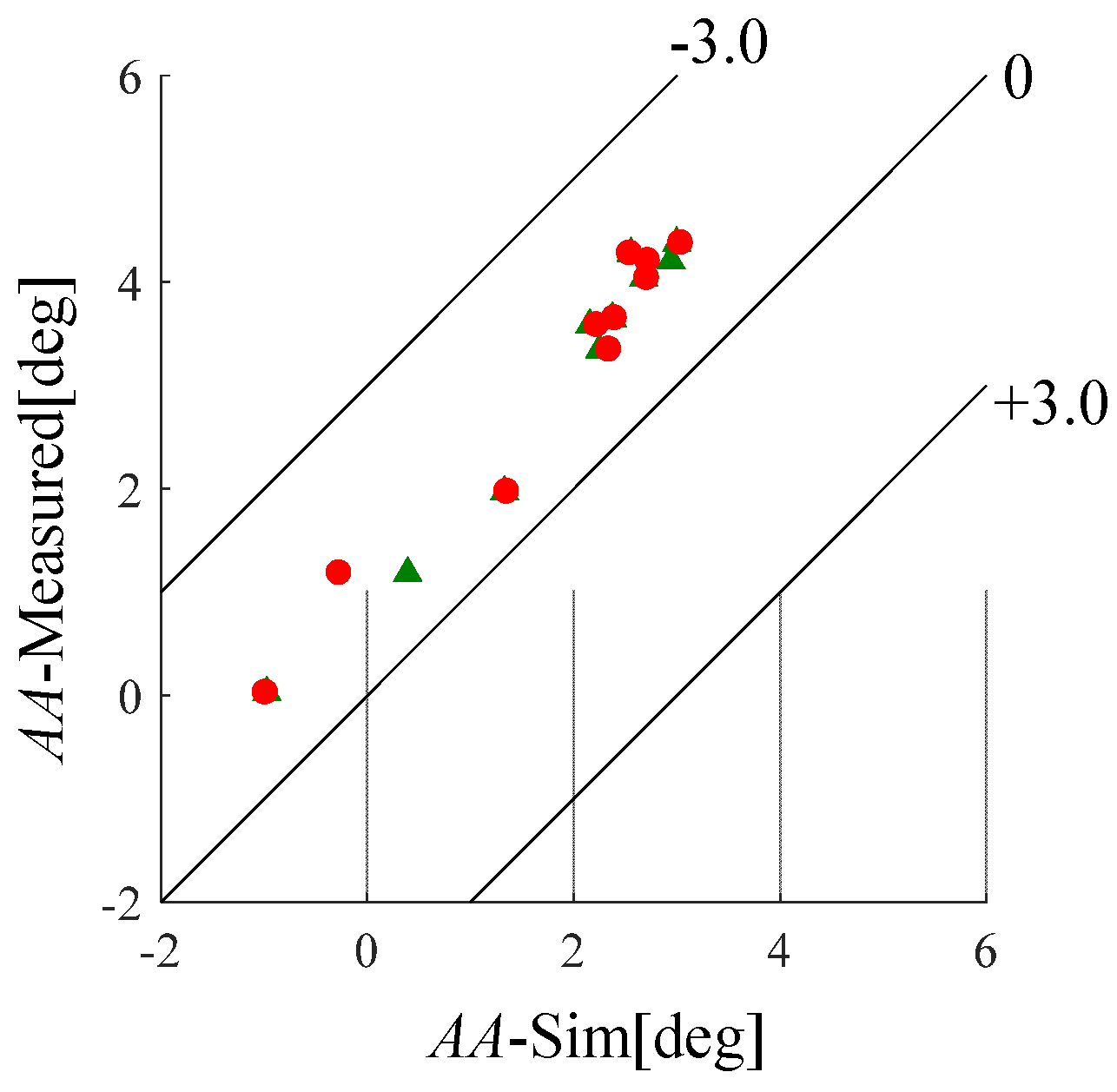
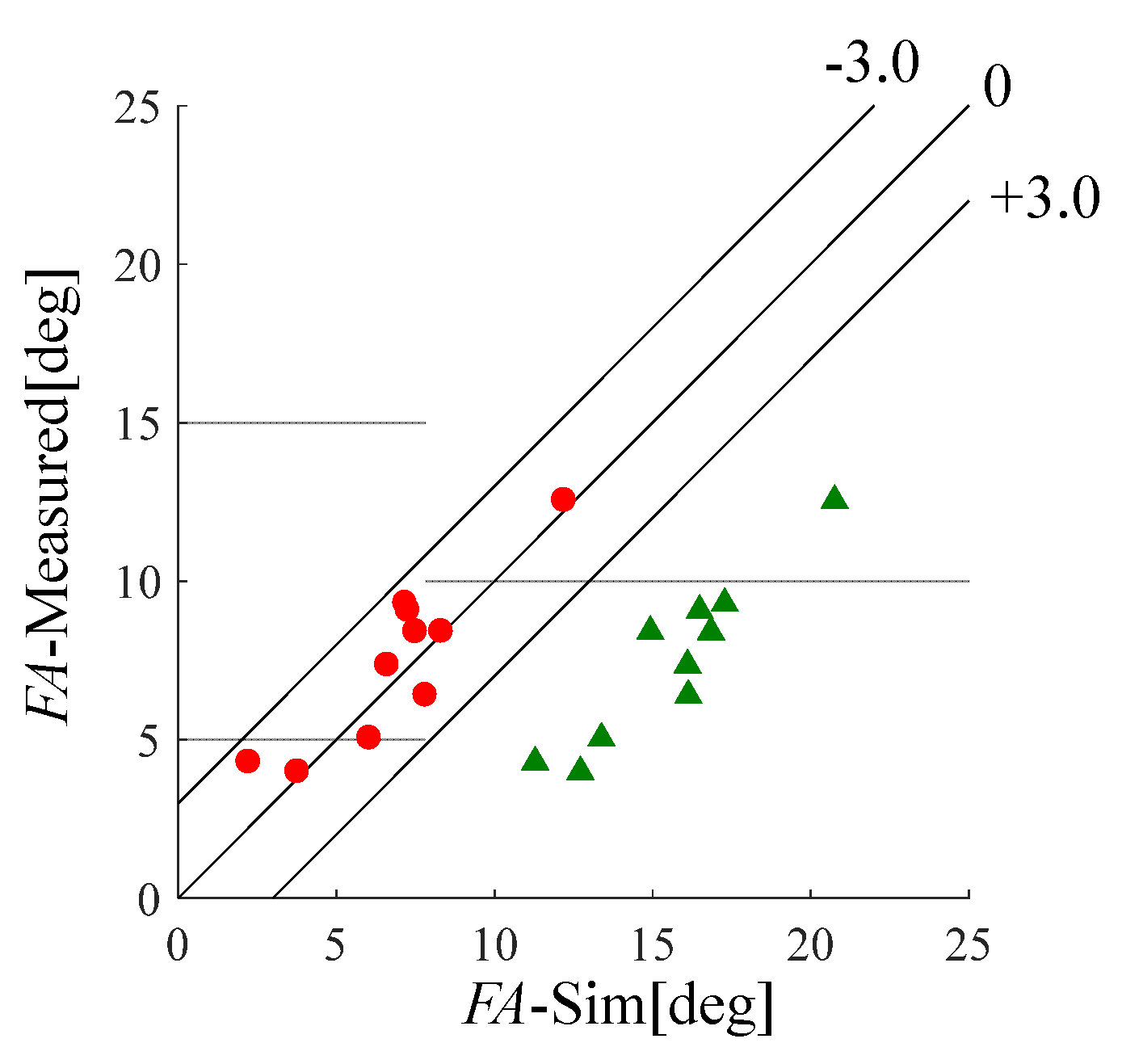
4.2. Comparison of Measured and Simulated Results of Club Head Kinematics
5. Conclusions
- (1)
- The deflection of the tip of the shaft was not influenced by the Head-torque generated by grip acceleration.
- (2)
- The HS and AA simulations was not influenced by the Head-torque generated by grip acceleration.
- (3)
- Considering the influence of the Head-torque generated by grip acceleration, the Path and FA simulations was close to the measured values.
References
- MacKenzie, S.J.; Boucher, D.E. The influence of golf shaft stiffness on grip and clubhead kinematics. J. Sports Sci. 2017, 35, 105–111. [Google Scholar] [CrossRef] [PubMed]
- Worobets, J.; Stefanyshyn, D. The influence of golf club shaft stiffness on clubhead kinematics at ball impact. Sports Biomech. 2012, 11, 239–248. [Google Scholar] [CrossRef] [PubMed]
- Tsujiuchi, N.; Koizumi, T.; Tomii, Y. Analysis of the influence of golf club design on the golf swing. Eng. Sport 2002, 4, 537–544. [Google Scholar]
- MacKenzie, S.J.; Sprigings, E.J. Understanding the mechanisms of shaft deflection in the golf swing. Sports Eng. 2010, 12, 69–75. [Google Scholar] [CrossRef]
- Sandhu, S.; Millard, M.; McPhee, J.; Brekke, D. 3D dynamic modelling and simulation of a golf drive. Procedia Eng. 2010, 2, 3243–3248. [Google Scholar] [CrossRef]
- Matsumoto, K.; Tsujiuchi, N.; Koizumi, T.; Ito, A.; Ueda, M.; Okazaki, K. The Influence of a Golf Club’s Inertia on Shaft Movement during the Golfer’s Swing. In Proceedings of the 11th conference of the International Sports Engineering Association, Procedia Engineering, Delft, The Netherland, 11–14 July 2016; Volume 147, pp. 360–365. [Google Scholar]
- Matsumoto, K.; Tsujiuchi, N.; Ito, A.; Ueda, M.; Okazaki, K.; Taiki, S. Effect of Inertia for Shaft Movement generated by a Golf Swing. In Proceedings of the 8th Asian Conference on Multibody Dynamics, Kanazawa, Japan, 7–10 August 2016. [Google Scholar]
- Iwatsubo, T.; Matsuhisa, H.; Inoue, Y.; Utsuno, H.; Kawamura, S.; Kanki, H.; Koizumi, T.; Shiohata, K.; Tsujiuchi, N.; Nakagawa, N. Basics of Vibration Engineering; Morikita Publishing Co., Ltd.: Tokyo, Japan, 2014; pp. 130–134. [Google Scholar]
- Komatsu, K. Machine Architecture Vibration Science FEM and Analysis of Response by MATLAB; Morikita Publishing Co., Ltd.: Tokyo, Japan, 2009; pp. 38–39. [Google Scholar]
- Nagamatsu, A. Modal Analysis; Baifukan CO., Ltd.: Tokyo, Japan, 1985; pp. 176–216. [Google Scholar]
- Matsumoto, K.; Tsujiuchi, N.; Ito, A.; Taiki, S.; Ueda, M.; Okazaki, K. Estimation of Club Head Posture during Golf Swing using three-dimensional FEM model. In Proceedings of the Symposium on Sports and Human Dynamics 2016, Yamagata, Japan, 9–11 December 2016. (In Japanese). [Google Scholar]


| Toe-Top (mm) | Face-Top (mm) | Toe-Impact (mm) | Face-Impact (mm) | |
|---|---|---|---|---|
| Sim(no-Head-torque) | 11.3 ± 2.7 | 9.9 ± 6.0 | 4.0 ± 2.3 | 12.9 ± 6.5 |
| Sim(Head-torque) | 10.0 ± 2.7 | 9.8 ± 6.0 | 3.5 ± 2.8 | 9.0 ± 6.1 |
| HS (m/s) | Path (deg) | AA (deg) | FA (deg) | |
|---|---|---|---|---|
| Sim(no-Head-torque) | 0.5 ± 0.4 | 0.6 ± 0.3 | 1.2 ± 0.3 | 8.1 ± 1.0 |
| Sim(Head-torque) | 0.5 ± 0.4 | 0.1 ± 0.2 | 1.2 ± 0.3 | 0.6 ± 1.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Furukawa, K.; Tsujiuchi, N.; Ito, A.; Matsumoto, K.; Ueda, M.; Okazaki, K. The Influence of the Grip Acceleration on Club Head Rotation during a Golf Swing. Proceedings 2018, 2, 241. https://doi.org/10.3390/proceedings2060241
Furukawa K, Tsujiuchi N, Ito A, Matsumoto K, Ueda M, Okazaki K. The Influence of the Grip Acceleration on Club Head Rotation during a Golf Swing. Proceedings. 2018; 2(6):241. https://doi.org/10.3390/proceedings2060241
Chicago/Turabian StyleFurukawa, Kazuki, Nobutaka Tsujiuchi, Akihito Ito, Kenta Matsumoto, Masahiko Ueda, and Kosuke Okazaki. 2018. "The Influence of the Grip Acceleration on Club Head Rotation during a Golf Swing" Proceedings 2, no. 6: 241. https://doi.org/10.3390/proceedings2060241
APA StyleFurukawa, K., Tsujiuchi, N., Ito, A., Matsumoto, K., Ueda, M., & Okazaki, K. (2018). The Influence of the Grip Acceleration on Club Head Rotation during a Golf Swing. Proceedings, 2(6), 241. https://doi.org/10.3390/proceedings2060241





