Analysis of Swing Movement in Ballroom Dancing ^†

Abstract

Natural rise and fall movement represents typical characteristics of the swing dances in ballroom dances. The rise and fall movements are analyzed in the mechanical point of view in the presentation. The biomechanics of the rise and fall movements were analyzed in terms of the potential energy and the velocity of the body. Some basic figures of Waltz are taken as examples with application suggestion to the other dances. A sinusoidal function is employed for vertical and horizontal movements in the analysis featuring the natural swing movement of the dancer’s body. The height of center of gravity of dancer and its vertical acceleration are quantitatively exhibited in graphs for each basic movement of the figures of these dances. It is shown that the maximum height in the movement depends on each figure in each dance and that it is limited by the acceleration analysis regardless of dancer’s height or weight.

1. Introduction

The ballroom dancing is a couple dance in a ballroom developed extensively in European societies. It has been systematized in England since in the middle of 20th century [1,2]. The dances are classified in categories of (modern) standard dances, and Latin American dances [3] and others. The modern standard dances include Waltz, Foxtrot, Tango, Quickstep, and Viennese Waltz, and the Latin American Dances include Rumba, Cha Cha Cha, Samba, Jive, and Paso doble. In the standard dances, the couple maintains contact hold, whereas in Latin American dances, non-contact positions are generally taken. Some important characteristics in the ballroom dancing are noted below;

• The music has a fixed tempo for each dance and is constant throughout,
• The movement of dance is based on natural human gait,
• The sequence of dance is not fixed in advance (non-sequential, or non-provisional).
• The man leads the dance movements and the lady follows.

Technique of ballroom dancing is generally recognized as internationally and has been defined in the syllabi by the two associations of dance teachers in U.K., ISTD (The Imperial Society of Teachers of Dancing) [4,5] and IDTA (International Dance Teachers Association) [6]. In these syllabi, the dancer’s movement is described precisely in the manner in which the position of each step, amount of turn between steps, Rise and Fall, footwork, and etc., are prescribed. However, in these books, most of the movements are shown without explanation, and even in the case of explanations give, most are rather from feelings or sense and not based on scientific theory. In this paper, the Rise and Fall movement or Swing movements in ballroom dancing is analyzed using aspects of mechanics. The purpose of the study is to give the dancers adequate advice on the swing movement in each figure of the dances. The movements referenced are those based on the syllabus by ISTD [4,5]. The analysis is focused to Waltz, Foxtrot, Quickstep, and Viennese Waltz which are sometimes called “Swing dances”. Tango is excluded since there is no Rise and Fall in Tango dancing.

The analysis of Rise and Fall is represented by the movement of center of gravity of dancers. Since contact hold is fundamentally taken in modern standard, the center of gravity can be regarded as that of the couple in the analysis.

2. Mechanical Energy Consideration and Expression of Rise and Fall as a Mathematical Function

2.1. Potential and Kinetic Energy Exchange in Rise and Fall Movement

The swing in dancing which is often referred to a pendulum movement is crucially important to dance elegantly with good balance. Focusing the vertical component, the swing is a reciprocal movement between the high stable position (Up) and the low stable position (Down). The highest vertical position of center of gravity (Up) measured from the “Down” position is taken as H. If the velocity at the “Up” is zero in any direction, and if there is no mechanical energy loss during the swing down action, the velocity at the “Down” position v becomes,

$$v=\sqrt{2gH},$$

(1)

where g is the acceleration of gravity on the surface of the earth. Taking an example, if the highest position H = 0.1 m, the swing velocity at “Down” position becomes around 1.4 m/s. There is some loss of energy and also additional energy is introduced by the dancer’s muscles. However, this simplified model without any loss or additional energy can be considered to represent an ideal natural movement in ballroom dancing.

The energy exchange is discussed in more detail taking the example of Waltz Natural Turn or Reverse Turn, the description of which is expressed as,

Count 1 (first beat in the bar (measure) in the music): Starting height (Down), Commence to rise e/o (end of) 1 (NFR in case of backward step), Count 2 (Second beat in the bar): Continue to rise, and Count 3(Third beat in the bar): Continue to rise, Lower e/o 3.

During this rising process, the maximum kinetic energy will be gained when the translational velocity is the largest, i.e., at the time around the middle of Count 2. After that, the velocity decreases and the kinetic energy is transformed to the potential energy increase due to the rising of the body. The largest potential energy is reached in the middle of Count 3 when the body position is the highest. At this instance, the feet are together and the velocities in vertical and horizontal directions are zero, so that the kinetic energy diminishes. At the starting position, the potential energy is in the minimum (Down). Although the starting velocity is not specified in the syllabi, it may not be large in natural sense. If so, the maximum kinetic energy in Count 2 comes partly from the potential energy on Count 3 of the previous bar but mainly from the energy exerted by the dancer’s muscle through the pressure between the foot and the floor. In fact, from Count 1 to 2, despite of the rising process, the velocity also increases meaning both the potential and kinetic energies increment. It is easier to input energy through muscle in the acceleration upward process (beginning of Rise) since the pressure between the foot and the floor is larger, than the deceleration process. If the Rise and Fall of Waltz basic figures is modelled as a swing motion, or simple pendulum motion, the swing up process can be explained naturally as the energy change from kinetic to potential, however, the swing down process in which the energy changes from the potential to kinetic involves dissipation.

In case of Foxtrot, taking the example of Feather action, i.e., Feather Step, Feather Finish or Feather ending, the lowering occurs in the end of penultimate step (Man’s right step, Count Q). This lowering step is not closed and increases the body movement in the horizontal direction, resulting that the ultimate step of Feather, Count S has considerable amount of velocity which is the start of next swing. The velocity is larger than that in the middle of the previous step Q, so that the potential energy can be regarded to change to the kinetic energy to some extent.

Quickstep has cases in which the feet are together in “Up” position and also cases in which the feet are open, so that they should be discussed separately. The former example is the 1–3 of Natural Turn and should be discussed in a similar manner as in Waltz. The latter example is Progressive Chassé in which the movement in the horizontal direction does not stop and is discussed as above in Foxtrot. Even in Waltz, there are cases in which the feet are open on Count 3, as in Spin Turn, Chassé from PP, etc., the energy discussions should be similar as in Foxtrot.

The starting movement in Waltz is reconsidered here. Many dancers start with opposite foot on the third beat of the previous bar, as a preparation step. Some dancers take this step with the footwork H, and other dancers with TH. In case of the footwork H, the movement of “Swing” is simply upward as explained above, while in case of TH, the dancers may suppose the previous step as a open finish such as Chassé from PP so that the swing down motion also involves. Considering these ways, it may be natural to take the feet open in the end of Count 3 after lowering the body. This allows an initial velocity in horizontal direction with the lowering in the end of Count 3. The potential energy stored on Count 3 is partly converted to the kinetic energy in the “Down” swing. These movements look like saving energy and thus look more natural than to lose energy.

2.2. Expression of Rise and Fall As a Mathematical Function

The free vibration function (natural vibration) is employed here to describe the natural dance movements. In the progression of movement, the continuity of the position (height) and its velocity are retained, however, the acceleration may change without continuity. Most of the Rise and Fall movements in Ballroom Dancing are monotonically without stopping in the middle.

The Rise and Fall is represented mechanically by the height h(t) of the center of gravity of dancers’ body as a function of time t. If the rising process is started at time t = 0, height h(t) = 0, vertical velocity dh(t)/dt = 0 and reaches to the maximum peak height h(t) = H and dh(t)/dt = 0 at t = T, the rising function is expressed as,

$$h\left(t\right)=\frac{H}{2}\left\{1-\cos \left(\pi \frac{t}{T}\right)\right\}$$

(2)

Similarly the lowering movement starting at time t = 0, height h(t) = H, vertical velocity dh(t)/dt = 0, and terminates at t = T, h(t) = 0, dh(t)/dt = 0 is expressed, as,

$$h\left(t\right)=\frac{H}{2}\left\{\cos \left(\pi \frac{t}{T}\right)+1\right\}$$

(3)

The period of the sinusoidal function is 2T. The acceleration in the vertical direction is given by differentiating twice by time. To understand the sensitivity of acceleration felt by the dancer, or to realize the force between the feet and the floor, the acceleration a in this analysis is expressed by adding the gravity g, that is the true acceleration. For example, the acceleration at the start of lowering is expressed as,

$$a=g-\frac{{\pi }^{2}H}{2T^2}$$

(4)

3. Rise and Fall in Each Figure

3.1. Rise and Fall in Waltz

The Rise and Fall movement in the Waltz is basically one bar unit type, that is starting to rise from the “Down” position in a bar and lowering ends within the bar. The Rise and Fall types are classified according to the timing of Rise, the rising modes, whether a plateau (Up) part exists or not, and the timing of lowering. The highest position depends on the type of dance. The followings Rise and Fall types in the Waltz classified by the author are:

Natural Turn type, Spin Turn type, Chassé from PP type, Turning Lock type, Man’s Telemark type, Lady’s Telemark type, Double Reverse Spin type, and No Rise and Fall type. Other figures not included in these types, such as Fallaway Reverse, Bounce Fallaway, Reverse Corté, Wing, Cross Hesitation, and Contra Check have some ambiguity in which the dancer may choose arbitrarily.

Some Rise and Fall types are explained in the following sub-sections. The tempo of Waltz is set to be 30 bpm in the analysis, namely, the length of one bar is 2 s, and one beat has 2/3 s. The Count 1, 2, 3 correspond to the beats in a bar but not always correspond to the step number.

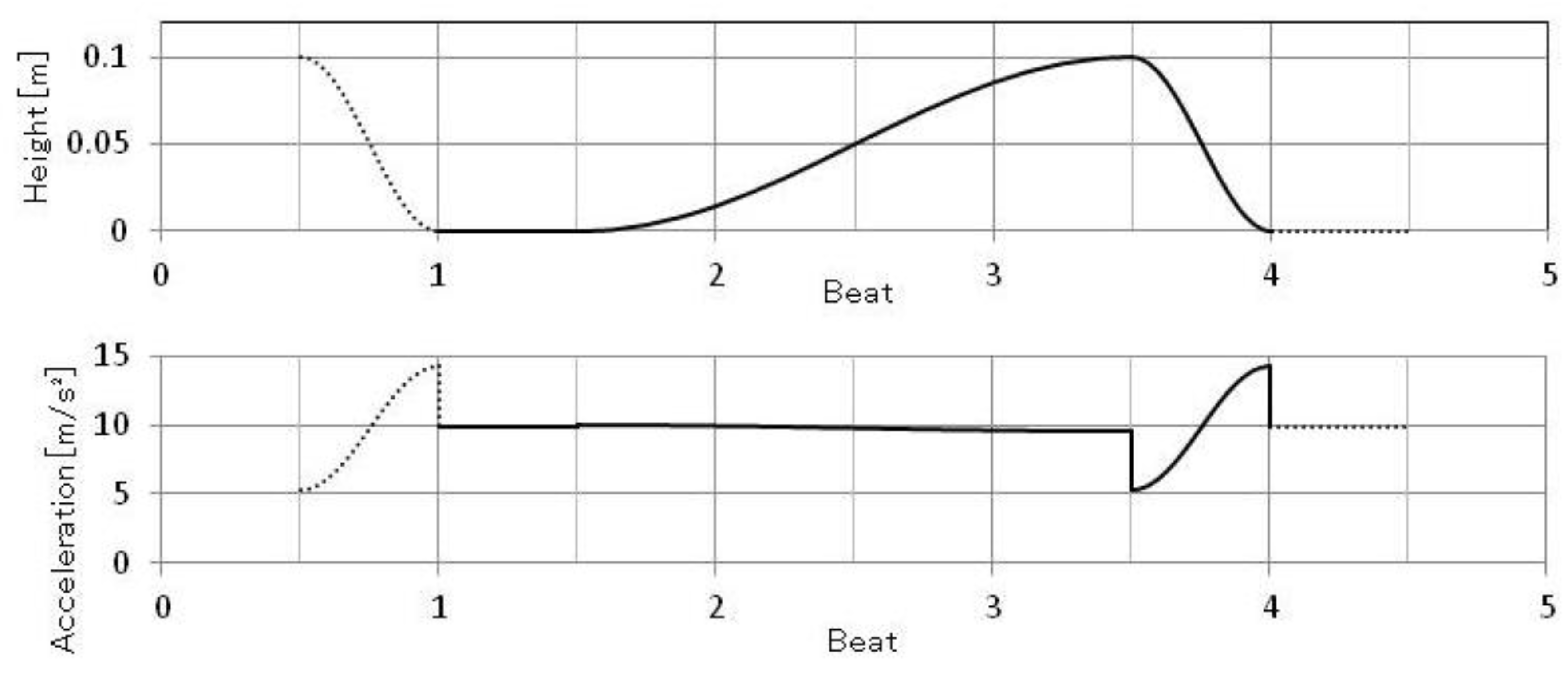
3.1.1. Natural Turn Type

This fundamental Rise and Fall type explained in the previous section include 1–3 of Natural Turn (Man & Lady), 4–6 of Natural Turn (Man & Lady), 1–3 of Reverse Turn (Man & Lady), 4–6 of Reverse Turn (Man & Lady), Closed Change, R & L, (Man & Lady), Cross Hesitation (Man & Lady). The Rise starts gradually from the end of Count 1 and continues to the middle of Count 3. The reason of the continuation of the Rise on 3 is that the step 3 (Count 3) is the closing feet step. Figure 1 shows the height of the center of gravity of dancer and its acceleration as a function of time. The highest position $H_{\mathrm{N}}$ occurs in the middle of Count 3 when the both feet are closed. The height at the half beat before the highest incident, which is the start of Count 3, is,

$$\frac{1}{2}\left(1+\frac{\sqrt{2}}{2}\right)H_{\mathrm{N}}=0.85H_{\mathrm{N}}$$

(5)

This height may be regarded as the height without closing feet on Count 3. This way of thinking will be applied also to other types of Rise and Fall in which the highest position occurs with feet open, such as Spin turn explained in the following sub-section. The acceleration shown in Figure 1 includes the gravity of the body, representing the force between the floor and the feet (in most case, supporting foot). The lowest acceleration (the maximum deceleration) occurs at the middle of the Count 3 (the end of rising). The figure shows the case in which the peak height is 100 mm and the tempo is 30 bpm, resulting in a maximum deceleration of approximately 4.44 ms⁻². The deceleration is proportional to the peak height under fixed tempo. If the maximum deceleration exceeds the gravity of the earth, the interactive force between the floor and the feet diminishes, meaning the limitation of the rising height, which is about 0.22 m. Thus, the limitation of Rise and Fall in Waltz is obtained to be about 0.22 m, and this does not depend on the dancer’s height, weight, muscle strength, nor techniques. It is noted in the rising process, the change of acceleration is relatively very small, since in this type, the rising is very gradual.

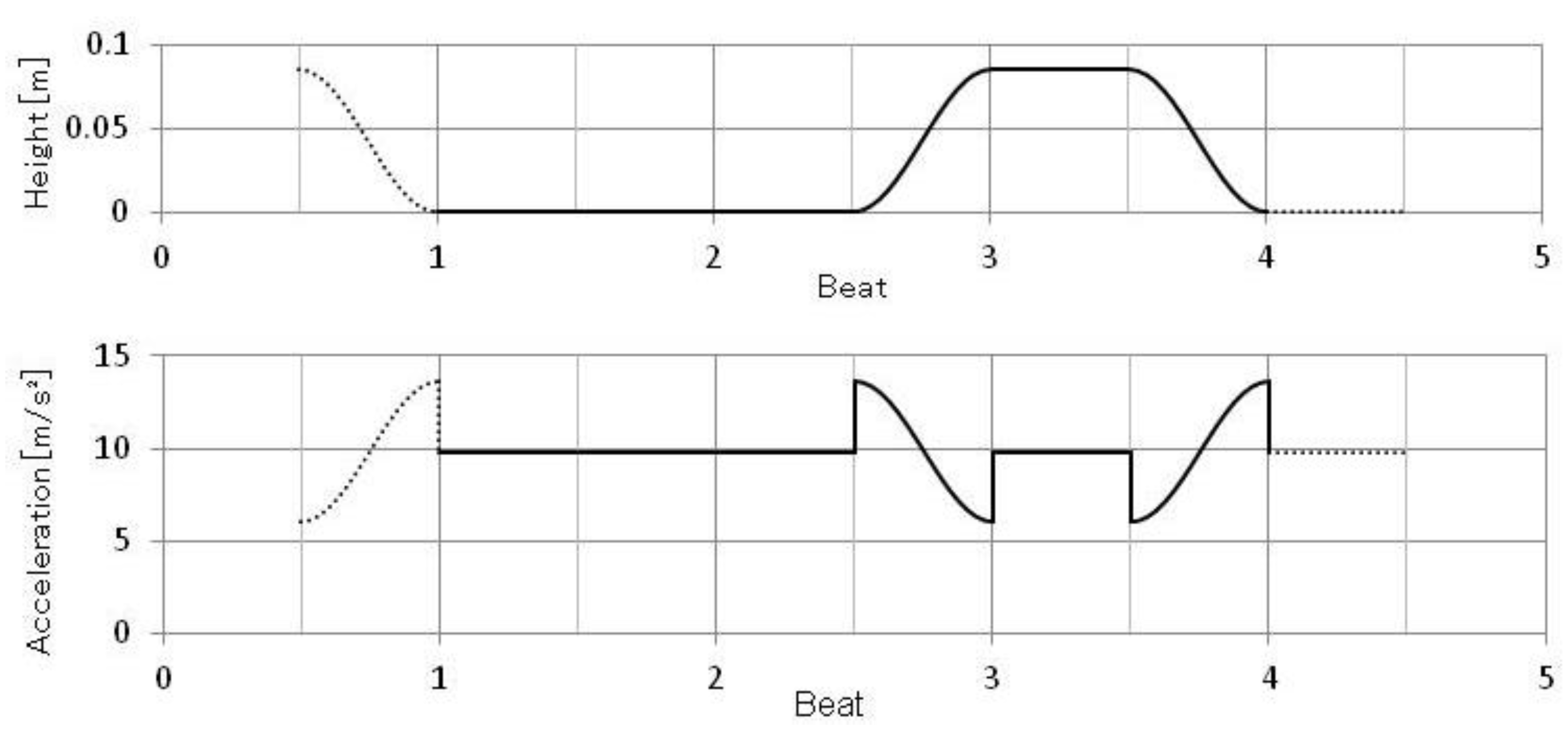
3.1.2. Spin Turn Type

This type includes 4–6 of Natural Spin Turn (Man & Lady), Impetus (Closed & Open, Man & Lady), Outside Spin (Man & Lady), 1–3 of Basic Weave (Man & Lady). The description of Rise and Fall is:

No rise (Down) from the first beat to the middle of second beat; Rise e/o 2, Up on 3, Lower e/o 3. The characteristics of this type are no rise in Count 1, rapid rise e/o Count 2, and “Up” in count 3. The reason of the “Up” is that the step on this count is not closing to the other foot but end in the open position. The height of “Up” is lower than the rising height of Natural turn as explained in the above sub-section. The height and the acceleration are shown in Figure 2. Compared with Natural Turn, the Rise is more rapid and accordingly the change of load (acceleration) is more remarkable. The duration of “Up” in Count 3 becomes shorter if the Turning Lock follows.

3.1.3. Other Type of Rise and Fall

Other types of Rise and Fall in Waltz and also in other swing dances can similarly be analyzed referring the description of Rise and Fall in the syllabi [4,5]. It is noted that in some figures, the rising process is over two or three steps, however, the lowering process is done on one step.

4. Limitation of Rise and Fall in Swing Dances

The normal lowering duration in Waltz, Foxtrot and Viennese Waltz is half of the beat. In case of Quickstep, the lowering is made on the Q Count, or on the S depending on the figure. Assuming the similar lowering pattern, the acceleration is proportional to the square of time. In order to feel the similar natural acceleration as in Waltz, the height is 9/16 in Foxtrot, 1/4 in Viennese Waltz, and about 0.2 or 0.4 in Quickstep if the height in Waltz is taken unity. The maximum possible height is given by setting Equation (4) zero, i.e., zero acceleration, as,

$$H=\frac{2g}{{\pi }^2}{T}^2,$$

(6)

On the other hand, the maximum acceleration occurs at the start of rise or the end of lowering as,

$$a_{\max }=g+\frac{{\pi }^{2}H}{2T^2}=2g$$

(7)

This corresponds to the twice of the body weight. It is noted that the accelerations shown here is only the vertical component, and the actual force felt by the feet includes the horizontal component. It should also be emphasized that the cases in which the whole body leaves the floor by jumping or leaping are excluded in the present analysis. The maximum possible height in each dance is exhibited in

Table 1. Maximum allowable Rise and Fall range in swing dances.

	Waltz	Foxtrot	Viennese Waltz	Quickstep
Tempo (bpm)	30	30	60	50
Beat length (s)	2/3	0.5	1/3	0.3
Lowering duration	Latter half of count 3 (half beat)	Latter half of count Q (half beat)	Latter half of count 3 (half beat)	Latter half of count Q (half beat)	Latter half of count S (one beat)
Maximum height (m)	0.221	0.124	0.055	0.045	0.179

. The dancers are advised not to make wasted effort to exceed these limits.

5. Conclusions

Rise and fall of Ballroom dancing is analyzed mechanically. The potential and kinetic energy exchange in Rise and Fall is discussed. Sinusoidal function is adapted as a natural rising and lowering movements. The Rise and Fall types in each dance are classified. The height and the vertical acceleration are shown for each standard figure. It is cleared that the rising height depends on each figure. The analysis has shown that each dance has its limitation of Rise and Fall and that it does not depends on the dancer’s height or weight. The results shown are from the theoretical analysis and the measurement of actual movement will be desired.