Abstract
An aerodynamic study was conducted on eleven high-end ‘aero-road’ helmets with the aim of determining whether a helmet can simultaneously have low drag and efficient cooling. The aerodynamic drag of each helmet was measured using a custom-built cycling manikin at a velocity of 40 km/h with a yaw angle range of 0° to ±25° and at velocities of 50 and 58 km/h at 0° yaw. Thermal testing of the cooling abilities of each helmet was conducted with a custom-built heated mannequin headform, which incorporated 36 thermocouples embedded within its surface. Contour plots of the temperature distributions over the head were created together with images obtained by a thermal camera. The results demonstrate that all the aero-road helmets are generally as cool as each other, however, there can be significant differences in the aerodynamic drag.
1. Introduction
At typical race speeds, aerodynamic drag accounts for greater than 90% of the total resistive force on a cyclist and the power required to maintain a constant speed is proportional to the velocity cubed [1]. Efforts to minimise the aerodynamic drag, one method being through the use of streamlined helmets, can greatly decrease the power demand required for cycling. It is common for professional and some amateur cyclists to use a low drag helmet as it has been shown that an aerodynamic helmet can produce a 4–7% total drag reduction compared to a conventional helmet [2]. However, most low-drag helmets have a significant thermal penalty.
Helmet cooling is provided via vents that supply airflow across the scalp of a rider, using forced convection to cool the head. However, these vents prevent a smooth flow of air over the helmet’s exterior, increasing the aerodynamic drag. Low drag helmets have minimal cooling vents and therefore can cause a rider’s head to overheat, creating discomfort, sweating, increasing fatigue and potentially reducing the performance of the cyclist [3]. A recent trend in road helmet design is to reduce the number of vents over the central section of the helmet, following observations by De Brynne et al. [4] that inlets in this region are not as effective as anterior or posterior openings.
Many studies that measure the aerodynamic drag or thermal efficiency of cycling helmets separately have been undertaken, however, there are few that have researched the effects of both simultaneously. One study completed by Alam et al. [5] used helmets that are now several generations old and have not benefited from extensive aerodynamic research during development. The objective of this current study was to investigate whether recently-developed high-end aero-road cycling helmets are able to be simultaneously thermally cool and aerodynamically low-drag.
2. Materials and Methods
2.1. Description of Helmets
Eleven different helmets were tested, the exact identity of which has been masked for anonymity reasons. The primary helmets considered were eight elite aero-road helmets deemed the best road helmet from the predominant cycling companies at the time of testing in 2016. Three different style helmets were also tested for comparison. These consisted of; two previous generation road cycling helmets where one was designed to be cool (#1) whilst the other was designed to provide low drag (#2), and a low-drag Time Trial (TT) helmet (#3). Additionally, helmet #4 was tested with the anterior cooling inlets covered over and the posterior outlets left open (#4a). The mannequin bare head (BH) was also tested as a baseline comparison.
2.2. Aerodynamic Drag Measurements
Drag testing was completed at the University of Adelaide blower wind tunnel. This is an open-jet blower tunnel with an octagonal test cross-section of 0.9 × 0.9 m and a top speed of 16.2 m/s. Drag measurements were collected with a bicycle and custom mannequin that had been positioned in a typical TT position. The mannequin is a fashion display mannequin with extensive modifications based on photographic analysis of the positions adopted by elite cyclists during racing. Particular care was taken to ensure that the location of the head relative to the torso and bicycle was accurate, allowing interactions between the helmet and body to accurately reflect real-world conditions. The model was mounted on a turntable that could yaw the model in a manner that allowed the head to remain positioned in the centre of the flow. The test model was fitted with two Loadstar (Fremont, CA, USA) single point load cells, one (Model RRP2, 50 kg) mounted at the base that measured the drag force for the entire rig, and a second (Model RSP1, 5 kg) mounted at the base of the neck of the mannequin that measured the drag force for the head alone. Both load cells measured the force along the bicycle axis, i.e., the drag force experienced by a cyclist rather than the aerodynamic axis drag. Testing was completed to determine if there was any significant difference between the two load cells and it was observed that although the magnitude differed, the relative difference between the two load cells was approximately consistent across the required range of yaw angles and flow speeds. This enabled further testing to be completed with the neck load cell alone.
All helmets were tested at a speed of 11.1 m/s (40 km/h) and through a yaw angle sweep of 0, 2.5, 5, 7.5, 10, 15, 20 and 25° in both positive and negative directions. This provided aerodynamic drag measurements across the range of yaw angles expected during typical cycling. Smaller increments were used at the more common lower yaw angles to provide higher resolution. Further testing was completed at speeds of 13.9 m/s (50 km/h) and 16.2 m/s (58 km/h) and a yaw angle of 0°. For each of the three testing speeds, the mannequin head angle and height was adjusted to reflect a realistic riding position for that respective speed. Testing at the slowest speed (40 km/h) had the head in an upright position, angled 30° from the vertical plane. The head angle increased to 38° for the 50 km/h test, and for the 58 km/h test, the head was lowered 20 mm and the angle adjusted to 60°. These positions were chosen from photographic analysis of competitive cyclists at a variety of velocities. The angles were defined by the angle of the headform reference line as outlined in AS/NZS 2512.1:2009 (Size K), the Australian helmet testing standard [6]. A custom jig was constructed that identically aligned all helmets with the headform reference line, using a helmet positioning index of 23 mm. This ensured that each helmet was consistently placed in the position that they had been designed and tested for.
2.3. Frontal Area
Each helmet was photographed alongside a reference area of known size and photo editing software was used to calculate the frontal area of the combined helmet and mannequin head. This was calculated for each of the 39 different head positions, resulting in a mean frontal area of 0.0574 m2 with a standard deviation (SD) of 0.0019 m2. The resultant blockage ratio was approximately 8.5% for the helmet and head, and 31% for the entire mannequin. However, for an open-jet tunnel, the effects of solid blockage are one-fourth of the equivalent for a closed-jet tunnel [7]. This results in a blockage ratio of 2.1% and 7.9% which are within acceptable bounds. The testing was completed as a comparison between configurations rather than to obtain exact magnitudes of drag forces, reducing the need to correct for blockage. Additionally, as the size difference between all helmets was minimal, each helmet would have been affected by the blockage equally. As such, blockage correction calculations were not undertaken.
The projected frontal area of all inlet vents at a head angle of 30° was measured in a similar fashion and the average inlet area per vent was calculated. There was a wide variation between the size and number of inlet vents with a minimum inlet area of 3.6 cm2 across 3 vents (1.2 cm2/vent, #2) to a maximum inlet area of 100 cm2 across 10 vents (10 cm2/vent, #1). The mean was 52.5 cm2 (SD = 32.2 cm2) and 7.9 cm2/vent (SD = 4.0 cm2/vent).
2.4. Thermal Measurements
Testing of the thermal performance of the helmets was completed in The University of Adelaide’s KC Wind Tunnel. This is a low-speed open-jet wind tunnel with a 0.5 × 0.5 m test section, and maximum speed of 30 m/s. A custom-built heated head was used to measure the thermal cooling properties of each helmet. The headform was based on head and face anthropomorphic measurements collected by Zhuang and Bradtmiller [8] who produced a 3D model of an average 50th percentile head. This model was 3D printed in ABS plastic which has a similar thermal conductivity to human skin, ensuring the heat would dissipate over the scalp at a realistic rate. The headform had 36 thermocouples embedded across the scalp surface and a heater mounted inside the head that distributed heat evenly across the surface.
Throughout all testing the thermal head was heated at a constant power that equated to a constant mean temperature of 38 °C in still air. Experimentation was completed with the head tilted forward 30° and at a velocity of 11.1 m/s where the head temperature decreased until steady sate conditions were achieved. For each helmet the temperature data from the thermocouples was constantly recorded for a period of 50 min. The wind tunnel was then turned off, the flow was blocked, the helmet removed, and thermograms of the head were immediately captured with a thermal camera placed at two different locations. The ambient temperature of the room was recorded throughout the experiment and used to determine the temperature difference from the scalp temperature. For all tests the mean ambient temperature was 24.9 °C (SD = 0.50 °C).
2.5. Measurement Error
To investigate the accuracy of the drag measurements, the complete yaw angle sweep of 16 drag data points was repeated twice for five different helmets. The resultant drag error was ±0.019 N (1.8%). A similar procedure was followed for testing the error of the thermal headform, producing a result of ±0.62 °C (1.8%). To measure the influence of helmet repositioning errors, the helmet was placed on the mannequin, the drag recorded, and then the helmet was replaced, six times in succession. This resulted in a helmet replacement error of ±0.0021 N (0.17%).
3. Results and Discussion
3.1. Drag Testing
The Wind Averaged Drag (WAD) was calculated at 11.1 m/s using the method described by Brownlie et al. [9] and is shown in Figure 1 alongside the drag data at zero yaw angle. All drag data sets have had the bare head drag value subtracted. The results were consistent with expectations, demonstrating that the TT helmet (#3) yielded the lowest drag at all positions and covering the vents in helmet #4a showed a drag advantage across all speeds. The range of aero-road helmets displayed significant variation between models, while previous-generation helmets displayed higher drag, particularly #1, which was designed for maximum ventilation. There was a minor difference between the WAD and drag at zero yaw for the same speed, with a +3.5% mean difference.
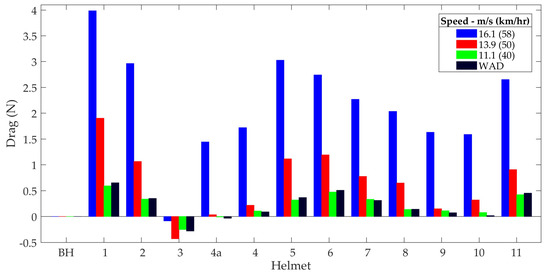
Figure 1.
Drag at 0° yaw and WAD difference from bare head for each of the helmets.
3.2. Thermal Testing
The cooling ability of all helmets was tested at the same conditions as for the WAD testing and is shown in Figure 2 as a contour plot of the temperatures recorded at each thermocouple across the head. Thermal images of the heated head at steady state conditions were also taken for analysis alongside the contour plots and are shown in Figure 3. Temperature distributions across the scalp are clearly visible in both figures with the cooler areas at the front of the head and warmer areas towards the rear. These variations are attributed to the airflow pattern across the scalp with the fastest-flowing, cool air at the front creating the greatest forced convection and heat transfer whilst the slower moving, warmer air at the rear provided less cooling. Also visible on the thermal images are locations of vents and channels by observing the clear delineation of cool areas along the airflow path and warmer areas where the helmet is in contact with the head.
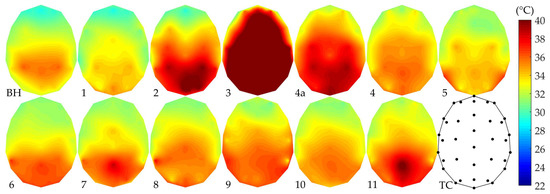
Figure 2.
Contour plots of the interpolated temperature across the mannequin headform. Diagram ‘TC’ displays the location of each thermocouple on the headform. This is an approximate model due to the inconsistencies of transforming 3D coordinates to a 2D plane.
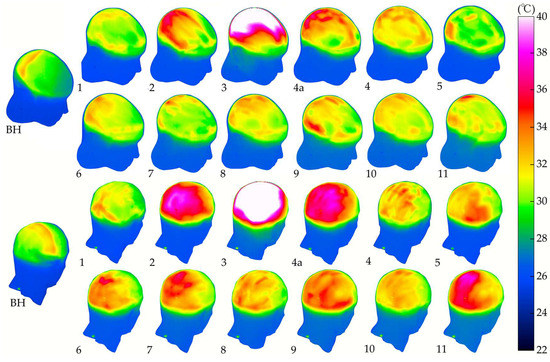
Figure 3.
Thermal images of the heated head taken from two different angles.
The rear of the head was the area that displayed most significant difference between helmets. The mean temperature for the headform rear-half was 35.5 °C (SD = 2.6 °C), whilst for the front-half the mean temperature was 32.6 °C (SD = 1.4 °C). This indicates a greater variation between helmets towards the rear of the head. Comparison of thermal images to the physical helmet showed that the coolest helmets were those with large vents and deep internal channels allowing fast-moving air to be drawn from the front, across the scalp, and out the rear without significant restriction of the flow area. This effect is most clearly demonstrated in helmets #4 and #4a where covering the anterior intake vents reduces the cooling at the rear, despite the posterior outlets remaining open.
3.3. Drag and Cooling Combined
A method of combining the aerodynamic drag and thermal cooling abilities of each helmet is to plot the mean temperature difference against the WAD (shown in Figure 4). The ambient temperature has been subtracted from the head temperature to account for any atmospheric changes between tests. The prominent outliers present in the group of helmets tested were the TT helmet (#3) and the two previous-generation helmets (#1, 2). A significant result is the effect of covering the vents in helmet #4 which simultaneously lowered the drag and increased the temperature.
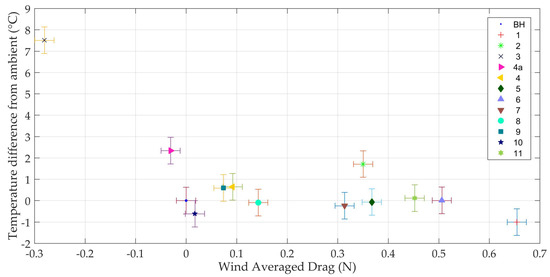
Figure 4.
Mean temperature difference from ambient versus WAD for each helmet at a velocity of 11.1 m/s. Both axes have had the values for the bare head subtracted to base all data around the bare head as the zero point.
A trend is evident when the outliers are removed and the primary focus helmets (high end aero-road helmets #4–11) are analysed. Generally speaking, it can be observed that while most helmets are equally cool, there are significant variations in drag production. Additionally, all helmets are approximately as cool as a bare head, indicating that thermal discomfort due to the use of a helmet should be minimal.
It was observed that for the range of helmets tested, vents across the central portion of the helmet proved to be relatively ineffective at cooling. Having no vents in this region has a minimal thermal penalty with the potential to significantly decrease the aerodynamic drag. This is most evident in the results from helmet #10 which was the second coolest helmet tested, yet had few vents and was the fastest unmodified aero-road helmet. Observing the thermal images, it is clear that #10 was able to draw airflow from the large anterior vents (12.5 cm2/vent) across the head, and out the posterior outlets in an efficient manner. In contrast, helmets that were similarly cool but with a smaller inlet area per vent had a much higher aerodynamic drag.
4. Conclusions
The results of this study demonstrate that contemporary high-end road cycling helmets are beginning to overcome the dichotomy of a fast and cool helmet. While there is still a clear distinction between a road and TT helmet, high-end aero-road helmets are able to reduce a rider’s aerodynamic drag with minimal thermal cost, reducing power demand without decreasing rider comfort.
Acknowledgments
This research was supported by Scott Sports SA. The authors would also like to acknowledge the help of Paul Grimshaw, Darcy Thompson-Bagshaw, Tom Goddard, Guy Page and Ben Whyte.
Conflicts of Interest
The authors declare no conflict of interest and the funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript and in the decision to publish the results.
References
- Kyle, C.R.; Burke, E.R. Improving the racing bicycle. Mech. Eng. 1984, 106, 34–45. [Google Scholar]
- Blair, K.; Sidelko, S. Aerodynamic Performance of Cycling Time Trial Helmets (P76). In The Engineering of Sport, 7th ed.; Estivalet, M., Brisson, P., Eds.; Springer: Paris, France, 2009; Volume 1, pp. 371–377. [Google Scholar]
- Ellis, A.J.; Bertolini, A.F.; Thompson, L.A. A review of research on bicycle helmet ventilation. Sports Eng. 2000, 3, 185–194. [Google Scholar] [CrossRef]
- De Bruyne, G.; Aerts, J.; Sloten, J.V.; Goffin, J.; Verpoest, I.; Berckmans, D. Quantification of local ventilation efficiency under bicycle helmets. Int. J. Ind. Ergon. 2012, 42, 278–286. [Google Scholar] [CrossRef]
- Alam, F.; Chowdhury, H.; Elmir, Z.; Sayogo, A.; Love, J.; Subic, A. An experimental study of thermal comfort and aerodynamic efficiency of recreational and racing bicycle helmets. In Proceedings of the 8th conference of the International Sports Engineering Association, Vienna, Austria, 12–16 July 2010; pp. 2413–2418. [Google Scholar]
- Standards Australia. Methods of Testing Protective Helmets; AS/NZS 2512; Standards Australia: Sydney, Australia, 2009. [Google Scholar]
- Rae, W.; Pope, A. Low-Speed Wind Tunnel Testing, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1984. [Google Scholar]
- Zhuang, Z.; Bradtmiller, B. Head-and-Face Anthropometric Survey of U.S. Respirator Users. J. Occup. Environ. Hyg. 2005, 2, 567–576. [Google Scholar] [CrossRef] [PubMed]
- Brownlie, L.; Ostafichuk, P.; Tews, E.; Muller, H.; Briggs, E.; Franks, K. The wind-averaged drag of competitive time trial cycling helmets. In Proceedings of the 8th conference of the International Sports Engineering Association (ISEA), Vienna, Austria, 12–16 July 2010. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
