Entropy Production in the Expanding Universe †
Abstract
1. Introduction
2. Particle Creation in the Expanding Universe
3. Particle Creation Entropy
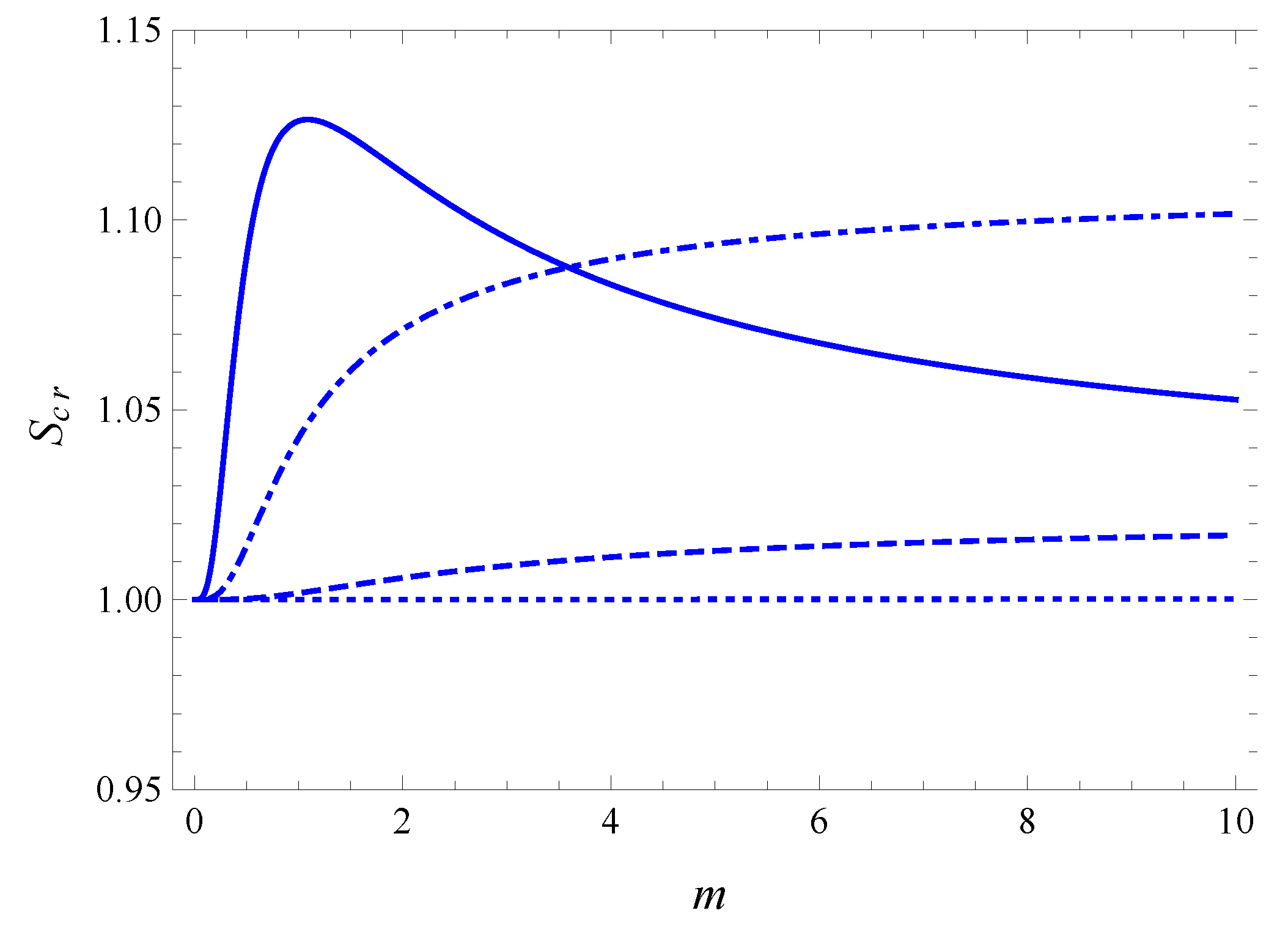
4. Interpretation of Results
5. Entanglement Entropy
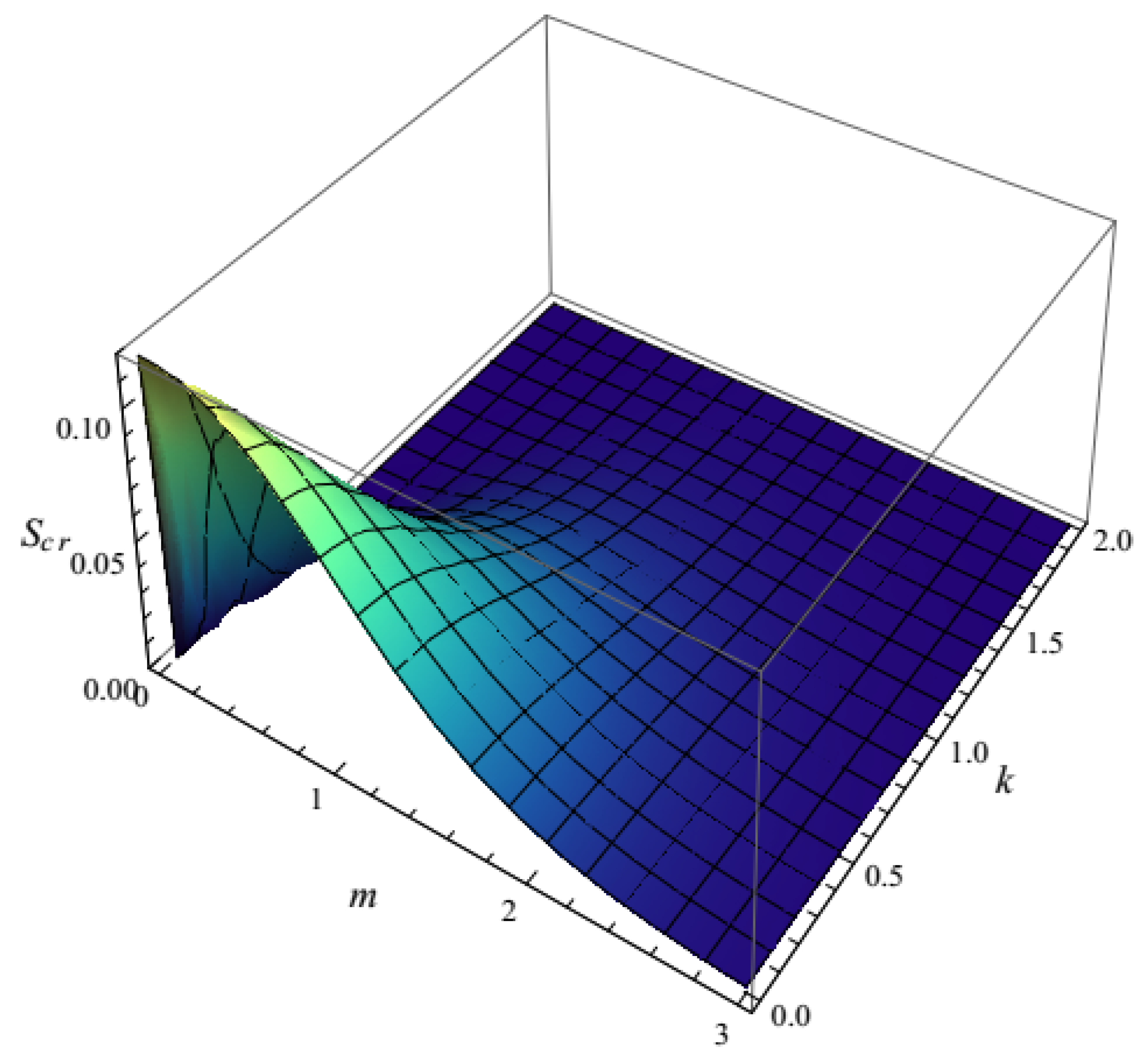
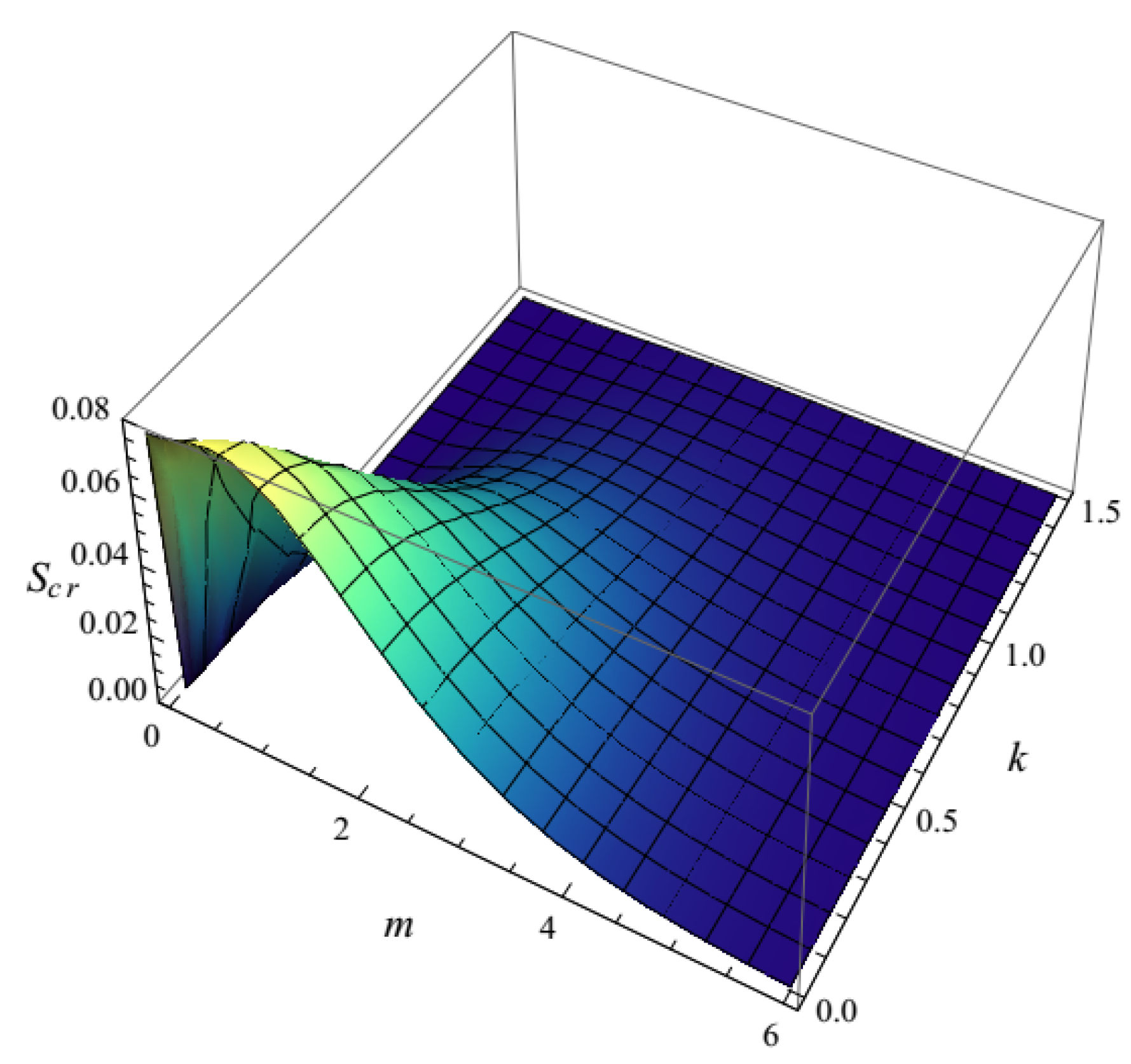
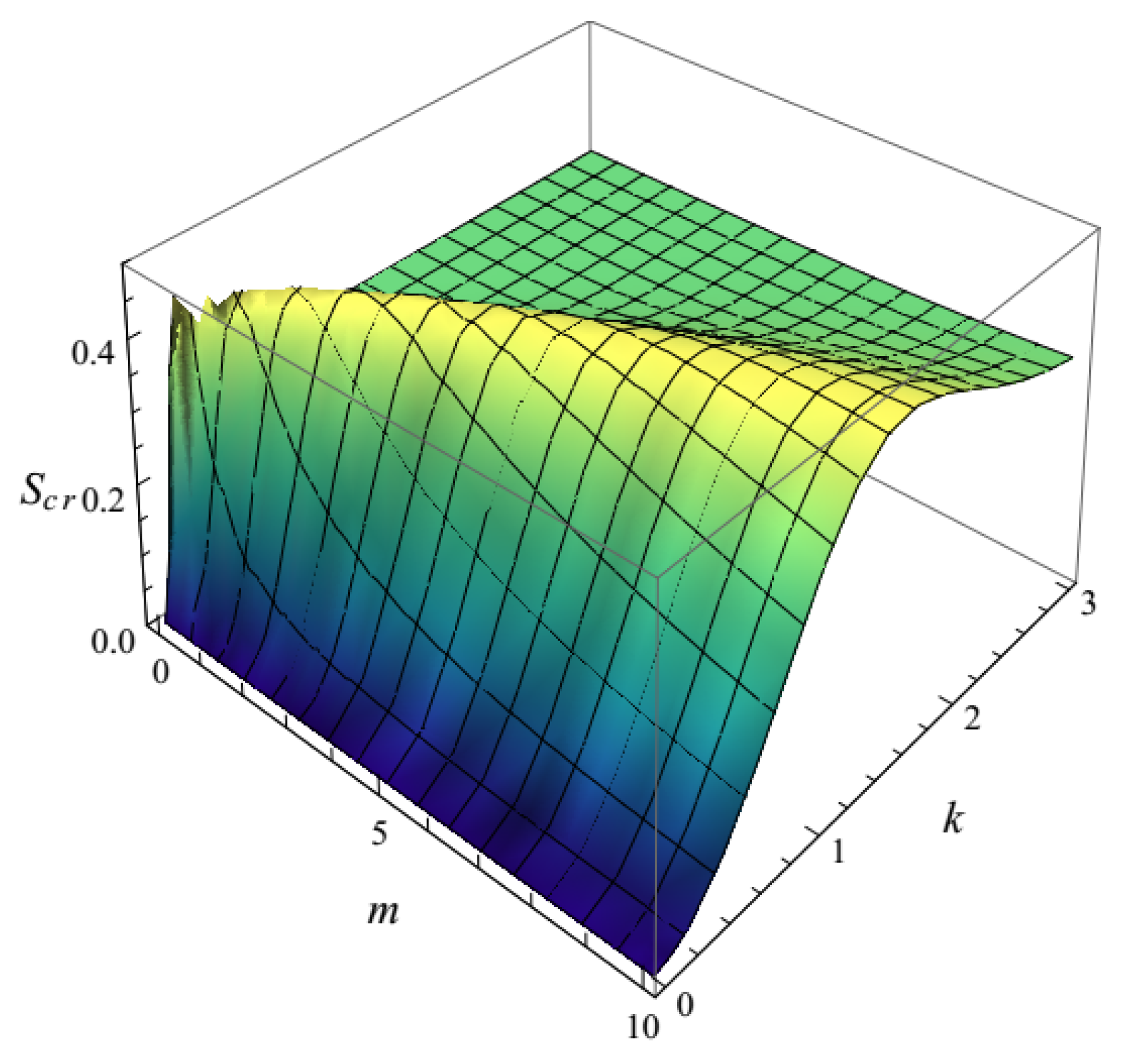
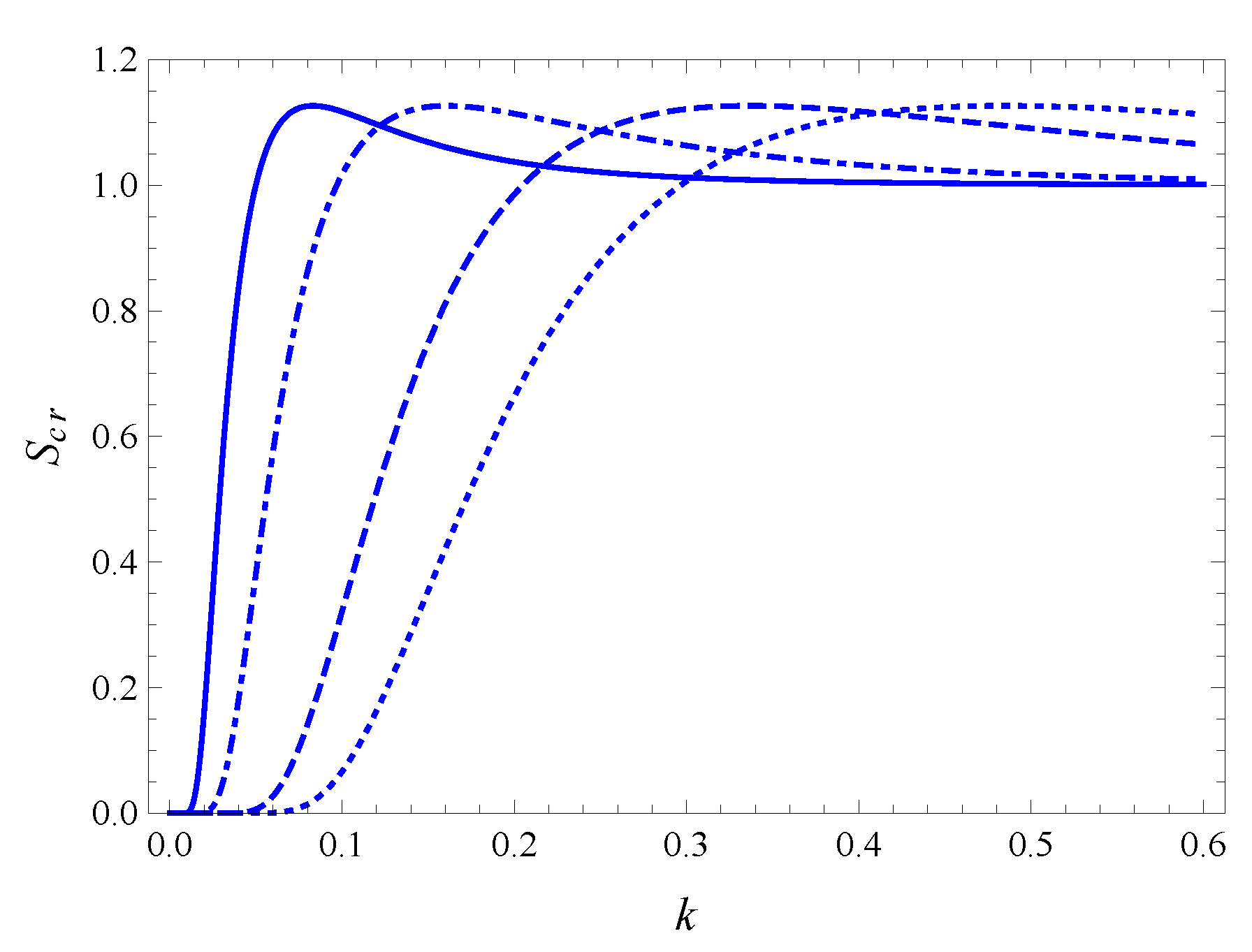
6. Entropy Production
7. Conclusions
Conflicts of Interest
References
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Ball, J.L.; Fuentes-Schuller, I.; Schuller, F.P. Entanglement in an expanding spacetime. Phys. Lett. A 2006, 359, 550–554. [Google Scholar] [CrossRef]
- Fuentes, I.; Mann, R.B.; Martín-Martínez, E.; Moradi, S. Entanglement of Dirac fields in an expanding spacetime. Phys. Rev. D 2010, 82, 045030. [Google Scholar] [CrossRef]
- Farahmand, M.; Mohammadzadeh, H.; Mehri-Dehnavi, H. Quantum thermodynamics and quantum entanglement entropies in an expanding universe. Int. J. Mod. Phys. 2017, 32, 1750066. [Google Scholar] [CrossRef]
- Mohammadzadeh, H.; Farahmand, M.; Maleki, M. Entropy production due to Lorentz invariance violation. Phys. Rev. D 2017, 96, 024001. [Google Scholar] [CrossRef]
- Martín-Martínez, E.; Menicucci, N.C. Entanglement in curved spacetimes and cosmology. Class. Quantum Gravity 2014, 31, 214001. [Google Scholar] [CrossRef]
- Ebadi, Z.; Mirza, B. Entanglement generation by electric field background. Ann. Phys. 2014, 351, 363–381. [Google Scholar] [CrossRef]
- Ebadi, Z.; Mirza, B. Entanglement generation due to the background electric field and curvature of space-time. Int. J. Mod. Phys. A 2015, 30, 1550031. [Google Scholar] [CrossRef]
- Mohammadzadeh, H.; Ebadi, Z.; Mehri-Dehnavi, H.; Mirza, B.; Rahimi, R. Entanglement of arbitrary spin modes in expanding universe. Quantum Inf. Process. 2015, 14, 4787–4801. [Google Scholar] [CrossRef]
- Pierini, R.; Moradi, S.; Mancini, S. The role of spin in entanglement generated by expanding spacetime. Int. J. Theor. Phys. 2016, 55, 3059–3078. [Google Scholar] [CrossRef][Green Version]
- Mann, R.B.; Ralph, T.C. Relativistic quantum information. Class. Quantum Gravity 2012, 29, 220301. [Google Scholar] [CrossRef]
- Benincasa, D.M.T.; Borsten, L.; Buck, M.; Dowker, F. Quantum information processing and relativistic quantum fields. Class. Quantum Gravity 2012, 31, 075007. [Google Scholar] [CrossRef][Green Version]
- Alsing, P.M.; Milburn, G.J. Teleportation with a uniformly accelerated partner. Phys. Rev. Lett. 2003, 91, 180404. [Google Scholar] [CrossRef] [PubMed]
- Alsing, P.M.; Fuentes-Schuller, I.; Mann, R.B.; Tessier, T.E. Entanglement of Dirac fields in noninertial frames. Phys. Rev. A 2006, 74, 032326. [Google Scholar] [CrossRef]
- Adesso, G.; Fuentes-Schuller, I.; Ericsson, M. Continuous-variable entanglement sharing in noninertial frames. Phys. Rev. A 2007, 76, 062112. [Google Scholar] [CrossRef]
- Mehri-Dehnavi, H.; Rahimi, R.; Mohammadzadeh, H.; Ebadi, Z.; Mirza, B. Quantum teleportation with nonclassical correlated states in noninertial frames. Quantum Inf. Process. 2015, 14, 1025–1034. [Google Scholar] [CrossRef]
- Helder, A.; de Souza, G.; Mansfield, P.; Sampaio, M. Alice and Bob in an expanding spacetime. EPL 2015, 111, 60001. [Google Scholar]
- Müller, R.; Lousto, C.O. Entanglement entropy in curved spacetimes with event horizons. Phys. Rev. D 1995, 52, 4512–4517. [Google Scholar] [CrossRef]
- Zare, S.; Raissi, Z.; Mohammadzadeh, H.; Mirza, B. Condensation of an ideal gas with intermediate statistics on the horizon. Eur. Phys. J. C 2012, 72, 2152. [Google Scholar] [CrossRef]
- Ebadi, Z.; Mirza, B.; Mohammadzadeh, H. Infinite statistics condensate as a model of dark matter. J. Cosmol. Astropart. Phys. 2013, 11, 057. [Google Scholar] [CrossRef]
- Parker, L. Particle creation in expanding universes. Phys. Rev. Lett. 1968, 21, 562. [Google Scholar] [CrossRef]
- Liu, N.; Goold, J.; Fuentes, I.; Vedral, V.; Modi, K.; Bruschi, D.E. Quantum thermodynamics for a model of an expanding universe. Class. Quantum Gravity 2016, 33, 035003. [Google Scholar]
- Campisi, M.; Hänggi, P.; Talkner, P. Colloquium: Quantum fluctuation relations: Foundations and applications. Rev. Mod. Phys. 2011, 83, 771–791. [Google Scholar] [CrossRef]
- Haouat, S.; Chekireb, R. On the Creation of Scalar Particles in a Flat Robertson–Walker Spacetime. Mod. Phys. Lett. A 2011, 26, 2639–2651. [Google Scholar] [CrossRef]
- Esposito, M.; Lindenberg, K.; van den Broeck, C. Entropy production as correlation between system and reservoir. New J. Phys. 2010, 12, 013013. [Google Scholar] [CrossRef]
- Strasberg, P.; Schaller, G.; Brandes, T. Quantum and information thermodynamics: A unifying framework based on repeated interactions. Phy. Rev. X 2017, 7, 021003. [Google Scholar] [CrossRef]
- Mukhanov, V. Physical Foundations of Cosmology; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Alsing, P.M.; McMahon, D.H.; Milburn, G.J. Teleportation in a non-inertial frame. J. Opt. B Quantum Semiclass. Opt. 2004, 6, S834. [Google Scholar] [CrossRef]
- Yurke, B.; Potasek, M. Obtainment of thermal noise from a pure quantum state. Phys. Rev. A 1987, 36, 3464. [Google Scholar] [CrossRef] [PubMed]
- Gerry, C.; Knight, P. Introductory Quantum Optics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Feldmann, T.; Kosloff, R. Performance of discrete heat engines and heat pumps in finite time. Phys. Rev. E 2000, 61, 4774–4790. [Google Scholar] [CrossRef]
- Del Campo, A.; Goold, J.; Paternostro, M. More bang for your buck: Super-adiabatic quantum engines. Sci. Rep. 2014, 4, 6208. [Google Scholar] [CrossRef]
- Plastina, F.; Alecce, A.; Apollaro, T.; Falcone, G.; Francica, G.; Galve, F.; Gullo, N.L.; Zambrini, R. Irreversible work and inner friction in quantum thermodynamic processes. Phys. Rev. Lett. 2014, 113, 260601. [Google Scholar] [CrossRef]
- Tasaki, H. Jarzynski relations for quantum systems and some applications. arXiv 2000, arXiv:cond-mat/0009244. [Google Scholar]
- Evans, D.J.; Cohen, E.; Morriss, G. Probability of second law violations in shearing steady states. Phys. Rev. Lett. 1993, 71, 2401–2404. [Google Scholar] [CrossRef] [PubMed]
- Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721. [Google Scholar] [CrossRef] [PubMed]
- Barnett, S.; Radmore, P.M. Methods in Theoretical Quantum Optics; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Unruh, W.G. Notes on black-hole evaporation. Phys. Rev. D 1976, 14, 870. [Google Scholar] [CrossRef]
- Bernard, C.; Duncun, A. Regularization and renormalization of quantum field theory in curved space-time. Ann. Phys. 1977, 107, 201–221. [Google Scholar] [CrossRef]
- Setare, M.R. Cosmological particle creation and dynamical Casimir effect. Int. J. Theor. Phys. 2004, 43, 2237–2242. [Google Scholar] [CrossRef]
- Moradi, S. Creation of Scalar and Dirac Particles in Asymptotically Flat Robertson-Walker Spacetimes. Int. J. Theor. Phys. 2008, 47, 2807–2818. [Google Scholar] [CrossRef]
- Grib, A.A.; Pavlov, Y.V. Superheavy particles in Friedmann cosmology and the dark matter problem. Int. J. Mod. Phys. D 2002, 11, 433–436. [Google Scholar] [CrossRef]
- Grib, A.A.; Pavlov, Y.V. Cold dark matter and primordial superheavy particles. Int. J. Mod. Phys. A 2002, 17, 4435–4439. [Google Scholar] [CrossRef]
- Grib, A.A.; Pavlov, Y.V. Quantum field theory in curved space-time and the early Universe. arXiv 2002, arXiv:gr-qc/0206040. [Google Scholar]
- Grib, A.A.; Pavlov, Y.V. On the cosmological coincidence between visible and hidden masses. Grav. Cosmol. Suppl. 2002, 8, 50–51. [Google Scholar]
- Vedral, V. Introduction to Quantum Information Science; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics; John Wiley and Sons: West Sussex, UK, 2007. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Broadbridge, P.; Zulkowski, P. Dark energy states from quantization of boson fields in a universe with unstable modes. Rep. Math. Phys. 2006, 57, 27–40. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farahmand, M.; Mohammadzadeh, H. Entropy Production in the Expanding Universe. Proceedings 2018, 2, 170. https://doi.org/10.3390/ecea-4-05037
Farahmand M, Mohammadzadeh H. Entropy Production in the Expanding Universe. Proceedings. 2018; 2(4):170. https://doi.org/10.3390/ecea-4-05037
Chicago/Turabian StyleFarahmand, Mehrnoosh, and Hosein Mohammadzadeh. 2018. "Entropy Production in the Expanding Universe" Proceedings 2, no. 4: 170. https://doi.org/10.3390/ecea-4-05037
APA StyleFarahmand, M., & Mohammadzadeh, H. (2018). Entropy Production in the Expanding Universe. Proceedings, 2(4), 170. https://doi.org/10.3390/ecea-4-05037



