Ion-Generating and Ion-Capturing Nanomaterials in Liquid Crystals †
Abstract
:1. Introduction
2. Results and Discussion
2.1. Model
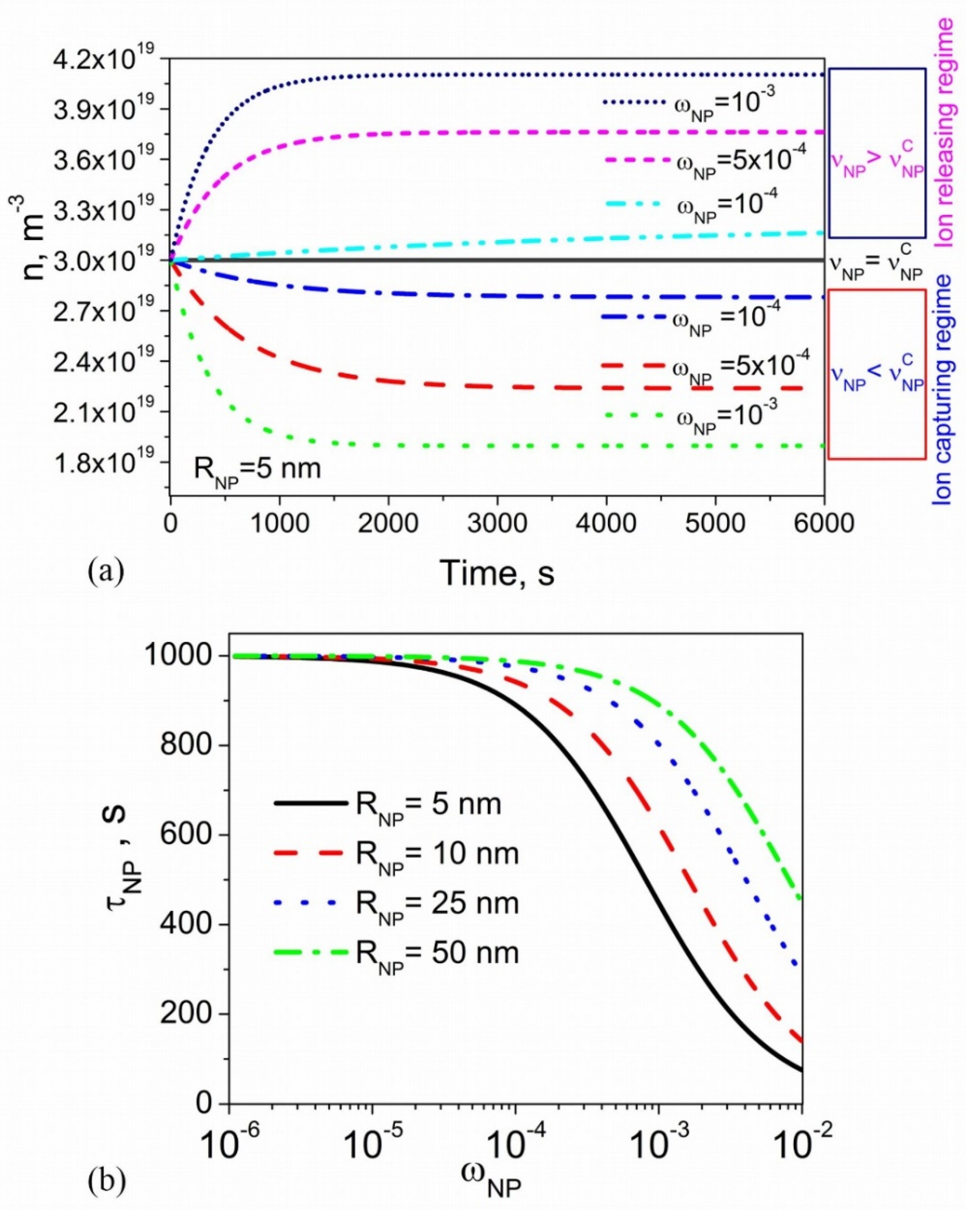
2.2. Kinetics of Ion-Capturing and Ion-Releasing Processes
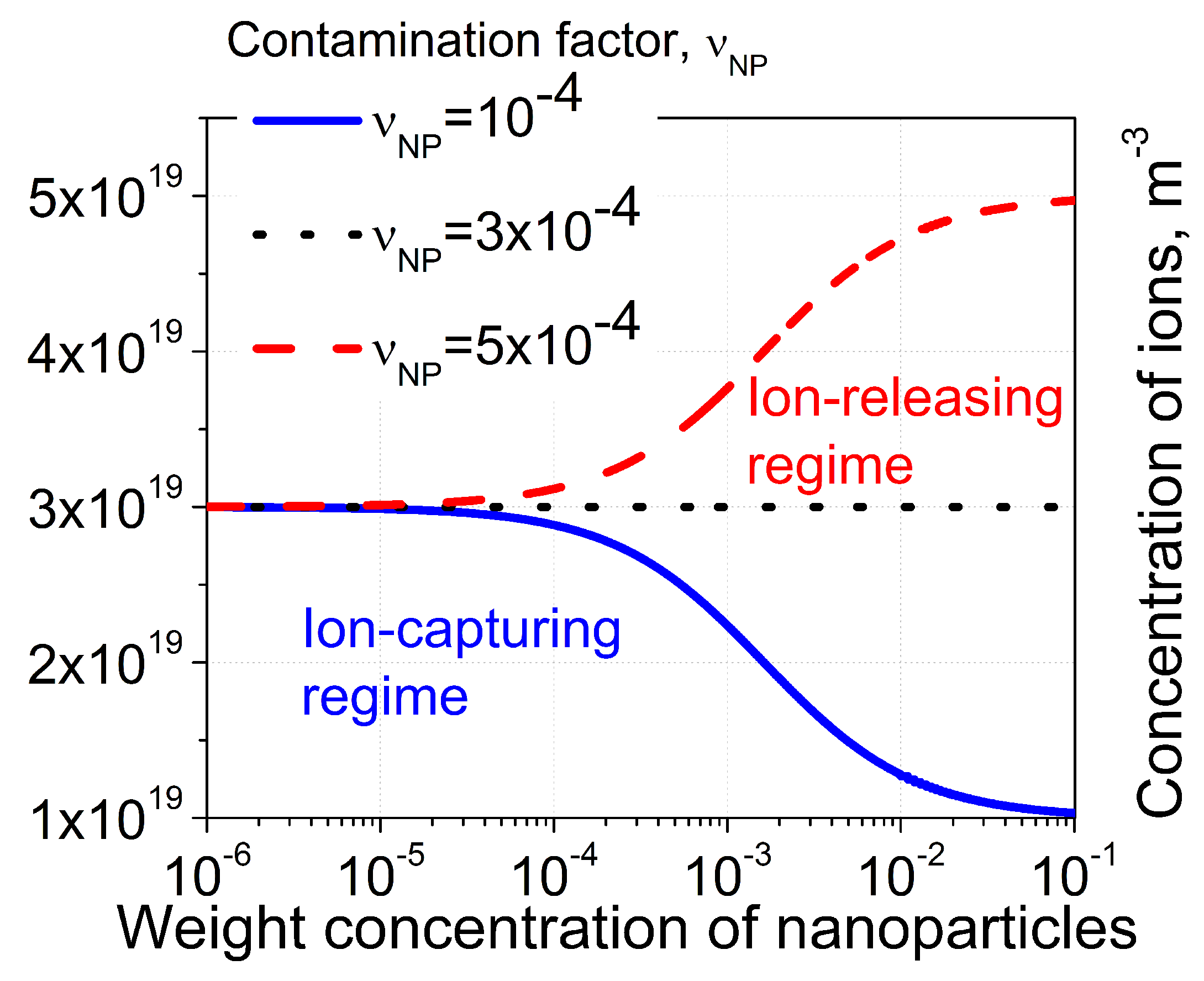
2.3. Steady-State Regime
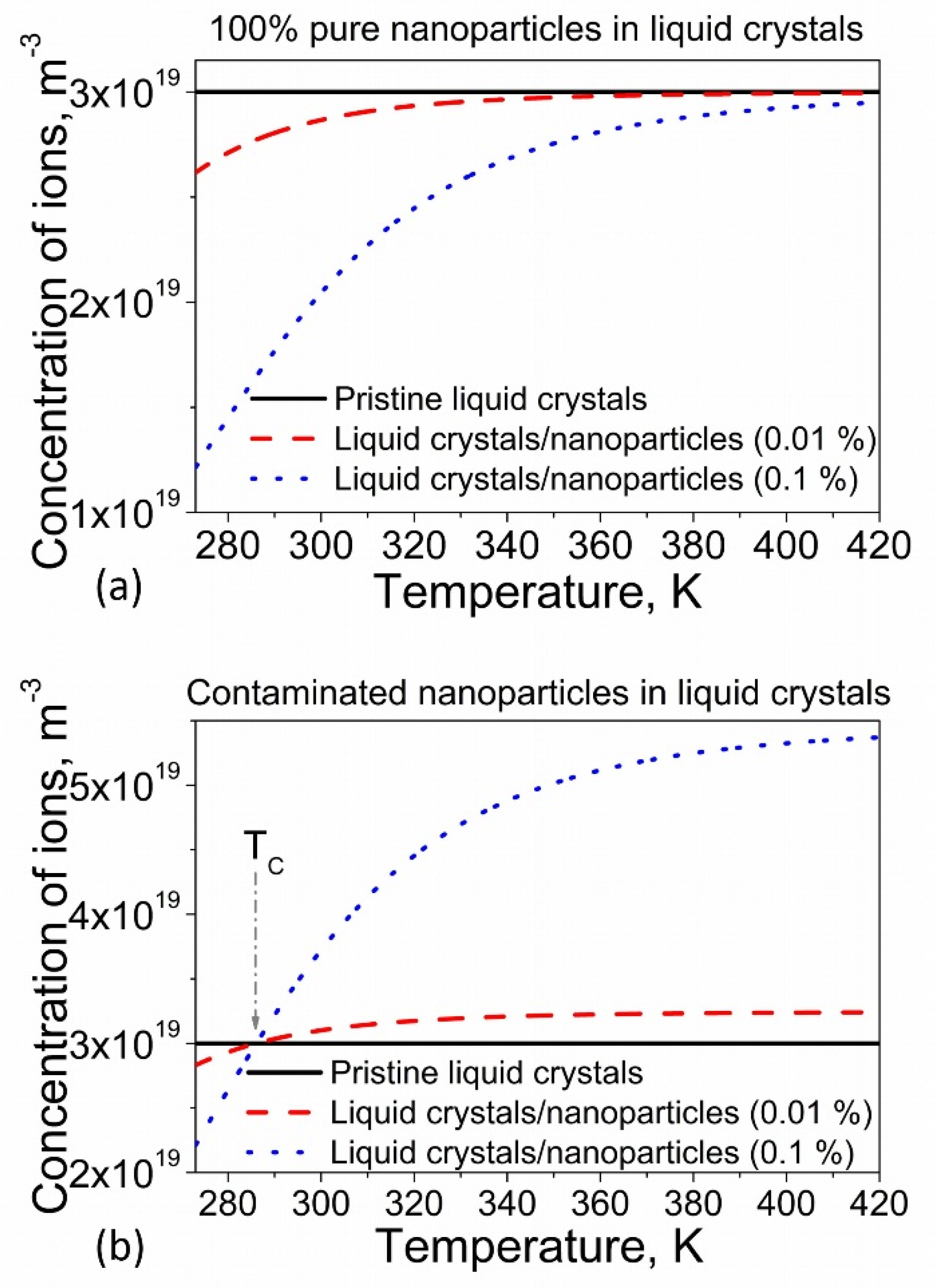
2.4. Temperature-Induced Effects
3. Case Studies: A Brief Survey
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| LCD | liquid crystal display |
References
- Yang, D.-K.; Wu, S.-T. Liquid Crystal Devices; John Wiley & Sons: Hoboken, NJ, USA, 2006; pp. 1–378. [Google Scholar]
- Chigrinov, V.G. Liquid Crystal Devices: Physics and Applications; Artech House: Boston, MA, USA, 1999; pp. 1–360. [Google Scholar]
- Abdulhalim, I. Non-display bio-optic applications of liquid crystals. Liq. Cryst. Today 2011, 20, 44–60. [Google Scholar] [CrossRef]
- De Sio, L.; Roberts, D.E.; Liao, Z.; Hwang, J.; Tabiryan, N.; Steeves, D.M.; Kimball, B.R. Beam shaping diffractive wave plates. Appl. Opt. 2018, 57, A118–A121. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-H.; Wang, Y.-J.; Reshetnyak, V. Liquid crystal lenses with tunable focal length. Liq. Cryst. Rev. 2017, 5, 111–143. [Google Scholar] [CrossRef]
- Geis, M.W.; Bos, P.J.; Liberman, V.; Rothschild, M. Broadband optical switch based on liquid crystal dynamic scattering. Opt. Express 2016, 24, 13812–13823. [Google Scholar] [CrossRef]
- Naemura, S. Electrical properties of liquid crystal materials for display applications. Mater. Res. Soc. Symp. Proc. 1999, 559, 263–274. [Google Scholar] [CrossRef]
- Neyts, K.; Beunis, F. Ion transport in liquid crystals. In Handbook of Liquid Crystals: Physical Properties and Phase Behavior of Liquid Crystals; Wiley-VCH: Weinheim, Germany, 2014; Volume 2, Chapter 11; pp. 357–382. [Google Scholar]
- Korniychuk, P.P.; Gabovich, A.M.; Singer, K.; Voitenko, A.I.; Reznikov, Y.A. Transient and steady electric currents through a liquid crystal cell. Liq. Cryst. 2010, 37, 1171–1181. [Google Scholar] [CrossRef]
- Blinov, L.M. Structure and Properties of Liquid Crystals; Springer: New York, NY, USA, 2010. [Google Scholar]
- Chang, R.; Richardson, J.M. The anisotropic electrical conductivity of MBBA containing tetrabutyl-ammonium tetraphenyl-boride. Mol. Cryst. Liq. Cryst. 1973, 28, 189–200. [Google Scholar] [CrossRef]
- Barnik, M.I.; Blinov, L.M.; Grebenkin, M.F.; Pikin, S.A.; Chigrinov, V.G. Electrohydrodynamic instability in nematic liquid crystals. Sov. Phys. JETP 1976, 42, 550–553. [Google Scholar]
- Naemura, S.; Sawada, A. Ionic conduction in nematic and smectic liquid crystals. Mol. Cryst. Liq. Cryst. 2003, 400, 79–96. [Google Scholar] [CrossRef]
- Hung, H.Y.; Lu, C.W.; Lee, C.Y.; Hsu, C.S.; Hsieh, Y.Z. Analysis of metal ion impurities in liquid crystals using high resolution inductively coupled plasma mass spectrometry. Anal. Methods 2012, 4, 3631–3637. [Google Scholar] [CrossRef]
- Murakami, S.; Naito, H. Electrode and interface polarizations in nematic liquid crystal cells. Jpn. J. Appl. Phys. 1997, 36, 2222–2225. [Google Scholar] [CrossRef]
- Mizusaki, M.; Enomoto, S.; Hara, Y. Generation mechanism of residual direct current voltage for liquid crystal cells with polymer layers produced from monomers. Liq. Cryst. 2017, 44, 609–617. [Google Scholar] [CrossRef]
- Kravchuk, R.; Koval’chuk, O.; Yaroshchuk, O. Filling initiated processes in liquid crystal cell. Mol. Cryst. Liq. Cryst. 2002, 384, 111–119. [Google Scholar] [CrossRef]
- Garbovskiy, Y. Time dependent electrical properties of liquid crystal cells: Unravelling the origin of ion generation. Liq. Cryst. 2018, 45, 1540–1548. [Google Scholar] [CrossRef]
- Chieu, T.C.; Yang, K.H. Transport properties of ions in ferroelectric liquid crystal cells. Jpn. J. Appl. Phys. 1989, 28, 2240–2246. [Google Scholar] [CrossRef]
- Murakami, S.; Naito, H. Charge injection and generation in nematic liquid crystal cells. Jpn. J. Appl. Phys. 1997, 36, 773–776. [Google Scholar] [CrossRef]
- Naemura, S.; Sawada, A. Ion Generation in Liquid Crystals under Electric Field. Mol. Cryst. Liq. Cryst. 2000, 346, 155–168. [Google Scholar] [CrossRef]
- De Vleeschouwer, H.; Verschueren, A.; Bougrioua, F.; Van Asselt, R.; Alexander, E.; Vermael, S.; Neyts, K.; Pauwels, H. Long-term ion transport in nematic liquid crystal displays. Jpn. J. Appl. Phys. 2001, 40, 3272–3276. [Google Scholar] [CrossRef]
- Kovalchuk, A.V.; Lavrentovich, O.D.; Linev, V.A. Electrical conductivity of γ-irradiated cholesteric liquid crystals. Sov. Tech. Phys. Lett. 1988, 14, 381–382. [Google Scholar]
- Naito, H.; Yoshida, K.; Okuda, M.; Sugimura, A. Transient Current Study of Ultraviolet-Light-Soaked States in n-Pentyl-p-n-Cyanobiphenyl. Jpn. J. Appl. Phys. 1994, 33, 5890–5891. [Google Scholar] [CrossRef]
- Barret, S.; Gaspard, F.; Herino, R.; Mondon, F. Dynamic scattering in nematic liquid crystals under dc conditions. I. Basic electrochemical analysis. J. Appl. Phys. 1976, 47, 2375–2377. [Google Scholar] [CrossRef]
- Barret, S.; Gaspard, F.; Herino, R.; Mondon, F. Dynamic scattering in nematic liquid crystals under dc conditions. II. Monitoring of electrode processes and lifetime investigation. J. Appl. Phys. 1976, 47, 2378–2381. [Google Scholar] [CrossRef]
- Lim, H.S.; Margerum, J.D.; Graube, A. Electrochemical properties of dopants and the DC dynamic scattering of a nematic liquid crystal. J. Electrochem. Soc. Solid State Sci. Technol. 1977, 124, 1389–1394. [Google Scholar]
- Rahman, M.; Lee, W. Scientific duo of carbon nanotubes and nematic liquid crystals. J. Phys. D Appl. Phys. 2009, 42, 063001. [Google Scholar] [CrossRef]
- Garbovskiy, Y.; Glushchenko, A. Liquid crystalline colloids of nanoparticles: Preparation, properties, and applications. Solid State Phys. 2011, 62, 1–74. [Google Scholar]
- Garbovskiy, Y.; Zribi, O.; Glushchenko, A. Emerging Applications of Ferroelectric Nanoparticles in Materials Technologies, Biology and Medicine. In Advances in Ferroelectrics; Peláiz-Barranco, A., Ed.; InTech: Rijeka, Croatia, 2012; ISBN 978-953-51-0885-6. [Google Scholar] [CrossRef]
- Mirzaei, J.; Reznikov, M.; Hegmann, T. Quantum dots as liquid crystal dopants. J. Mater. Chem. 2012, 22, 22350–22365. [Google Scholar] [CrossRef]
- Stamatoiu, O.; Mirzaei, J.; Feng, X.; Hegmann, T. Nanoparticles in liquid crystals and liquid crystalline nanoparticles. Top. Curr. Chem. 2012, 318, 331–394. [Google Scholar] [PubMed]
- Blanc, C.; Coursault, D.; Lacaze, E. Ordering nano- and microparticles assemblies with liquid crystals. Liq. Cryst. Rev. 2013, 1, 83–109. [Google Scholar] [CrossRef]
- Kumar, S. Discotic liquid crystal-nanoparticle hybrid systems. NPG Asia Mater. 2014, 6, e82. [Google Scholar] [CrossRef]
- Urbanski, M. On the impact of nanoparticle doping on the electro-optic response of nematic hosts. Liq. Cryst. Today 2015, 24, 102–115. [Google Scholar] [CrossRef]
- Klimusheva, G.; Mirnaya, T.; Garbovskiy, Y. Versatile Nonlinear-Optical Materials Based on Mesomorphic Metal Alkanoates: Design, Properties, and Applications. Liq. Cryst. Rev. 2015, 3, 28–57. [Google Scholar] [CrossRef]
- Yadav, S.P.; Singh, S. Carbon nanotube dispersion in nematic liquid crystals: An overview. Prog. Mater. Sci. 2016, 80, 38–76. [Google Scholar] [CrossRef]
- Mertelj, A.; Lisjak, D. Ferromagnetic nematic liquid crystals. Liq. Cryst. Rev. 2017, 5, 1–33. [Google Scholar] [CrossRef]
- Li, Q. (Ed.) Nanoscience with Liquid Crystals; Springer: Cham, Switzerland, 2014; p. 420. [Google Scholar]
- Lagerwall, J.P.F.; Scalia, G. Liquid Crystals with Nano and Microparticles; Series in Soft Condensed Matter; World Scientific Publishing Co: Singapore, 2016; Volume 7, pp. 461–920. [Google Scholar]
- Garbovskiy, Y.; Glushchenko, I. Nano-Objects and Ions in Liquid Crystals: Ion Trapping Effect and Related Phenomena. Crystals 2015, 5, 501–533. [Google Scholar] [CrossRef]
- Jian, B.R.; Tang, C.Y.; Lee, W. Temperature-dependent electrical properties of dilute suspensions of carbon nanotubes in nematic liquid crystals. Carbon 2011, 49, 910–914. [Google Scholar] [CrossRef]
- Tomylko, S.; Yaroshchuk, O.; Kovalchuk, O.; Maschke, U.; Yamaguchi, R. Dielectric properties of nematic liquid crystal modified with diamond nanoparticles. Ukr. J. Phys. 2012, 57, 239–243. [Google Scholar] [CrossRef]
- Wu, P.C.; Lisetski, L.N.; Lee, W. Suppressed ionic effect and low-frequency texture transitions in a cholesteric liquid crystal doped with graphene nanoplatelets. Opt. Express 2015, 23, 11195–11120. [Google Scholar] [CrossRef]
- Shukla, R.K.; Feng, X.; Umadevi, S.; Hegmann, T.; Haase, W. Influence of different amount of functionalized bulky gold nanorods dopant on the electrooptical, dielectric and optical properties of the FLC host. Chem. Phys. Lett. 2014, 599, 80–85. [Google Scholar] [CrossRef]
- Podgornov, F.V.; Wipf, R.; Stühn, B.; Ryzhkova, A.V.; Haase, W. Low-frequency relaxation modes in ferroelectric liquid crystal/gold nanoparticle dispersion: Impact of nanoparticle shape. Liq. Cryst. 2016, 43, 1536–1547. [Google Scholar] [CrossRef]
- Urbanski, M.; Lagerwall, J.P.F. Why organically functionalized nanoparticles increase the electrical conductivity of nematic liquid crystal dispersions. J. Mater. Chem. C 2017, 5, 8802–8809. [Google Scholar] [CrossRef]
- Podgornov, F.V.; Gavrilyak, M.; Karaawi, A.; Boronin, V.; Haase, W. Mechanism of electrooptic switching time enhancement in ferroelectric liquid crystal/gold nanoparticles dispersion. Liq. Cryst. 2018, 45, 1594–1602. [Google Scholar] [CrossRef]
- Tang, C.Y.; Huang, S.M.; Lee, W. Electrical properties of nematic liquid crystals doped with anatase TiO2 nanoparticles. J. Phys. D Appl. Phys. 2011, 44, 355102. [Google Scholar] [CrossRef]
- Chandran, A.; Prakash, J.; Gangwar, J.; Joshi, T.; Kumar Srivastava, A.; Haranath, D.; Biradar Ashok, M. Low-voltage electro-optical memory device based on NiO nanorods dispersed in a ferroelectric liquid crystal. RSC Adv. 2016, 6, 53873–53881. [Google Scholar] [CrossRef]
- Shcherbinin, D.P.; Konshina, E.A. Impact of titanium dioxide nanoparticles on purification and contamination of nematic liquid crystals. Beilstein J. Nanotechnol. 2017, 8, 2766–2770. [Google Scholar] [CrossRef] [PubMed]
- Kovalchuk, O.V.; Studenyak, I.P.; Izai, V.Y.; Rubak, S.O.; Pogodin, A.I.; Kopcansky, P.; Timko, M.; Gdovinova, V.; Mariano, J.; Kovalchuk, T.M. Saturation effect for dependence of the electrical conductivity of planar oriented liquid crystal 6CB on the concentration of Cu7PS6 nanoparticles. Semicond. Phys. Quantum Electron. Optoelectron. 2017, 20, 437–441. [Google Scholar] [CrossRef]
- Shcherbinin, D.P.; Konshina, E.A. Ionic impurities in nematic liquid crystal doped with quantum dots CdSe/ZnS. Liq. Cryst. 2017, 44, 648–655. [Google Scholar] [CrossRef]
- Konshina, E.; Shcherbinin, D. Comparison of the properties of nematic liquid crystals doped with TiO2 and CdSe/ZnS nanoparticles. J. Mol. Liq. 2017. [Google Scholar] [CrossRef]
- Shukla, R.K.; Liebig, C.M.; Evans, D.R.; Haase, W. Electro-optical behaviour and dielectric dynamics of harvested ferroelectric LiNbO3 nanoparticle-doped ferroelectric liquid crystal nanocolloids. RSC Adv. 2014, 4, 18529–18536. [Google Scholar] [CrossRef]
- Basu, R.; Garvey, A. Effects of ferroelectric nanoparticles on ion transport in a liquid crystal. Appl. Phys. Lett. 2014, 105, 151905. [Google Scholar] [CrossRef]
- Garbovskiy, Y.; Glushchenko, I. Ion trapping by means of ferroelectric nanoparticles, and the quantification of this process in liquid crystals. Appl. Phys. Lett. 2015, 107, 041106. [Google Scholar] [CrossRef]
- Hsiao, Y.G.; Huang, S.M.; Yeh, E.R.; Lee, W. Temperature-dependent electrical and dielectric properties of nematic liquid crystals doped with ferroelectric particles. Displays 2016, 44, 61–65. [Google Scholar] [CrossRef]
- Al-Zangana, S.; Turner, M.; Dierking, I. A comparison between size dependent paraelectric and ferroelectric BaTiO3 nanoparticle doped nematic and ferroelectric liquid crystals. J. Appl. Phys. 2017, 121, 085105. [Google Scholar] [CrossRef]
- Kumar, P.; Debnath, S.; Rao, N.V.S.; Sinha, A. Nanodoping: A route for enhancing electro-optic performance of bent core nematic system. J. Phys. Condens. Matter 2018, 30, 095101. [Google Scholar] [CrossRef] [PubMed]
- Garbovskiy, Y. Switching between purification and contamination regimes governed by the ionic purity of nanoparticles dispersed in liquid crystals. Appl. Phys. Lett. 2016, 108, 121104. [Google Scholar] [CrossRef]
- Garbovskiy, Y. Electrical properties of liquid crystal nano-colloids analysed from perspectives of the ionic purity of nano-dopants. Liq. Cryst. 2016, 43, 648–653. [Google Scholar] [CrossRef]
- Garbovskiy, Y. Impact of contaminated nanoparticles on the non-monotonous change in the concentration of mobile ions in liquid crystals. Liq. Cryst. 2016, 43, 664–670. [Google Scholar] [CrossRef]
- Garbovskiy, Y. Ions and size effects in nanoparticle/liquid crystal colloids sandwiched between two substrates. The case of two types of fully ionized species. Chem. Phys. Lett. 2017, 679, 77–85. [Google Scholar] [CrossRef]
- Garbovskiy, Y. Nanoparticle enabled thermal control of ions in liquid crystals. Liq. Cryst. 2017, 44, 948–955. [Google Scholar] [CrossRef]
- Garbovskiy, Y. Ions in liquid crystals doped with nanoparticles: Conventional and counterintuitive temperature effects. Liq. Cryst. 2017, 44, 1402–1408. [Google Scholar] [CrossRef]
- Garbovskiy, Y. The purification and contamination of liquid crystals by means of nanoparticles. The case of weakly ionized species. Chem. Phys. Lett. 2016, 658, 331–335. [Google Scholar] [CrossRef]
- Garbovskiy, Y. Ion capturing/ion releasing films and nanoparticles in liquid crystal devices. Appl. Phys. Lett. 2017, 110, 041103. [Google Scholar] [CrossRef]
- Garbovskiy, Y. Kinetics of Ion-Capturing/Ion-Releasing Processes in Liquid Crystal Devices Utilizing Contaminated Nanoparticles and Alignment Films. Nanomaterials 2018, 8, 59. [Google Scholar] [CrossRef] [PubMed]
- Garbovskiy, Y. Adsorption of ions onto nanosolids dispersed in liquid crystals: Towards understanding the ion trapping effect in nanocolloids. Chem. Phys. Lett. 2016, 651, 144–147. [Google Scholar] [CrossRef]
- Garbovskiy, Y. Nanoparticle—Enabled ion trapping and ion generation in liquid crystals. Adv. Condens. Matter Phys. 2018, 2018, 8914891. [Google Scholar] [CrossRef]
- Garbovskiy, Y. Adsorption/desorption of ions in liquid crystal nano-colloids: The applicability of the Langmuir isotherm, impact of high electric fields, and effects of the nanoparticle’s size. Liq. Cryst. 2016, 43, 853–860. [Google Scholar] [CrossRef]
- Barbero, G.; Evangelista, L.R. Adsorption Phenomena and Anchoring Energy in Nematic Liquid Crystals; Taylor & Francis: Boca Raton, FL, USA, 2006. [Google Scholar]
- Steffen, V.; Cardozo-Filho, L.; Silva, E.A.; Evangelista, L.R.; Guirardello, R.; Mafra, M.R. Equilibrium modeling of ion adsorption based on Poisson–Boltzmann equation. Colloids Surf. A Physicochem. Eng. Asp. 2015, 468, 159–166. [Google Scholar] [CrossRef]
- Batalioto, F.; Figueiredo Neto, A.M.; Barbero, G. Ion trapping on silica nanoparticles: Effect on the ζ-potential. J. Appl. Phys. 2017, 122, 164303. [Google Scholar] [CrossRef]
- Steffen, V.; Silva, E.A.; Evangelista, L.R.; Cardozo-Filho, L. Debya-Huckel approximation for simplification of ions adsorption equilibrium model based on Poisson-Boltzmann equation. Surf. Interfaces 2018, 10, 144–148. [Google Scholar] [CrossRef]
- Nanowerk Spotlight. Ionic Purity of Nanoparticles Is Key to Switching between Purification and Contamination Regimes in Liquid Crystal Devices. Available online: https://www.nanowerk.com/spotlight/spotid=42995.php (accessed on 30 March 2016).
- Nanowerk Spotlight. A Nanotechnology Approach to Purifying Liquid Crystals. Available online: https://www.nanowerk.com/spotlight/spotid=45659.php (accessed on 23 January 2017).
- Wu, P.W.; Lee, W. Phase and dielectric behaviors of a polymorphic liquid crystal doped with graphene nanoplatelets. Appl. Phys. Lett. 2013, 102, 162904. [Google Scholar] [CrossRef]
| Ion-Capturing Regime | No Change Regime | Ion-Releasing Regime | |
|---|---|---|---|
| Materials | Reported Effects | Physical Parameters |
| ) nanoparticles in nematic liquid crystals (E44) | Ion capturing effect [49] | [62] |
| Carbon nanotubes (CNT) in nematic liquid crystals (E7) | Ion capturing effect [42] | [62] |
| Diamond nanoparticles in nematic liquid crystals (E7) | Ion capturing effect [43] | [62] |
| Diamond nanoparticles in nematic liquid crystals (E7) | Ion releasing effect [43] | [62] |
| Graphene nano-flakes (GNF) in nematic liquid crystals (8OCB) | Ion capturing effect [79] | [62] |
| ) in liquid crystals | Ion capturing effect [55] | [62] |
| ) in nematic liquid crystals | Ion capturing effect [57] | [62] |
| ) in nematic liquid crystals (E44) | Temperature-induced release of ions [58] | [65] |
| nanoparticles in nematic liquid crystals (ZhK1282) | Ion releasing effect [51] | [71] |
| nanoparticles in nematic liquid crystals (ZhK1282) | Ion capturing effect [51] | [71] |
| core/shell nanoparticles in nematic liquid crystals (ZhK1289) | Ion releasing effect [53] | [71] |
| nanoparticles in nematic liquid crystals (6CB) | Ion releasing effect [52] | [71] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garbovskiy, Y. Ion-Generating and Ion-Capturing Nanomaterials in Liquid Crystals. Proceedings 2018, 2, 1122. https://doi.org/10.3390/IECC_2018-05257
Garbovskiy Y. Ion-Generating and Ion-Capturing Nanomaterials in Liquid Crystals. Proceedings. 2018; 2(14):1122. https://doi.org/10.3390/IECC_2018-05257
Chicago/Turabian StyleGarbovskiy, Yuriy. 2018. "Ion-Generating and Ion-Capturing Nanomaterials in Liquid Crystals" Proceedings 2, no. 14: 1122. https://doi.org/10.3390/IECC_2018-05257
APA StyleGarbovskiy, Y. (2018). Ion-Generating and Ion-Capturing Nanomaterials in Liquid Crystals. Proceedings, 2(14), 1122. https://doi.org/10.3390/IECC_2018-05257





