Simultaneous Identification of Thermal Diffusivity, Thickness, and Heating Center Point Based on Surface Temperature Variation Excited by Laser-Spot Heating ^†

Abstract

An infrared thermographic technique was developed for identifying the thermal diffusivity from temperature variation data of the specimen surface. Laser-spot heating is applied to the specimen surface for a certain period, and then, temperature variation in the surface is measured using infrared thermography. Since analytical solution for the temperature variation is expressed in terms of parameters including the thermal diffusivity, thickness and heating point position, the parameters are identified by fitting the analytical solution to the measured data. The developed technique was applied to a ceramic specimen for verification. It was shown that the thermal diffusivity can be identified with high accuracy if the thickness and heating point position are known in advance. Furthermore, it is confirmed that the thermal diffusivity, thickness, and heating point position can be simultaneously estimated with acceptable accuracy.

1. Introduction

Thermal diffusivity is one of the most representative thermal properties of materials, and its evaluation is important in many scientific and industrial fields. The laser flash method [1,2], periodic heat method [3] and temperature wave method [4] are standard methods to measure thermal diffusivity. The aim of the laser flush method is to evaluate thermal diffusivity by applying a short thermal pulse to the entire front surface of a material and observing the temperature variation on the rear surface. The periodic heat method and the temperature wave method evaluate thermal properties by analyzing the phase response of thermal waves generated by periodic heating. Both methods typically measure the phase difference between the front and rear surfaces of the sample to determine thermal diffusivity and thermal conductivity. However, these methods have the limitation that the specimen must be cut out if the rear surface of the sample is not accessible, which is not nondestructive. A recent study [5] has proposed a more practical method for identifying thermal diffusivity by measuring temperature variation in the material surface using a combination of laser spot and step heating. Nevertheless, this method requires the thickness of the sample to be known in advance. In this study, a method to accurately and efficiently identify thermal diffusivity by pulse-step laser-spot heating is established even when the specimen thickness is unknown.

2. Solution for Temperature Variation

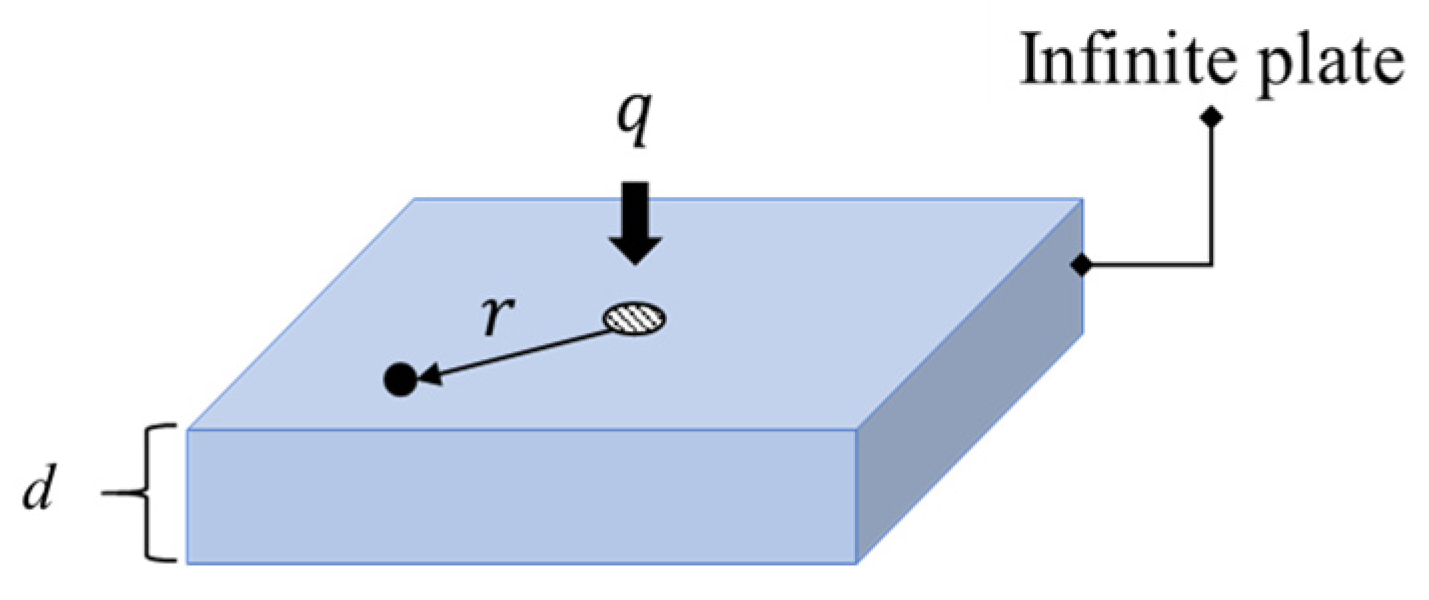
Assume that an infinite flat plate is subjected to step heating at a point from time t = 0 to t = t₁ as shown in Figure 1. The heat flux is expressed as

$$q\left(t\right)=\left\{\begin{array}{cc}0,& t<0,\\ q,& 0\le t<t_1,\\ 0,& t\ge t_1.\end{array}\right.$$

(1)

The theoretical solution for the surface temperature variation T(r, t) at a distance r from the heating point is given as [6,7]

$$T\left(r,t\right)=\left\{\begin{array}{cc}0,& t<0,\\ {\displaystyle \frac{q}{2\pi k}}{\sum }_{n=-\infty }^{\infty }{\displaystyle \frac{1}{\sqrt{r^2+4n^2{d}^2}}}erfc\left({\displaystyle \frac{\sqrt{r^2+4n^2{d}^2}}{\sqrt{4\alpha t}}}\right),& 0\le t<t_1,\\ {\displaystyle \frac{q}{2\pi k}}\sum _{n=-\infty }^{\infty }{\displaystyle \frac{1}{\sqrt{r^2+4n^2{d}^2}}}\left\{erf\left({\displaystyle \frac{\sqrt{r^2+4n^2{d}^2}}{\sqrt{4\alpha \left(t-t_1\right)}}}\right)-erf\left({\displaystyle \frac{\sqrt{r^2+4n^2{d}^2}}{\sqrt{4\alpha t}}}\right)\right\},& t\ge t_1.\end{array}\right.$$

(2)

$$r=\sqrt{{\left(x-x_0\right)}^2+{\left(y-y_0\right)}^2}$$

(3)

Here k is the thermal conductivity, d is the thickness, and α is the thermal diffusivity of the plate. In addition, x and y indicate the position of the temperature measurement point, and x₀, y₀ indicate the position of the heating point.

By applying Equation (2) in the fitting process to the surface temperature data obtained at various times and positions using the IR camera, it is possible to simultaneously identify the unknown parameters: thermal diffusivity α, thickness d, and the heating point position x₀ and y₀. If the thickness and heating position are known in advance, thermal diffusivity may be identified with higher accuracy due to the reduction in unknown parameters.

3. Experimental Method

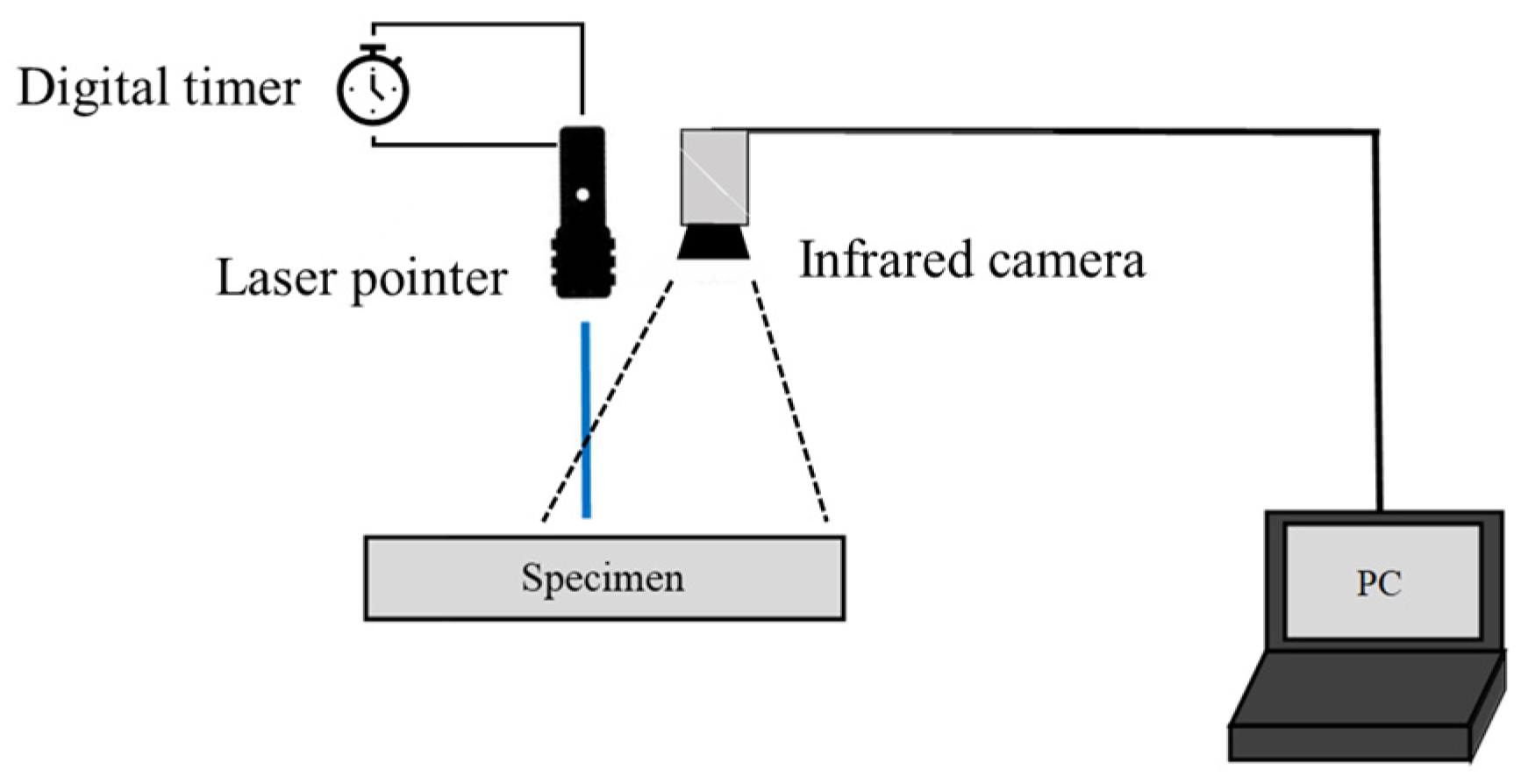
The experiment was carried out as illustrated in Figure 2. A laser beam (HTRLASER, Yiwu, China) was irradiated to the specimen, and surface temperature data was obtained by IR camera (Optris, Berlin, Germany). The heating period was precisely controlled using a digital timer (Omron, Kyoto, Japan). A ceramic plate (NISHIMURA ADVANCED CERAMICS CO.,LTD, Kyoto, Japan) made of alumina was used as a specimen. Experimental parameters are summarized in

Table 1. Experimental parameters.

Parameters	Values
Thickness: d	20 mm
Thermal diffusivity: α	7.7 × 10−6 m2/s
Thermal conductivity: k	21.95 W/m·K
Heat flux: q	1.05 W
Heating period: t1	10 s or 50 s
Measurement time	t = 0–50 s
Measurement radius	r = 0–20 mm

.

4. Results

Table 2. Thermal diffusivity and thickness identification error when thickness is unknown.

Heat Stop Time	Data Range		Identified Value and Error
	t	r	Thermal Diffusivity		Thickness
10 s (Pulse-step)	5–15 s	6–11 mm	8.3 × 10−6 m2/s	7.0%	13.4 mm	32.9%
50 s (Step)	5–32.5 s	4–9 mm	8.1 × 10−6 m2/s	4.4%	19.2 mm	3.9%

shows the identification results of thermal diffusivity and thickness in the case when the heating position is known. The time and radius data range used for the identification was determined to minimize the influence of error factors such as laser spot diameter and noise. These results indicate that, when the thickness is unknown, step heating (t₁ = 50 s) leads to smaller identification errors in both thermal diffusivity and thickness, whereas pulse-step heating (t₁ = 10 s) results in a larger error in thickness identification.

Table 3. Thermal diffusivity identification error when thickness is known.

Heat Stop Time	Data Range		Identified Value and Error (Thermal Diffusivity)
	t	r
10 s (Pulse-step)	5–15 s	6–11 mm	7.5 × 10−6 m2/s	3.5%
50 s (Step)	5–32.5 s	4–9 mm	8.0 × 10−6 m2/s	3.6%

shows the identification results of thermal diffusivity in the case when the thickness and the heating position are known. The accuracy of thermal diffusivity identification is improved in both methods compared to Table 2, with a particularly significant improvement observed in the case of pulse-step heating. These results indicate that stopping the heating midway slightly improves the accuracy.

5. Discussion

When the thickness is known, the pulse-step method yields slightly higher accuracy. This is considered to be due to the increased sensitivity of thermal diffusivity during fitting by using both the heating and cooling process. On the other hand, when the thickness is unknown, the accuracy of thermal diffusivity identification by the pulse-step method becomes inferior to that by the step method, and the accuracy of thickness identification is significantly decreased. This is considered to be because the thermal effect from the rear surface is not sufficiently reflected to the surface temperature. In fact, considering the thermal diffusion length shown below, the minimum time t′ at which the influence of the rear surface appears to the surface temperature is 13 s after the start of heating in this experiment.

$$d=2\sqrt{\alpha t^{\prime }}\iff t^{\prime }={\displaystyle \frac{d^2}{4\alpha }}$$

(4)

In summary, the results suggest that the pulse-step method, when the plate thickness is known, and the step method, when the thickness is unknown, enable more accurate identification of thermal diffusivity. To improve the accuracy of thermal diffusivity and thickness estimation in pulse-step heating, it is necessary to increase the heating time and sufficiently utilize the data range beyond 13 s after the start of heating.

6. Conclusions

A method to simultaneously identify the thermal diffusivity, thickness and heating point position by a laser spot heating technique was developed. Experiments were conducted to verify the method.

It has been shown that both the step heating and the pulse-step heating methods provided accurate identification of thermal diffusivity when the thickness is known in advance. In the case when the thickness is unknown, the step heating method resulted in higher accuracy than the pulse-step heating method. This is attributed to the need for sufficient heating and appropriate selection of the data range used for fitting, in order to capture the influence of the rear surface on the surface temperature.