Total Focusing in the Virtual Wave Domain: 3D Defect Reconstruction Using Spatially Structured Laser Heating †
Abstract
1. Introduction
2. Methodology
3. Total Focusing Method
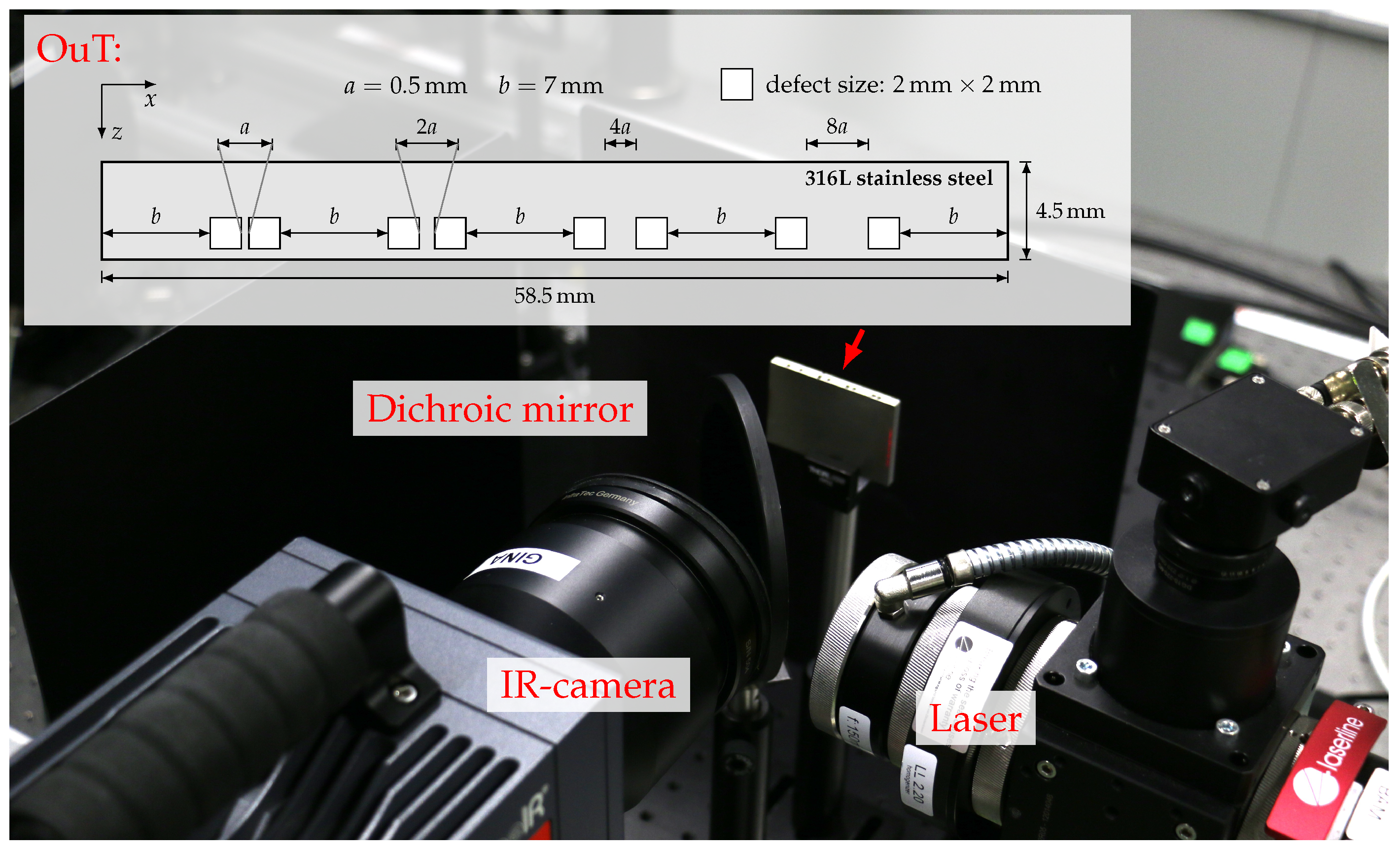
4. Experimental Setup
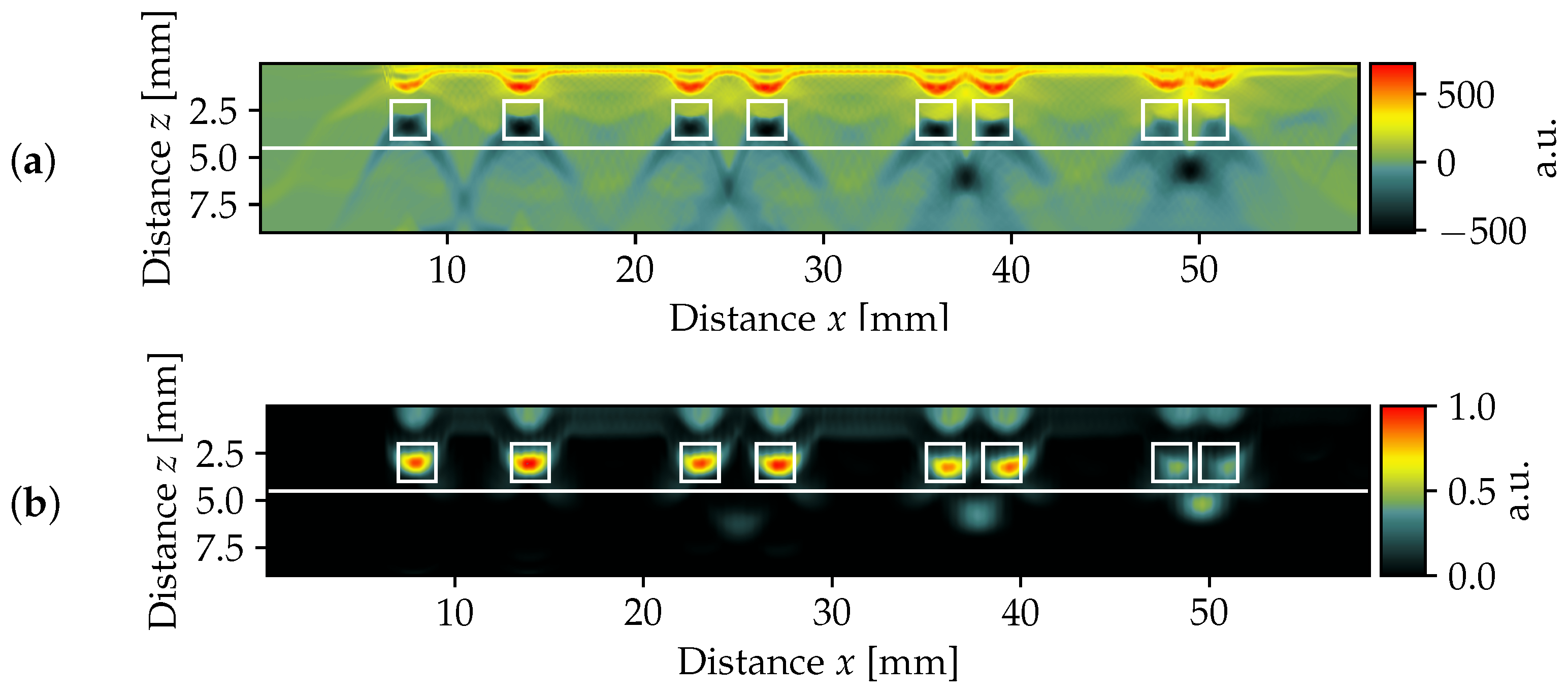
5. Results and Discussion
6. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Burgholzer, P.; Thor, M.; Gruber, J.; Mayr, G. Three-dimensional thermographic imaging using a virtual wave concept. J. Appl. Phys. 2017, 121, 105102. [Google Scholar] [CrossRef]
- Thummerer, G.; Mayr, G.; Haltmeier, M.; Burgholzer, P. Photoacoustic reconstruction from photothermal measurements including prior information. Photoacoustics 2020, 19, 100175. [Google Scholar] [CrossRef] [PubMed]
- Boyd, S. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends Mach. Learn. 2010, 3, 1–122. [Google Scholar] [CrossRef]
- Holmes, C.; Drinkwater, B.W.; Wilcox, P.D. Post-processing of the full matrix of ultrasonic transmit–receive array data for non-destructive evaluation. NDT E Int. 2005, 38, 701–711. [Google Scholar] [CrossRef]
- Sobczak, M.; Machynia, A.; Dworakowski, Z.; Roemer, J. Experimental Setup for Nondestructive Testing of Composite Structures Using Laser Spot Thermography. In Advances in Technical Diagnostics II; Springer Nature: Cham, Switzerland, 2023; pp. 75–84. [Google Scholar] [CrossRef]
- Lecompagnon, J.; Hirsch, P.D.; Rupprecht, C.; Ziegler, M. Nondestructive thermographic detection of internal defects using pixel-pattern based laser excitation and photothermal super resolution reconstruction. Sci. Rep. 2023, 13, 3416. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lecompagnon, J.; Rooch, L.; Hassenstein, C.; Ziegler, M. Total Focusing in the Virtual Wave Domain: 3D Defect Reconstruction Using Spatially Structured Laser Heating. Proceedings 2025, 129, 54. https://doi.org/10.3390/proceedings2025129054
Lecompagnon J, Rooch L, Hassenstein C, Ziegler M. Total Focusing in the Virtual Wave Domain: 3D Defect Reconstruction Using Spatially Structured Laser Heating. Proceedings. 2025; 129(1):54. https://doi.org/10.3390/proceedings2025129054
Chicago/Turabian StyleLecompagnon, Julien, Ludwig Rooch, Christian Hassenstein, and Mathias Ziegler. 2025. "Total Focusing in the Virtual Wave Domain: 3D Defect Reconstruction Using Spatially Structured Laser Heating" Proceedings 129, no. 1: 54. https://doi.org/10.3390/proceedings2025129054
APA StyleLecompagnon, J., Rooch, L., Hassenstein, C., & Ziegler, M. (2025). Total Focusing in the Virtual Wave Domain: 3D Defect Reconstruction Using Spatially Structured Laser Heating. Proceedings, 129(1), 54. https://doi.org/10.3390/proceedings2025129054





