Abstract
Jacopo Barozzi da Vignola played a significant role in the development of the theory and practice of prospective. The study presented here intends to highlight the theoretical contribution that the architect and painter has given to the history of perspective, through digital models that illustrate, clarify and allow to relate to each other—with the synthesis and effectiveness of the image—the main notions present in the treaty in order to trace, by comparing figures and texts, the scientific path that led to the formulation of the Two rules of practical perspective.
1. For a Current Study of the Two Rules
The treaty Two rules of practical perspective by Jacopo Barozzi da Vignola, published posthumously in 1583 by the mathematician Egnazio Danti [1,2] that integrates the manuscript [3] with wide comments, constitutes one of the fundamental contributions to the development of the method of perspective representation.
Just as in the De prospectiva pingendi by Piero della Francesca, the first scientific illustrated treatise on the subject, even in the Two rules the role of the image is fundamental and essential. A careful and progressive reading of the figures, together with that of the literary text accompanying them, provides significant clues to understanding the evolution of the authors’ thought in the subtle transition from one rule to the other.
The figures constitute the main structure on which the whole work is composed and mark its rhythm, starting with the first two parts in which definitions, theorems and problems are introduced, to continue with the next two, in which they illustrate the principles underlying the two rules. In this configuration, the text, more concise with regard to Vignola and considerably extended to Danti, comments on the construction and above all defines the role and importance of the figures progressively introduced with respect to the overall reasoning (Figure 1).

Figure 1.
Example of a definition in the first part of the Treaty. In this definition, Vignola illustrates the principle point as the point in which the perspectives of the lines perpendicular to the picture plane converge.
At a first reading, carried out with the preponderant filter of the present knowledge, the figures, apparently identical in morphology, seem for the most part repeat the same concepts, albeit with different levels of abstraction. By paying greater attention to the text and focusing on terms used and on the sequence and the connections between the reasoning gradually introduced, it is clear that the figures, albeit similar, refer to different geometric models. The perspective theory that is emerging is the result of two categories of observations, interconnected: the first, connected to Euclidean optics, are intended only to describe certain relationships between the entities of the plan; the other, evoking perspective views, on the other hand imply the concept of projection and section and, operating in three-dimensional space, investigate explicitly the visual experience phenomenon. In the first case, these are demonstrations that concern two-dimensional problems, synthesis and projection—as we perceive later—of operations that take place in three-dimensional space (Figure 2a). In the second case, we are faced with representations of operations occurring in the space and that find a two-dimensional synthesis on the paper sheet, also thanks to the use of representations in plan and elevation (Figure 2b).
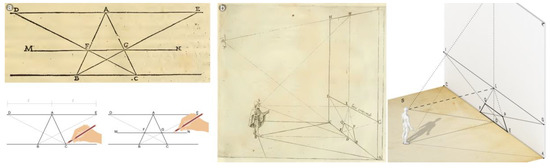
Figure 2.
(a) Illustration of the first theorem, first proposition, contained in the introductory part of the Treaty. The theorem deals with a plan geometry problem—regarding the parallelism between lines—that does not yet refer explicitly to prospective constructions, but is preparatory to it; (b) Illustration of the prospective construction of a square that implies the properties exhibited in the first theorem.
The previous critical tradition has seen numerous opposing opinions about it [4,5,6,7,8,9,10,11,12]. There are authors like Maria Walcher Casotti [4] who have supported the originality of Vignola’s contribution, identifying it in the passage from the first to the second rule, by attributing to him the formulation of concepts generally referred to later theorizing, as in the case of the vanishing points. Others, however, in addition to not recognizing the originality of the work contents, have not considered that there was significant differences between the two display rules, as reflected in the comments made by Judith Veronica Field [7] in comparing the two main figures of the Treaty depicting the two rules (the one relating to Chapter VI of the first rule, Figure 3a, and the other illustrating Chapter II of the second rule, Figure 3b, of which we will deal extensively).
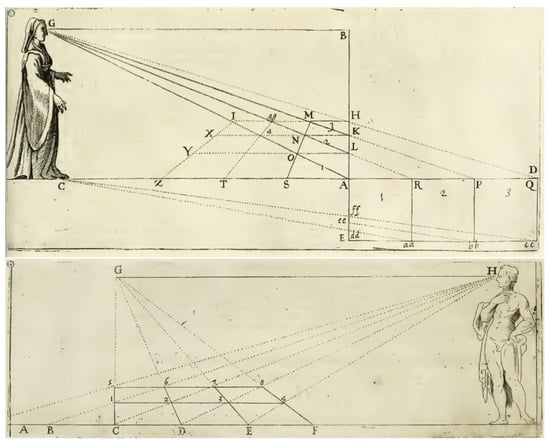
Figure 3.
Illustration of the two rules by Vignola. The first (a) is located in the sixth chapter of the First rule; the other (b) in the second chapter of the Second rule.
Moving from this wide tradition and operating with a critical approach, we analysed the most emblematic figures of the work, considered in their sequencing, through interpretative digital models that could explain their generative logic and highlight individual peculiarities. These models constitute complex digital images, in continuity with the related original figures, exhaustive synthesis of the content of the treaty and explicit manifestation of their interrelations.
2. The Two Rules of Vignola: Interpretative Models
The structure of the treaty, as emphasized in the preface by Danti, reveals the extent of the audience to which it is addressed: the parts dedicated to the two rules, which fully describe prospective constructions and are therefore directly related to artistic practice, are in fact preceded by two equally extensive sections. In these two parts Vignola and, above all, Danti deepen, through definitions, theorems and problems, the principles of optics on which the prospective theory is based, constituting a precious tool for understanding its evolutionary state with respect to the history of the method.
The second chapter, in particular, opens with a series of theorems that lay the theoretical basis of the method starting from considerations that belong to the field of plane geometry. For example, the first theorem (Figure 2a) shows that, given a triangle between two parallel lines, if we draw two straight lines from two points of the top line, equidistant from the top of the triangle and directed to its opposite vertices, belonging to the lower parallel, the straight line passing through the points of intersection between these lines and the sides of the triangle is parallel to its base. There is yet no reference in the proposition to the perspective space to which the figure seems to be alluding: the triangle vertex does not yet assume the value of principal point, the quadrilateral BCFG is not yet the perspective of a square (or of a rectangle), points D and E are still not distance points. It is merely a demonstration, which exploits the similarity between triangles, of a phenomenon that belongs to the plan, and which will subsequently justify spatial operations (Figure 2b).
The rules that Vignola introduces later are the expression of two different ways of thinking in space, even leading the same result. The first rule has no innovative elements compared to the previous tradition: in the preface, Danti refers to other authors who have dealt with perspective, citing in particular, in the order, Piero della Francesca, Daniele Barbaro, Sebastiano Serlio, Baldassarre da Siena (Baldassarre Peruzzi), Giacomo Andreotti da Cerchio, Giovan Cusin Frazesi (Jean Cousin), Pietro Cataneo, Leon Battista Alberti, Leonardo da Vinci, Albrecht Dürer, Giovacchino Fortio, Giovan Lencker, Venceslao Gianizzero Norimbergense, Viator (Jean Pèlerin), Federico Commandino). It reduces the perspective representation to a projection and section operation in which, obtaining the data in plan and elevation through projecting lines that intersect the picture plane, we come to the representation of the subject (Figure 3a). In the second rule, whose invention is explicitly attributed by Danti to Vignola, the perspective is built directly on the picture plane thanks to some observations, which will be crucial for the full theorization of the method in the following centuries. In fact, the point of distance intervenes explicitly in the construction, not merely as an overturning of the center of projection, but as a point of the perspective image in which converge the lines that are parallel and “diagonal” (inclined at 45°) with respect to the picture plane Figure 3b).
Before proceeding with the analysis of the two rules, and in order to better understand the value of the operations carried out in their application, it is important to understand what definitions are given of the main entities involved in the construction of the perspective (pp. 4–6 of the treatise):
- “Parallel lines”: lines that converge at a point on the horizon (and therefore, let’s add, they must be horizontal);
- “Principal point” (Figure 1): point of convergence of the “parallel lines” forming right angles with the “planar line”; it is “in front of the eye”, at same level, where the view of the observer is directed;
- “Point of distance”: corresponds to the projection center, and it is also “the one where end all diagonal lines”; it is “in the center of the eye” and it is always represented overturned on the picture plane, far from the principal point at a distance corresponding to the principal distance;
- “Particular point”: point of the horizon in which converge straight lines (and, of course, horizontal) that are not perpendicular to the picture plane;
- “Horizontal Line”: it is the horizon, the line at which principal point, point of distance and “particular points” belong;
- “Planar line”: in perspective, line parallel to the horizon. Planar lines are generally all parallel lines that remain parallel also in perspective (and are parallel to the horizon, “go to the center of the earth” and are therefore vertical) and “do not escape the eye”. Among them, the planar line is for Vignola and Danti the line of the plane, on which the observer stands, that is perpendicular to the lines converging in perspective in the principal point;
- “Parallel principal lines”: they converge to the principal point and are then perpendicular to the picture plane;
- “Parallel secondary lines”: they converge at a point different from the principal one and do not form right angles with the straight line;
- “Diagonal line”: passes through the corners of the perspective of the square and ends at the point of the distance.
As you can see from the careful reading of the treaty, the differentiation of the two rules is not clearly defined between the third and fourth chapter, and this makes it difficult to trace a clear boundary between the principles that apply to the individual rules; therefore, we will analyze the significant parts of the two rules, sometimes subverting the order of the propositions (we have to say that the present study focuses on propositions that directly contribute to the formulation of the two Rules, but the treatise addresses other important issues, relevant for the definition of the method and the practice of perspective, such as the question of the constrained view, the type of surface on which the perspective is realized, the use of prospective machines.).
2.1. The First Rule
The first rule is, as we said, directly and explicitly linked to the fundamental concept of projection and section of the visual pyramid and coincides with the second procedure illustrated by Piero della Francesca in the De prospectiva pingendi. An anticipation of this concept appears already among the theorems of the previous chapter, which show the results of the projection and section operation in a profile view, demonstrating the digression of apparent quantities of segments of equal measure (Figure 4a,b).
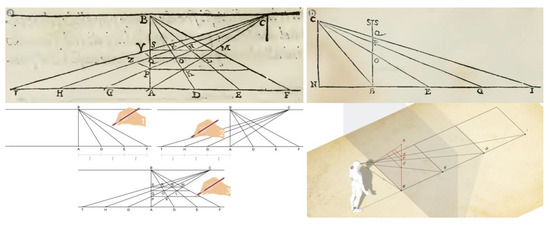
Figure 4.
(a) Illustration of the fourth theorem, fourth proposition, contained in the introductory part of the Treaty. The theorem deals with a plan geometry problem—regarding the relationship between triangles and the parallelism between lines—that does not yet refer explicitly to prospective constructions, but is propedeutic to it; (b) Illustration of the XXIII theorem, XXIX proposition, contained in the introductory part of the Treaty. This theorem refers to the reduction of the apparent sizes, showing the operation of projection and section in an elevation view. It involves the principles exposed in the fourth theorem.
In this prospective model, “five terms” of primary importance enable the perspective to be defined: the principal distance; the height of the point of view; the centered or decentralized position of the point of view with respect to the object, fixed the first two terms; the position of the picture plane; the scale of representation.
Let’s see in detail what this process implies. First, it is necessary to represent in plan and elevation the subject that, as Vignola suggests, must be placed beyond the picture with respect to the observer. Thanks to a double overturning that allows to superimpose and link perspective, plan and elevation of the subject, we get the measures that let us to find the position of the points as they appear in perspective from that point of view (Figure 5).

Figure 5.
The digital model that illustrates the principles of the prospective representation outlined in the first rule.
Considering the above definitions and studying the proposition, we can highlight two fundamental aspects related to this process: the principal point is used as the point where the lines perpendicular to the picture converge; the point of distance is used as the overturning of the projection center on the picture plane to relate the entities observed in a profile view and their image on the picture.
The overturning of the projection center, that allows representing the profile of the prospective model, is performed by using as hinge the vertical straight line passing through the principal point, overturning—as we say now—the vertical plane that projects the principal ray. The rule is subsequently more flexible, showing how this tilting can actually be displaced perpendicularly to the hinge (Figure 6a), for the principle shown in the third proposition of the introductory part (Figure 6b).
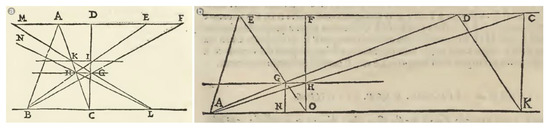
Figure 6.
The figure of Danti’s VI annotation (a), in the sixth chapter introducing the first rule, shows how it is possible to identify the perspective of the back side of a square even if we make a translation of the overturned point of distance and picture plane. The same principle had already been demonstrated in the first part of theorem III through a flat geometry exercise (b).
The subject chosen for the illustration of the first rule has peculiarities that make it easy and clear to apply the procedure and to read the image later. It is a series of contiguous squares, parallel and contiguous to the picture plane, placed in the left half of the perspective with respect to the projection center. The overturned plan is seen from the bottom upwards and therefore mirrored compared to the usual planar representation (this is because it would occupy the top half of the perspective, over the ground line, already used for the elevation). This particular condition of frontality and contiguity of the squares allows to introduce a special procedure, explained in the text, to speed up the construction of the perspective: instead of identify the location of all the points of the squares in plan, and determining in perspective only the dimension of the side of the square that belongs to the fundamental line, we trace the perspective of the line perpendicular to the picture plane, to which the squares are aligned, that allows to identify the vertices of the lined squares by intersection with the lines defining their heights (Figure 3a). This allows us to add another consideration to those previously expressed: lines parallel to the picture plane are parallel to each other even in perspective. This concept, already illustrated as a plane geometry operation, is also explained in the theorem XXVII, proposition XXXIII, where the link between the real shape of the subject and its perspective is shown (Figure 7a).
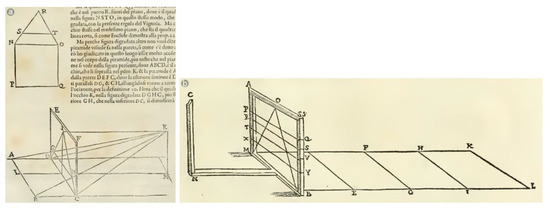
Figure 7.
The theorem XXVII, proposition XXXIII, illustrates the operation of projection and section, explaining the relationship between the objective figure and its perspective (a). The experimental verification of the theorem is instead illustrated by Danti in the annotation before the same proposition, where he describes an instrument that let us experience in the space the coincidence between the objective figure and its perspective (b).
In order to demonstrate the versatility of the rule, independently of the case previously illustrated, Vignola subsequently examines other planar figures, regular and irregular, extending then the application to solid shapes, although all of the represented objects continue to be placed in the left half-space of the picture to facilitate readability of the figure.
The correctness of the rule is finally proved experimentally through a physical model, a kind of prospective machine, which materializes the scheme of proposition XXXIII and allows the observer to verify the correspondence between the object and its representation on the picture (Figure 7b).
2.2. The Second Rule
The second rule, whose invention is attributed by Danti to Vignola (Egnazio Danti’s Preface to the Second Rule, p. 97 of the treatise), is introduced in the fourth and last chapter of the work in order to provide a more “convenient” procedure for the realization of a perspective, albeit acting in accordance with the first rule—such as underlined in the text.
The illustration of the second rule (Figure 3b and Figure 8) moves from an example of a prospective construction similar to the one used for the first, which is initially applied also in this second case to construct the perspective of the first square placed beyond the picture plane, contiguous to it and aligned to the principal point. The construction continues showing how, without translating the point of distance, the perspectives of the other squares can be identified, directly intersecting the lines that go to the point of distance with the ones converging at the principal point. What new principle intervenes to define this second rule, which, in the light of the examples shown, seems to act in the same way as the first one, as Judit Field points out? The conceptual difference is in effect in the different meaning assumed by the point of distance. This point not only acts as a center of projection overturned but it is used as the point of convergence of the “diagonal” lines (“Point of diagonal lines”, as Danti explains in note II of Chapter III of the second rule), that is the diagonals of the squares placed frontally in perspective, and then inclined by 45° with respect to the picture plane. In the examples he proposes, Vignola always uses a single point of distance. In Chapter VI of the second Rule (pp. 106–107), however, he explains that sometimes three different points of distance can be used, depending on the need: one placed symmetrically to the first with respect to the principal point, the others two on the vertical straight line belonging to the principal point, at the same distance from it). What were first projecting lines that allowed to locate on the picture plane the heights of the points beyond it, now become perspective straight lines in perspective, which intervene in defining the diagonals of the squares in perspective dividing them into triangles (Proposition XII, theorem XII, p. 23).
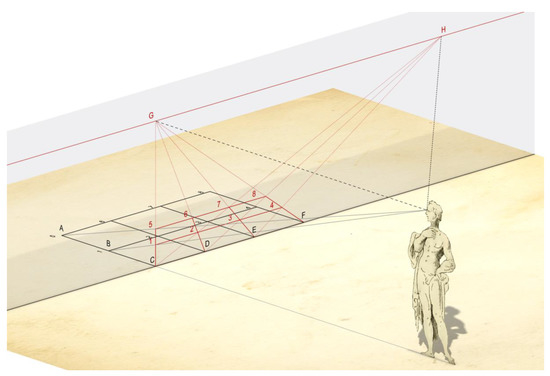
Figure 8.
The digital model that illustrates the principles of the prospective representation outlined in the second rule.
In this process, we see a first important step towards a direct conception of the prospective construction, which will find its full formalization only with the projective geometry and the introduction of the measurement concept. The use of the vanishing point of the diagonal lines allows, in conjunction with the use of the principal point in which the perpendicular lines of the picture coincide, to represent the perspective of each point of the subject identified as the intersection of the images of the perpendicular and “diagonal” lines who belong to it. This procedure, which Vignola explains, once again, using simple squares frontally represented, applies flexibly to planar figures and solid bodies of any shape, as seen, for example, in Chapter VII of the second rule. Here we can see that, without having the tools to directly control the “secondary parallel lines”, which are only said to converge in their “special points” distinct from the principal point (Figure 9a), Vignola builds the perspective of an octagon by points, using perpendicular and “diagonal” straight lines belonging to them (Figure 9b).
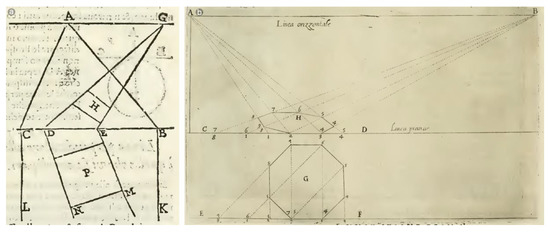
Figure 9.
(a) Representation of straight lines that are not perpendicular or parallel to the picture plane (definition XI). These lines converge in a point located on the horizon; (b) Perspective of an octagon realized with the application of the second rule (VII chapter of second rule).
The ambivalence of the point of distance, understood both as center of projection overturned and as convergence point of the “diagonal” lines, is not expressed immediately in the text but a careful, synchronous reading of the many propositions preceding the illustration of the rules allows us to understand its logical derivation. We have already discussed, within the first rule, of the point of distance as the overturning of the principal point. On the other and, the use of this point as the convergence point of the “diagonals” in perspective is deducible by a series of propositions that explain its geometric nature, first with abstract exercises of plane geometry (Figure 2a or Figure 10a), then resorting to more complex spatial models expressly referred to the prospective representation (Figure 10b). As can be seen from the definitions and the theorems, this use of the points of distance does not yet imply the concept of measurement as we mean it today, but derives from empirical observations related to the geometric properties of the square in perspective.

Figure 10.
Relationship between perspective of squares and their diagonals, converging in a point on the horizon (b), as previously shown in an exercise of plane geometry (a) in theorem XXIV.
Again, at the end of the explanation of the process, the authors rely on the experimental testing of what is stated, suggesting the use of the same prospective machine described above.
3. Conclusions
Vignola treatise, as we have seen, is an important testimony to the state of advancement of knowledge on the prospective representation, illustrated by a series of figures that manifest, although with the reiteration of the results, different aspects of evolving prospective science. The digital models made during the study, a complex representation of the various more significant propositions, allowed us to graphically define the two rules exposed in the treatise and clarify relationships with the definitions and the theorems outlined in the first part of the work. The comparison between the models has enabled us to highlight the gradual transition from the operations conducted through the use of plan and elevation representations, in the first rule, to operations performed directly on the perspective picture plane introducing entities such as the principal point and the point of distance, as result of precise empirical observations subsequently developed and defined in the projective geometry.
Conflicts of Interest
the author declares no conflict of interest.
References
- Da Vignola, J.B. Le Due Regole della Prospettiva Pratica; Cassa di Risparmio del Vignola; Arti Grafiche Tamari: Bologna, Italy, 1974. [Google Scholar]
- Egnatio, D. Les Deux Règles de la Perspective Pratique de Vignole; 1583, Trad. et éd. Critique (sic) par Pascal Dubourg Glatigny; CNRS Éditions: Paris, France, 2003. [Google Scholar]
- Da Vignola, J.B. Portione del Manoscritto Originale di Giacomo Barozzi da Vignola della Sua Prospettiva; Archivio Storico dell’Accademia Nazionale di San Luca: Roma, Italy.
- Walcher, C.M. Il Vignola; Istituto di Storia dell’Arte Antica e Moderna, n. 11: Trieste, Italy, 1960; Volume 2. [Google Scholar]
- Coolidge, J. (contributi di). La Vita e le Opere di Jacopo Barozzi da Vignola: 1507–1573, nel Quarto Centenario Della Morte; Cassa di Risparmi di Vignola: Vignola, Italy, 1974. [Google Scholar]
- Wolfgang, L. I Disegni, La Vita e le Opere di Jacopo Barozzi da Vignola 1507–1573 Nel Quarto Centenario della Morte; Cassa di Risparmio di Vignola: Italy, 1974. [Google Scholar]
- Field, J.V. The Invention of Infinity: Mathematics and Art in the Renaissance; Oxford University Press: UK, 1997. [Google Scholar]
- Ricci, M. Jacopo Barozzi da Vignola: La Vita e le Opere; Fondazione Cassa di Risparmio di Vignola: Vignola, Italy, 2002. [Google Scholar]
- Tuttle, R.J.; Adorni, B.; Frommel, C.L.; Thoenes, C. Vignola Jacopo Barozzi; Electa: Milano, Italy, 2002. [Google Scholar]
- Frommel, C.L.; Ricci, M.; Tuttle, R.J. Vignola e i Farnese; Atti del convegno Internazionale, Piacenza 18–20 Aprile 2002; Electa: Milano, Italy, 2003. [Google Scholar]
- Vv.Aa. Jacopo Barozzi da Vignola: Aggiornamenti Critici a 500 Anni Dalla Nascita; Comitato Nazionale per il Vignola; Novegrafie: Roma, Italy, 2008. [Google Scholar]
- Affanni, A.M.; Portoghesi, P. (a cura di). Studi su Jacopo Barozzi da Vignola; Atti del Convegno Internazionale di Studi; Gangemi Editore: Roma, Italy, 2012. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).