Ad Oculos. Images, Imagination and Abstract Thinking ^†

Abstract

The unusual edition of Elements of Euclid released for publishing in 1847 by Oliver Byrne offers the occasion to suggest a few elements for discussion on the uniqueness of the ‘representation’ of geometric-mathematical thinking—and more in general of the abstract thinking—enshrined in its ‘nature of a pure imaginative vision able to connect the intelligible with the tangible’. The purpose is, thus, a reasoning on images and communicative artefacts, that, when articulated, provide different variations of the idea of ‘transcription’ of complex theoretical structures from one language (that of abstract logic) to another (that of sensory experience), with a view to facilitate, ease and make more accurate the noetic process. Images able over time to facilitate the understanding of complex and abstract theoretical principles—since able to show them in an extremely concrete way, ad oculos,—and which at some points could reveal the horizons of art interpretation to inscrutable and figurative meaningless formulas.

1. Introduction

“To whatever height we place our concept and no matter how much we strive to abstract from sensitivity, they will still remain linked to figurative representations deemed precisely to make those concepts—otherwise non derived from experience—more suitable to empirical use!”

[E. Kant]

In his famous essay, Visual thinking [1], Rudolpf Arnhaim suggests a theory based on which communication isn’t just connected to image, but the same thinking is articulated according to the modalities arising from perception, above all the visual one. A non self-evident theory in a cultural setting deeply verb-centered like the coeval Western paradigm. By the way, today a renewed attention to the distinction between verbal and visual register is observable, in the processes of knowledge elaboration and dissemination as part of a discourse that is currently being developed around the meaning of iconic turn, or a turn toward the iconic dimension of those cultural phenomena being in contemporary times a countermelody of that linguistic turn codified by Rotry in 1967 [2]. «He intended to trace back every gnoseological issue—broadly intended—despite its many interpretations and nuances, to a matter of language, that had to be addressed with the help of linguistic tools (and of a semiotics based on it)» [3] (p. 16) [translator’s note: freely translated].

The considerations put forward in this short essay do not expect to deal with the entire visual domain in its complexity, but rather to suggest some comments on the uniqueness of the ‘representation’ of abstract thinking, enshrined in its «nature of a pure imaginative vision, able to connect the intelligible with the tangible» [4] (p. 17) [translator’s note: freely translated].

After all, the issue of communication of knowledge and of the forms of its possible ‘visual representation’ appears to be strictly linked to its same generative process. The thought, before even resulting in a logical and verbal formulation, singles out, articulates and organizes images and graphic patterns, based on figurative processes, concerning which it might be worth for the disciplines of representations to put forward some considerations; even more on such an occasion like the one offered by this meeting, that urges a reflection on the role of images in the process of knowledge construction by adopting an approach that leverages on the pedagogical and educational dimension. The purpose here, therefore, is to reason about images and communicative artefacts, that, when articulated provide different variations of the idea of ‘transcription’ of complex theoretical structures from one language (that of abstract logic) to another (that of sensory experience), with a view to facilitate, ease and make more accurate the noetic process.

At large, visually representing cognitive processes has always been an essential operation in several domains of thought production, both when the process is about to accomplish itself and when, after investigating, analyzing and sensing, it is useful and sometimes indispensable to communicate processes and information flows with a ‘touch of diagrammatic efficiency’, that only figurative representation is capable of. Giovanni Anceschi, in an attempt to master the subject of his research, very effectively distinguishes two phases involving two distinct forms of interaction between thought and image. The first is what Anceschi defines as the phase of notational capture, while the second is the phase of objectification of knowledge. The topic is fascinating and full of food for thought, because in both cases it concerns once again—and not in a banal way—the terms of an issue that is central to representation: the search for the ‘referential relationship’, i.e., the link in meaning that it has the task of ensuring between the dimension of signs (whether iconic or abstract) and the pragmatic dimension of the represented image (whether an object or a process).

In the complex definition of the scope and the meaning of this gesture, i.e., the gesture of transcription, it seems possible to reach an agreement on the fact that it conceptually represents an action of ‘transfer of information’ from a notational setting to another. The issue appears therefore to refer in essential terms to the processes of ‘mediation’ and, hence, it falls under the domain of languages, much more than that of ‘information’ per se, which in turn seems to be interested by an action that occurs and takes on a form at the level which, from Hjielmslev on, we got used to define as the level of expression, clearly distinct from the level of content. Indeed, the fact that we are dealing with, so to say, ‘expressive’ issues is confirmed by the same concept of in-formation, that seems to stress the need to give form—not ‘one’ form, but ‘one of the’ possible forms—to a fact or a system of facts with a view to make it understandable, transferable, communicable and, hence, useful for new experiments of meaning. A number of basic issues can be observed in this process, that fall under two distinct categories of problems for the representation: the first involves perspective, sensory and generally speaking aesthetic aspects related to the act of transcription; the second involves the cognitive, and more broadly, the cultural aspects implied by the same act. The first is intended to identify different levels of figurative schematization (or also different levels of iconicity), the second to define different levels of conceptual schematization (i.e., distinguishing different levels of interpretation, ‘reduction’, simplification, amplification of meaning). Both the two actions are clearly connected to the act of representation, particularly if the representation is intended not so much or at least not only as re-presenting, or presenting once again, in a way re-invoking in absentia, but rather as displaying, better showing off, making available to the view and somehow to the knowledge.

The topic takes on a special pedagogical meaning, if, in this scenario—that could be defined as that of the ‘informational images’ and that makes up a relevant heritage for the history of representation—the emphasis is put on the specific case of visualization of abstract concepts, where representation best expresses its unique nature of pure imaginative visuality: we are referring to the transcriptions from the mundus intellegibilis to the mundus sensibilis. In other words, those images that attempt to transfer the abstract into what can be experienced through the senses—above all the sight—by using iconic representations, considered unquestionably useful, precisely where the subject of knowledge is abstract or can’t be seen at all. Images that have been facilitating over time the understanding of complex and abstract theoretical principles, being they concretely demonstrated ad oculos and which have often provided a relevant contribution to the development of cognitive theories and processes acting as a field of understanding more than of description. The history of representation is dotted with this kind of images, which at some points could reveal the horizons of art interpretation to inscrutable and figurative meaningless formulas. It consists in a research field that mainly establishes a connection between the abstract mathematical thinking and aesthetic practices and which shows itself clearly in the avantgardes’ speculations. By the way, the issue was central in Modern thinking and yet it found unexpected anticipations in some of the experiences made in the pedagogical field towards the end of XIX century. With regard to the above, a special emblematic value is acquired by the work of Oliver Byrne who, when releasing for publishing in 1847 in London the most attractive edition ever of the first six books of the Elements of Euclid, suggests a daring shift from Euclid’s pure axiomatic geometry to its ‘sensory transcription’: its periods were made of coloured diagrams and symbols instead of letters and abstract formulas (Figure 1). Its unique beauty that seems belonging neither to ancient times or to Nineteen century represents an important anticipation of the mathematizing and abstract aesthetics that played such a major role in the development of XIX century’s avantgardes.

Figure 1. Oliver Byrne, The First Six Book of the Elements of Euclid, Londres, 1847. Book I Prop. XXXVII “Triangles on the same base and between the same parallels are equal”; Book I Prop. XXXVIII “Triangles on equal bases and between the same parallels are equal”.

2. Educational, Coloured, Eccentric. The Elements of Euclid by Oliver Byrne and Other Stories

Anachronistic, eccentric, seen by his contemporaries as a mere curiosity and almost ignored by the history of mathematics, the book released for publishing by Oliver Byrne in 1847 represents, viceversa, an operation that today appears to be extremely topical and that, considered broadly, perfectly meets the need to make visible our reasoning by way of principles of a blatant evidence.

Byrne’s book is entitled: The first six books of ‘The Elements of Euclid’ in wich coloured diagrams and symbols are used instead of letters for the greater ease of lerners. In the introduction Byrne clarifies that «my work has a greater aim than mere illustration: we do not introduce colours for the purpose of entertainment or to amuse by certain combinations of tint and form, but to assist the mind in its researches after truth» [5] (p. vii).

Hence, what emerges is a profound pedagogical meaning that Byrne—essentially a scientific popularizer—intends since the very beginning to convey to his work, by exposing, with an educational purpose, principles and theories to a ‘compromise with the visible’.

The didactic considerations used quite regularly in the book confirm a firm wish of providing the student with a tool to find a bearing in the universe of mathematics, considered as a ‘pure science’, while fully respecting the basic link between geometry-shape-form and yet grounding the intuition to the experience of sensory perception and above all the visual one. In this attempt Byrne lets his experience as a professor and the difficulties he run into while trying to teach his students lengthy formulas and complex demonstrations guide him. So, Byrne transforms Euclid’s declaratory scaffolding into periods made out of diagrams, colours and symbols, that fulfill a need to make complex reasoning ‘visible’, resorting to the principles of easiness, speed and blatant evidence. ‘Simplifying’ the learning process is Byrne’s stated purpose and right this perspective, clearly focused on teaching, should be the framing context for the use of that ‘system’ of symbols, diagrams and colours, featuring the most visible innovation of his Euclid (Figure 2). A ‘system’ of symbols where the communicative value is paramount: logic, concise and convincing. An ability to free the learning process from the burden of minuscule signs and hermetic formulas and to cast the dynamics of learning into the universe of immediate intuition, led by visual perception. The use of colours is thus essential since, as Byrne himself points out, they express themselves in mind at higher speeds than any other information and, hence, they are able to speed up the processes of learning and storage. Such a wide use of colour, the attention to the sensory dimension connected to it, shall certainly be attributed to the momentum gathered by the ‘colors theory’ after Goethe’s studies. We are clearly referring to the famous Zur Farbenlehre [6]. The use of primary colours, the attention to contrasts, the superposition of coloured surfaces, the traditional care for the chromatic balance in the page are visible confirmations of a mature chromatic sensitiveness, where the reference to the successive theories by Itten would be even more fitting. Already in his previous studies, Byrne had anticipated this consideration on the usefulness of colours for the representation of scientific discourses, contextualizing it within the broader debate on the supremacy of sight over the other senses, an eye-centered position featuring the majority of Western cultures. No doubt the attainment of his purpose was only acknowledged precisely after his 1847 publication, Euclid.

Figure 2. Oliver Byrne, The First Six Book of the Elements of Euclid, Londres, 1847. Book II Prop. VI; Book II Prop. VII.

Indeed, the major sign of modernity of Byrne’s work shall be identified right in his intention to shift the attention and the interest from scientific object per se to the ways it is presented and communicated. As such, Byrne was a precursor of an entire current of scientific illustration, that by using the colour and systems of symbols could demonstrate the unique ‘usefulness’ of the iconic representations, precisely where the object is not actually visible. The advantages brought up by figurative language, particularly the chromatic one, and the time saving in terms of perception and acquisition of concepts it enables are well-evident also in Chemical Atlas [7]—published in 1856 in New York—in whose title Livingstone Youman highlights the great usefulness of the iconic representation where the object is not visible at all.

Also Youman mentioned «series of beautifully colored diagrams… designed for the use of student», he too stressed the importance of colour to accelerate the processes of understanding. The stunning plates of his Atlas clearly confirm this. Moreover, they contain an interesting and peculiar mixture of different expressive codes. The iconic dimension of the landscape represented in Plate XII (Figure 3) is still affected by a clear romantic atmosphere, and yet the mixture with the system of symbols and arrows complementing the construction of the visual message claim its absolute expressive modernity. The same consideration applies to the ‘flame’ in Plate XI (Figure 4), where the evocative power of the phenomenon of combustion co-exists with the ‘simplification’ and the efficacy of diagrams used to represent the combinations of atoms and their exact proportions during the phenomenon of combustion.

Figure 3. Eduard L. Youman, Chemical Atlas, New York, 1856, Plate XII, Changes induced by vegetal and animal kingdoms to the atmosphere.

Figure 4. Eduard L. Youman, Chemical Atlas, New York, 1856, Plate XI, Chemistry of combustion and illumination: structure of flame.

Incredibly effective also the images in Plates V and VI (Figure 5), not only in terms of the educational efficacy of the simplification of chemical compounds between elements, but also for the extraordinary modernity of the formal expression and the quality of organization of visual elements which definitely recalls the figurative speculation of the Gestalt and anticipates the processes of schematization of the properties of forms in the investigations on the plastic organization of elements in the visual experience. To it the laws on perceptual organization defined by Georgy Kepes in his most famous work Language of vision [8] can be traced back.

Figure 5. Eduard L. Youman, Chemical Atlas, New York, 1856, Plate I and II, Metalloids and their compounds. Metals and their compounds with oxygen.

Equally effective in terms of simplification and visual synthesis is the work by Ezekiel Webster Dimond, The Chemistry of Combustion [9], published in 1867 in Worcester. Here, the complex chemical processes of combustion are explained with the plain and accurate language of images and elementary symbols, above all with the introduction of colours: red for acids, yellow for water, blue for nitrogen and black for carbon (Figure 6 and Figure 7).

Figure 6. Ezekiel W. Dimond, The Chimestry of combustion, Worcester 1867. Diagram 6. Representation of combustion of a given volume of hydrogen carbonate and its equivalent volume of oxygen.

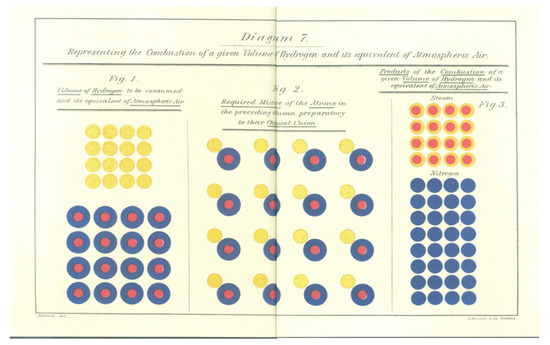
Figure 7. Ezekiel W. Dimond, The Chimestry of combustion, Worcester 1867. Diagram 7. Representation of combustion of a given volume of hydrogen and its equivalent volume in nature.

Byrne’s, therefore, is not an isolated case in the panorama of images, concerned in the visual representation of abstraction and learning processes, but it can be rightly assumed that his experiments on abstraction and simplification with symbols are a basic requirement for anyone who intends to embark on the analysis of the successive graphic and visual experiments in the field of scientific representation. The profound link between logic criterion and aesthetic emotion is quite renowned. It’s not infrequent that great mathematicians were also active artists and there are no doubts that up to the end of XIX century the mathematical thinking has played a major role in the more general cultural evolution at any time in history. The purpose is hereby to point out how this binomial—logic and aesthetic emotion—is a specific feature of the fascinating world of images, required to face the challenge of representing the un-representable. Specifically, the topic of visual representation has as a goal that of representing objects and processes finding no conventional visual equivalent. We are not referring only to the issue of the ‘reality’ of mathematics and geometry, but also of a great part of scientific representation that «relies on simplification, abstraction, classification, marking and schematization of the chaotic natural phenomena into orderly graphic forms» [translator’s note: freely translated]. Basically, what has been described by Bruno Latour as the ‘cascade’ of successive abstractions that remove scientific images from phenomenal chaos.

If we, then, consider that the contemporary scenario witnesses today to an unprecedented quantity of flow-charts, hypertexts, cognitive maps, graphics... whose goal is to build representational syntheses able to produce an ‘organized render’ of information through an action of representation which gets activated by processes of schematization and simplification, we can’t but conclude that Byrne’s experiments had well in advance detected a need for simplification and communicative efficacy, largely expressed today by computer graphics.

3. The Pedagogical Approach and the Critical Fortune

Byrne’s pedagogical mission is blatant and openly stated by the author since the very first lines of his book, which, by the way, is essentially the final outcome of a didactic and pedagogical interest permeating his entire scientific production [10]. His idea is to add, if you wish, to ‘overlap’ to Euclid’s logic system a graphic system made of symbols, colours and shapes whose efficacy and usefulness is constantly stressed by the same Byrne in an attempt to make his Euclid easy to memorize and fitting with the dynamics of experience and visual perception. Accordingly and within the framework of the considerations put forward hereby—far away from any value judgement on mathematical scientific thinking—Byrne’s work results extremely interesting. First, for the inclination, manifest in it, to optimize sensory skills and to experiment strategies of representation where the art of ‘showing’ overstretches by far the art of ‘saying’ and the interest is clearly shifted from the knowledge per se to the dynamics of its visual ‘presentation’ (Figure 8). What is striking in Byrne is the acknowledgment of the power of visual perception, that in a way anticipates the intellectual knowledge of the form. A reference to Pestalozzi can be observed already in the first pages of Byrne’s book and is a further confirmation of his strong educational aim. In his Lessons on the Observation of Number Relations [11], Pestalozzi makes a clear reference to a methodology, a pragmatics, necessary to learn mathematics in step with the development of thinking and following an approach pretty similar to the one adopted by Byrne in his effort to attain the same result with the use of symbols, diagrams and colours. Simplicity, speed and accuracy are the advocated features of the learning process in Euclid’s postulates, whose well-known obscuritas makes it even more required for the teacher to pay attention to the methodologies of representation, demonstrations and hence, ultimately to the educational medium as a whole. Let consider the problem of the postulates contained in Euclid’s Book V, the ‘obscure’ book as Galileo defined it for its being so far away from intuition. Therein, in particular, the introduction of a system of signs and symbols is functional to show the processes of understanding and storage.

Figure 8. Oliver Byrne, The First Six Book of the Elements of Euclid, Londres, 1847. Book III. Prop. I. Prob. To find a center of a given circle; Book III Prop.II Theor. A STRAIGHT line joining twopoint in the circumference of a circle.

As Heinrich Rickert stated, mathematics was not provided with a material basis, hence it has necessarily to ‘create it’! In this sense Byrne’s work doesn’t seem devoid of intuition. We can rather affirm that Byrne was a precursor of an entire current of research which, after him, will get to the acknowledgment that mathematics shall not be reduced, as with pure logic, to simple concepts and that the part played by intuition in its learning process is undeniable, since the mathema are made possible not by concepts, but rather by their construction [12]. Hilbert will define it as an ‘intuitive trend’ in the study of geometry [13]. A trend whose relevance deserves to be highlighted for the high heuristic value it is able to express and for the inner ability to stimulate an understanding and an acquisition of the ‘structures of order’ of the reality by way of ‘materialized abstractions’.

The above are, basically, arguments contained in the discourse about the usefulness of learning mathematical thinking, deemed as an effective ‘mediator’ for no matter what kind of learning—for the greater ease of learning—as already stated in the first Pestalozzi’s statements. But here they find a further clarification in the definition of the senses affected and in the explanation of a learning process, where the connection to them it’s not merely optional, but in a way sets the rules of it. Something urging an idea of optimization of a sensory reaction (sense perception) and an immediacy in representation (presentational immediacy), which are definitely contained in Byrne’s work as well and whose outcomes are, moreover, put in connection with successive experiences. For instance, those leading from the German pedagogical tradition straight to Pastolazzi, or to Froëbel’s ‘gifts’, to the progressive pedagogical theories of the beginning of XX century or to the Learning—Thought—Doing movement, initiated by John Dewey, a renowned US pedagogist. And from here the step to the passionating season of Bauhaus is very short! « Ellen Lupton and J. Abbot- Miller identify in fact Fröbel and Pestalozzi as the Bauhaus predecessors for pedagogics. And they prove this assumption using a comparison of texts and artefacts by Itten, Klee, Kandinskij ecc, with unique and rare documents by Fröbel and Pestalozzi, such as the book by Heinrich Pestalozzi and Christopher Buss, ABC der Anschauung, where Anschauung could be translated as the ability to imagine something, better if this is done with the eyes of mind» [14] (p. 16). For those who are familiar with the introductory studies of design, known as Basic Design, they’ll feel here like being at home here: both share an attention for the syntactic and elementary aspects of configuration.

Following this route, the attention to a sensory dimension of learning may also make us daring a comparison between Byrne’s work and that unique experience represented by the Methodology and the Educational materials ideated by Maria Montessori in the first years of XX century to facilitate the learning of mathematics and geometry. Objects featuring a clear and undeniable aesthetic value, but also—and mainly—by a forceful logic seduction power. Once again here shape and colour are amazing learning tools in a series of objects whose ‘representation’ of the logic and mathematical thinking conquers the three-dimensionality of physical space, gets in touch with the matter and caresses the field of design [15] (p. 16).

Specifically, ‘psyco-arithmetics’ and ‘psyco-geometry’ are the two domains that appear to be crucial to grasp the ‘representational’ dimension of the logic and mathematical space, which is activated thanks to the educational materials. Also in the case of Montessori the reference to Froëbel’s theories is a must. It’s actually true that Froëbel’s ‘perceptual path’ is dominated by mathematical thinking; he also stated that «teaching of numbers is the basic foundation for the teaching of shapes and quantities and the teaching of space in general» and also that «mathematics shall be rethought and treated more from a physical and dynamic perspective, as a product of nature and force» [16] (p. 297) [translator’s note: freely translated]. And yet, Montessori’s position in this regard was much more articulated. Montessori regarded mathematical thought as a stepwise «organization of scientific stimuli, inciting a psychic activity, of materialization of what is abstract and hence, of emancipation of intelligence» [17] (p. 82) [translator’s note: freely translated]. Montessori’s attention to the sensory dimension of learning appears here strong and clear: on one side the reference to an ‘aesthetics’ whose function is to become a learning vehicle and on the other an attention to the sensory dimension of learning itself, that can’t neglect its visual and formal perception, though not being limited to it and allowing the tactile dimension to unashamedly enter the noetic process.

Another peculiar commonality between Byrne and Montessori is the great number of detractors of their theories. Critics didn’t always reserve them rewarding opinions. There were quite a few doubts shed about the efficacy of Montessori ‘educational materials’ [18]. The most severe criticism addressed to Montessori assumes that her ‘materials’ imply intellectual distinctions that can be produced by an adult mind and hence, as in Dewey’s words «the idea that an apprentice using these materials may somehow assimilate the intelligence originally employed for his education is unsound» [translator’s note: freely translated]. Also regarding Byrne’s method critics had reservations. In the massive essay where Florian Cajori [19] deals with symbols and forms used in mathematics, Byrne’s Euclid deserves a non marginal place, although the same Cajori stated that Byrne’s work was not taken seriously enough and often approached with ‘curiosity’ more than a real scientific interest. Posterity was condescending with Byrne. Starting from Augustus De Morgan’s merciless judgement—his worst detractor—who authoritatively maintained (his comment is definitely directed to Byrne!) that those who introduce symbols in elementary geometry are somehow breaking that ‘mechanical relationship’ that every student establishes with it. The one between Byrne and De Morgan was a querelle holding the stage in the years around the half of XIX century, in it, which in the end is a dispute between formal logic and symbolic logic, we can spot the grounds of the crisis experienced by ‘iconic’ representation (Bieldvorstellung) of mathematics in those years.

Indeed, Byrne’s work is animated by this internal contradiction. Certainly anachronistic as regards mathematical thought (in those years the Outdated Euclid was being published and Lobacevskij undermined the axiomatic foundations of Euclidean geometry), he seemed glancing towards the past of scientific thinking; and yet, as regards the graphic expression «with his coloured diagrams and his blind trust in arbitrary forms of representation, […] he is, if you will, artistically modern» [20] (p. 44) [translator’s note: freely translated], by far in advance as regards figurative language and aesthetic sensitivity. Equally, Montessoris’ educational materials, if observed in the perspective of their aesthetics and of product standardization appear to become part—in an intense and original way—of the lively cultural debate having the merit of the creation of modern design culture and, more generally, of the same project culture in the modern sense. We can safely assume that the educational materials are the outcome of a project-composition activity that clearly shows a culture of modernity and that contains with unexpected forwardness the arguments which will feature the project of Modernity. Above all with regard the concept of ‘space’, that is developed in Montessori’s project as a ‘space of relations’ and, hence, as a ‘structure’ in a ‘configurative’ as well as formal way, as later on Paul Klee will greatly express.

If a final judgement for both Byrne and Montessori in terms of efficacy of their learning processes is still waiting for a verdict, we can’t deny the aesthetic sensitivity and an extraordinary figurative outcome in their work, thanks to which both Euclid’s plates by Byrne and the ‘objects’ by Montessori can rightly find a place in the scenario of Modernity. The reference to such a great part of the artistic avantgardes of XX century, to De Style to Mondrian to Constructivism, to Kandinsky of Point and line to plane, Klee and the cult for a mathematizing, abstract aesthetics, free from the idea of a figurative representation of space and reality that has been characterizing the culture of XX century, seem in a way be recalled in Byrne’s and Montessori’s logic and figurative outcomes.