Abstract
This study focuses on an analysis of perceiving the infinite “solid images” derived from the projective transformations of space in a relief perspective, with particular reference to Renaissance theatre scenery. Today it is possible to simulate the projective transformations of the scenic space in a parametric environment, dynamically. This parameterization allows to analyze the effects of visual perception of the scene, through the dynamic control of its projective transformations. The main objective of this study is the exploration of the places of the projective transformation straddling reality and illusion, where the metamorphosis of the space triggers changeable processes of perception.
1. Introduction
This study focuses on an analysis of perceiving the infinite “solid images” that derive from the projective transformations of the real space in a relief perspective, with particular reference to Renaissance theatre scenery.
The perception of an architectural space moves between two opposite poles. On the one hand, there are projective effects on vision that generate perspective images, and on the other hand, there is the objective space, as it is in the reality in which it is immersed.
The space in which we are found is perceived by our eyes following the laws of vision, which generate images characterized by the presence of deformations that we call apparent. This projective space, which is anisotropic, is processed by the mind; based on experience, it interprets the perspective images, reducing them to their original Euclidean space. The dynamics between the two perceptual systems-the vision and the mind-that are based on Gestalt studies on psychology and perception, further developed in research carried out by Rudolph Arnheim in the second half of the 1970s, give cause for reflection to expand on an area that cannot be easily situated in the known dichotomy of “as it looks” and “as it is” [1]. There is, in fact, a place in which the border between real space and apparent space is not clear. This is the place where the projective transformations of space take place, where it is possible to construct an infinite number of relief perspectives of a single architectural subject, dilated or contracted, placed between real and illusory space.
In a relief perspective, a unique one-to-one relationship is established between Euclidean space and the projective space that generates a contracted solid image. This image varies in a portion of space regulated by the distance between two planes: the vanishing plane, also called the first limit plane, and the trace plane, also called the collineation plane. The dilation of space follows the separation of these planes, the contraction follows their approach. It is thus simple to understand the two-dimensional image of a linear perspective as a particular case of relief perspective: the one where space contracts until the above-mentioned planes coincide in a single plane commonly known as the picture plane (Figure 1).
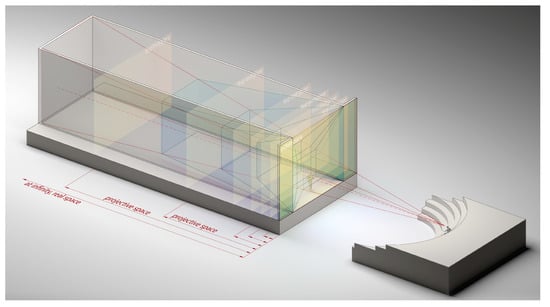
Figure 1.
Perspective transformation of solid space in a Renaissance theatre scenography.
If we imagine, for example, the Perspective gallery of Spada Palace in Rome, created around the mid-1600s by Francesco Borromini, we can observe the space “as it looks”, deluding spectators into believing they have in front of their eyes a gallery that is much longer with respect to its real dimensions. In this case, the space “as it is” does not represent the ideal gallery, but a phase of the projective transformation it is subject to. Since a relief perspective contains an infinite number of configurations that return the same ideal space, the gallery should be interpreted as a specific moment in the projective transformation process that takes the three-dimensional reality of space “as it is” to the two-dimensional perspective image of the space “as it looks”.
2. Projective Transformations of Scenic Space in Renaissance Theatre
In the history of representation, the control of contracting space in a relief perspective finds a documented area of experimentation in the scenography of Renaissance theatre. In fact, with the advent of court theatre, the modest sizes of the places where the scenes were hosted and the need to satisfy a favored point of view determined the construction of a contracted scenic space, generally parallelepiped in shape, designed according to a perspective system that we today would classify as frontal. Scenographic practice of the time shows an exemplary control of the projective transformations of the scenic box; famous examples of which include the Teatro Olimpico in Vicenza, designed in 1580 by Andrea Palladio and completed by Vincenzo Scamozzi, and the Teatro all’antica in Sabbioneta, designed by Scamozzi a few years later (Figure 2).
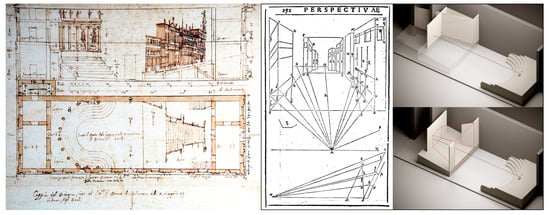
Figure 2.
Left: Vincenzo Scamozzi’s drawing for the scenography of the Theatre in Sabbioneta; Right: construction of the scenography in De Scenis treatise by Guidobaldo del Monte, 1600.
The same body of treatises accompanying the practice, as was usual, dedicates space to the construction of the scenery, considered a direct application of perspective. The treatises contain chapters dedicated to the art of fabricating the scene, among which we recall those by Sebastiano Serlio, Daniele Barbaro, and Lorenzo Sirigatti. Of undoubted interest is the chapter by Ignazio Danti in his Commentarii to Le due Regole della prospettiva pratica (The Two Rules of Practical Perspective) by Jacopo Barozzi da Vignola, published posthumously in 1583 [2]. However, it is with the scientific theorization of projective procedures at the base of perspective and in particular with the theorization of the punctum concursus (vanishing points) stated by Guidobaldo del Monte in 1600, that the control of the contraction of the scenic space becomes a method [3]. In De Scenis, the sixth book of Perspectivae libri sex, Guidobaldo describes the construction of the scene as the synthesis of two different operations. The first is the contraction of the scenic box, which takes the isotropic Euclidean space to the anisotropic scenic space. The second is the construction of the backdrop perspectives on the individual planes that compose the contracted scenic box, considered one by one as picture planes, all seen from the same point of view (Figure 2).
Guidobaldo demonstrates how the punctum concursus of the edges of the contracted scenic box are given by the intersection of the inclined plane of the stage with the straight line perpendicular to the backdrop plane passing through the eyes of the observer. Since this point is inaccessible due to the modest dimensions of the places in which the scenes were located, he then demonstrates how it is possible to use perspective to construct classes of lines in a generic position on all the surfaces of the scenic box, considering them to be the picture plane one by one.
The method proposed resolves the problem of controlling the contraction of the scenic space by reducing it to a set of plane cases. In fact, the relief perspective of the scenic box is decomposed into as many perspective planes as there are surfaces that compose it, these perspectives share the same centre of projection.
The universality of the method consists in applying the theory of the punctum concursus, which guarantee the possibility of representing lines in a generic position on planes oriented differently in a solid space. In this way, it is possible to control the contraction of the scenic space, using the process of projective transformation in any static configuration. Guidobaldo’s method therefore contains the prodromes of the relief perspective that would be theorized about two centuries later [4].
If in Guidobaldo’s perspective the projective transformation dealt only with the scenic box, because the research of the validity of theoretical projective reasoning, in the scenography of the time, the contraction of space regarded the overall setting of the scene and therefore the individual buildings that compose it.
The maturity demonstrated by the control of contracting the “solid space” of the scene, the capacity to create the illusion inside the illusion through the rigorous construction of a set of linear perspectives, and the scenographic practice of the time that experimented in the theatre the relief perspective, all led to enhancing the perception of the scene in the theatre of the late 1500s.
In the theatre, the contracted scenic box assumes one of an infinite number of configurations that, when observed from the centre of projection, all allude to the same ideal space. The choice of this contraction depends on two main factors: the dimensions of the spaces that host the scenes, and the dimensions of the usable space in which the players could act.
The privileged observer, who sees the scene from the centre of projection, has no perception of the projective transformations of the scenic space since the same image that would be seen if observing the real space is seen in any configuration. This is not true for other spectators, who move in the more or less wider surroundings of the limits of the restricted sight and who therefore have different perceptions of the real space, with respect to both the place they occupy and the greater or lesser contraction of the scenic space.
Today it is possible to simulate the projective transformations of the scenic space in a parametric environment by constructing an algorithm to generate the relief perspective on which the contraction of the space is based. By dynamically controlling of the projective transformation of the space, this parameterization allows us to analyze the effects of visual perception of the scene and at the same time, to systematizing some parameters, for example, the measurement of the “dimensions” of the restricted view, the effects of which can be controlled as the conformation of the scene is varied. The main objective of this analysis is the exploration of the places of the projective transformation straddling reality and illusion, where the metamorphosis of the space triggers sometimes-changeable processes of perception.
3. Dynamic Transformations between Affine Space and Projective Space
At the end of the 1800s, Wilhelm Fiedler demonstrated how linear perspective should be considered a particular case of relief perspective, and how other methods of representation derive from it [5]. To focus on this idea, we consider the operation of projection and section at the base of representation as a whole. The projecting lines, leaving a centre of projection, intersect the picture plane where the perspective image forms. There is a one-to-one correspondence between the class of points in the real plane and the two-dimensional class of image points in the picture plane. In a relief perspective, we replace the picture plane with an anisotropic scenic space, in geometry called projective space, which is overlaid on the real isotropic space, in geometry called affine space. There is the same one-to-one correspondence between the points of the real space and the points of the scenic space.
The depth of the scenic space measures the anisotropy in an interval between two limiting configurations: maximum dilation, in which the scenic space coincides with the real space; and maximum contraction, in which the scenic space instead reduces to a plane, as occurs in the particular case of the linear perspective (Figure 1).
In a linear perspective, the traces, the vanishing points, and the perspective images of the lines represented lie on the picture plane. In a relief perspective instead, the vanishing points lie on a plane called the first limit plane, or more simply, the vanishing plane, situated at a given distance from the centre of projection (principal distance or focal distance). The traces instead lie on a plane interposed between the observer and the first edge plane, called the collineation plane (or the trace plane), which contains points shared between the real space and the scenic space. The line in perspective, the image of the given line, crosses the projective space.
The front plane in a linear perspective passes through the eyes of the observer. This plane hosts the classes of points that, if projected from the centre of projection, meet the picture in a certain direction. Therefore, in the relief perspective, this plane, which is called the second limit plane, is necessarily separated from the centre of projection as much as the collineation plane is separated from the first limit plane (Figure 3).
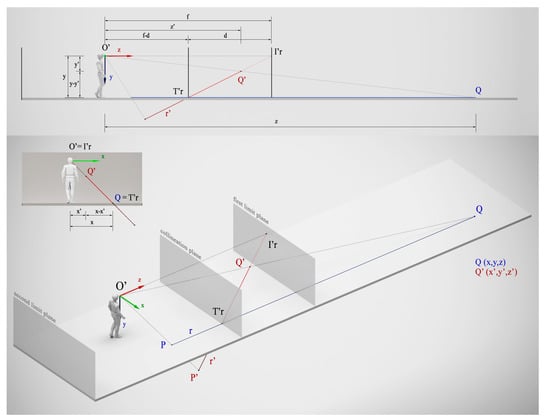
Figure 3.
Main elements of a relief perspective and geometric relationships at the base of the ratio between the coordinates of a point in the affine space and the coordinates of the same point in the projective space.
Today it is possible to rigorously build a relief perspective in the digital space and it is also possible to simulate the transformations between affine space and projective space, reproducing the contraction and expansion of space in a parametric environment and thus in a dynamic way [6].
This type of transformation can be made by calculating the coordinates of the points in the projective space with respect to those in the affine space and reiterating it for all of the infinite number of positions that the first limit plane can assume with respect to the collineation plane.
In fact, if we imagine placing the origin of a Cartesian coordinate system in the centre of projection oriented according to the pre-established axes, for example, with the z-axis coinciding with the principal distance, the set of transformations of all the points in the scene can be referred to this system. We therefore decompose the problem into three plane cases that resolve the calculation of the unknown coordinates in the zx-, zy-, and xy-planes, respectively. We first consider the case of the z-coordinates (Figure 3).
Due to similarity between triangles O’I’rQ’ and T’rQQ’, we have the following ratio:
z’:f = (z − z’):z − (f − d)
The lengths d, f, and z are known values; z is fixed because it corresponds to the position of the point in the affine space, and d and f vary with respect to the position that the first edge plane progressively assumes in the different transformation phases.
z’ = (fz)/(d + z)
The preceding relationship yields two more:
y’ = (fy)/(d + z)
x’ = (fx)/(d + z)
These relationships define the coordinates in the projective space starting from the affine space. The one-to-one nature of the projective relationships allows us to obtain the inverse relationships, which, starting from the projective space, yield the affine space:
z = (dz’)/(f − z’)
y = [y’(d + z)]/f
x = [x’(d + z)]/f
According to the objectives, these values can be implemented directly or inversely in a mathematical deformer that operates on a numerical model via the discrete representation of the entities. The relationships generate a model that reproduces the projective transformations of the space in a continuous way.
4. Perceptual Effects of the Projective Transformation of the Scene
The digital model, which is capable of simulating the projective transformation of the space, allows us to analyse and measure the illusory effect of the relief perspective of a scenic space, comparing it to the real space it refers to. It is clear that from the favoured point of view of the centre of projection, the collimation between the perspective image (which at this point we can define as a real “solid” image) and reality is perfectly verified despite the strength of the contraction of the scenic box.
Instead, we ask what happens when the observer is placed outside the restricted sight. What are the effects and what the variables that condition the alteration of the perception?
The object of experimentation is a model of the theatre of proportions similar to the theatre in Sabbioneta, reconstructed based on Vincenzo Scamozzi’s drawings.
In the case of a linear perspective, we can study the durability of the restricted sight, analysing three notable displacements of the observer with respect to the centre of projection: first, a horizontal movement perpendicular to the picture plane; second, a vertical movement parallel to the picture plane; and third, a horizontal movement that is also parallel to the picture plane [6].
The comparison between real space and the perceived scenic space when moving in these directions allows us to evaluate, and therefore measure, the tenacity of the illusion and to define a neighborhood around the centre of projection in which it is possible to move and perceive a space that geometrically conforms to the real space represented.
In the case of a relief perspective, this “measurement” is also conditioned by the contraction of the scenic space, which enhances or reduces the effects of compressing and dilating the space due to the above-mentioned movements. It alters the perception of depth and perspective, and therefore the real form of the object represented to which the perspective alludes. For the first displacement we imagine moving along the principal distance and we consider the configuration in which the first limit plane coincides with the collineation plane (the case of linear perspective). If the observer approaches the collineation plane, a scenic space is perceived that represents a real space that is more compressed than the true one. If, on the other hand, the observer moves away from the collineation plane, one will have the impression of viewing a more dilated space (Figure 4).
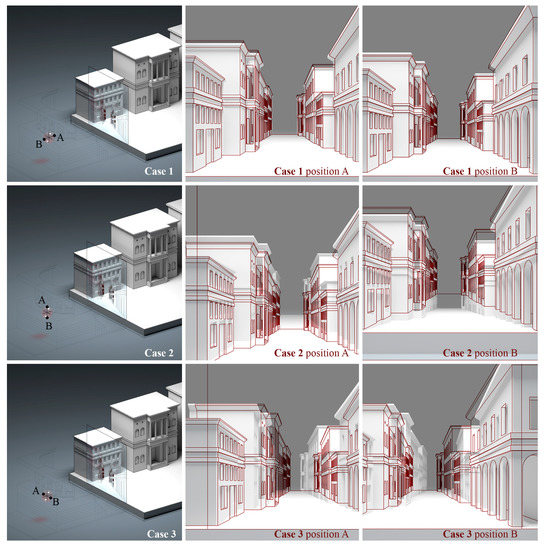
Figure 4.
Synoptic picture of the visual perception of the scene seen by an observer placed outside the restricted sight, according to three particular types of motion in case of a linear perspective.
Comparing the compression or dilation of the scenic space in this movement to the real space seen from the centre of projection, we see how the differences are modest for large displacements.
If we introduce the relief perspective, we see how this acts as an intervening accelerator, amplifying or reducing these effects. If we imagine the observer close to the collineation plane, outside the restricted sight and we dilate the scenic box, the effect of compressing the space is reduced. On the contrary, if the observer moves away from the collineation plane and we again dilate the scenic box, the extension is amplified, giving the impression that the spectator is found before an even deeper space (Figure 5).
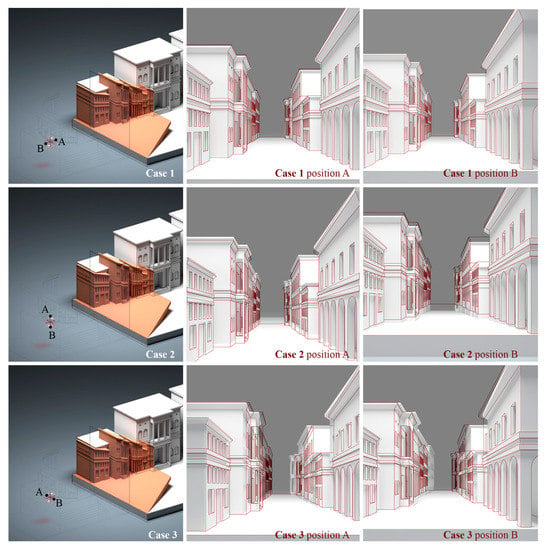
Figure 5.
Synoptic picture of the visual perception of the scene seen by an observer placed outside the restricted sight, according to three particular types of motion in case of a relief perspective.
We now imagine the second movement, wherein we make a vertical displacement, for example, situating the observer above the centre of projection. The horizon line would lose its coincidence with the effective horizon of the scene. If we want to restore the space represented by this perspective we should observe that the edges on the ground and at the top of the buildings would be inclined with respect to the horizon line the plane of the floor would therefore appear inclined: uphill if the observer moves upwards, and downhill if the observer moves downwards. This type of deformation allows for a certain margin when moving with respect to the restricted sight, even if it is less with respect to what was analysed above. But not all classes of lines react in the same way with respect to the observer’s displacement. In fact, if the images of the lines perpendicular to the frame are hardly affected by the vertical movement of the observer, one cannot say the same for the lines lying on the side planes, which represent horizontal lines parallel to the front of the scene. For this class of lines, which Guidobaldo in his scenography teaches us to represent on the wings, the illusion vanishes even for little movements of the centre of projection. If we introduce the relief perspective, we observe how this reduces, even in this case, the deformations produced by the displacement of the observer, expanding the boundaries of the restricted sight.
Finally, we imagine the third movement. In this case, the illusion also fails for small displacements around the centre of projection because the space represented is deformed and assumes, if restored, the form of an oblique prism. If we were to restore the real space which are view from this new perspective, we would find in front of a trapezoidal space. Even in this case, the expansion of the space introduced by the relief perspective widens the boundaries of the restricted sight reducing the perspective deformations (Figure 4 and Figure 5).
We can therefore determine a zone of “tolerance” for the restricted sight where the illusion is susceptible to tiny transformations that can be overlooked with respect to the perception of the overall scene. This zone is approximately ellipsoid shaped, situated with its major axis along the normal to the front of the scene, the intermediate axis in a vertical position, and the minor axis horizontal and parallel to the front of the scene. This tolerance is smallest for a linear perspective and increases noticeably in the case of a relief perspective, in which the space is enhanced, amplifying the perception of depth (Figure 6).
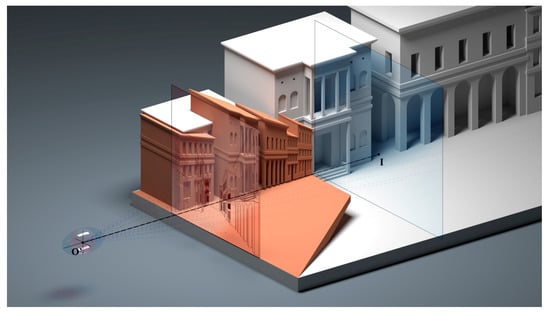
Figure 6.
Hypothesis on the size of the restricted sight in case of a linear perspective.
The measure of the illusion does not depend only on parameters of perspective, but also on a series of boundary conditions that contribute to revealing the perspective trick or amplifying its illusion.
In a theatre, the contracted box of the scene is not compared with the real space due to the darkness in which it is wrapped. In addition, there is no information about the space as it is, which lends credibility to the different interpretations of the form of the scenic space referred to by the perspective, which are generated observing the scene from points of view other than the centre of projection. In this artificial context, the observer can recognize in dimensional terms only architectural elements such as doors or windows and only if in ratio to the human scale; the observer cannot recognize the absolute dimensions of the spaces.
This abstraction of the real world does not increase the size of the restricted sight, but makes apparently deformed spaces plausible, alluding to real spaces different from those perceived from the centre of projection. The experience contributes to amplifying this extension, connecting the image of deformed spaces to apparently regular places and leading the observer into thinking that lines viewed as horizontal and orthogonal at the front of the scene are really so, ignoring the projective relationships of the perspective.
A perspective rendering has absolute metrical value if we have the length of a line whose orientation in space is known. This data is not used in the case of a theatre scene due to the illusion of the subject represented, so the restitution of the spaces observed, that is, the effective form of the illusory spaces, becomes an interpretational process whose own foundation is found in the perceptual experience.
A significant case in this sense is when the observer moves laterally to the margins of the scene. In this position, the main point of the perspective, O’0A, changes with respect to the effective principal point of the relief perspective, O’0. If we imagine to restore this perspective from the new centre of projection, we observe that the lines incident at O’0, which represented perpendicular lines at the front of the scene, now make a certain angle with respect to the frame, and therefore represent an oblique, prismatic space (Figure 7). This is generally ignored by the observer, whose visual experience and familiarity with common architecture suggest a state of perpendicularity that obscures any perspective consideration.
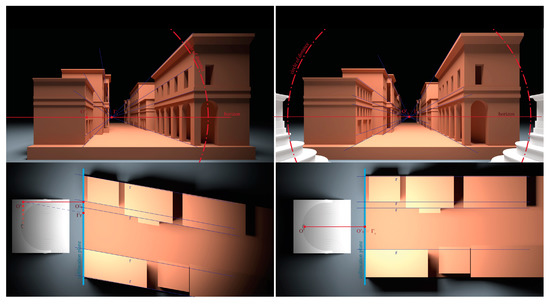
Figure 7.
Reconstruction of the real space starting from two perspective of the same solid perspective seen from two different points of view: the center of projection and a generic position of the observer.
Therefore, an observer can move within the theatre, approaching the front of the scene or moving away from it without the configuration of the apparent space losing any credibility. In the same way, the observer can move upwards or downwards, increasing or decreasing the apparent tilt of the stage, or laterally, sometimes altering the perspective and form of the space observed.
In addition, the contraction of the scenic space favours the overall perception of the scene. If we observe the contracted scene at the edge of the restricted sight by moving along the front, if the space is contracted, the wing most in perspective always remains visible, which does not occur if we substitute the real space for the contracted scene.
The contraction of the scenic space therefore extends the illusion to all the places in the theatre designed to observe the representation, in apparent contradiction to the concept of the Renaissance theatre, which was designed for a privileged spectator. Other devices seem to favour non-privileged points of view. This includes the depth of the real space alluded to by the scenic space. I In some cases, such as Guidobaldo’s scenography, the real space restored starting from the relief perspective of the scene appear particularly dilated; the spaces appear are unnatural with respect to a credible dimension because the buildings are excessively separated from each other. This distance, which is hardly perceived by the privileged observer, would have been perceived as unnatural if the real space were seen by a spectator in a decentralized position. The relief perspective—and therefore the contraction of the scenic space—compensates for this dilation, making the entire flat visible to a particularly decentralized spectator.
So far we have dealt with the empty scene without actors. The actor’s presence introduces a measure of the perspective space because it attributes dimensions to the buildings that can be compared to those of the human figure. The actor directly influences the design of the stage, where the useful space depends on the compatibility between human height and the height of some recognizable architectural elements that we are confronted with daily, such as the height and width of doors and windows. This ratio establishes a limit to the stage area used by the actor, beyond which the illusion is immediately revealed due to the paradoxes generated, making it seem to spectators that they are viewing giants act (Figure 8). If there is a physical limit beyond which the stage is not usable, we therefore wonder why a backdrop plane is not located there painted with a linear perspective as part of the flats. The reason rests on the fact that by introducing a linear perspective, one would again fall within the restricted sight, which the relief perspective in the theatre instead tends to invalidate.
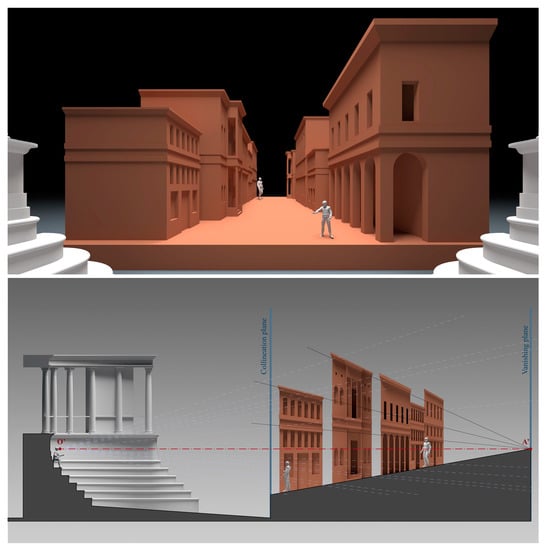
Figure 8.
The human figure and the measure of solid prospective space.
5. Conclusions
The goal of this experimentation was to explain the relationships that arise in a relief perspective between the space as it is and the space as it looks, with the aim of developing a method to measure the illusory power of the relief perspective in its infinite, changeable images.
We therefore studied the visual perception for an observer placed in a generic position with respect to the centre of projection, first in the plane case and then in the case of a dilation of the projective space. It was therefore seen how the case of the linear perspective establishes the most restrictive limits for the restricted sight and how the introduction of a relief perspective space is instead capable of increasing the dimensions sensibly and progressively.
In theatre scenography, the reduction of aberrations due to increasing the depth of the scenic space is not the only parameter to consider when studying the overall phenomenon of the illusion.
In particular, in Renaissance court theatre, in which the scene depicts outdoor, generally urban settings, there are an infinite number of solid images that satisfy the illusion for observers. Each image alludes to a real space that is geometrically different from the others, but which is anyway plausible. As a result, the spectator perceives the trick only through the direct comparison of the perspective scene with the human figure.
Thus, the court theatre, apparently designed for a privileged observer is, actually, an inclusive theatre, in which each spectator participates in the perspective illusion equally but in a different way, independently of the image and the phase of the process of projective transformation of the space in which the observer operates.
In sum, the relief perspective in theatre overcomes the restrictions of the restricted sight. Here the strength of illusion goes beyond the reasons of perspective. The spectator does not know the space as it is, but in an infinite number of solid images as it looks.
Author Contributions
Leonardo Baglioni and Marta Salvatore conceived and designed the experiments on the perceptual effects of the projective transformation of the scene completely sharing the methodology and the content. The authors continued the studies made by Riccardo Migliari beginning at the end of the 1990s on the theoretical foundation of relief perspective, reconsidering and developing the proportional ratios of direct and inverse formulas, on which the construction of the dynamic perspective machine is founded. Leonardo Baglioni, in addition, deepened the construction of the dynamic perspective machine from an operational point of view. Marta Salvatore, in addition, deepened the relationship between the relief perspective and the projective transformations of the scenographic space in the Renaissance theatre.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arnheim, R. The Dynamics of Architectural Form; University of California Press: Berkeley, CA, USA, 1977; ISBN 9780520035515. [Google Scholar]
- Mancini, F. Scenografia Italiana, dal Rinascimento all'età Romantica; Fratelli Fabbri: Milano, Italy, 1966. [Google Scholar]
- Del Monte, G. Perspectivae Libri Sex; Hieronymum Concordiam: Pesaro, Italy, 1600. [Google Scholar]
- Baglioni, L.; Salvatore, M. Projective principles at the basis of relief perspective in scenography of Guidobaldo del Monte. In Territories and Frontiers of Representation, Proceedings of the 39° Convegno Internazionale dei Docenti Delle Discipline Della Rappresentazione; Di Luggo, A., Giordano, P., Florio, R., Papa, L.M., Rossi, A., Zerlenga, O., Barba, S., Campi, M., Cirafici, A., Eds.; Di Luggo, A., Giordano, P., Florio, R., Papa, L.M., Rossi, A., Zerlenga, O., Barba, S., Campi, M., Cirafici, A., Eds.; Gangemi Editore International: Rome, Italy, 2017; pp. 267–276. ISBN 978-88-492-3507-4. [Google Scholar]
- Fiedler, G. Trattato di Geometria Descrittiva del Dr Guglielmo Fiedler; Successori Lemonier: Florence, Italy, 1874. [Google Scholar]
- Migliari, R. Ha la prospettiva un futuro. In Ikhnos, Analisi Grafica e Storia della Rappresentazione; Lombardi: Siracusa, Italy, 2005; pp. 133–160. ISBN 88-7260-161-4. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).