Vortex Motion State of the Dry Atmosphere with Nonzero Velocity Divergence ^†

Abstract

In the present work an analytical model of the vortex motion elementary state of the dry atmosphere with nonzero air velocity divergence is constructed. It is shown that the air parcel moves along the open curve trajectory of spiral geometry. It is found that for the case of nonzero velocity divergence the atmospheric elementary state presents an unlimited sequence of vortex cells transiting from one to another. On the other hand, at zero divergence, the elementary state presents a pair of connected vortices, and the trajectory is a closed curve. If in some cells the air parcel moves upward then in the adjacent cells it will move downward and vice versa. At reaching the cell middle height the parcel reverses the direction of rotation. When parcel moves upward, the motion is of anticyclonic type in the lower part of the vortex cell and of the cyclonic type in the upper part. When parcel moves downward, the motion is of anticyclonic type in the upper part of the vortex cell and of the cyclonic type in the lower part.

1. Introduction

It is well known that the geostrophic state is a two-dimensional basic state for large scale atmospheric motion [1,2,3]. But the atmospheric motions are three-dimensional. In the geostrophic state the motion cannot be convergence or divergence, and there is no vertical motion [4,5]. Because of surface frictional force, wind blows, and the motion is certainly upward or downward due to the continuous equation. Spiral structures of vortices in the atmosphere in different scales take place in these cases. Exact solutions of the Navier-Stokes equations for a three-dimensional vortex have been found out [6,7,8], of greater attracting is Sullivan’s two-cell vortex solution because the flow not only spirals in toward the axis and out along it, but also has a region of reverse flow near the axis.

A theoretical model of the vortex state of the atmosphere has been elaborated in [9,10] where the three-dimensional atmospheric vortex motion has been analyzed by considering dynamical equation, thermodynamical equation including Coriolis force, pressure gradient force and viscous force. It should be noted that a nondivergent motion has been studied in [9,10]. In this paper, we further develop the theoretical model of the vortex motion state of the atmosphere. The main goal of the study is to take proper account of the divergence term in the equations of motion.

2. Main Equations

In the local coordinate system the atmospheric state is described by the set of equations [1,2,3]:

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}=-\frac{1}{\mathsf{\rho }}\left(\frac{\partial p}{\partial x}\right)+\mathsf{\nu }{\nabla }^{2}u+2{\mathsf{\omega }}_{0z}v-2{\mathsf{\omega }}_{0y}w$$

(1)

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}=-\frac{1}{\mathsf{\rho }}\left(\frac{\partial p}{\partial x}\right)+\mathsf{\nu }{\nabla }^{2}u+2{\mathsf{\omega }}_{0z}v-2{\mathsf{\omega }}_{0y}w$$

(2)

$$\frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z}=-\frac{1}{\mathsf{\rho }}\left(\frac{\partial p}{\partial z}\right)-g+\mathsf{\nu }{\nabla }^{2}w+2{\mathsf{\omega }}_{0y}u$$

(3)

$$\frac{\partial \Delta T}{\partial t}+\left(v,\nabla \right)\Delta T=\mathsf{\kappa }{\nabla }^2\Delta T$$

(4)

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=\mathsf{\alpha }\left({\gamma }_{\mathrm{A}}-\gamma \right)w+\mathsf{\alpha }u\frac{\partial \Delta T}{\partial x}+\mathsf{\alpha }v\frac{\partial \Delta T}{\partial y}+\mathsf{\alpha }w\frac{\partial \Delta T}{\partial z}$$

(5)

Here $\Delta T=T-\overline{T}$; $T$, $\overline{T}$ are the air temperatures of disturbed and undisturbed atmosphere correspondingly.

The atmosphere statics equation:

$$\frac{\partial \overline{p}}{\partial x}=0, \frac{\partial \overline{p}}{\partial y}=0, -\frac{1}{\overline{\mathsf{\rho }}}\left(\frac{\partial \overline{p}}{\partial z}\right)-g=0$$

Let the atmospheric parameters have the form:

$$p=\overline{p}\left(z\right)+p^{\prime }\left(x,y,z,t\right), \Delta T=\overline{\Delta T}\left(z\right)+\mathsf{\theta }\left(x,y,z,t\right),\overline{ \Delta T}={\Delta }_{0}T-\Delta \gamma \cdot z, \Delta \gamma ={\gamma }_{\mathrm{a}}-\gamma .$$

The air density has the form $\mathsf{\rho }=\overline{\mathsf{\rho }}\left(1-\mathsf{\alpha }\Delta T\right)$. Neglecting the advective terms and proceeding to the dimensionless quantities, the set of equations can be written as

$$\frac{\partial u}{\partial t}=-\frac{\partial p^{\prime }}{\partial x}+\frac{1}{{\mathrm{Ro}}_L}v-\frac{1}{{\mathrm{Ro}}_H}w+\frac{1}{\mathrm{Re}}\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}+\frac{{\partial }^{2}u}{\partial z^2}\right)$$

(6)

$$\frac{\partial v}{\partial t}=-\frac{\partial p^{\prime }}{\partial y}-\frac{1}{{\mathrm{Ro}}_L}u+\frac{1}{\mathrm{Re}}\left(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}+\frac{{\partial }^{2}v}{\partial z^2}\right)$$

(7)

$$\frac{\partial w}{\partial t}=-\frac{\partial p^{\prime }}{\partial z}+\mathrm{Ri}\cdot \Delta T+\frac{1}{{\mathrm{Ro}}_H}u+\frac{1}{\mathrm{Re}}\left(\frac{{\partial }^{2}w}{\partial x^2}+\frac{{\partial }^{2}w}{\partial y^2}+\frac{{\partial }^{2}w}{\partial z^2}\right)$$

(8)

$$\frac{1}{\mathrm{Pr}\cdot \mathrm{Re}}\frac{\partial \mathsf{\theta }}{\partial t}=w+\frac{{\partial }^2\mathsf{\theta }}{\partial x^2}+\frac{{\partial }^2\mathsf{\theta }}{\partial y^2}+\frac{{\partial }^2\mathsf{\theta }}{\partial z^2}$$

(9)

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=\mathsf{\alpha }\left({\gamma }_{\mathrm{A}}-{\gamma }_{\mathrm{a}}\right)Hw$$

(10)

Differentiating by y and x and subtracting Equation (1) from Equation (2), we get

$$\frac{\partial \mathsf{\Omega }}{\partial t}=-\frac{1}{{\mathrm{Ro}}_L}D+\frac{1}{\mathrm{Re}}{\nabla }^2\mathsf{\Omega }+\frac{1}{{\mathrm{Ro}}_H}\frac{\partial w}{\partial y}$$

Here

$$\mathsf{\Omega }=\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}, D=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}$$

is the vertical vorticity and horizontal divergence correspondingly.

Analogously, differentiating and summing the Equations (6) and (7), we get

$$\frac{\partial D}{\partial t}=-\left(\frac{{\partial }^2{p}^{\prime }}{\partial x^2}+\frac{{\partial }^2{p}^{\prime }}{\partial y^2}\right)+\frac{\mathsf{\Omega }}{{\mathrm{Ro}}_L}-\frac{1}{{\mathrm{Ro}}_H}\frac{\partial w}{\partial x}+\frac{1}{\mathrm{Re}}{\nabla }^{2}D,$$

Thus we have

$$\frac{\partial \mathsf{\Omega }}{\partial t}+\frac{D}{{\mathrm{Ro}}_L}=\frac{1}{\mathrm{Re}}{\nabla }^2\mathsf{\Omega }+\frac{1}{{\mathrm{Ro}}_H}\frac{\partial w}{\partial y}$$

(11)

$$\frac{\partial D}{\partial t}-\frac{\mathsf{\Omega }}{{\mathrm{Ro}}_L}=-\left(\frac{{\partial }^2{p}^{\prime }}{\partial x^2}+\frac{{\partial }^2{p}^{\prime }}{\partial y^2}\right)+\frac{1}{\mathrm{Re}}{\nabla }^{2}D-\frac{1}{{\mathrm{Ro}}_H}\frac{\partial w}{\partial x}$$

(12)

$$\frac{\partial w}{\partial t}=-\frac{\partial p^{\prime }}{\partial z}+\mathrm{Ri}\cdot \mathsf{\theta }+\frac{1}{\mathrm{Re}}{\nabla }^{2}w+\frac{1}{{\mathrm{Ro}}_H}u$$

(13)

$$\frac{1}{\mathrm{PrRe}}\frac{\partial \mathsf{\theta }}{\partial t}=w+{\nabla }^2\mathsf{\theta }$$

(14)

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=\mathsf{\alpha }H\left({\gamma }_{\mathrm{A}}-{\gamma }_{\mathrm{a}}\right)\cdot w$$

(15)

Consider the atmospheric stationary state. Neglecting the advective terms, the Equations (11)–(15) can be transformed:

$$\frac{D}{{\mathrm{Ro}}_L}=\frac{1}{\mathrm{Re}}{\nabla }^2\mathsf{\Omega }+\frac{1}{{\mathrm{Ro}}_H}\frac{\partial w}{\partial y}$$

(16)

$$-\frac{\mathsf{\Omega }}{{\mathrm{Ro}}_L}=-\left(\frac{{\partial }^2{p}^{\prime }}{\partial x^2}+\frac{{\partial }^2{p}^{\prime }}{\partial y^2}\right)+\frac{1}{\mathrm{Re}}{\nabla }^{2}D-\frac{1}{{\mathrm{Ro}}_H}\frac{\partial w}{\partial x}$$

(17)

$$0=-\frac{\partial p^{\prime }}{\partial z}+\mathrm{Ri}\cdot \mathsf{\theta }+\frac{1}{\mathrm{Re}}{\nabla }^{2}w+\frac{1}{{\mathrm{Ro}}_H}u$$

(18)

$$0=w+{\nabla }^2\mathsf{\theta }$$

(19)

$$D+\frac{\partial w}{\partial z}=\mathsf{\alpha }H\left({\gamma }_{\mathrm{A}}-{\gamma }_{\mathrm{a}}\right)\cdot w$$

(20)

Excluding $\mathsf{\Omega }$, $D$, $\mathsf{\theta }$, $p^{\prime }$, we get the required partial differential equation:

$$\begin{array}{l}\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}\right)\left[\left({\nabla }^2{\nabla }^2-\mathrm{Ra}\right)w+\frac{\mathrm{Re}}{{\mathrm{Ro}}_H}{\nabla }^{2}u\right]+\left({\nabla }^2{\nabla }^2+\mathrm{Ta}\right)\frac{{\partial }^{2}w}{\partial z^2}-\\ \mathsf{\alpha }H\left({\gamma }_{\mathrm{A}}-{\gamma }_{\mathrm{a}}\right)\left({\nabla }^2{\nabla }^2+\mathrm{Ta}\right)\frac{\partial w}{\partial z}=-\frac{\mathrm{Re}}{{\mathrm{Ro}}_H}\frac{{\partial }^2{\nabla }^{2}w}{\partial z\partial x}-\frac{{\mathrm{Re}}^2}{{\mathrm{Ro}}_H{\mathrm{Ro}}_L}\frac{{\partial }^{2}w}{\partial z\partial y}\end{array}$$

(21)

where

$$\mathrm{Ra}=\mathrm{Ri}\cdot \mathrm{Re}=\frac{\mathsf{\kappa }}{\mathsf{\nu }}\frac{H^2{N}^2}{U^2}, \mathrm{Ta}=\frac{{\mathrm{Re}}^2}{{\left({\mathrm{Ro}}_L\right)}^2}$$

(22)

Ra is the Rayleigh number, Ta is the Taylor number.

3. Solution of the Main Equations

Assume that $w$ has the form:

$$w=X\left(x\right)Y\left(y\right)W\left(z\right), X\left(x\right)=\cos kx, Y\left(y\right)=\cos ky, W\left(z\right)=W_0\cdot \sin \left(n\mathsf{\pi }z\right)$$

(23)

Substituting Equation (23) into Equation (21), we get

$$\begin{array}{c}\left(2k^2\mathrm{Ra}-{\left(2k^2+n^2{\mathsf{\pi }}^2\right)}^3-n^2{\mathsf{\pi }}^2\mathrm{Ta}\right)w+\frac{\mathrm{Re}}{{\mathrm{Ro}}_H}\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}\right){\nabla }^{2}u+\\ \frac{\mathrm{Re}}{{\mathrm{Ro}}_H}\left(2k^2+n^2{\mathsf{\pi }}^2\right)W_{0}kn\mathsf{\pi }\cdot \sin kx\cdot \cos ky\cdot \cos \left(n\mathsf{\pi }z\right)-\\ \mathsf{\alpha }H\left({\gamma }_{\mathrm{A}}-{\gamma }_{\mathrm{a}}\right)\left[{\left(2k^2+n^2{\mathsf{\pi }}^2\right)}^2+\mathrm{Ta}\cdot n\mathsf{\pi }\right]W_0\cdot \cos kx\cdot \cos ky\cdot \cos \left(n\mathsf{\pi }z\right)=\\ W_0\frac{{\mathrm{Re}}^2}{{\mathrm{Ro}}_L{\mathrm{Ro}}_H}kn\mathsf{\pi }\cdot \cos kx\cdot \sin ky\cdot \cos \left(n\mathsf{\pi }z\right)\end{array}$$

We seek the expression of u in the form:

$$u=-W_0\cdot \left(A\cdot \sin kx\cdot \cos ky+B\cdot \cos kx\cdot \sin ky+C\cdot \cos kx\cdot \cos ky\right)\cdot \cos \left(n\mathsf{\pi }z\right)$$

Substituting, we get

$$\begin{array}{c}\left[2k^2\mathrm{Ra}-n^2{\mathsf{\pi }}^2\mathrm{Ta}-{\left(2k^2+n^2{\mathsf{\pi }}^2\right)}^3\right]W_0\cdot \cos kx\cdot \cos ky\cdot \sin \left(n\mathsf{\pi }z\right)-\\ \frac{\mathrm{Re}}{{\mathrm{Ro}}_H}k\left(2kA-n\mathsf{\pi }\right)\left(2k^2+n^2{\mathsf{\pi }}^2\right)W_0\cdot \sin kx\cdot \cos ky\cdot \cos \left(n\mathsf{\pi }z\right)-\\ \left[\frac{\mathrm{Re}}{{\mathrm{Ro}}_H}2k^2\left(2k^2+n^2{\mathsf{\pi }}^2\right)B+\frac{{\mathrm{Re}}^2}{{\mathrm{Ro}}_L{\mathrm{Ro}}_H}kn\mathsf{\pi }\right]W_0\cdot \cos kx\cdot \sin ky\cdot \cos \left(n\mathsf{\pi }z\right)-\\ \left\{\frac{\mathrm{Re}}{{\mathrm{Ro}}_H}2k^2\left(2k^2+n^2{\mathsf{\pi }}^2\right)C+\mathsf{\alpha }H\left({\gamma }_{\mathrm{A}}-{\gamma }_{\mathrm{a}}\right)\left[{\left(2k^2+n^2{\mathsf{\pi }}^2\right)}^2+{\mathrm{Ta}}^{2}n\mathsf{\pi }\right]\right\}\times \\ W_0\cdot \cos kx\cdot \cos ky\cdot \cos \left(n\mathsf{\pi }z\right)=0\end{array}$$

From here we have

$$\begin{array}{c}{\mathrm{Ra}}_{\mathrm{cr}}=\frac{{\left(2k^2+n^2{\mathsf{\pi }}^2\right)}^3+n^2{\mathsf{\pi }}^2\mathrm{Ta}}{2k^2}, A=\frac{n\mathsf{\pi }}{2k}, B=-\frac{\mathrm{Re}}{{\mathrm{Ro}}_L}\frac{\mathsf{\pi }n}{2k\left(2k^2+n^2{\mathsf{\pi }}^2\right)},\\ C=-\frac{{\mathrm{Ro}}_H}{\mathrm{Re}}\mathsf{\alpha }H\left({\gamma }_{\mathrm{A}}-{\gamma }_{\mathrm{a}}\right)\left[1+\frac{n^2{\mathsf{\pi }}^2}{2k^2}+\mathrm{Ta}\frac{n\mathsf{\pi }}{2k^2\left(2k^2+n^2{\mathsf{\pi }}^2\right)}\right]\end{array}$$

Finally

$$\frac{u}{W_0}=-\left(\frac{n\mathsf{\pi }}{2k}\cdot \sin kx\cdot \cos ky-\frac{\mathrm{Re}}{{\mathrm{Ro}}_L}\frac{\mathsf{\pi }n}{2k\left(2k^2+n^2{\mathsf{\pi }}^2\right)}\cdot \cos kx\cdot \sin ky+C\cdot \cos kx\cdot \cos ky\right)\cos \left(n\mathsf{\pi }z\right)$$

(24)

$$\begin{array}{c}v=\frac{W_0}{k}\cdot \cos kx\cdot \sin ky\cdot \left[\mathsf{\alpha }H\left({\gamma }_{\mathrm{A}}-{\gamma }_{\mathrm{a}}\right)\cdot \sin \left(n\mathsf{\pi }z\right)-n\mathsf{\pi }\cdot \cos \left(n\mathsf{\pi }z\right)\right]+\\ W_0\cdot \cos kx\left[\left(\frac{n\mathsf{\pi }}{2k}+C\right)\sin ky-\frac{\mathrm{Re}}{{\mathrm{Ro}}_L}\frac{\mathsf{\pi }n}{2k\left(2k^2+n^2{\mathsf{\pi }}^2\right)}\cdot \cos ky\right]\cos \left(n\mathsf{\pi }z\right)\end{array}$$

(25)

$$w=W_0\cdot \cos kx\cdot \cos ky\cdot \sin \left(n\mathsf{\pi }z\right)$$

(26)

Figure 1 shows the velocity field in accordance with Equations (24)–(26). It is seen that the air parcel motion have a three-dimensional spiral structure.

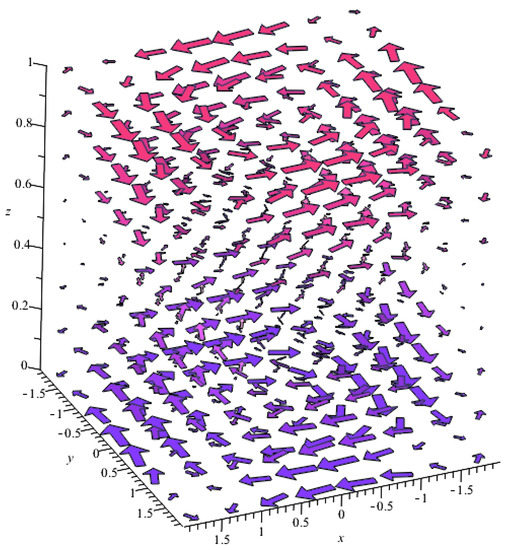
Figure 1. Velocity field of the vortex motion.

Figure 2 shows the calculated air parcel trajectory in accordance with Equations (24)–(26).

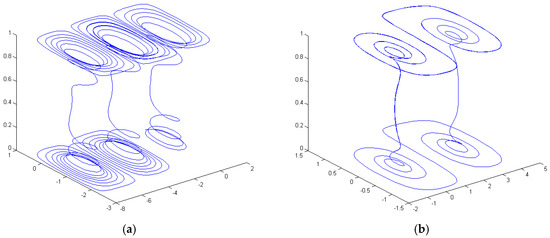
Figure 2. The air parcel trajectory. (a) At non-zero divergence; (b) The divergence is equal to zero.

As is seen from Figure 2a, the air parcel trajectory is an unclosed curve. In other words the parcel passes from one vortex cell to another. Thus, one can see that the basic state of the atmosphere in the case of non-zero divergence is a sequence of connected vortex cells. On the other hand, at zero divergence, the air parcel trajectory is a closed curve and the atmospheric state is a pair of connected vortices (Figure 2b).

The expression for the velocity divergence can be obtained from Equation (20):

$$\begin{array}{c}D=\mathsf{\alpha }H\left({\gamma }_{\mathrm{A}}-{\gamma }_{\mathrm{a}}\right)\cdot w-\frac{\partial w}{\partial z}=\\ W_0\cdot \cos kx\cdot \cos ky\cdot \left[\mathsf{\alpha }H\left({\gamma }_{\mathrm{A}}-{\gamma }_{\mathrm{a}}\right)\sin \left(n\mathsf{\pi }z\right)-n\mathsf{\pi }\cdot \cos \left(n\mathsf{\pi }z\right)\right].\end{array}$$

The expression for the temperature disturbance can be obtained from Equation (19):

$$\mathsf{\theta }=\frac{W_0}{2k^2+n^2{\mathsf{\pi }}^2}\cdot \cos kx\cdot \cos ky\cdot \sin \left(n\mathsf{\pi }z\right)$$

The expression for the pressure disturbance can be obtained from Equation (18):

$$\begin{array}{c}{p}^{\prime }=\left[\frac{\left(2k^2+{\mathsf{\pi }}^2{n}^2\right)}{\mathrm{Re}}-\frac{\mathrm{Ri}}{2k^2+n^2{\mathsf{\pi }}^2}\right]\frac{W_0}{\mathsf{\pi }n}\cdot \cos kx\cdot \cos ky\cdot \cos \left(n\mathsf{\pi }z\right)+\\ \left[\frac{n\mathsf{\pi }}{2k}\cdot \sin kx\cdot \cos ky-\left(\frac{\mathrm{Re}}{{\mathrm{Ro}}_L}\frac{\mathsf{\pi }n}{2k\left(2k^2+n^2{\mathsf{\pi }}^2\right)}\cdot \sin ky+C\cdot \cos ky\right)\cdot \cos kx\right]\times \\ \times \frac{W_0}{{\mathrm{Ro}}_H\cdot n\mathsf{\pi }}\cdot \sin \left(n\mathsf{\pi }z\right).\end{array}$$

The expression for the vorticity can be obtained from Equation (17):

$$\begin{array}{c}\mathsf{\Omega }=-2k^2\frac{{\mathrm{Ro}}_L{W}_0}{\mathsf{\pi }n}\left[\frac{\left(2k^2+{\mathsf{\pi }}^2{n}^2\right)}{\mathrm{Re}}-\frac{\mathrm{Ri}}{2k^2+n^2{\mathsf{\pi }}^2}\right]\cdot \cos kx\cdot \cos ky\cdot \cos \left(n\mathsf{\pi }z\right)+\\ 2k^2{\mathrm{Ro}}_L\left[\frac{n\mathsf{\pi }}{2k}\cdot \sin kx\cdot \cos ky-\left(\frac{\mathrm{Re}}{{\mathrm{Ro}}_L}\frac{\mathsf{\pi }n}{2k\left(2k^2+n^2{\mathsf{\pi }}^2\right)}\cdot \sin ky+C\cdot \cos ky\right)\cdot \cos kx\right]\times \\ \frac{W_0}{{\mathrm{Ro}}_H\cdot n\mathsf{\pi }}\cdot \sin \left(n\mathsf{\pi }z\right)+\\ \frac{{\mathrm{Ro}}_L}{\mathrm{Re}}{W}_0\left(2k^2+{\mathsf{\pi }}^2{n}^2\right)\cdot \cos kx\cdot \cos ky\cdot \left[\mathsf{\alpha }H\left({\gamma }_{\mathrm{A}}-{\gamma }_{\mathrm{a}}\right)\sin \left(n\mathsf{\pi }z\right)-n\mathsf{\pi }\cdot \cos \left(n\mathsf{\pi }z\right)\right]-\\ \frac{{\mathrm{Ro}}_L}{{\mathrm{Ro}}_H}{W}_{0}k\cdot \cos kx\cdot \cos ky\cdot \sin \left(n\mathsf{\pi }z\right).\end{array}$$

Figure 3 and Figure 4 show the fields of vorticity, temperature, divergence, and pressure at the altitudes $z=0.5$ (lower part of the vortex cell) and $z=1.5$ (upper part of the vortex cell) correspondingly.

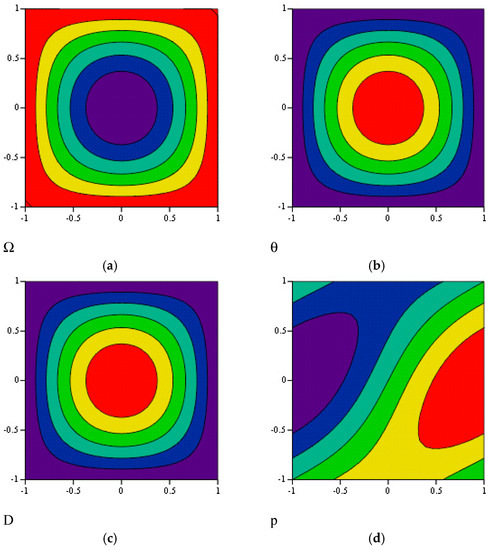
Figure 3. The calculated fields of vorticity (a), temperature (b), divergence (c), and pressure (d) in lower part of the vortex cell (at $z=0.5$).

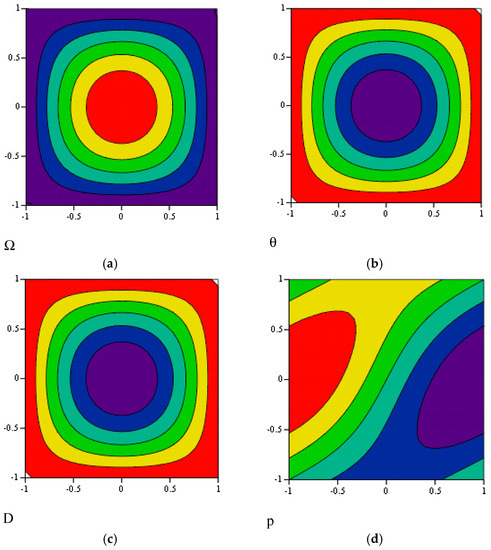
Figure 4. The calculated fields of vorticity (a), temperature (b), divergence (c), and pressure (d) in upper part of the vortex cell (at $z=1.5$).

As is seen, if the motion field in the lower part of the cell has a cyclonic vorticity, then in the upper part it has an anticyclonic vorticity and vice versa. The cyclonic center is heated; the anticyclonic center is cooled. The temperature field correlates with the pressure field.

4. Conclusions

In the present study the mathematical model of the stationary three-dimensional vortex state of the atmosphere at nonzero divergence has been developed. The expressions for the vortex velocity components have been derived. It is shown that at zero divergence, the elementary state of the atmosphere presents a pair of connected vortices, and the air parcel trajectory is a closed curve. For the case of nonzero velocity divergence the atmospheric elementary state presents an unlimited sequence of vortex cells transiting from one to another, and the air parcel trajectory is an unclosed curve. The pressure isolines are unclosed at nonzero divergence. The centers of cyclonic vorticity, velocity divergence and temperature maximum in the lower part of the cell coincide with the pressure ridge. The center of anticyclonic vorticity in the upper part of the cell coincides with the pressure hollow.