Trend Assessment for a CO2 and CH4 Data Series in Northern Spain †
Abstract
1. Introduction
2. Data and Methods
2.1. Data Acquisition and Calibration
2.2. Site Location
2.3. Mathematical Procedure
2.3.1. Harmonic Function
2.3.2. Kernel Function
2.3.3. Local Linear Function
3. Results and Discussion
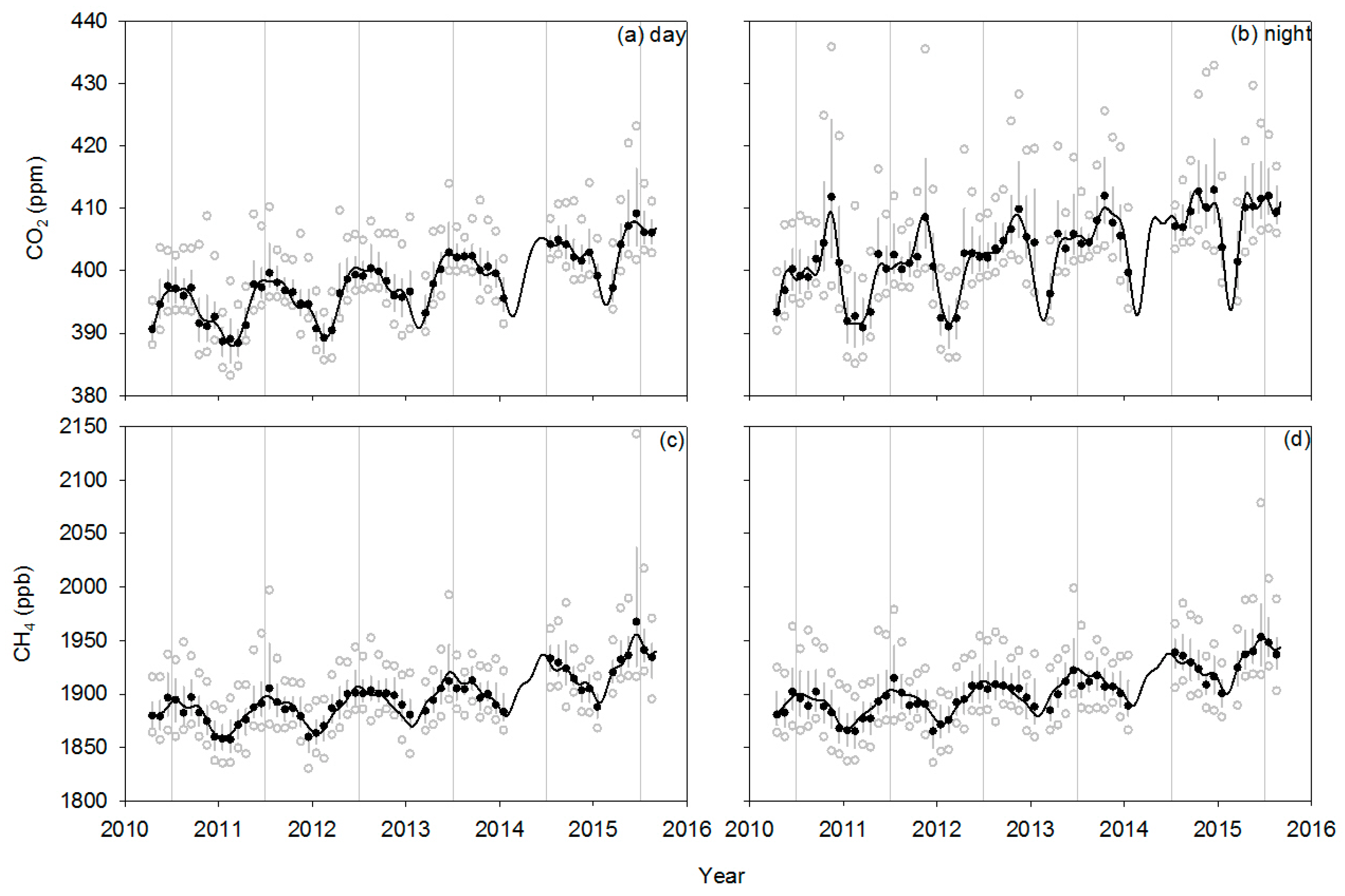
3.1. CO2 and CH4 Mixing Ratio Evolution
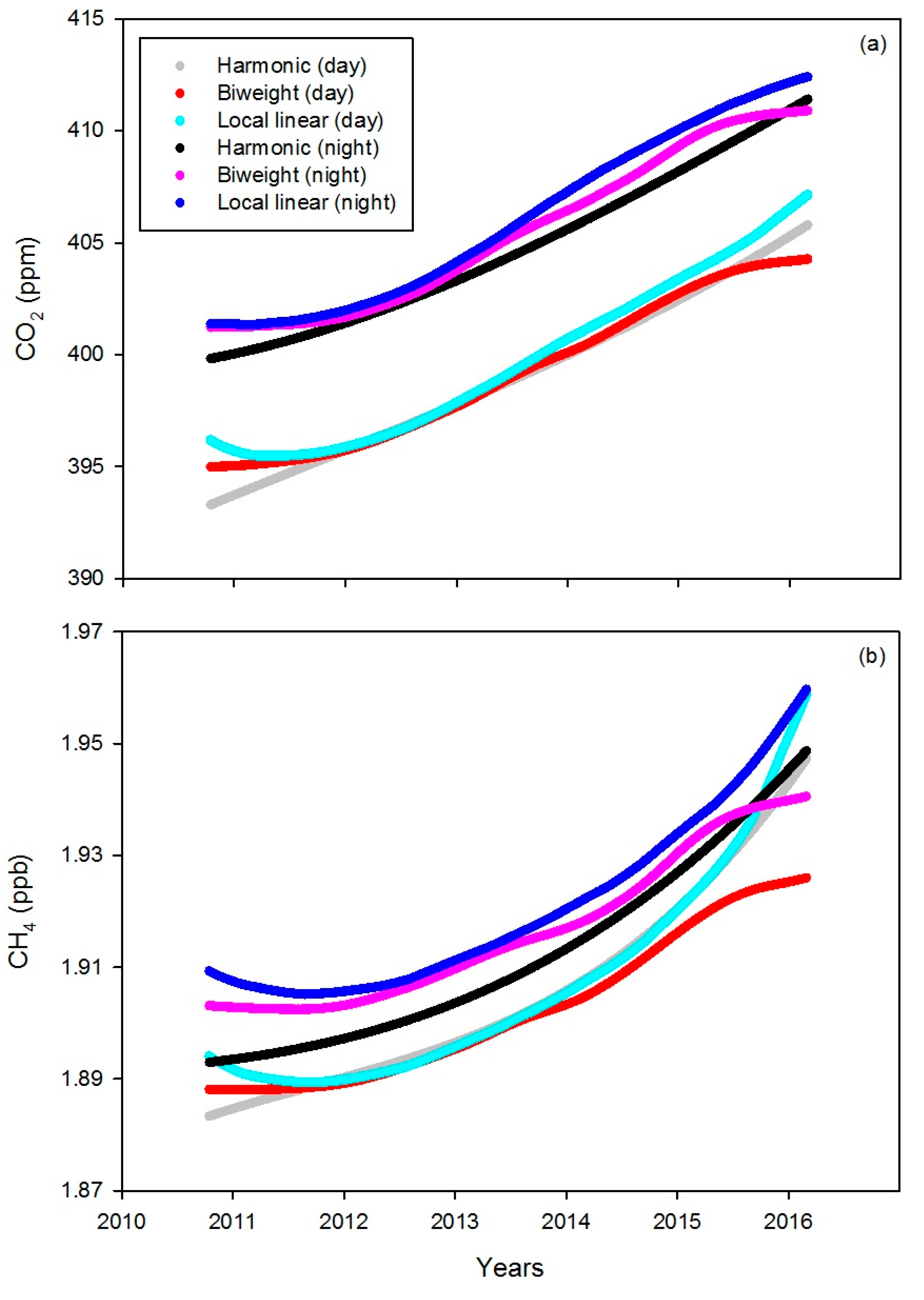
3.2. Data Trend Evolution
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Pérez, I.A.; Sánchez, M.L.; García, M.Á.; Pardo, N. Carbon dioxide at an unpolluted site analysed with the smoothing kernel method and skewed distributions. Sci. Total Environ. 2013, 456, 239–245. [Google Scholar] [CrossRef] [PubMed]
- Pickers, P.A.; Manning, A.C. Investigating bias in the application of curve fitting programs to atmospheric time series. Atmos. Meas. Tech. 2015, 8, 1469–1489. [Google Scholar] [CrossRef]
- Artuso, F.; Chamard, P.; Piacentino, S.; Sferlazzo, D.M.; De Silvestri, L.; di Sarra, A.; Meloni, D.; Monteleone, F. Influence of transport and trends in atmospheric CO2 at Lampedusa. Atmos. Environ. 2009, 43, 3044–3051. [Google Scholar] [CrossRef]
- Anderson-Cook, C.M. A second order model for cylindrical data. J. Stat. Comput. Simul. 2000, 66, 51–65. [Google Scholar] [CrossRef]
- Sánchez, M.L.; Pérez, I.A.; García, M.A. Study of CO2 variability at different temporal scales recorded in a rural Spanish site. Agric. For. Meteorol. 2010, 150, 1168–1173. [Google Scholar] [CrossRef]
- Fernández-Duque, B.; Pérez, I.A.; Sánchez, M.L.; García, M.Á.; Pardo, N. Temporal patterns of CO2 and CH4 in a rural area in northern Spain described by a harmonic equation over 2010–2016. Sci. Total. Environ. 2017, 593, 1–9. [Google Scholar] [CrossRef]
- Cleveland, W.S. Robust locally weighted regression and smoothing scatterplots. J. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- Pérez, I.A.; Sánchez, M.L.; García, M.Á.; Pardo, N. Trend analysis of CO2 and CH4 recorded at a semi-natural site in the northern plateau of the Iberian Peninsula. Atmos. Environ. 2017, 151, 24–33. [Google Scholar] [CrossRef]
- Pérez, I.A.; Sánchez, M.L.; García, M.Á.; Pardo, N. Daily patterns of CO2 in the lower atmosphere of a rural site. Theor. Appl. Climatol. 2015, 122, 195–205. [Google Scholar] [CrossRef]
- De Haan, P. On the use of density kernels for concentration estimations within particle and puff dispersion models. Atmos. Environ. 1999, 33, 2007–2021. [Google Scholar] [CrossRef]
- Lorimer, G.S. The Kernel method for air quality modelling-I. Mathematical foundation. Atmos. Environ. 1986, 20, 1447–1452. [Google Scholar] [CrossRef]
- Donnelly, A.; Broderick, B.; Misstear, B. Relating background NO2 concentrations in air to air mass history using non-parametric regression methods: Application at two background sites in Ireland. Environ. Model. Assess. 2012, 17, 363–373. [Google Scholar] [CrossRef]
- Crosson, E.R. A cavity ring-down analyzer for measuring atmospheric levels of methane, carbon dioxide, and water vapor. Appl. Phys. B 2008, 92, 403–408. [Google Scholar] [CrossRef]
- Rella, C.W.; Chen, H.; Andrews, A.E.; Filges, A.; Gerbig, C.; Hatakka, J.; Karion, A.; Miles, N.L.; Richardson, S.J.; Steinbacher, M.; et al. High accuracy measurements of dry mole fractions of carbon dioxide and methane in humid air. Atmos. Meas. Tech. 2013, 6, 837–860. [Google Scholar] [CrossRef]
- Pérez, I.A.; Sánchez, M.L.; García, M.Á.; Pardo, N. Features of the annual evolution of CO2 and CH4 in the atmosphere of a Mediterranean climate site studied using a nonparametric and a harmonic function. Atmos. Pollut. Res. 2016, 7, 1013–1021. [Google Scholar] [CrossRef][Green Version]
- García, M.Á.; Sánchez, M.L.; Pérez, I.A. Differences between carbon dioxide levels over suburban and rural sites in Northern Spain. Environ. Sci. Pollut. Res. 2012, 19, 432–439. [Google Scholar] [CrossRef] [PubMed]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2006; Volume 91, Chapter 3. [Google Scholar]
- Sánchez, M.L.; García, M.A.; Pérez, I.A.; Pardo, N. CH4 continuous measurements in the upper Spanish plateau. Environ. Monit. Assess. 2014, 186, 2823–2834. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Tang, J.; Shi, G.; Nakazawa, T.; Aoki, S.; Sugawara, S.; Wen, M.; Morimoto, S.; Patra, P.K.; Hayasaka, T.; et al. Temporal and spatial variations of the atmospheric CO2 concentration in China. Geophys. Res. Lett. 2008, 35, L03801. [Google Scholar] [CrossRef]
- Zhu, C.; Yoshikawa-Inoue, H. Seven years of observational atmospheric CO2 at a maritime site in northernmost Japan and its implications. Sci. Total Environ. 2015, 524, 331–337. [Google Scholar] [CrossRef]
- Fang, S.X.; Tans, P.P.; Dong, F.; Zhou, H.; Luan, T. Characteristics of atmospheric CO2 and CH4 at the Shangdianzi regional background station in China. Atmos. Environ. 2016, 131, 1–8. [Google Scholar] [CrossRef]
- Nisbet, E.G.; Dlugokencky, E.J.; Bousquet, P. Methane on the Rise—Again. Atmos. Sci. 2014, 343, 493–495. [Google Scholar] [CrossRef] [PubMed]
- Vermeulen, A.T.; Hensen, A.; Popa, M.E.; van den Bulk, W.C.M.; Jongejan, P.A.C. Greenhouse gas observations from Cabauw Tall Tower (1992–2010). Atmos. Meas. Tech. 2011, 4, 617–644. [Google Scholar] [CrossRef]

| Kernel Function | a K(u) |
|---|---|
| Epanechnikov | (3/4) (1 − u2) |
| Biweight | (15/16) (1 − u2)2 |
| Gaussian | (2π)−1/2 exp (−0.5u2) |
| Rectangular | 1/2 |
| Triangular | 1 − |u| |
| Tricubic | (70/81) (1 − |u|3)3 |
| Statistic | CO2 (ppm) | CH4 (ppb) | ||
|---|---|---|---|---|
| Day | Night | Day | Night | |
| Median | 397.91 | 403.24 | 1.8966 | 1.9024 |
| Interquartile range | 5.01 | 7.98 | 0.0284 | 0.0315 |
| 10th percentile | 394.34 | 397.87 | 1.8737 | 1.8772 |
| 90th percentile | 405.72 | 414.74 | 1.9368 | 1.9446 |
| Function | CO2 (ppm) | CH4 (ppb) | ||
|---|---|---|---|---|
| Day | Night | Day | Night | |
| Harmonic | 399.05 | 404.77 | 1.9054 | 1.9121 |
| Biweight kernel | 399.17 | 405.44 | 1.9023 | 1.9164 |
| Local weighted | 399.74 | 406.01 | 1.9064 | 1.9204 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández-Duque, B.; Pérez, I.A.; García, M.Á.; Pardo, N.; Sánchez, M.L. Trend Assessment for a CO2 and CH4 Data Series in Northern Spain. Proceedings 2017, 1, 146. https://doi.org/10.3390/ecas2017-04147
Fernández-Duque B, Pérez IA, García MÁ, Pardo N, Sánchez ML. Trend Assessment for a CO2 and CH4 Data Series in Northern Spain. Proceedings. 2017; 1(5):146. https://doi.org/10.3390/ecas2017-04147
Chicago/Turabian StyleFernández-Duque, Beatriz, Isidro A. Pérez, M. Ángeles García, Nuria Pardo, and M. Luisa Sánchez. 2017. "Trend Assessment for a CO2 and CH4 Data Series in Northern Spain" Proceedings 1, no. 5: 146. https://doi.org/10.3390/ecas2017-04147
APA StyleFernández-Duque, B., Pérez, I. A., García, M. Á., Pardo, N., & Sánchez, M. L. (2017). Trend Assessment for a CO2 and CH4 Data Series in Northern Spain. Proceedings, 1(5), 146. https://doi.org/10.3390/ecas2017-04147







