Information: Subjective or Objective? ^†

Abstract

We consider the derivation of information in both organic and inorganic systems, that is both for organisms and solid state physics, and conclude that information is always subjective, although this presents less of a problem in inorganic systems, where the simplicity of a measurement’s ecosystem implies that information tends towards being objective.

1. Introduction

The target of this paper is to draw a comparison between information in living systems and information in inorganic contexts. The two representative contexts we will refer to are those of an organism and of solid state physics. We have published extensively elsewhere on the properties of a model hierarchy (e.g., [1]; and most recently [2,3]), and to reproduce the entire derivation would be inappropriate for this extended abstract. Consequently, we will restrict ourselves to the brief sketch which follows, in the hope that this attenuated version is sufficiently comprehensible.

2. Natural Model Hierarchy

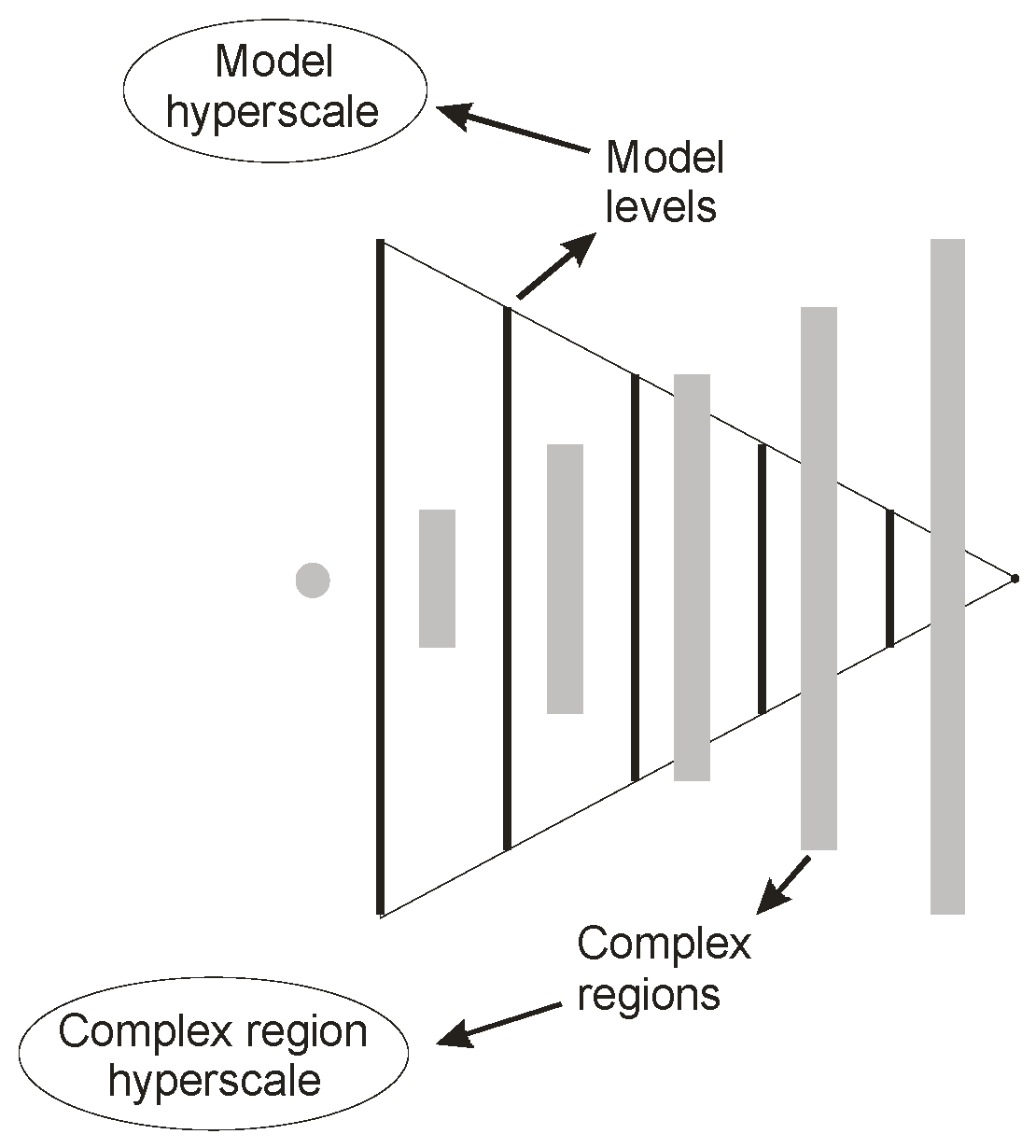
Figure 1 illustrates the general form of a model hierarchy in the example of an organism. The hierarchy is pictured ‘on its side’ to support the view that no one level of organization is ultimately dominant. Each organizational level constitutes a model of an entire organism at a specific structural scale, as indicated, and as opposed to conventional hierarchical representation, for example Salthe’s [4] compositional hierarchy, where a single constitutional element is presented at each level. The model hierarchy appears to be the parent [5] of both compositional hierarchy and subsumption hierarchy [4]. Although Figure 1 is presented in structural terms, such a hierarchy can also be represented in terms of function, and it automatically includes any required aspects of heterarchy. Regions between adjacent levels are extremely complex in Rosen’s [6] sense, and these embody the locally scaled internal representations of the organism’s ecosystem. Each organizational level is partially closed and partially open to the rest of the hierarchy, and direct access to individual levels from outside or from other internal levels is limited.

The hierarchy automatically creates a pair of approximate models of itself [5], one for the organizational levels, one for the complex regions (see Figure 2), which we refer to as hyperscales [7].

Ultimately these integrate, giving a singular metascalar representation (as illustrated in Figure 3) which is the real identity of the organism [5]. This corresponds with the identification of information with the integration of data (the model level hyperscale) and context (the complex region hyperscale) [2].

3. Solid State Physics

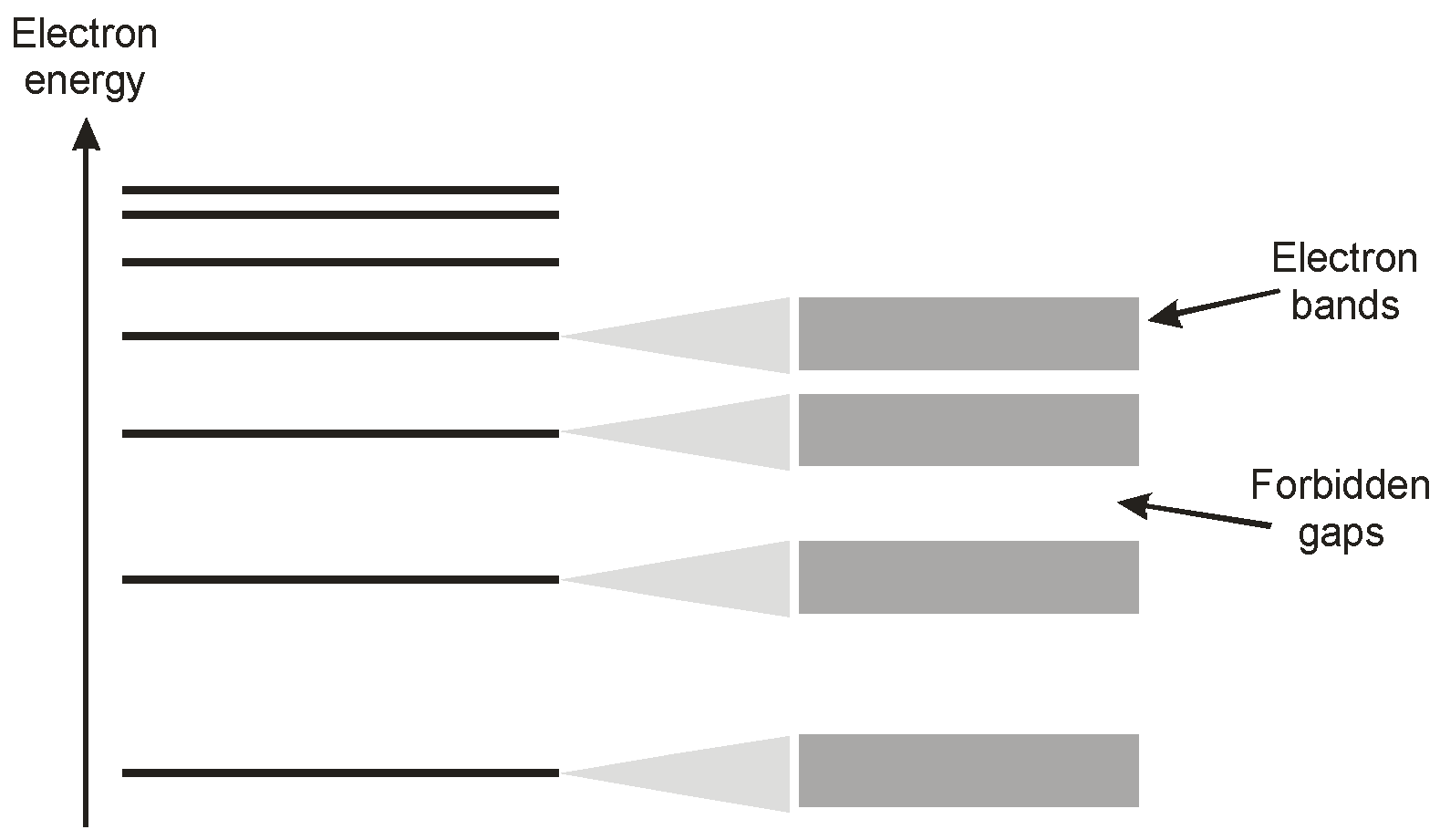
Our next task is to describe formulation of the electronic properties of solid state physics. We start with a single atom, which exhibits a sequence of electron energetic levels spreading outward from the nucleus, as indicated in Figure 4.

In a crystal consisting of a myriad of closely packed atoms these energy levels broaden, following the Pauli exclusion principle [8], to a set of energetic bands, as illustrated in Figure 5. Adjacent bands are separated by ‘forbidden regions’ as indicated.

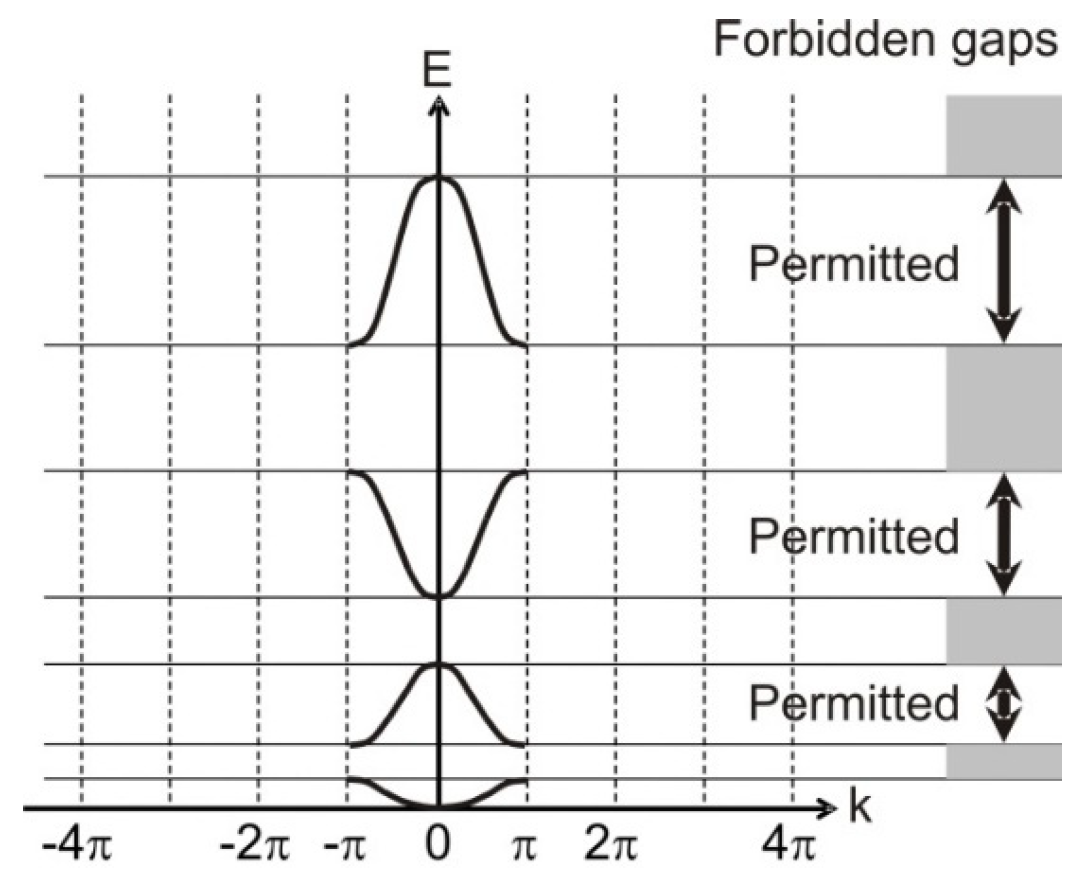
A parallel mathematical derivation of this context following the Kronig-Penney model [8] yields the equivalent arrangement of bands shown in Figure 6.

Similarity between the electronic band structure and the organism model hierarchy is already apparent. The horizontally extended regions of Figure 6—called Brillouin zones—fold in to the central region to give Figure 7—an apparent equivalence to the generation of the model-level hyperscale in an organism.

The second ecosystemic hyperscale is here relatively simple, as in the inorganic case it collapses down to a simple set of parameters of temperature, pressure, magnetic field, … At the highest level of organization, electronic conduction is controlled by two aspects. Firstly, the electrons themselves, secondly, the regions from which they may be absent, called ‘holes’. The holes’ properties are those of the electrons’ ecosystems. Consequently, conductivity in a crystal is derived from the properties of both electrons and their ecosystems—an apparent mirroring of metascale in an organism.

4. Comparing Natural Hierarchy and Solid State Physics

The coupling feature between these two systems appears to be the relationship between process and structure, where both are intimately connected in an organism, and where process is virtually absent from a crystal. This gives us a way of characterizing system properties, including information, in the two situations. We believe that the higher level characteristic of complementarity can best represent this coupling, and that objectivity or subjectivity in a given context can be referred to the degree of its presence in a context, or of its absence.

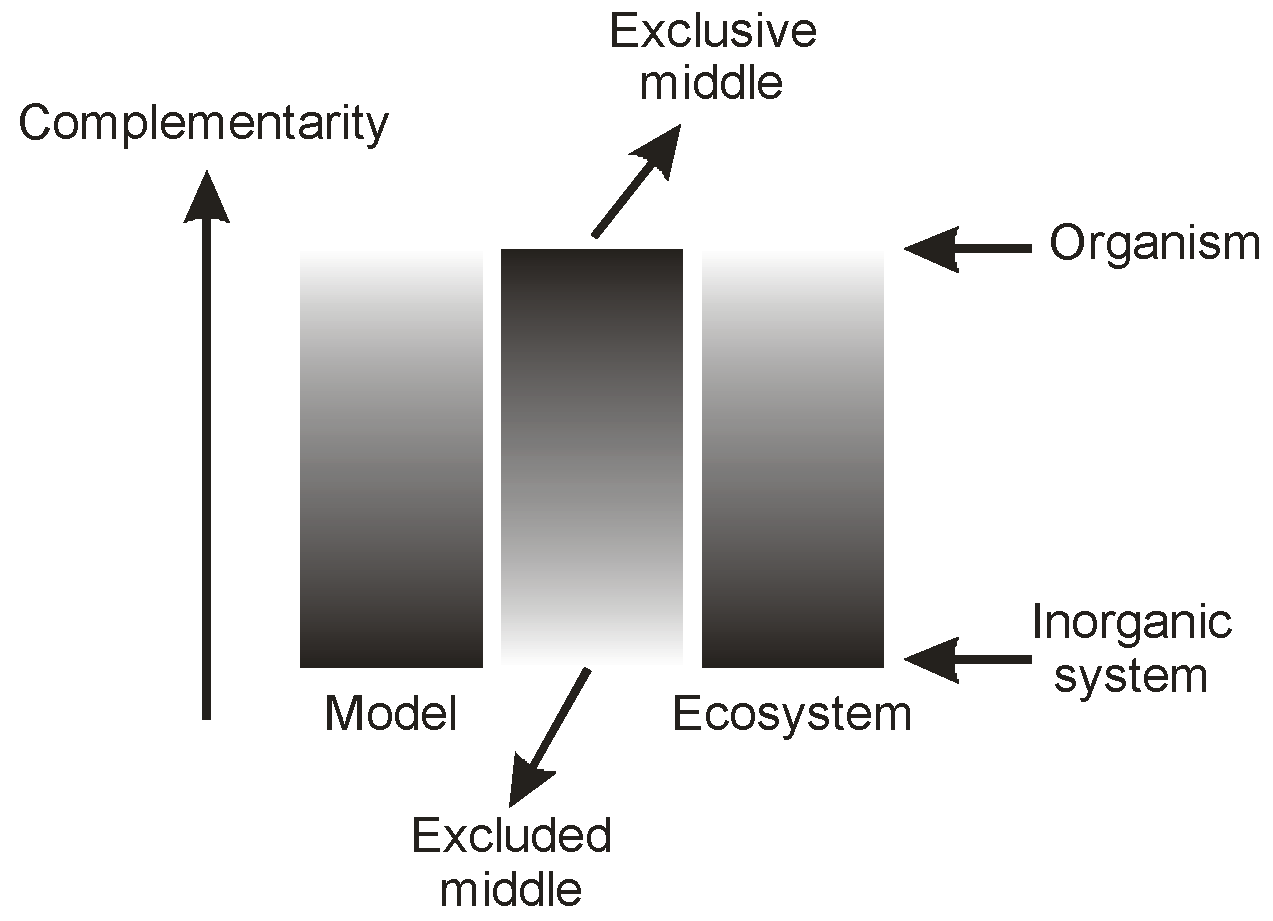
Figure 8 attempts to picture this relationship. It should be noted that we do not suggest that the implied coupling is linear: this is shown in the Figure merely to establish the sense of the relationship between complementarity and objectivity/subjectivity. Interestingly, this relationship resembles one that we have published earlier [5] between complementarity and the excluded or exclusive middle in bilateral contexts, such as in Brenner’s [9] Logic in Reality (see Figure 9). Increase in system complementarity corresponds to a decrease in the accessibility of the bilateral ‘end-points’ of the system, and a focusing of system properties on the mid-region.

We have earlier published an investigation of information in living systems (Cottam et al., 2016) which concluded, following Havel’s [10] propositions of the natures of subjectivity and objectivity, that information in organisms is fundamentally subjective, and exclusive in character. This corresponds to the preponderance of complementarity in living systems, as we indicated in Figure 8. On the other hand, complementarity in inorganic systems is lacking, and measures of information derived in these systems are fundamentally objective, in Havel’s [10] sense.