Fundamental Law of Information: Proved by Both Numbers and Characters in Conjugate Matrices †
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. The Fundamental Law of Information Proved by Both Brain and Computer
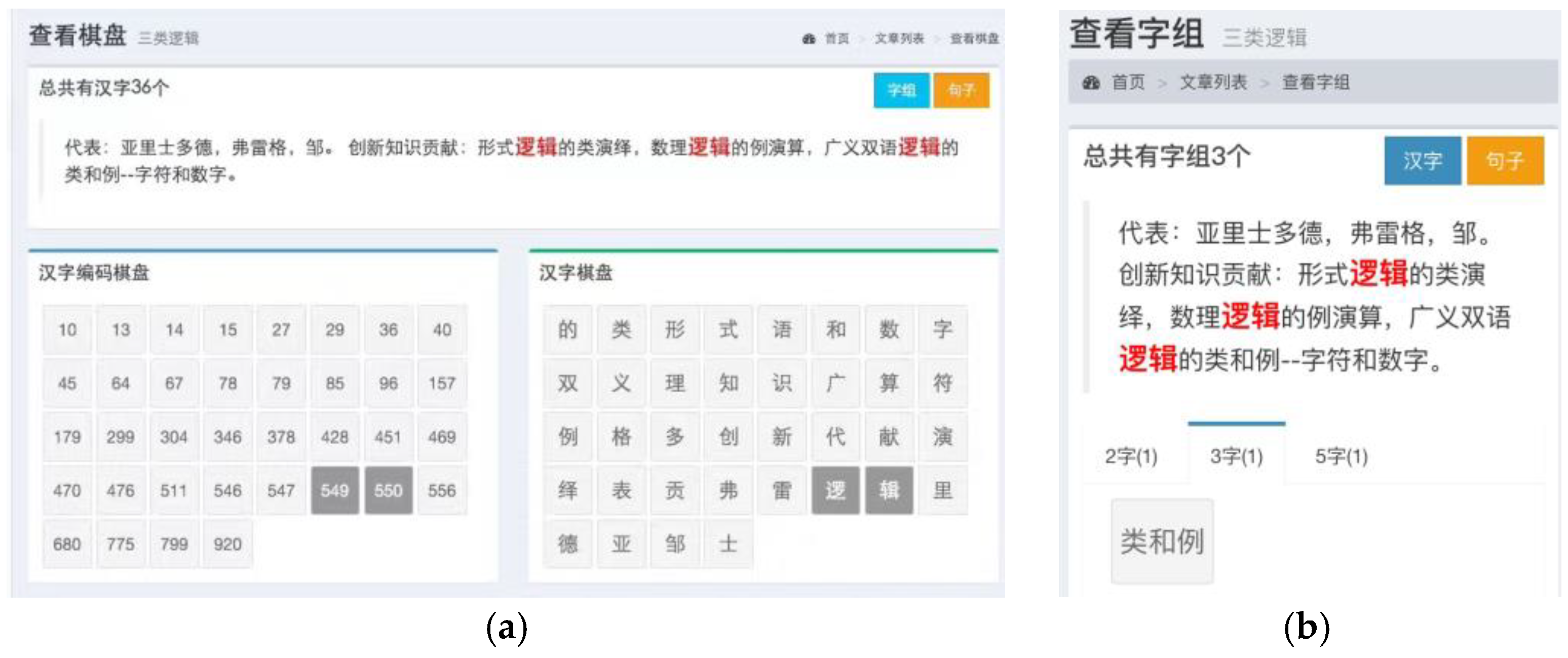
3.1.1. Proved by Logic
- Aristotle’s formal logic based on language with letters or characters;
- Frege’s mathematical logic based on arithmetic with numbers;
- Zou’s generalized bilingual logic of sequence and position with both characters and numbers.
- (1)
- Formal Logic using letters-based deduction for the abstract class;
- (2)
- Mathematical Logic using numbers-based calculation for the case;
- (3)
- Generalized Bilingual Logic using both characters and numbers for the class-case.
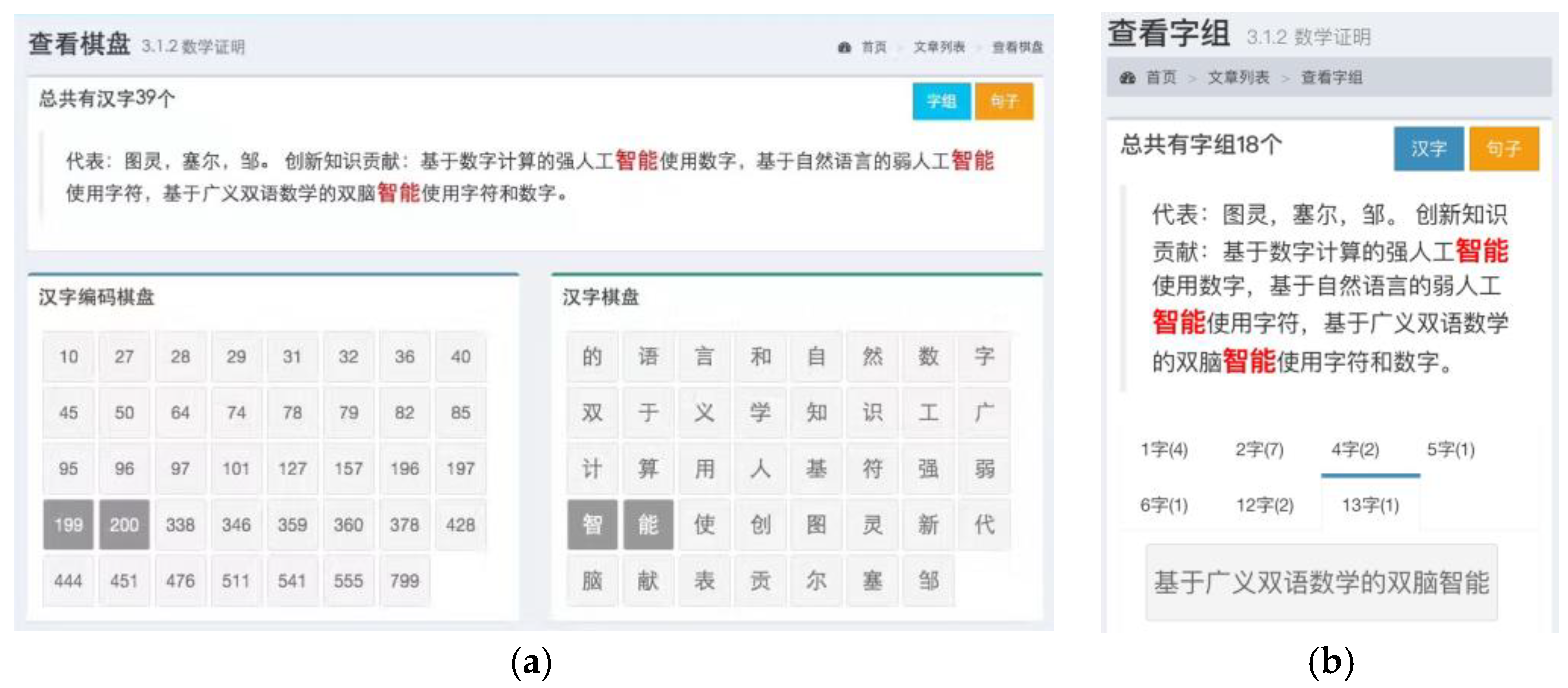
3.1.2. Proved by Mathematics
- Turing’s Strong Artificial Intelligence based on Digital Computation;
- Searle’s Weak Artificial Intelligence based on Natural Language;
- Zou’s Generalized Intelligence based on Bilingual Mathematics.
- (1)
- Strong Artificial Intelligence based on Digital Computation by using numbers;
- (2)
- Weak Artificial Intelligence based on Natural Language by using letters or characters;
- (3)
- Generalized Intelligence based on Bilingual Mathematics by using the both.
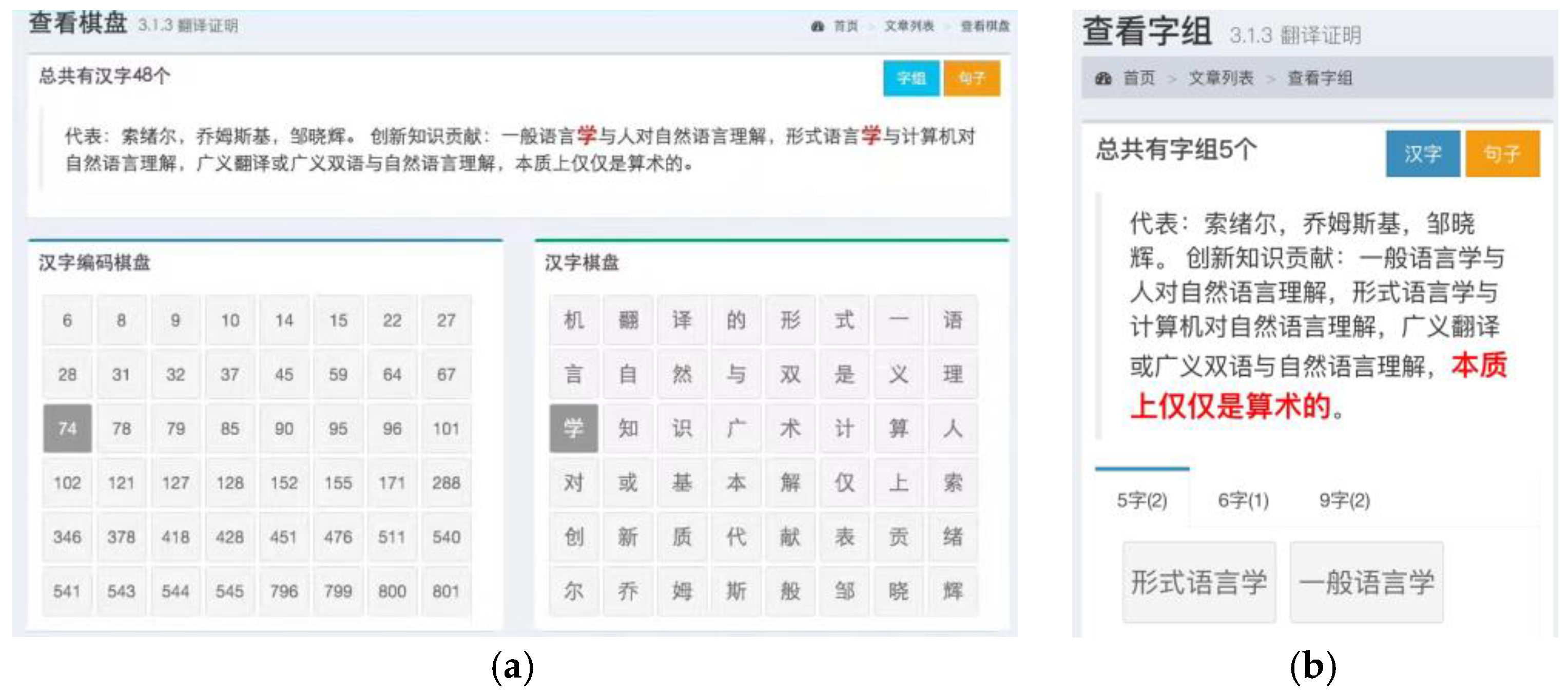
3.1.3. Proved by Translation
- Saussure’s general linguistics using natural language;
- Chomsky’s formal linguistics using formal language;
- Zou’s generalized bilingual linguistics using both on surfaces, essentially only arithmetic.
- (1)
- General Linguistic View for human’s natural language understanding;
- (2)
- Formal Linguistic View for computer’s natural language understanding;
- (3)
- Generalized Bilingual Linguistic View for both of human brain and computer.
3.2. The Digital and Textual Twin Matrices
3.3. Three Kinds of Identity: Mathematical Information Law
- (1)
- The identity of the algebra is not only the solution of the algebraic equation, but also the lattice of the matrix—can be filled in numbers to facilitate the calculation or statistics of the numerator, and the algebraic equation is associated with the geometric pattern, accurately record and express a specific grid in which the specific order and place. (1) This identity records the solution of a particular equation, either a periodic function, a distribution function, or a similar function, whose polynomials represent pure digital relationships. The constraint condition is determined by (2) is ultimately determined by (3).
- (2)
- The identity of the twin, on the one hand, represents the functional relationship between the digital systems, and on the other hand, representing the functional relationship between the text system or the character system, and the performance of the two Linkage function (with twin relationship). (2) is the linkage of the linkage equation, from the linkage function—links (1) and (3) linkage function.
- (3)
- The identity of the text, not only Chinese characters, but also can be the form of English words, or other language system. The relationship between the various character systems, there are strict constraints, usually with the convention of the corresponding relationship or referral as a basis. Thus, (3) the identity, the actual record of the bilingual relationship between the contract is a mixed function—the need for man-machine collaboration to decompose its polynomial (because it is not formal, the need to help indirectly through the linkage function to achieve its formalization).
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Beziau, J.-Y. What is “Formal Logic”? In Proceedings of the XXII World Congress of Philosophy, Seoul, Korea, 30 July–5 August 2008; Volume 13, pp. 9–22. [Google Scholar]
- Chiswell, I. Mathematical Logic; Oxford University Press: Northamptonshire, UK, 2007. [Google Scholar]
- Turing, A.M. Computing Machinery and Intelligence. Mind 1950, 49, 433–460. [Google Scholar] [CrossRef]
- Searle, J.R. Minds, Brains and Programs. Behav. Brain Sci. 1980, 3, 417–457. [Google Scholar] [CrossRef]
- Taylor, J.M.; Raskin, V.; Hempelmann, C.F. From Disambiguation Failures to Common-Sense Knowledge Acquisition: A Day in the Life of an Ontological Semantic System. In Proceedings of the 2011 IEEE/WIC/ACM International Conferences on Web Intelligence and Intelligent Agent Technology (WI-IAT 2011), Lyon, France, 22–27 August 2011. [Google Scholar]
- Ludwig, D. Overlapping Ontologies and Indigenous Knowledge. From Integration to Ontological Self-Determination. Stud. Hist. Philos. Sci. 2016, 59, 36–45. [Google Scholar] [CrossRef]
- De Saussure, F. Selections from the Course in General Linguistics. In The Continental Philosophy Reader; Kearney, R., Rainwater, M., Eds.; Routledge: London, UK, 1996. [Google Scholar]
- Chomsky, N. Syntactic Structures, 2nd ed.; De Gruyter Mouton: Hague, The Netherlands, 1957. [Google Scholar]
- Zou, X. Collaborative Intelligent Computing System: Theoretical Model with Its Application. In Proceedings of the 2012 AAAS Annual Meetings, Vancouver, BC, Canada, 16–20 February 2012. [Google Scholar]
- Zou, X. Basic Law of Information: The Fundamental Theory of Generalized Bilingual Processing. In Proceedings of the SIS Summit Vienna 2015—The Information Society at the Crossroads, Vienna, Austria, 3–7 June 2015. [Google Scholar]
- Zou, X. Fundamental Law of Information Proved by Brain and Computer. Online resource: http://blog.sciencenet.cn/home.php?mod=space&uid=94143&do=blog&id=1056171 (accessed on 21 May 2017).

| Attributes | Concept | Types |
|---|---|---|
| Formal | Logic | class |
| Mathematical | Logic | Case |
| Bilingual | Logic | class and case |
| Attributes | Concept | Types |
|---|---|---|
| Artificial | Intelligence | Strong |
| Artificial | Intelligence | Weak |
| Generalized | Intelligence | Bilingual |
| Attributes | Concept | Types |
|---|---|---|
| General | Linguistics | |
| Formal | Arithmetic | |
| Bilingual | Linguistics | Arithmetic |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, X.; Zou, S.; Ke, L. Fundamental Law of Information: Proved by Both Numbers and Characters in Conjugate Matrices. Proceedings 2017, 1, 60. https://doi.org/10.3390/IS4SI-2017-03927
Zou X, Zou S, Ke L. Fundamental Law of Information: Proved by Both Numbers and Characters in Conjugate Matrices. Proceedings. 2017; 1(3):60. https://doi.org/10.3390/IS4SI-2017-03927
Chicago/Turabian StyleZou, Xiaohui, Shunpeng Zou, and Lijun Ke. 2017. "Fundamental Law of Information: Proved by Both Numbers and Characters in Conjugate Matrices" Proceedings 1, no. 3: 60. https://doi.org/10.3390/IS4SI-2017-03927
APA StyleZou, X., Zou, S., & Ke, L. (2017). Fundamental Law of Information: Proved by Both Numbers and Characters in Conjugate Matrices. Proceedings, 1(3), 60. https://doi.org/10.3390/IS4SI-2017-03927





