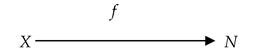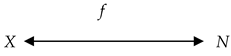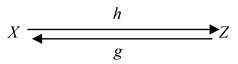Bidirectional Named Sets as Structural Models of Interpersonal Communication ^†

Abstract

Treating communication as information exchange between systems, we employ the most fundamental structure in mathematics, nature and cognition, which is called a named set or a fundamental triad because it has been useful in a variety of areas such as networks and networking, physics, information theory, mathematics, logic, database theory and practice, artificial intelligence, mathematical linguistics, epistemology and methodology of science, to mention but a few. Here we use structural models based on the theory of named sets for description and analysis of interpersonal communication explicating its structural regularities.

1. Introduction

There are different models of communication (cf., for example, [1,2,3]). They distinguish two basic types of communication—interpersonal communication and intrapersonal communication. Interpersonal communication is information exchange between different systems. For instance, human-computer communication is interpersonal. Intrapersonal communication is information exchange in one system. For instance, communication in the World Wide Web is intrapersonal with respect to the World Wide Web. Here we use structural models based on the theory of named sets [4] for description and analysis of interpersonal communication explicating its structural regularities.

Being the most fundamental structure in mathematics, nature and cognition (as it is demonstrated in [4,5,6], named sets (also called fundamental triads) have been useful in a variety of areas such as networks and networking, physics, information theory, mathematics, logic, database theory and practice, artificial intelligence, mathematical linguistics, epistemology and methodology of science, to mention but a few. Application of named set theory to communication theory is based on the fact that communication as an information exchange has the intrinsic structure of a named set.

In the next section, we consider elements of named set theory necessary for communication studies, which are exposed in Section 3.

2. Named Sets and Fundamental Triads

We consider three primary types of named sets and fundamental triads [4].

A basic fundamental triad or a basic named set has the following form (1).

(1)

It is a triad X = (X, f, I), in which X and N are two objects and f is a correspondence (e.g., a binary relation) between X and I. With respect to X, X is called the support of X, N is called the component of names (reflector) or set of names of X, and f is called the naming correspondence (reflection) of X. Note that here, f is not necessarily a mapping or a function.

The standard example is a basic named set (fundamental triad), in which X consists of people, N consists of their names and f is the correspondence between people and their names. Another example is a basic named set (fundamental triad), in which X consists of things, N consists of their names and f is the correspondence between things and their names [7].

It is necessary to make a distinction between triples and triads. A triple is any set with three elements, while a triad is a system of three connected elements (components). It is worthy of note that mathematicians introduced the concept of a triple in an abstract category [8]. In essence, such a triple is a triad that consists of three fundamental triads and thus is a triad of the second order [4]. Understanding of the complex nature of the categorical triple made mathematicians to change the name of this structure and now it is always called a monad [9]. Interestingly, this shows connection between fundamental triads and Leibniz monads.

A bidirectional fundamental triad or a bidirectional named set has the following form (2).

(2)

It is also a triad D = (X, f, Y), in which the naming relation f goes in two directions.

We have an example of a bidirectional named set when two people are exchanging messages, e.g., be e-mails, messaging or talking to one to another. In this case, X and Z are people while f and g are messages that go from one person to another.

Note that when mathematicians or computer scientists use connections without direction such as those that are used, for example, in general graphs [10], these connections actually have both directions and are more explicitly represented by the union of directed connections h and g.

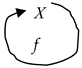
A cyclic fundamental triad or a cyclic named set has the following form (3)

(3)

The following graphic form (4) can also describe it.

(4)

An example of a cyclic named set is a subatomic particle, such as an electron, which acts on itself (cf., for example, [11]).

Another example of a cyclic named set is a computer network. In it, X consists of computers and f contains all connections between them.

Let us obtain some simple properties of named sets related to their compositions.

Proposition 1.

• (a) The sequential composition of basic named sets is a basic named set.
• (b) The sequential composition of bidirectional named sets is a bidirectional named set.
• (c) The sequential composition of cyclic named sets is a cyclic named set.

In many cases, a bidirectional named set can be decomposed into the inverse composition of two basic named sets as it is demonstrated in the following diagram, which is a decomposition of Diagram (2).

(5)

Here f = [h, g] or f = h ∪ g. Thus, a decomposed bidirectional named set D is denoted by D = (X, [h, g], Z) and has two components, which are basic named sets:

• The direct component X = (X, f, Z)
• The inverse component Y = (Z, g, X)

Proposition 2.

A bidirectional named set D is equal to the inverse composition of its components X and Y.

For instance, the set-theoretical bidirectional named set

X = (X = {1, 2, 3}, f, Z = {a, b})

with the naming correspondence (a binary relation in this case)

f = {(1, a), (3, b), (2, a), (b, 1), (a, 3)}

is decomposable the inverse composition of the direct component Z = (X, h, Z) and inverse component Y = (Z, g, X) where

h = {(1, a), (3, b), (2, a)} ⊆ X × Y

and

g = {(b, 1), (a, 3)} ⊆ Y × X

We see that in this case, f = h ∪ g.

This shows how it is possible to construct bidirectional named sets using inverse composition of basic named sets [4].

Inverse composition of basic named sets X = (X, f, I) and Y = (Y, g, J) is defined as

X ≬ Y = (X, f, I) ≬ (Y, g, J) = (X ∪ J, f ∪ g⁻¹, I ∪ Y)

The inverse composition of named sets X and Y is equal to the sequential composition of X and the involution Y^o of Y, i.e.,

X ≬ Y = X ∘ Y^o

Although any bidirectional named set is the inverse composition of basic named sets, it is a fundamental structure such as a set, graph, category, fuzzy set or multiset. In more detail, relations between basic and bidirectional named sets are studied elsewhere.

There are also other compositions of named sets [4].

If X = (X, r, I) and Y = (Y, q, J) are named sets, then their sequential composition X ∘ Y is the named set (X, r_oq_o, J) where r_o = r ∩ (X × (I ∩ Y)) and q_o = q ∩ ((I ∩ Y) × J).

Example 1

. Superposition of functions is the sequential composition of the corresponding named sets in the case when I = Y.

Example 2

. Composition of morphisms in categories is the sequential composition of the corresponding named sets.

If X = (X, r, I) and Y = (Y, q, J) are named sets, then their parallel composition X ⊕ Y is

X ⊕ Y = (X, f, I) ⊕ (Y, g, J) = (X ∪ J, f ∪ g, I ∪ Y)

An important special case of inverse composition is cyclic composition of named sets.

If X = (X, r, Y) and Y = (Y, q, X) are two named sets, in which the support of X coincides with the reflector of Y and the support of Y coincides with the reflector of X, then their cyclic composition has the form

X © Y = (X, r, Y) © (Y, q, X) = (X, r∘q, X)

If X = (X, r, Y) and Y = (Y, q, Z) are two named sets, then their chain composition is a named set chain (Burgin, 2011) and has the form

V = [X, Y]

3. Interpersonal Communication

People understand communication either as a process of information exchange or as a result of such a process. In addition, communication can include exchange of ideas, thoughts and/or opinions. However, everything that is transmitted in communication comes through information exchange. As a result, it is natural to treat communication as a system of information transmissions, which can be organized in a sequence or go concurrently. The action of information transmission has the structure of a basic named set (6), in which its support and reflector have the roles of a sender and receiver.

(6)

Communication as a pure exchange of information in the form of messages has the structure (7) of a decomposed bidirectional named set, in which the naming relation represents messaging.

(7)

Here each participant acquires the two-folded role of a Sender/Receiver.

Note that both the Sender and Receiver can be not only individuals but also groups of individuals, devices, e.g., computers, birds, animals and other living beings.

Connections t, f and g between the Sender and the Receiver have three components:

-

Communication space, e.g., a channel or a system of channels, is the medium, in which communication goes and which allows sending messages from the sender to the receiver

-

A system of messages, e.g., one message, where a message is the object sent (transmitted)

-

A context consists of conditions (environment) in which communication goes

Messages are carriers of information and usually have three components:

-

The physical component of a message, e.g., electrical signals or piece of paper with some text.

-

The structural component of a message, e.g., text or picture

-

The mental component of a message, e.g., the meaning of a text

Contexts usually have one of the following three types:

-

Individual contexts

-

Group contexts

-

General contexts

A context determines how information is transmitted and also have three components:

-

The physical component of a context, e.g., conditions, in which information is sent and received

-

The structural component of a context, e.g., language of the message

-

The mental component of a context, e.g., knowledge of the sender and receiver

Besides, there is such a phenomenon as self-communication. Self-communication is communication self-directed in the elaboration and sending of the message, self-selected in the reception of the message, and self-defined in terms of the formation of the communication space. Self-communication is special case of intrapersonal communication. Self-communication is represented by the following cyclic named set (8), in which X is both the Sender and the Receiver.

(8)

Another important case of intrapersonal communication represented by a cyclic named set is communication in networks, such as the Internet, where each node can be both a receiver and sender. This process is also naturally modeled by a cyclic named set, in which X is the whole network.

A combination of network communication and self-communication is called mass self-communication.

Enhanced communication as an exchange of information with information processing, which includes information organization, is the sequential composition (9) of two cyclic and one bidirectional named sets.

(9)

According to the general theory of information, information for a system R is a capacity to change an infological system IF(R) of the system R.

There are three basic forms of information organization:

All considered above types and schemas represented direct communication. Mediated communication has the structure of a chain (10) of bidirectional named sets (fundamental triads):

(10)

In a sequential communication, all messages are linearly ordered in time and transmission of each of them does not intersect in time with transmission of another one.

There are different types of messages in communication:

-

The starting message m₀ is the first message in communication.

-

The concluding message m_f is the last message in communication.

-

A feedback message is an outcoming message caused by some incoming message.

-

A direct feedback message is an outcoming message caused by the previous incoming message.

-

An initializing message is a message that is not a feedback message.

Messages allow construction of characteristic structures of communication.

Communication thread L consists of an initializing message called the root of L and a sequence of direct feedback messages, in which the first element is the feedback to the initializing message and each next element is the direct feedback to the previous element.

Communication leaping thread H consists of an initializing message called the root of H and a sequence of direct feedback messages, in which the first element is the feedback to the initializing message and each next element is the feedback to the previous element but not necessarily direct feedback.

Note that a communication thread is also a communication leaping thread.

Communication multithread is the union of communication threads with a common root.

Communication leaping multithread is the union of communication threads, which have a common root and can be leaping.

Note that a communication thread is also a communication multithread and a communication multithread is also a communication leaping multithread.

Communication hyperthread is the union of communication threads.

Communication leaping hyperthread is the union of communication threads, some of which can be leaping.

This gives us different types of communication.

-

Communication is linear if it consists of a single communication thread.

-

Communication is branching if it contains, at least, one communication multithread.

-

The most general is concurrent communication.

Two communication threads are disjoint if each of them does not have a feedback message to a message from another one.

Communication is disjoint if it consists of disjoint communication threads.

Explication of structural peculiarities of communication is aimed at better organization of interpersonal communication in both human society and networks of artificial devices such as cell phone networks or the Internet.