Computing with Nature †
Abstract
1. Introduction
- Why conventional computation is irreversible, while processes of simple physical systems are always reversible? Irreversibility (breaking time-reversal symmetry) is coming with increased complexity and is manifested in systems far from equilibrium. If the Turing machine computing operates at the lowest level of complexity, why is it irreversible?
- Reflection on implementations of computation in natural or physical systems is usually expressed in terms of causality. However, the concept of causality is absent in formalisms of physical theories. It is more a (doubtful) philosophical concept used in interpretation of physical theories or just a convenient expression to describe components of a system (“The revolution of Earth around Sun is caused by gravitational force of the mass of Sun”—the obvious physical nonsense as Earth is not revolving around Sun). The questioning of the cause as physical concept goes back at least to Bertrand Russells essay from 1917: “All philosophers, of every school, imagine that causation is one of the fundamental axioms or postulates of science, yet, oddly enough, in advanced sciences such as gravitational astronomy, the word ‘cause’ never occurs…” [12]. Naturalized computation should be described in terms of interaction not cause.
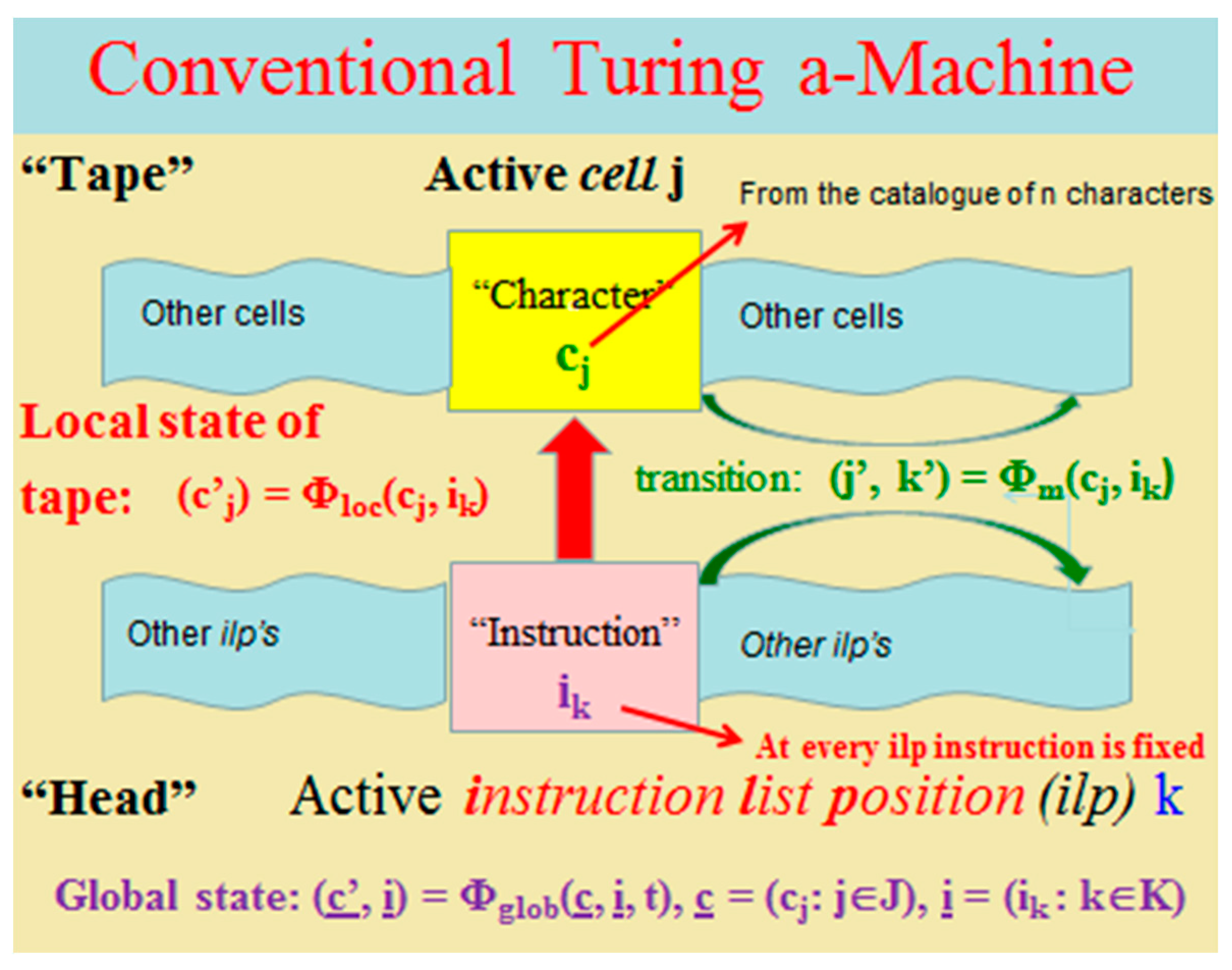
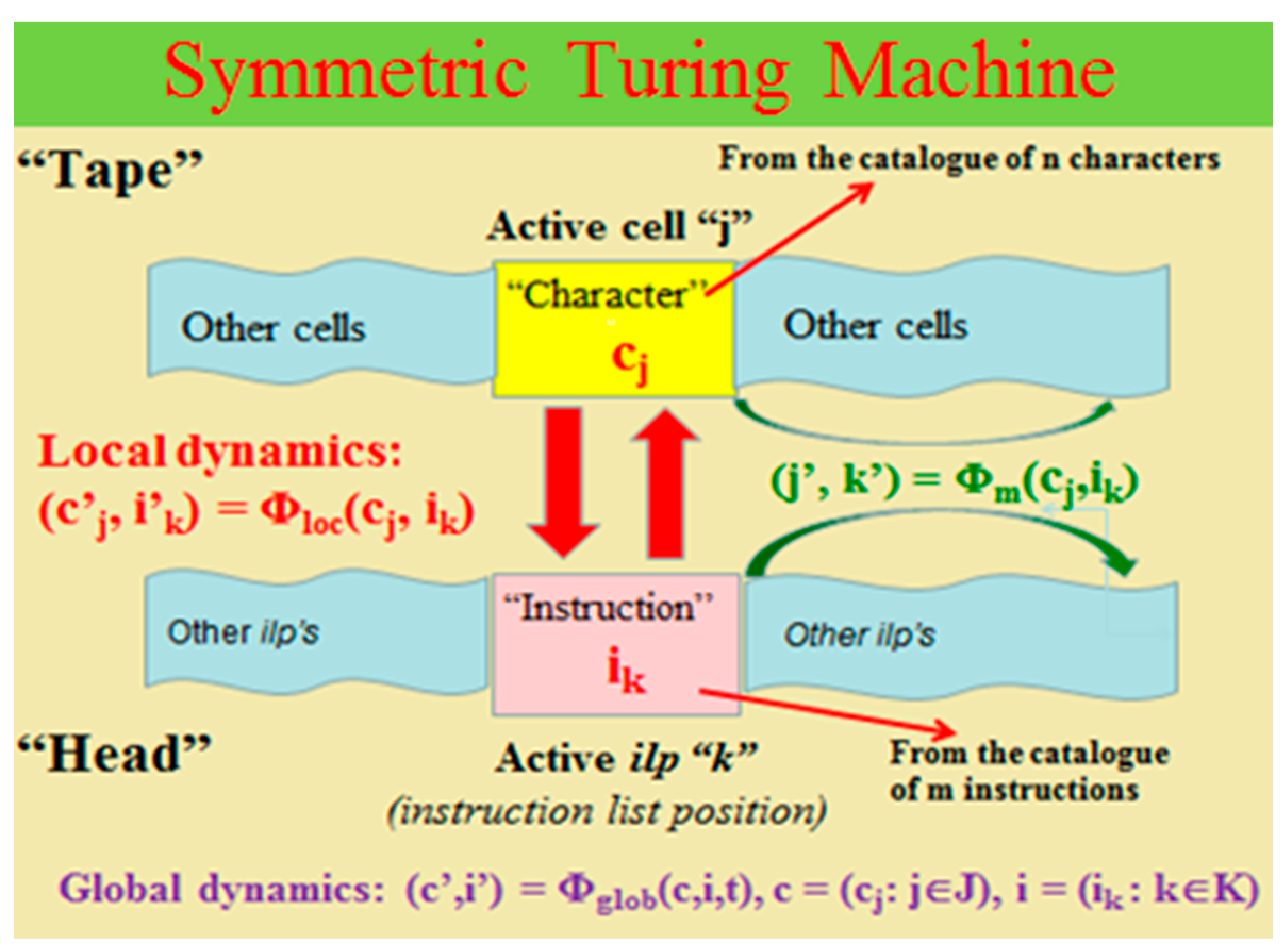
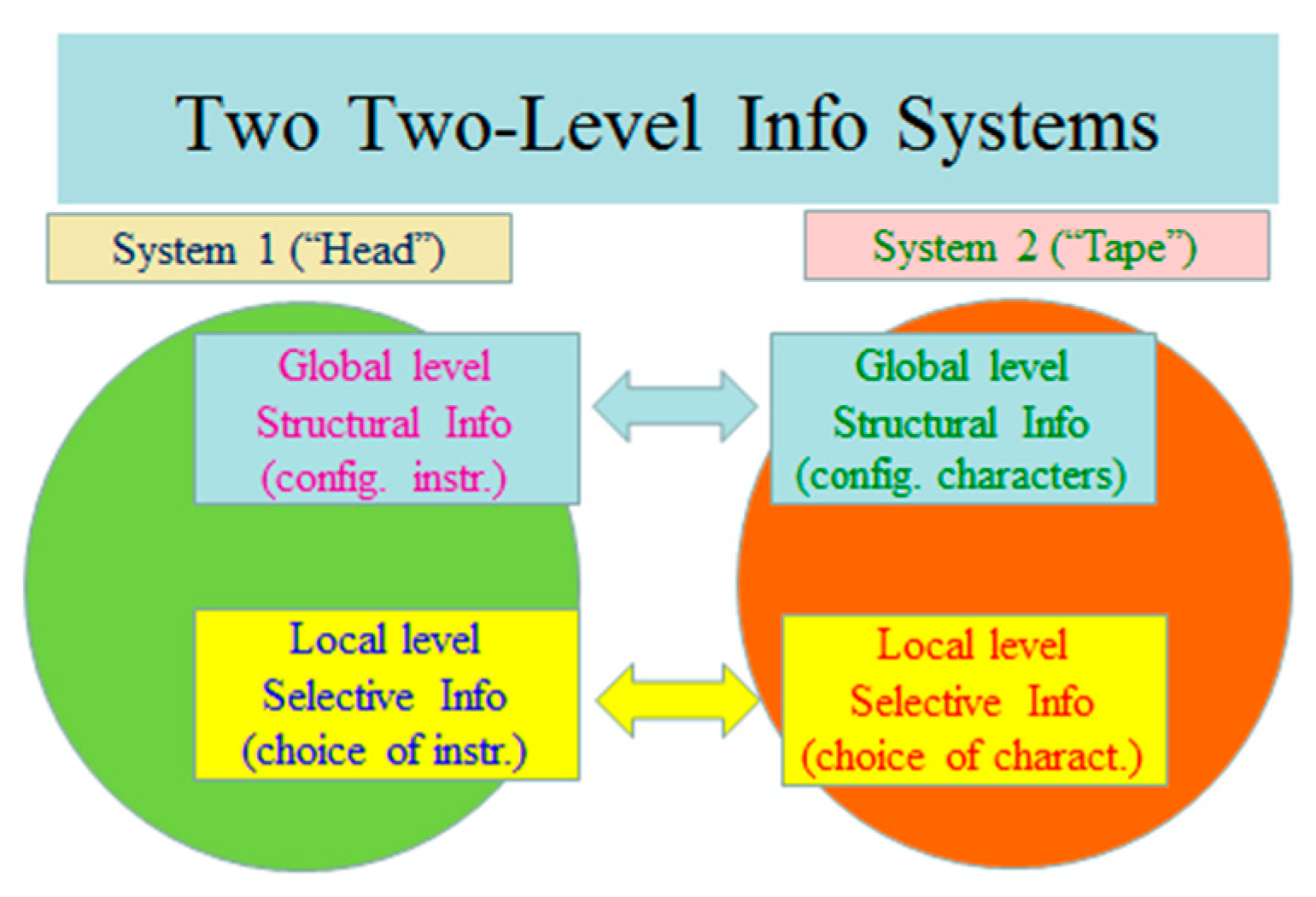
- More careful reflection on the way Turing derived the description of his a-machine shows that the description involves some arbitrary elements probably coming from the original vision of the “human computer” performing calculation. There is no reason to insist that the entire content of the instructions has to be located in one central place with primary control function (head) and that the head has to have more active role in the computation than the tape.
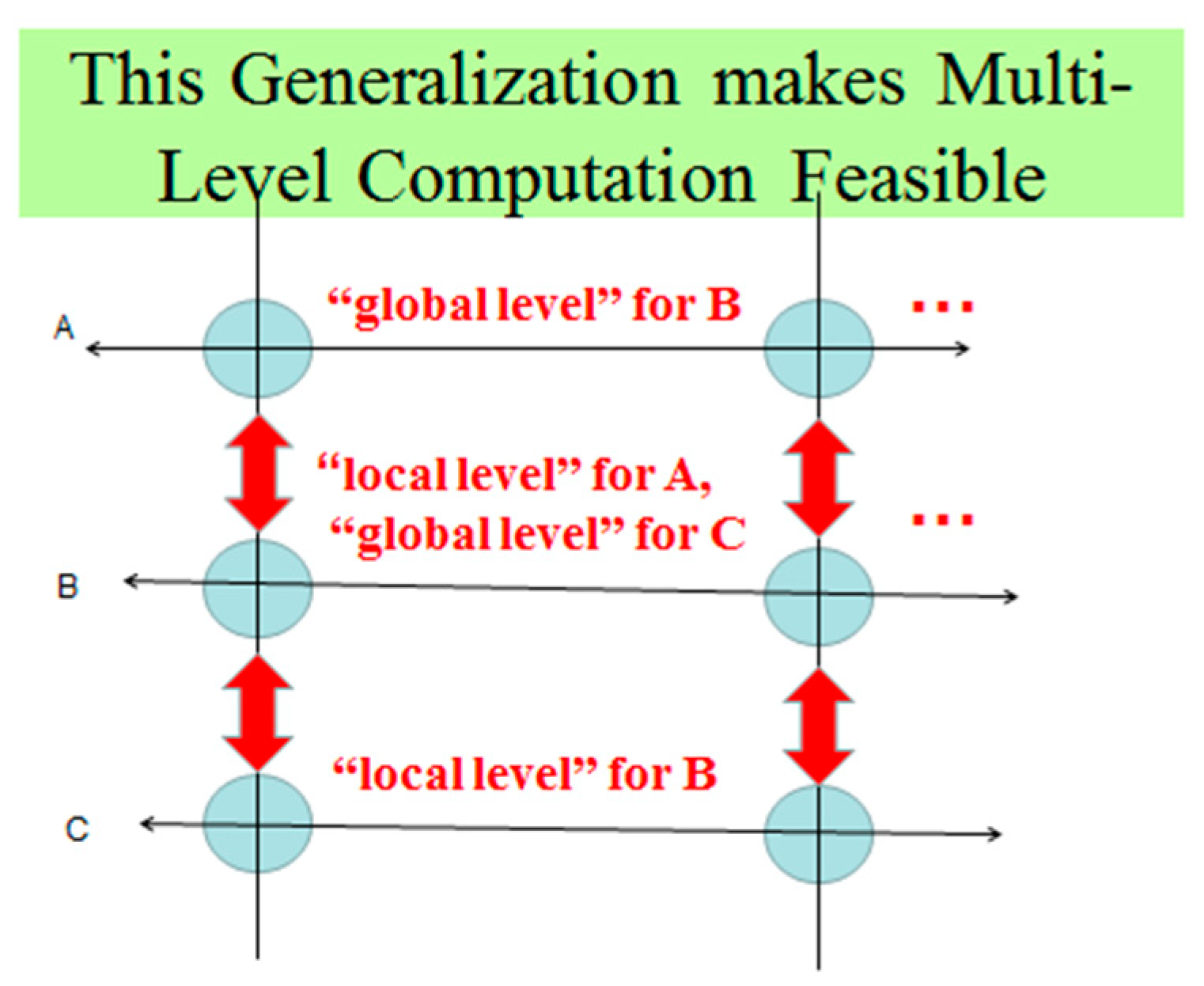
- Natural systems are typically of a complex hierarchical architecture. Natural computation should be generalized to make multilevel simultaneous computation possible.
2. Another Form of Morphological Computing
Conflicts of Interest
References
- Turing, A.M. On computable numbers, with an application to the Entscheidungsproblem. Proc. Lond. Math. Soc. Ser. 1936, 42, 230–265, cor. 43, 544–546. [Google Scholar]
- Searle, J.R. Is the Brain a Digital Computer? In Presidential Address to the American Philosophical Association; The American Philosophical Association, University of Delaware: Newark, NJ, USA, 1990; Available online: http://users.ecs.soton.ac.uk/harnad/Papers/Py104/searle.comp.html/ (accessed on 21 December 2013).
- Copeland, B.J.; Proudfoot, D. Alan Turing’s forgotten ideas in computer science. Sci. Am. 1999, 280, 76–81. [Google Scholar] [CrossRef]
- Adamatzky, A. Slime mould processors, logic gates and sensors. Philos. Trans. R. Soc. 2015, 37320140216. [Google Scholar] [CrossRef][Green Version]
- Adamatzky, A.; Martinez, G.J. (Eds.) Designing Beauty: The Art of Cellular Automata. Emergence, Complexity and Computation; Springer: Berlin/Heidelberg, Germany, 2016; Volume 2. [Google Scholar]
- Hagiya, M.; Konagaya, A.; Kobayashi, S.; Saito, H.; Murata, S. Molecular Robots with Sensors and Intelligence. Acc. Chem. Res. 2014, 47, 1681–1690. [Google Scholar] [CrossRef]
- Hagiya, M.; Wang, S.; Kawamata, I.; Murata, S.; Isokawa, T.; Peper, F. On DNA-Based Gellular Automata. In Proceedings of the 13th International Conference on Unconventional Computation and Natural Computation, London, ON, Canada, 14–18 July 2014; Ibarra, O.H., Kari, L., Kopecki, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8553, pp. 177–189. [Google Scholar]
- Kim, S.-J.; Naruse, M.; Aono, M. Harnessing the Computational Power of Fluids for Optimization of Collective Decision Making. Philosophies 2016, 1, 245–260. [Google Scholar] [CrossRef]
- Kim, S.-J.; Aono, M.; Nameda, E. Efficient decision-making by volume-conserving physical object. New J. Phys. 2015, 17, 083023. [Google Scholar] [CrossRef]
- Morita, K. An 8-state simple reversible triangular cellular automaton that exhibits complex behavior. In AUTOMATA 2016; Cook, M., Neary, T., Eds.; LNCS 9664; Springer: Berlin/Heidelberg, Germany, 2016; pp. 70–184. [Google Scholar]
- Schroeder, M.J. From Proactive to Interactive Theory of Computation. In Proceedings of the 6th AISB Symposium on Computing and Philosophy: The Scandal of Computation—What is Computation? Bishop, M., Erden, Y.J., Eds.; The Society for the Study of Artificial Intelligence and the Simulation of Behaviour, Institute of Psychiatry, King’s College: London, UK, 2013; pp. 47–51. [Google Scholar]
- Russell, B. Mysticism and Logic, and Other Essays; Unwin: London, UK, 1963. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schroeder, M.J. Computing with Nature. Proceedings 2017, 1, 178. https://doi.org/10.3390/IS4SI-2017-04022
Schroeder MJ. Computing with Nature. Proceedings. 2017; 1(3):178. https://doi.org/10.3390/IS4SI-2017-04022
Chicago/Turabian StyleSchroeder, Marcin J. 2017. "Computing with Nature" Proceedings 1, no. 3: 178. https://doi.org/10.3390/IS4SI-2017-04022
APA StyleSchroeder, M. J. (2017). Computing with Nature. Proceedings, 1(3), 178. https://doi.org/10.3390/IS4SI-2017-04022



