Estimation Method of Leaf Nitrogen Content of Dominant Plants in Inner Mongolia Grassland Based on Machine Learning
Abstract
1. Introduction
2. Materials and Methods
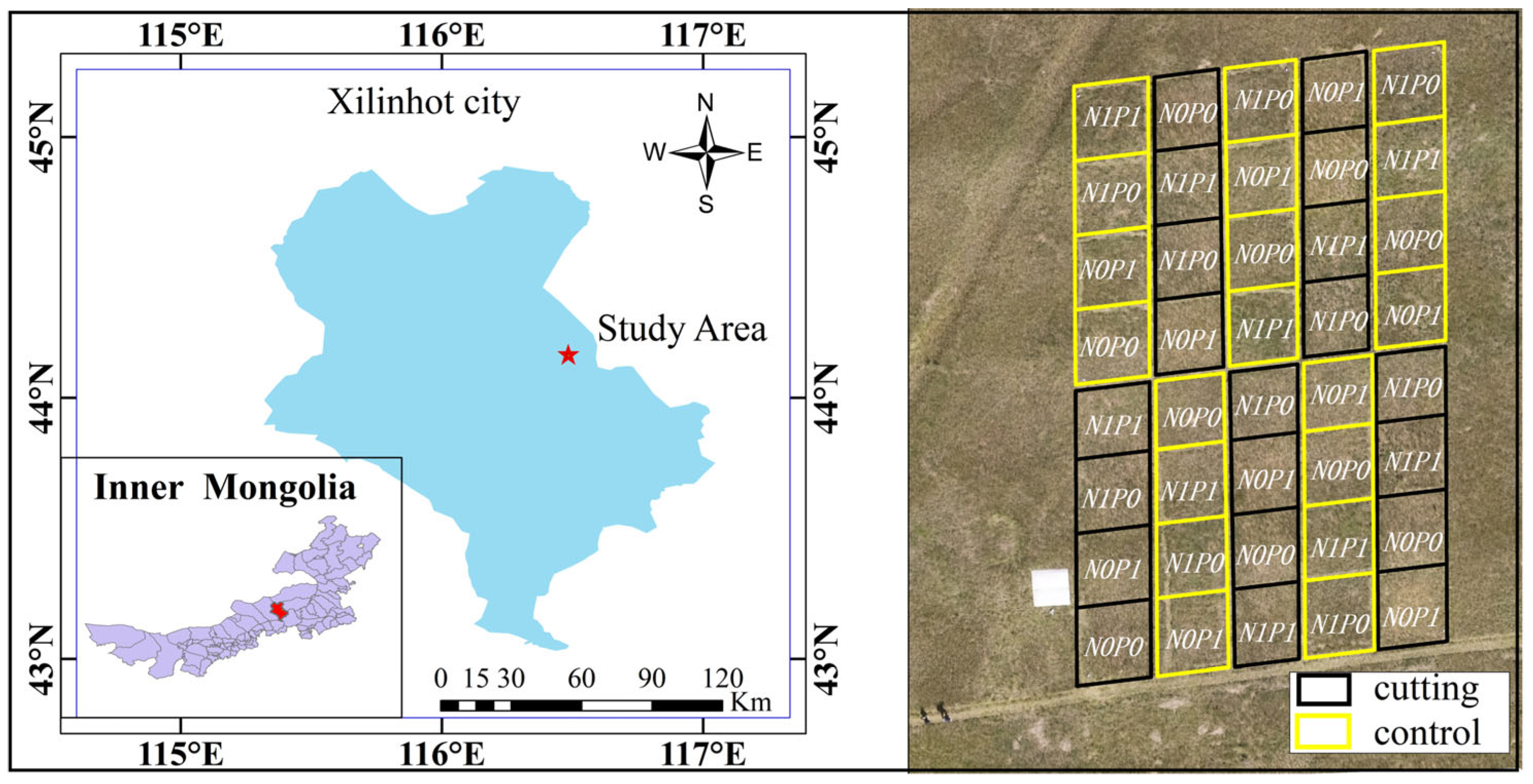
2.1. Overview of the Study Area and Experimental Design
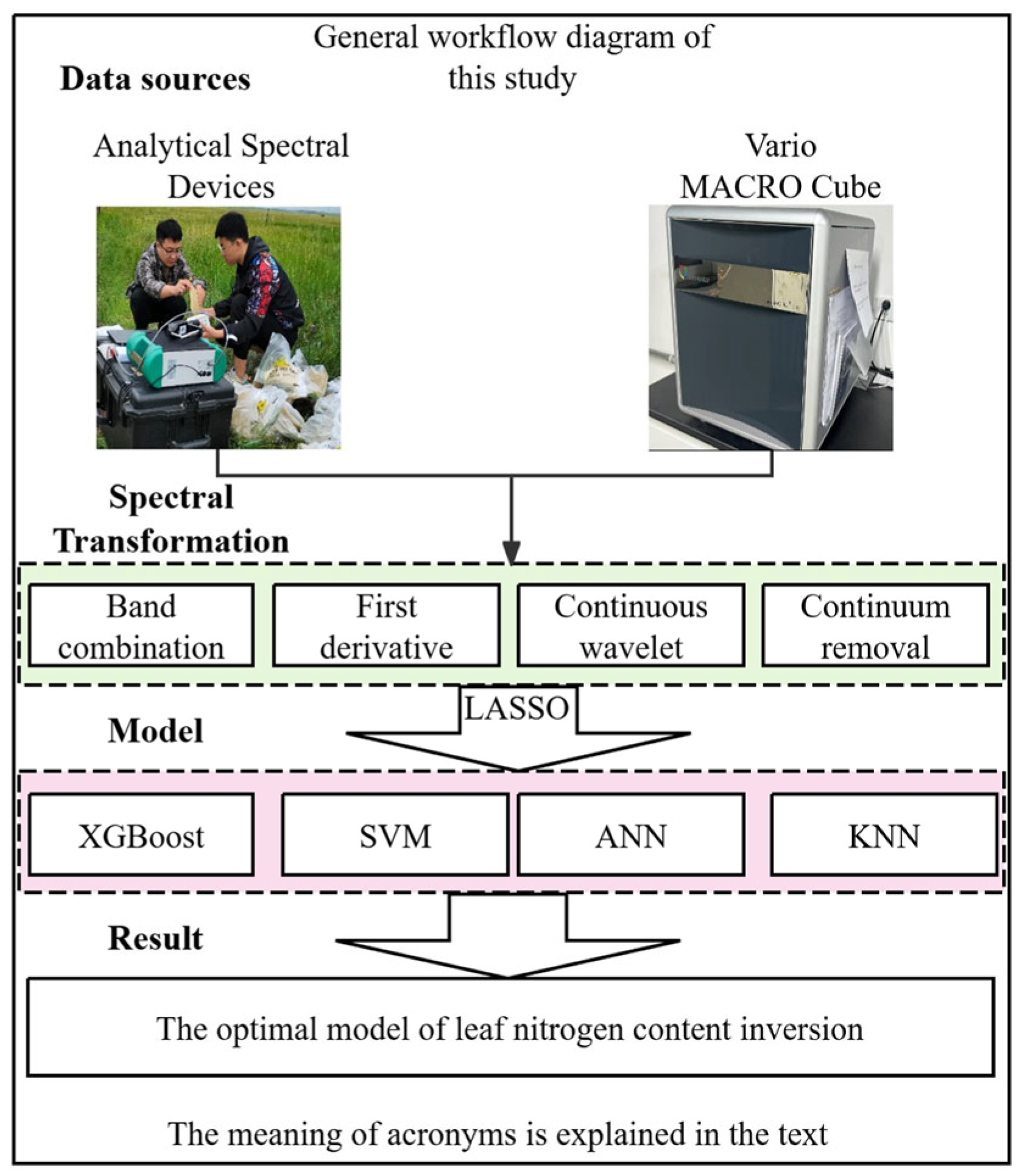
2.2. Data Observation
2.3. Research Methodology
2.3.1. Data Preprocessing
2.3.2. Variable Screening Methods
2.3.3. Modeling Algorithms
2.4. Model Validation
3. Results and Analyses
3.1. LNC Statistical Analysis of L. chinensis and C. squarrosa
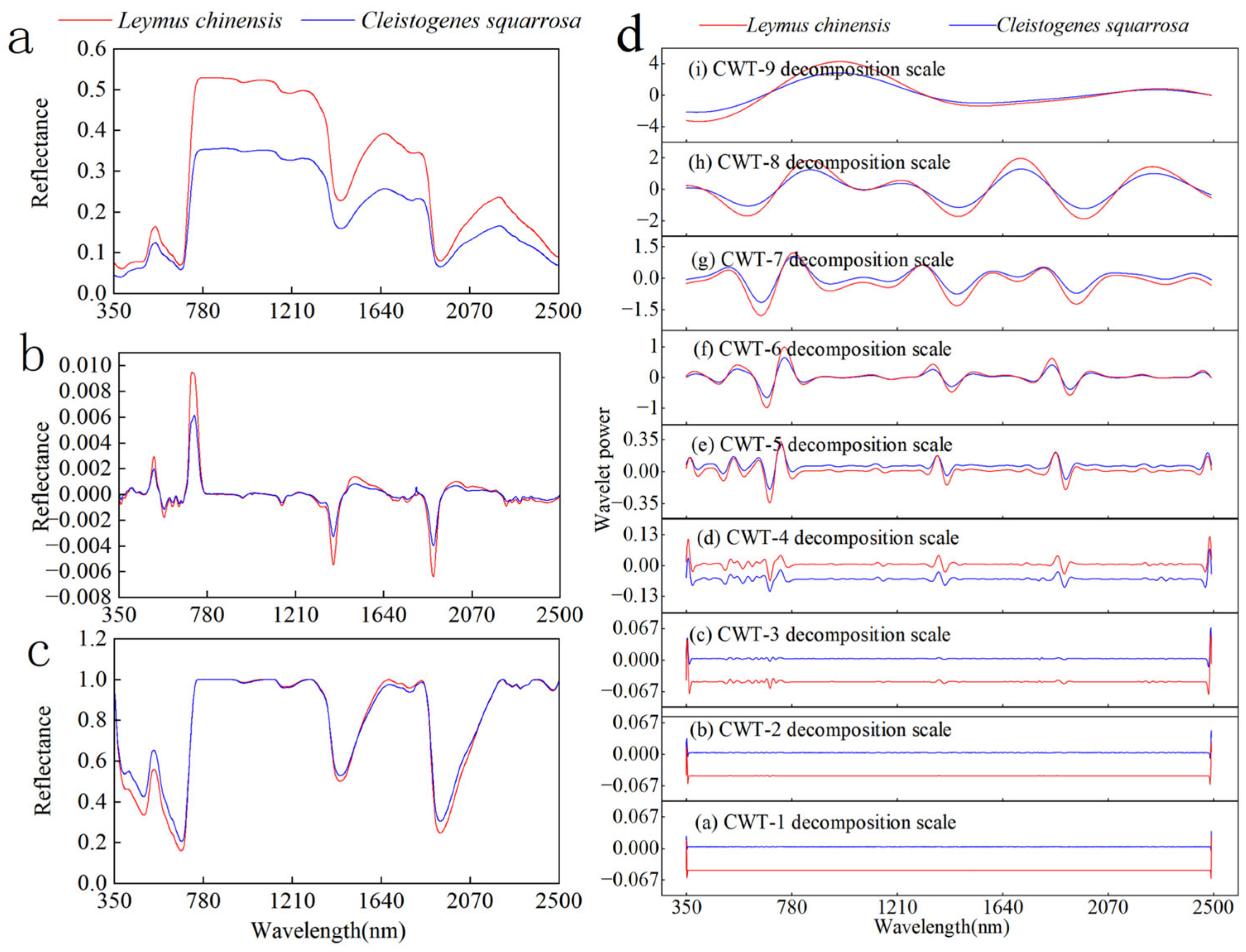
3.2. Hyperspectral Feature Analysis Under Different Transform Methods
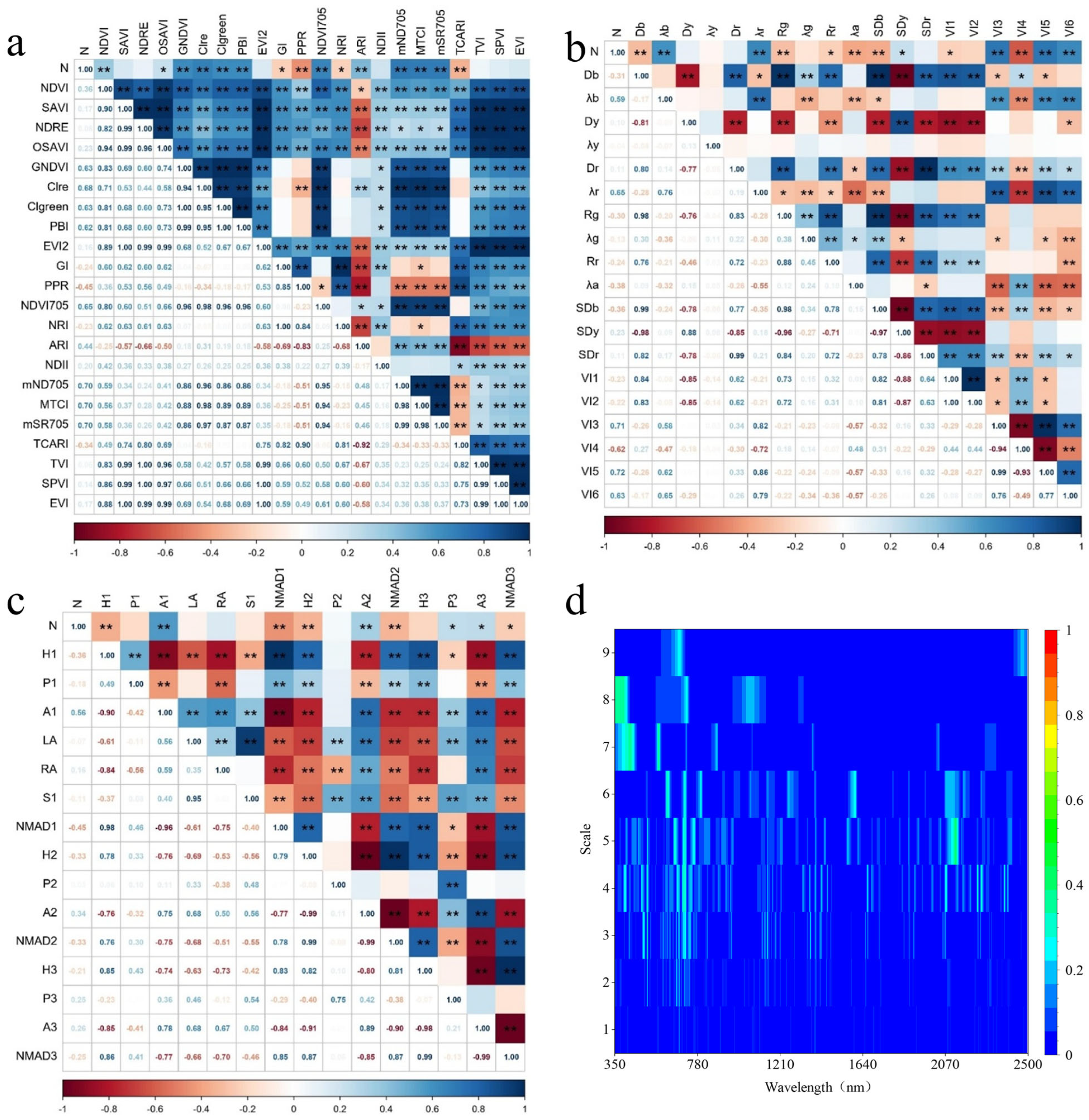
3.3. Correlation Analysis Between Vegetation LNC and Spectral Parameters
3.3.1. Relationship Between L. chinensis LNC and Spectral Variables Under Different Transformations
3.3.2. Relationships Between C. squarrosa LNC and Spectral Variables Under Different Transformations
3.4. LASSO Feature Parameter Screening Results
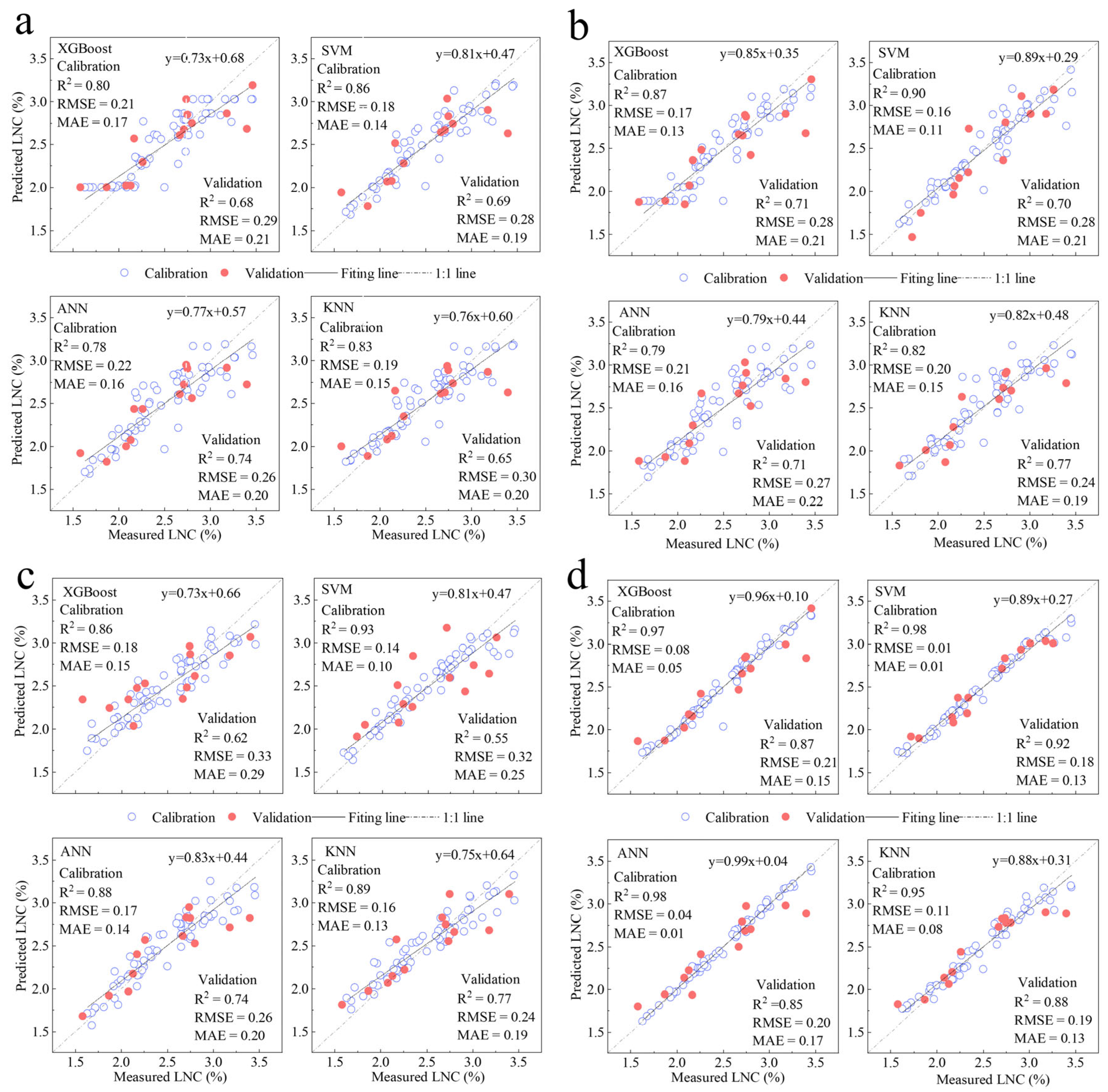
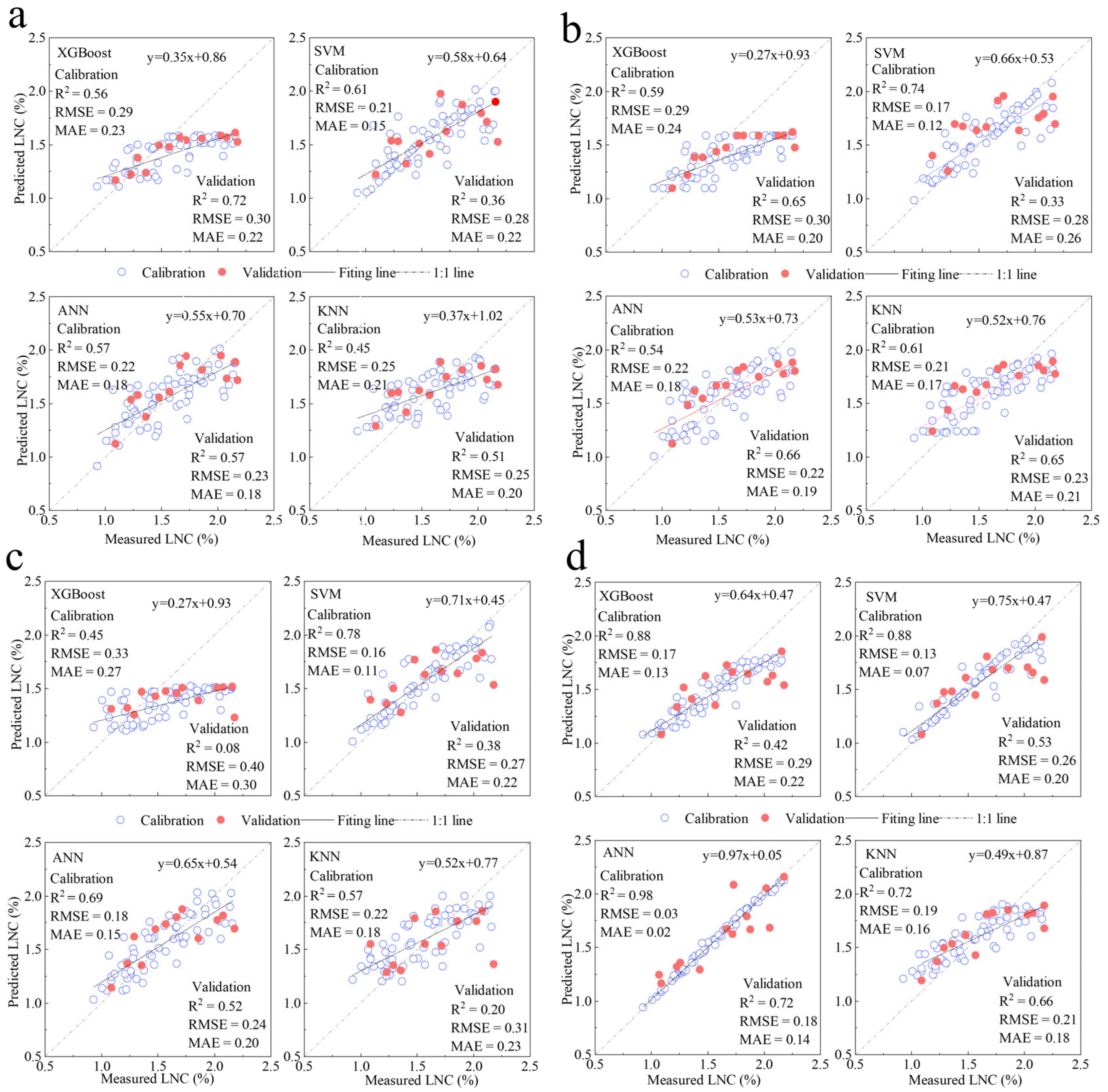
3.5. LNC Model Construction and Accuracy Evaluation
3.5.1. L. chinensis LNC Model Construction and Accuracy Evaluation
3.5.2. C. squarrosa LNC Model Construction and Accuracy Evaluation
4. Discussion
4.1. Nitrogen-Sensitive Band Analysis
4.2. Screening Parameter Analysis
4.3. Prediction Model Analysis
5. Conclusions
- Different spectral transformations can highlight spectral information. The original spectral curves for the two grassland plants, L. chinensis and C. squarrosa, exhibit similar shapes and align with the spectral reflectance curves typical of green vegetation. After the FDT, the positive extreme value of L. chinensis is greater than that of C. squarrosa at a wavelength of about 716 nm, and the reflectance of L. chinensis in the red-edge range increases at a faster rate. After the CWT, obvious green peaks and red valleys are observed at the fourth to sixth scales, which are conducive to discovering and extracting subtle spectral features. Upon implementing the CRT, three absorption valleys become apparent within the visible and near-infrared wavelength ranges, while a “double-valley” configuration is observed in the blue and red light ranges. Compared to the initial spectral curves, these spectral changes improve the spectral characteristics, expand the spectral data, and facilitate the extraction of spectral features.
- Dimensionality reduction can effectively prevent data overfitting. Four sets of variables are obtained using the LASSO method: LASSO-VI variables, LASSO-hyperspectral feature variables, LASSO-CR parameters, and LASSO-wavelet coefficients. The number of feature variables after screening is significantly reduced compared to before, and the number of variables of L. chinensis is smaller than that of C. squarrosa. The LASSO-wavelet coefficients decrease the most (with that of L. chinensis decreasing from 19,359 to 59 and that of C. squarrosa decreasing from 19,359 to 63). The screening process eliminates variables that exhibit zero variance, those with near-zero variance, and those that display high autocorrelation. This approach reduces data redundancy during the modeling phase while also decreasing the dimensionality of the hyperspectral data.
- Among the 16 constructed multivariate nitrogen inversion models utilizing four sets of spectral variables for L. chinensis, the model employing SVM and wavelet coefficients exhibits the highest performance. It achieves an R2 value of 0.98 on the training dataset, with corresponding RMSE and MAE metrics of 0.02 and 0.03, respectively. The validation dataset results in an R2 of 0.92, alongside RMSE and MAE values of 0.18 and 0.13. The approximate 6% accuracy difference between the training and validation datasets indicates the model’s stability and reliability. For the 16 multivariate nitrogen inversion models developed for C. squarrosa using four spectral variable sets, the ANN model based on wavelet coefficients demonstrates superior performance. The training dataset yields an R2 of 0.98, with RMSE and MAE values of 0.03 and 0.02, respectively. However, the validation dataset shows an R2 of 0.72, accompanied by RMSE and MAE values of 0.18 and 0.14. These results provide essential insights for developing a rapid, efficient, and non-destructive estimation model for leaf nitrogen content in typical grassland plant species.
- Using wavelet transform sensitive parameters as independent variables for leaf nitrogen content inversion of L. chinensis and C. squarrosa, two typical grassland plants in Inner Mongolia, yields the best results, serving as a reference for choosing spectral transformation methods and regression models in future monitoring of nitrogen content in grassland vegetation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| N | Nitrogen |
| ASD | Analytical Spectral Devices |
| FDT | First-order Derivative Transformation |
| CWT | Continuous Wavelet Transformation |
| CRT | Continuum Removal Transformation |
| LASSO | Least Absolute Shrinkage and Selection Operator |
| XGBoost | Extreme Gradient Boosting |
| SVM | Support Vector Machine |
| ANN | Artificial Neural Network |
| KNN | K-Nearest Neighbors |
| CNC | Canopy Nitrogen Concentration |
| LNC | Leaf Nitrogen Content |
| SMLR | Stepped-Multiple Linear Regression |
| SVR | Support Vector Regression |
| GA-ELM | Genetic Algorithm–Extreme Learning Machine |
| VI | Vegetation Indices |
| Max | Maximum |
| Min | Minimum |
| Mean | Arithmetic Mean |
| SD | Standard Deviation |
| CV | Coefficient of Variation |
References
- Wang, Z.; Ma, Y.; Zhang, Y.; Shang, J. Review of remote sensing applications in grassland monitoring. Remote Sens. 2022, 14, 2903. [Google Scholar] [CrossRef]
- Reinermann, S.; Asam, S.; Kuenzer, C. Remote sensing of grassland production and management—A review. Remote Sens. 2020, 12, 1949. [Google Scholar] [CrossRef]
- Yang, X.; Xu, B.; Zhu, X.; Jin, Y.; Li, J.; Zhao, F.; Chen, S.; Guo, J.; Ma, H.; Yu, H. A monitoring indicator system for remote sensing of grassland vegetation growth and suitability evaluation—A case study of the Xilingol Grassland in Inner Mongolia, China. Int. J. Remote Sens. 2015, 36, 5105–5122. [Google Scholar] [CrossRef]
- Bangira, T.; Mutanga, O.; Sibanda, M.; Dube, T.; Mabhaudhi, T. Remote Sensing Grassland Productivity Attributes: A Systematic Review. Remote Sens. 2023, 15, 2043. [Google Scholar] [CrossRef]
- Riggs, C.E.; Hobbie, S.E.; Bach, E.M.; Hofmockel, K.S.; Kazanski, C.E. Nitrogen addition changes grassland soil organic matter decomposition. Biogeochemistry 2015, 125, 203–219. [Google Scholar] [CrossRef]
- He, J.-S.; Wang, L.; Flynn, D.F.; Wang, X.; Ma, W.; Fang, J. Leaf nitrogen: Phosphorus stoichiometry across Chinese grassland biomes. Oecologia 2008, 155, 301–310. [Google Scholar] [CrossRef]
- Beeri, O.; Phillips, R.; Hendrickson, J.; Frank, A.B.; Kronberg, S. Estimating forage quantity and quality using aerial hyperspectral imagery for northern mixed-grass prairie. Remote Sens. Environ. 2007, 110, 216–225. [Google Scholar] [CrossRef]
- Mutanga, O.; Adam, E.; Adjorlolo, C.; Abdel-Rahman, E.M. Evaluating the robustness of models developed from field spectral data in predicting African grass foliar nitrogen concentration using WorldView-2 image as an independent test dataset. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 178–187. [Google Scholar] [CrossRef]
- Gao, J.; Liang, T.; Yin, J.; Ge, J.; Xie, H. Estimation of Alpine Grassland Forage Nitrogen Coupled with Hyperspectral Characteristics during Different Growth Periods on the Tibetan Plateau. Remote Sens. 2019, 11, 2085. [Google Scholar] [CrossRef]
- Poonsak, M.; Wasinee, W. Estimations of Nitrogen Concentration in Sugarcane Using Hyperspectral Imagery. Sustainability 2018, 10, 1266. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, J.; Xiong, S.; Zhang, Z.; Wei, Q.; Zhang, W.; Feng, W.; Ma, X. Hyperspectral assessment of leaf nitrogen accumulation for winter wheat using different regression modeling. Precis. Agric. 2021, 22, 1634–1658. [Google Scholar] [CrossRef]
- Yu, F.; Feng, S.; Du, W.; Wang, D.; Guo, Z.; Xing, S.; Jin, Z.; Cao, Y.; Xu, T. A study of nitrogen deficiency inversion in rice leaves based on the hyperspectral reflectance differential. Front. Plant Sci. 2020, 11, 573272. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Y.; Wang, Y.; Cheng, J.; Li, F.Y. Preferences for different nitrogen forms in three dominant plants in a semi-arid grassland under different grazing intensities. Agric. Ecosyst. Environ. 2022, 333, 107959. [Google Scholar] [CrossRef]
- Wu, N.; Liu, G.; Yang, Y.; Song, X.; Bai, H. Dynamic monitoring of net primary productivity and its response to climate factors in native grassland in Inner Mongolia using a light-use efficiency model. Acta Prataculturae Sin. 2020, 29, 1–10. [Google Scholar] [CrossRef]
- Wang, R.; Dong, J.; Jin, L.; Sun, Y.; Baoyin, T.; Wang, X. Improving the Accuracy of Vegetation Index Retrieval for Biomass by Combining Ground-UAV Hyperspectral Data—A New Method for Inner Mongolia Typical Grasslands. Phyton 2024, 93, 387–411. [Google Scholar] [CrossRef]
- Geng, Q.; Ma, X.; Peng, F.; Zhu, Z.; Li, Q.; Xu, D.; Ruan, H.; Xu, X. Consistent responses of the C:N:P stoichiometry of green leaves and fine roots to N addition in poplar plantations in eastern coastal China. Plant Soil 2023, 485, 377–394. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Barnes, E.; Clarke, T.; Richards, S.; Colaizzi, P.; Haberland, J.; Kostrzewski, M.; Waller, P.; Choi, C.; Riley, E.; Thompson, T. Coincident detection of crop water stress, nitrogen status and canopy density using ground based multispectral data. In Proceedings of the Fifth International Conference on Precision Agriculture, Bloomington, MN, USA, 16–19 July 2000; p. 6. [Google Scholar]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef]
- Rao, N.R.; Garg, P.; Ghosh, S.; Dadhwal, V. Estimation of leaf total chlorophyll and nitrogen concentrations using hyperspectral satellite imagery. J. Agric. Sci. 2008, 146, 65–75. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Peñuelas, J.; Gamon, J.; Fredeen, A.; Merino, J.; Field, C. Reflectance indices associated with physiological changes in nitrogen-and water-limited sunflower leaves. Remote Sens. Environ. 1994, 48, 135–146. [Google Scholar] [CrossRef]
- Gitelson, A.; Merzlyak, M.N. Spectral reflectance changes associated with autumn senescence of Aesculus hippocastanum L. and Acer platanoides L. leaves. Spectral features and relation to chlorophyll estimation. J. Plant Physiol. 1994, 143, 286–292. [Google Scholar] [CrossRef]
- Schleicher, T.D.; Bausch, W.C.; Delgado, J.A.; Ayers, P.D. Evaluation and refinement of the nitrogen reflectance index (NRI) for site-specific fertilizer management. In Proceedings of the 2001 ASAE Annual Meeting, Sacramento, CA, USA, 29 July–1 August 2001; p. 1. [Google Scholar]
- Gitelson, A.A.; Merzlyak, M.N.; Chivkunova, O.B. Optical properties and nondestructive estimation of anthocyanin content in plant leaves. Photochem. Photobiol. 2001, 74, 38–45. [Google Scholar] [CrossRef]
- Hunt, E.R., Jr.; Rock, B.N. Detection of changes in leaf water content using near-and middle-infrared reflectances. Remote Sens. Environ. 1989, 30, 43–54. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P. The MERIS terrestrial chlorophyll index. Int. J. Remote Sens. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Vincini, M.; Frazzi, E.; D’Alessio, P. Angular dependence of maize and sugar beet VIs from directional CHRIS/Proba data. In Proceedings of the 4th ESA CHRIS PROBA Workshop, Piacenza, Italy, 19–21 September 2006; pp. 19–21. [Google Scholar]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Wang, X.; Xu, G.; Feng, Y.; Peng, J.; Gao, Y.; Li, J.; Han, Z.; Luo, Q.; Ren, H.; You, X. Estimation Model of Rice Aboveground Dry Biomass Based on the Machine Learning and Hyperspectral Characteristic Parameters of the Canopy. Agronomy 2023, 13, 1940. [Google Scholar] [CrossRef]
- Li, C.; Chen, P.; Ma, C.; Feng, H.; Wei, F.; Wang, Y.; Shi, J.; Cui, Y. Estimation of potato chlorophyll content using composite hyperspectral index parameters collected by an unmanned aerial vehicle. Int. J. Remote Sens. 2020, 41, 8176–8197. [Google Scholar] [CrossRef]
- Kong, B.; Yu, H.; Du, R.; Wang, Q. Quantitative estimation of biomass of alpine grasslands using hyperspectral remote sensing. Rangel. Ecol. Manag. 2019, 72, 336–346. [Google Scholar] [CrossRef]
- Zhang, J.; Pu, R.; Loraamm, R.W.; Yang, G.; Wang, J. Comparison between wavelet spectral features and conventional spectral features in detecting yellow rust for winter wheat. Comput. Electron. Agric. 2014, 100, 79–87. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Fan, Y.; Cheng, Y.; Wu, X.; Zhang, J.; Wang, B.; Wang, X.; Yong, T.; Liu, W. Evaluating photosynthetic pigment contents of maize using UVE-PLS based on continuous wavelet transform. Comput. Electron. Agric. 2020, 169, 105160. [Google Scholar] [CrossRef]
- Gu, X.; Wang, Y.; Sun, Q.; Yang, G.; Zhang, C. Hyperspectral inversion of soil organic matter content in cultivated land based on wavelet transform. Comput. Electron. Agric. 2019, 167, 105053. [Google Scholar] [CrossRef]
- Lin, D.; Li, G.; Zhu, Y.; Liu, H.; Li, L.; Fahad, S.; Zhang, X.; Wei, C.; Jiao, Q. Predicting copper content in chicory leaves using hyperspectral data with continuous wavelet transforms and partial least squares. Comput. Electron. Agric. 2021, 187, 106293. [Google Scholar] [CrossRef]
- Zhuang, T.; Zhang, Y.; Li, D.; Schmidhalter, U.; Ata-Ui-Karim, S.T.; Cheng, T.; Liu, X.; Tian, Y.; Zhu, Y.; Cao, W.; et al. Coupling continuous wavelet transform with machine learning to improve water status prediction in winter wheat. Precis. Agric. 2023, 24, 2171–2199. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, W.; Qiao, H.; Xu, C.; Guo, J.; Si, H.; Wang, J.; Xiong, S.; Ma, X. Estimation of leaf nitrogen content in winter wheat based on continuum removal and discrete wavelet transform. Int. J. Remote Sens. 2023, 44, 5523–5547. [Google Scholar] [CrossRef]
- Huang, Z.; Turner, B.J.; Dury, S.J.; Wallis, I.R.; Foley, W.J. Estimating foliage nitrogen concentration from HYMAP data using continuum removal analysis. Remote Sens. Environ. 2004, 93, 18–29. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Gao, J.; Meng, B.; Liang, T.; Feng, Q.; Ge, J.; Yin, J.; Wu, C.; Cui, X.; Hou, M.; Liu, J. Modeling alpine grassland forage phosphorus based on hyperspectral remote sensing and a multi-factor machine learning algorithm in the east of Tibetan Plateau, China. ISPRS J. Photogramm. Remote Sens. 2019, 147, 104–117. [Google Scholar] [CrossRef]
- Moghimi, A.; Pourreza, A.; Zuniga-Ramirez, G.; Williams, L.E.; Fidelibus, M.W. A novel machine learning approach to estimate grapevine leaf nitrogen concentration using aerial multispectral imagery. Remote Sens. 2020, 12, 3515. [Google Scholar] [CrossRef]
- Sudu, B.; Rong, G.; Guga, S.; Li, K.; Zhi, F.; Guo, Y.; Zhang, J.; Bao, Y. Retrieving SPAD values of summer maize using UAV hyperspectral data based on multiple machine learning algorithm. Remote Sens. 2022, 14, 5407. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Tatnall, A.R. Introduction neural networks in remote sensing. Int. J. Remote Sens. 1997, 18, 699–709. [Google Scholar] [CrossRef]
- Wang, L.; Chang, Q.; Li, F.; Yan, L.; Huang, Y.; Wang, Q.; Luo, L. Effects of growth stage development on paddy rice leaf area index prediction models. Remote Sens. 2019, 11, 361. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Z.; Jiang, T.; Li, X.; Li, Y. Evaluation of the effectiveness of multiple machine learning methods in remote sensing quantitative retrieval of suspended matter concentrations: A case study of Nansi Lake in North China. J. Spectrosc. 2021, 2021, 1–17. [Google Scholar] [CrossRef]
- Alexander, J.; Hubert, H.; Ellen, A.H.; Andreas, B.; Jens, B.; Georg, B. Investigating the Potential of a Newly Developed UAV-Mounted VNIR/SWIR Imaging System for Monitoring Crop Traits—A Case Study for Winter Wheat. Remote Sens. 2021, 13, 1697. [Google Scholar] [CrossRef]
- Stroppiana, D.; Fava, F.; Boschetti, M.; Brivio, P.A. Estimation of Nitrogen Content in Herbaceous Plants Using Hyperspectral Vegetation Indices; Hyperspectral Indices and Image Classifications for Agriculture and Vegetation; CRC Press: Boca Raton, FL, USA, 2019; Volume 2. [Google Scholar]
- Clevers, J.G.P.W.; Gitelson, A.A. Remote estimation of crop and grass chlorophyll and nitrogen content using red-edge bands on Sentinel-2 and -3. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 344–351. [Google Scholar] [CrossRef]
- Cho, M.A.; Skidmore, A.K. A new technique for extracting the red edge position from hyperspectral data: The linear extrapolation method. Remote Sens. Environ. 2006, 101, 181–193. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K.; Kumar, L.; Ferwerda, J. Estimating tropical pasture quality at canopy level using band depth analysis with continuum removal in the visible domain. Int. J. Remote Sens. 2005, 26, 1093–1108. [Google Scholar] [CrossRef]
- Li, X.; Shi, Z.; Bai, T.; Chen, B.; Lv, X.; Zhang, Z.; Zhou, B. A Study on the Estimation Model of Hyperspectral Reflectivity and Leaf Nitrogen Content of Cotton Leaves. IEEE Access 2023, 11, 74228–74238. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, C.; Hill, J.; Buddenbaum, H.; Werner, W.; Schuler, G. Retrieval of chlorophyll and nitrogen in Norway spruce (Picea abies L. Karst.) using imaging spectroscopy. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 17–26. [Google Scholar] [CrossRef]
- Skidmore, A.K.; Ferwerda, J.G.; Mutanga, O.; Wieren, S.E.V.; Peel, M.; Grant, R.C.; Prins, H.H.T.; Balcik, F.B.; Venus, V. Forage quality of savannas—Simultaneously mapping foliar protein and polyphenols for trees and grass using hyperspectral imagery. Remote Sens. Environ. 2010, 114, 64–72. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Red edge shift and biochemical content in grass canopies. Isprs J. Photogramm. Remote Sens. 2007, 62, 34–42. [Google Scholar] [CrossRef]
- Yi, Q.X.; Huang, J.F.; Wang, F.M.; Wang, X.Z.; Liu, Z.Y. Monitoring rice nitrogen status using hyperspectral reflectance and artificial neural network. Environ. Sci. Technol. 2007, 41, 6770–6775. [Google Scholar] [CrossRef]
- Schwarz, G.E. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Murray, A.B. Reducing model complexity for explanation and prediction. Geomorphology 2007, 90, 178–191. [Google Scholar] [CrossRef]
- Corbier, C.; Ugalde, H.M.R. Robust Estimation of Balanced Simplicity-Accuracy Neural Networks-Based Models. J. Dyn. Syst. Meas. Control 2016, 138, 051001. [Google Scholar] [CrossRef]
- Thorp, K.R.; Wang, G.; Bronson, K.F.; Badaruddin, M.; Mon, J. Hyperspectral data mining to identify relevant canopy spectral features for estimating durum wheat growth, nitrogen status, and grain yield. Comput. Electron. Agric. 2017, 136, 1–12. [Google Scholar] [CrossRef]
- Fu, Y.; Yang, G.; Li, Z.; Li, H.; Li, Z.; Xu, X.; Song, X.; Zhang, Y.; Duan, D.; Zhao, C.; et al. Progress of hyperspectral data processing and modelling for cereal crop nitrogen monitoring. Comput. Electron. Agric. 2020, 172, 105321. [Google Scholar] [CrossRef]
- Peerbhay, M.K. Remote sensing of key grassland nutrients using hyperspectral techniques in KwaZulu-Natal, South Africa. J. Appl. Remote Sens. 2017, 11, 036005. [Google Scholar] [CrossRef]
- Hunt, E.R.; Doraiswamy, P.C.; Mcmurtrey, J.E.; Daughtry, C.S.T.; Perry, E.M.; Akhmedov, B. A visible band index for remote sensing leaf chlorophyll content at the canopy scale. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 103–112. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Kooistra, L. Using hyperspectral remote sensing data for retrieving total canopy chlorophyll and nitrogen content. In Proceedings of the 2011 3rd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lisbon, Portugal, 6–9 June 2011. [Google Scholar]
- Chakraborty, S.K.; Mahanti, N.K.; Mansuri, S.M.; Tripathi, M.K.; Kotwaliwale, N.; Jayas, D.S. Non-destructive classification and prediction of aflatoxin-B1 concentration in maize kernels using Vis–NIR (400–1000 nm) hyperspectral imaging. J. Food Sci. Technol.-Mysore 2020, 58, 437–450. [Google Scholar] [CrossRef] [PubMed]
- Remote sensing of forage nutrients: Combining ecological and spectral absorption feature data. ISPRS J. Photogramm. Remote Sens. 2012, 72, 27–35. [CrossRef]
- Cao, C.; Wang, T.; Gao, M.; Li, Y.; Li, D.; Zhang, H. Hyperspectral inversion of nitrogen content in maize leaves based on different dimensionality reduction algorithms. Comput. Electron. Agric. 2021, 190, 106461. [Google Scholar] [CrossRef]
- Ma, C.; Zhai, L.; Li, C.; Wang, Y. Hyperspectral Estimation of Nitrogen Content in Different Leaf Positions of Wheat Using Machine Learning Models. Appl. Sci. 2022, 12, 7427. [Google Scholar] [CrossRef]
- Cheng, T.; Rivard, B.; Sánchez-Azofeifa, A. Spectroscopic determination of leaf water content using continuous wavelet analysis. Remote Sens. Environ. 2011, 115, 659–670. [Google Scholar] [CrossRef]
- Sabzi, S.; Pourdarbani, R.; Rohban, M.H.; García-Mateos, G.; Arribas, J.I. Estimation of nitrogen content in cucumber plant (Cucumis sativus L.) leaves using hyperspectral imaging data with neural network and partial least squares regressions. Chemom. Intell. Lab. Syst. 2021, 217, 104404. [Google Scholar] [CrossRef]
- Eshkabilov, S.; Lee, A.; Sun, X.; Lee, C.W.; Simsek, H. Hyperspectral imaging techniques for rapid detection of nutrient content of hydroponically grown lettuce cultivars. Comput. Electron. Agric. 2021, 181, 105968. [Google Scholar] [CrossRef]

| Name | Computing Formula | Reference |
|---|---|---|
| Two-band VI | ||
| Normalized difference VI (NDVI) | [18] | |
| Soil adjustment VI (SAVI) | [19] | |
| Normalized difference red edge index (NDRE) | [20] | |
| Optimized soil adjusted VI (OSAVI) | [21] | |
| Green normalized difference VI (GNDVI) | [22] | |
| Chlorophyll red-edge index (Clre) | [23] | |
| Chlorophyll greenness index (Clgreen) | [23] | |
| Plant biochemical index (PBI) | [24] | |
| Plant pigment ratio (PPR) | [24] | |
| Two-band enhanced VI (EVI2) | [25] | |
| Greenness index (GI) | [26] | |
| Red-edge normalized difference VI (NDVI705) | [27] | |
| Nitrogen reflectance index (NRI) | [28] | |
| Anthocyanin reflectance index (ARI) | [29] | |
| Normalized difference infrared index (NDII) | [30] | |
| Three-band VI | ||
| Modified normalized difference index (mND705) | [31] | |
| Modified scale VI (mSR705) | [31] | |
| Meris terrestrial chlorophyll index (MTCI) | [32] | |
| Transformed chlorophyll absorption ratio index (TCARI) | [33] | |
| Triangular VI (TVI) | [34] | |
| Spectral polygon VI (SPVI) | [35] | |
| Enhanced VI (EVI) | [36] |
| Type | Name | Definition and Calculation Method | Reference |
|---|---|---|---|
| Spectral area and positional parameters | Db | Maximum value of the first-order derivative spectrum within 490–530 nm of the blue edge | [37] |
| λb | The wavelength position corresponding to Db | [37] | |
| Dy | Maximum value of the first-order derivative spectrum within 560–640 nm at the yellow edge | [37] | |
| λy | The wavelength position corresponding to Dy | [37] | |
| Dr | Maximum value of the first-order derivative spectrum within 680–760 nm at the red edge | [37] | |
| λr | The wavelength position corresponding to Dr | [37] | |
| Rg | Green peak reflectance, maximum reflectance in the wavelength range of 520–560 nm | [37] | |
| λg | The wavelength position corresponding to Rg | [38] | |
| Rr | Red valley reflectance, maximum reflectance in the wavelength range of 650–690 nm | [38] | |
| λa | The wavelength position corresponding to Rr | [38] | |
| SDb | Integration of FDS in the blue-edge wavelength range of 490–530 nm | [38] | |
| SDy | Integration of FDS in the yellow-edge wavelength range of 560–640 nm | [38] | |
| SDr | Integration of FDS in the red-edge wavelength range of 680–760 nm | [38] | |
| The ratio of spectral area to positional parameters | VI1 | Ratio of green peak reflectance, Rg, to red valley reflectance, Rr | [39] |
| VI2 | Normalized values of green peak reflectance, Rg, and red valley reflectance, Rr | [39] | |
| VI3 | Ratio of the area of the red side, SDr, to the area of the blue side, SDb | [39] | |
| VI4 | Ratio of the area of the red side, SDr, to the area of the yellow side, SDy | [39] | |
| VI5 | Normalized values for the area of the red edge, SDr, and the area of the blue edge, SDb | [39] | |
| VI6 | Normalized values for the area of the red edge, SDr, and the area of the yellow edge, SDy | [39] |
| Name | Definition |
|---|---|
| Maximum absorption depth, H1 | Maximum absorption value in the first absorption peak |
| Absorption band wavelength, P1 | Wavelength corresponding to the maximum absorption depth (H) in the first absorption peak |
| The total area of the absorption peak, A1 | Integration of the depth of the band within the start and end wavelengths in the first absorption peak |
| Left area of absorption peak, LA | Integral area of the left absorption peak in the first absorption peak |
| The right area of absorption peak, RA | Integral area of the right absorption peak in the first absorption peak |
| Symmetry, S1 | Ratio of left area (LA) to right area (RA) in the first absorption peak |
| Maximum absorption depth for area normalization, NMAD1 | Ratio of the maximum depth of absorption of the first absorption peak (H1) to the total area of the absorption peak (A1) |
| Maximum absorption depth, H2 | Maximum absorption value in the second absorption peak |
| Absorption band wavelength, P2 | Wavelength corresponding to the maximum absorption depth (H) in the second absorption peak |
| Total area of absorption peak, A2 | Integration of the depth of the band within the start and end wavelengths in the second absorption peak |
| Maximum absorption depth for area normalization, NMAD2 | Ratio of the maximum depth of absorption of the second absorption peak (H1) to the total area of the absorption peak (A1) |
| Maximum absorption depth, H3 | Maximum absorption value in the third absorption peak |
| Absorption band wavelength, P3 | Wavelength corresponding to the maximum absorption depth (H) in the third absorption peak |
| Total area of absorption peak, A3 | Integration of band depths within the start and end wavelengths in the third absorption peak |
| Maximum absorption depth for area normalization, NMAD3 | Ratio of the maximum depth of absorption of the third absorption peak (H1) to the total area of the absorption peak (A1) |
| Vegetation | Data | Sample Size | Max | Min | Mean | SD | CV |
|---|---|---|---|---|---|---|---|
| L. chinensis | Total | 76 | 3.46 | 1.58 | 2.51 | 0.47 | 18.89 |
| Training set | 63 | 3.46 | 1.63 | 2.51 | 0.47 | 18.61 | |
| Test set | 13 | 3.4 | 1.58 | 2.49 | 0.52 | 21.01 | |
| C. squarrosa | Total | 76 | 2.18 | 0.93 | 1.57 | 0.33 | 21.26 |
| Training set | 63 | 2.16 | 0.93 | 1.56 | 0.33 | 20.92 | |
| Test set | 13 | 2.18 | 1.09 | 1.66 | 0.36 | 21.54 |
| Vegetation | Type of Spectral Variable | Number of Variables | Variable |
|---|---|---|---|
| L. chinensis | VI variable | 2 | mND705, TCARI |
| Hyperspectral feature variable | 3 | λr, SDy, VI3 | |
| CR variable | 6 | P1, A1, RA, S1, P2, A2 | |
| Wavelet coefficient variable | 59 | Scale1: WF528, WF595, WF602, WF622, WF625, WF710; Scale2: WF596, WF611, WF631, WF642, WF662, WF670, WF709, WF760, WF1096, WF1109, WF1759, WF2240; Scale3: WF630, WF642, WF2222, WF2239, WF2251; Scale4: WF594, WF611, WF759, WF851, WF1483, WF1544, WF1626, WF1690, WF2189, WF2238, WF2300, WF2319; Scale5: WF772, WF1227, WF1692, WF2091, WF2144; Scale6: WF350, WF631, WF1147, WF1298, WF1609, WF1800, WF2171, WF2254; Scale7: WF579, WF724, WF1710, WF2337; Scale8: WF386, WF1039, WF1149; Scale9: WF773. WF1852, WF2269, WF2500; | |
| C. squarrosa | VI variable | 4 | mND705, PPR, ARI, NDII |
| Hyperspectral feature variable | 4 | r, VI4, VI6 | |
| CR variable | 7 | P1, A1, RA, S1, P2, NMAD2, P3 | |
| Wavelet coefficient variable | 63 | Scale1: WF351, WF666, WF676, WF687, WF688, WF690; Scale2: WF350, WF508, WF524, WF642, WF689, WF719, WF720, WF1137, WF1146, WF2302; Scale3: WF522, WF642, WF1146, WF1168; Scale4: WF368, WF680, WF954, WF1145, WF1540, WF2241, WF2361, WF2381; Scale5: WF522, WF770, WF1311, WF1566, WF1692, WF1761, WF2127; Scale6: WF363, WF514, WF631, WF905, WF964, WF1141, WF1259, WF1394, WF1489, WF1708, WF2166, WF2259, WF2486; Scale7: WF579, WF727, WF1062, WF1380, WF2296; Scale8: WF406, WF733, WF1084, WF1309, WF2118, WF2412; Scale9: WF700, WF1329, WF2085, WF2482; |
| Input Variable | Model | T-R2 | T-RMSE | T-MAE | V-R2 | V-RMSE | V-MAE |
|---|---|---|---|---|---|---|---|
| LASSO-VI variable | XGBoost | 0.80 | 0.21 | 0.17 | 0.68 | 0.29 | 0.21 |
| SVM | 0.86 | 0.18 | 0.14 | 0.69 | 0.28 | 0.19 | |
| ANN | 0.78 | 0.22 | 0.16 | 0.74 | 0.26 | 0.20 | |
| KNN | 0.83 | 0.19 | 0.15 | 0.65 | 0.30 | 0.20 | |
| LASSO-hyperspectral feature variable | XGBoost | 0.87 | 0.17 | 0.13 | 0.71 | 0.28 | 0.21 |
| SVM | 0.90 | 0.16 | 0.11 | 0.70 | 0.28 | 0.21 | |
| ANN | 0.79 | 0.21 | 0.16 | 0.71 | 0.27 | 0.22 | |
| KNN | 0.82 | 0.20 | 0.15 | 0.77 | 0.24 | 0.19 | |
| LASSO-CR parameter | XGBoost | 0.86 | 0.18 | 0.15 | 0.62 | 0.33 | 0.29 |
| SVM | 0.93 | 0.14 | 0.10 | 0.55 | 0.32 | 0.28 | |
| ANN | 0.88 | 0.17 | 0.14 | 0.74 | 0.26 | 0.20 | |
| KNN | 0.89 | 0.17 | 0.13 | 0.77 | 0.24 | 0.19 | |
| LASSO-wavelet coefficient | XGBoost | 0.97 | 0.08 | 0.05 | 0.87 | 0.21 | 0.15 |
| SVM | 0.98 | 0.02 | 0.03 | 0.92 | 0.18 | 0.13 | |
| ANN | 0.98 | 0.04 | 0.03 | 0.85 | 0.20 | 0.17 | |
| KNN | 0.95 | 0.11 | 0.08 | 0.88 | 0.19 | 0.13 |
| Input Variable | Model | T-R2 | T-RMSE | T-MAE | V-R2 | V-RMSE | V-MAE |
|---|---|---|---|---|---|---|---|
| LASSO-VIvariable | XGBoost | 0.56 | 0.29 | 0.23 | 0.72 | 0.30 | 0.22 |
| SVM | 0.61 | 0.21 | 0.15 | 0.36 | 0.28 | 0.22 | |
| ANN | 0.57 | 0.22 | 0.18 | 0.57 | 0.23 | 0.18 | |
| KNN | 0.45 | 0.25 | 0.21 | 0.51 | 0.25 | 0.20 | |
| LASSO-hyperspectral feature variable | XGBoost | 0.59 | 0.29 | 0.24 | 0.65 | 0.30 | 0.20 |
| SVM | 0.74 | 0.17 | 0.12 | 0.33 | 0.28 | 0.26 | |
| ANN | 0.54 | 0.22 | 0.18 | 0.66 | 0.22 | 0.19 | |
| KNN | 0.61 | 0.21 | 0.17 | 0.65 | 0.23 | 0.21 | |
| LASSO-CR parameter | XGBoost | 0.45 | 0.33 | 0.27 | 0.10 | 0.39 | 0.30 |
| SVM | 0.78 | 0.16 | 0.11 | 0.38 | 0.27 | 0.22 | |
| ANN | 0.69 | 0.18 | 0.15 | 0.52 | 0.24 | 0.20 | |
| KNN | 0.57 | 0.22 | 0.18 | 0.20 | 0.31 | 0.23 | |
| LASSO-wavelet coefficient | XGBoost | 0.88 | 0.17 | 0.13 | 0.29 | 0.42 | 0.22 |
| SVM | 0.87 | 0.13 | 0.07 | 0.26 | 0.53 | 0.20 | |
| ANN | 0.98 | 0.03 | 0.02 | 0.72 | 0.18 | 0.14 | |
| KNN | 0.72 | 0.19 | 0.16 | 0.21 | 0.66 | 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, L.; Wang, X.; Dong, J.; Wang, R.; Wen, H.; Sun, Y.; Wu, W.; Zhang, Z.; Kang, C. Estimation Method of Leaf Nitrogen Content of Dominant Plants in Inner Mongolia Grassland Based on Machine Learning. Nitrogen 2025, 6, 70. https://doi.org/10.3390/nitrogen6030070
Jin L, Wang X, Dong J, Wang R, Wen H, Sun Y, Wu W, Zhang Z, Kang C. Estimation Method of Leaf Nitrogen Content of Dominant Plants in Inner Mongolia Grassland Based on Machine Learning. Nitrogen. 2025; 6(3):70. https://doi.org/10.3390/nitrogen6030070
Chicago/Turabian StyleJin, Lishan, Xiumei Wang, Jianjun Dong, Ruochen Wang, Hefei Wen, Yuyan Sun, Wenbo Wu, Zhihang Zhang, and Can Kang. 2025. "Estimation Method of Leaf Nitrogen Content of Dominant Plants in Inner Mongolia Grassland Based on Machine Learning" Nitrogen 6, no. 3: 70. https://doi.org/10.3390/nitrogen6030070
APA StyleJin, L., Wang, X., Dong, J., Wang, R., Wen, H., Sun, Y., Wu, W., Zhang, Z., & Kang, C. (2025). Estimation Method of Leaf Nitrogen Content of Dominant Plants in Inner Mongolia Grassland Based on Machine Learning. Nitrogen, 6(3), 70. https://doi.org/10.3390/nitrogen6030070









