Abstract
In centrifugal compressors, Mild Surge (MS) leads to unstable operation. Previous experimental work on a centrifugal compressor designed and built by Safran Helicopter Engines (SafranHE) showed that MS corresponds to the pulsation of an alternate stall pattern at the Helmholtz frequency of the test rig on two channels in the radial diffuser. The present contribution experimentally investigates the impact of the Inlet Guide Vane (IGV) stagger angle on this alternate flow and numerically studies the topology of this pulsating alternate flow. The experimental investigation is performed with unsteady pressure sensors, and shows that the IGV stagger angle only impacts the pulsation frequency of the alternate flow pattern. This change is explained by the dependence of the Helmholtz frequency on the compressor inlet section. The topological analysis of the average flow field, computed from wall-resolved Unsteady Reynolds-Averaged Navier–Stokes (URANS) simulations, demonstrates that the saddle point (major critical point) in the corner hub/suction side of the stalled blade migrates upstream while staying in the corner if the mass flow rate decreases. One main blade over two is stalled on both sides because the flow originating from this corner separation circumvents the trailing edge and migrates upstream along the pressure side. In the simulation, the pulsation of the alternate stall is coupled with the reflection of acoustic waves on the inlet and outlet planes, regarded as an environmental effect.
1. Introduction
The operating range of a compressor is limited at low mass flow rate by the development of aerodynamic instabilities. Unlike axial compressors, centrifugal compressors can continue to provide work input to the flow despite the presence of separated flow areas thanks to the Coriolis force (see Appendix A). As a result, more complex flow structures and paths to surge may occur. The path to surge includes Mild Surge (MS) at the Helmholtz frequency of the compressor on the test bench, as found in several studies [1,2,3]. Engine manufacturers try to avoid MS, as it can provoke mechanical failure.
MS has previously been observed at partial rotation speed in a research centrifugal compressor stage featuring a radial diffuser with an odd number of channels which was designed and manufactured by Safran Helicopter Engines (SafranHE) [4,5]. In this particular case, the MS corresponds to the pulsation of the alternate pattern on two channels in the radial diffuser. To the best of the authors’ knowledge, such a pattern is quite unique, as no other publication dealing with this kind of behavior can be found in the literature with regard to aeronautical centrifugal compressors. Nevertheless, similar flow characteristics have been observed in hydraulic pumps with an even number of blades [6,7]. The experimental detection of the alternate pattern (time-independent or pulsating) is explained in detail in [4], and a short summary is provided below.
The pressure sensors distributed over the entire circumference (on the test rig) at the diffuser leading edge may be projected onto one single passage or two adjacent passages. Indeed, the existence of an alternate pattern over two channels requires that the channel to which the sensor belongs be respected. For illustration purposes, two numerical static pressure maps in the radial diffuser are plotted in Figure 1 for (a) a periodic flow and (b) an alternate flow. These numerical flow fields are probed at the same positions of the experimental sensors at the diffuser inlet. The pressure profiles and correspond to the projection in one passage and two passages, respectively. If the flow is similar in each channel (periodic case), the two pressure profiles and overlap each other. On the contrary, if a two-channel pattern exists in the diffuser (alternate case), the two profiles are very different. Furthermore, the saw-tooth profile rendered by the projection is obviously non-physical. The alternate rate based on these two projections is defined in Equation (1) in order to quantify the level of alternation and the lack or existence of an alternate pattern. The alternate rate corresponds to the area between the two projections and . In this illustration, the alternate rate is 42 times higher in the alternate case than in the periodic case. Therefore the alternate rate is a good indicator to detect the existence of an alternate flow.
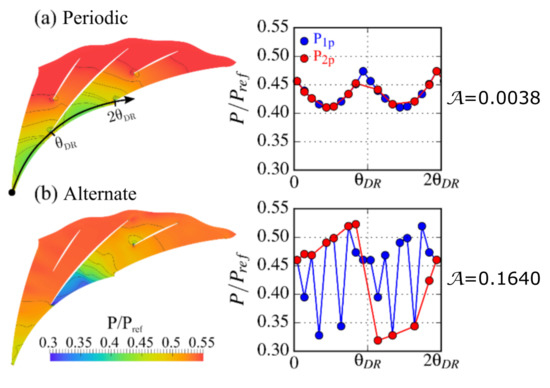
Figure 1.
Illustration of the alternate rate on two numerical static pressure maps.
The present work experimentally investigates the impact of the Inlet Guide Vane (IGV) stagger angle on this alternate flow and numerically studies the topology of this pulsating alternate flow. The analysis is performed at a partial rotation speed, denoted “C” in previous work [4], at an IGV stagger angle of .
First, the impact of the IGV stagger angle on the occurrence of the alternate flow is experimentally studied. Then, wall-resolved Unsteady Reynolds-Averaged Navier–Stokes (URANS) simulations are performed to analyse the flow topology (which is not experimentally available) and are validated against experimental data (performance and unsteady pressure measurements). The pulsation of the alternate stall is finally compared between experimental and numerical environments.
2. Methodology
2.1. Test Case
The test case is a research centrifugal compressor stage designed and manufactured by SafranHE. The compressor stage includes four blade rows: an axial IGV, an unshrouded backswept splittered impeller (IMP), a splittered vaned Radial Diffuser (RD), and axial Outlet Guide Vanes (OGV). A meridional scheme of the compressor is provided in Figure 2.
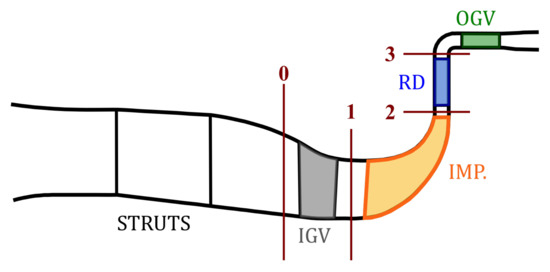
Figure 2.
Meridional view of the compressor stage (0: IGV inlet, 1: IGV outlet/IMP inlet, 2: IMP outlet/RD inlet, 3: RD outlet).
The overall stage total-to-static pressure ratio is around 4. The Mach number based on the peripheral velocity at the exit radius of the impeller is around 1.2 at maximal rotation speed.
2.2. Experimental Setup
The test rig is extensively instrumented; 130 steady sensors (temperature and pressure) are used for the monitoring and the performance measurements and 52 unsteady pressure sensors manufactured by Kulite Semiconductor Product, Inc. are embedded in the shroud and in the hub at different locations. More details on the experimental setup can be found in [4,8].
2.3. Numerical Setup
URANS simulations were run with the elsA software [9] developed at Office National d’Etudes et de Recherches Aérospatiales (ONERA). The code is based on a cell-centered finite volume method. The computational domain corresponds to the compressor spatial periodicity and includes several pairs of radial diffuser channels. The mesh is multiblock structured and includes around 50 million cells. It was built by SafranHE with in-house best practices, and the y+ values in the whole domain are between one and five.
The numerical parameters and boundary conditions are provided in Table 1. A time step convergence study shows that around 1200 steps of the main blade passing render an appropriate resolution, which leads to a physical time step with an order of magnitude of s.

Table 1.
Boundary conditions and numerical parameters.
A single impeller revolution was completed within 24 h on 168 cores of the cluster COBALT at the Centre de Calcul Recherche et Technologie (CCRT), representing around 4000 CPU hours. Certain simulations required more than 40 impeller revolutions, leading to approximately 200,000 CPU hours.
To compute the pressure ratios, the numerical static pressure field was probed according to the position of the experimental sensors, enabling a fair comparison between the numerical and experimental data.
2.4. Topological Analysis
Topological analysis was performed according to the work of Délery [10] and its extension to turbomachinery flows as suggested by Duquesne et al. [11]. In the following, 2D streamlines at the first cells are used as a proper approximation of the skin friction field.
3. Results
3.1. Experimental Investigation
3.1.1. IGV Stagger Angle of
This part corroborates the results presented in [4] (at rotation speed C) with data registered during a new experimental campaign.
Figure 3 shows the total-to-static pressure ratio , the steady alternate rate , and the unsteady alternate rate temporal standard deviation as functions of the standard mass flow rate . The significance level of , represented by a green dashed line, originates from the difference in discretization between the two projections (in one passage) and (in two passages), as previously explained in Figure 1. Here, a significance level of 0.012 is chosen corresponding to the maximal discretization error numerically observed from periodic flows over the whole compressor map. The unsteady alternate rate is calculated using the pressure signals registered by unsteady pressure sensors at the diffuser inlet (see [4] for more details).
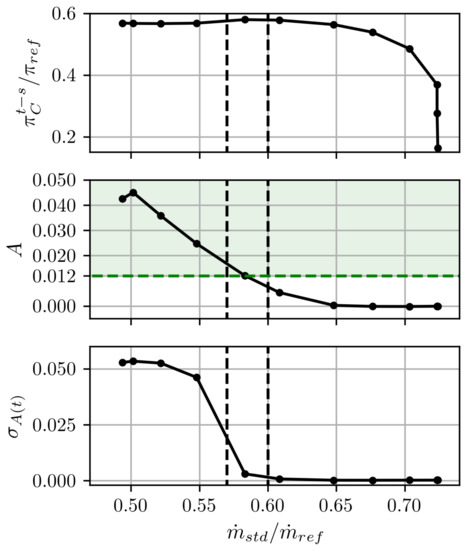
Figure 3.
Evolution of the alternate pattern with respect to standard mass flow rate at an IGV stagger angle of : total-to-static pressure ratio (top), steady alternate rate (middle), and unsteady alternate rate standard deviation (bottom).
In Figure 3, three groups of operating points can be observed:
- If , the steady alternate rate is lower than the significance level, meaning that the flow is periodic.
- If , the steady alternate rate is very similar to the significance level, while the unsteady alternate rate standard deviation remains close to zero. Therefore, an alternate flow arises over two channels while remaining steady.
- If , the steady alternate rate becomes higher than the significance level and the unsteady alternate rate standard deviation is of the same order of magnitude as the steady alternate rate. These are the signs of a pulsating alternate flow over two channels. The pressure ratio of the whole stage slightly decreases as well.
A 2D view of the flow at the radial diffuser inlet is shown in Figure 4. It shows the circumferential profiles of the steady static pressure P and standard deviation of the unsteady static pressure as a function of the standard mass flow rate . The three groups of operating points are now found again; if , the steady pressure profile differs a great deal between the two channels and the unsteady pressure standard deviation increases all around the circumference. This increase is especially pronounced around the leading edge of the blade separating the two channels (around ), revealing that this blade is of great interest.
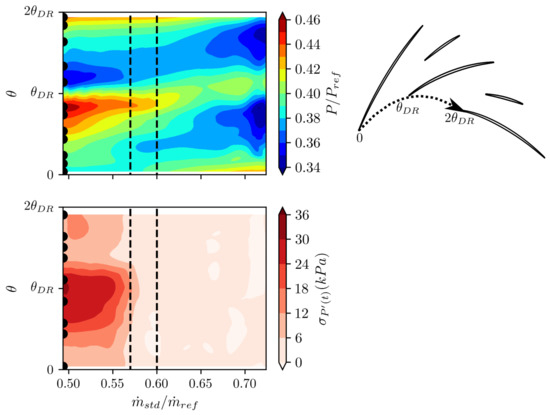
Figure 4.
Evolution of the alternate pattern with respect to standard mass flow rate at the radial diffuser inlet and an IGV stagger angle of : steady static pressure (top) and unsteady static pressure standard deviation (bottom).
The frequency content of these unsteady pressure fluctuations observed at the diffuser inlet is now investigated. Figure 5 shows the unsteady pressure average spectrum and the unsteady alternate rate spectrum , both obtained for the last stable operating point and at an IGV stagger angle of . The spectrum on the left is computed by averaging the spectra of unsteady pressures registered by all the diffuser inlet sensors (the same sensors that are used to compute the alternate rate). Both spectra and include a major peak at around 11 Hz and its harmonics. The unsteady pressure fluctuations plotted in Figure 4 are therefore linked to the pulsation of the alternate flow pattern at a frequency of 11 Hz. This frequency is close to the Helmholtz frequency (16 Hz) of the compressor mounted on the test rig, as stated in previous work [5]. This assumption is now discussed considering variation of the IGV stagger angles.
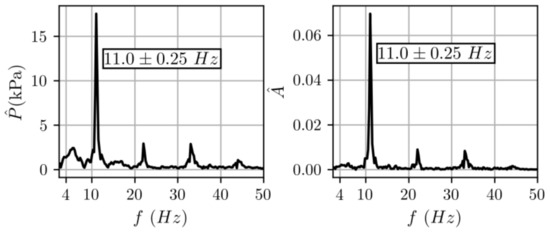
Figure 5.
Frequency content for the last stable operating point and for an IGV stagger angle of : unsteady pressure average spectrum (left) and unsteady alternate rate spectrum (right).
3.1.2. Impact of IGV Stagger Angle on the Helmholtz Frequency
Figure 6 shows the total-to-static pressure ratio , the steady alternate rate , and the unsteady alternate rate standard deviation as functions of the standard mass flow rate at three IGV stagger angles: , , and . The differences in choked mass flow between the IGV stagger angles have been discussed in previous work [8]. The shape of the characteristic curves is similar at the three IGV stagger angles; the pressure ratio decreases by a few operating points before surge. These operating points present an unsteady alternate rate standard deviation of the same order of magnitude as the steady alternate rate. At all of these IGV angles and at near-surge conditions, an alternate flow over two channels pulsates with almost the same alternate rate standard deviation.
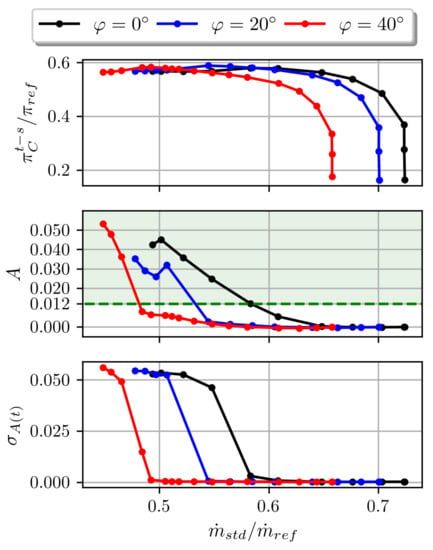
Figure 6.
Evolution of the alternate pattern with respect to standard mass flow rate at at IGV stagger angles of , , and : total-to-static pressure ratio (top), steady alternate rate (middle), and unsteady alternate rate standard deviation (bottom).
The unsteady pressure average spectrum (average of spectra of unsteady pressures at the diffuser inlet) obtained for the last stable operating point is plotted for each IGV stagger angle in Figure 7. The MS frequency corresponding to the major peak (shown in the label) decreases when the IGV stagger angle increases.
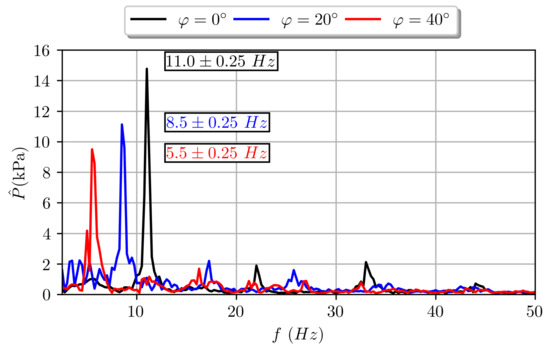
Figure 7.
Unsteady pressure average spectrum for the last stable operating point at IGV stagger angles of , , and .
According to the literature [1,2,3], MS occurs at the Helmholtz frequency, , for which the expression is provided by Equation (2):
where a is the speed of sound, is the compressor inlet section, is the downstream plenum volume, and is the compressor duct length.
In Equation (2), only the compressor inlet section depends on the IGV stagger angle. It can be simplified by the IGV passage width by reducing the geometrical dimension from 3D to 2D. This geometric modeling provides the theoretical frequency ratio in Equation (3):
The variation of the IGV passage width is schematized in Figure 8. Eventually, the passage width at the IGV stagger angle can be expressed using the passage width at the IGV stagger angle and the IGV chord in Equation (4).
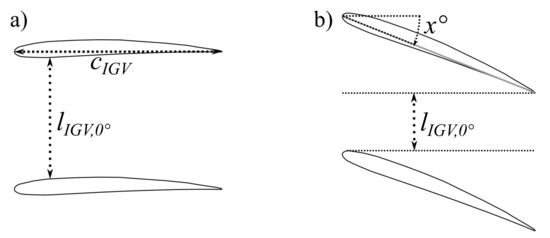
Figure 8.
Variation of the passage width with respect to the IGV stagger angle: (a) stagger angle and (b) stagger angle .
Table 2 provides the experimentally measured MS frequency , the experimental frequency ratio , and the theoretical frequency ratio for each IGV stagger angle from Equation (3). The use of frequency ratios suppresses the impact of choosing other geometrical dimensions on the calculation of the Helmholtz frequency. The selection of these other geometrical dimensions, especially the length, , is indeed not simple.

Table 2.
Experimental MS frequency, experimental MS frequency ratio, and theoretical MS frequency ratio at each IGV stagger angle.
At an IGV stagger angle of , the theoretical and experimental frequency ratios are very close. At an IGV stagger angle of , the theoretical ratio is around 25% lower than the experimental one. This discrepancy at an IGV stagger angle of is due to (i) wide partial gaps at the hub and shroud, and (ii) the decrease of the aerodynamic passage section due to thicker boundary layers. Nevertheless, the aforementioned two-dimensional modeling is consistent with the experimental evolution of the Helmholtz frequency as a function of the IGV stagger angle. This modeling reinforces the link between the stall pulsations and the Helmholtz frequency observed at an IGV stagger angle of .
The reasons for the occurence of this alternate stall are investigated in the following section. Flow fields obtained through numerical simulations are analyzed for this purpose because no such data are available experimentally. This analysis is only outlined at an IGV stagger angle of because the behavior of the alternate stall is independent of the IGV stagger angle according to experimental results (except for the pulsation frequency, which is discussed below in the case of numerical simulations).
3.2. Validation of Numerical Simulations
The total-to-static pressure ratio of the compressor stage and the static-to-static pressure ratio of the radial diffuser are plotted as functions of the standard mass flow rate in Figure 9. Data are drawn from tests, RANS simulations, and three converged URANS simulations.
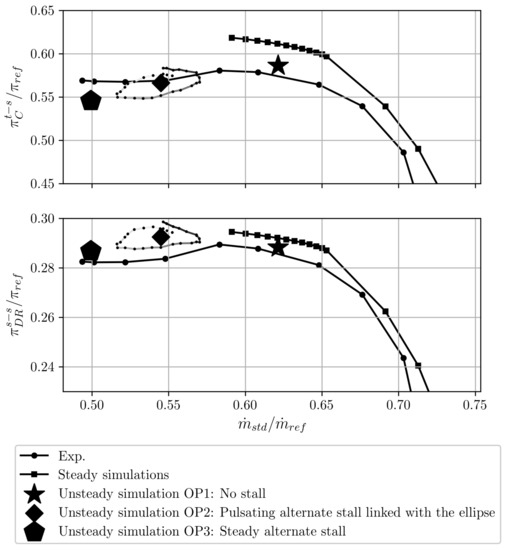
Figure 9.
Performance comparison between experimental and numerical data: total-to-static pressure ratio of the compressor stage (top) and static-to-static pressure ratio of the radial diffuser (bottom).
RANS simulations significantly overestimate the pressure ratio of the compressor stage, by around 6.3% at the maximum efficiency operating point. This overestimation is caused by: (i) the cut of shock waves by mixing planes (see [12]), and (ii) the inability of these simulations to detect an alternate stall on two channels in the radial diffuser. Furthermore, the surge mass flow rate predicted by RANS simulations is higher than the experimental one. This is due to the outlet boundary condition, which is a back pressure in the case of RANS simulations. Indeed, the latter condition cannot describe the positive slope of the characteristic curve. Therefore, RANS simulations are not considered in the following.
The first URANS simulation, OP1, is performed at the peak efficiency operating point according to experimental data. There is no significant stall at this operating point, and the simulation converges conventionally on the temporal period of the compressor.
A more throttled URANS simulation, OP2, displays a particular behavior: it converges on a temporal period equal to around eight impeller revolutions. This temporal period corresponds to a frequency of 71 Hz. During this period, the performance of the compressor draws an ellipse which is linked to the pulsation of the alternate stall in the radial diffuser at the same frequency. This numerical frequency is different from the experimental one (11 Hz; see Figure 5) because the environmental effects differ between experiments and numerical simulations. Despite this frequency difference, which is further explained below, the behavior of the alternate stall is qualitatively similar between experiments and numerical simulations. Therefore, the amplitude of the performance fluctuations and of the pressure fluctuations obtained numerically at OP2 are compared to the experimental ones below.
The OP3 URANS simulation near the experimental surge mass flow rate exhibits the alternate stall in the radial diffuser as well, however, the latter is now steady in the simulation, in contrast with OP2. This difference in behavior between the experimental and numerical results in OP3 is explained by the potential resonance of the alternate stall with environmental effects, as presented later.
3.2.1. OP2: Performance Fluctuations
The performance fluctuations at OP2 are due to the pulsation of the alternate stall in the radial diffuser, as shown below. These fluctuations in the simulation are unusually high. Therefore, their realism should be assessed by comparing them with experimental data.
The unsteady pressure ratio fluctuations of the IGV and the impeller put together are compared between experimental and numerical data in Table 3. The values are of the same order of magnitude. It has to be noted that neither the unsteady pressure ratio of the radial diffuser nor of the whole compressor can be calculated, because the unsteady pressure sensors are not numerous enough at the radial diffuser outlet.

Table 3.
Comparison of performance fluctuation amplitude at OP2 between experimental and numerical data.
Regarding mass flow rate fluctuations, they are not measured but rather recreated using the characteristic slope and pressure ratio fluctuations (quasi-stationary assumption). Again, Table 3 shows that the experimental and numerical values are similar.
The numerical performance fluctuations at OP2 can thus be considered realistic. A comparison of experimental and numerical pressure fluctuations occuring in the radial diffuser at OP2 can now be attained.
3.2.2. OP2: Pressure Fluctuations in the Radial Diffuser
As explained in the introduction, the MS in this compressor corresponds to the pulsation of the alternate stall on two channels in the radial diffuser. The pressure fluctuations at OP2 at the hub during an MS period are compared in Figure 10. These fluctuations are extracted during a single MS period in the simulation (the computational cost allows for the simulation of only a few MS periods), whereas they are averaged around 40 MS periods in the test. In both cases, the beginning of an MS period is arbitrarily set to the instant when the unsteady alternate rate is minimal.
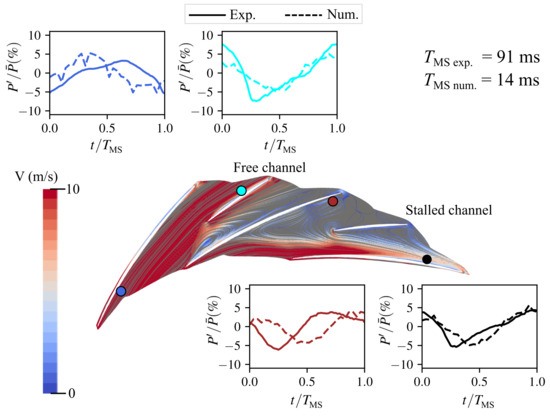
Figure 10.
Comparison of pressure fluctuations at the radial diffuser hub during an alternate stall period at OP2 between experimental and numerical data.
The streamlines computed from the average flow field (colored to represent their velocity) are plotted at the hub in the middle of Figure 10 to enable the visualization of the flow topology. It can be seen that the left channel is free and the right one is stalled.
The location of four unsteady pressure sensors is shown for this flow topology as well. At each sensor, the amplitude of pressure fluctuations, P, is similar between the experimental and numerical data. Therefore, the pressure fluctuations obtained numerically can be considered reliable.
3.3. Average Flow Topology Analysis
A flow topology analysis is now performed on these validated simulations in order to identify the root causes of the stall. The impact of the mass flow rate on the average flow topology is first analyzed; then, a 3D analysis of OP2 is performed, helping to determine the origins of the stall.
3.3.1. Change in the Average Flow Topology with Decreasing Mass Flow Rate
The change in the low Mach number zones (deduced from the average flow field) with the mass flow rate is illustrated in Figure 11. The isosurface at is plotted for the three operating points, OP1, OP2, and OP3, simulated and previously shown in Figure 9. Due to the flow alternate behavior at OP2 and OP3, this isosurface is plotted in two channels, a free channel and a stalled channel. The flow fields are viewed from the diffuser outlet (see the eye scheme at the upper right corner).
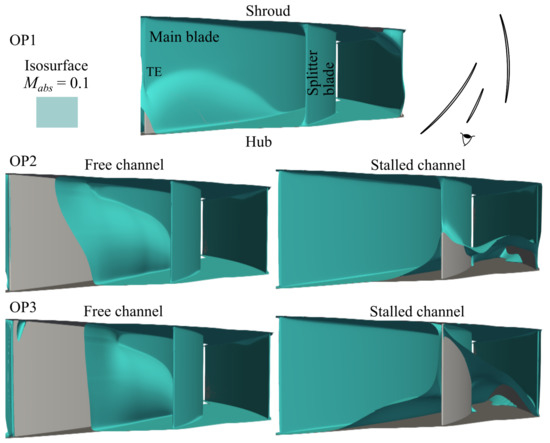
Figure 11.
Change in low Mach number zones with decreasing mass flow rate: isosurface viewed from the diffuser outlet.
At OP1, there are two low Mach number zones: (i) the corner pressure side of a main blade/hub from a third of the chord, and (ii) the corner suction side of a main blade/shroud from 60% of the chord.
OP2 and OP3 both exhibit low Mach number zones at the same locations, although they are wider at OP3 than OP2.
In the free channel, a low Mach number zone (i’) covers the pressure side of the main blade on the second half of the chord from hub to shroud. The extension of this zone does not significantly change from OP2 to OP3. This zone might originate from the extension upstream and towards the shroud of the low Mach number zone (i) in the corner pressure side of a main blade/hub at OP1.
In the stalled channel, a low Mach number zone (iii) begins in the corner suction side of the main blade/hub and expands farther than the splitter blade at OP2. This zone does not originate from a low Mach number zone observed at OP1. At OP3, this zone almost reaches the shroud at the splitter blade trailing edge. A large portion of the passage is therefore blocked.
These low Mach number zones are likely related to critical points. Therefore, an analysis of streamlines at first cells from the walls is performed to identify these critical points. The streamlines colored by the velocity at the hub are plotted for the three operating points in Figure 12. The streamlines at the shroud are not shown, because no interesting critical point could be identified there.

Figure 12.
Change in streamlines colored by the velocity at the hub with decreasing mass flow rate.
At OP1, the Focus Point (FP) related to the corner separation at the pressure side of a main blade/hub is near the trailing edge.
At OP2, the FP migrates upstream along the pressure side to around 15% of the chord in the free channel. In the stalled channel, a Saddle Point (SP) appears at around 30% of the chord in the corner suction side/hub. Although this SP does not exist at OP1, the friction lines already deviate from the suction side of the main blade. In the following, the blade located between these two critical points is called the stalled blade.
At OP3 the FP does not move compared to OP2, which is consistent with the observations previously made for the free channel in Figure 11. In the stalled channel, the SP migrates upstream towards around 20% of the chord.
As the flow topology is very similar between OP2 and OP3, the following analysis focuses on OP2, for which a 3D analysis is proposed.
3.3.2. 3D Analysis at OP2
There are 38 SPs and 32 FPs on two channels of the radial diffuser. Nevertheless, two main topological structures can be identified corresponding to the low Mach number zones previously shown in Figure 11: (i) the SP in the corner suction side/hub in the stalled channel, and (ii) the FP related to the corner separation at the pressure side of the stalled blade/hub in the free channel.
Figure 13 focuses on the average topological structure in the stalled channel. Figure 13a shows the friction lines colored by the velocity and the location of the important SP which marks the beginning of the low velocity zone. The view orientation is provided by the eye scheme at the upper left corner. Three 3D streamlines generated from the SP are plotted in Figure 13b. These streamlines are colored by the span height to make their 3D behavior easier to understand. The direction of the streamline starting at 60% of span height on the suction side is reversed at around 95% of the chord, and from this points it constitutes a separating line of the SP. A second stream line starting at 20% of span height on the suction side makes a u-turn at around 80% of the chord, does not go back to the SP, and moves away more quickly from the suction side before circumventing the splitter blade leading edge. Last, a third streamline remains stuck to the hub and moves towards the adjacent blade pressure side, where it delimits the low velocity zone in the stalled channel.
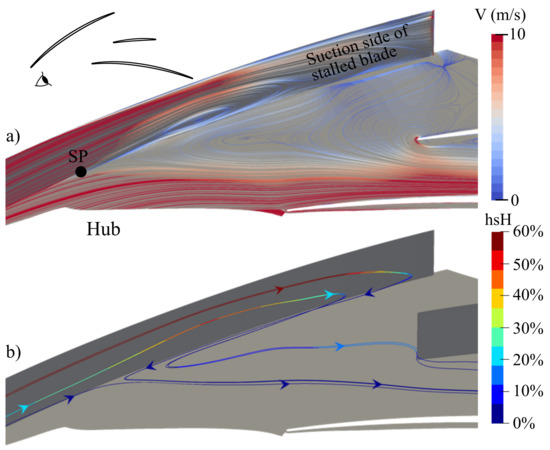
Figure 13.
Topological structure at the corner suction side of the stalled blade/hub in the stalled channel at OP2: (a) friction lines colored by the velocity and (b) 3D streamlines generated from the SP and colored by the span height.
The average topological structure in the free channel is shown in Figure 14. Figure 14a shows the friction lines colored by the velocity and the location of the important FP. A 3D streamline generated from the FP is colored by the span height in Figure 14b. The direction of this streamline shows that the FP is a reattachment one.
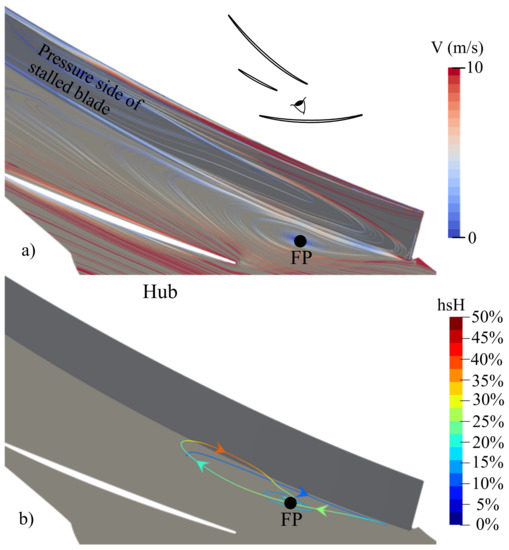
Figure 14.
Topological structure at the corner pressure side of the stalled blade/hub in the free channel at OP2: (a) friction lines colored by the velocity and (b) 3D streamlines generated from the FP and colored by the span height.
3.3.3. Origins of the Stall on Both Pressure and Suction Sides of a Blade
At OP2 and OP3, one main blade over two is stalled on both the pressure and suction sides. The flow at the diffuser inlet is well aligned with the main blade leading edge according to the URANS simulations. The stalls on both sides are therefore not due to an incidence issue.
For OP2, Figure 15 shows friction lines colored according to the velocity at the diffuser hub and a radial cut of the static pressure at the diffuser outlet. The stall on the suction side, which begins at the SP, is related to a high adverse pressure gradient. At the trailing edge of the stalled blade, near the hub, the flow moves from the suction side towards the pressure side as indicated by the black arrow. The fluid then moves upstream and reattaches at the FP. The stall on the pressure side is therefore due to the reversal of low-energy fluid coming from the suction side.
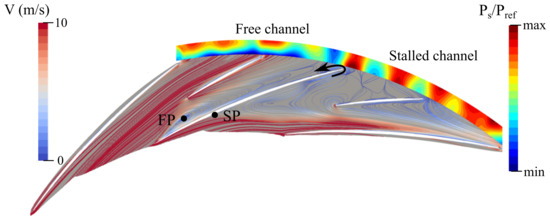
Figure 15.
Friction lines colored according to the velocity at the diffuser hub and the static pressure radial cut at the diffuser outlet at OP2.
3.4. Pulsating Alternate Flow Pattern at OP2
At OP2, the pressure fluctuations at the hub plotted in Figure 10 might be related to a pulsation of the alternate flow pattern in the simulation.
The isosurface colored by the span height is plotted during an MS period in Figure 16. The OP2 ellipse in the plane mass flow rate/total-to-static pressure ratio (already plotted in Figure 9) is recalled in the middle of Figure 16. As previously mentioned, this ellipse corresponds to an MS period of the compressor stage equal to approximately eight impeller revolutions (71 Hz). In Figure 16, each star symbol of the ellipse corresponds to the average performance over a compressor temporal period (one third of an impeller revolution). For eight of these compressor periods (highlighted with a black dot on the ellipse) the isosurface coloured by the span height is plotted. The stalled and free channels are pointed out at , and do not swap positions with each other for the rest of the MS period.
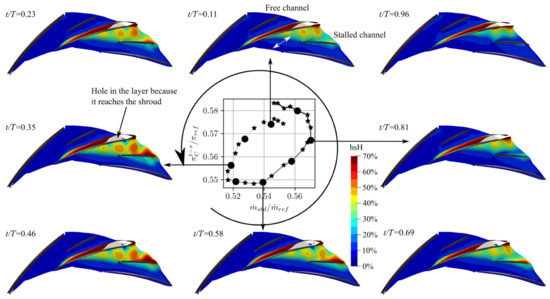
Figure 16.
Change in the isosurface colored by the span height during an alternate stall period at OP2.
In the stalled channel, the low Mach number zone is located in the corner suction side of the stalled blade/hub, as in the average flow field (see the stalled channel at OP2 in Figure 11). The upstream limit of this zone fluctuates during the MS period, as indicated with the white double arrow at . This limit is located the furthest downstream when the pressure ratio is at its maximum at , whereas it is the furthest upstream when the pressure ratio is at its minimum at . This migration is strongly related to that of the SP, previously shown in Figure 13. At , it should be noted that the low Mach number zone spreads over as much as 50% of the span at certain locations.
3.4.1. Assumption of Breathing Stall in URANS Simulation
The reason for this alternate pattern pulsation in the numerical simulation is now investigated. The first intuitive assumption is the occurence of a Helmholtz resonance, as in the test rig; however, (i) the domain volume downstream of the outlet guide vanes is too small to form a Helmholtz resonator, and (ii) additional numerical simulations (not shown in this article) reveal that the pulsation frequency does not depend on the IGV stagger angle, which is not consistent with experimental results (see Figure 7). These two points prove the Helmholtz resonance assumption to be false.
Another hypothesis is that the pulsation of this alternate pattern is related to the breathing of the separation bubble. Weiss et al. [13] and Mohammed-Taifour et al. [14] studied the unsteady behavior of a separation bubble due to an adverse pressure gradient. The unsteadiness of the separation bubble related to its breathing occurs at a Strouhal number of around 0.01. Here, the Strouhal number (calculated with the same methodology) is equal to 0.03. Although this similar order of magnitude indicates that the alternate pattern pulsation might correspond to the breathing of the separation bubble in the stalled channel, it could be argued that turbulence modeling in URANS simulation might not be able to grasp this breathing. Therefore, the presence of acoustic waves in the numerical domain is checked in the following.
3.4.2. Reflection of Acoustic Waves on the Inlet and Outlet Planes
The frequency content of the static pressure fluctuations registered during an MS period at the shroud is plotted along the meridional abscissa in Figure 17.

Figure 17.
Frequency content of static pressure fluctuations at the shroud during an MS period at OP2: (a) evolution in the meridional plane and (b) spectra at meridional abscissa I, II, and III.
In Figure 17a, the static pressure fluctuations are very high from the radial diffuser leading edge to the domain outlet, with a frequency band spreading in the range between 55 and 85 Hz. These fluctuations contain nodes and anti-nodes which indicate the reflection of acoustic waves on the outlet plane. The pulsation frequency of the alternate stall is around 71 Hz, corresponding to the middle of the frequency band, which is large because only one period of the alternate stall is considered for the calculation of the Fourier transform. The reflection of the acoustic waves on the outlet plane is therefore linked to the pulsation of the alternate stall.
Because of the low frequency of these fluctuations, it might be an acoustic planar mode, which which according to Bontemps [15] could travel upstream. Figure 17b shows the spectra of static pressure fluctuations at locations I, II, and III, which are plotted with vertical dotted lines in Figure 17a. At each location, the frequency of 71 Hz is observed, meaning that the acoustic waves exist from the inlet plane to the radial diffuser leading edge. These waves are not visible in Figure 17a because the amplitudes are too low.
In a nutshell, acoustic waves at 71 Hz are present in the whole simulated domain; they reflect off the inlet and the outlet planes and resonate with the alternate stall in the radial diffuser.
3.4.3. Two Different Resonators: Helmholtz Mode in the Experiments versus Acoustic Planar Mode in the Numerical Simulations
The environmental influence on the resonance of the alternate stall pulsation is depicted in Figure 18. It shows the magnitude spectrum related to the breathing of a separation bubble according to the work of Weiss et al. [13]. The experimental and numerical frequencies of the pulsation are respectively plotted in green and pink. While the frequencies differ by a factor of 6, both are within the frequency range in which breathing of the separation bubble may occur. The separation breathing might catch on the Helmholtz frequency during the test and on the frequency of reflected acoustic waves during the simulation.
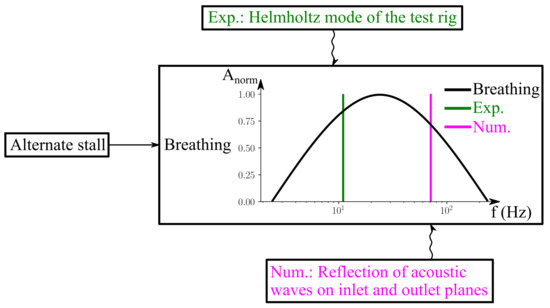
Figure 18.
Resonator difference for alternate stall pulsation between experiments and numerical simulations.
4. Discussion
Previous work [4] has reported a pulsating alternate flow pattern on two channels in the radial diffuser of a research centrifugal compressor stage designed by SafranHE. This pulsation occurred at the Helmholtz frequency of the test rig.
The present experimental and numerical study draws the following conclusions:
- Variation of the IGV stagger angle only impacts the pulsation frequency of the alternate flow pattern in the tests. This is explained by the dependence of the Helmholtz frequency on the compressor inlet section.
- Thanks to a topological analysis of the average flow field (computed from URANS simulation) on two radial diffuser adjacent channels, it is observed that the SP (major critical point) in the corner hub/suction side of the stalled blade migrates upstream while staying in the corner if the mass flow rate decreases. One main blade over two is stalled on both sides because the flow originating from this corner separation circumvents the trailing edge and migrates upstream along the pressure side.
- Although the same phenomenon occurs in both the experiment and the numerical simulation, the pulsation frequency of the alternate flow pattern is different. The experimental pulsation is related to the Helmholtz mode of the compressor on the test rig. The numerical pulsation occurs with the reflection of acoustic waves on the inlet and the outlet planes of the simulated domain.
Three research prospects are identified:
- A coupled CFD simulation, 1D for the test rig and 3D for the compressor stage, might predict the same frequency pulsation of the alternate flow as in the tests.
- URANS turbulence models are deemed to be inaccurate in stalled areas. Therefore, a wall-resolved Large Eddy Simulation (LES) might provide a better description of the flow in stalled areas. However, it should be noted that this simulation is not easily affordable because the mesh should contain at least several billions of cells.
- Finally, stall control using boundary layer suction might extend the operating range of the compressor. These tests will be carried out in 2022 within the framework of the European FLORA project.
Author Contributions
N.P.: methodology, formal analysis, investigation, writing—original draft preparation; M.B.: writing-review and editing; P.D.: writing—review and editing, supervision; I.T.: writing—review and editing, supervision, funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This project has received funding from the Clean Sky 2 Joint Undertaking under the European Union’s Horizon 2020 research and innovation programme under grant agreement N°820099. This publication reflects only the author’s view, and the JU is not responsible for any use that may be made of the information it contains.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank SAFRAN Helicopter Engines which supported this study. Pierre Laucher, Sebastien Goguey, Gilbert Halter and Benoit Paoletti are kindly thanked for manufacturing the test bench and supporting the measurements.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Latin Symbols | |
| A | Alternate rate |
| Mass flow | |
| p | Pitch |
| P | Pressure |
| r | Radius |
| V | Absolute velocity |
| W | Relative velocity |
| Greek Symbols | |
| Pressure ratio | |
| IGV stagger angle | |
| Rotation speed | |
| Circumferential direction | |
| Subscripts | |
| ref | Reference (value) |
| std | Standard |
| 0 | IGV inlet |
| 1 | IMP inlet |
| 2 | RD inlet |
| 3 | RD outlet |
| Superscripts | |
| s-s | Static-to-static |
| t | Total |
| t-s | Total-to-static |
| Abbreviations | |
| C | Compressor (IGV + IMP + RD) |
| CCRT | Centre de Calcul Recherche et Technologie |
| FP | Focus Point |
| IGV | Inlet Guide Vane |
| IMP | Impeller |
| LES | Large Eddy Simulation |
| MS | Mild Surge |
| ONERA | Office National d’Etudes et de Recherches Aérospatiales |
| OGV | Outlet Guide Vane |
| RD | Radial Diffuser |
| RANS | Reynolds-Averaged Navier–Stokes |
| SafranHE | Safran Helicopter Engines |
| SP | Saddle Point |
| URANS | Unsteady Reynolds-Averaged Navier–Stokes |
Appendix A. Links between the Centrifugal and Coriolis Forces and the Work Input
Euler’s Equation (A1) includes two terms, the deflection work due to the blades, and work which appears similar to the centrifugal force work. However, the following argumentation derived from Trébinjac’s turbomachinery course proves that this work actually originates from the Coriolis force.
Figure A1 shows forces acting on the fluid in the plane () and a meridional view with the definition of the angle .
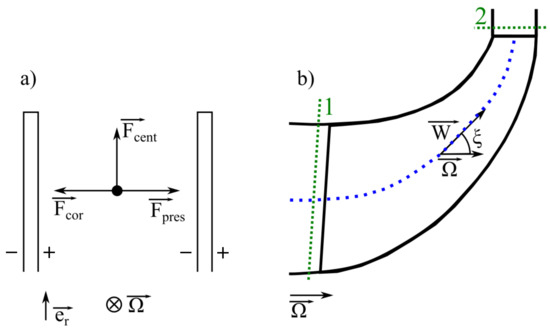
Figure A1.
Scheme of forces in (a) centrifugal impeller and (b) frame.
Appendix A.1. Analysis in the Circumferential Direction
The centrifugal force does not produce work along the circumferential direction because it is collinear to the radial direction.
The circumferential component of the elementary Coriolis force acting on a fluid element with a mass is
The related work is
and
It is assumed that the relative velocity is included in the meridional plane, as follows:
The mathematical integration provides:
The change in stagnation enthalpy related to Coriolis force is:
The term in Euler’s Equation (A1) is therefore due to the work related to the Coriolis force.
Appendix A.2. Analysis in the Rotating Frame of Reference
In the rotating frame of reference, the Coriolis force does not produce work because it is orthogonal to the relative velocity . The centrifugal force is collinear to the relative velocity and the related work is:
The rothalpy is preserved in the rotating frame of reference:
Therefore,
The change in radius leads to an energy transfer from the centrifugal force to a pressure increase.
Appendix A.3. Summary of Forces’ Roles
The sources of work input and pressure increase are compared between axial and centrifugal geometries in Table A1.

Table A1.
Comparison of sources of work input and pressure increase between axial and centrifugal geometries.
Table A1.
Comparison of sources of work input and pressure increase between axial and centrifugal geometries.
| Geometry Type | Work | Pressure Increase |
|---|---|---|
| Axial | Deflection | Decrease of relative velocity W |
| Centrifugal | Deflection and Coriolis force | Decrease of relative velocity W and centrifugal force |
References
- Fink, D.A.; Cumpsty, N.A.; Greitzer, E.M. Surge dynamics in a free-spool centrifugal compressor system. J. Turbomach. 1992, 114, 321–332. [Google Scholar] [CrossRef]
- Galindo, J.; Serrano, J.R.; Climent, H.; Tiseira, A. Experiments and modelling of surge in small centrifugal compressor for automotive engines. Exp. Therm Fluid Sci. 2008, 32, 818–826. [Google Scholar] [CrossRef]
- Zheng, X.; Liu, A. Phenomenon and mechanism of two-regime-surge in a centrifugal compressor. J. Turbomach. 2015, 137, 081007. [Google Scholar] [CrossRef]
- Moënne-Loccoz, V.; Trébinjac, I.; Poujol, N.; Duquesne, P. Detection and analysis of an alternate flow pattern in a radial vaned diffuser. Int. J. Turbomach. Propuls. Power 2020, 5, 2. [Google Scholar] [CrossRef] [Green Version]
- Moënne-Loccoz, V.; Trébinjac, I.; Poujol, N.; Duquesne, P. Low frequency stall modes of a radial vaned diffuser flow. Mech. Ind. 2019, 20, 805. [Google Scholar] [CrossRef]
- Sano, T.; Nakamura, Y.; Yoshida, Y.; Tsujimoto, Y. Alternate Blade Stall and Rotating Stall in a Vaned Diffuser. JSME Int. J. Ser. B Fluids Therm. Eng. 2002, 45, 810–819. [Google Scholar] [CrossRef] [Green Version]
- Pedersen, N.; Larsen, P.S.; Jacobsen, C.B. Flow in a Centrifugal Pump Impeller at Design and Off-Design Conditions—Part I: Particle Image Velocimetry (PIV) and Laser Doppler Velocimetry (LDV) Measurements. J. Fluids Eng. 2003, 125, 61–72. [Google Scholar] [CrossRef]
- Poujol, N.; Trébinjac, I.; Duquesne, P. Effects of Inlet Guide Vanes on the Performance and Stability of an Aeronautical Centrifugal Compressor. J. Turbomach. 2021, 143, 101010. [Google Scholar] [CrossRef]
- Cambier, L.; Gazaix, M.; Heib, S.; Plot, S.; Poinot, M.; Veuillot, J.P.; Boussuge, J.F.; Montagnac, M. An Overview of the Multi-Purpose elsAFlow Solver; Aerospace Lab.: Palaiseau, France, 2011; pp. 1–15. [Google Scholar]
- Délery, J. Three-Dimensional Separated Flow Topology: Critical Points, Separation Lines and Vortical Structures; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Duquesne, P.; Chanéac, J.; Mondin, G.; Dombard, J. Guidelines for flow separation analysis in turbomachinery. Int. J. Turbomach. Propuls. Power 2022. under review. [Google Scholar] [CrossRef]
- Benichou, E.; Trébinjac, I. Application of an analytical method to locate a mixing plane in a supersonic compressor. J. Energy Power Eng. 2015, 9, 91–101. [Google Scholar]
- Weiss, J.; Mohammed-Taifour, A.; Schwaab, Q. Unsteady Behavior of a Pressure-Induced Turbulent Separation Bubble. AIAA J. 2015, 53, 2634–2645. [Google Scholar] [CrossRef]
- Mohammed-Taifour, A.; Weiss, J. Unsteadiness in a large turbulent separation bubble. J. Fluid Mech. 2016, 799, 383–412. [Google Scholar] [CrossRef]
- Bontemps, T. Flottement Fan et Couplage Acoustique: Analyse et Modélisation. Ph.D. Thesis, École Centrale de Lyon, Écully, France, 2020. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).