Impact of Leakage Inlet Swirl Angle in a Rotor–Stator Cavity on Flow Pattern, Radial Pressure Distribution and Frictional Torque in a Wide Circumferential Reynolds Number Range ^†

Abstract

In the side-chambers of radial turbomachinery, which are rotor–stator cavities, complex flow patterns develop that contribute substantially to axial thrust on the shaft and frictional torque on the rotor. Moreover, leakage flow through the side-chambers may occur in both centripetal and centrifugal directions which significantly influences rotor–stator cavity flow and has to be carefully taken into account in the design process: precise correlations quantifying the effects of rotor–stator cavity flow are needed to design reliable, highly efficient turbomachines. This paper presents an experimental investigation of centripetal leakage flow with and without pre-swirl in rotor–stator cavities through combining the experimental results of two test rigs: a hydraulic test rig covering the Reynolds number range of $4\times {10}^5\le Re\le 3\times {10}^6$ and a test rig for gaseous rotor–stator cavity flow operating at $2\times {10}^7\le Re\le 2\times {10}^8$. This covers the operating ranges of hydraulic and thermal turbomachinery. In rotor–stator cavities, the Reynolds number $Re$ is defined as $Re=\mathsf{\Omega }\raisebox{1ex}{$b^2$}\!\left/ \!\raisebox{-1ex}{$\nu $}\right.$ with angular rotor velocity $\mathsf{\Omega }$, rotor outer radius b and kinematic viscosity $\nu$. The influence of circumferential Reynolds number, axial gap width and centripetal through-flow on the radial pressure distribution, axial thrust and frictional torque is presented, with the through-flow being characterised by its mass flow rate and swirl angle at the inlet. The results present a comprehensive insight into the flow in rotor–stator cavities with superposed centripetal through-flow and provide an extended database to aid the turbomachinery design process.

1. Introduction

In rotor–stator cavities, which are found in all radial turbomachines, complex flow patterns occur and influence axial thrust on the shaft as well as disc-friction torque. During the design phase of radial turbomachinery, to design axial bearings reliably we have to know the maximum axial thrust on the shaft with sufficient precision. Moreover, if the geometry of the cavities is designed carefully, losses due to friction can be minimised and efficiency maximised.

The first thorough experimental study of turbulent rotor–stator cavity flow was conducted by Daily and Nece [1], who designed a test rig able to reach Reynolds numbers up to $Re={10}^7$. Based on their torque and velocity distribution measurements, they identify two turbulent flow regimes in which rotor and stator boundary layers are either merged or separated. When these layers are separated, velocity measurements indicate the existence of a fluid core in the cavity middle, where radial velocity is negligible and circumferential velocity varies only with radius, not with axial coordinate. The existence of these flow regimes depends on circumferential Reynolds number $Re$ and relative axial gap width, defined as the ratio of axial gap width to disc outer radius. They also provide empirical correlations for the torque coefficient $c_M$ for each flow regime, allowing turbomachinery designers to estimate disc torque and machine efficiency during the design phase.

In [2], models for rotor–stator cavity flow with through-flow are introduced which are based on assumed velocity profiles and wall shear stress measurements. The models allow for the calculation of radial pressure distribution and axial thrust for the cases of closed cavity and centripetal through-flow. Additionally, in the through-flow case, they take into account the angular momentum flux into the cavity. This paper tests the validity of these models at a large Reynolds number range.

Radtke and Ziemann [3] experimentally investigated not only closed rotor–stator cavities, but also centripetal and centrifugal through-flow with and without preswirl alongside variations of the cavity geometry. We compare our measurement results to theirs.

Poncet et al. [4] investigated turbulent flow with separated boundary layers in a rotor–stator cavity with and without centripetal through-flow in the Reynolds number range of $1.04\times {10}^6\le Re\le 4.2\times {10}^6$ at relative cavity widths of $0.024\le G\le 0.048$. In their paper, Laser Doppler Anemometry measurements of core swirl ratio are compared to predictions based on measurements of radial pressure distribution. Using the $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$7$}\right.$ power law for the boundary layer velocity profiles, they derived a theoretical model for the core swirl ratio $K\left(r\right)$ which is calibrated using the measurement results. The validity of their model is reported for a wide range of Reynolds numbers and through-flow mass fluxes.

Poncet et al. [5] proposed a new Reynolds stress turbulence model suitable for numerical investigations of rotor–stator cavity flow that is reported to be superior to k-$\epsilon$ turbulence models for this application. They investigated the mean flow structure, the core swirl ratio, the radial pressure distribution and turbulence statistics for closed cavities, and centripetal as well as centrifugal through-flow. Their paper gives a comprehensive summary of flow structures with separated boundary layers inside rotor–stator cavities.

Will [6] investigated centripetal and centrifugal flow in a rotor–stator cavity, using analytical, experimental and numerical methods. He developed a new one-dimensional flow model of core swirl ratio, assuming separated boundary layers and using the logarithmic law of the wall.

Wang et al. [7] performed particle image velocimetry measurements in a water-filled microscale rotor–stator cavity made of glass with smooth compared to hydrophobic discs at low Reynolds numbers. They found a reduction of torque of more than 50% when using hydrophobic rotors, which was attributed to a thin air layer between disc and liquid in the case of hydrophobic rotor surfaces and to a reduction of turbulence intensity.

In the present study, experimental results of two rotor–stator test rigs are combined to study how disc torque, radial pressure distribution and axial thrust are influenced by Reynolds number, cavity width, centripetal through-flow and angular momentum flux into the cavity. The small test rig is operated with water, can be equipped with different discs with an outer radius of $b=110 \mathrm{m}\mathrm{m}$ each and is made of PMMA (Plexiglass). It covers a Reynolds number range of $3.8\times {10}^5\le Re\le 3.2\times {10}^6$ and an axial gap width range of $0.0182\le G\le 0.0728$. A more detailed description can be found in [8,9,10]. The large test rig, first introduced by Barabas et al. [11], can reach Reynolds numbers up to $Re=2.5\times {10}^8$ since it has a large disc radius and is operated with carbon dioxide. Relative gap widths of $0.0125\le G\le 0.0375$ are investigated in this test rig. Both rigs allow the superimposition of centripetal through-flow with different inlet swirl angles. Only corotating inlet swirl is investigated.

2. Rotor–Stator Cavity Test Rigs, Measurement Procedures and Uncertainty Calculation

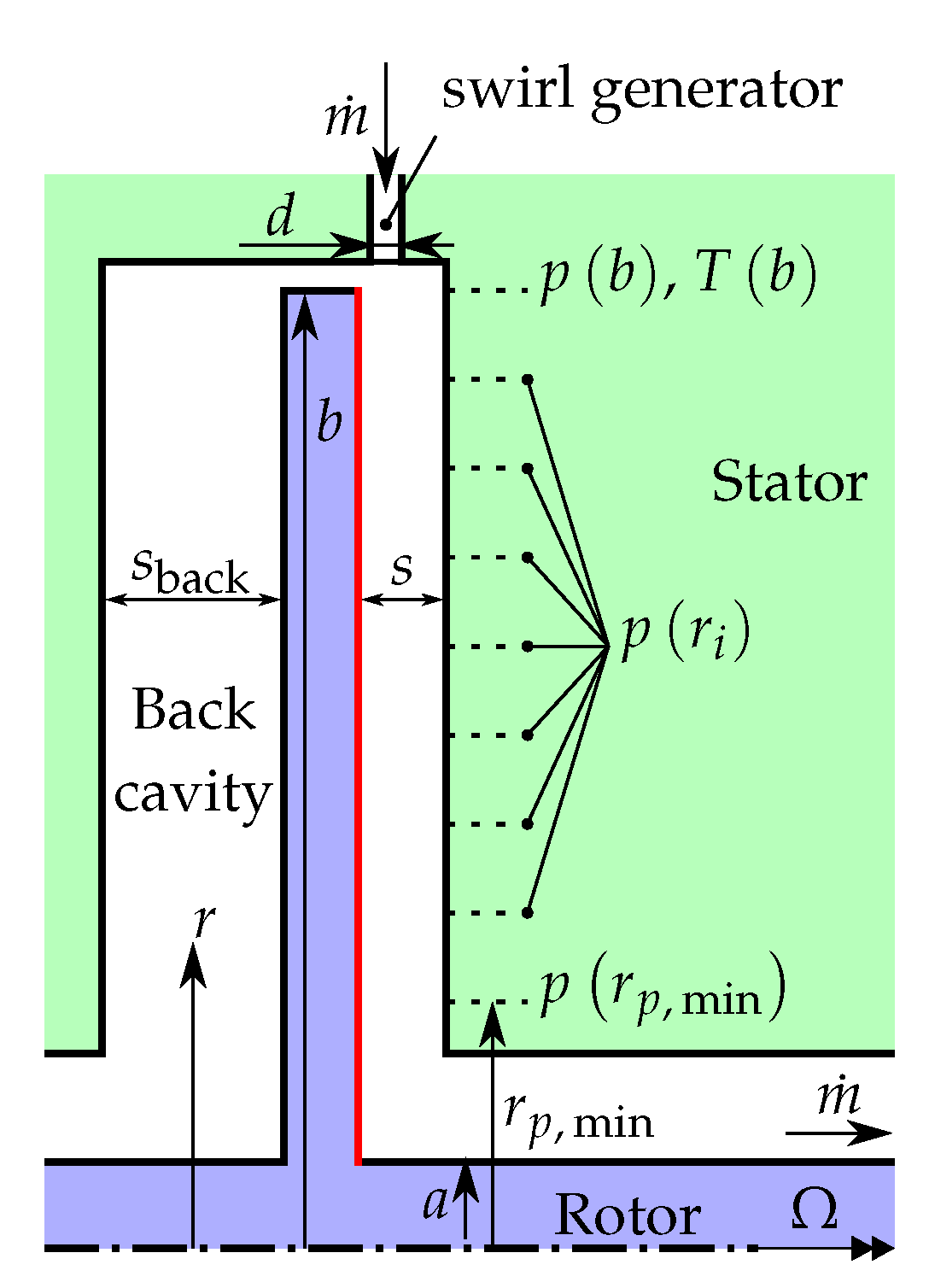
A schematic of the large rotor–stator test rig used in this study is given in Figure 1. The rotor has angular velocity $\mathsf{\Omega }$, outer radius b and hub radius a. Cavity width is given by distance s. Through-flow with mass flow rate $\dot{m}$ enters the cavity through a centripetal swirl generator, which has inlet width d, and exits axially at the hub. Swirl generators are changed to create through-flow with different inlet swirl angles $\alpha$. In the case of a closed cavity, the swirl generator is replaced by a ring structure, resulting in a cylindrical shroud without any opening. The rig is cooled by water to remove the heat generated by fluid friction.

A detailed drawing of the small test rig can be seen in ([10], Figure 33), including the sensors used. It is constructed similarly to the large test rig but does not have a hub in its front cavity. Additionally, it does not need to be cooled.

To determine the axial force resulting from the radial pressure distribution in the front cavity of the small test rig, the following measurement technique was used; greater detail is given in [10]. Tension–compression force transducers and a linear ball bearing are used to measure the axial thrust on the rotor and the shaft. The sum of the axial forces on both parts is given by

$$F_{\mathrm{a}}=F_{\mathrm{ab}}-F_{\mathrm{af}}=\underset{A_{\mathrm{b}}}{\int }{p}_{\mathrm{b}}\left(r\right)\mathrm{d}A-\underset{A_{\mathrm{f}}}{\int }{p}_{\mathrm{f}}\left(r\right)\mathrm{d}A=-\pi a^{2}p\left(b\right)-\pi {\mathsf{\Omega }}^2\rho \left[c_{F\mathrm{b}}\left[b^4-a^4\right]-c_{F\mathrm{f}}{b}^4\right]$$

(1)

where $F_{\mathrm{a}}$ is the axial force measured by tension–compression force transducers, and $F_{\mathrm{ab}}$ and $F_{\mathrm{af}}$ are the axial forces due to the pressure $p_{\mathrm{b}}$ in the back and the pressure $p_{\mathrm{f}}$ in the front cavity, respectively. The radial pressure distribution in the back and front cavity is characterised by the axial thrust coefficients $c_{F\mathrm{b}}$ and $c_{F\mathrm{f}}$, respectively, which are defined as

$$\begin{array}{cc}\hfill c_{F\mathrm{b}}& =\frac{\pi \left[b^2-a^2\right]p\left(r=b\right)-F_{\mathrm{ab}}}{\pi \rho {\mathsf{\Omega }}^2\left[b^4-a^4\right]}\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill c_{F\mathrm{f}}& =\frac{\pi b^{2}p\left(r=b\right)-F_{\mathrm{af}}}{\pi \rho {\mathsf{\Omega }}^2{b}^4}.\hfill \end{array}$$

(3)

In the case of a closed cavity without through-flow and equal widths of the front and back cavity ($s=s_{\mathrm{back}}$), identical flow structures in the front and back cavity are assumed, which leads to the assumption $c_{F\mathrm{b}}=c_{F\mathrm{f}}$. In this test rig configuration, the axial thrust coefficient

$$c_{F\mathrm{b}}=\frac{F_{\mathrm{a}}+\pi a^{2}p\left(r=b\right)}{\pi \rho {\mathsf{\Omega }}^2{a}^4}$$

(4)

of the back cavity is calculated from measurements of the net axial thrust $F_{\mathrm{a}}$. The measured coefficient $c_{F\mathrm{b}}$ is transformed into a correlation, which is then used to calculate the axial thrust coefficients $c_{F\mathrm{f}}$ in the front cavity from net axial force $F_{\mathrm{a}}$ measurements using Equation (1) in different test rig configurations.

The large test rig has nine taps to measure radial pressure distribution, to which differential pressure transducers are connected to measure the pressure differences $p\left(r=b\right)-p\left(r_i\right)$ directly (see Figure 1). In addition, temperature and absolute pressure are measured at the outer radius b. From these measurements, density $\rho$ and kinematic viscosity $\nu$ are calculated. The radial pressure distribution in the small test rig is measured at twelve distinct radial positions; density and kinematic viscosity are assumed to be constant [10]. The pressure coefficient

$$c_p\left(r\right)=\frac{p\left(r=b\right)-p\left(r\right)}{\rho {\mathsf{\Omega }}^2{b}^2}$$

(5)

is a dimensionless measure of static pressure $p\left(r\right)$ relative to that at disc outer radius b.

The axial thrust coefficient $c_F$ can be calculated using the pressure coefficient $c_p$ by

$$c_F=\frac{2}{b^2-r_{p,\min }^2}\underset{r_{p,\min }}{\overset{b}{\int }}{c}_p\left(r\right)r \mathrm{d}r$$

(6)

and this procedure is employed for the large test rig. The minimal pressure measurement radius is denoted by $r_{p,\min }$ (see Figure 1). The integral is approximated using the trapezoidal rule, i.e., pressure coefficient $c_p$ is assumed to vary linearly with the radius r between two adjacent pressure measurement taps.

The torque coefficient

$$c_M=2\frac{M_{\mathrm{front}}}{\rho {\mathsf{\Omega }}^2{b}^5}$$

(7)

measures the fluid friction torque $M_{\mathrm{front}}$ on the front-facing side of the disc, indicated by a red line in Figure 1. It is calculated as follows for both test rigs (see [10]): the overall torque $M_{\mathrm{all}}$ is measured between the motor and the coupling, and includes the friction torque $M_{\mathrm{friction}}$ generated by the bearings and the fluid friction on the shaft. The fluid friction in the back cavity is modelled by a correlation, $c_{M,\mathrm{back}}$, and the friction on the cylindrical outer rotor surface is given by the correlation $c_{M,\mathrm{cylindrical}}$. This leads to

$$c_M=2\frac{M_{\mathrm{all}}-M_{\mathrm{friction}}\left(\rho ,\mathsf{\Omega }\right)}{\rho {\mathsf{\Omega }}^2{b}^5}-c_{M,\mathrm{back}}-c_{M,\mathrm{cylindrical}}$$

(8)

where $M_{\mathrm{friction}}\left(\rho ,\mathsf{\Omega }\right)$ is a correlation derived from measurements with no disc installed. In the large test rig, this is conducted at different CO₂ pressure levels p and the shaft rotating at varying angular velocities $\mathsf{\Omega }$. In the small test rig, only the angular velocity $\mathsf{\Omega }$ is varied [10].

The correlation $c_{M,\mathrm{back}}$ is found by setting the front and back cavity widths equal, $s=s_{\mathrm{back}}$, with the test rigs in the closed cavity configuration and by assuming $c_{M,\mathrm{back}}=c_{M,\mathrm{front}}$. The overall torque $M_{\mathrm{all}}$ at varying angular velocities $\mathsf{\Omega }$ and pressure levels p in the large test rig is measured, then $c_{M,\mathrm{back}}$ is found from

$$2c_{M,\mathrm{back}}=2\frac{M_{\mathrm{all}}-M_{\mathrm{friction}}\left(\rho ,\mathsf{\Omega }\right)}{\rho {\mathsf{\Omega }}^2{b}^5}-c_{M,\mathrm{cylindrical}}.$$

(9)

In [3], a correlation $c_{M,\mathrm{cylindrical}}$ is given which predicts the friction on the cylindrical outer rotor surface in rotor–stator cavities. It is assumed that this correlation holds for the friction on this surface in the large test rig, although extrapolation to Reynolds numbers higher than those investigated by Radtke and Ziemann [3] is required. This correlation is used in the torque coefficient calculation in the large test rig case. The friction on the cylindrical outer rotor surface is neglected in the small test rig [10].

For the large test rig, the calculation of torque coefficient uncertainties includes measurement uncertainties for the following quantities: overall torque $M_{\mathrm{all}}$, breakaway torque, temperature T, absolute static pressure p, angular rotor velocity $\mathsf{\Omega }$ and manufacturing tolerances. The uncertainty of the correlation $c_{M,\mathrm{cylindrical}}$ is not known and not included in the calculation, meaning that the torque coefficient uncertainties calculated here provide a lower bound; in reality they may be higher. To calculate these uncertainties, the first-order error propagation method is used as presented in [12]. Uncertainties of measurements in the small test rig are taken from [10].

The curve fit and model parameter uncertainty calculations are carried out as presented in [13]; the method is briefly summarised here. Let $\mathbf{x}={\left(x_1,\cdots ,x_n\right)}^T$ be a column vector of measured values with associated covariances $u\left(x_i,x_j\right)$ and $\mathbf{y}={\left(y_1,\cdots ,y_m\right)}^T$ be a column vector of unknown model parameters. The column vector of model equations is given by $\mathbf{M}\left(\mathbf{x},\mathbf{y}\right)=0$. The measured values $\mathbf{x}$ will most likely not fulfil the model $\mathbf{M}\left(\mathbf{x},\mathbf{y}\right)=0$ for any vector of model parameters $\mathbf{y}$; therefore, the vector $\mathbf{x}$ is replaced by a column vector $\mathbf{z}={\left(z_1,\cdots ,z_n\right)}^T$ of free parameters that should fulfil the model equations $\mathbf{M}\left(\mathbf{z},\mathbf{y}\right)=0$ while minimising the squared error norm ${\chi }^2$. This error norm assigns a high weight to measurement results with low uncertainties and vice versa. The problem is solved, using a column vector $\mathbf{b}$ of Lagrange multipliers, for the unknown column vector $\mathbf{w}={\left({\mathbf{b}}^T,{\mathbf{y}}^T,{\mathbf{z}}^T\right)}^T$ by finding a Karush–Kuhn–Tucker point ${\mathbf{w}}^{*}$ of the Lagrange function

$$\mathcal{L}\left(\mathbf{x},\mathbf{w}\right)=\frac{1}{2}{\chi }^2+{\mathbf{M}}^T\left(\mathbf{z},\mathbf{y}\right)·\mathbf{b}=\frac{1}{2}{\left[\mathbf{z}-\mathbf{x}\right]}^T·{\mathbf{U}}_{xx}^{-1}·\left[\mathbf{z}-\mathbf{x}\right]+{\mathbf{M}}^T\left(\mathbf{z},\mathbf{y}\right)·\mathbf{b}.$$

(10)

Here, ${\left({\mathbf{U}}_{xx}\right)}_{ij}=u\left(x_i,x_j\right)$ are components of the matrix ${\mathbf{U}}_{xx}$ of measurement covariances. The Karush–Kuhn–Tucker conditions for this problem, which are solved for $\mathbf{w}$, read

$${\mathbf{M}}^{*}\left(\mathbf{x},\mathbf{w}\right)=\left(\begin{array}{c}\frac{\partial \mathcal{L}}{\partial \mathbf{b}}\left(\mathbf{x},\mathbf{w}\right)\\ \frac{\partial \mathcal{L}}{\partial \mathbf{y}}\left(\mathbf{x},\mathbf{w}\right)\\ \frac{\partial \mathcal{L}}{\partial \mathbf{z}}\left(\mathbf{x},\mathbf{w}\right)\end{array}\right)=\left(\begin{array}{c}\mathbf{M}\left(\mathbf{z},\mathbf{y}\right)\\ \frac{\partial {\mathbf{M}}^T}{\partial \mathbf{y}}\left(\mathbf{z},\mathbf{y}\right)·\mathbf{b}\\ \mathbf{z}-\mathbf{x}+{\mathbf{U}}_{xx}·\frac{\partial {\mathbf{M}}^T}{\partial \mathbf{z}}\left(\mathbf{z},\mathbf{y}\right)·\mathbf{b}\end{array}\right)=0.$$

(11)

A solution ${\mathbf{w}}^{*}$ to these conditions includes the vector ${\mathbf{y}}^{*}$ of optimal model parameters.

The covariances $u\left(w_i^{*},w_j^{*}\right)$, including the covariances $u\left(y_i^{*},y_j^{*}\right)$ of optimal model parameters ${\mathbf{y}}^{*}$, are derived by first order error propagation and are given by

$$\begin{array}{cc}\hfill {\mathbf{U}}_{w^{*}{w}^{*}}& =\mathbf{Q}\left(\mathbf{w}={\mathbf{w}}^{*}\right)·{\mathbf{U}}_{xx}·{\mathbf{Q}}^T\left(\mathbf{w}={\mathbf{w}}^{*}\right)\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill \mathbf{Q}\left(\mathbf{w}\right)& =-{\left[\frac{\partial {\mathbf{M}}^{*}}{\partial \mathbf{w}}\left(\mathbf{x},\mathbf{w}\right)\right]}^{-1}·\frac{\partial {\mathbf{M}}^{*}}{\partial \mathbf{x}}\left(\mathbf{x},\mathbf{w}\right).\hfill \end{array}$$

(13)

Here, ${\left({\mathbf{U}}_{w^{*}{w}^{*}}\right)}_{ij}=u\left(w_i^{*},w_j^{*}\right)$ are the components of the matrix ${\mathbf{U}}_{w^{*}{w}^{*}}$ of covariances of the vector ${\mathbf{w}}^{*}$. The standard uncertainties $u\left(y_i^{*}\right)$ are then given by $u\left(y_i^{*}\right)=\sqrt{u\left(y_i^{*},y_i^{*}\right)}$.

If the uncertainties of the measured values are unknown, the curve fit method reduces to calculating the Karush–Kuhn–Tucker point ${\mathbf{y}}^{*}$ that minimises the squared error norm $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\mathbf{M}}^T\left(\mathbf{x},{\mathbf{y}}^{*}\right)·\mathbf{M}\left(\mathbf{x},{\mathbf{y}}^{*}\right)$. In this case, all measured values $\mathbf{x}$ are equally weighted.

3. Closed Cavity

The flow in a closed cavity with a cylindrical shroud but without preswirl guide vanes is taken as the reference configuration, the configuration originally studied by Daily and Nece [1]. In this section, the dependency of the torque coefficient, the pressure coefficient and the axial thrust coefficient on the circumferential Reynolds number and the relative axial gap width are investigated. In later sections, the influence of centripetal through-flow is compared to this reference configuration.

3.1. Torque Coefficient

In the radial turbomachinery design process, frictional losses in side chambers should be minimised. The gap width has a significant influence on frictional losses; the correlations by Daily and Nece [1] showed that disc torque is minimal in the transition zone between the two flow regimes. Moreover, they found that for merged and separated boundary layers, the torque coefficient $c_M$ is proportional to $R{e}^{-0.25}$ and $R{e}^{-0.20}$, respectively.

Figure 2 compares torque measurements of closed cavities with hydraulically smooth discs from the small, water-operated test rig from [10], the large carbon dioxide test rig, and the test bench used by Radtke and Ziemann [3], and gives the correlations provided by Daily and Nece [1]. All uncertainties shown as error bars in figures are 99% ($2.576$ standard deviations) confidence intervals; all those quoted in text are 68% (1 standard deviation) intervals.

The low torque coefficient values of the small test rig are a result of the hydrophobic properties of the material used and its low surface roughness: PMMA is used for both the disc and the casing; its transparency implies that its surface is very smooth. In the large, carbon dioxide operated test rig, the installed disc is polished and hydraulically smooth at all Reynolds numbers investigated. Optical measurements of the disc surface do not show any significant roughness. In contrast, the shroud and the casing are rough, the roughness of the latter being approximately 10 $\mathsf{\mu }$$\mathrm{m}$ tip-to-tip. Moreover, holes are drilled in the cylindrical outer disc surface for balancing purposes, which increases the torque. All these aspects influence torque magnitude and make a direct comparison of the different test rig results difficult. Therefore, only the behaviour of the torque coefficients with varying Reynolds number and different axial gap widths is investigated.

For the small test rig, the change in torque coefficient with increasing Reynolds number shows a good correlation with the results of Daily and Nece [1], with torque coefficient being proportional to $R{e}^{-0.253\pm 0.01}$ and $R{e}^{-0.223\pm 0.009}$ for the small cavity width $G=0.0182$ and the large cavity width $G=0.0728$, respectively. According to Daily and Nece [1], measurements at the small cavity width $G=0.0182$ are in the merged boundary layer regime, while those at the large cavity width $G=0.0728$ feature separated boundary layers. In this range of Reynolds number up to $Re=4\times {10}^6$ and with incompressible fluids, no deviation from the predictions made by Daily and Nece [1] can be seen.

The large test rig and that of Radtke and Ziemann [3] are operated with compressible gases, carbon dioxide and air, respectively. Furthermore, they operate in Reynolds number regions of $Re\ge 3\times {10}^6$. Torque data from these test rigs show that by increasing the Reynolds number $Re$, the torque coefficient $c_M$ decreases significantly more slowly than in the Reynolds number range of $Re\le 4\times {10}^6$: the largest torque coefficient decrease is proportional to $R{e}^{-0.134\pm 0.003}$ (large test rig, $G=0.0125$), while the slowest is proportional to $R{e}^{-0.07}$ ([3], $G=0.0125$), as shown by the curve fits in Figure 2. This suggests that the regimes introduced by Daily and Nece [1] cannot reliably be applied to rotor–stator cavities at Reynolds numbers $Re\ge {10}^7$. It is important to note that the behaviour of the torque coefficient differs for each test rig with respect to the relative cavity width: the data by Radtke and Ziemann [3] show that with increasing relative cavity width, the exponent c in $c_M\propto R{e}^c$ decreases, while the data from the large test rig show the opposite: with increasing relative cavity width, the exponent c increases.

3.2. Radial Pressure Distribution

A radial pressure gradient develops in rotor–stator cavities, which exerts axial thrust on the rotor disc or on the shaft in a radial turbomachine. To predict this precisely, the radial pressure distribution must be known for the operating point of the machine.

Kurokawa and Sakuma [2] proposed two models to calculate the core swirl ratio $K=\raisebox{1ex}{$u_{\phi }$}\!\left/ \!\raisebox{-1ex}{$\mathsf{\Omega }r$}\right.$ (with circumferential velocity $u_{\phi }$ at the cavity middle $z=\raisebox{1ex}{$s$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$) and the pressure coefficient $c_p\left(r\right)$. Both models are applicable to rotor–stator cavity flow without through-flow as well as with centripetal through-flow. Each model is based on the characteristics of one of the two flow regimes identified by Daily and Nece [1]. The interference gap model assumes the absence of a rotating core, the presence of boundary layers on the rotor and the stator with a thickness of half the cavity width each, and velocity distributions according to the $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$7$}\right.$ power law. In the non-interference gap model, a rotating core with axially constant circumferential and vanishing radial velocity is assumed to exist between the boundary layers. The models take into account the circumferential Reynolds number $Re$; additionally, the interference gap model includes the relative cavity width G, but the non-interference gap model does not. In the case of closed cavity flow, no other variables are taken into account.

Figure 3 shows the variation of the radial pressure distribution for a range of circumferential Reynolds numbers at a small cavity width. Measurement data for the small test rig are taken from [10]. According to Kurokawa and Sakuma [2], only the small test rig operates in the non-interference gap region and all other measurements are at operating conditions with interfering boundary layers. Measurements in the Reynolds number range of $1.5\times {10}^6\le Re\le 2.6\times {10}^7$ show that with increasing Reynolds number, the radial pressure gradient increases, and at $Re\approx 2.6\times {10}^7$ the radial pressure gradient is greatest. However, although the Kurokawa and Sakuma models predict similar behaviour with increasing Reynolds numbers in this range, their predictions deviate significantly from the observed data, especially at low relative radii $\raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$b$}\right.$. In addition, a further increase of the Reynolds number $Re$ to the range of $Re\ge 3\times {10}^7$ leads to a decrease of the radial pressure gradient, while the models by Kurokawa and Sakuma [2] predict a continued increase. Note that in the small test rig, the changes in radial pressure gradient with Reynolds number are small for the relative cavity width $G=0.0182$ [10], thus only one representative set of measurements is shown.

3.3. Axial Thrust Coefficient

In Figure 4, axial thrust coefficients $c_F$ are plotted against Reynolds numbers $Re$ for different relative cavity widths G alongside predictions by the models given in Kurokawa and Sakuma [2]. The axial thrust coefficient decreases as cavity width increases and as Reynolds number increases. For the small test rig, $c_F$ decreases significantly faster with increasing Reynolds number than for the large test rig. Moreover, with small relative cavity width $G=0.0182$, the decrease in axial thrust coefficient slows down for Reynolds numbers $Re\ge 2\times {10}^6$, and thus its slope in this range is much closer to the slope of the axial thrust coefficients obtained from the large test rig. This change in slope indicates a change in flow characteristics, for example, an increasing influence of turbulence. Further research is needed to investigate this phenomenon.

Considering the whole Reynolds number range of $3.8\times {10}^5\le Re\le 2.5\times {10}^8$ and all axial gap widths investigated, a continuous decrease of axial thrust coefficients with increasing Reynolds numbers is apparent. There is no hint of discontinuities or other phenomena in the Reynolds number range where no measurement data are available. Fitting the axial thrust coefficients $c_F$ measured in the small and the large test rig to a curve results in the empirical approximation

$$c_F=3.76\times {10}^{-2}+2.28\times {10}^{-2}{\left[{10}^{-7}Re\right]}^{-0.505}.$$

(14)

This curve is plotted in Figure 4 as a brown dotted line.

It is again apparent that the flow models by Kurokawa and Sakuma [2] fail to capture the variation of axial thrust with Reynolds number, but the influence of different cavity widths is reproduced qualitatively. Measurements published by Radtke and Ziemann [3] are much closer to predictions by Kurokawa and Sakuma [2] than to the results of the small and the large test rig, and do not show any significant influence of the cavity width.

4. Centripetal Through-Flow

In a radial turbomachine, superposed centripetal through-flow can occur in a side chamber, significantly influencing the coefficients investigated earlier. The mass flow through the cavity is given by the through-flow coefficient

$$c_D=\frac{\dot{m}}{\rho \mathsf{\Omega }{b}^3}$$

(15)

with $c_D<0$ for centripetal through-flow. The small and large test rigs can operate at through-flow coefficient ranges of $-6.64\times {10}^{-3}\le c_D\le 0$ and $-1.45\times {10}^{-3}\le c_D\le 0$, respectively.

A significant amount of angular momentum can be carried into the rotor–stator cavity if the inflow has a circumferential velocity component; this angular momentum flow is given by the coefficient

$$c_L=\frac{{\dot{m}}^{2}tan\alpha }{4{\pi }^2{\rho }^2{b}^5{\mathsf{\Omega }}^{2}d}$$

(16)

where $\alpha$ is the preswirl guide vane angle relative to the radial direction. With a preswirl angle of $\alpha =0^{\circ }$, radial inflow occurs and no angular momentum flows into the cavity, resulting in an angular momentum coefficient of $c_L=0$. Corotational swirl corresponds to preswirl angles of $\alpha >0^{\circ }$, with the angular momentum coefficient $c_L$ being positive. The small test rig covers the range of $0\le c_L\le 9.6\times {10}^{-5}$ and the large one $0\le c_L\le 1.6\times {10}^{-5}$.

It is important to note that computational fluid dynamics simulations along with measurements in the small test rig not presented here show a significant influence of centripetal inlet area on the results: a jet develops at the inlet, with smaller inlet areas generating higher velocity jets for the same mass flow rate. The inlet gap widths d are $3.75\times {10}^{-3}$ and $1.82\times {10}^{-2}$ times the disc radius b for the large and small test rig, respectively. Results are presented separately.

4.1. Large Test Rig

The large test rig has four different configurations: in addition to the closed cavity, one of three different preswirl guide vanes for centripetal through-flow may be installed. The preswirl angles investigated are 0, 26 and 52${}^{\circ }$.

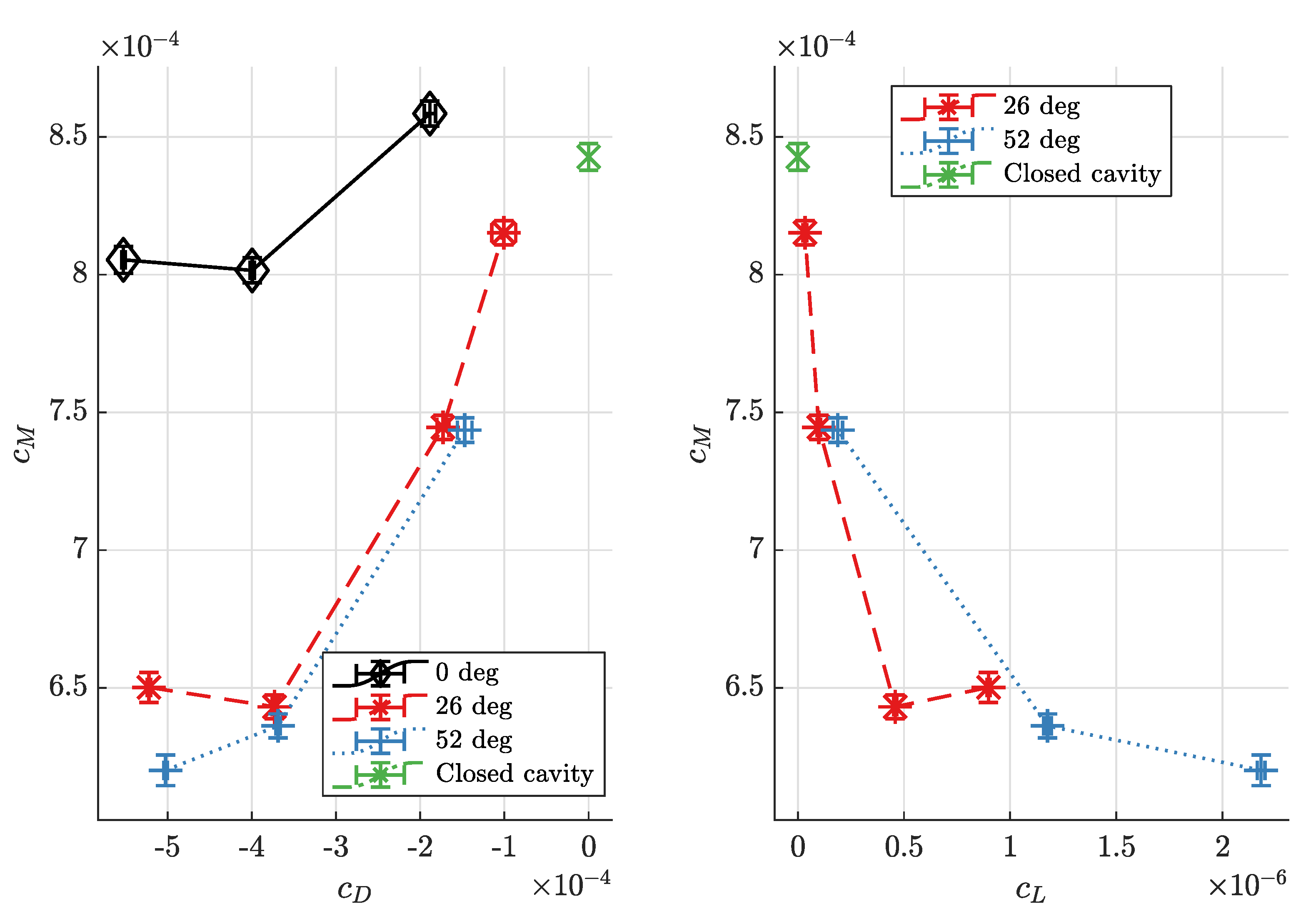
Figure 5 illustrates the torque coefficients $c_M$ measured with and without centripetal through-flow for a relative gap width of $G=0.0125$ and in the Reynolds number range of $7.5\times {10}^7\le Re\le 9.6\times {10}^7$. It is apparent that with increasing centripetal mass flow ($c_D$ decreasing below zero), the torque coefficient $c_M$ first decreases, reaches a minimum and then increases to higher values than that of the closed cavity configuration. The torque coefficient minima are all found at through-flow mass flux coefficients of $c_D\approx -6.1\times {10}^{-4}$, but at different angular momentum flow coefficients $c_L$. This indicates that the point where the minima occur depends only on mass flow, and not on inlet swirl angle. However, the torque coefficient values strongly depend on the angular momentum flow into the cavity, with high preswirl angles leading to lower torque coefficients at the same mass flux coefficients.

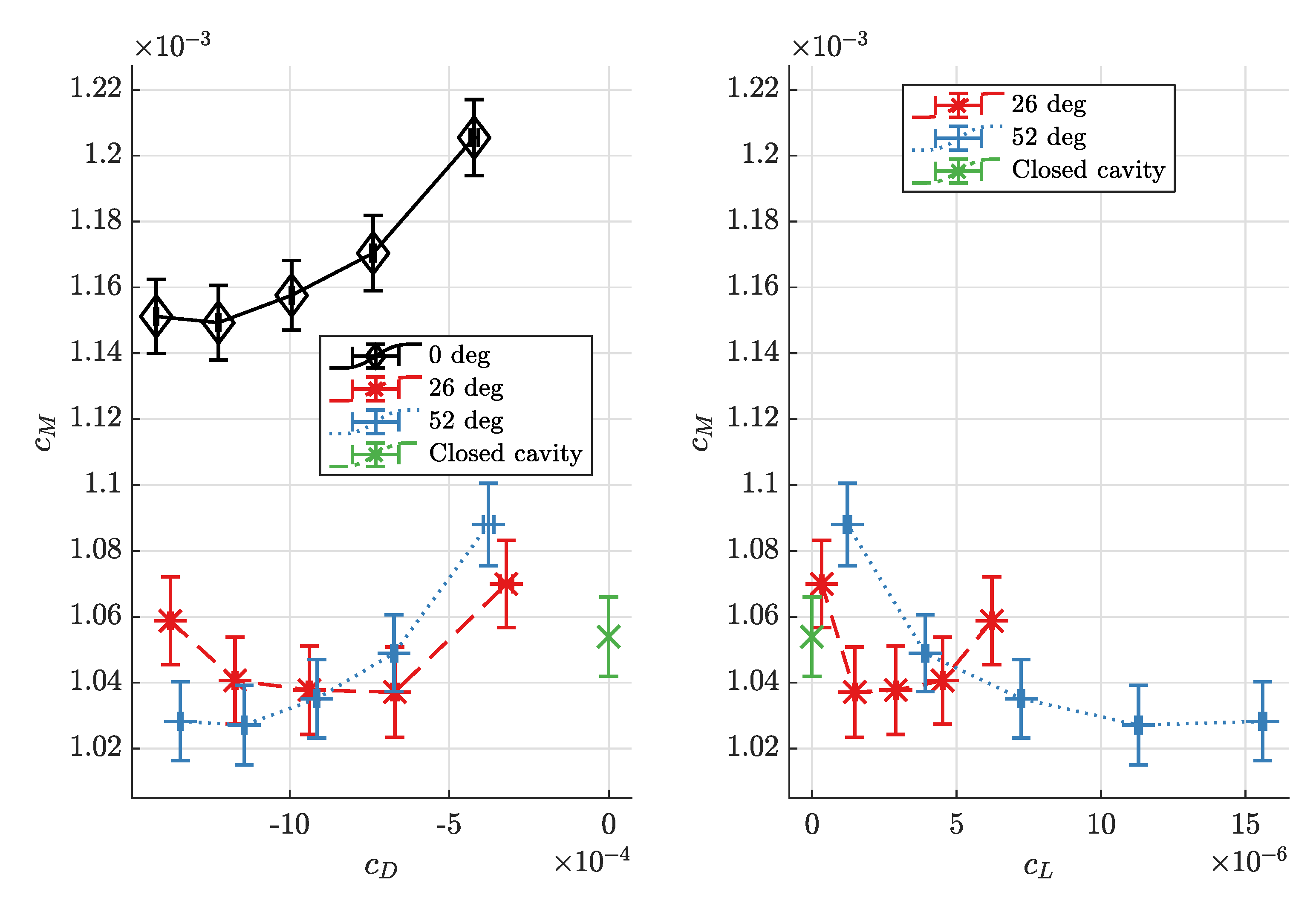
For large Reynolds numbers of $Re\ge 1.8\times {10}^8$ shown in Figure 6, the decline of torque coefficients from radial inflow to a preswirl angle of 26${}^{\circ }$ is much larger than for the moderate Reynolds numbers in Figure 5, but the torque coefficients at preswirl angles 26${}^{\circ }$ and 52${}^{\circ }$ differ significantly only at high through-flow mass flux (small through-flow coefficient values $c_D<0$). Minimum torque coefficients are found at $c_D\approx -3.7\times {10}^{-4}$ for radial inflow and the 26${}^{\circ }$ preswirl angle, but at $c_D\le -5\times {10}^{-4}$ for the 52${}^{\circ }$ preswirl angle. For this gap width and Reynolds number range, the angular momentum flux entering the cavity plays an important role: for radial inflow, where by definition $c_L=0$, the minimum torque coefficient is $c_M=8\times {10}^{-4}$, but with increasing angular momentum inflow in the case of corotating preswirl, the torque coefficient quickly drops to values below $6.5\times {10}^{-4}$.

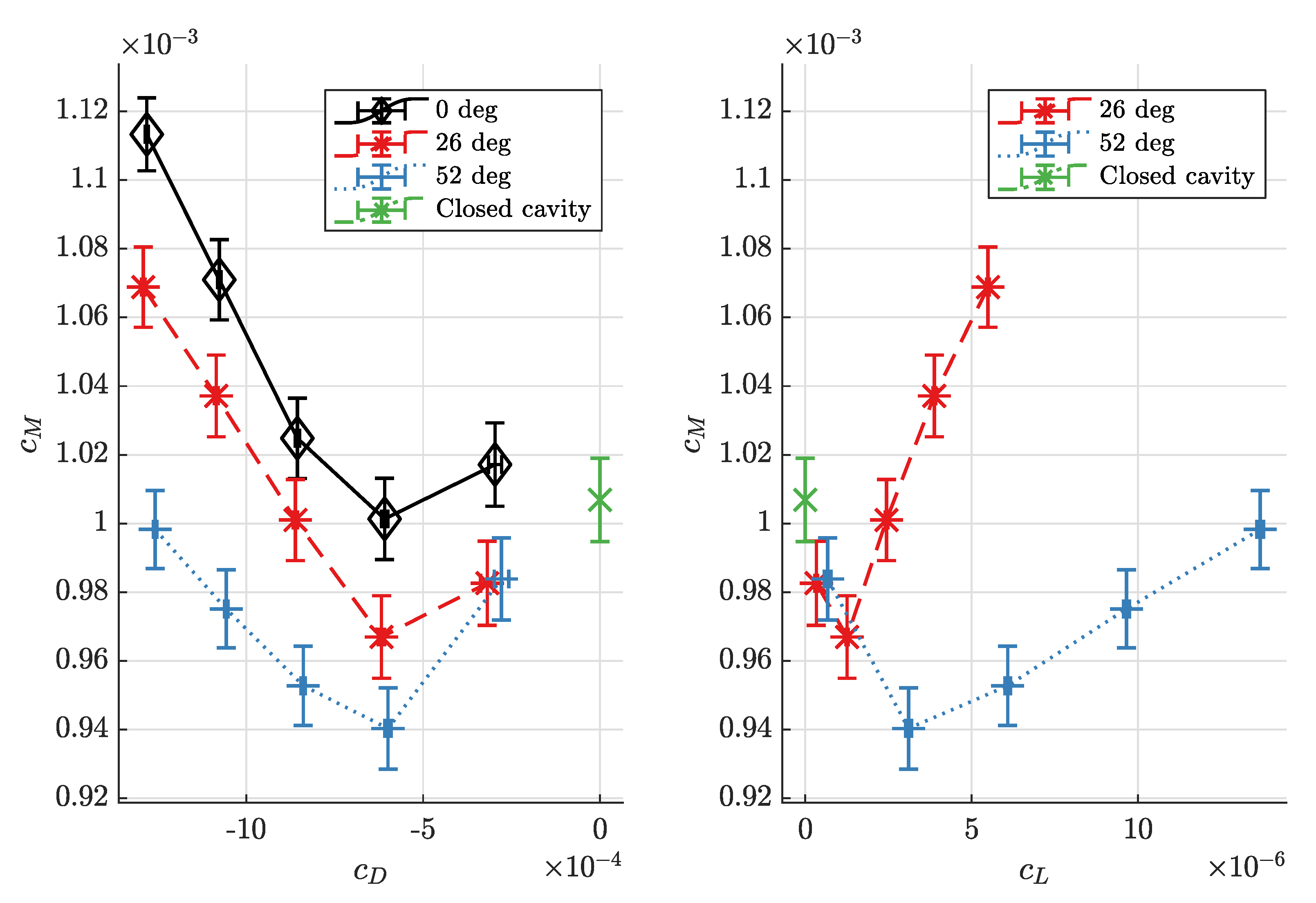
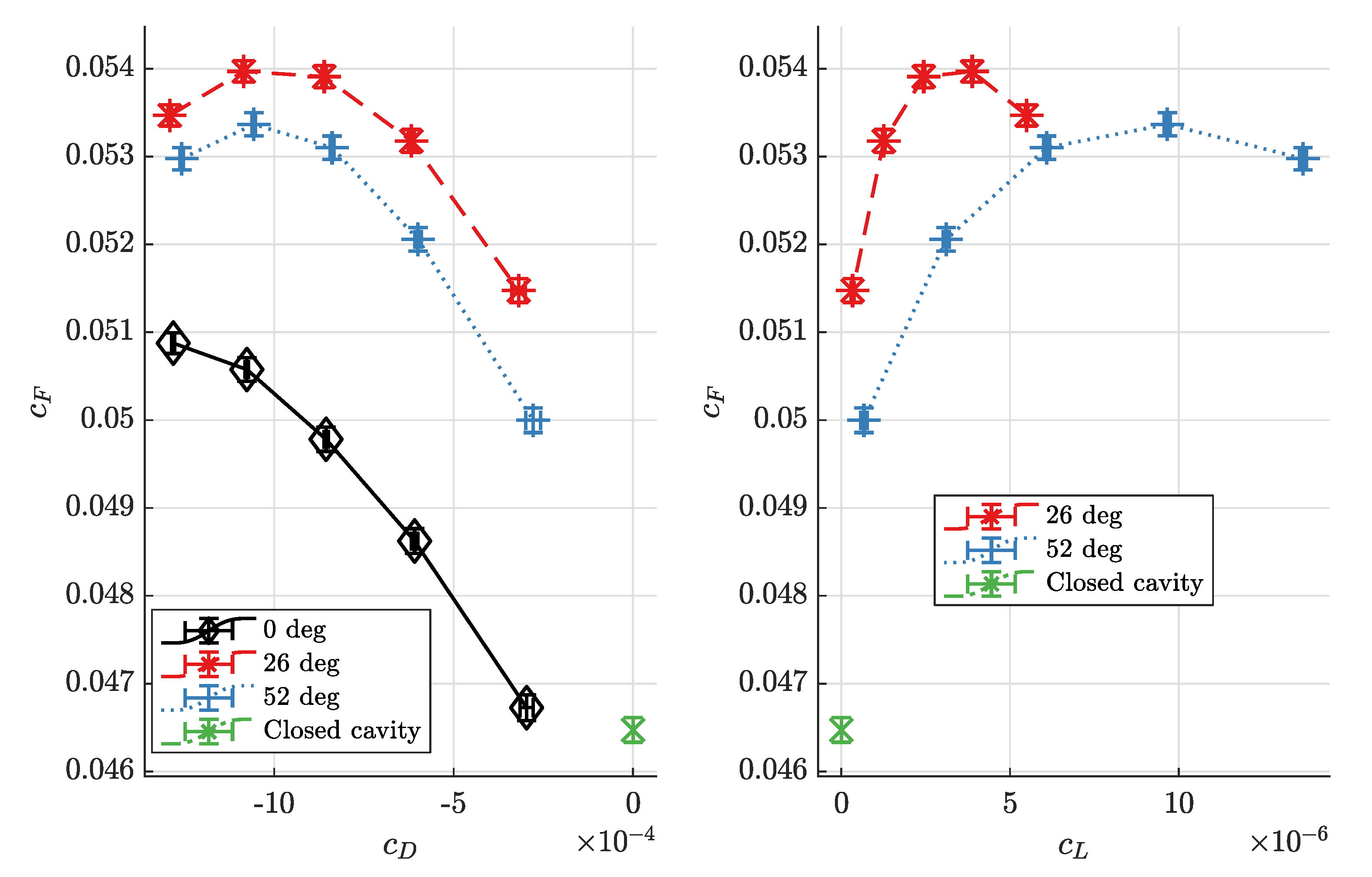
With a relative cavity width of $G=0.0375$ and a Reynolds number of $7.5\times {10}^7\le Re\le 9.6\times {10}^7$, the torque coefficient behaves as shown in Figure 7. The only difference in experimental set-up from that of Figure 5 is that the cavity width is three times larger. Again, torque coefficients are significantly higher with radial inflow ($\alpha =0^{\circ }$, no preswirl) than with preswirl, but while a difference between preswirl angles of 26${}^{\circ }$ and 52${}^{\circ }$ is observed at the smaller cavity width, no significant difference is observed here. For this larger cavity width, the minima of the torque coefficient seem to be shifted to smaller through-flow mass flux coefficients compared to the small cavity width, but this conclusion is not certain since the uncertainties of the measured torque coefficient are about as large as the change in the torque coefficients itself.

The explanation for greater torque coefficients in the case of radial inflow, which has been observed, is as follows. If through-flow enters the cavity radially, i.e., with a preswirl angle of $\alpha =0^{\circ }$, it creates a large gradient in the axial direction between the circumferential velocities of the fluid and disc close to its outer radius. This gives rise to a large drag, resulting in torque coefficients significantly higher than in the closed cavity or the centripetal through-flow case with corotating preswirl. The difference in circumferential velocity between the inflow and the disc is smaller with corotating preswirl, therefore the velocity gradient, drag and torque coefficient decrease.

The development of axial thrust coefficients with centripetal through-flow is shown in Figure 8 for the same measurements that are shown in Figure 5 ($G=0.0125$, $7.5\times {10}^7\le Re\le 9.6\times {10}^7$): centripetal through-flow significantly increases the thrust coefficient as essentially it is an accelerated flow which results in a larger radial pressure gradient. With increasing centripetal mass flow (decreasing $c_D$), the axial thrust coefficient reaches a maximum for preswirl angles of 26${}^{\circ }$ and 52${}^{\circ }$ at a through-flow coefficient of $c_D\approx -1.1\times {10}^{-3}$. For radial inflow, it seems that the thrust coefficient converges towards a maximum, too, which is outside of the investigated through-flow mass flux range. For this gap width and Reynolds number, centripetal through-flow with preswirl angles of 26${}^{\circ }$ and 52${}^{\circ }$ generates higher axial thrust coefficients compared to radial inflow with a preswirl angle of 0${}^{\circ }$. The small differences in the axial thrust coefficients between measurements with preswirl angles of 26${}^{\circ }$ and 52${}^{\circ }$ are not considered significant, because the experiment at the preswirl angle of 52${}^{\circ }$ was conducted at a slightly higher Reynolds number than those for 26${}^{\circ }$. The angular momentum coefficient $c_L$ alone is again insufficient to describe the axial thrust behaviour because multiple different axial thrust coefficient values are observed for one angular momentum coefficient value.

To investigate the influence on axial thrust of mass and angular momentum flow into the cavity, the radial pressure distribution of the closed cavity configuration and the centripetal through-flow case with 52${}^{\circ }$ preswirl angle is plotted in Figure 9. To provide a better view of the pressure gradients, markers and error bars are omitted. With increasing centripetal through-flow, the pressure at relative radii of $\raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$b$}\right.<0.7$ decreases as indicated by larger pressure coefficient values $c_p$. Simultaneously, the pressure at relative radii of $0.75<\raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$b$}\right.<1$ increases, leading to lower pressure coefficients compared to the closed cavity configuration. Since in the computation of axial thrust coefficients the pressure coefficients are weighted with the radial position r, a small pressure increase at large radii can balance larger pressure drops at small radii. This happens at the maxima of axial thrust coefficients as at this point a change in the radial pressure distribution does not cause a change in $c_F$.

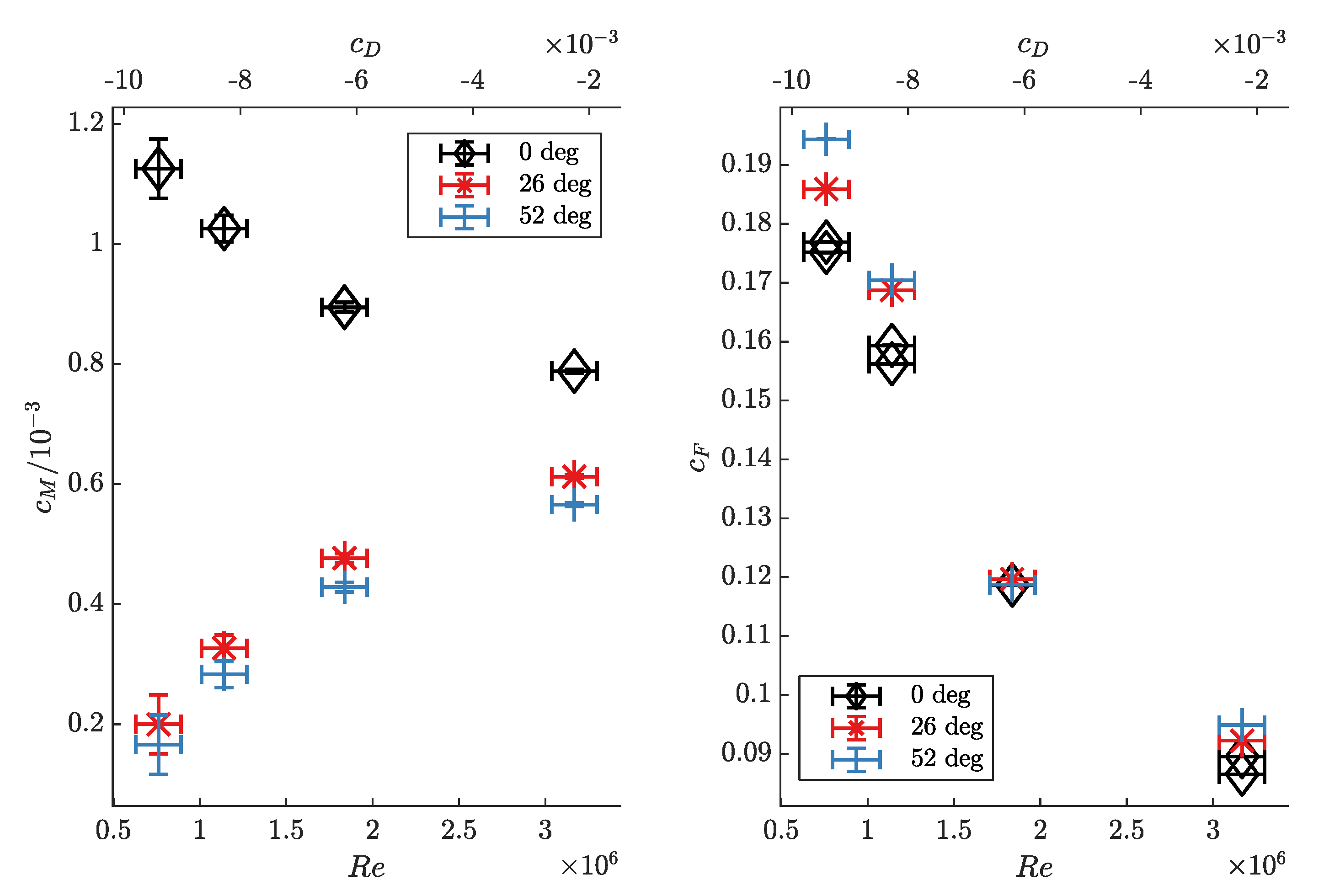
4.2. Small Test Rig

In Figure 10, axial thrust coefficients $c_F$ and torque coefficients $c_M$ measured in the small test rig with the cavity closed are compared to those obtained with radial inflow for the small relative cavity width of $G=0.0182$. The result shows an almost linear increase of thrust and torque coefficient with decreasing through-flow coefficient $c_D$, with the slope depending on the circumferential Reynolds number: as Reynolds number increases, the slopes $\raisebox{1ex}{$\partial c_M$}\!\left/ \!\raisebox{-1ex}{$\partial c_D$}\right.$ and $\raisebox{1ex}{$\partial c_F$}\!\left/ \!\raisebox{-1ex}{$\partial c_D$}\right.$ decrease.

In comparison to the results of the large test rig, it appears that the torque coefficient minima, observed in the large test rig for moderate through-flow mass flow rates and radial inflow, do not appear. The axial thrust coefficients of the large test rig with radial inflow, plotted in Figure 8, increase with decreasing through-flow coefficients, just as in the small test rig. However, in the large test rig, this increase decelerates with decreasing through-flow coefficients, while, in the small test rig, no deceleration is observable.

In Figure 11, the influence of preswirl angle on torque and axial thrust coefficient for the small test rig is presented. It is important to note that, in this figure, the Reynolds number of the data points is found on the lower horizontal axes while the through-flow coefficient is found on the upper ones. The torque coefficient behaviour with varying preswirl angles is similar to that observed in the large test rig: when the preswirl angle increases from 0${}^{\circ }$ (radial inflow) to 26${}^{\circ }$, the torque coefficient drops sharply, while a further increase of the preswirl angle to 52${}^{\circ }$ only leads to a marginal decrease of the torque coefficient compared to the results with a preswirl angle of 26${}^{\circ }$. Regarding the thrust coefficient, it is found that an increase of the preswirl angle increases the thrust coefficient, as in the large test rig. Interestingly, this increase is very small at the operating point $Re\approx 2\times {10}^6$, $c_D\approx -3\times {10}^{-3}$, but larger at all other points.

5. Conclusions

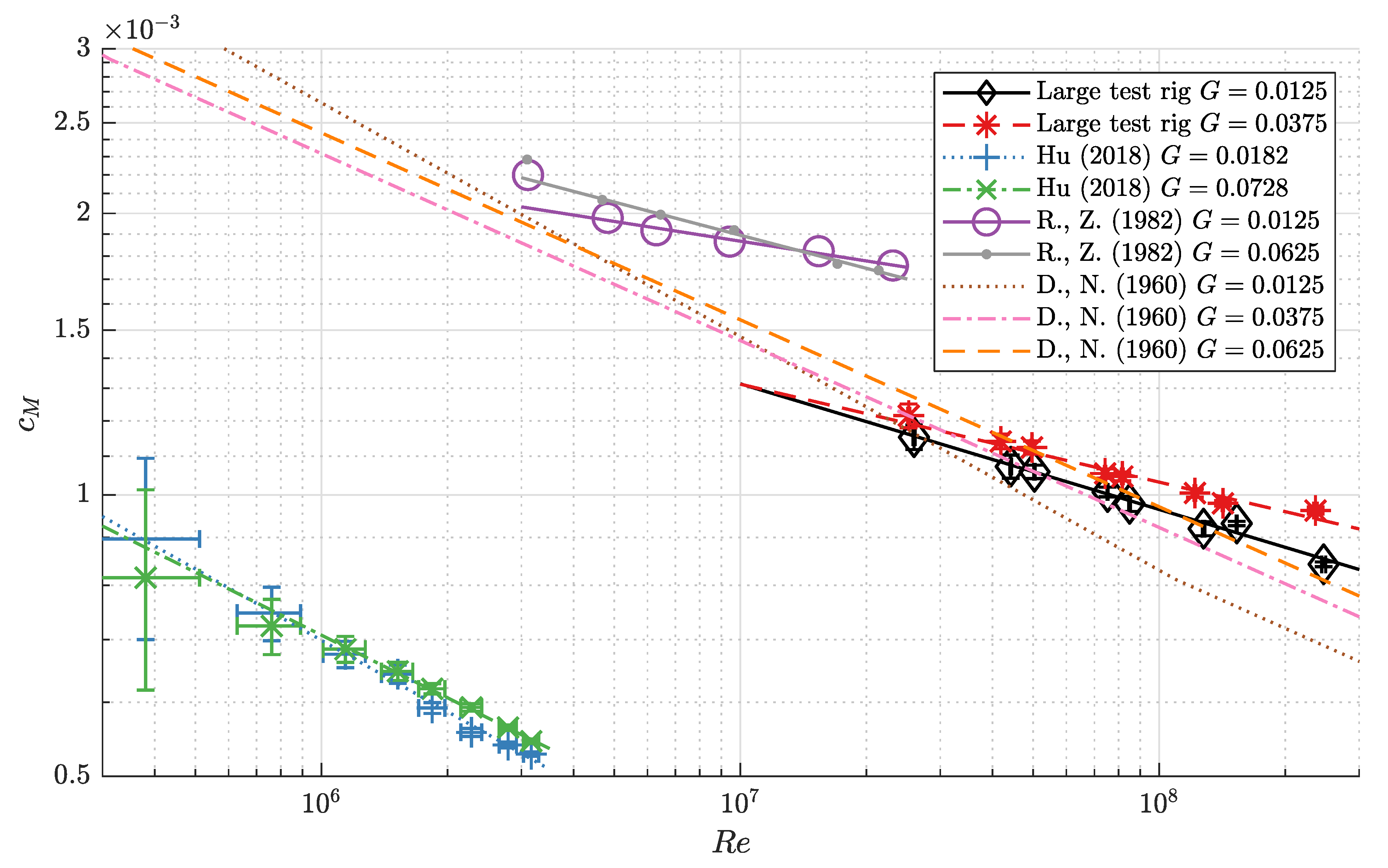
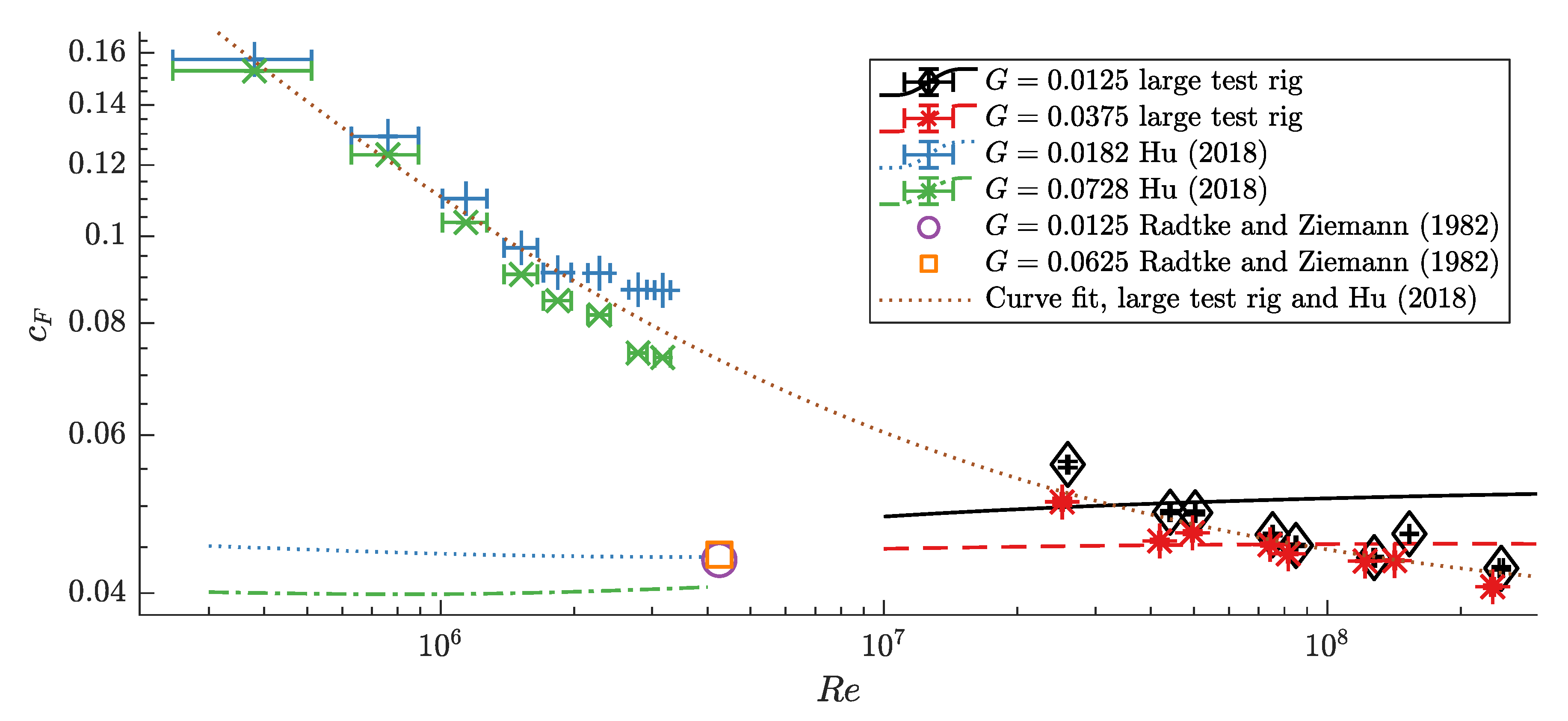
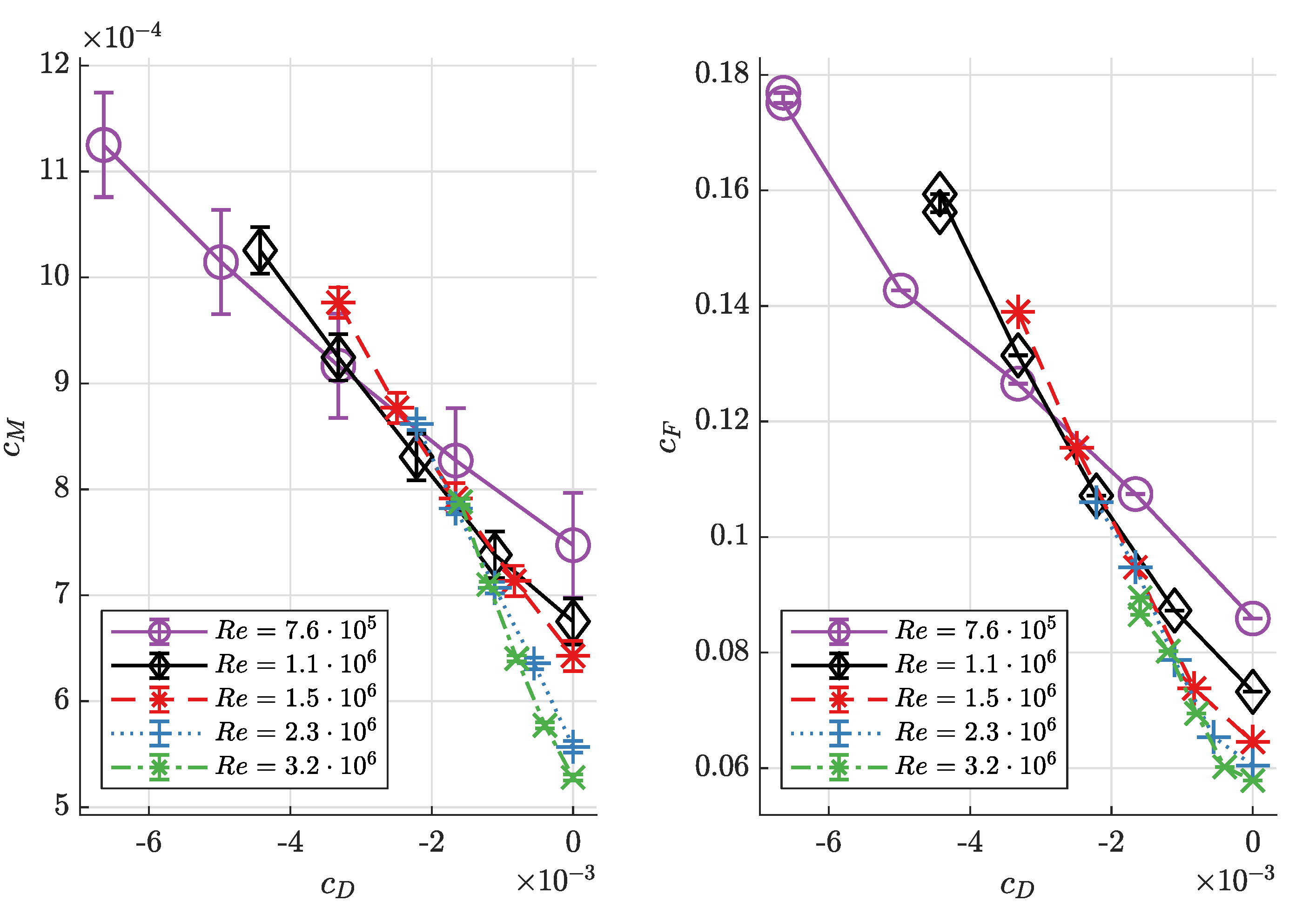
In the closed cavity configuration and in the Reynolds number range of $Re\le 3.2\times {10}^6$, the decrease of torque coefficient with increasing Reynolds number behaves in the same way as found experimentally by Daily and Nece [1] and as predicted by Kurokawa and Toyokura [14]. For Reynolds numbers $Re\ge 3\times {10}^6$, torque coefficient decreases significantly more slowly with increasing Reynolds number. This behaviour is observed in two different test rigs with two different compressible fluids (the large carbon-dioxide-operated test rig used here and the air-operated test rig built by Radtke and Ziemann [3]).

In both the small and large test rigs and in the closed cavity case, axial thrust coefficient is found to decrease with increasing Reynolds number. Neither of the models proposed by Kurokawa and Sakuma [2] predicts this behaviour. In the large test rig at the small cavity width, the radial pressure gradient decreases with increasing Reynolds number. However, the model by Kurokawa and Sakuma [2] applicable to this case predicts the opposite behaviour. However, these models capture the influence of the relative axial gap width qualitatively: with increasing Reynolds number, axial thrust coefficient decreases; with increasing cavity width, axial thrust coefficient increases.

In the large test rig with centripetal through-flow, as mass flow coefficient decreases, torque coefficient first decreases to a minimum and then increases. The torque coefficient minima are found at different mass flow coefficients, depending on the specific Reynolds number, relative axial gap width, and preswirl angle. Such minima are not found in the small, water-operated test rig, where in contrast centripetal through-flow with radial inflow increases torque coefficients.

In both the large and small test rigs, increasing the preswirl angle from 0${}^{\circ }$ to 26${}^{\circ }$ leads to a reduction of torque coefficient. No significant differences between preswirl angles of 26${}^{\circ }$ and 52${}^{\circ }$ were observed, with one exception: in the large test rig, at Reynolds numbers in the range of $7.5\times {10}^7\le Re\le 9.6\times {10}^7$, at the small cavity width of $G=0.0125$, and when the preswirl angle was increased to 52${}^{\circ }$, a further reduction of torque coefficient was observed.

For the small gap width $G=0.0125$ and a Reynolds number range of $7.5\times {10}^7\le Re\le 9.6\times {10}^7$, a mass flow coefficient of $c_D<0$ with any preswirl angle investigated lead to a larger axial thrust coefficient than that of the closed cavity configuration without through-flow. Characteristic maxima of axial thrust coefficients are observed for preswirl angles of 26${}^{\circ }$ and 52${}^{\circ }$. For radial inflow, the coefficients seem to converge towards a maximum, which lies outside the test rig’s operating range. Almost the same behaviour of axial thrust coefficients is observed in the small test rig with radial inflow, where centripetal through-flow increases the axial thrust coefficients, but no signs of maxima are found. Preswirl angle was also found to influence axial thrust coefficient, with an increase in preswirl angle resulting in an increase in the coefficient in both the large and small test rigs.

Finally, the increase of axial thrust coefficient with centripetal through-flow and a preswirl angle of 52${}^{\circ }$ observed in the large test rig is a result of the pressure increasing at relative radii of $\raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$b$}\right.>0.75$ and decreasing at relative radii of $\raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$b$}\right.<0.7$ compared to the radial pressure distribution of the closed cavity case.