High Resolution Experimental and Computational Methods for Modelling Multiple Row Effusion Cooling Performance †
Abstract
:1. Introduction
2. Materials and Methods
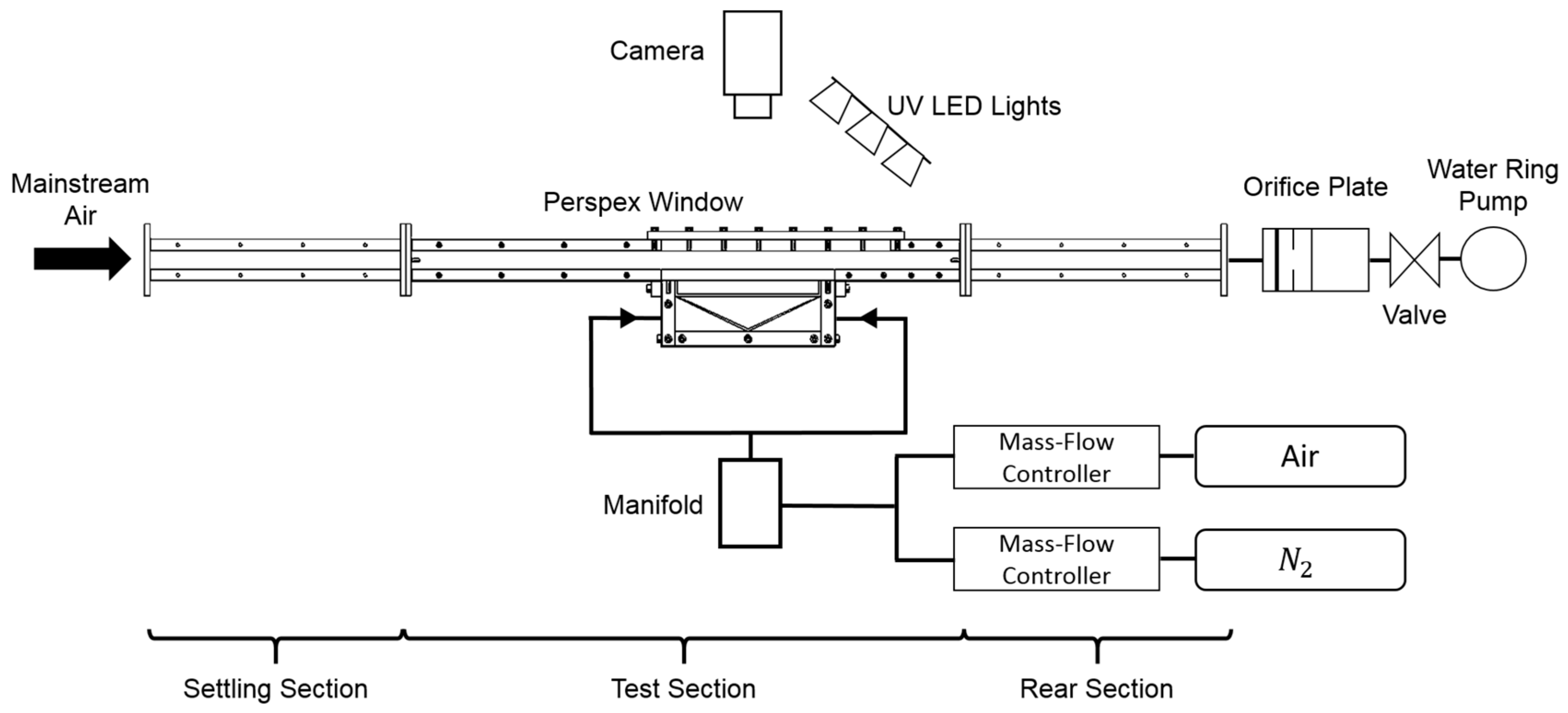
2.1. Experimental Setup
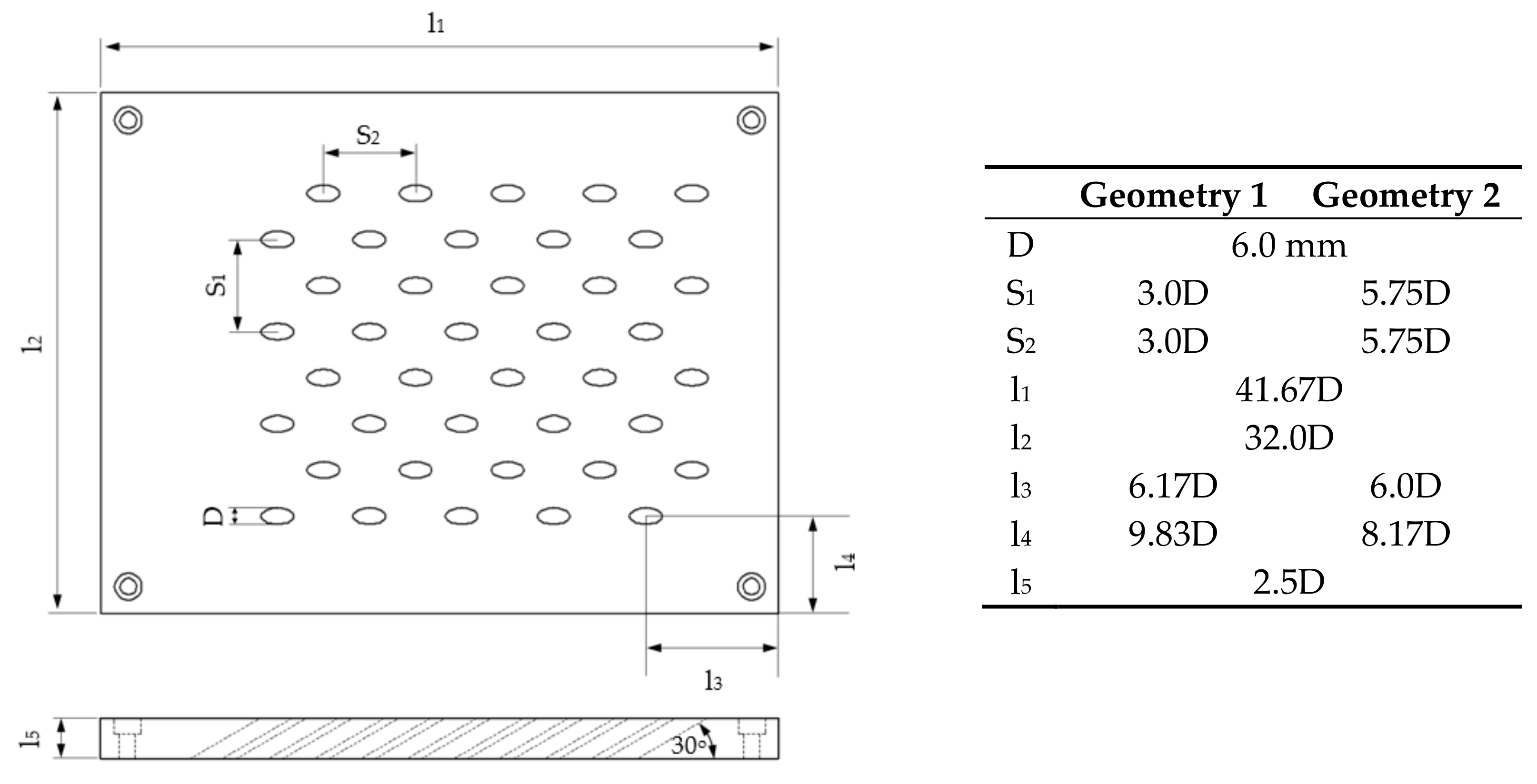
2.2. Flat-Plate Effusion Cooling Geometries
2.3. Pressure Sensitive Paint Measurement Methodology
2.4. Computational Simulations
2.5. Passive Scalar Tracking CFD Methodology
2.6. Multi-Hole CFD Domain and Setup
2.7. Single Hole CFD Domain, Setup and Superposition Method for Multi-Row Modelling
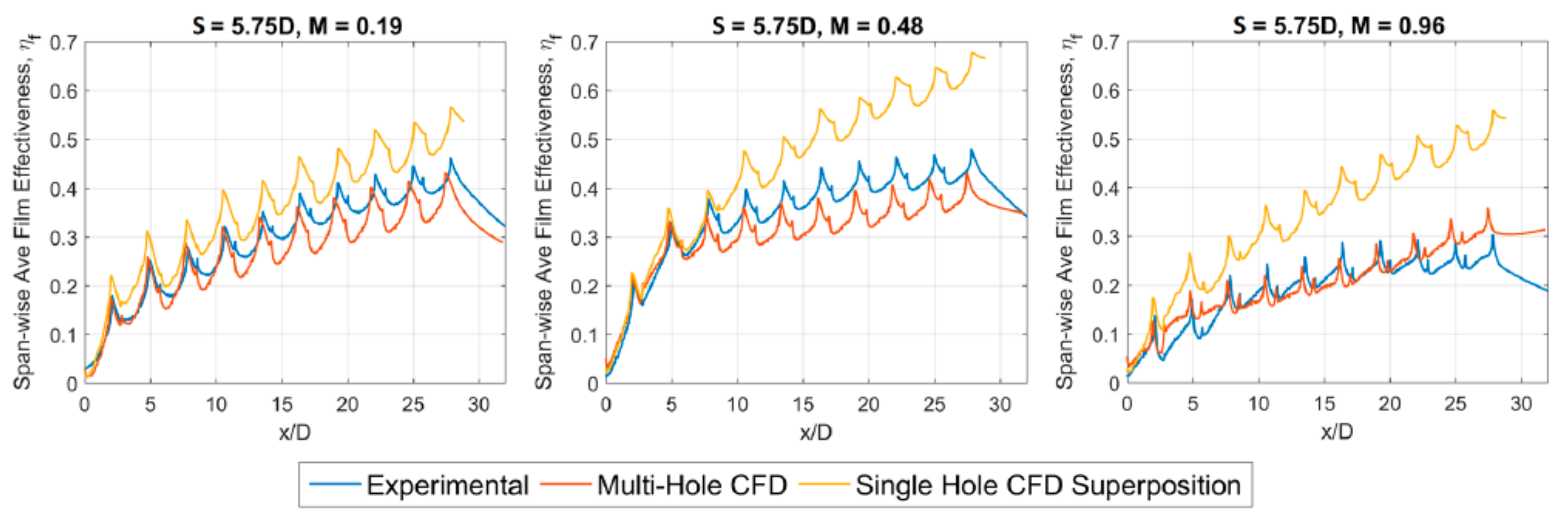
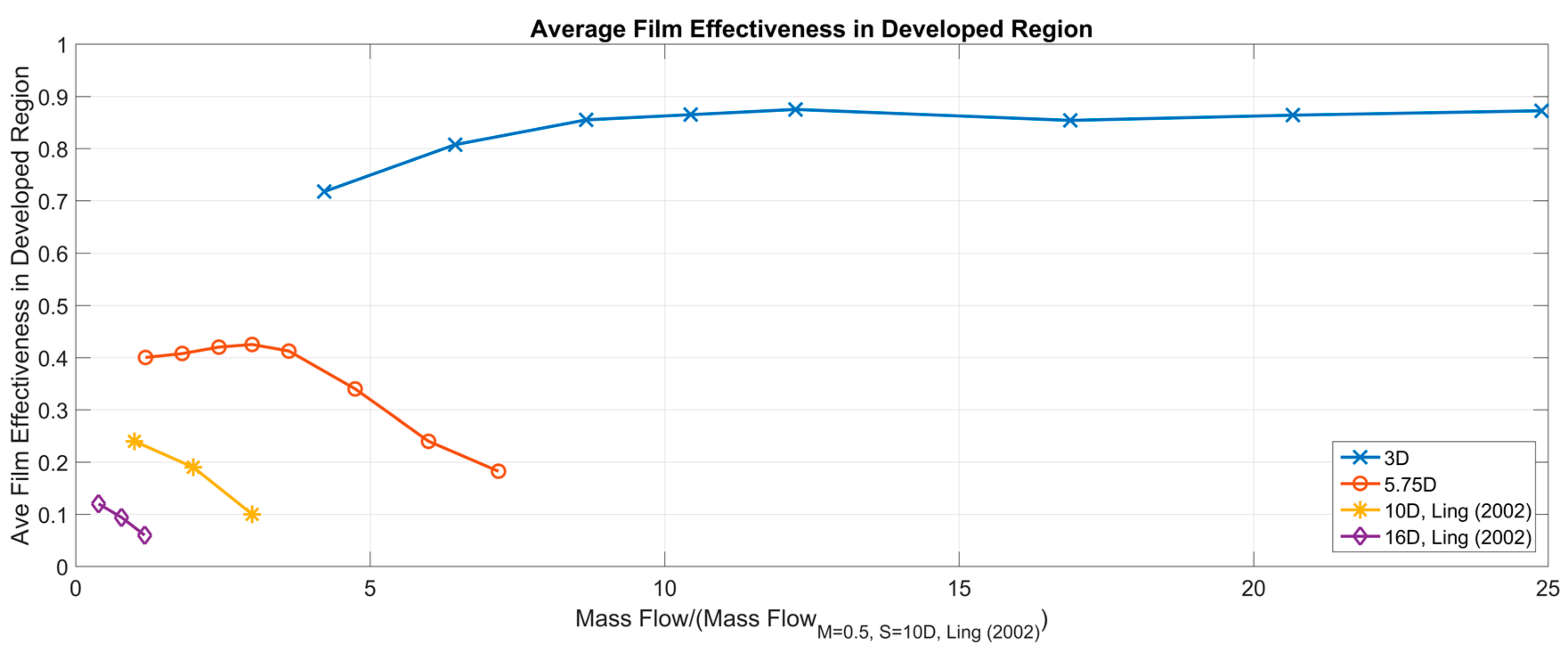
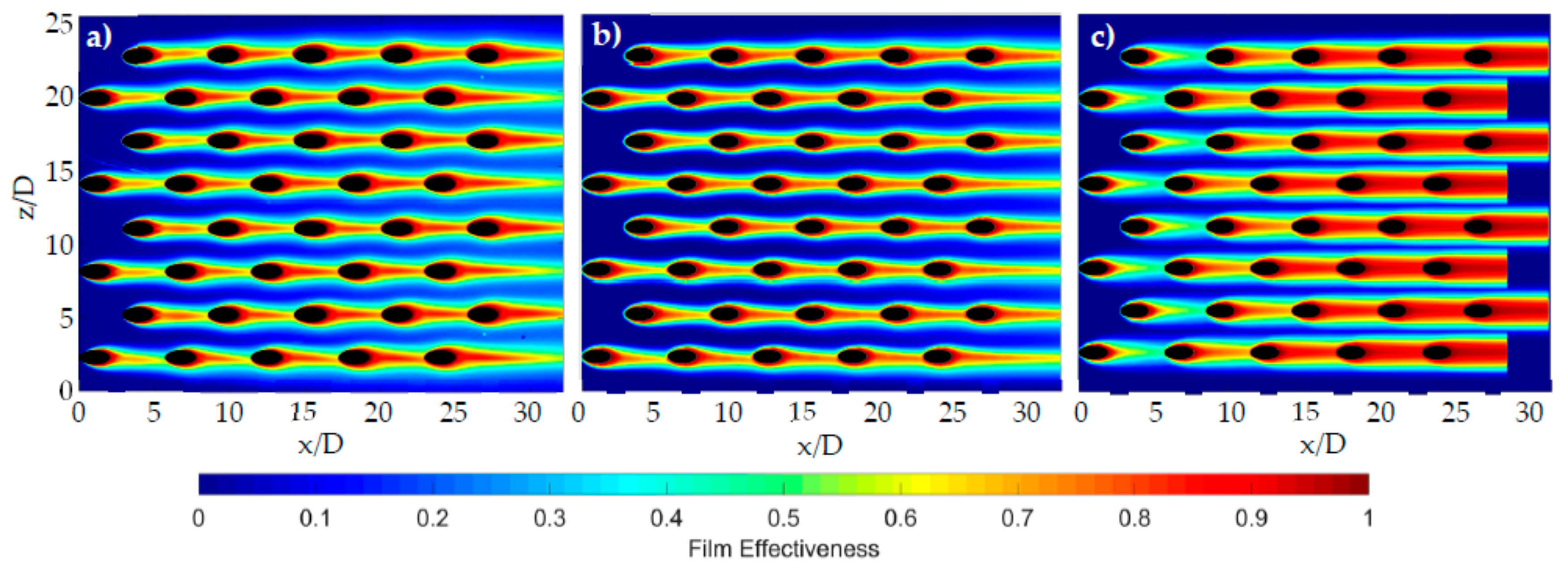
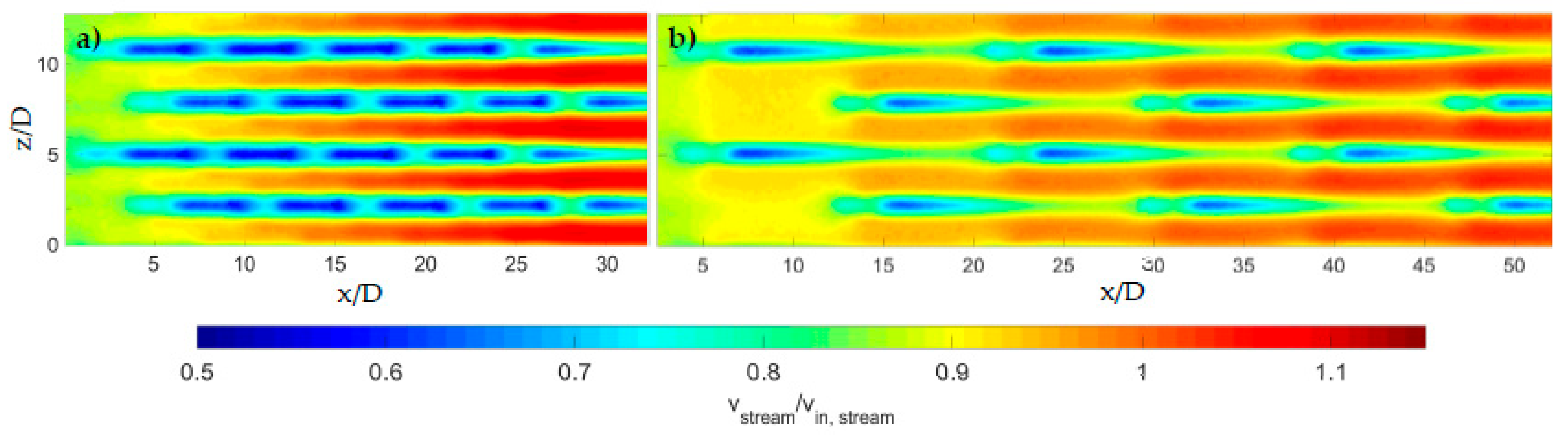
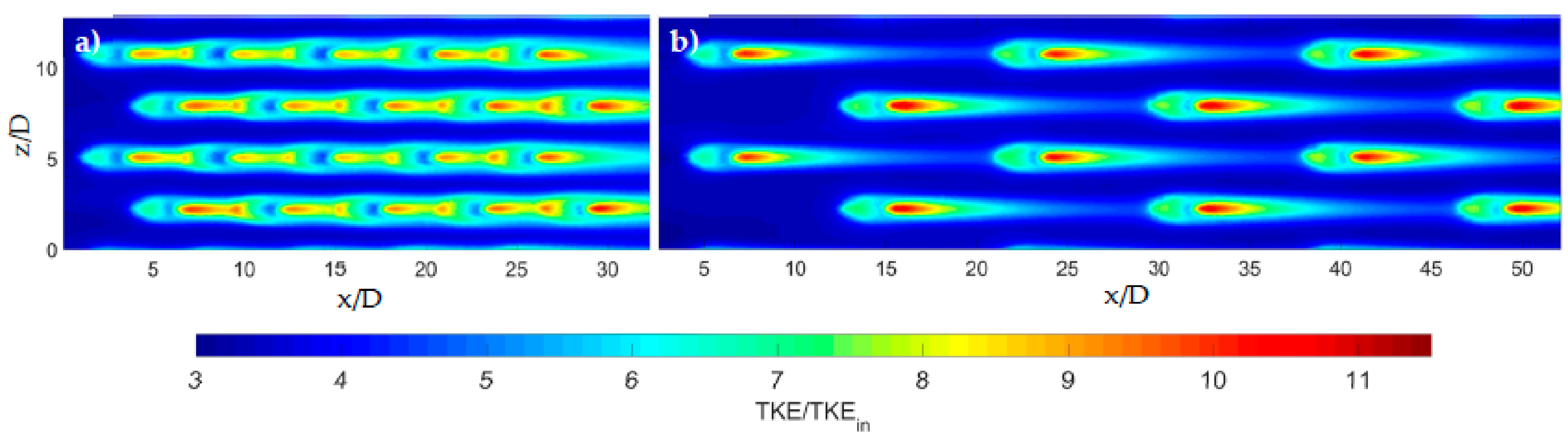
3. Results and Discussion
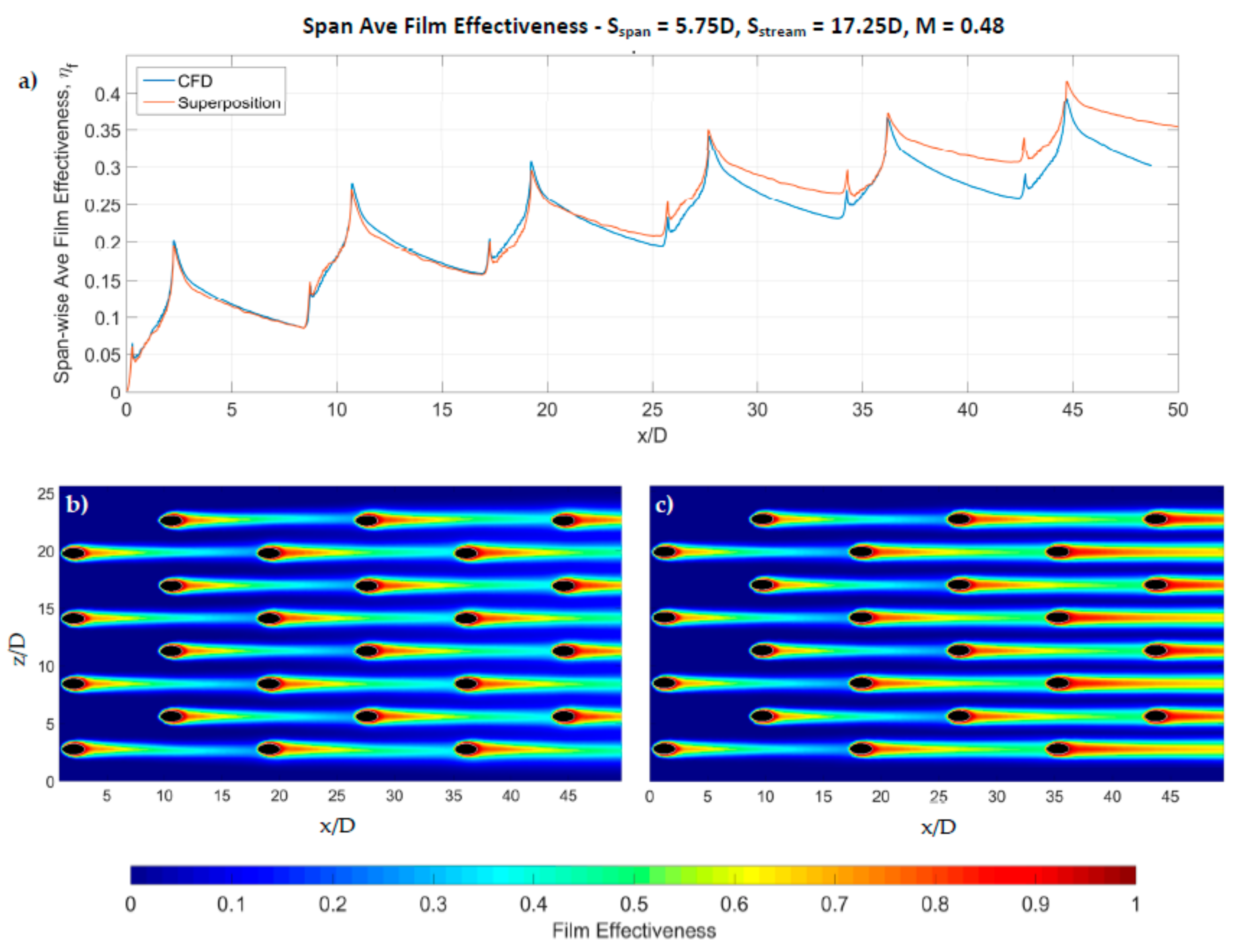
Further Investigation of Superposition in Effusion Cooling Performance Modelling
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| C | Mass Fraction |
| CFD | Computational Fluid Dynamics |
| cp | Specific Heat Capacity (J/K, const. p) |
| D | Diameter (m) |
| HP | High Pressure |
| k | Thermal Conductivity (W/m.k) |
| M | Blowing Ratio () |
| P | Non-Dimensional Pitch (-) |
| Partial Pressure of Oxygen | |
| Pr | Prandtl Number (-) |
| PSP | Pressure-Sensitive Paint |
| S | Pitch (m) |
| s | Source Term |
| Span | Spanwise Component |
| Stream | Streamwise Component |
| T | Temperature (K) |
| t | Time (s) |
| TET | Turbine Entry Temperature |
| TKE | Turbulent Kinetic Energy (J/kg) |
| xn | Direction Vector |
| v | Velocity (m/s) |
| Greek Characters | |
| α | Thermal Diffusivity (m2/s) |
| Γ | Diffusivity (m2/s) |
| Film Effectiveness | |
| μ | Dynamic Viscosity (Pa s) |
| Density (kg/m3) | |
| φ | Scalar Quantity |
| Subscripts | |
| aw | Adiabatic Wall |
| c | Coolant Condition |
| e | Exit Condition |
| in | Inlet Condition |
| l | Laminar Condition |
| t | Turbulent Condition |
| w | Wall |
| ∞ | Mainstream Condition |
References
- Broomfield, R.W.; Ford, D.A.; Bhangu, J.K.; Thomas, M.C.; Frasier, D.J.; Burkholder, P.S.; Harris, K.; Erickson, G.L.; Wahl, J.B. Development and turbine engine performance of three advanced rhenium containing superalloys for single crystal and directionally solidified blades and vanes. J. Eng. Gas Turbines Power 1998, 120, 595–608. [Google Scholar] [CrossRef]
- Ireland, P.T. The Potential Impact of Propulsion Technology on Emissions and Energy Security. In Energy, Transport & the Environment: Addressing the Sustainable Mobility Paradigm; Inderwildi, O., King, D.S., Eds.; Springer: London, UK, 2012; pp. 435–448. [Google Scholar]
- Krewinkel, R. A review of gas turbine effusion cooling studies. Int. J. Heat Mass Transf. 2013, 66, 706–722. [Google Scholar] [CrossRef]
- Andrews, G.E.; Asere, A.A.; Gupta, M.L.; Mkpadi, M.C. Full coverage discrete hole film cooling: The influence of hole size. In Proceedings of the American Society of Mechanical Engineers (ASME) 1985 International Gas Turbine Conference and Exhibit, Houston, TX, USA, 18–21 March 1985; p. V003T09A003. [Google Scholar]
- Gustafsson, K.M.B.; Johansson, T.G. An Experimental Study of Surface Temperature Distribution on Effusion-Cooled Plates. J. Eng. Gas Turbines Power 2001, 123, 308–316. [Google Scholar] [CrossRef]
- Crawford, M.E.; Kays, W.M.; Moffat, R.J. Full-Coverage Film Cooling on Flat, Isothermal Surfaces: A Summary Report on Data and Predictions; NASA Contractor Report 3219; Stanford University: Stanford, CA, USA, 1980.
- Foster, N.W.; Lampard, D. The Flow and Film Cooling Effectiveness Following Injection through a Row of Holes. J. Eng. Power 1980, 102, 584–588. [Google Scholar] [CrossRef]
- Gustafsson, B. Experimental Studies of Effusion Cooling. Ph.D. Thesis, Chalmers University of Technology, Goteborg, Sweden, 2001. [Google Scholar]
- Baldauf, S.; Schulz, A.; Wittig, S. High-Resolution Measurements of Local Effectiveness From Discrete Hole Film Cooling. J. Turbomach. 2001, 123, 758–765. [Google Scholar] [CrossRef]
- Krawciw, J.; Martin, D.; Denman, P. Measurement and Prediction of Adiabatic Film Effectiveness of Combustor Representative Effusion Arrays. In Proceedings of the American Society of Mechanical Engineers (ASME) Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015; p. V05BT12A035. [Google Scholar]
- Hu, Y.; Ji, H. Numerical study of the effect of blowing angle on cooling effectiveness of an effusion cooling. In Proceedings of the American Society of Mechanical Engineers (ASME) Turbo Expo 2004: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004; pp. 877–884. [Google Scholar]
- Andreini, A.; Facchini, B.; Picchi, A.; Tarchi, L.; Turrini, F. Experimental and theoretical investigation of thermal effectiveness in multiperforated plates for combustor liner effusion cooling. J. Turbomach. 2014, 136, 091003. [Google Scholar] [CrossRef]
- Ceccherini, A.; Facchini, B.; Tarchi, L.; Toni, L. Adiabatic and overall effectiveness measurements of an effusion cooling array for turbine endwall application. In Proceedings of the American Society of Mechanical Engineers (ASME) Turbo Expo 2008: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008; pp. 775–788. [Google Scholar]
- Andrei, L.; Andreini, A.; Bianchini, C.; Caciolli, G.; Facchini, B.; Mazzei, L.; Picchi, A.; Turrini, F. Effusion Cooling Plates for Combustor Liners: Experimental and Numerical Investigations on the Effect of Density Ratio. Energy Procedia 2014, 45, 1402–1411. [Google Scholar] [CrossRef]
- Cerri, G.; Giovannelli, A.; Battisti, L.; Fedrizzi, R. Advances in effusive cooling techniques of gas turbines. Appl. Therm. Eng. 2007, 27, 692–698. [Google Scholar] [CrossRef]
- Manzhao, K.; Huiren, Z.; Songling, L.; Hepeng, Y. Internal heat transfer characteristics of Lamilloy configurations. Chin. J. Aeronaut. 2008, 21, 28–34. [Google Scholar] [CrossRef]
- Sweeney, P.C.; Rhodes, J.F. An Infrared Technique for Evaluating Turbine Airfoil Cooling Designs. J. Turbomach. 1999, 122, 170–177. [Google Scholar] [CrossRef]
- ANSYS. Fluent User Guide (Release 16.2); ANSYS: Pittsburgh, PA, USA, 2015. [Google Scholar]
- Wong, T.H.; Ireland, P.T.; Self, K.P. Film Cooling Effectiveness Measurements on Trailing Edge Cutback Surface and Lands Following Novel Cross Corrugated Slot Geometry. In Proceedings of the American Society of Mechanical Engineers (ASME) Turbo Expo 2016, Seoul, Korea, 13–17 June 2016; p. V05CT19A024. [Google Scholar]
- Gurram, N.; Ireland, P.T.; Wong, T.H.; Self, K.P. Study of Film Cooling in the Trailing Edge Region of a Turbine Rotor Blade in High Speed Flow Using Pressure Sensitive Paint. In Proceedings of the American Society of Mechanical Engineers (ASME) Turbo Expo 2016, Seoul, Korea, 13–17 June 2016; p. V05CT19A023. [Google Scholar]
- Han, J.-C.; Rallabandi, A.P. Turbine Blade Film Cooling Using PSP Technique. Front. Heat Mass Transf. 2010, 1, 013001. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef]
- Han, J.-C. Fundamental gas turbine heat transfer. J. Therm. Sci. Eng. Appl. 2013, 5, 021007. [Google Scholar] [CrossRef]
- Kirollos, B.; Povey, T. An Energy-Based Method for Predicting the Additive Effect of Multiple Film Cooling Rows. J. Eng. Gas. Turbines Power 2015, 137, 122607. [Google Scholar] [CrossRef]
- Thomas, M.; Povey, T. A novel scalar tracking method for optimising film cooling systems. Proc. Inst. Mech. Eng. Part J. 2016, 230, 3–15. [Google Scholar] [CrossRef]
- Sellers, J.P. Gaseous Film Cooling with Multiple Injection Stations. AIAA J. 1963, 1, 2154–2156. [Google Scholar] [CrossRef]
- Ling, J.C.; Ireland, P.T.; Turner, L. Full coverage film cooling for combustor transition sections. In Proceedings of the American Society of Mechanical Engineers (ASME) Turbo Expo 2002: Power for Land, Sea, and Air, Amsterdam, The Netherlands, 3–6 June 2002; pp. 1011–1021. [Google Scholar]
- Murray, A.V.; Ireland, P.T.; Rawlinson, A.J. An Integrated Conjugate Computational Approach for Evaluating the Aerothermal and Thermomechanical Performance of Double-Wall Effusion Cooled Systems. In Proceedings of the American Society of Mechanical Engineers (ASME) Turbo Expo 2017, Charlotte, NC, USA, 26–30 June 2017; p. V05BT22A015. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Murray, A.V.; Ireland, P.T.; Wong, T.H.; Tang, S.W.; Rawlinson, A.J. High Resolution Experimental and Computational Methods for Modelling Multiple Row Effusion Cooling Performance. Int. J. Turbomach. Propuls. Power 2018, 3, 4. https://doi.org/10.3390/ijtpp3010004
Murray AV, Ireland PT, Wong TH, Tang SW, Rawlinson AJ. High Resolution Experimental and Computational Methods for Modelling Multiple Row Effusion Cooling Performance. International Journal of Turbomachinery, Propulsion and Power. 2018; 3(1):4. https://doi.org/10.3390/ijtpp3010004
Chicago/Turabian StyleMurray, Alexander V., Peter T. Ireland, Tsun Holt Wong, Shaun Wei Tang, and Anton J. Rawlinson. 2018. "High Resolution Experimental and Computational Methods for Modelling Multiple Row Effusion Cooling Performance" International Journal of Turbomachinery, Propulsion and Power 3, no. 1: 4. https://doi.org/10.3390/ijtpp3010004
APA StyleMurray, A. V., Ireland, P. T., Wong, T. H., Tang, S. W., & Rawlinson, A. J. (2018). High Resolution Experimental and Computational Methods for Modelling Multiple Row Effusion Cooling Performance. International Journal of Turbomachinery, Propulsion and Power, 3(1), 4. https://doi.org/10.3390/ijtpp3010004




