Liquid Droplet Breakup Mechanisms During the Aero-Engine Compressor Washing Process ^†

Abstract

The study of the dynamics during droplet breakup is fascinating to engineers. Some industrial applications include fire extinguishing by sprinkler systems, painting of various components, washing processes, and fuel spraying in internal combustion engines, which involve the interaction between liquid droplets, gaseous flow field, and walls. In this work, washing operations effectiveness of civil aviation aircraft engines is analyzed. Periodic washing operations are necessary to slow down the effects of particle deposition, e.g., gas turbine fouling, to reduce the specific fuel consumption and the environmental impact of the gas turbine operation. This analysis describes the dynamics in the primary breakup, related to the breakup of droplets due to aerodynamic forces, which occur when the droplets are set in motion in a fluid domain. The secondary breakup is also considered, which more generally refers to the impact of droplets on surfaces. The latter is studied with particular attention to dry surfaces, investigating the limits for different breakup regimes and how these limits change when the impact occurs with surfaces characterized by different wettability. Surfaces with different roughness are also compared. All the tested cases are referred to surfaces at ambient temperature. Dimensionless numbers generalize the analysis to describe the droplet behavior. The analysis is based on several data reported in the open literature, demonstrating how different washing operations involve different droplet breakup regimes, generating a non-trivial data interpretation. Impact dynamics, droplet characteristics, and erosion issues are analyzed, showing differences and similarities between the literature data proposed in the last twenty years. Washing operation and the effects of gas turbine fouling on the aero-engine performance are still under investigation, demonstrating how experiments and numerical simulations are needed to tackle this detrimental issue.

1. Introduction

Many researchers have studied fouling by highlighting which areas of the compressor are most susceptible to it. Similarly, the restoring strategy was developed to clean the blade and vane surface, recovering the initial performance of the unit as reported in [1]. During engine washing, one of the issues is related to the injected droplet sizes as highlighted in [2,3]. Smaller droplets are carried by the air stream without being able to penetrate the boundary layer and thus without impacting the surfaces to be cleaned. In addition, there is an increase in air temperature during the compression phase, which causes the smaller droplets to evaporate completely. In contrast, large droplets can penetrate the boundary layer and impact the airfoils. At the same time, their size should not be excessive, as they may cause wear and tear as highlighted in [4,5]. In addition, due to centrifugal force, large droplets are pushed away toward the engine case without reaching the airfoils. Therefore, due to the centrifugal force and the rising temperature that occurs in the compression phase, higher cleaning effectiveness of the early stages of the compressor is achieved, and the removed dirt redeposits on the airfoils of the aft stages in agreement with [3]. Thus, the main challenge of the washing process is determining the droplet size that ensures optimal washing efficiency. The difficulties encountered in the engine washing process are related to several factors, such as primary droplet breakup, secondary droplet breakup, temperature, droplet inertia, and surface properties. The primary breakup occurs when a droplet is set in motion within a fluid domain. After that, the droplet reduces its size continuously until it reaches a size where it becomes airborne by the airflow itself. Therefore, properly analyzing such breakup mechanisms is useful in understanding the distance at which the nozzles should be positioned to the inlet section of the compressor to prevent excessive fragmentation of the droplet to reach a size where it becomes airborne. As can easily be understood, the answer is not univocal but depends on multiple physical factors, especially concerning the constraints imposed by the geometry of the intake duct and the position of the inlet as shown in [4]. The secondary breakup takes place when a drop impacts a solid surface. In this case, the breakup mechanisms are related to both the kinematic characteristics of the drop and the surface characteristics of the airfoil. When a droplet hits a surface, it may bounce or deposit on it, either breaking or following a mechanism called splash-breakup, after which numerous smaller secondary drops are generated. This work is an extended version of a conference paper presented at the 16th European Turbomachinery Conference (ETC16) [6], where the authors created a database based on the open literature for the analysis of washings in aero-engine compressors.

Aim of the Paper and Novelty

Data from various articles in the open literature regarding aero-engine compressor washings are considered and tabulated. An explanation of the different mechanisms of rupture is conducted, and finally, graphs are made to identify the mechanisms of droplet breakup. The aim is to analyze the state of the art of compressor washing test to outline which breakup regime was obtained in previous numerical and experimental investigations. The effectiveness of different breakup mechanisms for compressor washings are analyzed and included in the discussion. The novelty is based on the correlation between the fundamental theory of droplet secondary breakup mechanisms and the actual data reported in the literature obtained from experimental and numerical analyses. The study of droplet–substrate interaction is fundamental to improve the washing effectiveness, and thus the data post-process here presented will be useful in adequately designing the proper washing conditions.

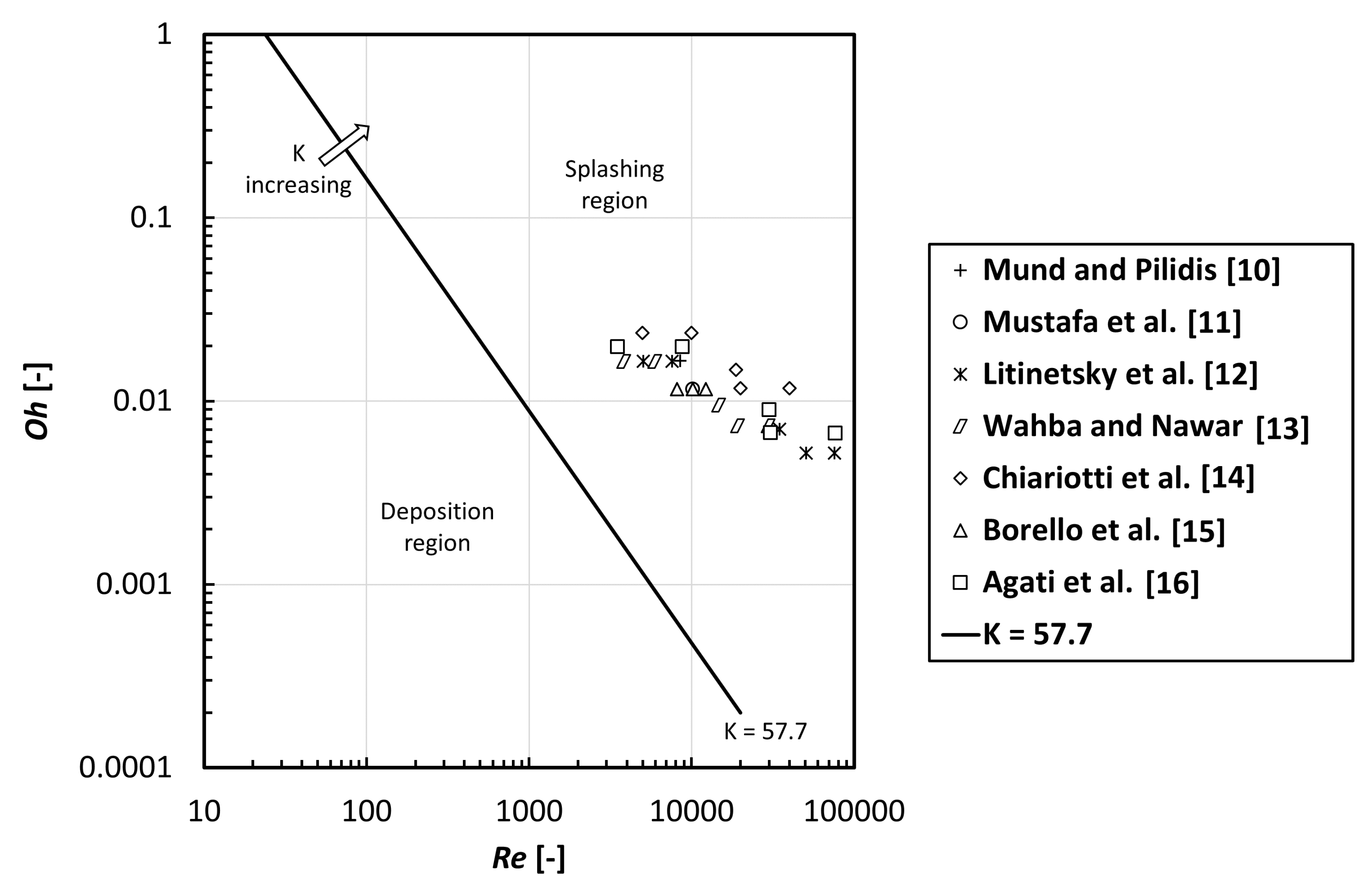
2. Literature Database

Here several studies reported in the literature regarding numerical analysis and experimental tests related to compressor washing are collected.

Table 1. Numerical studies.

Reference	D [µm]	V [m/s]	WTAR
[10]	50	170	0.20
[11]	100	100	0.16
[12]	50–500	100–150	0.22
[13]	50–250	75–116	0.60
[14]	25–100	200–400	-
[15]	100	80–120	-
[16]	35–305	100–250	0.25–1.00

shows the summary of the data related to the numerical analysis. Similarly, in

Table 2. Experimental studies. R.V. = reference velocity assumed by the authors; Ma = from Mach number.

Reference	D [µm]	V [m/s]	WTAR	Note
[2]	50–250	100	-	R.V.
[9]	25	100	0.43–3.00	R.V.
[9]	75	100	0.43–3.00	R.V.
[9]	200	100	0.43–3.00	R.V.
[17]	50–150	100	0.20	-
[18]	50–250	100	0.02	-
[8]	50–150	11–100	0.20	Ma
[19]	55.1–80.2	105	-	-
[7]	120	99–149	0.10–0.50	Ma
[20]	25	20–34	1.66–1.93	-
[21]	20	35	1.00–3.18	-
[21]	50	35	1.00–3.18	-
[21]	100	35	1.00–3.18	-

, the data about experimental tests are organized. For each analysis, the droplet diameter (single value or range if provided) and the flow velocity (single value or range if provided or indicated) are reported. When the droplet velocity is not provided, it is assumed to be equal to the velocity of the flow field. All analyses in Table 1 are based on water as a cleaning media. Considering the experimental contributions (see Table 2), the data provided for the water tests are collected in [7]. Differently from the numerical dataset, the data coming from the experimental test have to be interpreted. The velocity range reported for [7,8] is inferred from the Mach number. For tests on engines (reported in [2,9]), a reference velocity of 100 m/s is adopted.

To create a comprehensive picture of the data, starting from the range proposed in Table 1 and Table 2, the data are post-processed as follows. For each contribution, the range’s lowest, average, and highest values are considered. This means that for each contribution reporting ranges for droplet diameter and velocity, the non-dimensional number (Re, We and Oh) is computed by using couples ($V_{min}-D_{min}$), ($V_{min}-D_{max}$), ($V_{max}-D_{min}$), ($V_{max}-D_{max}$), and ($V_{ave}-D_{ave}$). With this strategy, the entire combination of droplet and velocity can be covered, generating an extended dataset that represents the literature findings.

3. Droplet Breakup Mechanisms

The breakup process can be divided into two types: primary and secondary. Primary breakup occurs when the droplet breaks while moving within an airflow. The secondary breakup occurs when a droplet impacts a surface. The characteristics that most influence this process are fluid properties (density, viscosity, etc.), droplet characteristics (diameter, shape, etc.), and impact conditions (i.e., velocity). Comprehension of these phenomena is essential for predicting the characteristics of the drop after breakup and thus understanding the behavior of secondary drops following breakup. To study and classify the mechanisms of droplet breakage, reference is made to the dimensionless Reynolds ($Re$), Weber ($We$), and Ohnesorge ($Oh$) numbers, which are given below.

$$Re={\displaystyle \frac{\rho ·V·D}{\mu }}$$

$$We={\displaystyle \frac{\rho ·V^2·D}{\gamma }}$$

$$Oh={\displaystyle \frac{\mu }{\sqrt{\rho ·\gamma ·D}}}={\displaystyle \frac{\sqrt{\mathrm{We}}}{\mathrm{Re}}}$$

3.1. Primary Breakup Mechanism

Concerning primary breakup, five mechanisms of droplet breakup can be distinguished according to the Weber number as reported in [22].

• The vibrational breakup occurs for lower Weber number values ($We\le 12$). The flow interacts with the droplet and produces a vibration of natural amplitude. The flow amplifies the oscillation, driving the droplet to breakup and forming large fragments.
• The bag breakup occurs for higher Weber numbers ($12<We\le 50$) and is characterized by forming a hollow bag in which a thin film of liquid is placed downstream of a more massive toroidal ring. The bag breaks out at a specific instant, generating many small fragments.
• The bag and stamen breakup is a transition mechanism with characteristics common to the bag breakup with $50<We\le 100$.
• Sheet stripping($100<We\le 350$) distinctly differs from the two rupture mechanisms discussed. No bags are formed, but a thin sheet of liquid forms on the peripheral circumference of the deformed droplet, from which droplets are continuously stripped.
• For higher Weber numbers ($We>350$), waves of large amplitude but small wavelengths are formed on the surface of the windward droplet. The action of the flow on itself continuously erodes the crests of the waves. This process is called wave crest stripping. For the largest Weber numbers, waves characterized by large amplitude and wavelength are formed on the droplet’s surface. This process is called catastrophic breakup. This leads to a multi-stage process in which fragments are subject to further breakup. This cascading process continues until each fragment reaches a critical value of the lower Weber number. Subsequently, the fragments are affected by the breakup mechanisms described above.

3.2. Secondary Breakup Mechanisms

Secondary breakup concerns the study of the interaction between a droplet and a solid surface. A droplet impacting a solid surface may rebound, deposit on the surface, or fragment into a significant number of secondary droplets, a phenomenon known as splashing. The present section focuses on the interaction that occurs when a droplet impacts a dry surface with a temperature such that the droplet’s breakup regime is unaffected. It is crucial to study secondary breakup mechanisms as they have direct influence on the cleaning ability of surfaces.

3.2.1. Low Weber Number

When a droplet impacts perpendicularly on a surface, it moves through a gas that must be displaced before contact with the surface occurs. As the droplet approaches the surface, the gas at the interface experiences an increase in pressure due to viscosity. This elevated pressure is strong enough to deform the droplet, changing its shape before contact. Two different cases can be distinguished. If $We$ < 4, it is observed that contact between drop and surface does not occur. A droplet is skating on an air film and bouncing without contacting the surface. This phenomenon has been observed for both hydrophilic and hydrophobic surfaces. If $We$ < 70, the contact surface assumes a ring shape, inside which a disk of air remains trapped. For both cases, after the impact, bouncing occurs.

3.2.2. Intermediate Weber Number

A droplet impacts the surface directly for larger Weber numbers, although entrapment of air bubbles within it may still occur. At this point, the droplet can have different behaviors depending on the properties of the surface. First, the drop spreads over the surface, until it reaches a certain extent. Finally, the drop contracts to minimize its surface energy and may bounce back or deposit on the surface. It is possible to describe the spreading phenomenon through the spreading factor, defined as the ratio of the maximum radius obtained from the extension of the droplet on the surface to the initial radius of the droplet. Some researchers have studied the evolution of spreading factor through time as summarized in [23]. Contraction, rebound, or deposition of the drop on the surface can be controlled by changing the wettability properties of the surface and surface tension of the drop.

3.2.3. Higher Weber Number

When the Weber number increases, the droplet could either deposit on the surface or fragment, generating a large number of secondary droplets, defined as splashing. The relation proposed in [24] incorporates the inertial, viscous, and surface tension terms:

$$K=Oh·R{e}^{1.25}$$

(1)

defines whether the impact falls into the deposition or splashing regime. Specifically, when $K<57.7$ deposition occurs, while for $K>57.7$ splashing occurs. In [24], tests were conducted considering surface roughness and wettability. Authors observed two distinct splash regimes, called prompt splash and corona splash. These types are driven by surface roughness, contact angle, surface tension, and ambient pressure. It is seen that these two types of splash always take place simultaneously and that there is no clear distinction between the two regimes. The differences between these two types of splashing are the size of the secondary droplets and how they are generated. In prompt splash, the secondary droplets originate directly from the edge of the advancing lamella. The early secondary droplets that form are very small in size. In the corona splash, the lamella rises from the surface due to viscous and surface tension actions and takes on the shape of a corona. At the apex of the lamella, many droplets of smaller size than in the prompt splash are released.

Different contact angles characterize hydrophilic surfaces but do not show different results. This indicates that the contact angle for these types of surfaces does not influence the breakup characteristics. There is a prevalence of prompt splash over corona splash, which only occurs for higher values of the Weber number. A reduction in the deposition regime is noted for hydrophobic surfaces with increasing contact angle. For super-hydrophobic surfaces, corona splash is prevalent, and only for these drop bounce occurs.

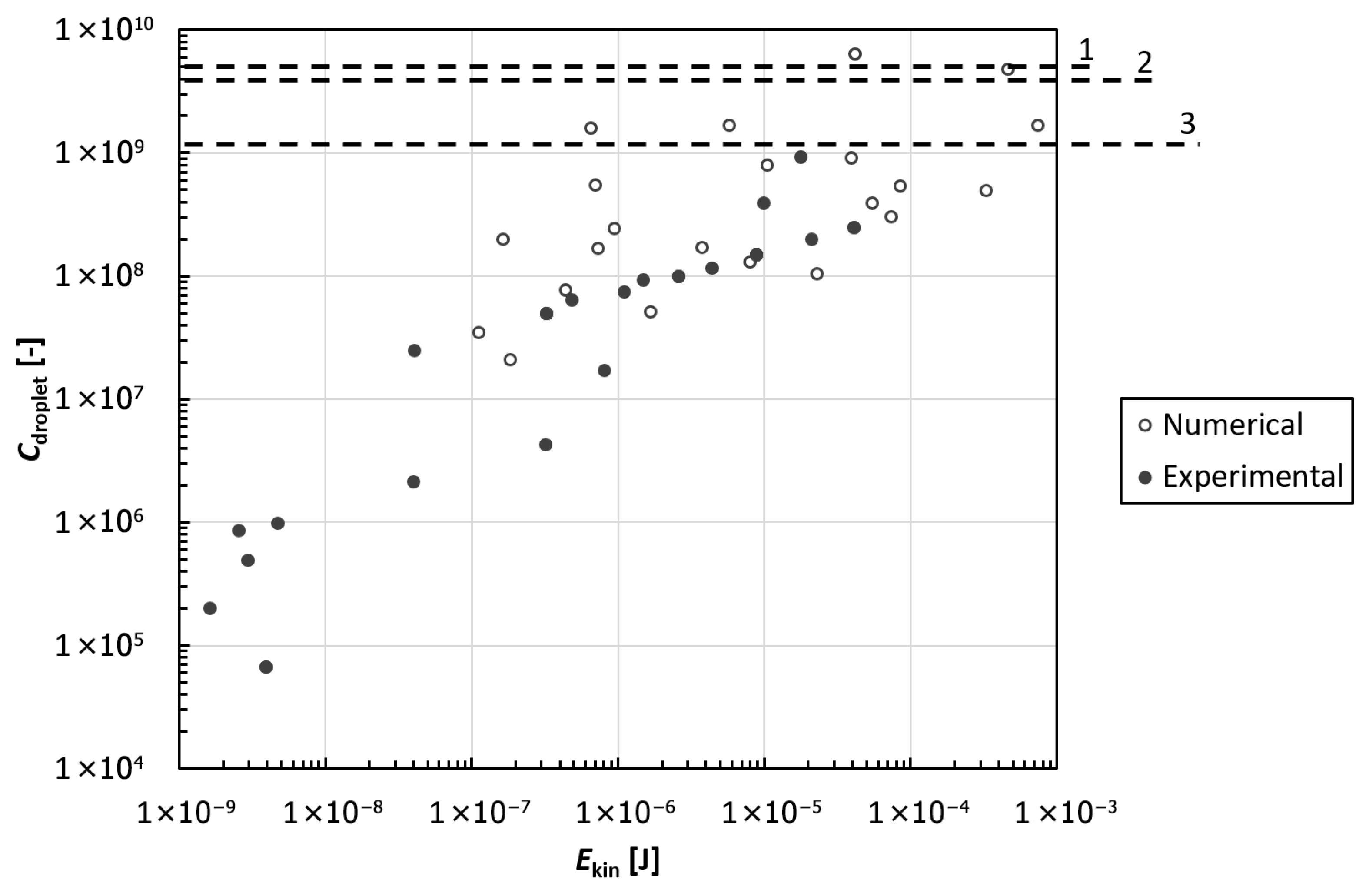
4. Results

The first analysis of the data reported in Table 1 and Table 2 is related to the $We-Re$ plane. Figure 1 reports all the data divided according to the numerical or experimental source. The data (droplet diameter and velocity) included in the literature contribution are used to compute the droplet Weber and Reynolds numbers. In the presence of diameter and velocity range, the aforementioned strategy (based on a combination of the lowest, average, and highest values of each range) was adopted. In the $We-Re$ chart, the limits related to $We=200$ and $We=800$ are indicated according to [25] representing the thresholds for the deposition and splashing regions. The droplet breakup could depend on the surface’s wettability [25]. In this case, no data are reported in the considered literature to assess the contact angle, even if it is possible to consider representative contact angles in the range of 50° to 90°, typical for water and metals. Looking at the available information, only a few experimental data belong to the Deposition region ($We<200$) while the majority of contributions (experimental and numerical) are located in the splashing region. There is an interesting over-imposition region between numerical and experimental data in a Weber range of 4000–70,000 and in a Reynolds range of 3000–40,000 where the data are localized. This means that it is possible to correlate experimental and numerical findings characterized with similar values of non-dimensional numbers. At the same time, this preliminary analysis shows how it is possible to discover the results and the effects of washing operation without a precise assessment of the material characteristics involved in the study.

The numerical data reported in Table 1 are shown in the $Oh-Re$ plane of Figure 2. According to the literature findings [25], the $Oh-Re$ plane is divided according to the reference line of $K=57.7$ that determines the division of the plane into two regions Splashing and Deposition. The literature data from numerical analysis correspond to the Splashing region. In particular, the data are characterized by a relatively high Reynolds number with an almost constant Ohnesorge number, which varies in the range of 0.0052–0.0235. From the Reynolds number point of view, the maximum values are reached in [16] and [12] in which droplet diameters equal to 305 µm and 500 µm, respectively, were considered. The lowest value refers to [13], in which a sensitivity analysis was performed using different nozzle positions and droplet diameters. In the paper, the droplet tracks and velocity show how the inlet bell mouth acceleration determines the modification of the droplet velocity from the nozzle to the engine inlet.

From the experimental point of view, in Figure 3, the data in the $Oh-Re$ appear characterized by lower values of Reynolds number and slightly greater values for Ohnesorge number. One contribution [8] belongs to the Deposition region. This analysis uses a stationary cascade that can control the deposition and washing mechanisms. Such experimental setup was also used in [18], where the greatest droplet diameter generates the highest Reynolds number value. Tests in [20,21] create a set of data close to the limit $K=57.7$. These data are obtained using a small-scale compressor unit operated in a quasi-idle regime. Experimental tests are generally characterized by a lower droplet velocity that generates a set of impact conditions closer to the Deposition region.

Figure 4 shows a bar chart reporting 12 bins obtained by considering the value of parameter K defined in the Equation (1), from the Deposition-to-Splashing threshold ($K=57.7$) to the highest values. From such data organization, it is clear how the experimental data are characterized by values of K lower than those obtained for the numerical data. Seven experimental conditions are located in the region $K<357$, while the same number characterizes the numerical data for a region with $K>3000$. The secondary breakup process depends not only on the dynamic of the droplet (diameter and velocity) but also on the surface characteristics such as surface roughness and wettability. As reported in [25], the numerical and experimental analyses collected in the present work can generate splashing or deposition phenomena (greater K values) as a function of the contact angle between water and surface. According to the surface characteristics, the droplet impacts involved in contributions located on the left-hand side can generate a deposition instead of a splashing phenomenon as shown in Figure 4.

It is reasonable to assume that for both the rebound and deposition cases, the droplet cannot clean the airfoil surface because, in the first case, the droplet rebounds without determining any cleaning effect on the surface. In contrast, in the second case, depositing on the surface creates a film that obstructs the correct cleaning of the below surface. Aiming to perform a successful cleaning, it is desirable to introduce a droplet into the compressor with a splash breakup regime, which is characterized by more energy and should provide a cleaning action toward the impacted surface. The last analysis is devoted to comparing the literature to erosion behavior. Engine washing parameters are selected as a compromise between the restoring capability (which imposes a greater water flow rate and droplet diameter) and the preservation of the compressor section integrity, which could be impacted by erosion generated by droplet impact [7]. The methodology reported in [5] is adopted to assess the erosion risks. The basic theory is related to the dynamic crack propagation driven by the impact characteristics of the droplet. The theory is based on a threshold value of the constant $C_{\mathit{blade}}$ based on the material characteristics of the blade.

$$C_{\mathit{blade}}={\displaystyle \frac{{\sigma }_s·K_{IC}^2}{2·E·C_s}}$$

(2)

where ${\sigma }_s$ is the yield strength, $K_{IC}$ is the fracture toughness, E is the elastic modulus, and $C_s$ is the speed of sound in the solid. Following the line of thought reported in [5], the same constant, called $C_{\mathit{droplet}}$, can be calculated also using the droplet impact characteristics

$$C_{\mathit{droplet}}={\rho }^2·V^3·D$$

(3)

Comparing the two constants obtained using the droplet characteristics and the material characteristics, it is possible to assess if the droplet impact generates erosion issues ($C_{\mathit{droplet}}>C_{\mathit{blade}}$) or not ($C_{\mathit{droplet}}<C_{\mathit{blade}}$). In Figure 5, the values of the constant $C_{\mathit{droplet}}$ are reported against the droplet kinetic energy $E_{kin}$. The chart shows three thresholds for the constant $C_{\mathit{blade}}$ related to stainless steel, titanium alloy, and aluminum alloy blade material, in line with the analysis in [5]. Such thresholds give just a reference value. Each case should be compared with the proper $C_{\mathit{blade}}$ according to the blade material characteristics. The comparison shows that all experimental analyses are located in the safe region where the droplet impact does not determine erosive phenomena. Only a few numerical data belong to the unsafe conditions (due to the impact velocity of the droplet), and it has to be considered that the thresholds are just a reference and not based on the specific characteristics of the blade involved in such analyses. It is important to note that it is impossible to determine an univocal answer regarding the best droplet size for online washing. This is because each washing system must be designed for each application considered.

5. Conclusions

In this paper, a literature survey about gas turbine compressor washing is carried out. In particular, the analysis proposes a data post-process of relevant non-dimensional numbers to organize and extract general information about the dynamic and splashing regime at which the experimental and numerical tests are carried out. Using non-dimensional numbers allows for interpretation and cross-correlation with different literature sources. Looking at the relevant non-dimensional number obtained in the studies of droplet impact, the literature data are organized, enhancing the completeness of the results by introducing the splash regime and the droplet primary and secondary breakup mechanisms. The analysis highlights how droplet size and impact velocity must be realized to reach the proper impact regime on the compressor blade surface. Based on the literature data, operating parameters should be set to obtain splashing conditions as secondary breakup behavior to increase the washing effectiveness, i.e., for $K>57.7$ (Equation (1)). According to this assumption, the droplets’ size for an approaching impact velocity of 50 m/s should be, for example, at least greater than 6 µm. In addition, the data post-process allows the setup of a general starting point for further investigations to increase the efficiency and reliability of the compressor washing process.