Comparison of Different Strategies to Include Structural Mechanics in the Optimization Process of an Axial Turbine’s Runner Blade
Abstract
1. Introduction
2. Design Tool
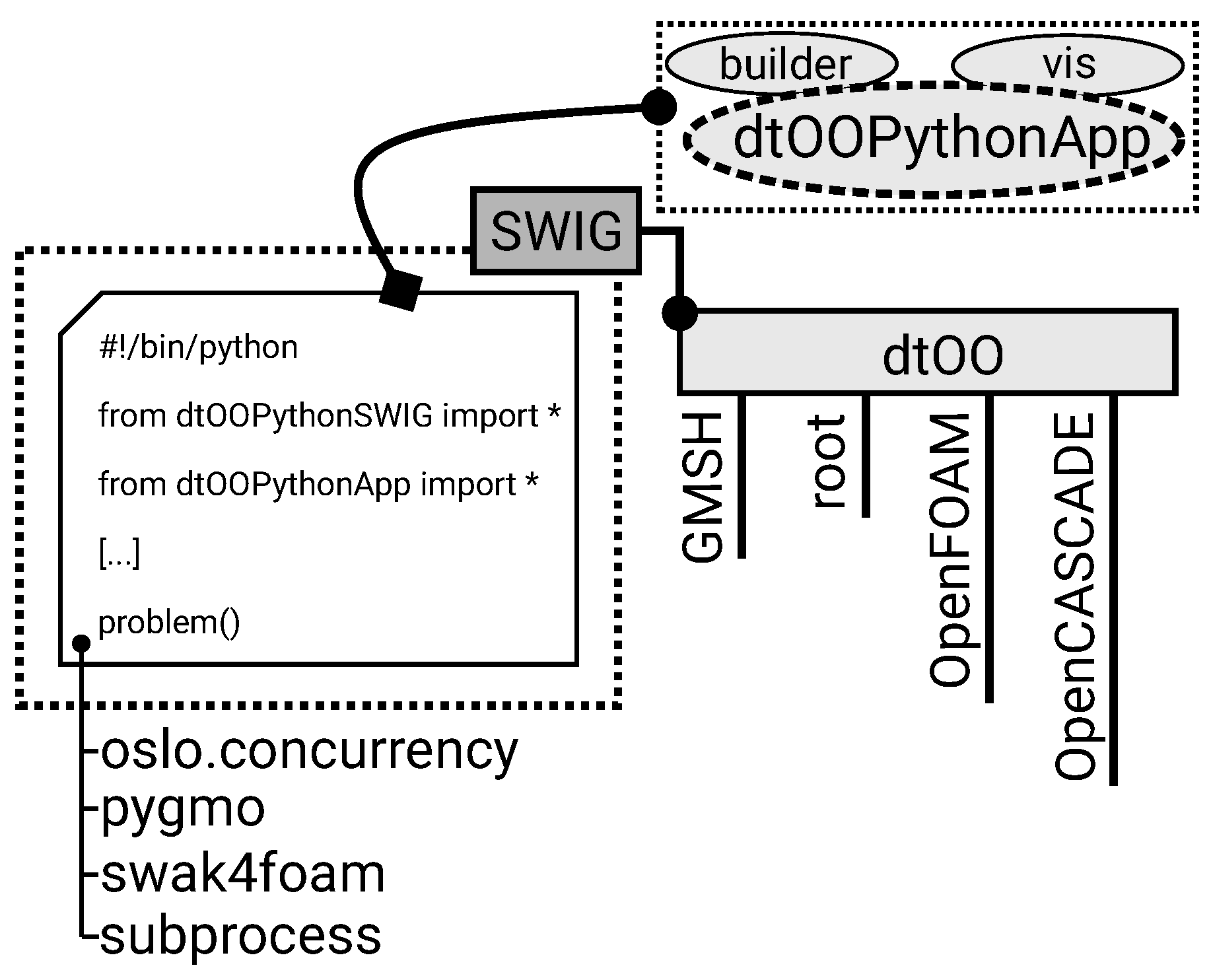
2.1. Code Structure
2.2. Python Interface
| Listing 1. Source code for creating a meanplane. |
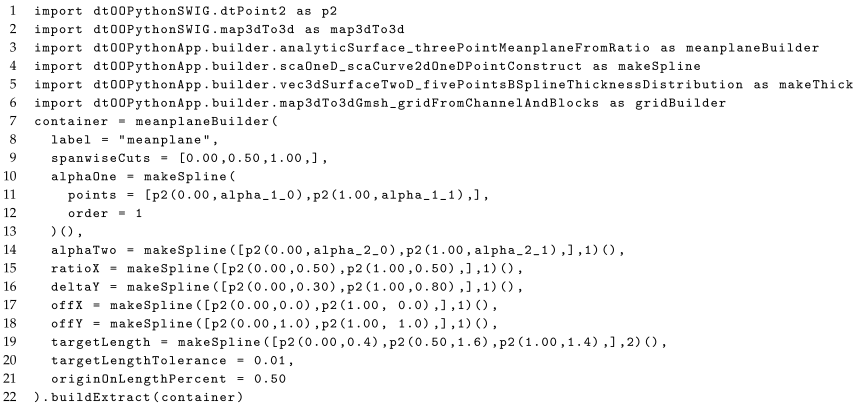 |
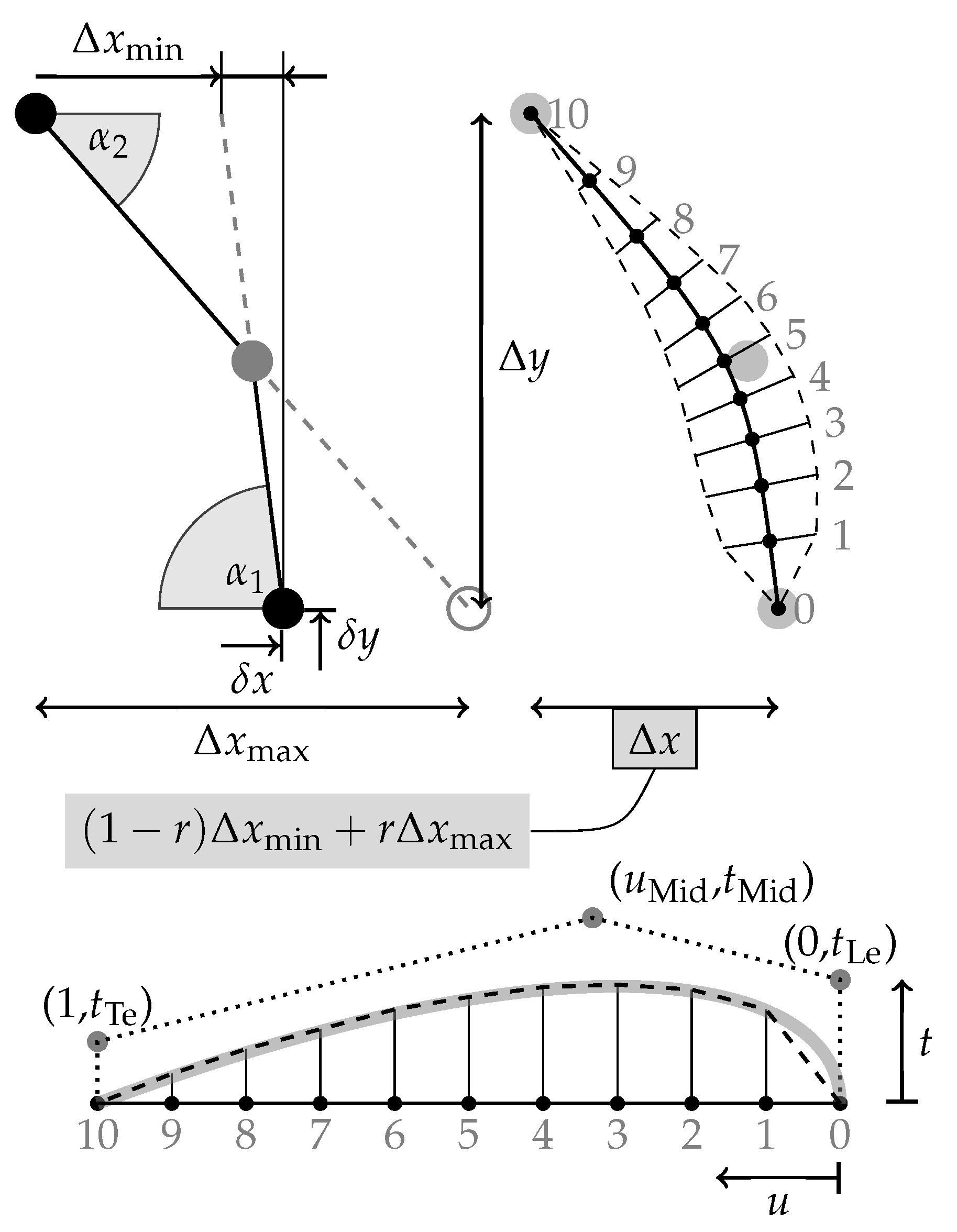
| Listing 2. Source code for creating the thickness distribution. |
 |
| Listing 3. Source code for creating a computational grid. |
 |
3. Models
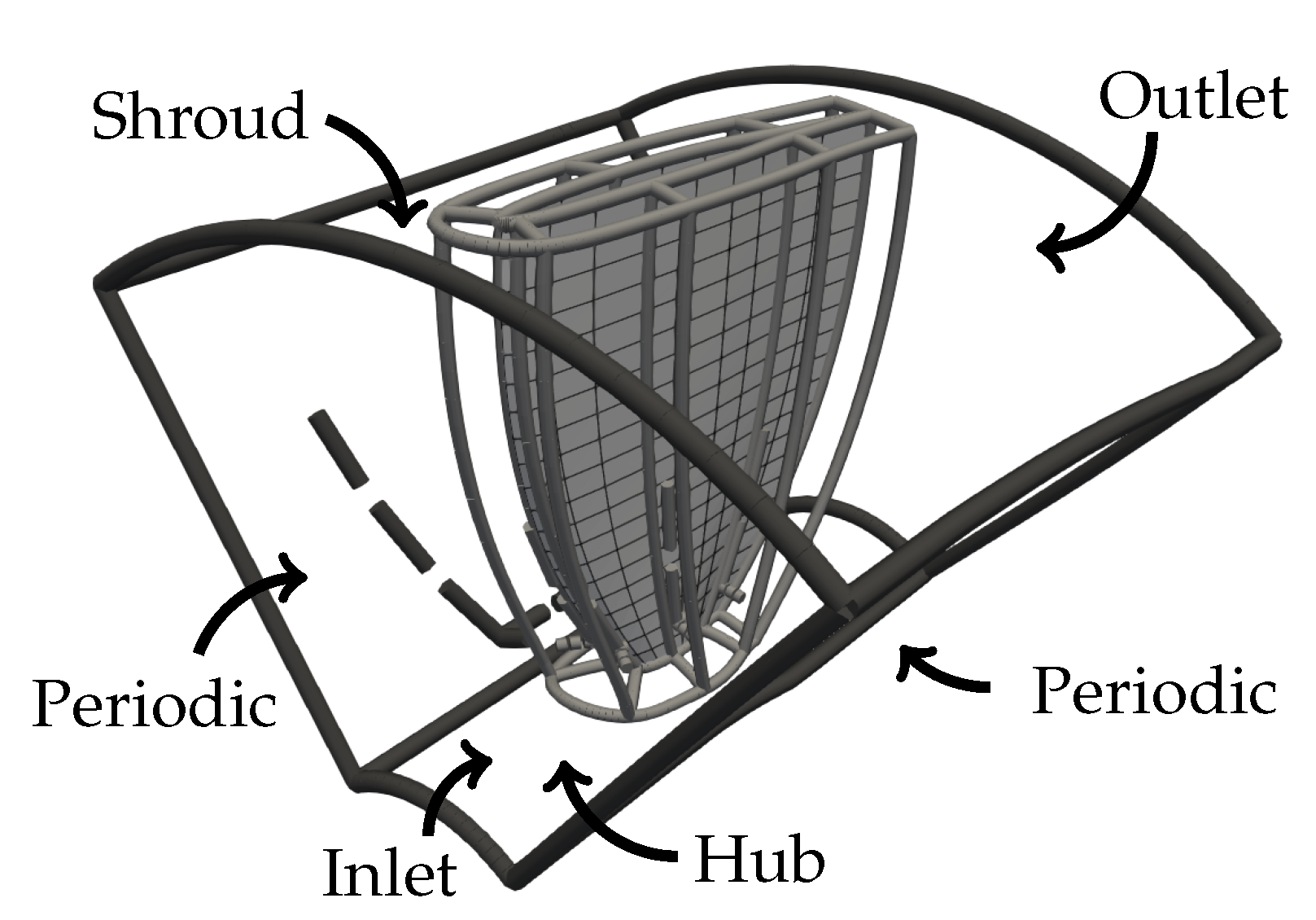
3.1. Numerical Setup
3.2. Optimization Setups
3.2.1. Scalar Objective Function
- Minimize
- If both individuals are infeasible, the individual with the lower constraint violation is chosen.
- If only one individual is feasible, the feasible individual is chosen.
- If both individuals are feasible, the individual with the lower fitness value is chosen.
3.2.2. Multi-Objective Optimization with Resolution of the Pareto Front
- Minimize
3.2.3. Parallelization and Initialization
4. Results
4.1. Scalar Objective Function
4.2. Multi-Objective Optimization with Resolution of the Pareto Front
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CAD | Computer Aided Design |
| CFD | Computational Fluid Dynamics |
| CSM | Computational Structural Mechanics |
| DE | Differential evolution algorithm |
| DOF | Degree of freedom |
| dtOO | Design tool Object-Oriented |
| GMSH | GNU Mesh |
| NSGA-II | Nondominated sorting genetic algorithm II |
| NSGA-III | Nondominated sorting genetic algorithm III |
| OpenCASCADE | Open Computer Aided Software for Computer Aided Design and Engineering |
| OpenFOAM | Open Field Operation and Manipulation |
| root | Cern ROOT |
| SEM | Standard error of the mean |
| SWIG | Simplified Wrapper and Interface Generator |
References
- Cui, Y.; Geng, Z.; Zhu, Q.; Han, Y. Review: Multi-objective optimization methods and application in energy saving. Energy 2017, 125, 681–704. [Google Scholar] [CrossRef]
- Luo, C.; Song, L.; Li, J.; Feng, Z. A Study on Multidisciplinary Optimization of an Axial Compressor Blade Based on Evolutionary Algorithms. J. Turbomach. 2012, 134, 054501. [Google Scholar] [CrossRef]
- Song, L.; Luo, C.; Li, J.; Feng, Z. Automated multi-objective and multidisciplinary design optimization of a transonic turbine stage. Proc. Inst. Mech. Eng. Part A J. Power Energy 2012, 226, 262–276. [Google Scholar] [CrossRef]
- Joly, M.M.; Verstraete, T.; Paniagua, G. Multidisciplinary design optimization of a compact highly loaded fan. Struct. Multidisc. Optim. 2014, 49, 471–483. [Google Scholar] [CrossRef]
- Chirkov, D.V.; Ankudinova, A.S.; Kryukov, A.E.; Cherny, S.G.; Skorospelov, V.A. Multi-objective shape optimization of a hydraulic turbine runner using efficiency, strength and weight criteria. Struct. Multidisc. Optim. 2018, 58, 627–640. [Google Scholar] [CrossRef]
- Song, Y.H.; Guo, P.C.; Sun, L.G.; Zhou, H.T.; Luo, X.Q. Multidisciplinary design optimization on the splitter blade of high head Francis turbine. IOP Conf. Ser. Earth Environ. Sci. 2018, 163, 012032. [Google Scholar] [CrossRef]
- Li, C.; Wang, J.; Guo, Z.; Song, L.; Li, J. Aero-mechanical multidisciplinary optimization of a high speed centrifugal impeller. Aerosp. Sci. Technol. 2019, 95, 105452. [Google Scholar] [CrossRef]
- Sen-chun, M.; Hong-biao, Z.; Ting-ting, W.; Xiao-hui, W.; Feng-xia, S. Optimal design of blade in pump as turbine based on multidisciplinary feasible method. Sci. Prog. 2020, 103, 0036850420982105. [Google Scholar] [CrossRef]
- Zhang, J.; Zangeneh, M. Multidisciplinary and multi-point optimisation of radial and mixed-inflow turbines for turbochargers using 3D inverse design method. In Proceedings of the 14th International Conference on Turbochargers and Turbocharging, London, UK, 11–12 May 2021; CRC Press: London, UK, 2020; pp. 263–277. [Google Scholar] [CrossRef]
- Thandayutham, K.; Samad, A. Hydrostructural Optimization of a Marine Current Turbine Through Multi-fidelity Numerical Models. Arab. J. Sci. Eng. 2020, 45, 935–952. [Google Scholar] [CrossRef]
- Lian, Y.; Liou, M.S. Aerostructural Optimization of a Transonic Compressor Rotor. J. Propuls. Power 2006, 22, 880–888. [Google Scholar] [CrossRef]
- Siller, U.; Voß, C.; Nicke, E. Automated Multidisciplinary Optimization of a Transonic Axial Compressor. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009; p. 863. [Google Scholar] [CrossRef]
- Joly, M.M.; Verstraete, T.; Paniagua, G. Integrated multifidelity, multidisciplinary evolutionary design optimization of counterrotating compressors. Integr. Comput.-Aided Eng. 2014, 21, 249–261. [Google Scholar] [CrossRef]
- Teichel, S.; Verstraete, T.; Seume, J. Optimized Multidisciplinary Design of a Small Transonic Compressor for Active High-Lift Systems. Int. J. Gas Turbine Propuls. Power Syst. 2017, 9, 19–26. [Google Scholar] [CrossRef] [PubMed]
- Deng, Q.; Shao, S.; Fu, L.; Luan, H.; Feng, Z. An Integrated Design and Optimization Approach for Radial Inflow Turbines—Part II: Multidisciplinary Optimization Design. Appl. Sci. 2018, 8, 2030. [Google Scholar] [CrossRef]
- Lachenmaier, N.; Baumgärtner, D.; Schiffer, H.P.; Kech, J. Gradient-Free and Gradient-Based Optimization of a Radial Turbine. Int. J. Turbomach. Propuls. Power. 2020, 5, 14. [Google Scholar] [CrossRef]
- Pierret, S.; Filomeno Coelho, R.; Kato, H. Multidisciplinary and multiple operating points shape optimization of three-dimensional compressor blades. Struct. Multidisc. Optim. 2007, 33, 61–70. [Google Scholar] [CrossRef]
- Verstraete, T.; Alsalihi, Z.; Van den Braembussche, R.A. Multidisciplinary Optimization of a Radial Compressor for Microgas Turbine Applications. J. Turbomach. 2010, 132, 031004. [Google Scholar] [CrossRef]
- Bannikov, D.V.; Yesipov, D.V.; Cherny, S.G.; Chirkov, D.V. Optimization design of hydroturbine rotors according to the efficiency-strength criteria. Thermophys. Aeromech. 2010, 17, 613–620. [Google Scholar] [CrossRef]
- Van den Braembussche, R.A.; Alsalihi, Z.; Verstraete, T.; Matsuo, A.; Ibaraki, S.; Sugimoto, K.; Tomita, I. Multidisciplinary Multipoint Optimization of a Transonic Turbocharger Compressor. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; Volume 8, pp. 903–913. [Google Scholar] [CrossRef]
- Aissa, M.H.; Verstraete, T. Metamodel-Assisted Multidisciplinary Design Optimization of a Radial Compressor. Int. J. Turbomach. Propuls. Power 2019, 4, 35. [Google Scholar] [CrossRef]
- Deb, K. An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
- Tismer, A. Entwicklung einer Softwareumgebung zur automatischen Auslegung von hydraulischen Maschinen mit dem Inselmodell. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, 2020. Available online: https://d-nb.info/1220692778/34 (accessed on 31 January 2025).
- Tismer, A. ihs-ustutt/dtOO. 2024. Available online: https://github.com/ihs-ustutt/dtOO (accessed on 31 January 2025).
- Tismer, A.; Schlipf, M.; Riedelbauch, S. Sensitivity Study of the Numerical Setup for an Automatic Optimization Procedure for a Hydraulic Machine. In Proceedings of the VII European Congress on Computational Methods in Applied Sciences and Engineering, Crete Island, Greece, 5–10 June 2016; Volume VII. [Google Scholar] [CrossRef]
- Brun, R.; Rademakers, F.; Canal, P.; Naumann, A.; Couet, O.; Moneta, L.; Vassilev, V.; Linev, S.; Piparo, D.; GANIS, G.; et al. root-project/root: v6.18/02; Zenodo: Geneva, Switzerland, 2020. [Google Scholar] [CrossRef]
- Biscani, F.; Izzo, D. A parallel global multiobjective framework for optimization: pagmo. J. Open Source Softw. 2020, 5, 2338. [Google Scholar] [CrossRef]
- Gamma, E.; Helm, R.; Johnson, R.; Vlissides, J.M. Design Patterns: Elements of Reusable Object-Oriented Software, 1st ed.; Addison-Wesley Professional: Boston, MA, USA, 1994. [Google Scholar]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Cohoon, J.P.; Hegde, S.U.; Martin, W.N.; Richards, D. Punctuated Equilibria: A Parallel Genetic Algorithm. In Proceedings of the Second International Conference on Genetic Algorithms and Their Application, Cambridge, MA, USA, 28–31 July 1987; pp. 148–154. [Google Scholar]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Iman, R.L.; Helton, J.C.; Campbell, J.E. An Approach to Sensitivity Analysis of Computer Models: Part I—Introduction, Input Variable Selection and Preliminary Variable Assessment. J. Qual. Technol. 1981, 13, 174–183. [Google Scholar] [CrossRef]
- Herman, J.; Usher, W. SALib: An open-source Python library for Sensitivity Analysis. J. Open Source Softw. 2017, 2, 97. [Google Scholar] [CrossRef]
- Iwanaga, T.; Usher, W.; Herman, J. Toward SALib 2.0: Advancing the accessibility and interpretability of global sensitivity analyses. Socio-Environ. Syst. Model. 2022, 4, 18155. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Janczyk, M.; Pfister, R. Understanding Inferential Statistics: From A for Significance Test to Z for Confidence Interval, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Jain, H.; Deb, K. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point Based Nondominated Sorting Approach, Part II: Handling Constraints and Extending to an Adaptive Approach. IEEE Trans. Evol. Comput. 2014, 18, 602–622. [Google Scholar] [CrossRef]




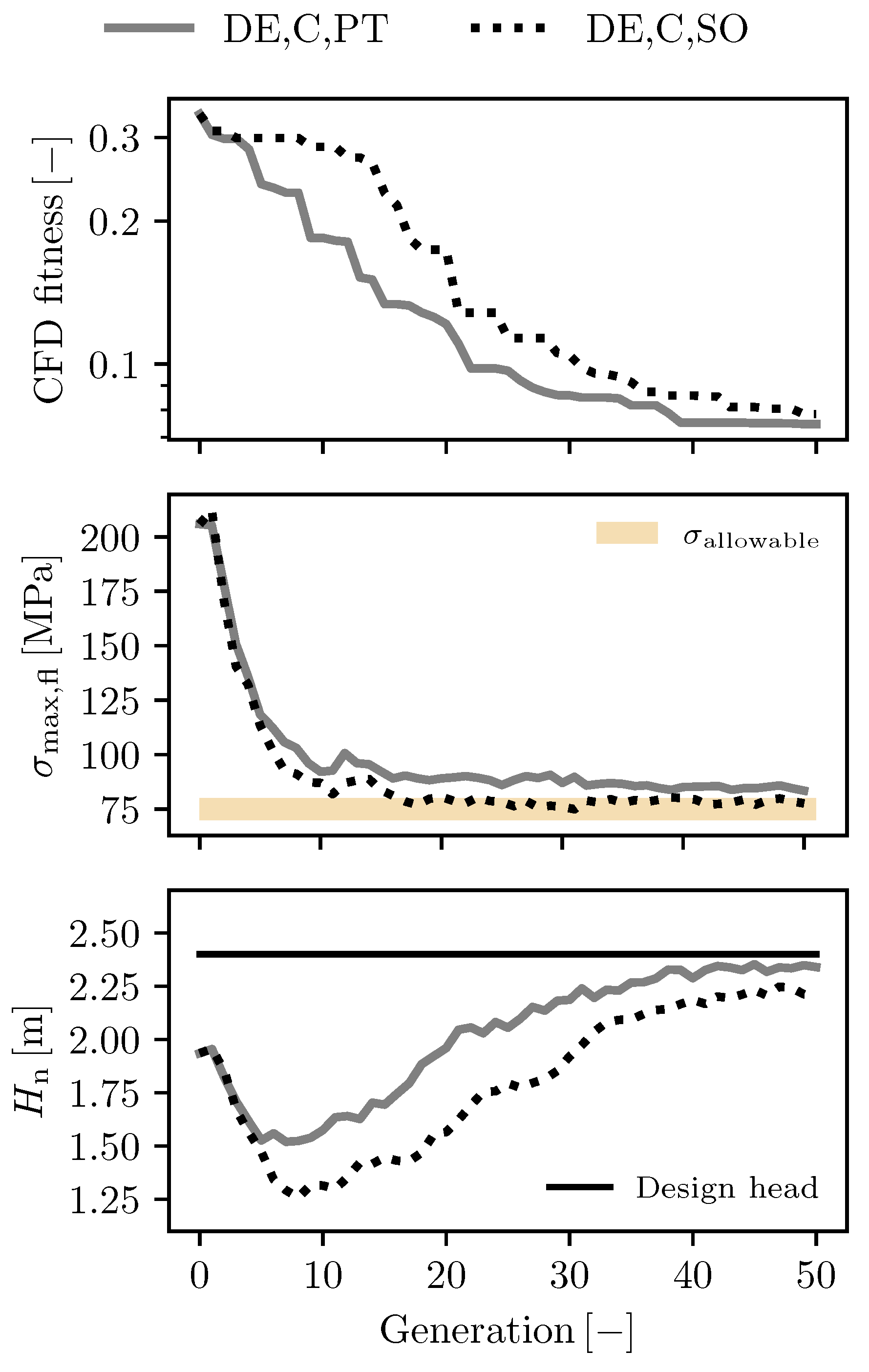
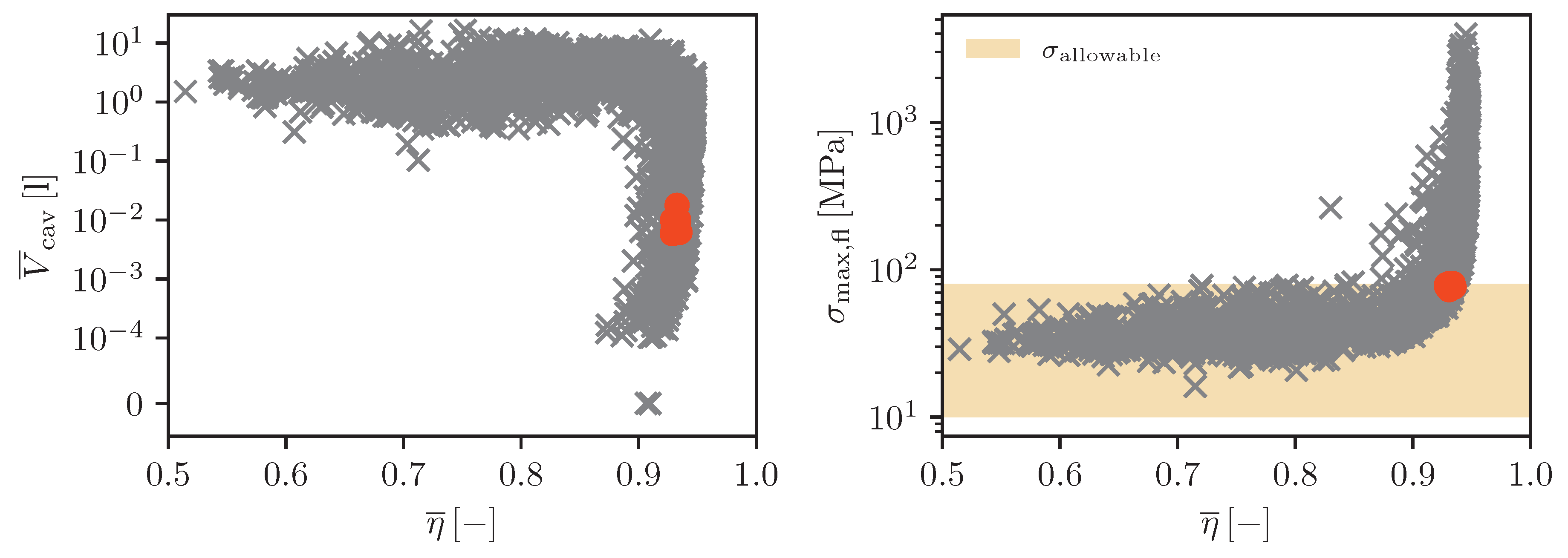
| Integration Structural Mechanics | |
|---|---|
| setup(DE,C,PT) | Constraint, penalty term |
| setup(DE,C,SO) | Constraint, selection operator |
| setup(DE,O) | Objective |
| setup(DE,O,H) | Objective, lower weighted head |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the EUROTURBO. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Fraas, S.; Tismer, A.; Riedelbauch, S. Comparison of Different Strategies to Include Structural Mechanics in the Optimization Process of an Axial Turbine’s Runner Blade. Int. J. Turbomach. Propuls. Power 2025, 10, 38. https://doi.org/10.3390/ijtpp10040038
Fraas S, Tismer A, Riedelbauch S. Comparison of Different Strategies to Include Structural Mechanics in the Optimization Process of an Axial Turbine’s Runner Blade. International Journal of Turbomachinery, Propulsion and Power. 2025; 10(4):38. https://doi.org/10.3390/ijtpp10040038
Chicago/Turabian StyleFraas, Stefan, Alexander Tismer, and Stefan Riedelbauch. 2025. "Comparison of Different Strategies to Include Structural Mechanics in the Optimization Process of an Axial Turbine’s Runner Blade" International Journal of Turbomachinery, Propulsion and Power 10, no. 4: 38. https://doi.org/10.3390/ijtpp10040038
APA StyleFraas, S., Tismer, A., & Riedelbauch, S. (2025). Comparison of Different Strategies to Include Structural Mechanics in the Optimization Process of an Axial Turbine’s Runner Blade. International Journal of Turbomachinery, Propulsion and Power, 10(4), 38. https://doi.org/10.3390/ijtpp10040038





