Investigation of Mixture Modelling Algorithms as a Tool for Determining the Statistical Likelihood of Serological Exposure to Filariasis Utilizing Historical Data from the Lymphatic Filariasis Surveillance Program in Vanuatu
Abstract
1. Introduction
2. Materials and Methods
2.1. Survey Sites for the 2005 TAS1/C Survey in Vanuatu
2.2. Survey Sites for the 2008 Targeted Child Survey in Vanuatu
2.3. Human Ethics
2.4. Filariasis CELISA
2.5. Mixture Modelling Statistical Methods
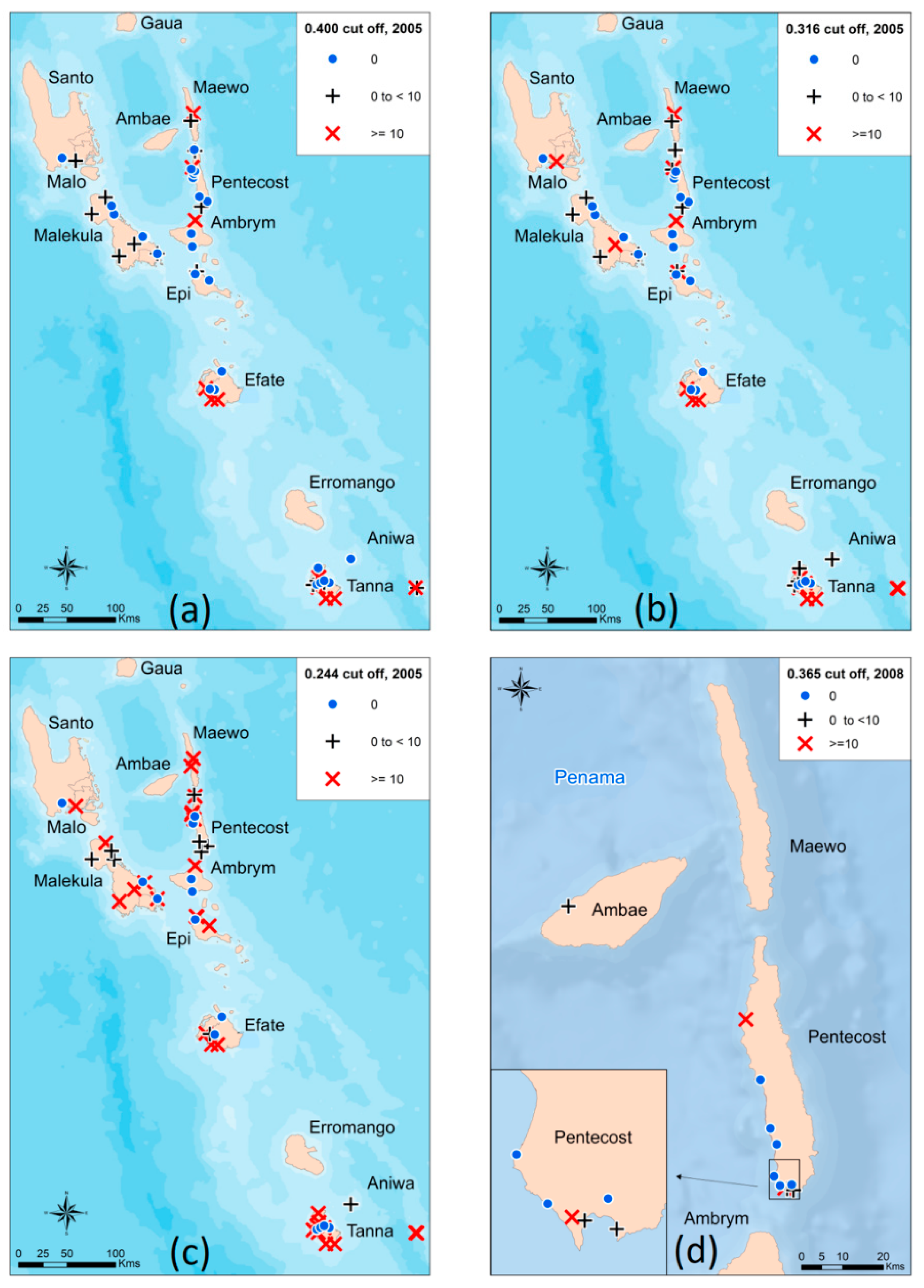
2.6. Prevalence Mapping
3. Results
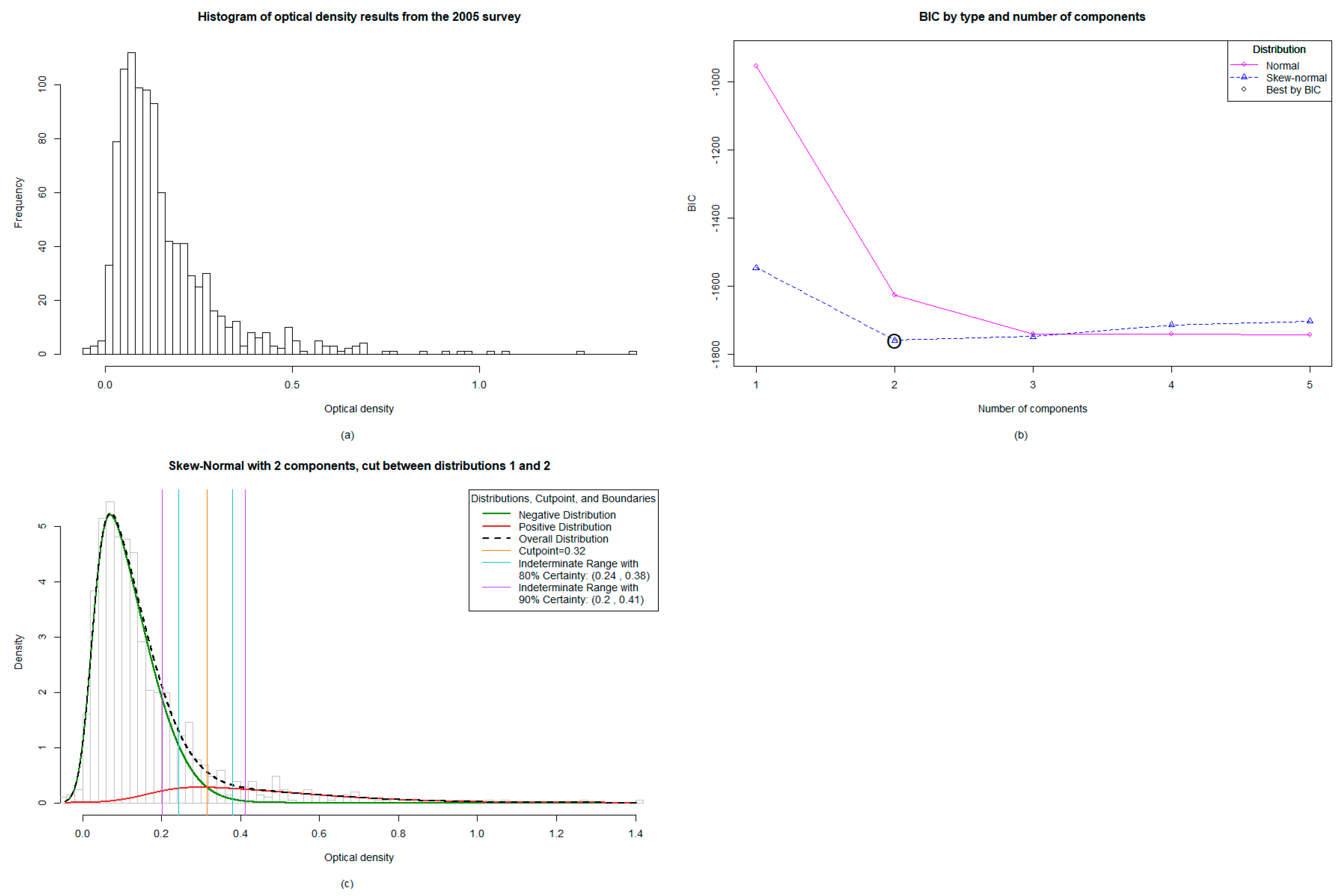
3.1. Spread of the OD Values across Both Years; 2005 and 2008.
3.2. The Mixture Modelling Algorithm for the 2005 TAS 1 Survey Data
3.3. Mixture Modelling Algorithms suggest a Higher Antibody Prevalence of Children from the TAS1 Survey in 2005 Utilizing both the Absolute Cut-off Value and the Lower 80% Certainty Cut-off Value
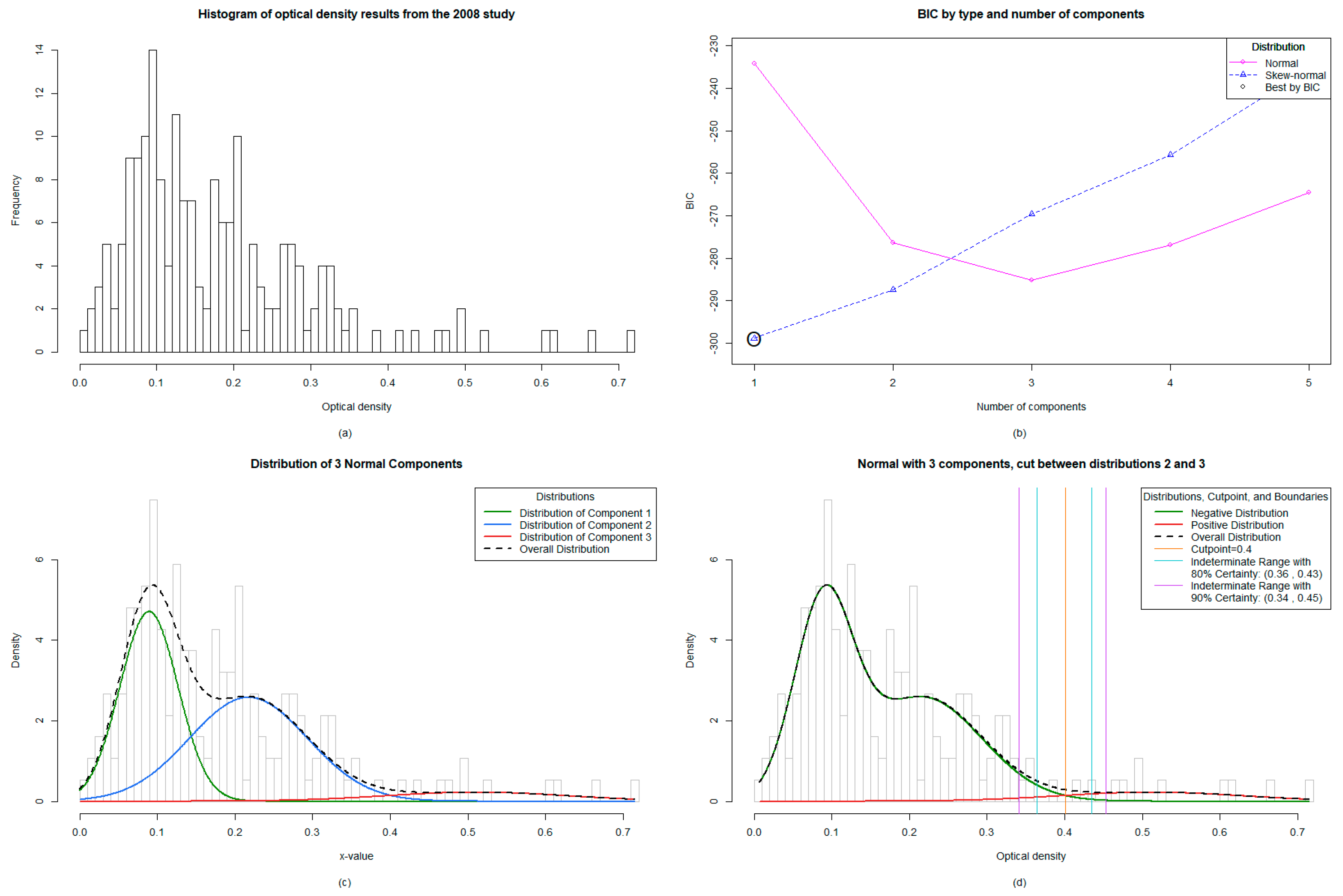
3.4. The Mixture Modelling Algorithm for the 2008 Targeted Child Survey Data
3.5. Antibody Prevalence from the 2008 Survey Remains Unchanged with New Mixture Modelling Absolute Cut-off Value and Increases Slightly with Lower 80% Certainty Threshold Cut-off Value
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Global programme to eliminate lymphatic filariasis: progress report, 2017. Wkly Epidemiol. Rec. 2018, 44, 589–604. [Google Scholar]
- Rebollo, M.P.; Bockarie, M.J. Can Lymphatic Filariasis Be Eliminated by 2020? Trends Parasitol. 2017, 33, 83–92. [Google Scholar] [CrossRef] [PubMed]
- Ichimori, K.; Graves, P.M. Overview of PacELF-the Pacific Programme for the Elimination of Lymphatic Filariasis. Trop. Med. Health 2017, 45, 34. [Google Scholar] [CrossRef] [PubMed]
- Won, K.Y.; Sambou, S.; Barry, A.; Robinson, K.; Jaye, M.; Sanneh, B.; Sanyang, A.; Gass, K.; Lammie, P.J.; Rebollo, M. Use of Antibody Tools to Provide Serologic Evidence of Elimination of Lymphatic Filariasis in The Gambia. Am. J. Trop. Med. Hyg. 2018, 98, 15–20. [Google Scholar] [CrossRef] [PubMed]
- Lammie, P.J.; Weil, G.; Noordin, R.; Kaliraj, P.; Steel, C.; Goodman, D.; Lakshmikanthan, V.B.; Ottesen, E. Recombinant antigen-based antibody assays for the diagnosis and surveillance of lymphatic filariasis - a multicenter trial. Filaria J. 2004, 3, 9. [Google Scholar] [CrossRef] [PubMed]
- Mladonicky, J.M.; King, J.D.; Liang, J.L.; Chambers, E.; Pa’au, M.; Schmaedick, M.A.; Burkot, T.R.; Bradley, M.; Lammie, P.J. Assessing transmission of lymphatic filariasis using parasitologic, serologic, and entomologic tools after mass drug administration in American Samoa. Am. J. Trop. Med. Hyg. 2009, 80, 769–773. [Google Scholar] [CrossRef]
- Washington, C.H.; Radday, J.; Streit, T.G.; Boyd, H.A.; Beach, M.J.; Addiss, D.G.; Lovince, R.; Lovegrove, M.C.; Lafontant, J.G.; Lammie, P.J.; et al. Spatial clustering of filarial transmission before and after a Mass Drug Administration in a setting of low infection prevalence. Filaria J. 2004, 3, 3. [Google Scholar] [CrossRef][Green Version]
- Weil, G.J.; Kastens, W.; Susapu, M.; Laney, S.J.; Williams, S.A.; King, C.L.; Kazura, J.W.; Bockarie, M.J. The impact of repeated rounds of mass drug administration with diethylcarbamazine plus albendazole on bancroftian filariasis in Papua New Guinea. PLoS Negl. Trop. Dis. 2008, 2, e344. [Google Scholar] [CrossRef]
- Joseph, H.; Maiava, F.; Naseri, T.; Silva, U.; Lammie, P.; Melrose, W. Epidemiological assessment of continuing transmission of lymphatic filariasis in Samoa. Ann. Trop. Med. Parasitol. 2011, 105, 567–578. [Google Scholar] [CrossRef]
- Rao, K.V.N.; Eswaran, M.; Ravi, V.; Gnanasekhar, B.; Narayanan, R.B.; Kaliraj, P.; Jayaraman, K.; Marson, A.; Raghavan, N.; Scott, A.L. The Wuchereria bancrofti orthologue of Brugia malayi SXP1 and the diagnosis of bancroftian filariasis. Mol. Biochem. Parasitol. 2000, 107, 71–80. [Google Scholar] [CrossRef]
- Dissanayake, S.; Xu, M.; Piessens, W.F. A cloned antigen for serological diagnosis of Wuchereria bancrofti microfilaremia with daytime blood samples. Mol. Biochem. Parasitol. 1992, 56, 269–277. [Google Scholar] [CrossRef]
- Joseph, H.; Clough, A.; Peteru, A.; Crawley, S.; Pulu, T.; Maiava, F.; Melrose, W. Exploratory study investigating factors influencing mass drug administration (MDA) compliance for lymphatic filariasis in Samoa. Samoa Med. J. 2010, 3, 12–25. [Google Scholar]
- Joseph, H.; Maiava, F.; Naseri, T.; Taleo, F.; Ake, M.; Capuano, C.; Melrose, W. Application of the Filariasis CELISA Antifilarial IgG(4) Antibody Assay in Surveillance in Lymphatic Filariasis Elimination Programmes in the South Pacific. J. Trop. Med. 2011, 2011, 492023. [Google Scholar] [CrossRef] [PubMed]
- Joseph, H.; Moloney, J.; Maiava, F.; McClintock, S.; Lammie, P.; Melrose, W. First evidence of spatial clustering of lymphatic filariasis in an Aedes polynesiensis endemic area. Acta Trop. 2011, 120, S39–S47. [Google Scholar] [CrossRef]
- Joseph, H.M.; Melrose, W. Applicability of the Filter Paper Technique for Detection of Antifilarial IgG(4) Antibodies Using the Bm14 Filariasis CELISA. J. Parasitol. Res. 2010, 2010, 594687. [Google Scholar] [CrossRef]
- Lau, C.L.; Sheridan, S.; Ryan, S.; Roineau, M.; Andreosso, A.; Fuimaono, S.; Tufa, J.; Graves, P.M. Detecting and confirming residual hotspots of lymphatic filariasis transmission in American Samoa 8 years after stopping mass drug administration. PLoS Negl. Trop. Dis. 2017, 11, e0005914. [Google Scholar] [CrossRef]
- Gass, K.; Beau de Rochars, M.V.; Boakye, D.; Bradley, M.; Fischer, P.U.; Gyapong, J.; Itoh, M.; Ituaso-Conway, N.; Joseph, H.; Kyelem, D.; et al. A multicenter evaluation of diagnostic tools to define endpoints for programs to eliminate bancroftian filariasis. PLoS Negl. Trop. Dis. 2012, 6, e1479. [Google Scholar] [CrossRef]
- Masson, J.; Douglass, J.; Roineau, M.; Aye, K.S.; Htwe, K.M.; Warner, J.; Graves, P.M. Concordance between Plasma and Filter Paper Sampling Techniques for the Lymphatic Filariasis Bm14 Antibody ELISA. Trop. Med. Infect. Dis. 2017, 2, 6. [Google Scholar] [CrossRef]
- World Health Organization. Lymphatic Filariasis: Monitoring and Epidemiological Assessment of Mass Drug Administration: A Manual for National Elimination Programmes; World Health Organization: Geneva, Switzerland, 2011. [Google Scholar]
- World Health Organization. The PacELF Way: Towards Elimination of Lymphatic Filariasis 1999–2005; World Health Organization: Geneva, Switzerland, 2006. [Google Scholar]
- Allen, T.; Taleo, F.; Graves, P.M.; Wood, P.; Taleo, G.; Baker, M.C.; Bradley, M.; Ichimori, K. Impact of the Lymphatic Filariasis Control Program towards elimination of filariasis in Vanuatu, 1997–2006. Trop. Med. Health 2017, 45, 8. [Google Scholar] [CrossRef]
- Taleo, F.; Taleo, G.; Graves, P.M.; Wood, P.; Kim, S.H.; Ozaki, M.; Joseph, H.; Chu, B.; Pavluck, A.; Yajima, A.; et al. Surveillance efforts after mass drug administration to validate elimination of lymphatic filariasis as a public health problem in Vanuatu. Trop. Med. Health 2017, 45, 18. [Google Scholar] [CrossRef]
- Lin, T.I.; Lee, J.C.; Yen, S.Y. Finite Mixture Modelling Using the Skew Normal Distribution. Stat. Sin. 2007, 17, 909–927. [Google Scholar]
- McLachlan, G.; Peel, D. Finite Mixture Models; John Wiley & Sons: New York, NY, USA, 2000; p. 68. [Google Scholar]
- Pereira, J.R.; Marques, L.A.; Da Costa, J.M. An Empirical Comparison of EM Initialization Methods and Model Choice Criteria for Mixtures of Skew-Normal Distributions. Rev. Colomb. Estad. 2012, 35, 3. [Google Scholar]
- Karlis, D.; Xekalaki, E. Choosing initial values for the EM algorithm for finite mixtures. J. Comput. Stat. Data Anal. 2003, 41, 577–590. [Google Scholar] [CrossRef]
- Thematic Mapping. Simplified Country Borders. 2018. Available online: www.thematicmapping.org/downloads/world_borders.php (accessed on 24 September 2018).
- ESRI Oceans Basemap. 2018. Available online: https://www.arcgis.com/home/item.html?id=6348e67824504fc9a62976434bf0d8d5 (accessed on 5 January 2019).
- Won, K.Y.; Robinson, K.; Hamlin, K.L.; Tufa, J.; Seespesara, M.; Wiegand, R.E.; Gass, K.; Kubofcik, J.; Nutman, T.B.; Lammie, P.J.; et al. Comparison of antigen and antibody responses in repeat lymphatic filariasis transmission assessment surveys in American Samoa. PLoS Negl. Trop. Dis. 2018, 12, e0006347. [Google Scholar] [CrossRef] [PubMed]
- Dylewski, J.S.; Rasmussen, L.; Mills, J.; Merigan, T.C. Large-scale serological screening for cytomegalovirus antibodies in homosexual males by enzyme-linked immunosorbent assay. J. Clin. Microbiol. 1984, 19, 200–203. [Google Scholar] [PubMed]
- Lau, C.L.; Won, K.Y.; Lammie, P.J.; Graves, P.M. Lymphatic Filariasis Elimination in American Samoa: Evaluation of Molecular Xenomonitoring as a Surveillance Tool in the Endgame. PLoS Negl. Trop. Dis. 2016, 10, e0005108. [Google Scholar] [CrossRef]
- Lau, C.L.; Won, K.Y.; Becker, L.; Soares Magalhaes, R.J.; Fuimaono, S.; Melrose, W.; Lammie, P.J.; Graves, P.M. Seroprevalence and spatial epidemiology of Lymphatic Filariasis in American Samoa after successful mass drug administration. PLoS Negl. Trop. Dis. 2014, 8, e3297. [Google Scholar] [CrossRef]
| Province | Island | Village | Number of Samples | % Prevalence |
|---|---|---|---|---|
| Malampa | Ambrym | Maat | 20 | 10 |
| Nova—Londre | 27 | 11.1 | ||
| Sameou | 26 | 0 | ||
| Maranata | 5 | 0 | ||
| Malekula | Dravai/Lamap | 53 | 1.9 | |
| P.R.V. | 36 | 0 | ||
| Wala Mainland | 24 | 0 | ||
| Pikaier | 19 | 5.3 | ||
| Lawa | 14 | 7.1 | ||
| Melken | 19 | 5.3 | ||
| Pandeur | 16 | 0 | ||
| Paama | Liro | 26 | 3.8 | |
| Sanma | Santo | Malotau | 16 | 0 |
| Tanavoli | 19 | 5.3 | ||
| Penama | Ambae | Lovositarivue | 2 | 0 |
| Maewo | Naviso | 31 | 38.7 | |
| Rembu | 6 | 0 | ||
| Nasawa | 14 | 7.1 | ||
| Pentecost | Baie Barrier | 39 | 0 | |
| Abwatunbuliva | 19 | 5.38 | ||
| Lalbung | 18 | 5.6 | ||
| Laone | 19 | 0 | ||
| Leravinanposvi | 21 | 0 | ||
| Likasak | 4 | 0 | ||
| Melsisi | 4 | 0 | ||
| Namaram | 17 | 23.5 | ||
| Pannas | 11 | 0 | ||
| Shefa | Efate | Erakor | 17 | 17.6 |
| Eratap | 14 | 14.3 | ||
| Mele | 15 | 0 | ||
| Paonangisu | 15 | 0 | ||
| Rango Rango | 22 | 0 | ||
| Epi | Brisbane | 11 | 0 | |
| Lamenu Bay | 26 | 3.8 | ||
| Mate | 9 | 0 | ||
| Tafea | Aniwa | Ikaokao | 39 | 0 |
| Futuna | Iasoa | 9 | 11.1 | |
| Matangi | 15 | 6.7 | ||
| Tanna | Eniai | 20 | 0 | |
| Fetukai | 30 | 20 | ||
| Ipai | 14 | 7.1 | ||
| Ikakahak | 30 | 43.3 | ||
| Ikapow | 1 | 0 | ||
| Imafen | 48 | 0 | ||
| Imereupow | 50 | 4 | ||
| Isiai | 8 | 12.5 | ||
| Lahwenuwi | 10 | 0 | ||
| Lenaken | 24 | 4.2 | ||
| Lenawawa | 16 | 0 | ||
| Lounapaio | 9 | 11.1 | ||
| Lounapkao | 10 | 0 | ||
| Lowkwaria | 40 | 7.5 | ||
| TOTAL | 1027 | 6.4 |
| Province | Island | Village | Number of samples | % prevalence |
|---|---|---|---|---|
| Penama | Ambae | Nanako | 14 | 7.1 |
| Pentecost | Bai Martelli | 17 | 5.9 | |
| Hot Wota | 1 | 0 | ||
| Londar | 29 | 10.3 | ||
| Lonlebule | 2 | 0 | ||
| Namaram | 12 | 41.7 | ||
| Pannas | 1 | 0 | ||
| Point Cross | 74 | 1.4 | ||
| Ranliae | 4 | 0 | ||
| Ranputor | 1 | 0 | ||
| Vansemakul | 1 | 0 | ||
| Wanur | 31 | 0 | ||
| TOTAL | 187 | 5.9% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joseph, H.; Sullivan, S.; Wood, P.; Melrose, W.; Taleo, F.; Graves, P. Investigation of Mixture Modelling Algorithms as a Tool for Determining the Statistical Likelihood of Serological Exposure to Filariasis Utilizing Historical Data from the Lymphatic Filariasis Surveillance Program in Vanuatu. Trop. Med. Infect. Dis. 2019, 4, 45. https://doi.org/10.3390/tropicalmed4010045
Joseph H, Sullivan S, Wood P, Melrose W, Taleo F, Graves P. Investigation of Mixture Modelling Algorithms as a Tool for Determining the Statistical Likelihood of Serological Exposure to Filariasis Utilizing Historical Data from the Lymphatic Filariasis Surveillance Program in Vanuatu. Tropical Medicine and Infectious Disease. 2019; 4(1):45. https://doi.org/10.3390/tropicalmed4010045
Chicago/Turabian StyleJoseph, Hayley, Sarah Sullivan, Peter Wood, Wayne Melrose, Fasihah Taleo, and Patricia Graves. 2019. "Investigation of Mixture Modelling Algorithms as a Tool for Determining the Statistical Likelihood of Serological Exposure to Filariasis Utilizing Historical Data from the Lymphatic Filariasis Surveillance Program in Vanuatu" Tropical Medicine and Infectious Disease 4, no. 1: 45. https://doi.org/10.3390/tropicalmed4010045
APA StyleJoseph, H., Sullivan, S., Wood, P., Melrose, W., Taleo, F., & Graves, P. (2019). Investigation of Mixture Modelling Algorithms as a Tool for Determining the Statistical Likelihood of Serological Exposure to Filariasis Utilizing Historical Data from the Lymphatic Filariasis Surveillance Program in Vanuatu. Tropical Medicine and Infectious Disease, 4(1), 45. https://doi.org/10.3390/tropicalmed4010045






