Figure 1.
Conceptual overview of the GCT taxonomy, categorising gaze clusters by count, target presence, and temporal alignment.
Figure 1.
Conceptual overview of the GCT taxonomy, categorising gaze clusters by count, target presence, and temporal alignment.
Figure 2.
Box plot showing the number of rows per CSV file across all recording rounds, used to assess dataset size variability.
Figure 2.
Box plot showing the number of rows per CSV file across all recording rounds, used to assess dataset size variability.
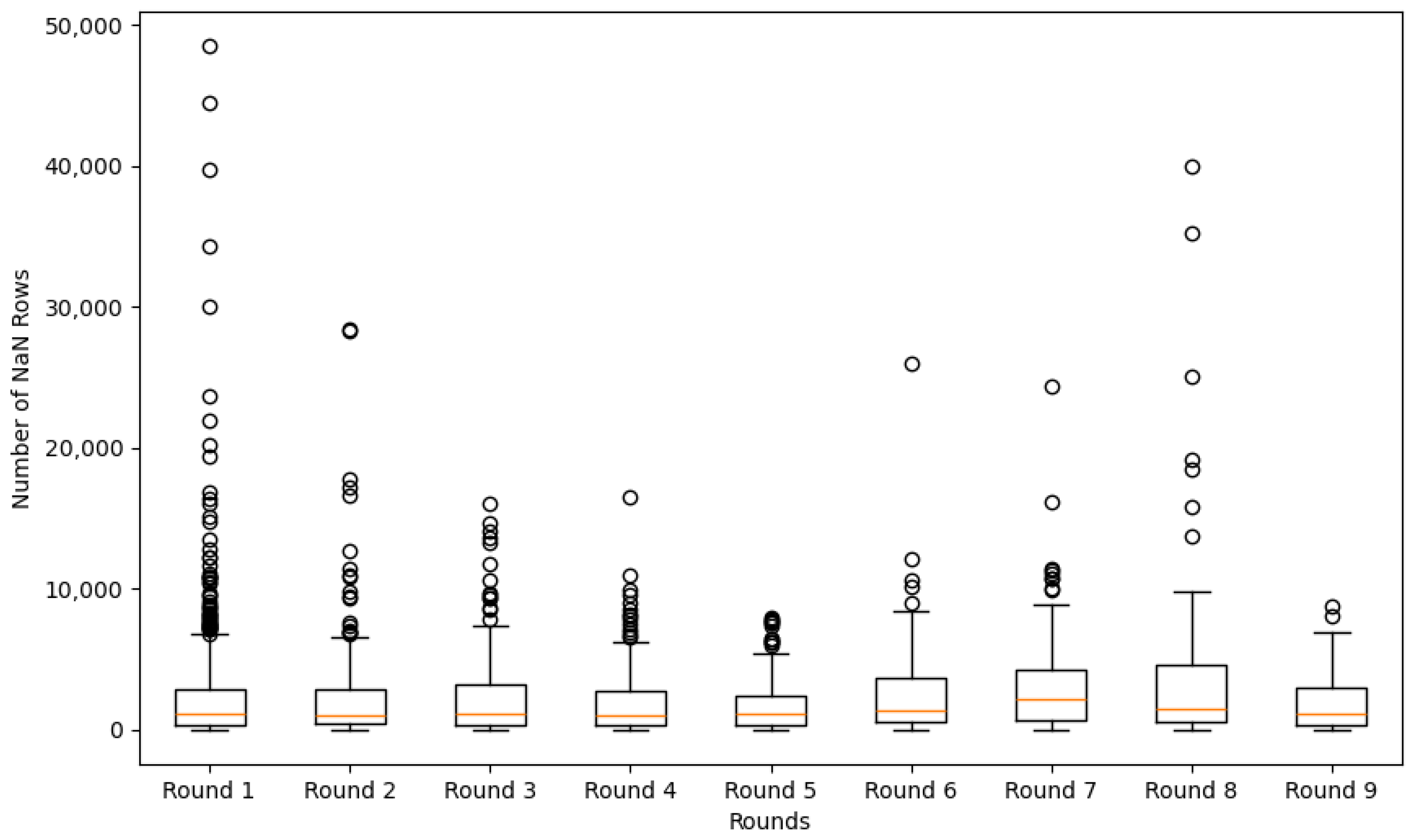
Figure 3.
Box plot of missing (NaN) rows per CSV file across rounds, indicating data quality and sparsity distribution.
Figure 3.
Box plot of missing (NaN) rows per CSV file across rounds, indicating data quality and sparsity distribution.
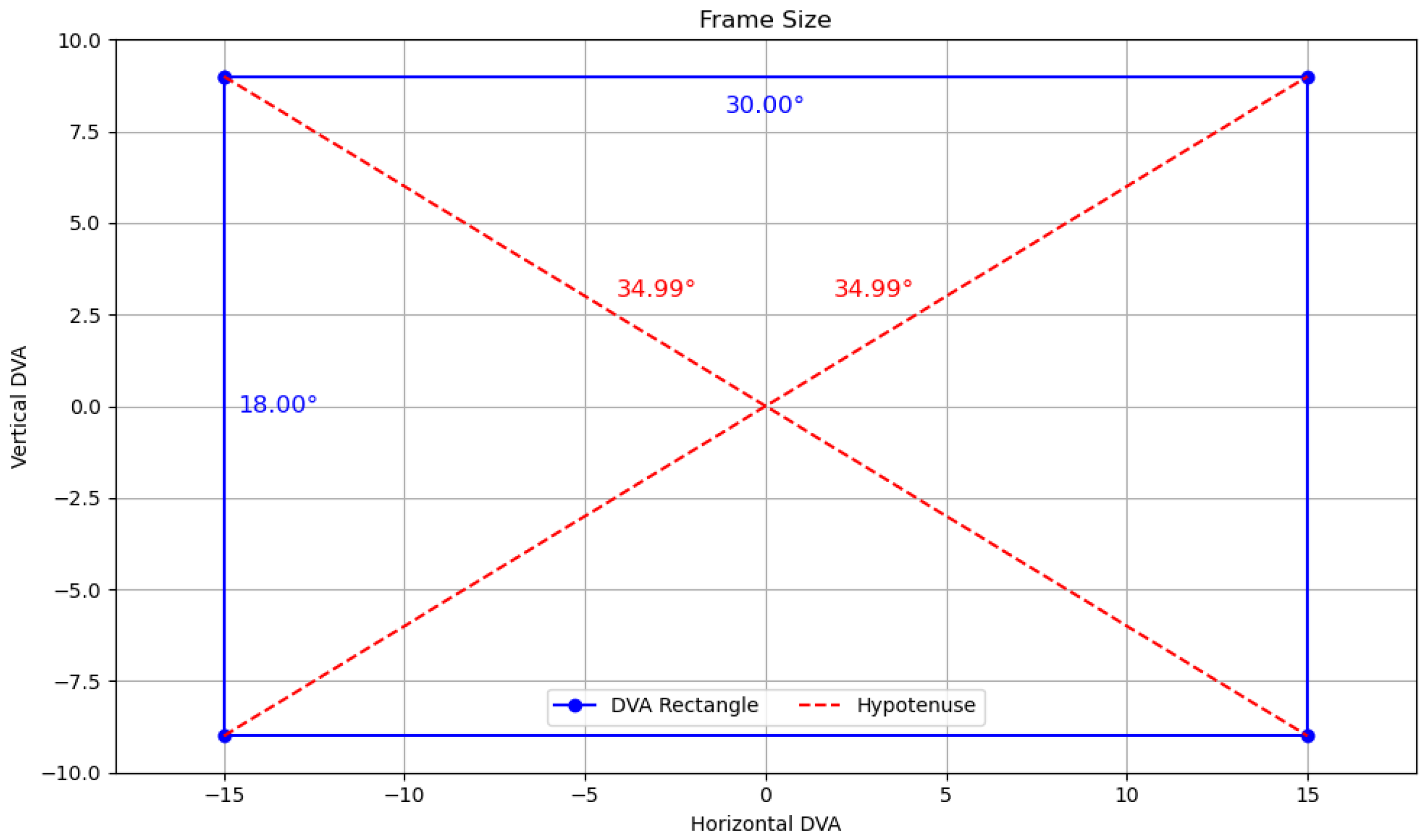
Figure 4.
Visualisation of the screen frame used in the Random Saccade task, bounded within ±15° horizontal and ±9° vertical DVA.
Figure 4.
Visualisation of the screen frame used in the Random Saccade task, bounded within ±15° horizontal and ±9° vertical DVA.
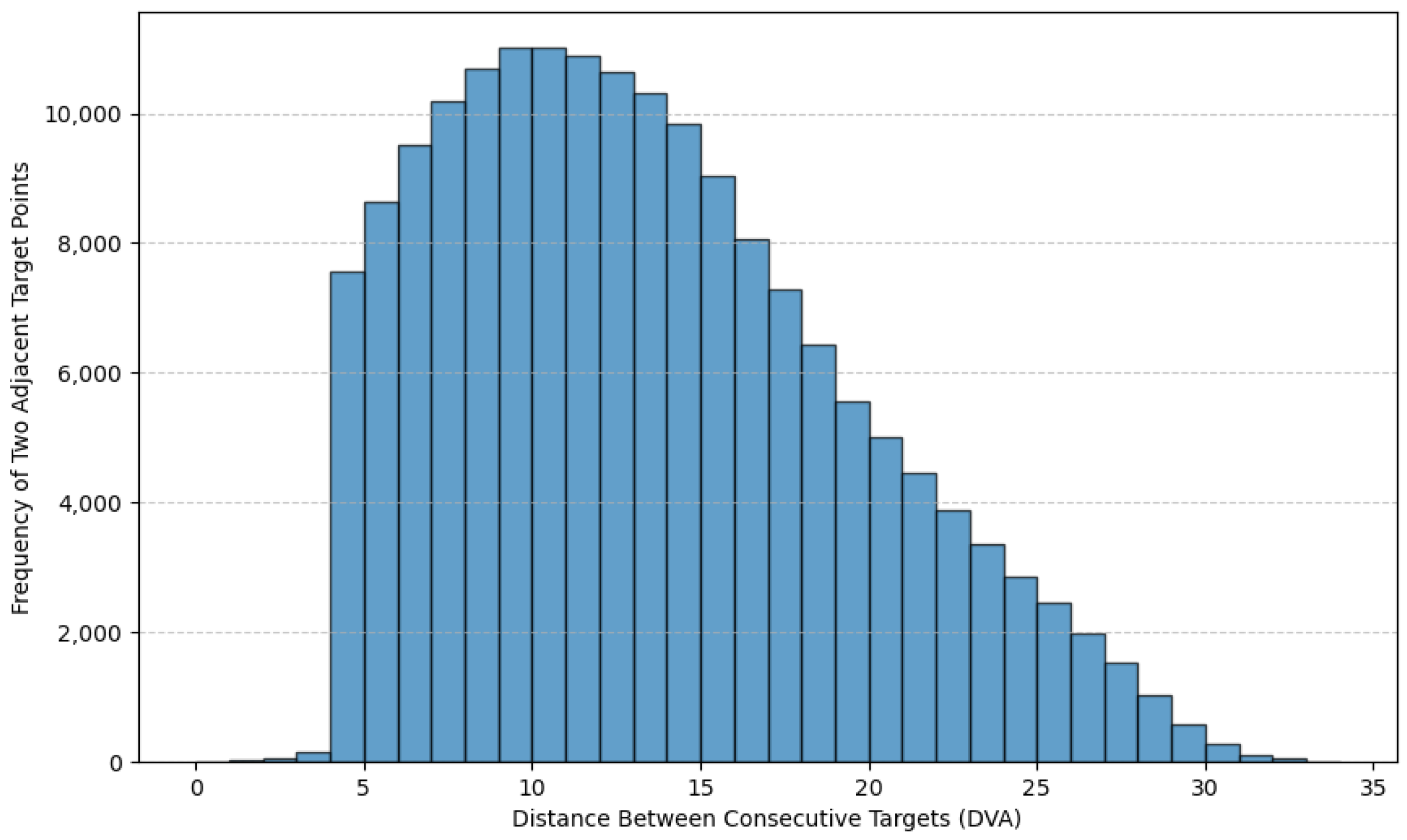
Figure 5.
Distribution of spherical distances between adjacent target points, confirming task constraints of >2 dva displacement.
Figure 5.
Distribution of spherical distances between adjacent target points, confirming task constraints of >2 dva displacement.
Figure 6.
Classification of gaze points as inside or outside the defined display frame, based on target coordinate bounds.
Figure 6.
Classification of gaze points as inside or outside the defined display frame, based on target coordinate bounds.
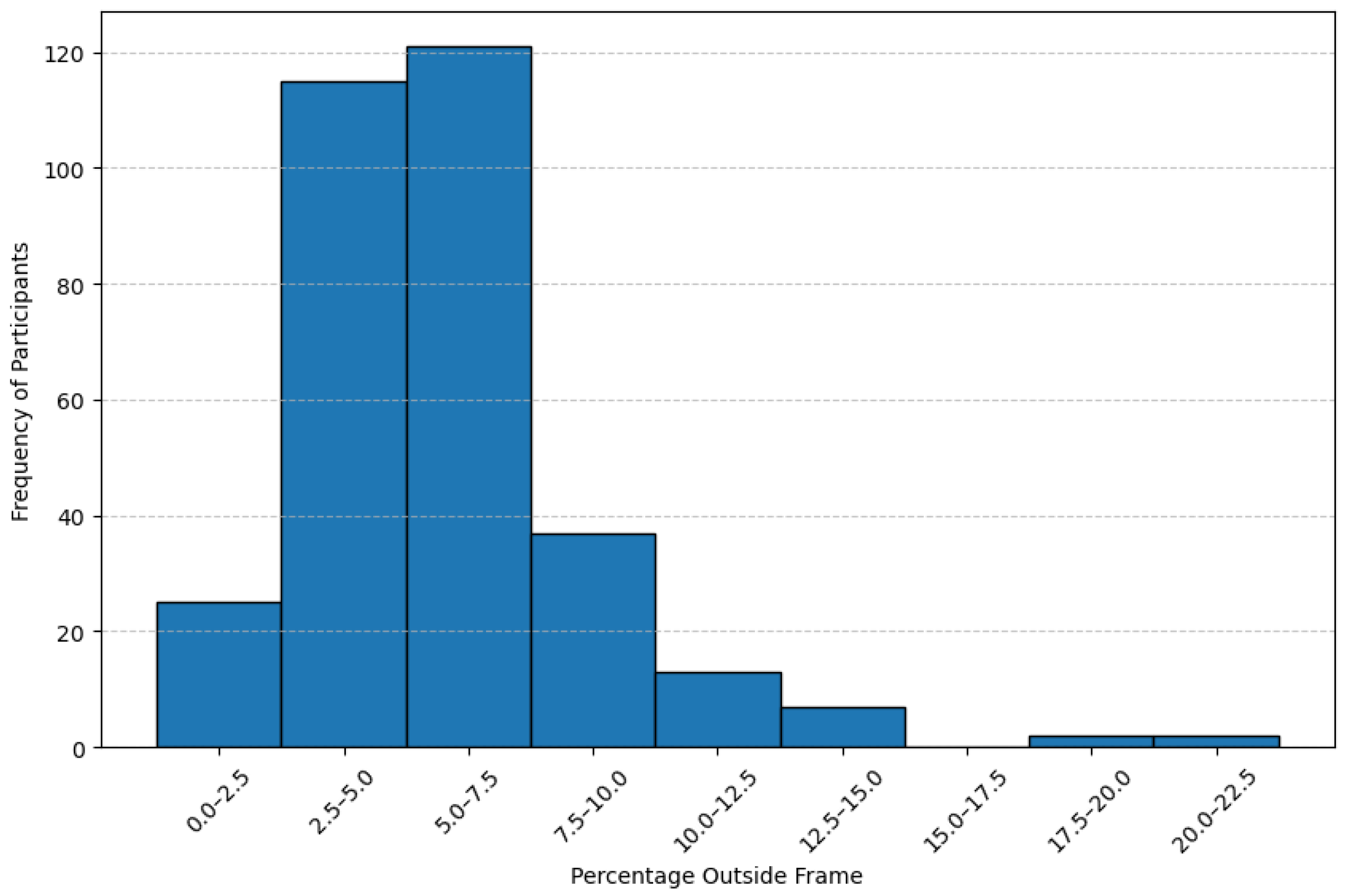
Figure 7.
Distribution of the percentage of gaze points falling outside the frame across all participants.
Figure 7.
Distribution of the percentage of gaze points falling outside the frame across all participants.
Figure 8.
NaN distribution among participants, categorised by the percentage of missing gaze points in each recording session.
Figure 8.
NaN distribution among participants, categorised by the percentage of missing gaze points in each recording session.
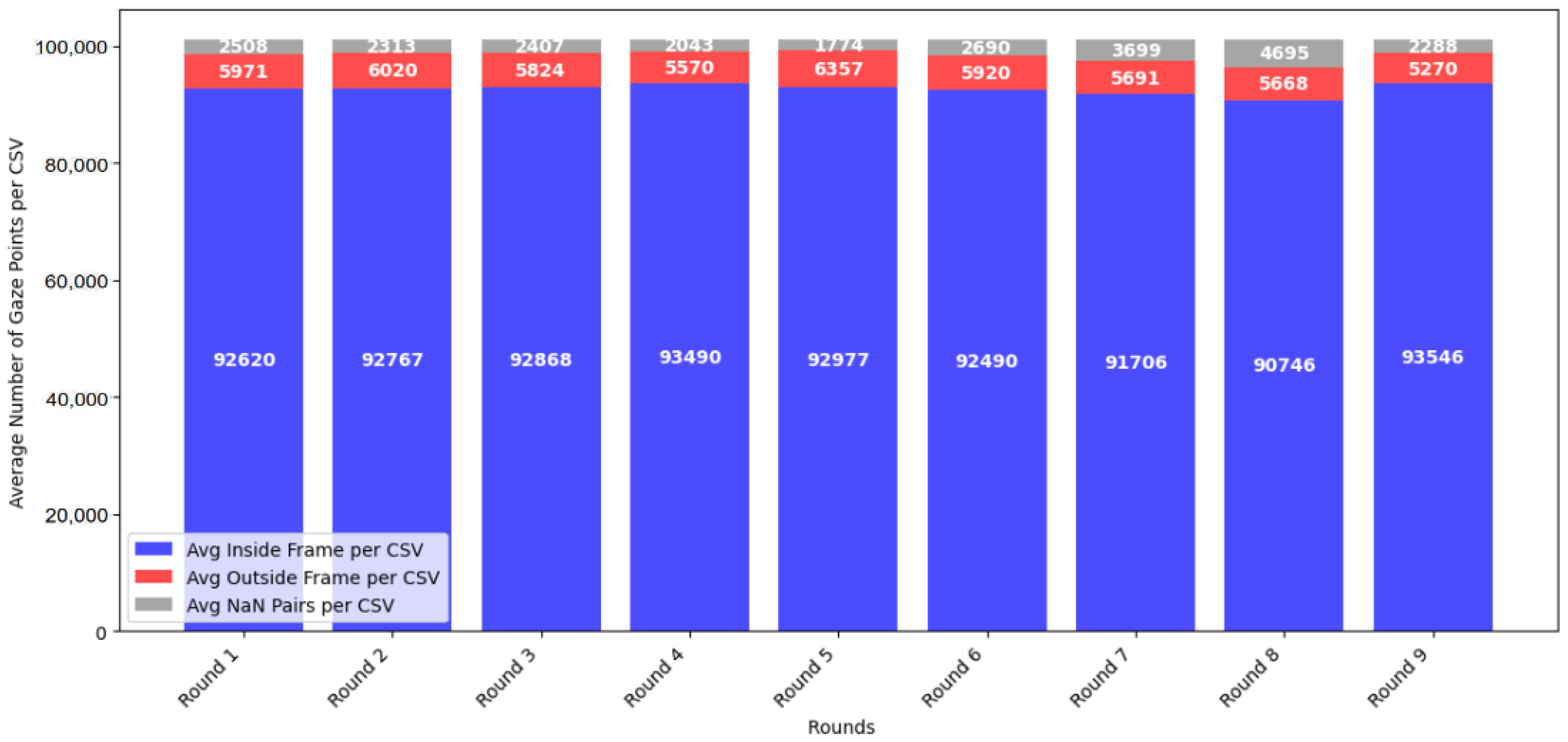
Figure 9.
Average distribution of inside-frame, outside-frame, and NaN gaze points across all participant sessions.
Figure 9.
Average distribution of inside-frame, outside-frame, and NaN gaze points across all participant sessions.
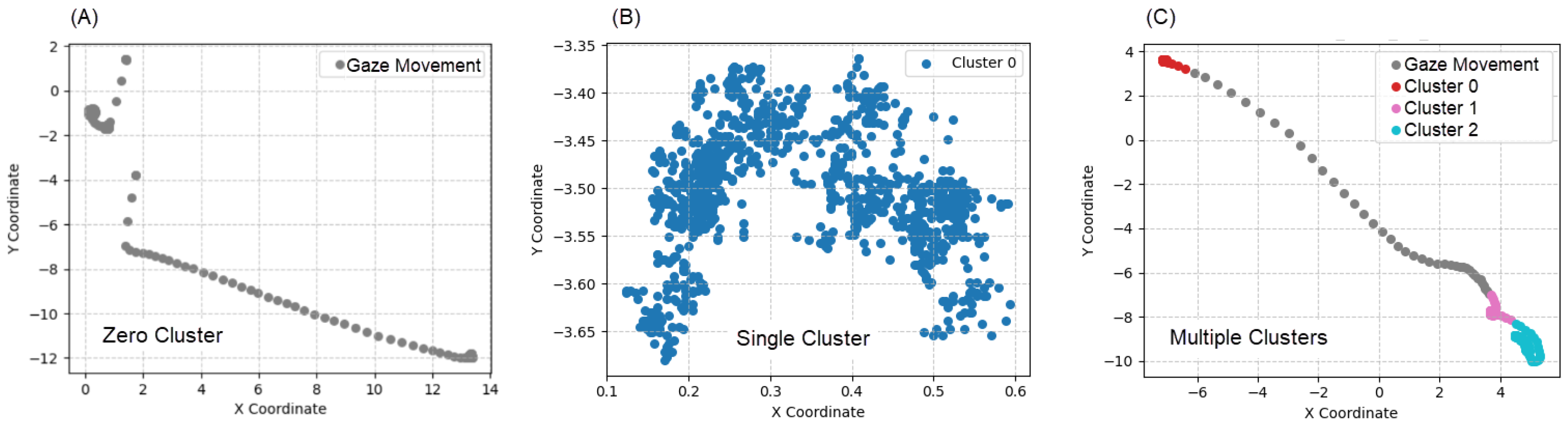
Figure 10.
Cluster examples by count type: (A) Zero Cluster. (B) Single Cluster. (C) Multiple Clusters.
Figure 10.
Cluster examples by count type: (A) Zero Cluster. (B) Single Cluster. (C) Multiple Clusters.
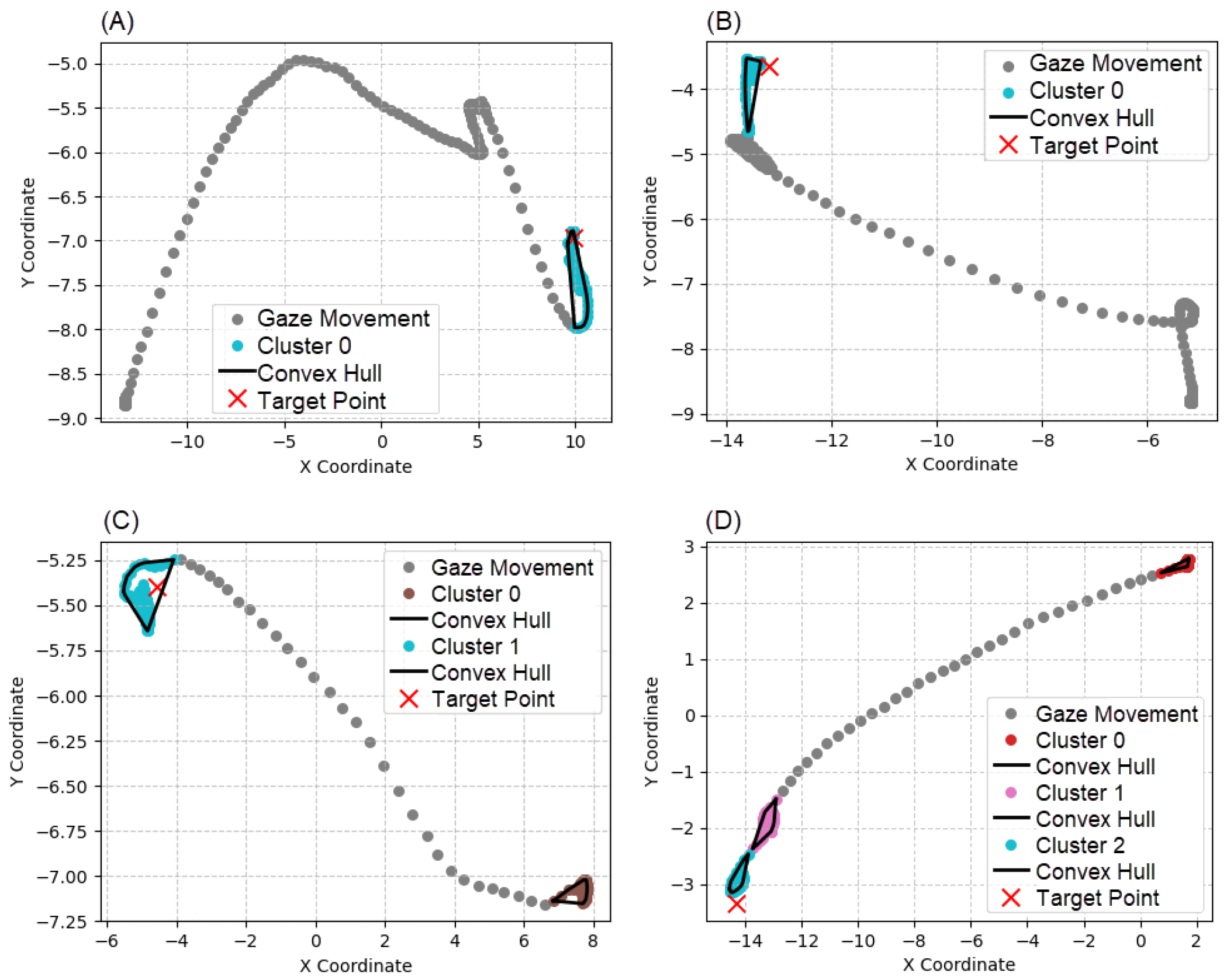
Figure 11.
Examples of target point presence relative to clusters: (A) Single cluster, target inside. (B) Single cluster, target outside. (C) Multiple clusters, target inside. (D) Multiple clusters, target outside.
Figure 11.
Examples of target point presence relative to clusters: (A) Single cluster, target inside. (B) Single cluster, target outside. (C) Multiple clusters, target inside. (D) Multiple clusters, target outside.
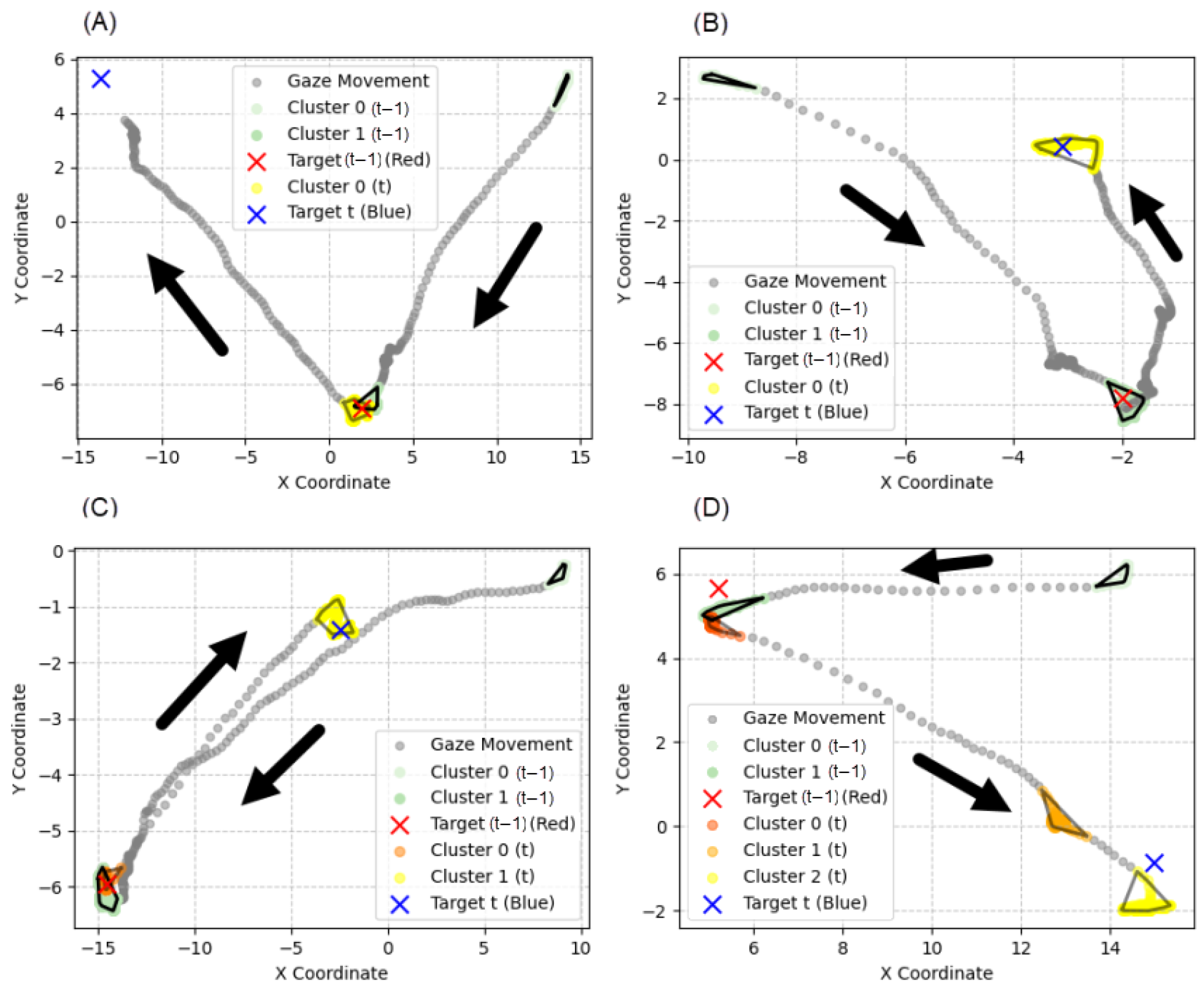
Figure 12.
Examples of temporal relationships between clusters and targets: (A) Delayed single cluster. (B) Not-delayed single cluster. (C) Delayed multiple clusters. (D) Not-delayed multiple clusters. The arrows represent the direction of gaze movement.
Figure 12.
Examples of temporal relationships between clusters and targets: (A) Delayed single cluster. (B) Not-delayed single cluster. (C) Delayed multiple clusters. (D) Not-delayed multiple clusters. The arrows represent the direction of gaze movement.
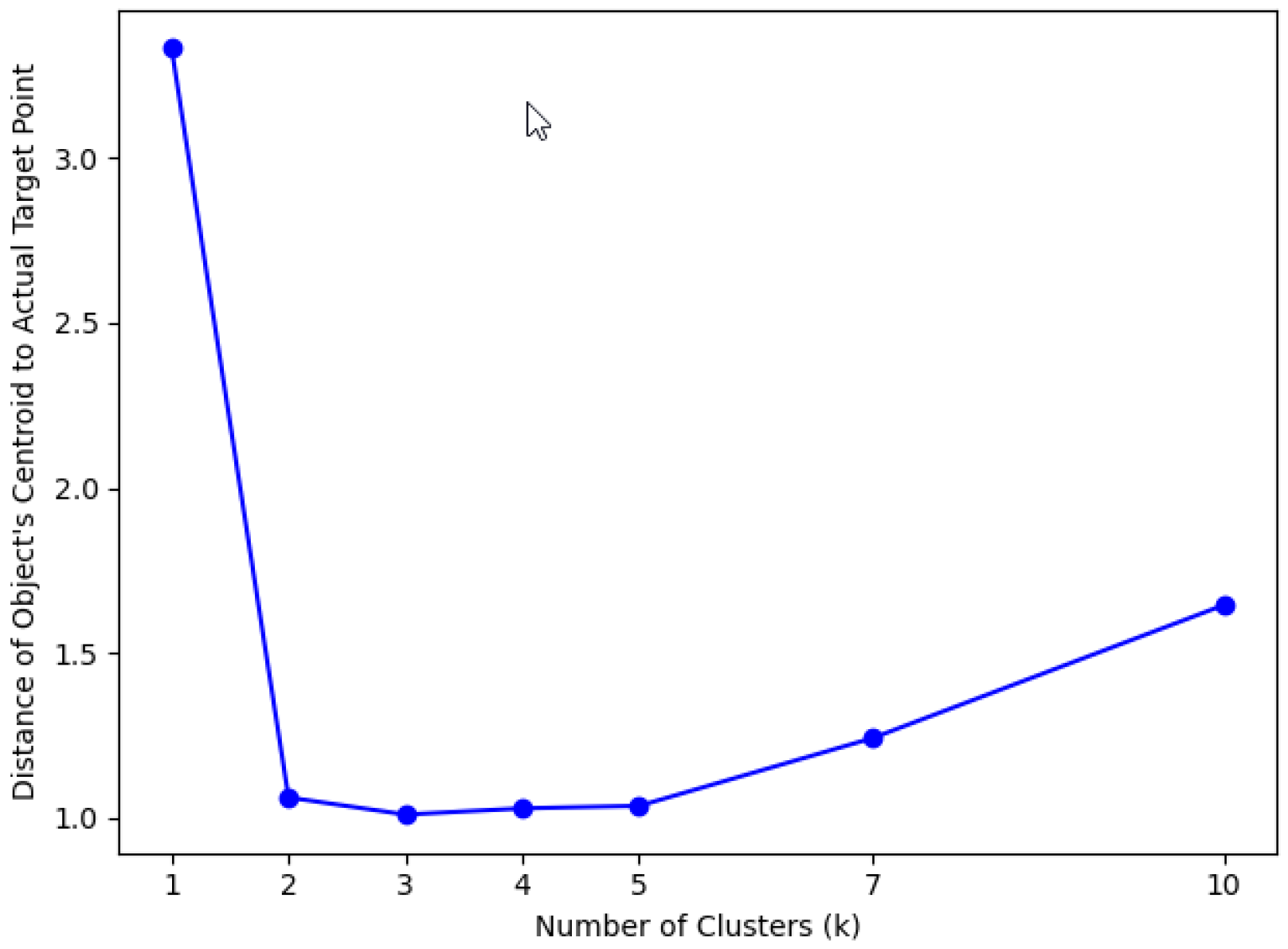
Figure 13.
Object extraction accuracy using k-NN under different window sizes and k values.
Figure 13.
Object extraction accuracy using k-NN under different window sizes and k values.
Figure 14.
Accuracy comparison using k-NN with varying k values on the gaze dataset.
Figure 14.
Accuracy comparison using k-NN with varying k values on the gaze dataset.
Figure 15.
Accuracy comparison using k-Means clustering with different k values.
Figure 15.
Accuracy comparison using k-Means clustering with different k values.
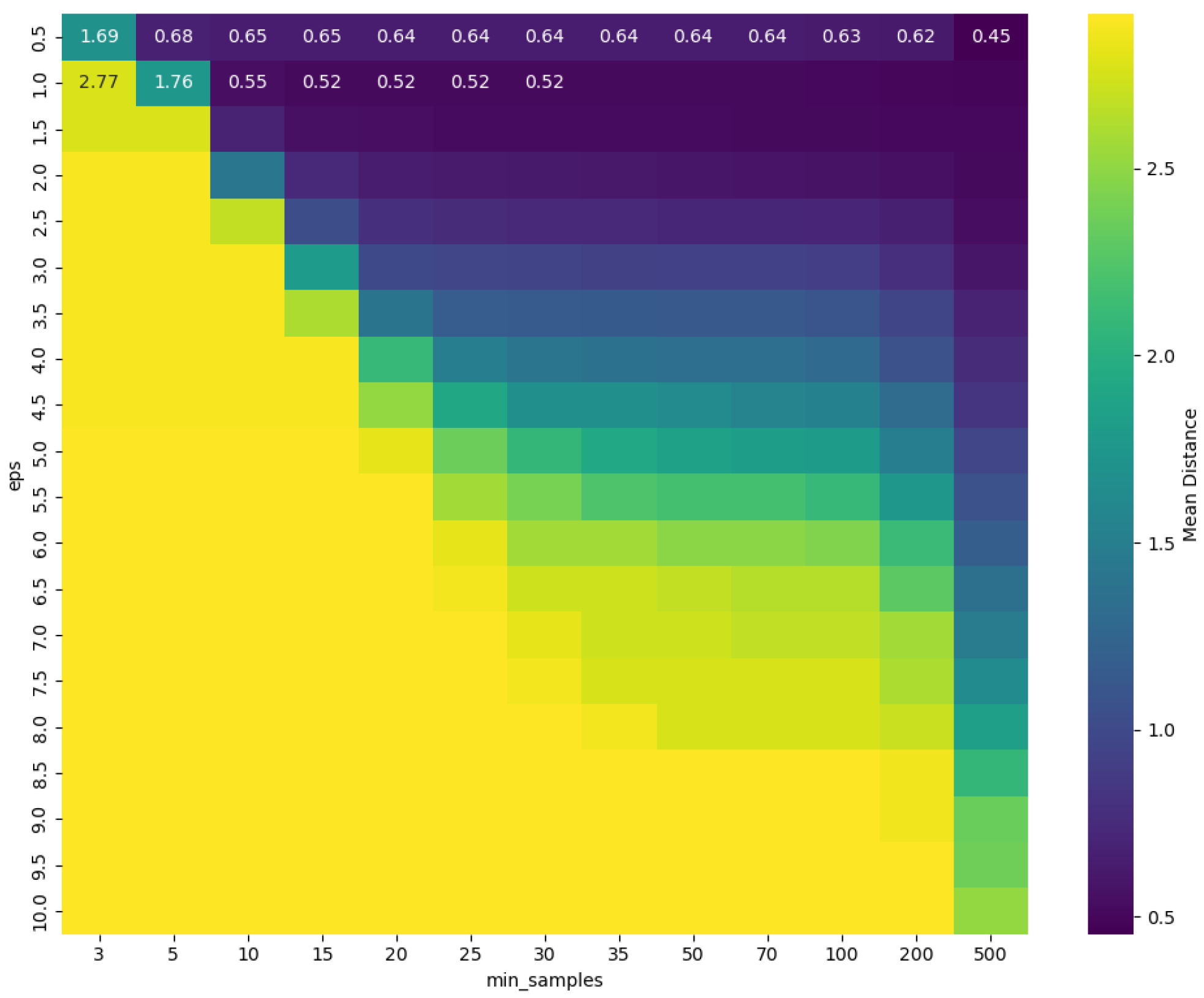
Figure 16.
DBSCAN hyperparameter tuning for object extraction performance.
Figure 16.
DBSCAN hyperparameter tuning for object extraction performance.
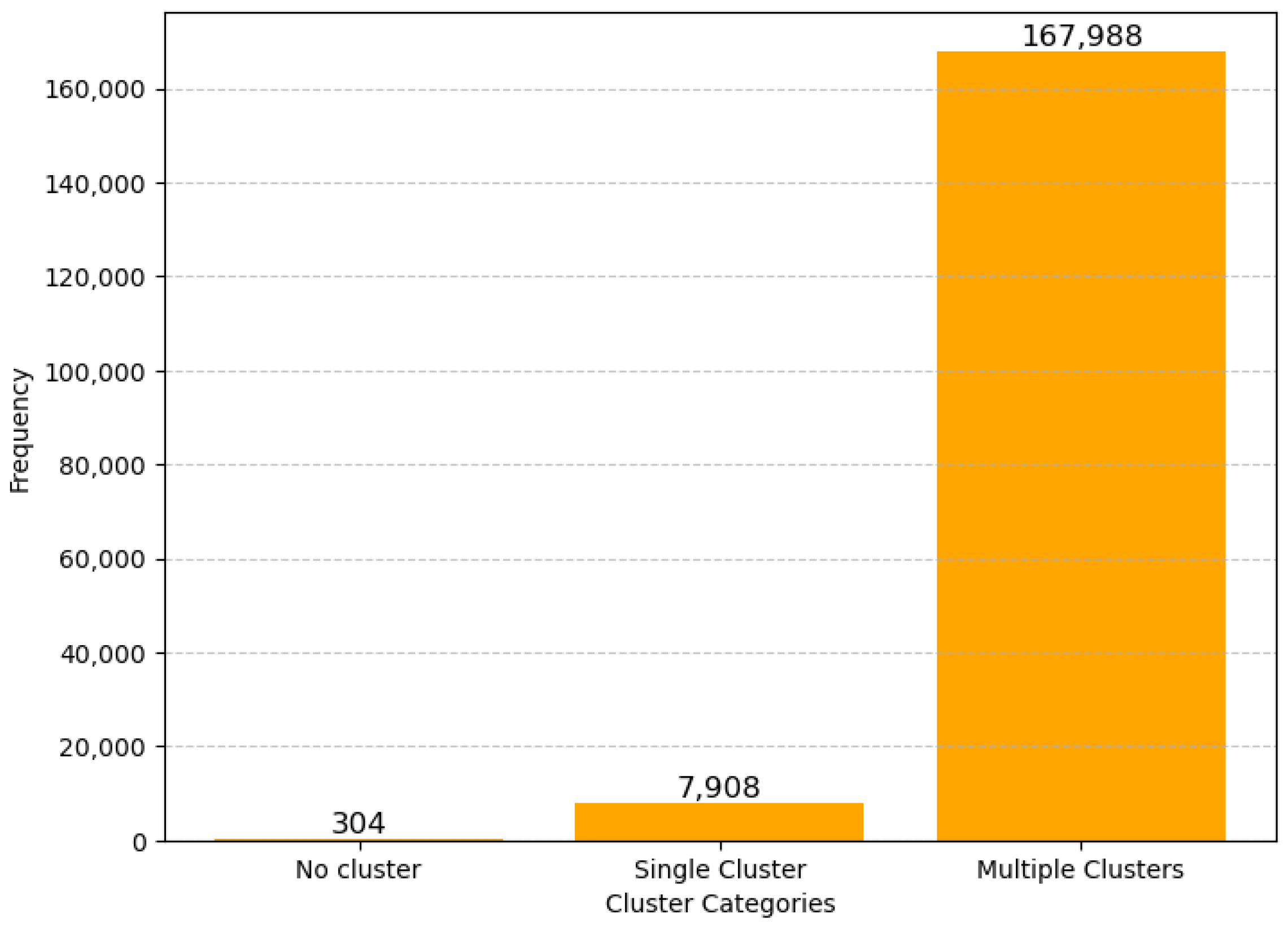
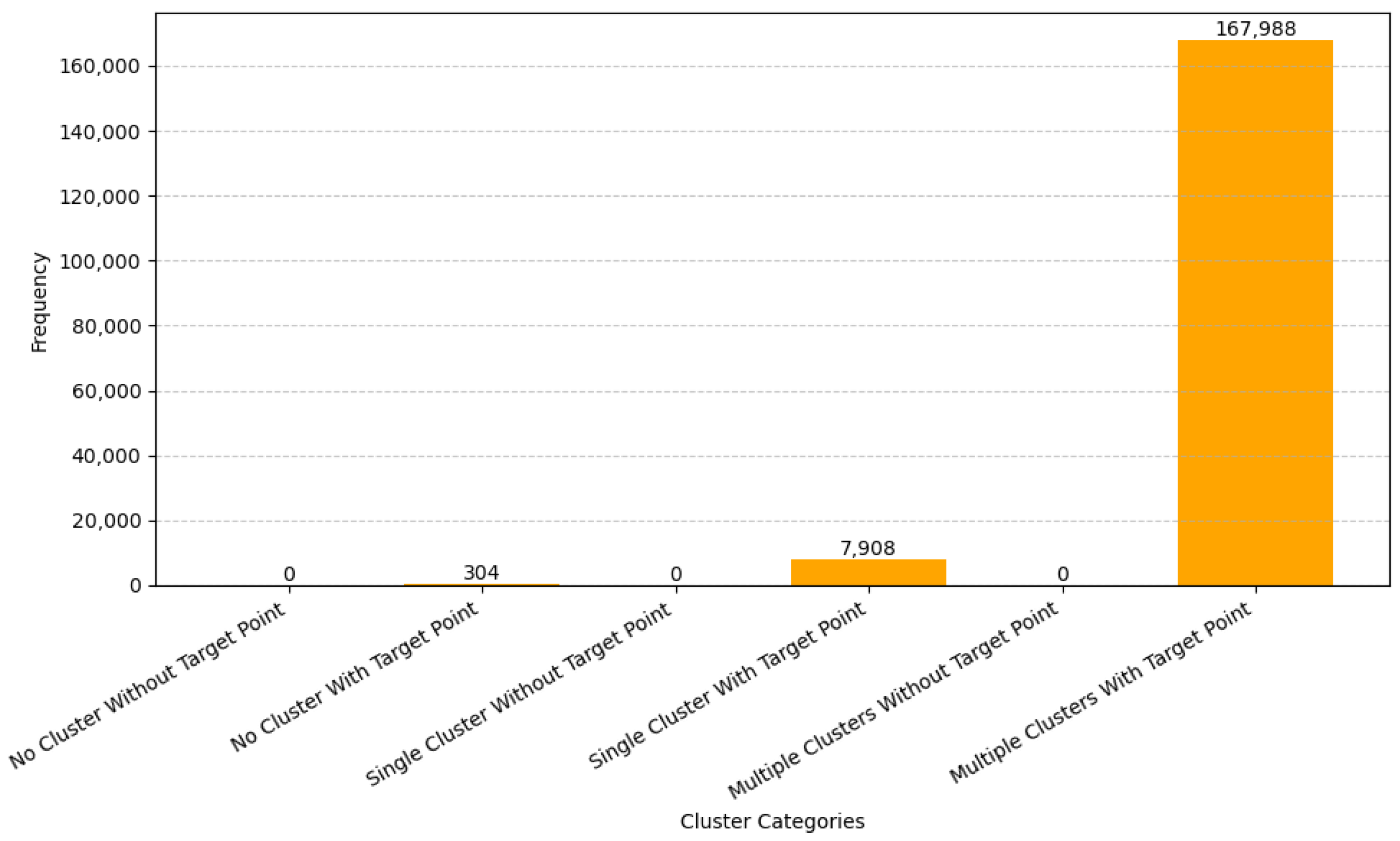
Figure 17.
Frequency distribution of cluster count classifications across the dataset.
Figure 17.
Frequency distribution of cluster count classifications across the dataset.
Figure 18.
Stacked percentage distribution of cluster counts across different recording rounds.
Figure 18.
Stacked percentage distribution of cluster counts across different recording rounds.
Figure 19.
Distribution of clusters by presence or absence of the target point within them.
Figure 19.
Distribution of clusters by presence or absence of the target point within them.
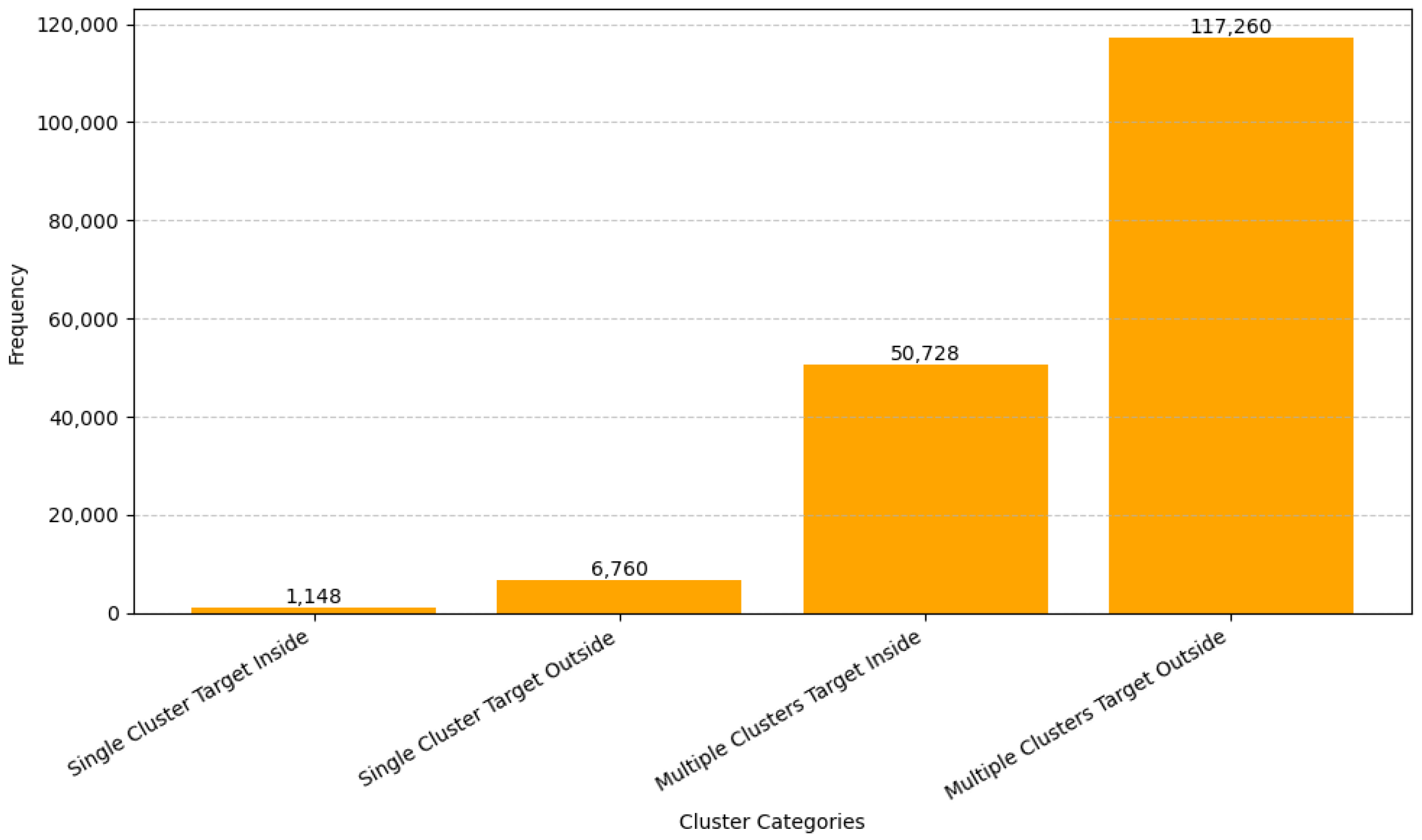
Figure 20.
Distribution of combined cluster and target presence relationships (e.g., inside/outside).
Figure 20.
Distribution of combined cluster and target presence relationships (e.g., inside/outside).
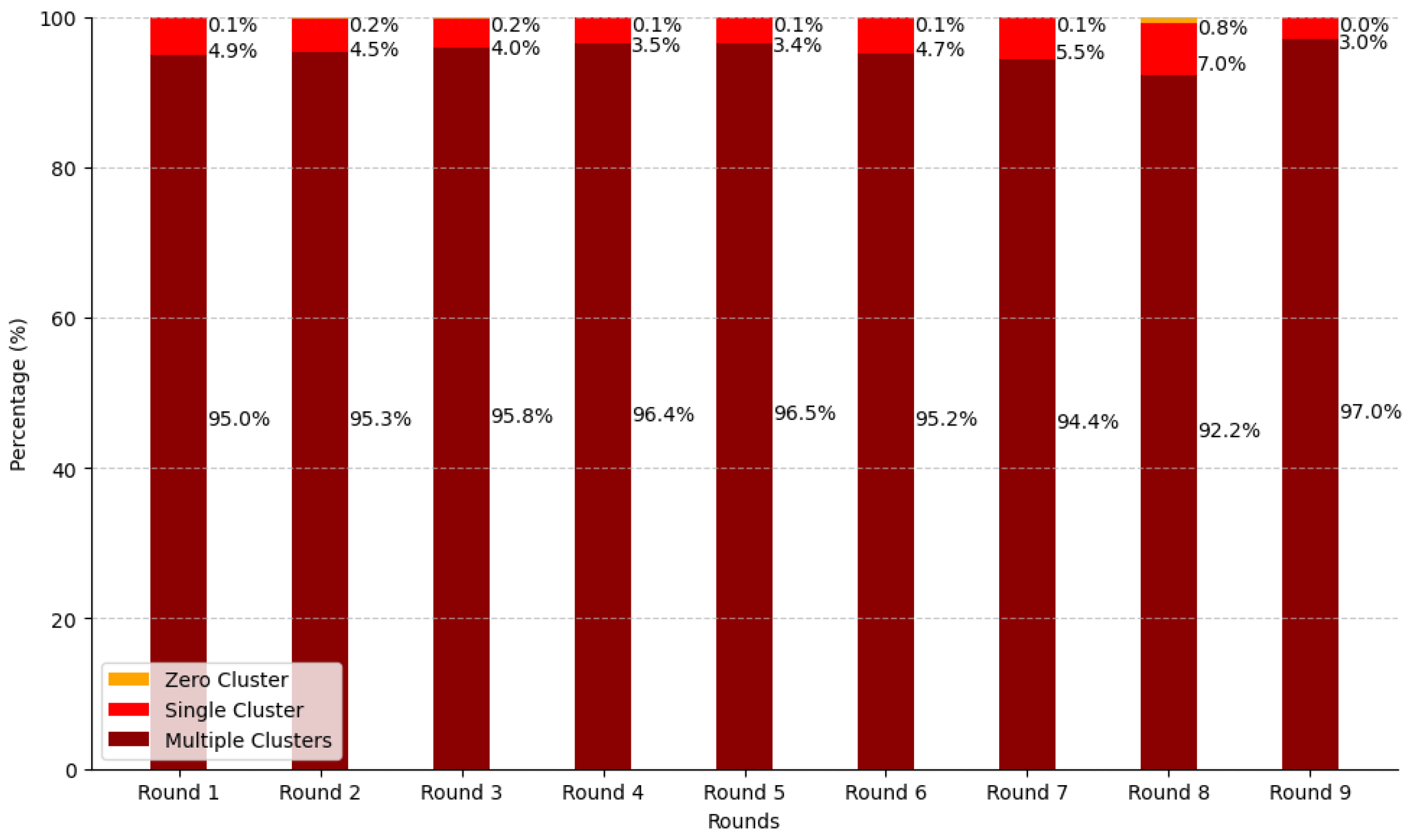
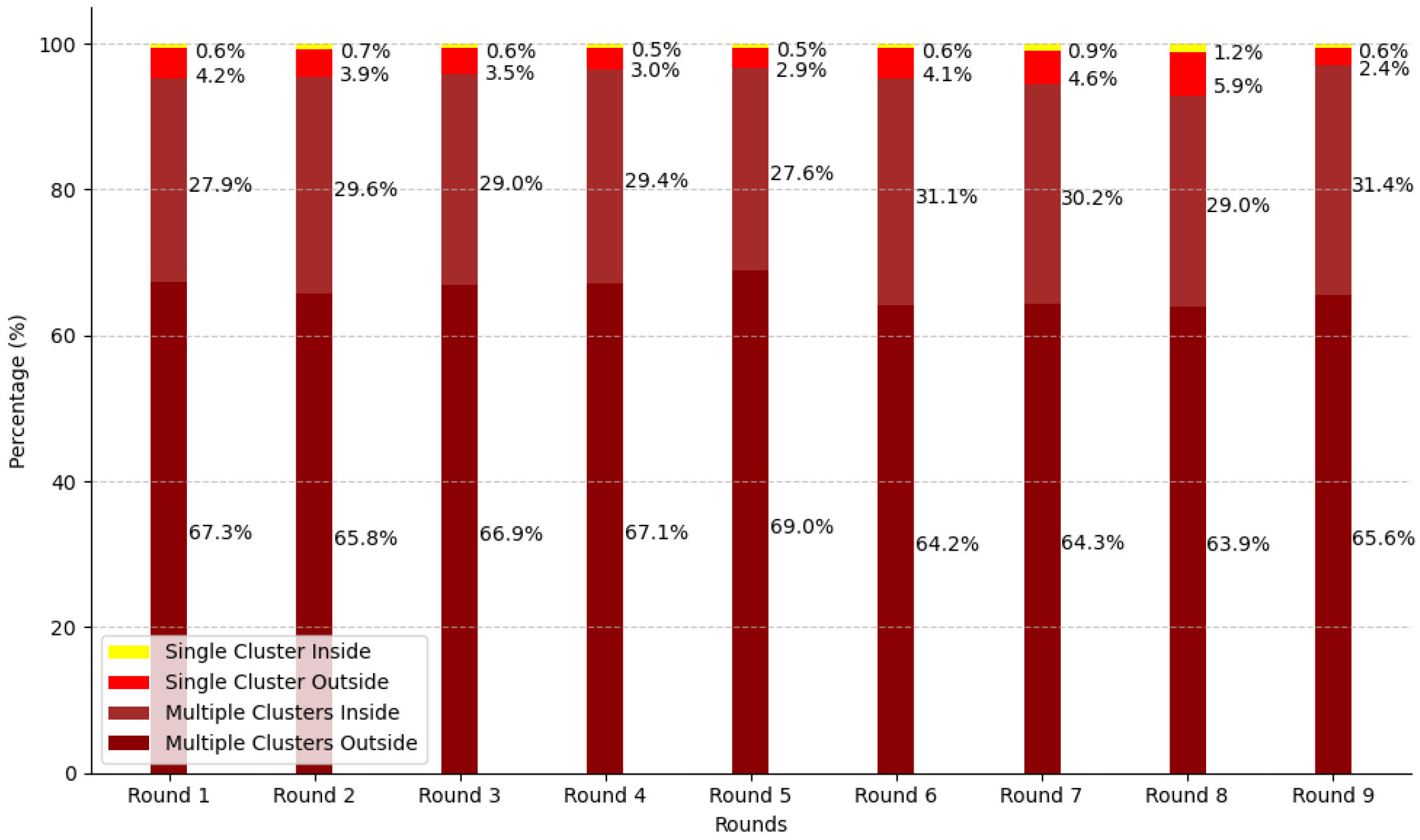
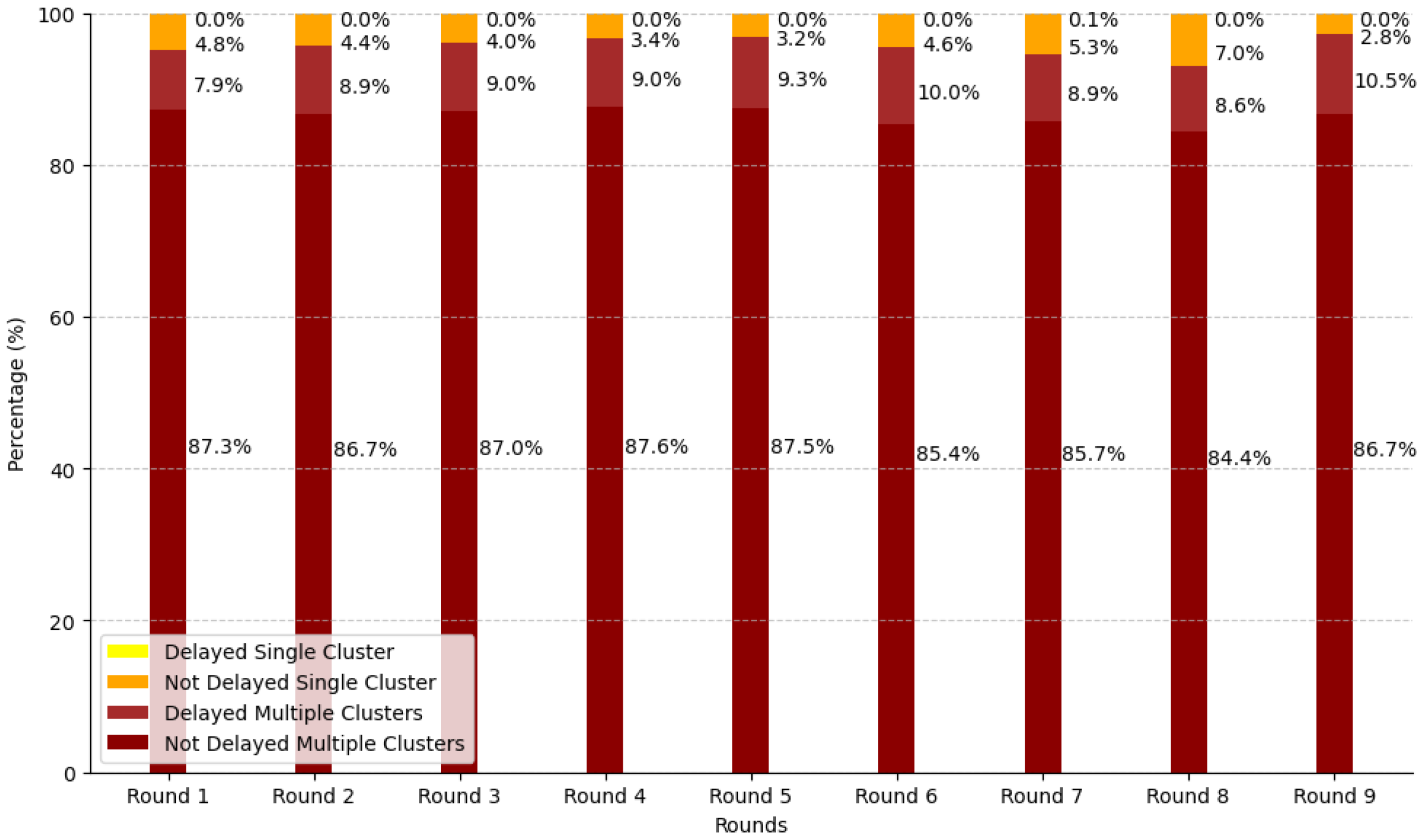
Figure 21.
Stacked cluster distribution across rounds in percentage. The chart shows the proportion of different cluster categories per round.
Figure 21.
Stacked cluster distribution across rounds in percentage. The chart shows the proportion of different cluster categories per round.
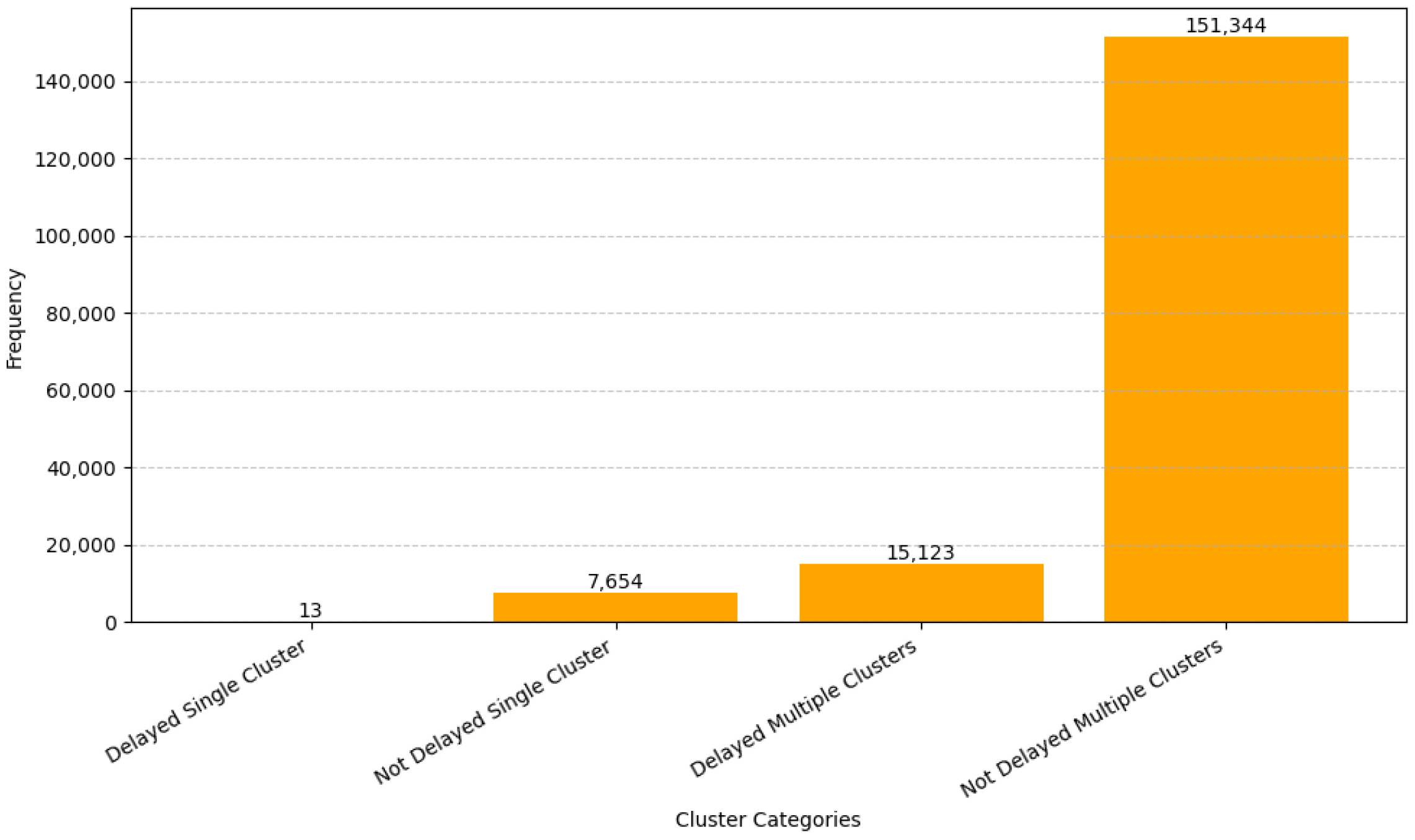
Figure 22.
Distribution of delayed and not-delayed cluster–target relationships.
Figure 22.
Distribution of delayed and not-delayed cluster–target relationships.
Figure 23.
Percentage distribution of temporal cluster–target relationships across rounds.
Figure 23.
Percentage distribution of temporal cluster–target relationships across rounds.
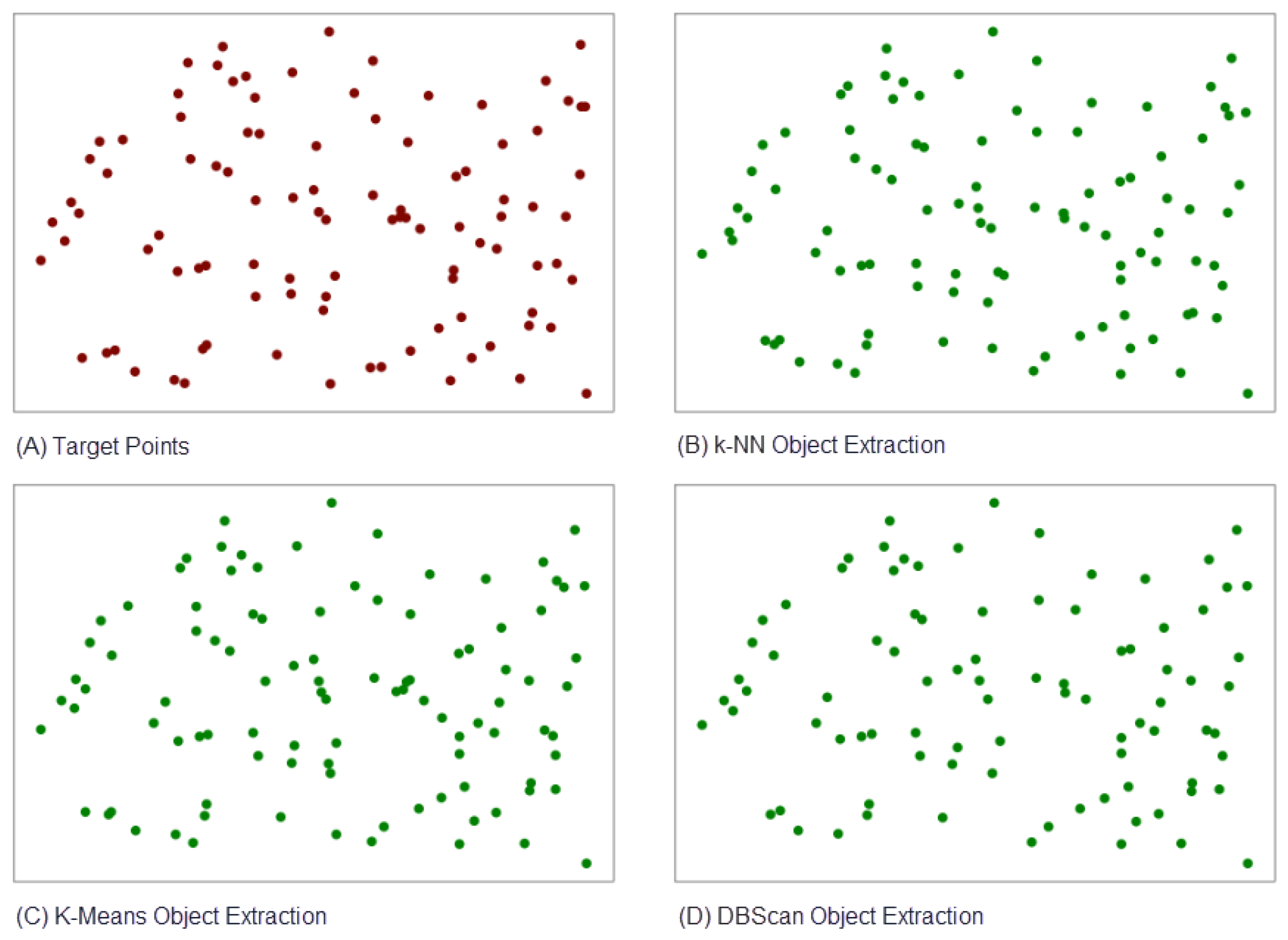
Figure 24.
Example of Comparison Target Points and other object extraction methodologies result. (A) Target Points as ground truth for (B) k-NN Object Extraction, (C) K-Means Object Extraction, and (D) DBScan Object Extraction.
Figure 24.
Example of Comparison Target Points and other object extraction methodologies result. (A) Target Points as ground truth for (B) k-NN Object Extraction, (C) K-Means Object Extraction, and (D) DBScan Object Extraction.
Table 1.
Overview of clustering methods applied to gaze data across prior studies. Includes participant count, task type, clustering technique, and key findings.
Table 1.
Overview of clustering methods applied to gaze data across prior studies. Includes participant count, task type, clustering technique, and key findings.
| Study | Participants | Year | Task | Clustering Method | Main Findings |
|---|
| Nyström et al. [28] | 10 | 2010 | Event Detection | Adaptive Thresholds, Data-driven Filtering | Emphasised filtering raw gaze data to accurately produce velocity and acceleration profiles, indirectly influencing clustering outcomes. |
| Kumar et al. [29] | 40 | 2019 | Reading (Metro Maps) | Hierarchical Clustering | Utilised clustering to identify gaze behaviour groups, aiding interpretation of fixation and saccade metrics and facilitating visual exploration of reading patterns. |
| Hsiao et al. [30] | 61 | 2021 | Visual Stimuli | Co-clustering, EMHMM | Identified consistent eye-movement patterns across varying stimulus layouts by estimating individual Hidden Markov Models (HMMS) and applying co-clustering. |
Table 2.
Summary of exploratory data attributes across dataset rounds, including number of rows, NaN percentages, and gaze-point distributions.
Table 2.
Summary of exploratory data attributes across dataset rounds, including number of rows, NaN percentages, and gaze-point distributions.
| Round | Files | Participants | 100-Gaze Pairs Group | Target Points | Total Pairs (in Million) | % NaN Pairs | % Inside Frame Pairs | % Outside Frame |
|---|
| 1 | 644 | 322 | 64,400 | 64,400 | 65.1 M | 2.48 | 91.61 | 5.91 |
| 2 | 272 | 136 | 27,200 | 27,200 | 27.4 M | 2.29 | 91.76 | 5.95 |
| 3 | 210 | 105 | 21,000 | 21,000 | 21.2 M | 2.38 | 91.86 | 5.76 |
| 4 | 202 | 101 | 20,200 | 20,200 | 20.4 M | 2.02 | 92.47 | 5.51 |
| 5 | 156 | 78 | 15,600 | 15,600 | 15.7 M | 1.76 | 91.96 | 6.29 |
| 6 | 118 | 59 | 11,800 | 11,800 | 11.9 M | 2.66 | 91.48 | 5.86 |
| 7 | 70 | 35 | 7000 | 7000 | 7.0 M | 3.66 | 90.71 | 5.63 |
| 8 | 62 | 31 | 6200 | 6200 | 6.2 M | 4.64 | 89.75 | 5.61 |
| 9 | 28 | 14 | 2800 | 2800 | 2.8 M | 2.26 | 92.52 | 5.21 |
Table 3.
Summary of Target Point Statistics. The variables and refer to the horizontal and vertical coordinates of the predefined target point shown during the Random Saccade task.
Table 3.
Summary of Target Point Statistics. The variables and refer to the horizontal and vertical coordinates of the predefined target point shown during the Random Saccade task.
| Metric | Min Value | Max Value | Stated Min | Stated Max | Difference Min | Difference Max |
|---|
| −14.702561 | 15.305838 | −15 | 15 | 0.297439 | −0.305838 |
| −9.367647 | 8.604543 | −9 | 9 | −0.367647 | 0.395457 |
Table 4.
Adjacent target displacement statistics in degrees of visual angle (DVA), representing average spatial movement between successive target points.
Table 4.
Adjacent target displacement statistics in degrees of visual angle (DVA), representing average spatial movement between successive target points.
| Round | Average Distance (DVA, Spherical) | Minimum Distance (DVA, Spherical) | Maximum Distance (DVA, Spherical) |
|---|
| Round 1 | 13.466467 | 0.382884 | 33.444873 |
| Round 2 | 13.484046 | 1.092978 | 32.346398 |
| Round 3 | 13.506172 | 0.318144 | 33.653568 |
| Round 4 | 13.460669 | 2.126197 | 33.475838 |
| Round 5 | 13.429277 | 1.036157 | 32.816737 |
| Round 6 | 13.516743 | 0.263403 | 32.397405 |
| Round 7 | 13.461173 | 0.765831 | 32.358234 |
| Round 8 | 13.520144 | 0.582597 | 31.629944 |
| Round 9 | 13.208448 | 3.434669 | 31.539671 |
Table 5.
Statistics of gaze point values, showing minimum and maximum data distribution across the entire dataset.
Table 5.
Statistics of gaze point values, showing minimum and maximum data distribution across the entire dataset.
| Metric | Min Value | Max Value |
|---|
| x | −52.241819 | 51.263111 |
| y | −41.153931 | 36.633323 |
Table 6.
Average object extraction accuracy across different clustering methods. Accuracy is calculated based on centroid-to-target distances.
Table 6.
Average object extraction accuracy across different clustering methods. Accuracy is calculated based on centroid-to-target distances.
| Object Extraction Method | Average Distance Accuracy Compared to Target Points |
|---|
| K-NN | 90.51% |
| K-means | 90.61% |
| DBscan | 90.87% |
Table 7.
Summary comparison of clustering methods (k-NN, k-Means, DBSCAN) based on the types of cluster classifications produced.
Table 7.
Summary comparison of clustering methods (k-NN, k-Means, DBSCAN) based on the types of cluster classifications produced.
| Cluster Type | k-NN (k = 5) | k-Means (k = 3) | DBScan ( = 0.5, Min_samples = 500) |
|---|
| Cluster Count (CC) | | | |
| No cluster | No | No | No |
| Single cluster | Yes | Yes | Yes |
| Multiple clusters | Need Vote | Need Vote | Need Vote |
| Cluster–Target Presence (C–TP) | | | |
| No cluster with target point | No | No | No |
| No cluster without target point | No | No | No |
| Single cluster with target point | Yes | Yes | Yes |
| Single cluster without target point | No Data | No Data | No Data |
| Multiple clusters with target point | Need Vote | Need Vote | Need Vote |
| Multiple clusters without target point | No Data | No Data | No Data |
| Cluster–Target Relationship (C–TR) | | | |
| Single cluster, target inside | Yes | Yes | Yes |
| Single cluster, target outside | No | No | No |
| Multiple clusters, target inside | Need Vote | Need Vote | Need Vote |
| Multiple clusters, target outside | No | No | No |
| Temporal Cluster–Target Relationship (TC–TR) | | | |
| Delayed single cluster | Yes | Yes | Yes |
| Not-delayed single cluster | No | No | No |
| Delayed multiple clusters | Need Vote | Need Vote | Need Vote |
| Not-delayed multiple clusters | No | No | No |
Table 8.
Benchmark comparison between the proposed GCT and prior works. Summarises task types, metrics, and applicability to gaze analysis. The “N/A” values in the table represent instances where neither of the prior works reported standard classification metrics such as accuracy, precision, recall, or F1-score.
Table 8.
Benchmark comparison between the proposed GCT and prior works. Summarises task types, metrics, and applicability to gaze analysis. The “N/A” values in the table represent instances where neither of the prior works reported standard classification metrics such as accuracy, precision, recall, or F1-score.
| Method | Task/Dataset | Accuracy | Precision | Recall | F1-Score | Notes |
|---|
| GCT (k-NN, k-Means, DBSCAN) | Random Saccade (GazeBase) | 90.5–90.9% | ∼93–95% | ∼93–95% | ∼93–95% | Supervised centroid-to-target classification; validated on 176,200 samples |
| Kumar et al. [29] | Static map reading | N/A | N/A | N/A | N/A | Hierarchical clustering; no classification metrics reported |
| Hsiao et al. [30] | Scene perception (natural images) | N/A | N/A | N/A | N/A | EMHMM + co-clustering; evaluated using log-likelihood, not accuracy |