Marine Applications and Design of High-Efficiency Small-Scale Gas Turbines

Abstract

In today’s era of heightened environmental awareness, industries and means of transport are under increasing pressure to minimize their ecological footprint. In particular, small-scale power plants for the marine sector pose environmental challenges due to their pollutant emissions. One promising technology to address this purpose is represented by small-scale gas turbines. In this work, the design of a radial turbine and a centrifugal compressor for a 5 MW engine to be employed onboard ships is developed. After a one-dimensional design, the project involves the aerodynamic and structural design optimization of the two machines using fluid dynamic and structural simulation software. The final configuration obtained by the optimization process and its performance are analyzed, demonstrating that the use of a radial architecture for the construction of a 5 MW small gas-turbine assembly for marine propulsion is feasible. Both the compressor and the turbine optimization procedures led to final values of polytropic efficiencies that were three percentage points larger than the first-guess design machine values, simultaneously allowing for reductions in stress usage factors by more than 38% and 32% for the compressor and the turbine, respectively.

1. Introduction

In the last decades particular attention has been paid to the reduction and minimization of the ecological footprint of industries and means of transport. Regulatory bodies worldwide are focusing on implementing stringent measures to govern the pollutant emissions from these facilities [1]. In this framework, small-scale power plants used in the marine sector play a crucial role in terms of pollutants.

The imperative to address environmental concerns within the marine sector arises from the recognition of its substantial contributions to air and water pollution [2,3]. Small ships often rely on small-scale power plants for propulsion and onboard energy needs. These power plants, usually based on reciprocating diesel engines, can emit pollutants such as sulfur oxides (SO_x), nitrogen oxides (NO_x), particulate matter (PM), and greenhouse gases (GHGs), contributing to air and water pollution.

Moreover, shipping operations are often conducted in sensitive marine ecosystems, magnifying the environmental impact of pollutant emissions. The combustion of fossil fuels in marine power plants further exacerbates their environmental footprint, underscoring the urgency of regulatory intervention to mitigate these impacts.

Sulphur oxides (SO_x) and nitrogen oxides (NO_x) are major contributors to air pollution, leading to respiratory problems, acid rain formation, and the formation of harmful ground-level ozone [4]. Particulate matter (PM) poses serious health risks [5], particularly to vulnerable populations, and can also contribute to respiratory and cardiovascular diseases, as well as atmospheric haze.

In addition to their local environmental effects, the emissions from marine power plants also contribute to global climate change. Carbon dioxide (CO₂) is a major greenhouse gas responsible for trapping heat in the Earth’s atmosphere, leading to global warming and its associated impacts, such as sea-level rise and extreme weather events [6]. Methane (CH₄), although less abundant, is even stronger than CO₂ in trapping heat over shorter time frames.

International organizations such as the International Maritime Organization (IMO) have identified and developed the mechanisms needed to achieve the limitation or reduction of GHG emissions from international shipping [7] and implemented effective regulatory frameworks, specifically tailored to maritime operations aimed at reducing emissions from ships and their associated power plants. These regulations include emission standards, fuel quality requirements, and incentives for adopting cleaner technologies.

One promising technology for reducing emissions from small-scale power plants in the marine sector is represented by small gas turbines in simple or regenerative configuration. These turbines are compact, lightweight, and highly efficient, making them well-suited for use on ships, where space and weight constraints are critical considerations. Small gas turbines utilize advanced combustion processes and waste heat recovery systems to maximize energy efficiency and minimize pollutant emissions.

By capturing and reusing waste heat from the turbine exhaust, regenerative systems can significantly reduce fuel consumption and emissions of greenhouse gases such as CO₂ and CH₄. Additionally, advanced combustion technologies enable small-scale gas turbines to achieve lower emissions of NO_x and PM compared to conventional power plant designs. Gas turbine design for the marine sector demands a delicate balance of efficiency, reliability, and compactness. These turbines must meet the stringent requirements imposed by the unique operational environments of ships.

In this work, the possible design of a radial turbine and centrifugal compressor for an engine to be employed onboard ships as a small gas turbine, i.e., up to 5 MW output power, is developed, considering cycle analysis, as well as aerodynamic, and structural design. To this purpose, in this work, the design of the radial turbine and the centrifugal compressor installed in a small gas turbine for marine applications, with an electrical output power of 5 MW, is proposed and developed.

The design starts from the preliminary design phase, based on the study of the thermodynamic cycle and its main characteristics, which define the boundary conditions for the main components of the plant and in particular, the compressor and the turbine. After a preliminary design phase of the machines, based on the one-dimensional design and the use of the fundamental equations of turbomachinery, the project involves the aerodynamic and structural optimization of the two components.

This phase is conducted using fluid dynamic and structural simulation software, capable of exploring the different geometric configurations of the machines, with the aim of identifying a configuration capable of increasing aerodynamic performance and at the same time satisfying the structural constraints imposed by the specific and challenging application. The final configuration and its performance are critically analyzed.

2. International Regulations on Marine Transport Emissions

Marine transport pollutants due to the required propulsion power and on-bord energy service consumptions are regulated by international legislation nowadays since they influence global warming and the local quality of air.

The IMO (the International Marine Organization of the UN) defines the limits of emissions in specific sea areas designated as ECAs—Emission Control Areas—as well as in the rest of global areas (MARPOL Convention Annex VI).

Sea areas with limits on sulfur oxides ${\mathrm{SO}}_{\mathrm{x}}$ are called SECAs (Sulphur Oxide Control Areas), while sea areas with limits on nitric oxides ${\mathrm{NO}}_{\mathrm{x}}$ are called NECAs (Nitric Oxide Control Areas). ECAs include both SECA and NECA limits. Furthermore, the IMO provides commitments for the limitation of greenhouse gases (GHGs).

2.1. Sulfur Oxides

Sulfur oxides are directly dangerous for human life, attacking the respiratory system, eyes, skin, and mucous membranes. They also cause corrosion on metallic structures.

Sulfur pollution is normally evaluated in terms of percentage of sulfur mass in mass of fuel. The sulfur content limits for marine applications have been changed in the last decades: nowadays, the sulfur content should be limited to 0.5% outside of SECAs (from 1 January 2020) and to 0.1% inside SECAs (from 1 January 2015).

The sulfur content is mainly a matter of fuel composition and the distillation process. In general, heavier fuel oils (HFOs) have a higher sulfur residual content compared to lighter marine diesel oil (MDO) or marine gas oil (MGO). Scrubber devices can be also used to clean exhaust gas; however, the main solution is the use of low sulfur content fuel.

LNG fuel can feed both diesel cycle engines and Joule–Brayton cycle engines (gas turbine engines).

The GT exhaust gases from LNG combustion, regardless of the exact composition of the LNG fuel, have a negligible content compared to the lowest limit of 0.10% [8].

2.2. Nitric Oxides

Nitric oxides, even in low concentrations (from 0.2 mg/m³ air), are dangerous for the respiratory system. They can be evaluated in terms of volumetric percentage of ${\mathrm{NO}}_{\mathrm{x}}$ in the exhaust gases (for a certain percentage of oxygen) or, in a more practical and unambiguous unit, as g/${\mathrm{kWh}}_{\mathrm{thermal}}$ produced or, even better, as g/${\mathrm{kWh}}_{\mathrm{electric}}$ produced, which, additionally, involves the efficiency of the energy conversion from thermal to electric.

The nitric oxides emissions of marine engines are regulated by amendment 2010 to Annex VI. These limits have been applied through three different periods of time, relevant to the ship construction, defined as “Tiers” (Levels) and three different categories of engines, based on their rotational speed (Figure 1):

-

Tier 1: represents the maximum level of admissible pollution (17–9.8 g/kWh) and it holds for engines installed before end 2010.

-

Tier 2: reduces to 14.4–7.7 g/kWh the level of admissible pollution from engines installed after January 2011.

-

Tier 3: furtherly reduces the level of admissible emissions to 3.4–2.0 g/kWh. It holds for engines installed after January 2016 and for all the ships travelling in NECA areas.

The reduction of nitric oxide pollution using LNG or mixture of hydrogen and natural gas, particularly in ports, is strategical, especially considering the ongoing and increasingly stringent emission limits.

While hydrogen combustion is inherently free from carbon oxide emissions, it is crucial to recognize that, when hydrogen or a mixture of hydrogen and natural gas is used, ${\mathrm{NO}}_{\mathrm{x}}$ production can still occur, depending on the combustion process and temperature.

Ammonia is a good ${\mathrm{H}}_2$ carrier and therefore a promising fuel for zero carbon emissions. However, technical difficulties related to low LHV, low burning velocity, large ${\mathrm{NO}}_{\mathrm{x}}$ production, prevent the immediate use of ammonia with the available GT technology.

A main drawback of ammonia as fuel is just related to its chemical composition that results in exceedingly large value of ${\mathrm{NO}}_{\mathrm{x}}$ in the exhaust gases ranging from 500 to 1000 ppm, according to [9].

2.3. Greenhouse Gases

GHG emissions are measured in terms of equivalent kg of CO₂ per Energy unit in kWh or gCO₂ per energy unit in MJ, featuring an index of emission suitable to compare the fuel performance. The energy unit can be referred to the thermal energy provided by the fuel combustion or to the electric or mechanical energy according to the end user. Referring to useful is more correct and avoids misleading even in case of CHP.

The Energy Efficiency Design Index (EEDI) [10], introduced by IMO in 2011 through amendments of MARPOL Annex VI is a design parameter based on general vessel performance, indicating the quantity of CO₂ emission per cargo unit per nautical mile. Given the general applicability of the EEDI, specific formulations were introduced to fit the diversity of modern ship types. A general definition for the EEDI is reported in the following equation:

$$EEDI=\left(C{O}_2\right)ME+\left(C{O}_2\right)AE+\left(C{O}_2\right)SG/M-\left(C{O}_2\right)ET /fi·CAP·v_{ref}$$

(1)

Each of the first three (CO₂) terms represent the carbon emissions associated to nominal operations for Main Engines (ME), Auxiliary Engines (AE) and Shaft Generators (SG) or other Motors/Systems present onboard for propulsion. The latter quantifies the CO₂ saved by the implementation of Efficiency Technologies (ET), such as Waste Heat Recovery (WHR), Cogeneration, hybrid propulsion, exhaust gas post-treatment among the most common. Each term is calculated as the set of engines Specific Fuel Consumption (SFC), Carbon emission coefficients (C), rated power (P), adjusted with non-dimensional coefficients ($fi$) set by IMO itself. The denominator represents vessel cargo capacity at a given cruise speed ($v_{ref}$). Capacity (CAP) can be defined using two different measures: Passenger, Ro-Pax and cruise vessels employ Gross Tons (GT) as a measure of internal volume of the vessel, whereas almost all ships dedicated to goods or resource transport employ Dead-Weight Tons (DWT), which indicates the total weight to be carried onboard.

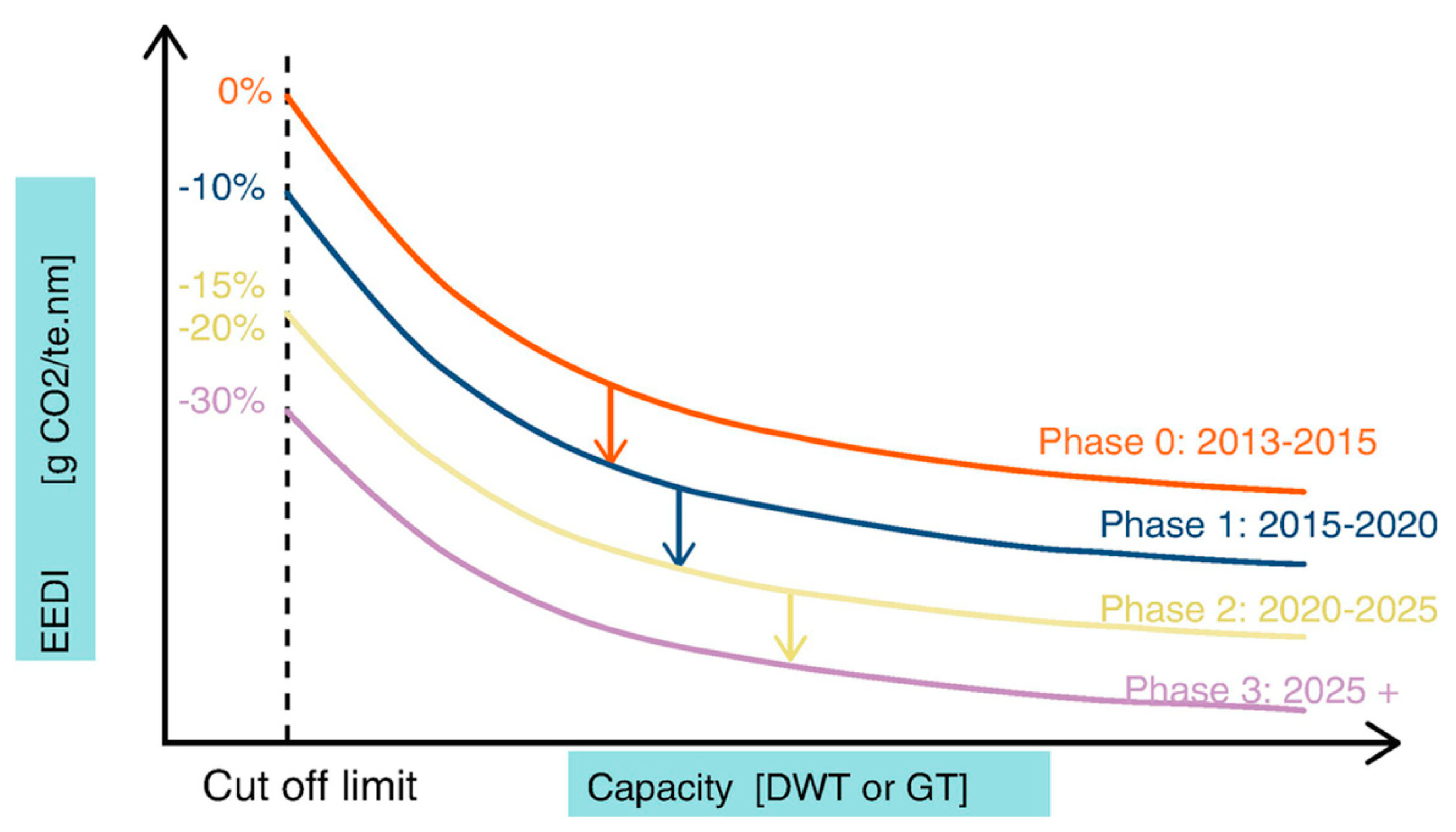
Regulations concerning EEDI came in force from 2013, with an initial Phase 0 of two years. The index must be calculated for operating ships and through the design of new vessels and it has to be compliant with the references set by IMO. Starting from 2015, the reference EEDI has been decreased gradually every 5 years, with a Phase 1 (from 2015 to 2019) reduction of 10% and a Phase 2 (from 2020 to 2024) of 15 to 20%, depending on the specific ship type. Starting from 2025, Phase 3 reduction will be characterized by a 30% decrease in the EEDI for almost all operating ships. The gradual modification of EEDI over time (shown in Figure 2) is a measure aiming to reduce the carbon footprint over the years and push the marine sector towards less carbon intensive technological development.

In July 2023 the 2023 IMO GHG Strategy has been adopted, aiming at net-zero GHG emissions by or around 2050. Intermediate objective is to reduce by 2030 CO₂ emissions by at least 40%, compared to 2008, through further improvement of energy efficiency for new ships.

In September 2023 the Parliament and the European Council have approved the EU Regulation 2023/1805 [7] on the use of renewable and low-carbon fuels in maritime transport and have laid down additional rules to limit GHG and impose On-shore Power Supply (OPS) or zero-emission technology in ports under the jurisdiction of a Member State:

Annex 1 of the Regulation applies to all ships to transport passengers or cargo for commercial purposes, regardless of their flag, characterized by gross tonnages above 5000 GT.

Evaluation of GHG includes both Tank to Wake (TtW) and Well-to-Tank (WtT) emissions, in other words, real emissions produced by fuel combustion and equivalent emissions associated to fuel production. All possible marine fuels are classified and evaluated in terms of TtW and WtT: fossil fuels (including HFO, LFO, MGO, LNG, H₂, NH₃, methanol), biofuels (including ethanol, biodiesel, bio-LNG, bio-methanol) and renewable fuels of non-biological origin (RFNBO) also called e-fuels (including e-LNG, e-H₂, e-NH₃).

3. Selection of Fuel and Engine

In October 2023 Nippon Kaiji Kyokai has issued a document on the Pathway to Zero Emissions in International Shipping to understand the 2023 IMO GHG Strategy and develop the possible scenarios for the years 2030 and 2040 concerning the use of new technologies and new fuels for three different conditions of future marine transport volumes increase compared to 2021, namely +25% (base case), +49% (high case), +14% (low case) for three levels of efficiency improvement (17%, 23%, 30%). In all the transition cases, an LNG invariant percentage of 10% has been considered. To achieve the IMO GHG Strategy checkpoints, a variable percentage of zero emission fuels, ranging from 21% (for the low-volume case with a larger efficiency improvement achievement) to 42% (for the high-volume case and a lower efficiency improvement achievement) by 2030, and ranging from 78% to 87% for 2040. These figures seem highly improbable to occur. Most probably, the LNG share in the near- to medium-term could achieve a larger value compared to 10%, considering that in 2021 the share was already 7% and that several efforts for production, distribution, and bunkering have already been implemented.

Among the fuels, those having the lowest WtW GHG emission factors are LPG (74 g/MJ) and LNG (76 g/MJ).

The efficiency of the power conversion systems is a fundamental parameter in determining the operational costs of a ship missions and directly influences the amount of emissions once the type of fuel and the power for propulsion and onboard energy request have been fixed.

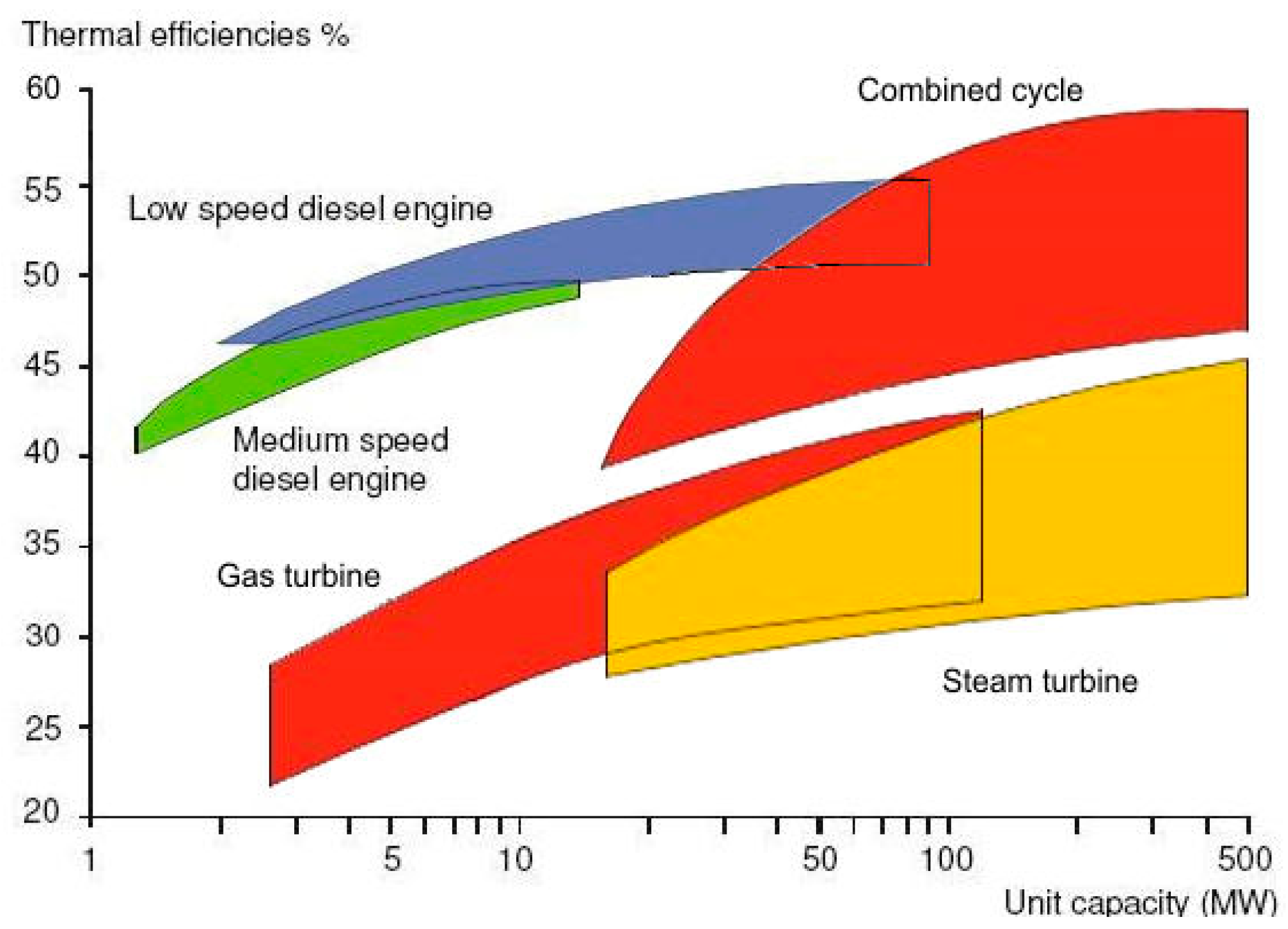
The efficiency of large units of low-speed reciprocating engines, nowadays, can reach 50% and more, and smaller engines have efficiencies larger than 40%. Even though the large units of aeroderivative gas turbine engines reach 40% efficiency and more, there is still an efficiency gap of more than 5 points among the two power conversion solutions. However, considering the large units, the introduction of gas-turbine combined-cycle (GTCC) engines for marine applications allows efficiencies higher than those of low-speed reciprocating engines (Figure 3).

Even though this solution is not new, it is still uncommon for commercial ships up to now.

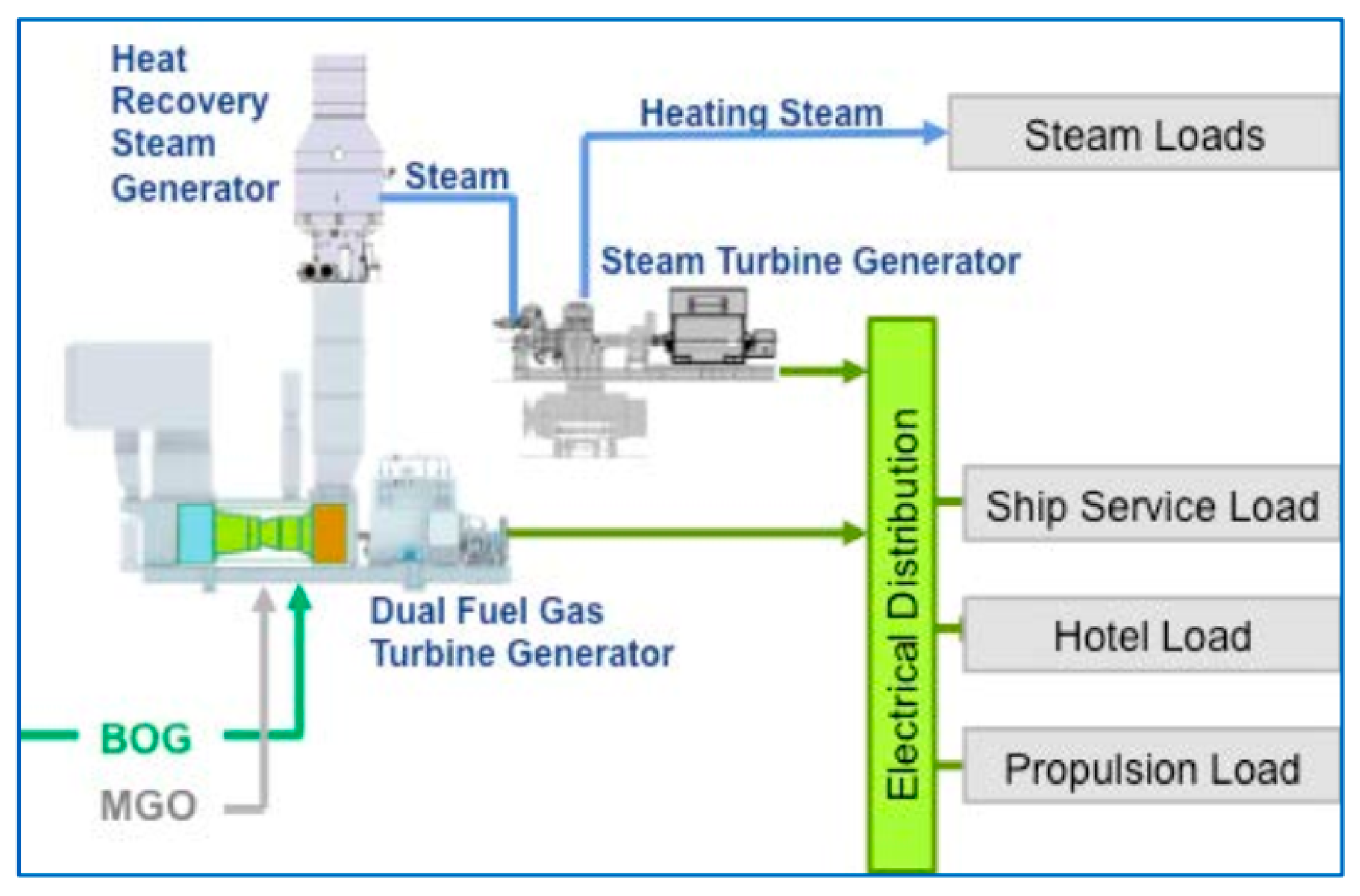
The GTCC marine conversion systems with gas and steam turbines seem to be especially suited for benefiting from the new electric propulsion architecture, since both gas turbine and steam turbine electric generators can provide electric energy to the ship’s internal grid, and the propulsive electric motors are mechanically decoupled from the engines. This is the COmbined Gas turbine Electric and Steam (COGES) power conversion and propulsion system (Figure 4). At the same time, part of the available steam can also be properly utilized by onboard users to meet heat requirements, especially in the case of cruise ships [13]. Moreover, this kind of plants pave the way for low- or zero-carbon fuels, with noteworthy environmental benefits [14].

One of the most important advantages of gas turbine-based conversion systems burning LNG, with the current lean premixed combustion technology that limits the combustion temperature to about 1800 K, is the ${\mathrm{NO}}_{\mathrm{x}}$ emission level, which attains values of the order of 0.1–0.2 g/kWh, namely one order of magnitude lower than the IMO Tiers III-prescribed limits in ECAs. Diesel engines, even when fueled with LNG, due to combustion process at higher temperature, generate about one order of magnitude larger values of $N{O}_x$, which, however, could still meet the Tiers III requirements.

Another advantage of the gas turbine-based engines compared to diesel engines is the more favorable power-to-weight ratio and power-to-volume ratio, which allow saving space on the ship and increasing the paying load (from +30 to +70 TEU—twenty-foot equivalent unit—or up to 50 cabins in large container ships and cruise ships, respectively). Finally, gas turbine engines reduce noise, vibration, the amount of lubricating oil, maintenance intervals, and simplify auxiliary systems.

The costs of the components for gas turbine-based power conversion systems are larger due to the more advanced aeroderivative technology and materials necessary to withstand larger continuous temperatures and outstanding centrifugal loadings of turbine and compressor bladings.

For limited power propulsion or auxiliary power generation onboard units, which are mainly employed at berth, less advanced technologies, simplified architecture, and less demanding performance can be acceptable and can be implemented by employing and extending to larger power the already-developed concepts and technologies of micro and small gas turbines.

The selection of fuel, engine, and onboard energy system architecture is a complex and non-unique solution problem, which would require evaluating several economic, environmental, technological, and regulatory aspects, and therefore is far beyond the present study objectives. Taking into consideration the above-reported information on marine transport emission regulation and the knowledge on small gas turbine energy systems, a possible logical solution for limited power propulsion or auxiliary power generation onboard units, to be mainly employed at berth, is here proposed.

A power range of about 1 to 10 MW_el per unit has been selected according to a previous analysis from the authors [16], focusing on the engine sizes adopted aboard presently operating vessels. A radial turbomachine architecture, driving the choice to a 5 MWe engine power configuration, has been selected to achieve a compact solution, especially concerning axial length. The main challenge of the present design is the achievement of competitive performances comparable to axial GTs and marine diesel engines with similar sizes.

4. Cycle Analysis

Since 2018, the authors have developed studies on the feasibility of GT-combined cycles for marine engines below 10 MW_el of power [16,17,18,19]. These studies have considered, as the main turbomachine components, a full radial single-stage compressor-turbine GT architecture of new design and a single-stage, high-speed compact FINCANTIERI steam turbine that can provide power in the range of 500–2000 kW, operating with superheated steam up to 60 bar.

The authors also conducted an extensive examination of thermodynamic cycles, comparing their performance, estimated dimensions, and weight with commercial engines installed aboard passenger ships [16]. The findings highlighted the viability of a single-cycle small gas turbine, producing up to 5000 kW_el of net electric power, which can be employed as a competitive power unit, also offering openness to co-generation strategies. When incorporated into a combined-cycle setup, this proposed plant can generate up to 7000 kW_el, while effectively meeting the heat demand onboard ships.

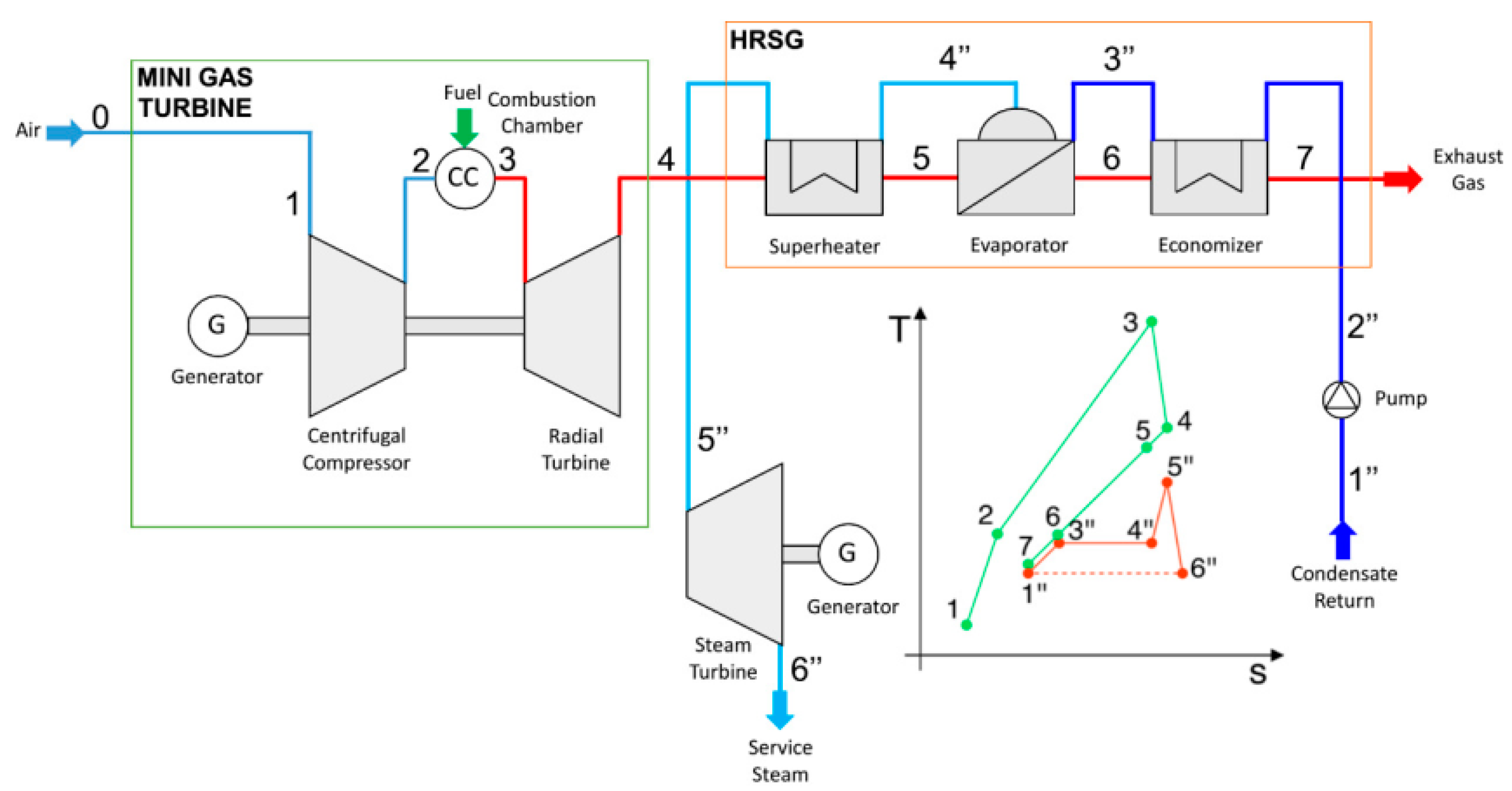
A full radial gas turbine system of 5000 kW_el l and a 6.5 pressure ratio compressor serve as the main power generator engine and a source of high enthalpy flow capable to drive a bottoming steam turbine cycle with admission of superheated steam at 40 bar and 450 °C and exhaust at both 3 bar (counterpressure configuration) and 0.05 bar (condenser configuration).

A general scheme of the combined-cycle power generation system and the combined cycle in T-s plane taken from [17] is reported for clarity in Figure 5.

The input data, starting from the maximum pressure ratio (β) allowed by the single-stage configuration for both the compressor and turbine, alongside the maximum turbine inlet temperature (TIT) imposed by the uncooled architecture adopted for the turbine and polytropic turbine and compressor efficiencies, as well as other necessary assumptions, are reported in

Table 1. Combined-cycle input data and assumptions.

Performance	Value
Compressor pressure ratio [-]/Turbine pressure ratio	6.5/6.0
Compressor efficiency [-]	0.84
Turbine inlet temperature [°C]	950
Turbine efficiency [-]	0.90
Steam turbine inlet temperature [°C]	450
Steam turbine inlet pressure [bar]	40
Steam turbine efficiency [-]	0.75
Heat recovery steam generator effectiveness [-]	0.80
Fuel lower heating value [MJ/kg]	49.5
Electric generator efficiency [-]	0.98
Mechanical efficiency [-]	0.98

.

The relevant thermodynamic and performance parameters of the combined-cycle power conversion system under study, calculated by means of an in-house-developed Excel code and verified by means of the GateCycle code, are reported in

Table 2. The relevant thermodynamic and performance parameters of the combined-cycle power system.

Performance	Counterpressure	Condensing
Steam turbine exhaust pressure [Pa]	0.05	3.0
Total electric power [kW]	6017	7098
Thermal power from fuel [kW]	17,348	17,348
Small gas-turbine electric power [kW]	5000	5000
Steam turbine electric power [kW]	1017	2098
Steam-to-gas turbine power ratio [-]	0.20	0.42
Combined-cycle electric efficiency [-]	0.347	0.409
CHP recuperated thermal power [kW]	4789	-
Steam mass flow rate [kg/s]	2.13	2.40
Steam turbine outlet temperature [°C]	161	33
CHP efficiency [%]	0.628	-
Thermal efficiency [%]	0.28	-
Air-to-steam mass flow-rate ratio [-]	11.51	10.21
Electricity-to-heat ratio [-]	0.81	-
Fuel mass flow rate [kg/s]	0.354	0.354
Gas turbine mass flow rate [kg/s]	24.46	24.46
Gas turbine outlet temperature [°C]	509	509
Stack temperature [°C]	207	120

.

5. Compressor and Turbine Design

Table 3. Compressor and turbine design objectives.

Performance	MU	Compressor	Turbine
$P_{t,in}$	[bar]	1.01	6.26
$T_{t,in}$	[K]	293	1223
$\dot{m}$	[kg/s]	24.11	24.46
$PR$	[-]	6.5	6
${\eta }_{tt}$	[-]	0.82	0.90
$n$	[rpm]	15,000	15,000

outlines the design objectives extrapolated from cycle design.

In selecting rotational speed (ω) and target design efficiencies, specific speed was a key parameter. Specific speed is defined by the formula:

$$n_s=\omega ·\sqrt{\dot{m}/{\rho }_{ref}}/\left(\mathsf{\Delta }{h}_{is}^{0.75}\right)$$

(2)

where the ${\rho }_{ref}$ rotor is the total outlet density for the compressor and the static exit density for the turbine, determined through the classical statistical maps outlined by Rodgers in [20], and further refined for high-performance centrifugal impellers by Van den Braembussche [21], as well as for axial and radial turbines by Glassman [22] and Baskharone [23], respectively. Starting from thermodynamic cycle analysis, an appropriate specific speed was selected to achieve a balance between the machine performance parameters. The calculated values for specific speed (ns) were 0.35 for the compressor and 0.68 for the turbine. The rotational speed of both rotors (reported in Table 3) has been chosen to be lower than in other similar applications [24,25,26].

The choice to use a radial turbomachine type presents significant benefits, particularly regarding the compact design of the compressor [21]. The pressure ratio specified in Table 1 was intentionally selected to allow for a single-stage unit. This decision, however, introduces additional aerodynamic challenges, such as flow recirculation in the compressor due to strong adverse pressure gradients. It is noteworthy that this consideration does not apply to the turbine. Typically, as the specific speed increases, axial gas turbines tend to deliver more power, with higher efficiency [23]. However, radial gas turbines prove to be more efficient when the specific speed is low (n_s < 0.77). Notably, the current assessment, with an n_s of 0.68, further endorses the use of a radial turbine, estimating an efficiency up to 7% higher than that of comparable axial turbines for the same design objective.

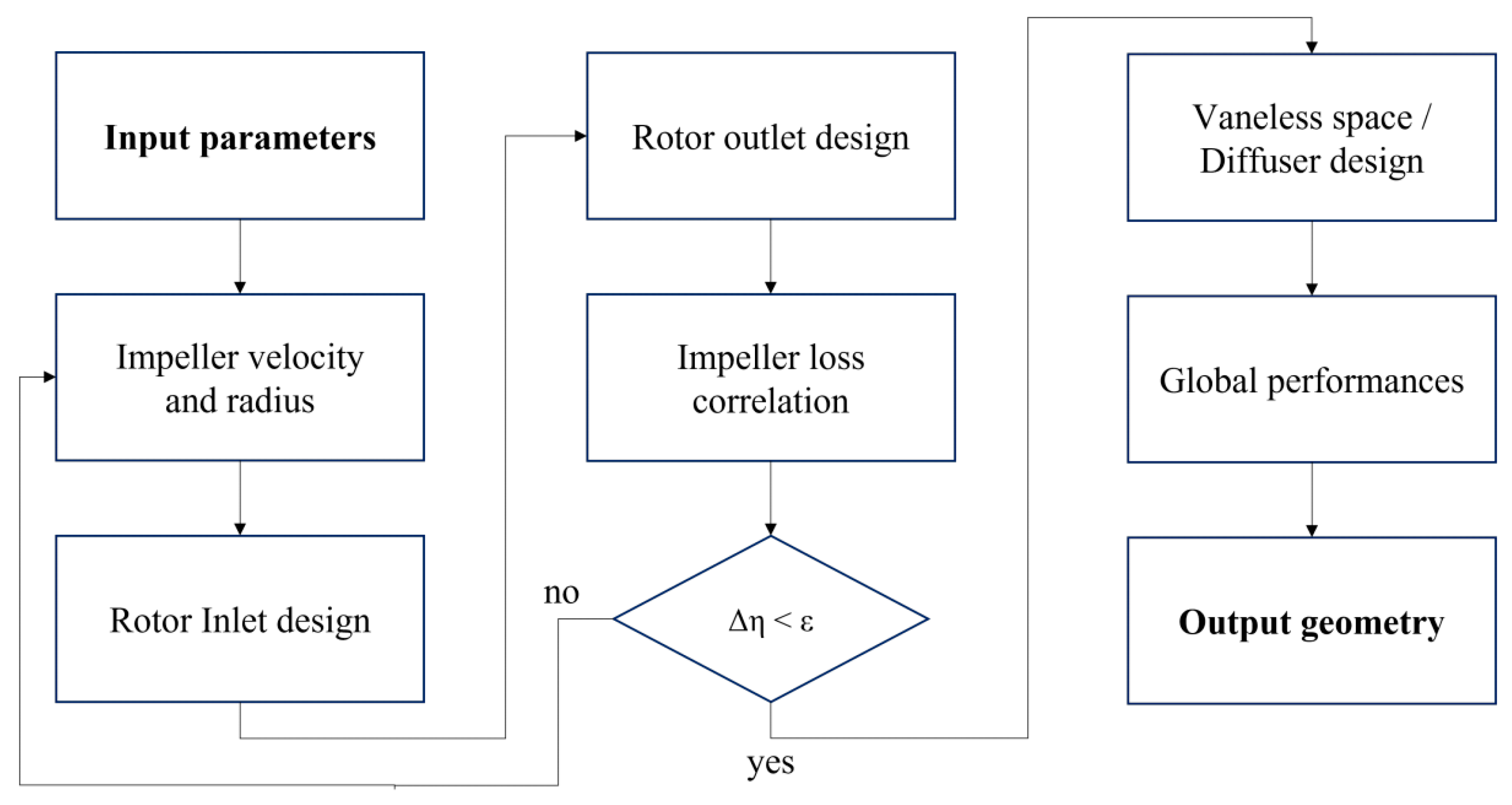
5.1. Compressor 1D Design

The design of the centrifugal compressor heavily relied on the data provided in Table 3, serving as foundational parameters for the implemented procedure. Calculations were conducted using an in-house Matlab code, whose logic is illustrated in Figure 6 and summarized as follows.

Initially, the impeller radius and tip velocity are evaluated starting from the compressor operating conditions and the inlet flow thermodynamic state, considering a preliminary estimation of the backsweep angle. The design of the impeller inlet follows a procedure outlined in the literature [27]. The design of the impeller tip is finalized by applying the continuity equation at the rotor outlet. Loss correlations [28] are employed in an internal loop to estimate the impeller efficiency until stable convergence is reached. To achieve a balance between flow guidance at the impeller outlet and efficiency, the number of blades is adjusted through an external loop.

Successively, a vaneless or wedged diffuser duct is designed to complete the machine. The code provides an assessment of the overall performance of the machine, considering both rotor and diffuser effects, along with the corresponding geometry, tailored for the specific application.

The introduction of the backsweep angle aimed to mitigate the impact of the Coriolis forces on the blade surface, thereby enhancing machine efficiency, with a slight increase in radius. The target pressure ratio is obtained by gradually increasing the outlet radius up to get the peripheral velocity needed [21]. The blade count is adjusted based on the impeller efficiency estimation, with the option to use splitter blades if needed.

Furthermore, the impeller tangential speed (U) and diameter have been determined through the Euler work Equation (D) [26].

Non-dimensional blockage factors have been inputted at all machine sections to consider the growing boundary layers along the channel. The standard coefficients for rotor inlet and outlet, typically around 5% for high-performance compressors, are utilized. The rotor isentropic total-to-total efficiency is estimated, incorporating the effects of supersonic flows, according to works reported in [21,28], to account for the supersonic flow effects. Loss correlations consider various factors, including incidence, skin friction, diffusion, recirculation, and shocks. The performance estimation updates loss components iteratively until the convergence criteria are met. Subsequently, the diffuser is designed, with the opportunity for the user to choose between a bladeless or a wedged one. The vaneless space radius ratio is fixed at 1.10, modelled via logarithmic spiral approximation. The impeller outlet flow angle determines the wedge geometry and fluid properties, with introduced loss coefficients for frictional loss in case of a vaneless diffuser. The described procedure was tested and calibrated on a high-pressure ratio centrifugal compressor from the literature documented by Krain et al. [25], ensuring a fair robustness in the geometry and performance prediction, as highlighted by the results reported in

Table 4. Centrifugal compressor design: procedure validation.

	Krain et al. [25]	1D Procedure
$Impeller inlet radius \left[\mathrm{mm}\right]$	54.0	55.1
$Impeller inlet blade height \left[\mathrm{mm}\right]$	48.0	45.1
$\mathrm{Impeller} \mathrm{outlet} \mathrm{radius} \left[\mathrm{mm}\right]$	112.0	113.2
$Impeller outlet blade height \left[\mathrm{mm}\right]$	10.2	9.7
$Pressure ratio [-]$	6.10	6.17
$Isentropic efficiency [-]$	84.0	84.7

.

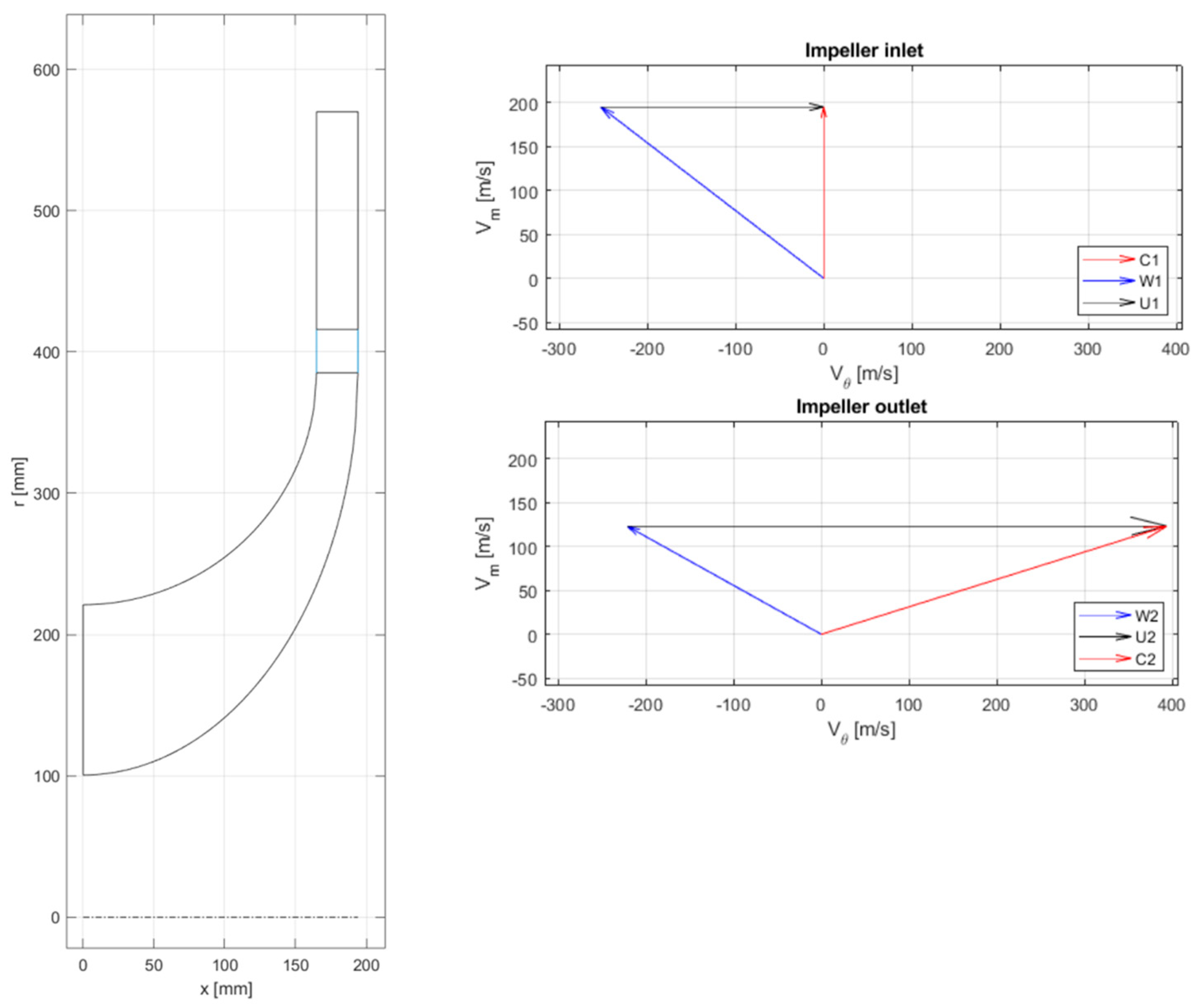
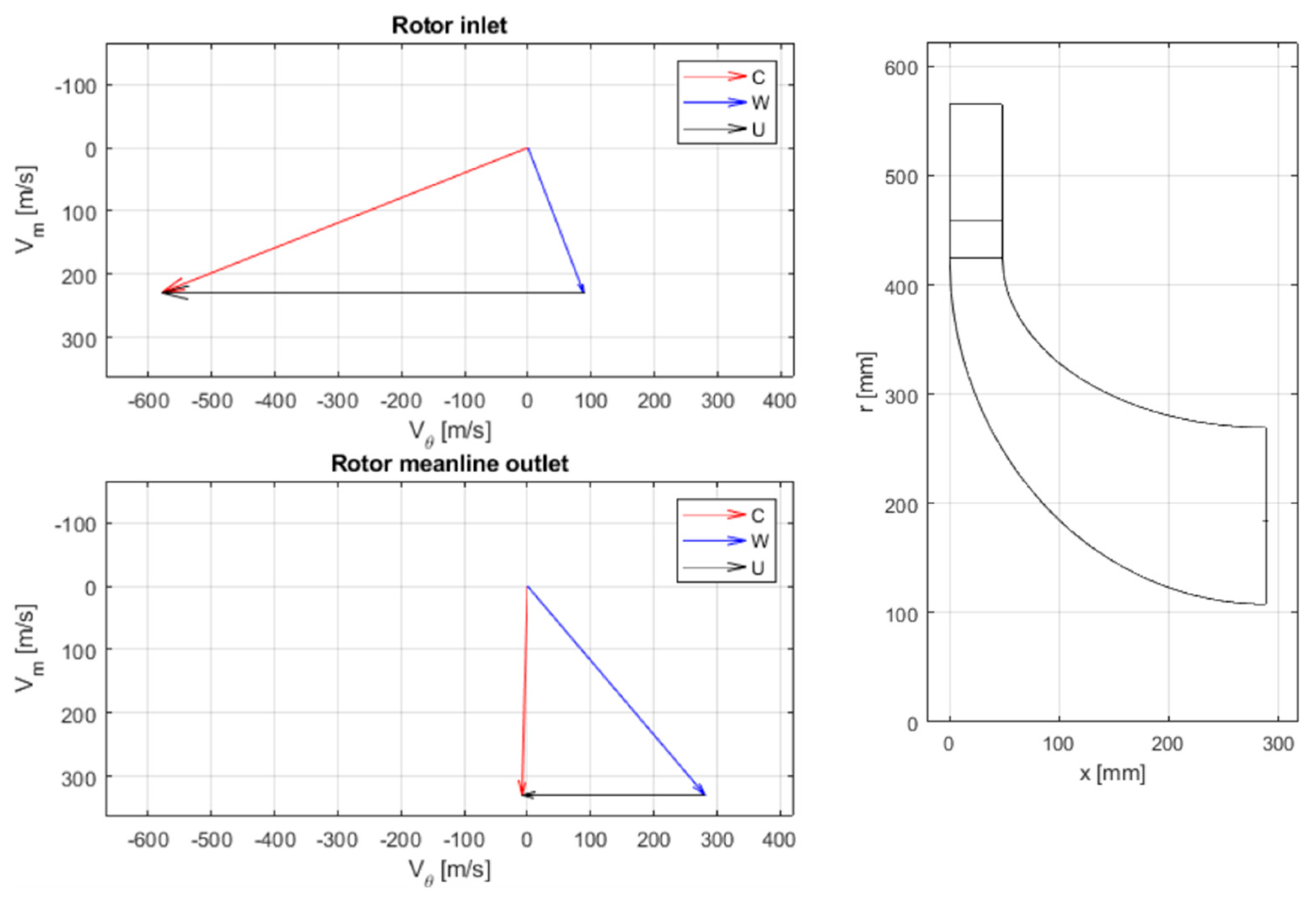
For the parameters specified in the present case (pressure ratio: 6.50, backsweep angle: 45°, specific speed: 0.38), the total-to-total isentropic efficiency is estimated at 82%, with a converged blade count of 26 and a 570 mm radius at the diffuser outlet, leading to a radially compact machine. Figure 7 shows the output of the procedure in terms of meridional channel representation and impeller inlet and outlet velocity diagrams, obtained as the first-guess estimation for the compressor design in the actual application.

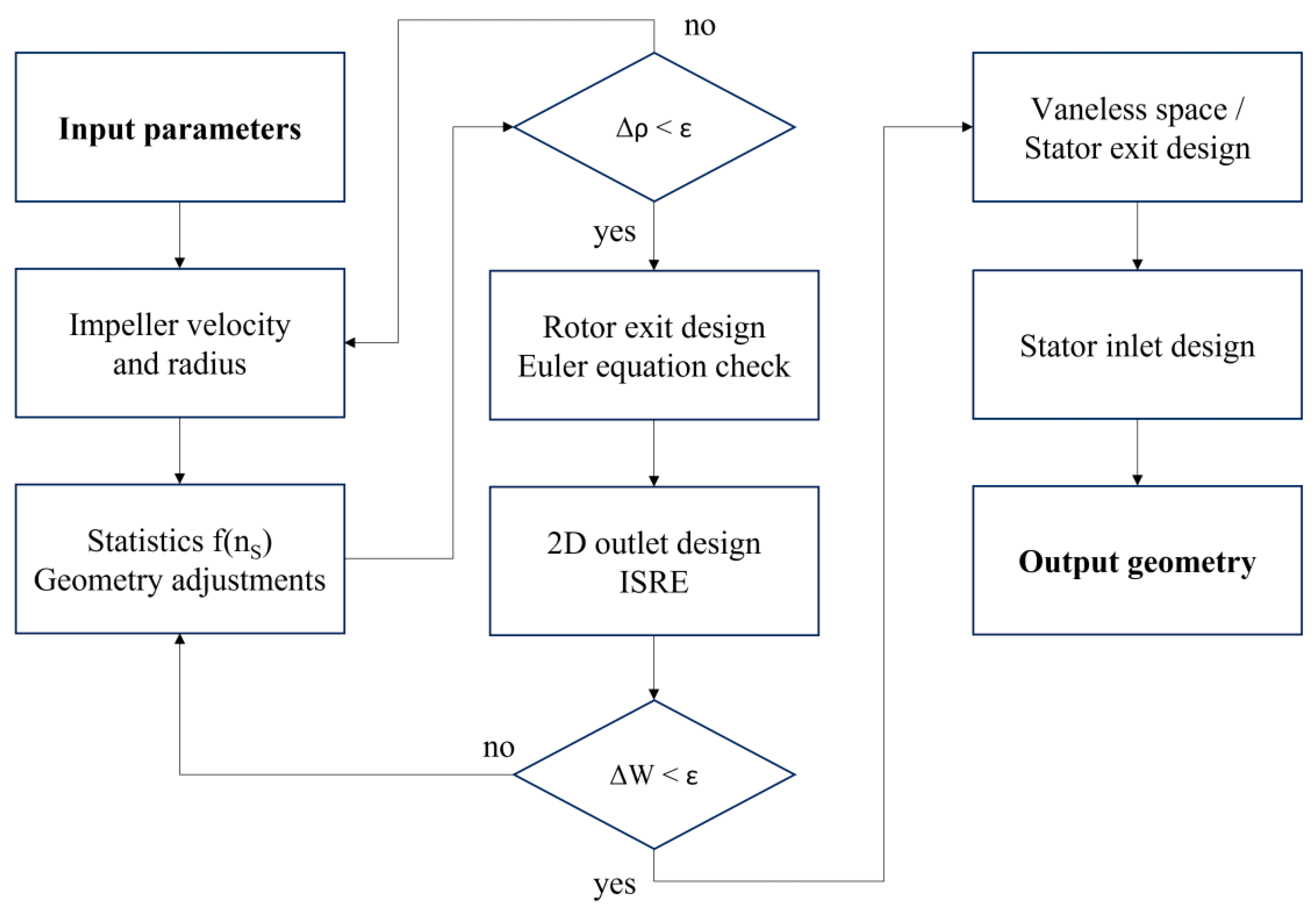
5.2. Turbine 1D Design

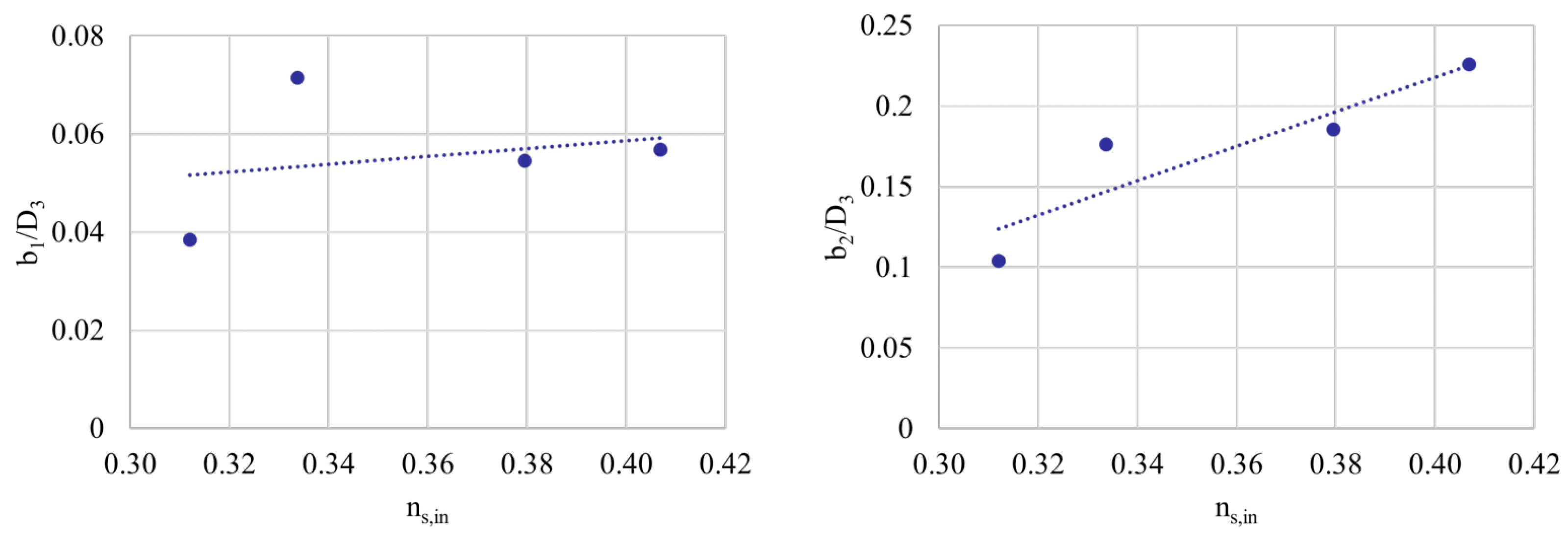
The initial turbine design primarily followed the approach outlined by Barsi et al. [29], with enhancements focusing on the rotor outlet. Statistical trends, derived from comparable radial turbines, were utilized to establish the non-dimensional geometric parameters based on a global factor (an example is shown in Figure 8).

Geometry determination was facilitated through an iterative process using an in-house Matlab program, outlined in Figure 9.

The inputs included the gas inlet thermodynamic state, flow angle, operating conditions (predefined mass flow rate and rotational speed), target expansion ratio, total-to-total isentropic efficiency, and the desired outlet mean-radius flow angle. The procedure could incorporate swept blades at the rotor inlet, similar to the compressor impellers, but the current design favored radial blades to simplify the manufacturing and reduce bending stress, providing mechanical advantages. The desired stator inlet flow angle was based on parallel research on radial turbine combustors for power applications in the 1 to 10 MW range. Starting from the given boundary conditions, the initial step involves estimating the density at the rotor inlet and calculating the corresponding specific speed. This specific speed is then utilized as the input value for statistical regression used for the first-guess evaluation of geometry.

All equations utilized are derived from trends observed in the available literature and a selection of few commercial models [24,30,31]. Notably, Figure 8 emphasizes the rarity of this turbine type. The Opra OP16 gas turbine engine is the most comparable to the present machine, delivering 1.8 MW_el of net electrical power [24]. The output tendencies are automatically compared and adjusted at each iteration based on established geometrical constraints from literature sources to prevent the generation of impractical shapes [32,33,34]. Subsequently, the rotor diameter is determined using the target work and the load coefficient. Then, the Stanitz slip model is employed to estimate the optimal incidence angle for the radially straight blades [22,27].

The adopted model adheres to Dixon’s guidelines [26], as the Coriolis forces’ effects at the rotor inlet are accounted for by adopting relations similar to those observed at a compressor impeller outlet. A mean-line analysis is conducted across machine sections to solve the turbomachinery kinematics and the energy equation. Additionally, static and total quantities based on the isentropic flow principles are evaluated through a density-based loop on continuity [27]. The design of the rotor outlet in two dimensions is accomplished using the isentropic radial equilibrium equation (ISRE), adopting the forced vortex law C_θ(r) = k r, with the hypothesis of isentropic flow. The calculation is extended along the radius, assuming negligible radial velocity (Cr) at the turbine exit, with the mean line tangential velocity established by the desired mean outlet angle of the rotor. To avoid vortex breakdown, the tangential velocity at the blade outlet hub is set to zero, whereas a positive tangential velocity component is preferred at the diffuser inlet to energize and stabilize the boundary layers. The output of the ISRE procedure in the outlet section of the turbine consists in the determination of the main geometric characteristics (blade angle) along the radial direction. Then, the Euler equation is used to verify work exchange. If a significant difference comes out, the procedure is iterated, adopting a new turbine inlet diameter. To design the diffuser, classical performance maps for conical diffusers [35] are adopted.

To test the 1D design procedure, a radial turbine with a high-pressure ratio (PR) has been selected from the literature [32]. The rotor inlet relative flow angle (−20 degrees) is aligned with the recommendations found in the literature. The outlet absolute flow angle ranges from 0 degrees at the blade hub to 10 degrees near the tip.

The meridional channel obtained for the radial turbine (Figure 10) is compact and comparable to gas turbines with a similar power output. However, the design is significantly larger than that of conventional radial turbomachines, such as micro-GTs and turbochargers, challenging the rotor mechanical integrity. Opting for an uncooled machine simplifies manufacturing but requires heavy, high-temperature-resistant materials such as nickel-based alloys.

6. Multidisciplinary Optimization Design

The utilization of the commercial software Cadence/Autoblade [36] has been instrumental in selecting an optimal set of parametric curves and determining the most suitable geometric topology. This allows designers to adeptly handle various geometric shapes using a limited number of key parameters.

For the radial compressor, to achieve the transition from axial to radial configuration, both the hub and shroud contours adopt a consistent geometric pattern comprising an axial line segment, a Bezier curve with four control points, and a radially directed line segment (see Figure 11). The impeller assembly consists of a main blade and a splitter blade. The main blade camber is parameterized at three spanwise sections with a five-point Bezier curve. Similarly, a four-point Bezier curve is used to define the half-thickness law on each spanwise section.

The diffuser row comprises straight wedge-shaped blades, characterized by their cylindrical, unleaned, and non-tapered design. Even after imposing the necessary constraints, the compressor parametric geometrical model boasts 26 degrees of freedom.

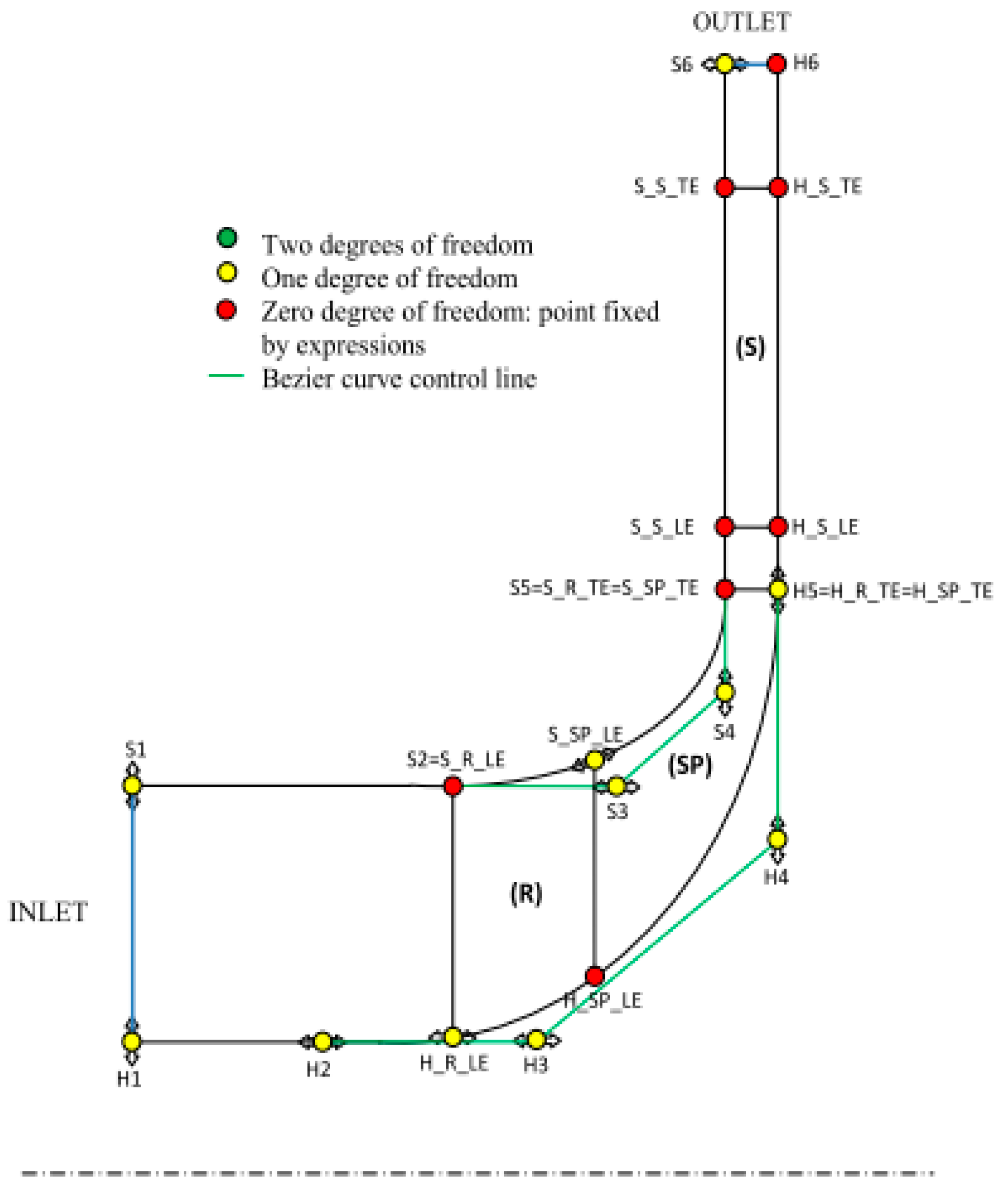
The Bezier curves adopted for the geometry description in the automatic tool for turbine optimization are shown in Figure 12. A simple Bezier curve is adopted for the stator row camber line, while a simple two-parameter law is used to add the thickness to the camber curve. Conversely, a four-point Bezier curve is adopted for both the rotor row camber line and thickness law.

Overall, the optimization procedure for the turbine will manage a total of 22 design parameters, ensuring a refined and efficient outcome. These free geometric parameters were varied using sampling methods to identify parameter combinations and the geometries associated with them.

6.1. Features of Fluid and Solid Meshes, Boundary Conditions and FEA

The entire fluid domain has been meshed using Cadence/IGG Autogrid 5. To streamline interfacing with the optimization environment, a Python script has been devised to automatically handle the multirow configuration. For each involved row, a multi-block hexahedral structured mesh is constructed. In total, the mesh comprises approximately 4 million cells for the compressor and 3.2 million cells for the turbine. Both meshes were tested for grid independency using the pressure ratio and the mass flow rate as reference values for the compressor and turbine, respectively, together with isentropic efficiencies to evaluate the mesh reliability.

The computational fluid dynamics (CFD) calculations are orchestrated through Cadence/FineTurbo, utilizing the Cadence/Euranus Navier-Stokes equations solver. Employing a RANS steady approach [36], the turbulence phenomenon is accurately represented using the two-equation SST (Shear Stress Transport) model [37]. At solid walls, a no-slip boundary condition is assumed, while the rotation periodicity conditions are adopted to synchronize periodic surfaces. Additionally, the interface between the impeller and diffuser rows is managed through a mixing plane approach.

The solid mesh is generated using the open-source software GMSH [38], integrated into a Python procedure developed in-house. This comprehensive procedure seamlessly combines the aerodynamic optimization algorithm implemented in Fine/Design 3D with CalculiX [39], a freely available open-source finite element analysis (FEA) tool. Each sample is analyzed for its aerodynamic performance using CFD and is also evaluated for its structural behavior.

6.2. Optimization Process Strategy

For the generation of the database, given the multitude of variables involved in the optimization process, a 25× random sampling for the compressor and a 15× random sampling for the turbine have been selected. More refined Design of Experiments (DoE) techniques would incur prohibitively high computational costs. However, these algorithms are based on a random selection of the possible combinations between the different parameters suitable to be sufficiently “sparse” and “uniformly distributed” within the space itself. For the present case, the database samples are 700 and 350, randomly selected from the available options, for compressor and turbine, respectively.

The optimization procedure aims at minimizing a single objective function, which comprises various dimensionless penalty terms, based on structural or aerodynamic parameters. The objective function is convex, due to the parabolic nature of these penalty terms, ensuring the existence of a minimum. Each parabolic penalty term is assigned a weighting coefficient, able to make the different contributions almost equivalent. In the optimization function of the centrifugal compressor (Equation (3)), six penalty terms—three aerodynamic (Equations (4)–(6)) and three structural (Equations (7)–(9))—are used.

$$F=F_{aero}+F_{struct}=P_{{\eta }_{istt}}+P_{{\beta }_{tt}}+P_{M{a}_C}+P_{stress}+P_{freq,low}+P_{freq,high}$$

(3)

$$P_{{\eta }_{istt}}=W_{{\eta }_{istt}}{\left(\frac{1-{\eta }_{istt}}{0.1}\right)}^2 if {\eta }_{istt}<1$$

(4)

$$P_{{\beta }_{tt}}=\{\begin{array}{l}{W}_{{\beta }_{tt}}{\left(\frac{4.5-{\beta }_{tt}}{1}\right)}^2 if {\beta }_{tt}<4.5\\ 0 if {\beta }_{tt}\ge 4.5\end{array}$$

(5)

$$P_{M{a}_C}=\{\begin{array}{l}{W}_{M{a}_c}{\left(\frac{1-M{a}_c}{1}\right)}^2 if M{a}_c\ge 1\\ 0 if M{a}_c<1\end{array}$$

(6)

$$P_{stress}=\{\begin{array}{l}{W}_{stress}{\left(\frac{{\sigma }_{max}}{{\sigma }_{all}}\right)}^2 if {\sigma }_{max}\ge {\sigma }_{all}\\ 0 if {\sigma }_{max}<{\sigma }_{all}\end{array}$$

(7)

$$P_{freq,low}=\{\begin{array}{l}{W}_{freq,low}{\left(\left|\frac{f_{eigfr}}{f_{exc\_low}}-1\right|\right)}^2 if \left|\frac{f_{eigfr}}{f_{exc\_low}}-1\right|\le 0.05\\ 0 if \left|\frac{f_{eigfr}}{f_{exc\_low}}-1\right|>0.05\end{array}$$

(8)

$$P_{freq,high}=\{\begin{array}{l}{W}_{freq,high}{\left(\left|\frac{f_{eigfr}}{f_{exc\_high}}-1\right|\right)}^2 if \left|\frac{f_{eigfr}}{f_{exc\_high}}-1\right|\le 0.05\\ 0 if \left|\frac{f_{eigfr}}{f_{exc\_high}}-1\right|>0.05\end{array}$$

(9)

Regarding the aerodynamic considerations, the objective function aims at maximizing the total-to-total isentropic efficiency, ensuring an absolute subsonic flow condition at the diffuser inlet and respecting the design absolute total pressure ratio. The structural objectives include keeping the maximum Von Mises stress in the impeller below the allowable stress value and preventing rotor resonances.

The objective function for geometry optimization for the radial turbine comprises several penalty terms (Equation (10)): four aerodynamic (Equations (11)–(14)) and three structural (Equations (15)–(17)).

$$F=F_{aero}+F_{struct}=P_{\dot{m}}+P_{{\eta }_{istt}}+{\displaystyle \sum }_{i=1}^4{P}_{min,{\alpha }_{out,i}}+{\displaystyle \sum }_{i=1}^4{P}_{MAX,{\alpha }_{out,i}}+P_{stress}+P_{freq,low}+P_{freq,high}$$

(10)

$$P_{\dot{m}}=W_{\dot{m}}{\left(\frac{{\dot{m}}_{nom}-\dot{m}}{{\dot{m}}_{nom}}\right)}^2$$

(11)

$$P_{{\eta }_{istt}}=W_{{\eta }_{istt}}{\left(\frac{1-{\eta }_{istt}}{0.1}\right)}^2$$

(12)

$$P_{min,{\alpha }_{out,i}}=\{\begin{array}{l}{W}_{min,{\alpha }_{out,i}}{\left(\frac{{\alpha }_{out,min,i} - {\alpha }_{out,i}}{{\alpha }_{out,min,i}}\right)}^2 if {\alpha }_{out,i}\ge {\alpha }_{out,min,i}\\ 0 if {\alpha }_{out,i}<{\alpha }_{out,min,i}\end{array}$$

(13)

$$P_{MAX,{\alpha }_{out,i}}=\{\begin{array}{l}{W}_{MAX,{\alpha }_{out,i}}{\left(\frac{{\alpha }_{out,MAX,i} - {\alpha }_{out,i}}{{\alpha }_{out,MAX,i}}\right)}^2 if {\alpha }_{out,i}\ge {\alpha }_{out,MAX,i}\\ 0 if {\alpha }_{out,i}<{\alpha }_{out,MAX,i}\end{array}$$

(14)

$$P_{stress}=\{\begin{array}{l}{W}_{stress}{\left(\frac{{\sigma }_{max}}{{\sigma }_{all}}\right)}^2 if {\sigma }_{max}\ge {\sigma }_{all}\\ 0 if {\sigma }_{max}<{\sigma }_{all}\end{array}$$

(15)

$$P_{freq,low}=\{\begin{array}{l}{W}_{freq,low}{\left(\left|\frac{f_{eigfr}}{f_{exc\_low}}-1\right|\right)}^2 if \left|\frac{f_{eigfr}}{f_{exc\_low}}-1\right|\le 0.05\\ 0 if \left|\frac{f_{eigfr}}{f_{exc\_low}}-1\right|>0.05\end{array}$$

(16)

$$P_{freq,high}=\{\begin{array}{l}{W}_{freq,high}{\left(\left|\frac{f_{eigfr}}{f_{exc\_high}}-1\right|\right)}^2 if \left|\frac{f_{eigfr}}{f_{exc\_high}}-1\right|\le 0.05\\ 0 if \left|\frac{f_{eigfr}}{f_{exc\_high}}-1\right|>0.05\end{array}$$

(17)

The penalty function allows for ensuring the design mass flow rate, maintaining the tangential velocity along the spanwise direction at the exit within a desired range, and maximizing the overall total-to-total efficiency.

To begin, an allowable stress, based on yield strength, expressed as a function of temperature, is determined using a safety factor and appropriately defined constants. Von Mises stresses at each blade node are then compared to the allowable stresses. Additionally, to prevent the eigenfrequencies from falling within the 0.95–1.05 range of the exciting frequencies, penalty functions similar to those defined for the compressor case are employed. Consequently, the objective function for structural analysis is derived as the sum of the aforementioned terms.

6.3. Compressor Results

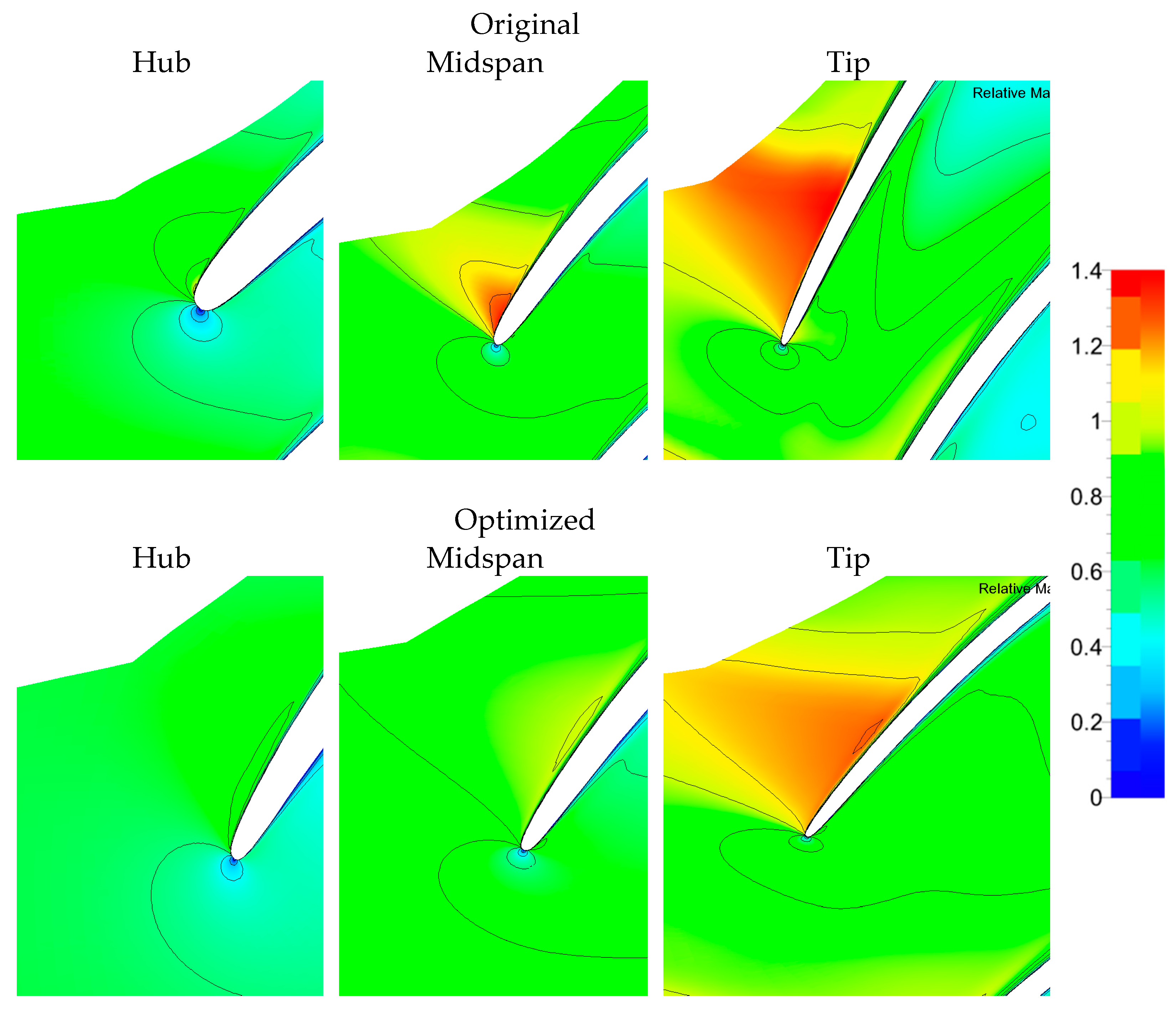
The optimization process has achieved convergence after 35 iterations. This paragraph showcases the optimized configuration, highlighting the differences from the original design and the impacts of the new geometric arrangement on both aerodynamic and structural assessment. In the optimized configuration depicted in Figure 13, it is clear how the relative Mach number is generally reduced in all sections, and that the maximum relative Mach number at the blade tip inlet section has been reduced from 1.35 to 1.2.

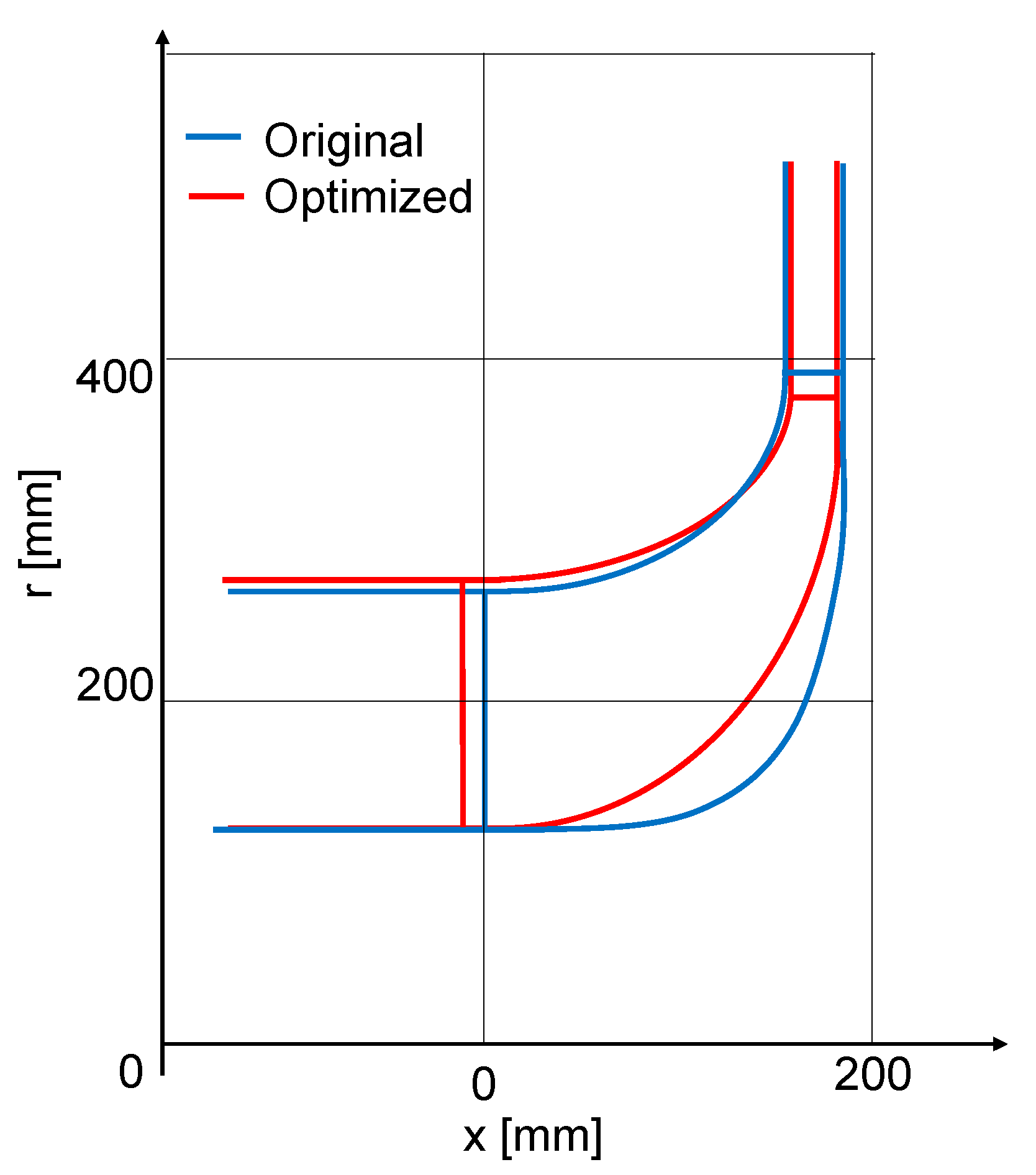
Notably, the region characterized by supersonic relative flow has undergone a significant reduction. This decrease in the relative Mach number primarily originates from the reduction in the inlet blade tip speed, achieved through a reduction in the inlet radius (see Figure 14), while the inlet meridional velocity remains relatively constant.

In terms of blade-to-blade geometrical characteristics, the reduction in blade thickness serves to alleviate the impact of the shock waves. Nevertheless, it is the specific absence of camber curvature at the leading edge (LE) that plays the most crucial role in minimizing the shock wave effects. Figure 13 further demonstrates how there is an improved flow incidence at the leading edge for both the main blade and the splitter. Additionally, the distribution of blade loading shows a more uniform profile along the entire length of the blade.

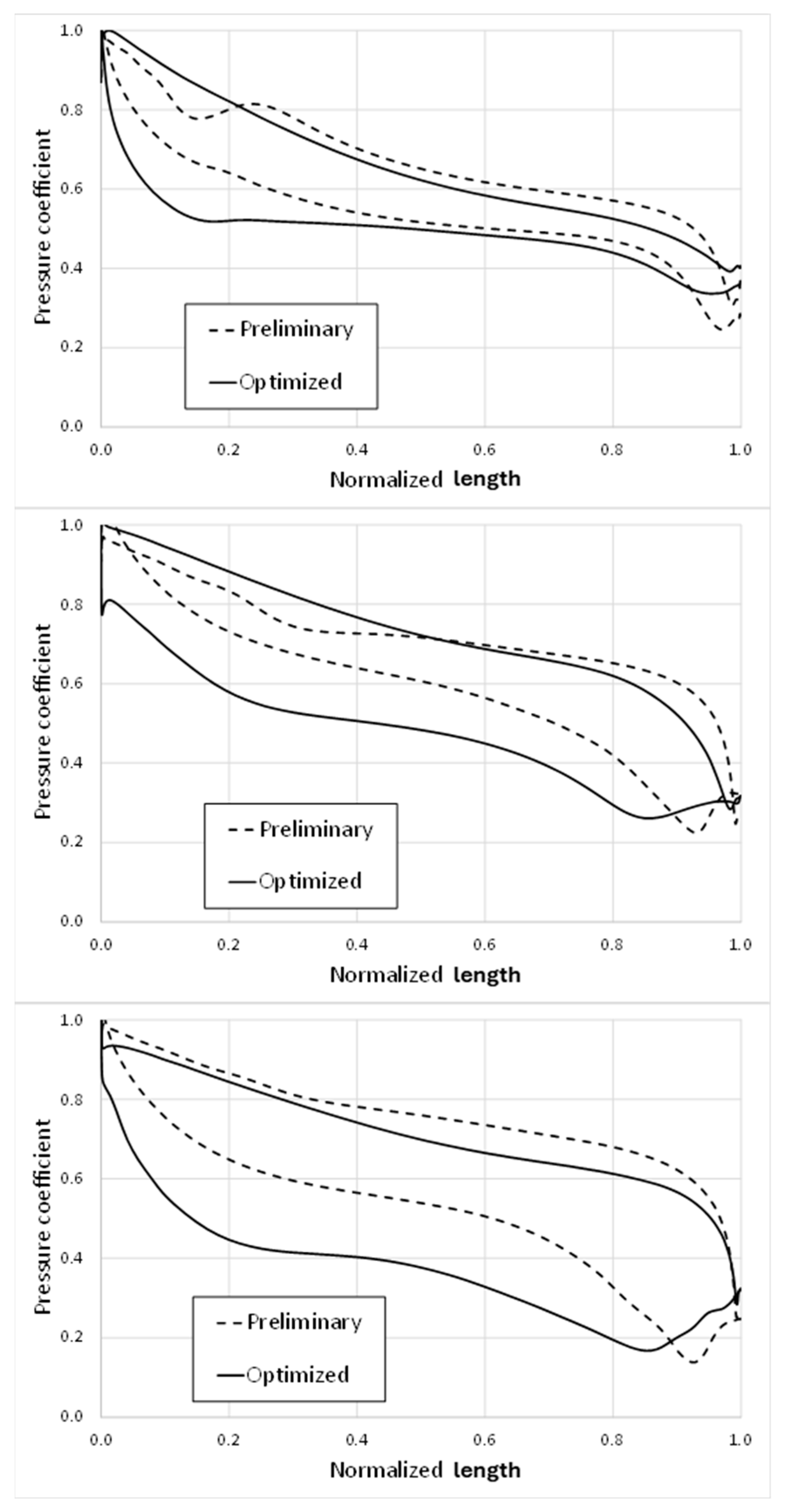
The analysis of the pressure coefficient diagrams (Figure 15) reveals an increase in blade loading in the optimized configuration. This trend aligns well with achieving a comparable absolute total pressure ratio, despite using 22 blades instead of 24 in the optimized configuration.

Figure 16 demonstrates a decrease in the maximum value of the absolute Mach number in the optimized configuration. This is accomplished by decreasing the absolute velocity magnitude at the impeller exit, which is facilitated by an increase in the backswept angle. As a result, the optimized configuration maintains the same impeller work addition, but achieves it through a higher peripheral velocity and a reduced circumferential absolute velocity. This leads to an unloaded impeller blade and a decreased absolute velocity at the diffuser inlet, affecting the impeller structural design by elevating the centrifugal force and necessitating greater backswept angles. This notable aerodynamic–structural interaction underscores the criticality of multidisciplinary optimization for high-efficiency turbomachines.

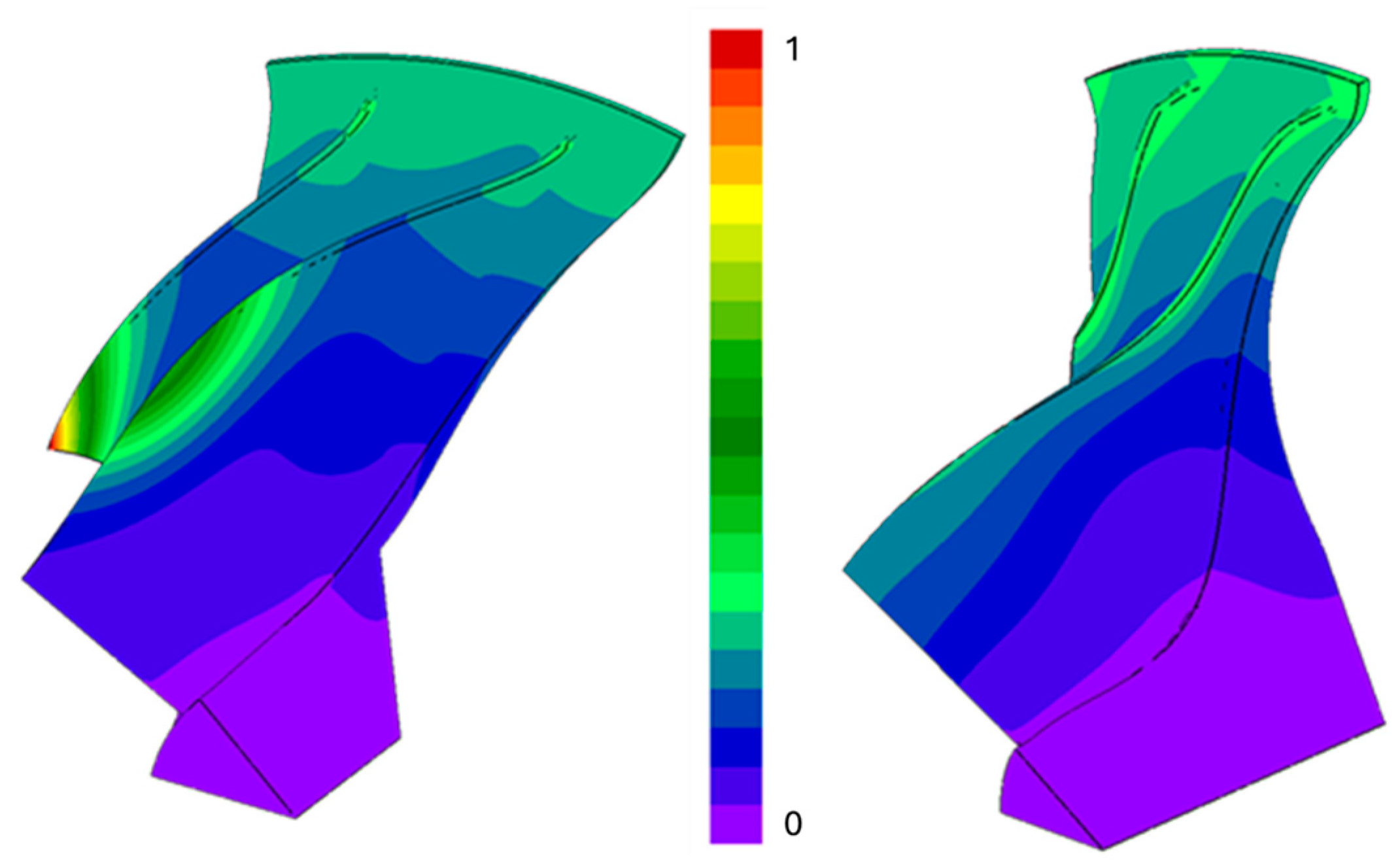
Turning to structural optimization, the Von Mises stress field for both the preliminary and optimized configurations showcases similar maximum Von Mises stress contours, even though the optimized setup reveals a more uniform stress distribution. Although the maximum Von Mises stress was not a restricting factor during the optimization phase, careful material selection and parameter adjustments contributed to alleviating stress distribution throughout the impeller. Looking at displacement, as shown in Figure 17, the maximum displacement of the original impeller is located at the tip of the splitter. In the optimized configuration, the maximum displacement is notably reduced to about 40% of the maximum original blade displacement.

In terms of dynamic behavior, the initial configuration shows resonances with the first four Engine Orders (EO) and with the number of stators downstream of the impeller. However, the optimization process has involved modifying the blade design to satisfy all dynamic assessment criteria. For a comprehensive overview,

Table 5. Compressor design: optimization results.

	Original	Optimized	Variation
$\dot{m} \left[\mathrm{kg}/\mathrm{s}\right]$	$24.11$	$24.11$	[imposed]
${\eta }_{t-t} [-]$	$81.05$	$83.89$	+3.5%
${\beta }_{t-t} [-]$	$5.42$	$6.48$	+19.6%
$Power \left[\mathrm{MW}\right]$	$4.26$	$5.49$	+28.9%
$Inlet relative Ma at tip [-]$	$1.2$	$0.83$	−30.8%
$Absolute Mach at diffuser inlet [-]$	$1.4$	$0.98$	−30.0%
$Stress usage factor [-]$	$1.54$	$0.95$	−38.3%
$Rotor outlet diameter \left[\mathrm{m}\right]$	$0.780$	$0.754$	−3.3%

summarizes the original and optimized performances.

6.4. Turbine Results

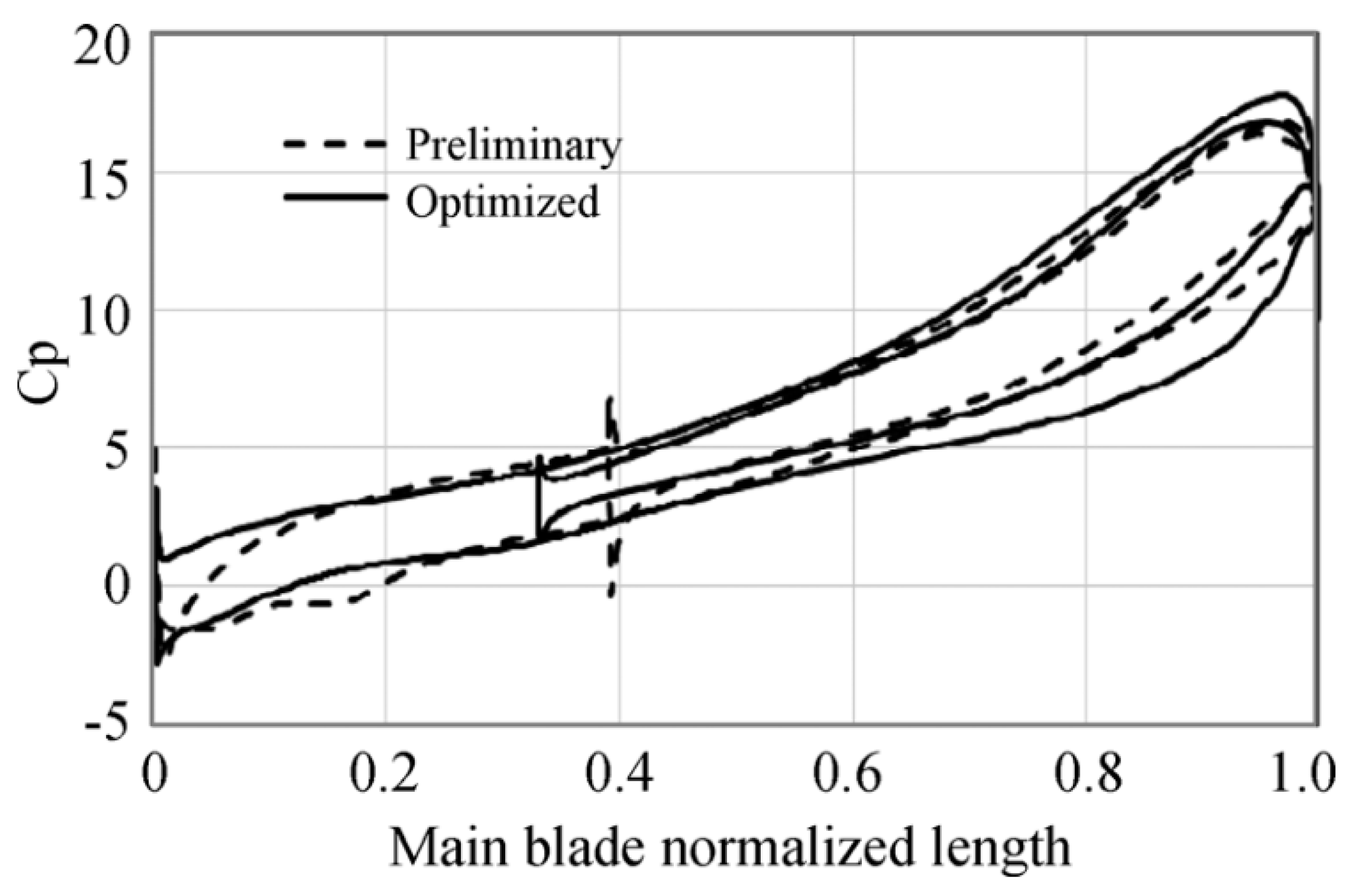
Thirty iterations have been employed to conduct the optimization process. Delving into the fundamental factors steering the discussed optimization procedure, Figure 18 illustrates the blade loading distributions represented by the static pressure coefficient (cp) at hub, midspan, and tip sections. The small pressure coefficient fluctuations close to the blade trailing edge are related to numerical wiggles, which are usually present in blade numerical analyses and do not alter the overall numerical results.

From the comparison between the preliminary and optimized aerodynamic loading, a relevant area increase appears for all the blade sections.

Zooming in on the midspan section provides particularly enlightening insights. Indeed, in this section, the intersection of the pressure and suction side lines just behind the impeller leading edge for the preliminary case, which is depicted by dashed curves, highlights the region on the pressure side characterized by a pressure lower than that at the suction side, due to a negative incidence angle present in the original case. This induces a reduction in the aerodynamic force between the blade and the flow, with a consequent decrease in work exchange, which makes the optimization procedure particularly important for this blade section.

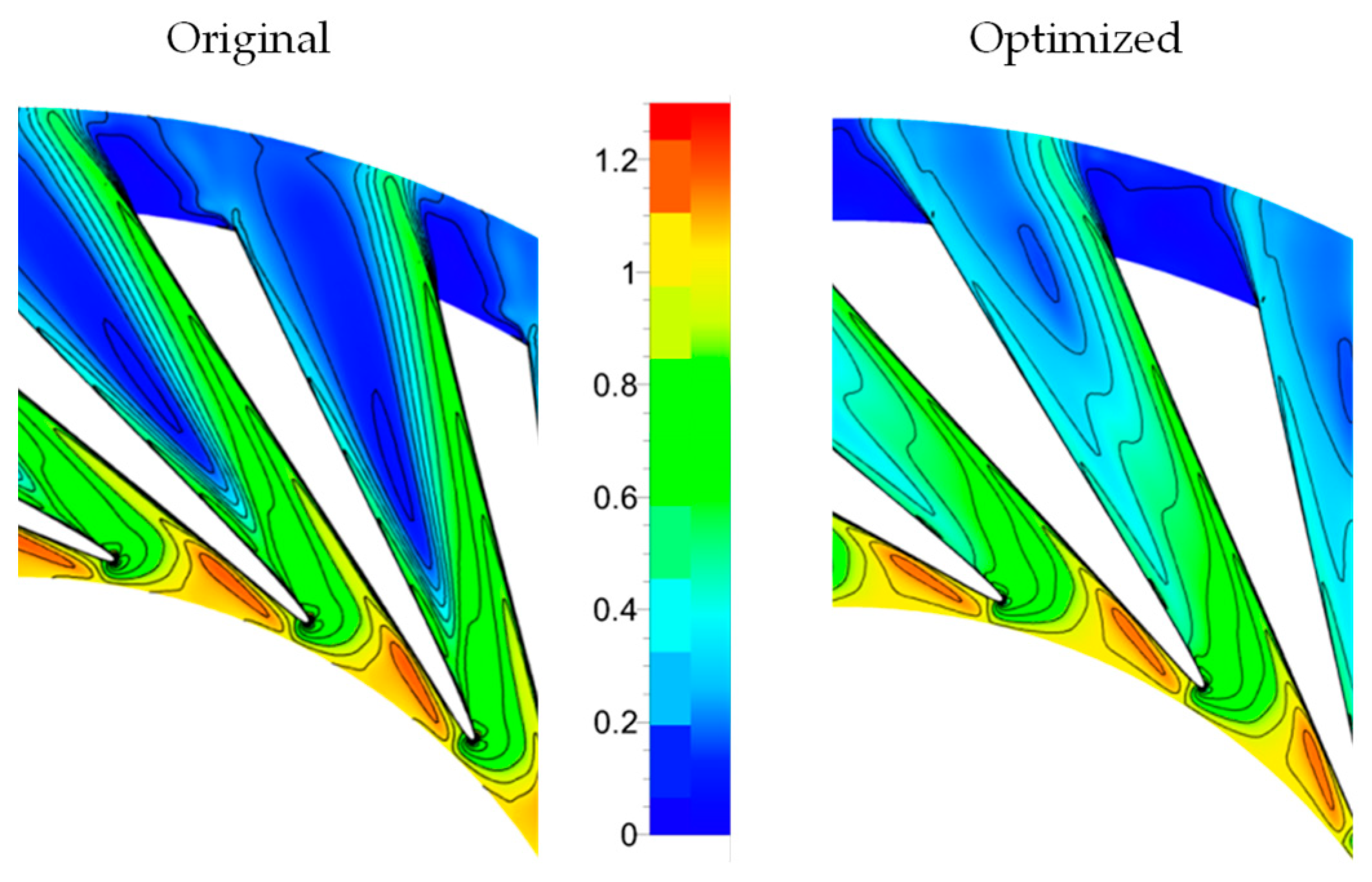
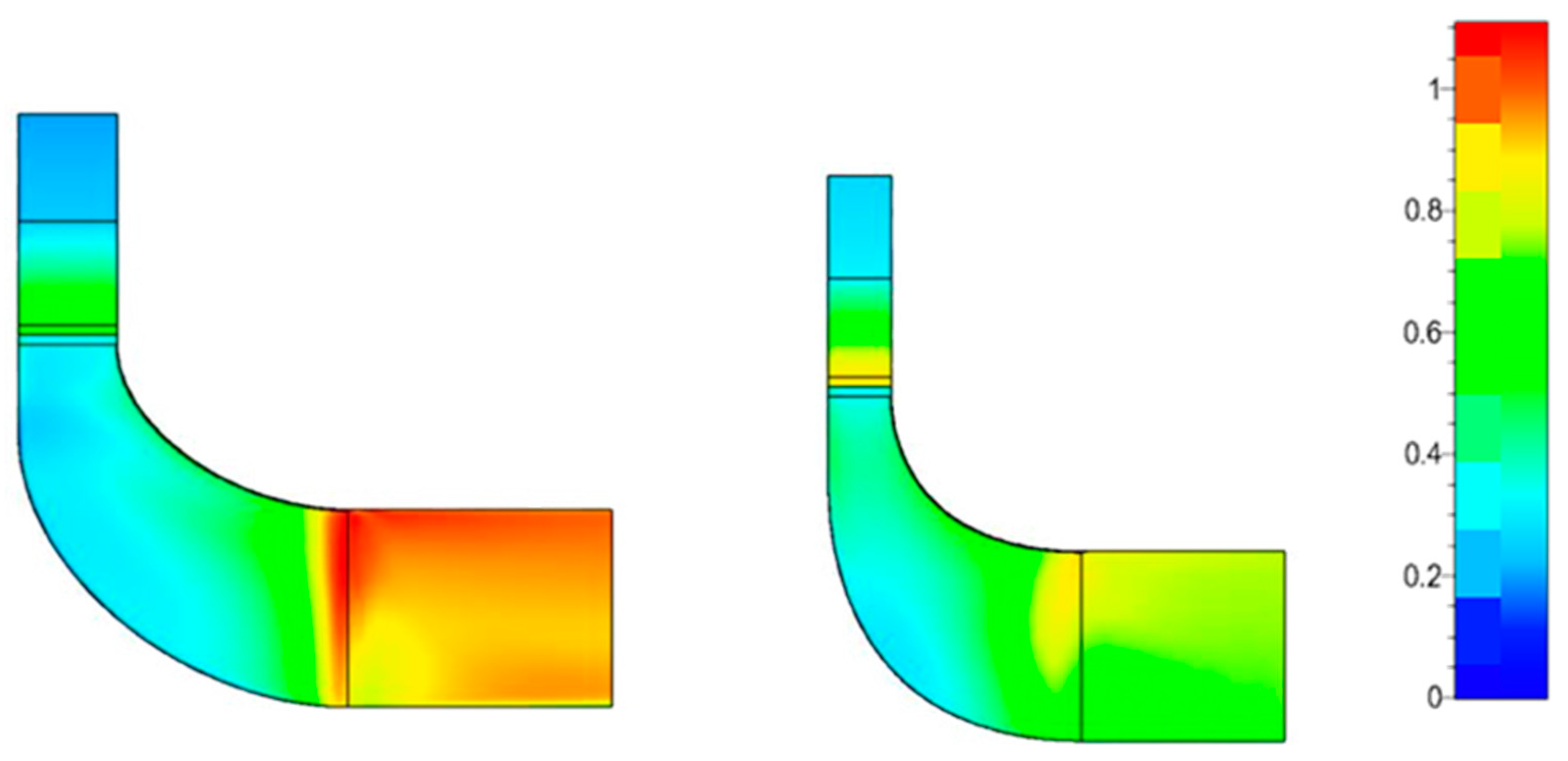
The optimized configuration achieves a higher Mach number at the trailing edge of the stator blade due to the increased absolute tangential velocity, as illustrated in the color plot of Figure 19, displaying the distribution of absolute Mach numbers in the meridional plane. Additionally, Figure 19 highlights the flow regions at the rotor exit characterized by Mach numbers greater than 1.

The significant boundary layer losses stem from the steep pressure increase on the suction side of the blade exit, as evident in the pressure coefficient distribution of Figure 18 for the baseline configuration. This is exacerbated by the high relative Mach number inherent to the original case, resulting in an excessive mass flow rate through the turbine compared to the target value.

Hence, the optimization procedure effectively reduces the mass flow rate by decreasing the meridional channel mean radius (and increasing the absolute flow angle) at the stator outlet while maintaining the same blade height (see Figure 19). Simultaneously, it decreases the relative flow angle at the impeller outlet section. This leads to an expansion increase in the stator and a reduction in the rotor, consequently boosting the absolute velocity at the stator exit and diminishing the relative Mach number at the rotor exit.

Moreover, the stress usage factor is also reduced by more than 32% compared to the original configuration, which was characterized by high stress in the midspan zone due to an excessively high lean angle.

In addition, in the final configuration, the optimization tool has adjusted the blade design to circumvent any potential resonances, both for the first Engine Order (EO) and the Number of Pole Pairs (NPF). The performance of both the original and optimized configurations is summarized in

Table 6. Radial turbine design: optimization results.

	Original	Optimized	Variation
$\dot{m} \left[\mathrm{kg}/\mathrm{s}\right]$	$26.41$	$24.72$	−6.4%
${\eta }_{t-t} [-]$	$88.2$	$91.2$	+3.4%
$Power \left[\mathrm{MW}\right]$	$8.82$	$10.89$	+23.5%
$Rotor outlet Ma [-]$	$1.2$	$0.83$	−30.8%
$Outlet flow angle \left[\mathrm{deg}\right]$	$24.4$	$3.7$	−84.8%
$Stress usage factor [-]$	$1.4$	$0.95$	−32.1%
$Rotor inlet diameter \left[\mathrm{m}\right]$	$0.90$	$0.87$	−3.3%

.

7. Conclusions and Recommendations

This paper analyzed the possibility of adopting small-scale gas turbines in the marine sector, starting from their capability of complying with marine transport emission regulations, which are due to the strong impact that pollutant emissions have on global warming, local air quality, and human health.

Thus, after an in-depth analysis of the regulations governing the reduction of pollutant emissions in marine applications, the design of a radial turbine and a centrifugal compressor for a marine small gas turbine, targeting a 5 MW power output, has been explored. The process included a concept design based on thermodynamic cycle analysis, and a one-dimensional turbomachine design. Additionally, aerodynamic and structural optimization was conducted using CFD and FEA simulation software to enhance performance while meeting challenging application constraints. The critical analysis of the final configuration confirmed the feasibility of a radial architecture for a small gas turbine system for naval propulsion up to 5 MW_el, despite the challenges in aerodynamic performance and mechanical stresses. This compact gas turbine assembly can constitute the top part of a gas-steam combined-cycle power conversion system that can produce up to 7 MW_el useful power, with an overall cycle efficiency of about 41%, which is an interesting value for a 7 MW_el unit.

Both the compressor and turbine optimization procedures led to an increase in machine efficiency, with the final values of turbine and compressor polytropic efficiencies in line (or even better than, according to the CFD simulation on the optimized geometries) those utilized for the combined-cycle efficiency evaluation, hence confirming the correctness of the approach. As far as the compressor optimization is concerned, notable changes included a decreased maximum relative Mach number, reduced supersonic flow, and smoother blade loading. In addition, structural enhancements have been observed, with lower stress levels and a smoother stress map. Modifying the blade design has addressed dynamic behavior, ensuring that all dynamic assessment criteria are met.

On the other hand, the optimization process applied to the turbine also improved the machine performance by addressing aerodynamic issues such as the boundary layer separation affecting the front part of the pressure side in the original blade. Moreover, adjustments to the tangential component of absolute velocity and meridional channel parameters led to improved performance. The mechanical concerns were also alleviated by redistributing stress concentrations and mitigating the bending stresses on the blade.

Overall, these findings underscore the effectiveness of the optimization procedure in enhancing the aerodynamic and structural performance of the turbine design.

The multidisciplinary optimization demonstrates that the full radial compact GT group, in a combined-cycle configuration to enhance efficiency and power, has passed through the concept and preliminary design phases. It complies with the most stringent regulations of pollutant emissions and, when fed with e-LNG in the future, will also configure a marine power system with zero GHG emissions.