Numerical Study of Bearing Strength of Infilled Concrete in Large Diameter CFST Column Reinforced by Shear Stoppers
Abstract
1. Introduction
2. Finite Element Analysis for Bearing Strength of Infilled Concrete
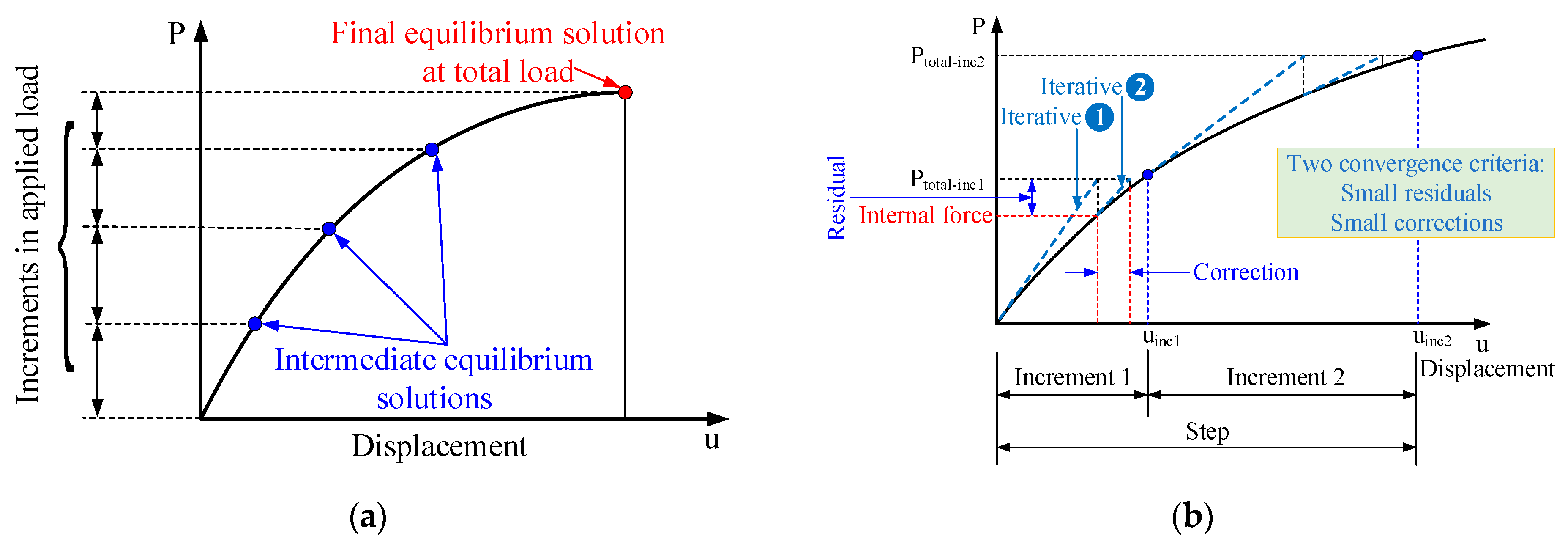
2.1. Algorithm
- Updating the tangential stiffness matrix ;
- Seeking the solution of the linear equation system for , and the estimated solution is provided as ;
- Computing the internal force vector based on , and the equilibrium convergence must be checked after each increment with two conditions: (i) must be within tolerances and (ii) increment .
2.2. Tangential Stiffness Matrix
2.3. Load Vector
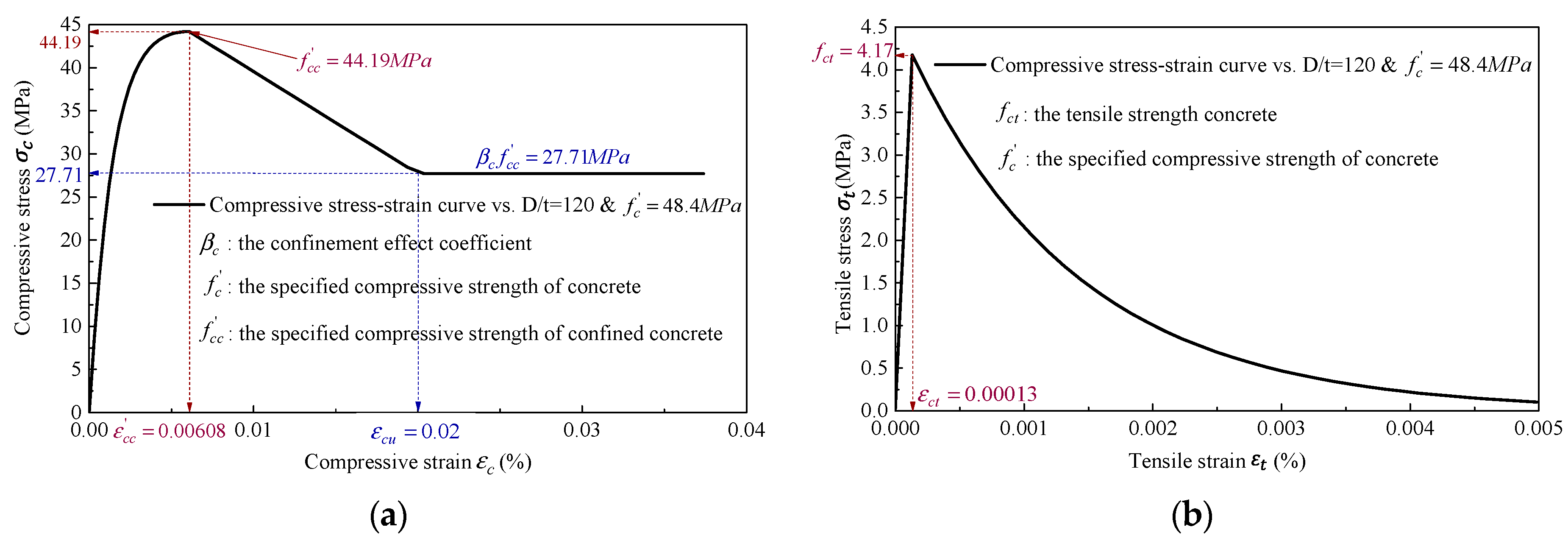
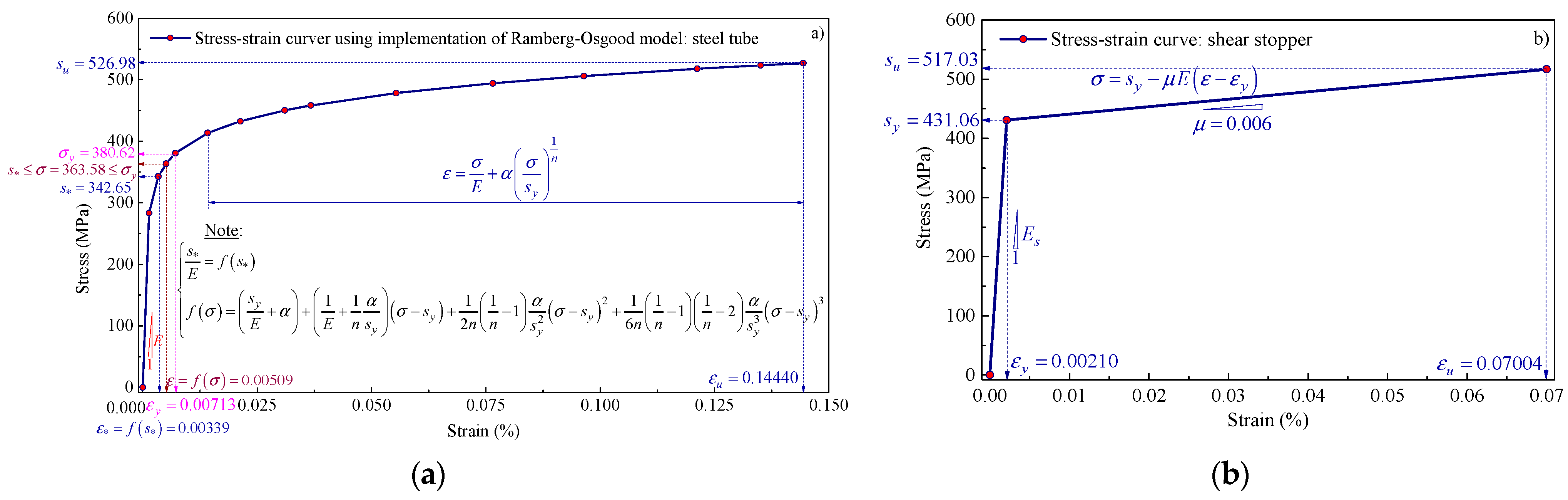
2.4. Material Model
2.4.1. Concrete
2.4.2. Steel
2.5. Contact Formulation
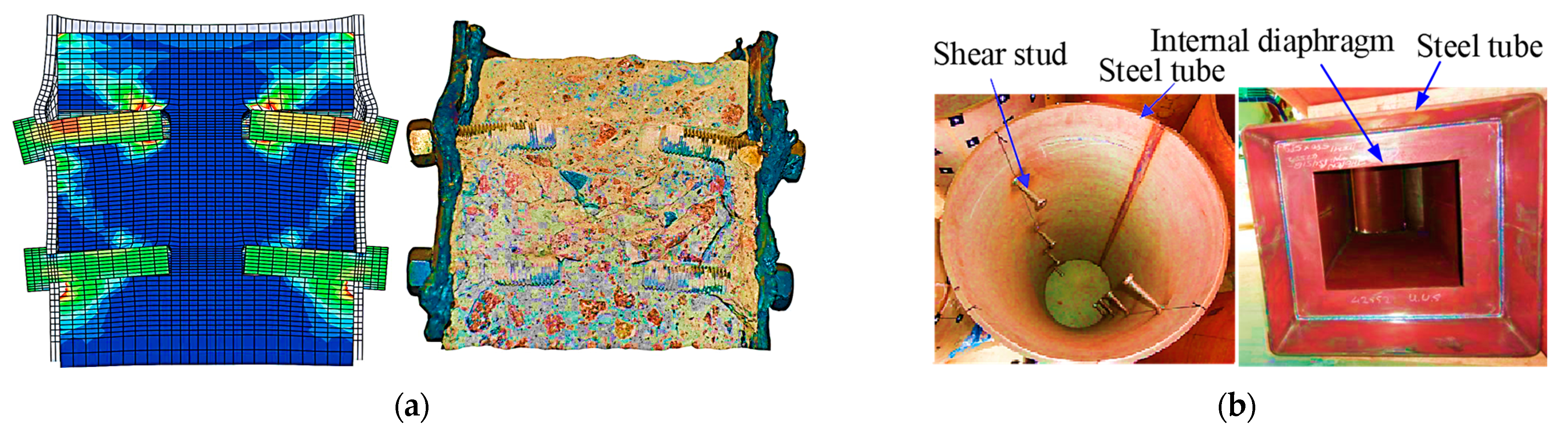
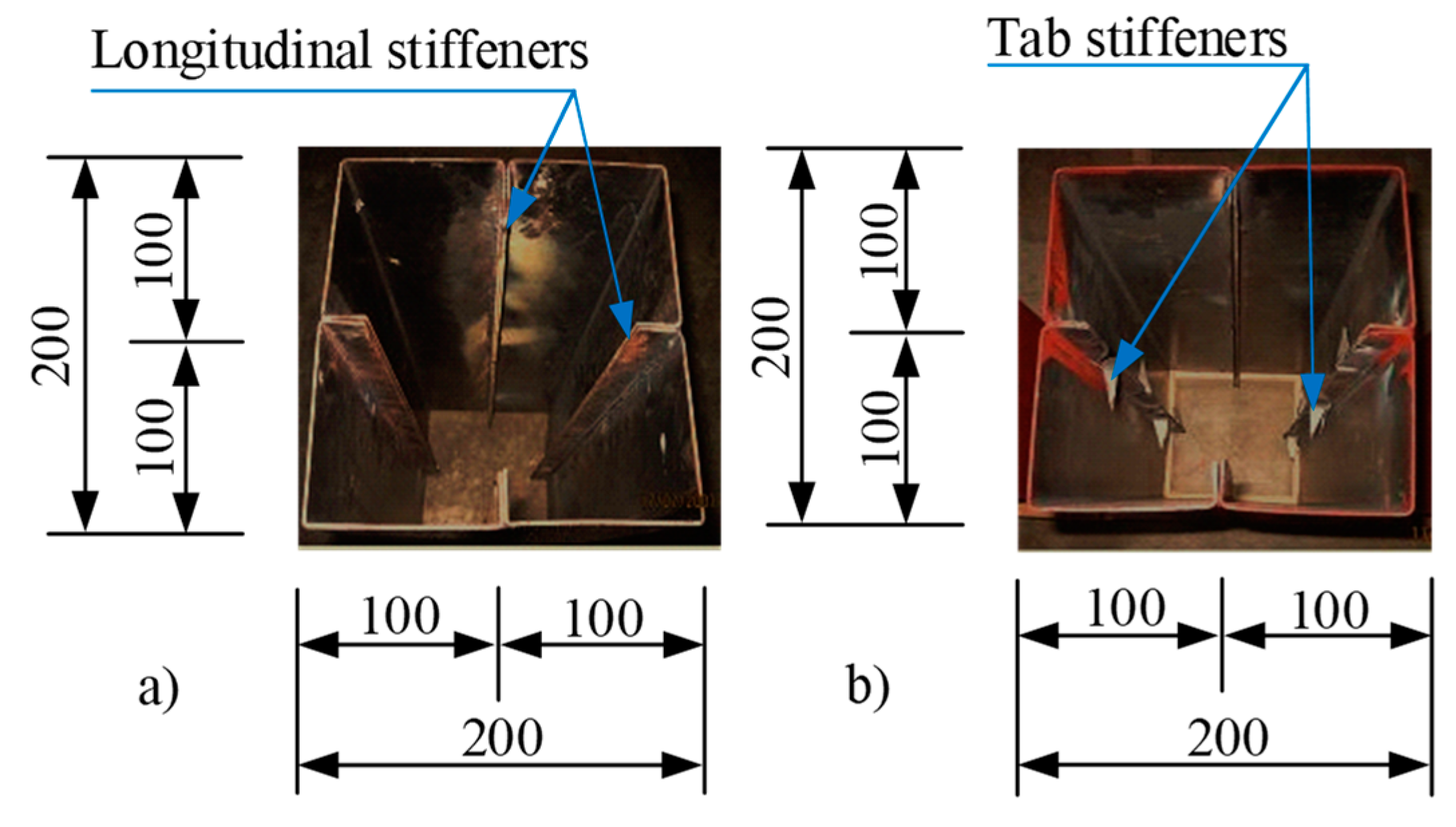
2.6. Geometrical and Mechanical Properties of Simulation Models
2.7. Mesh Generation and Working Principal Diagram
3. Results and Discussion
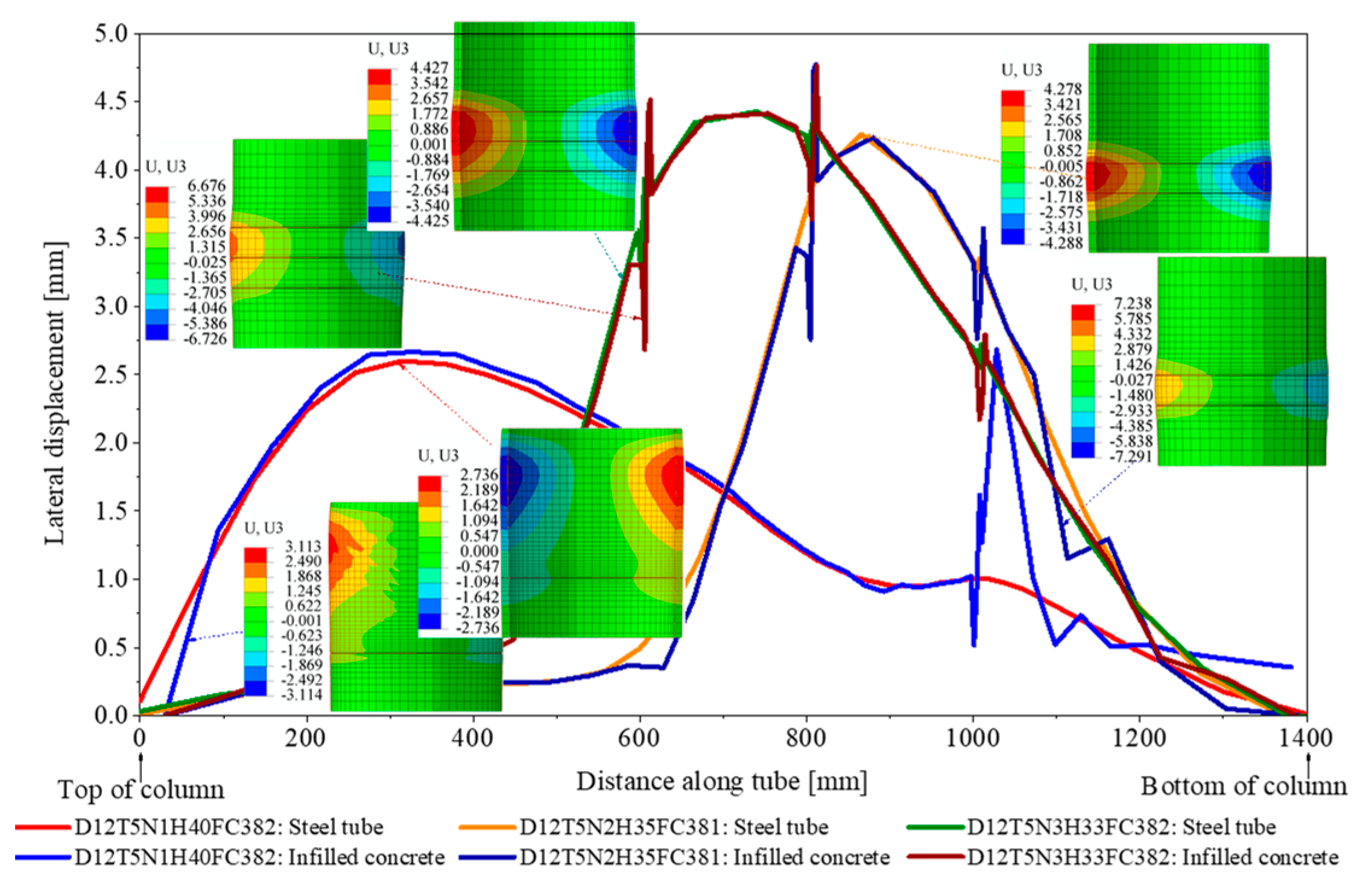
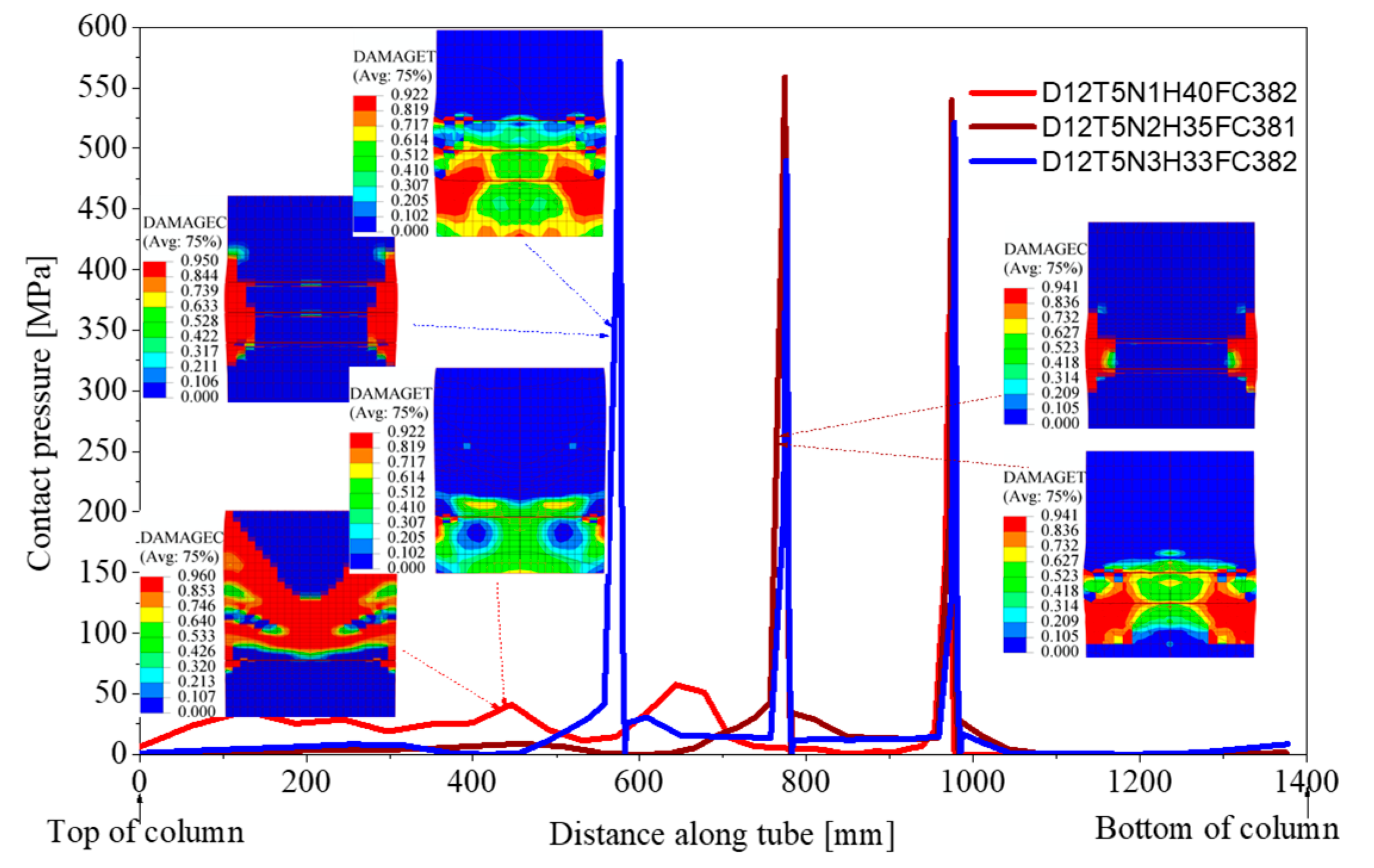
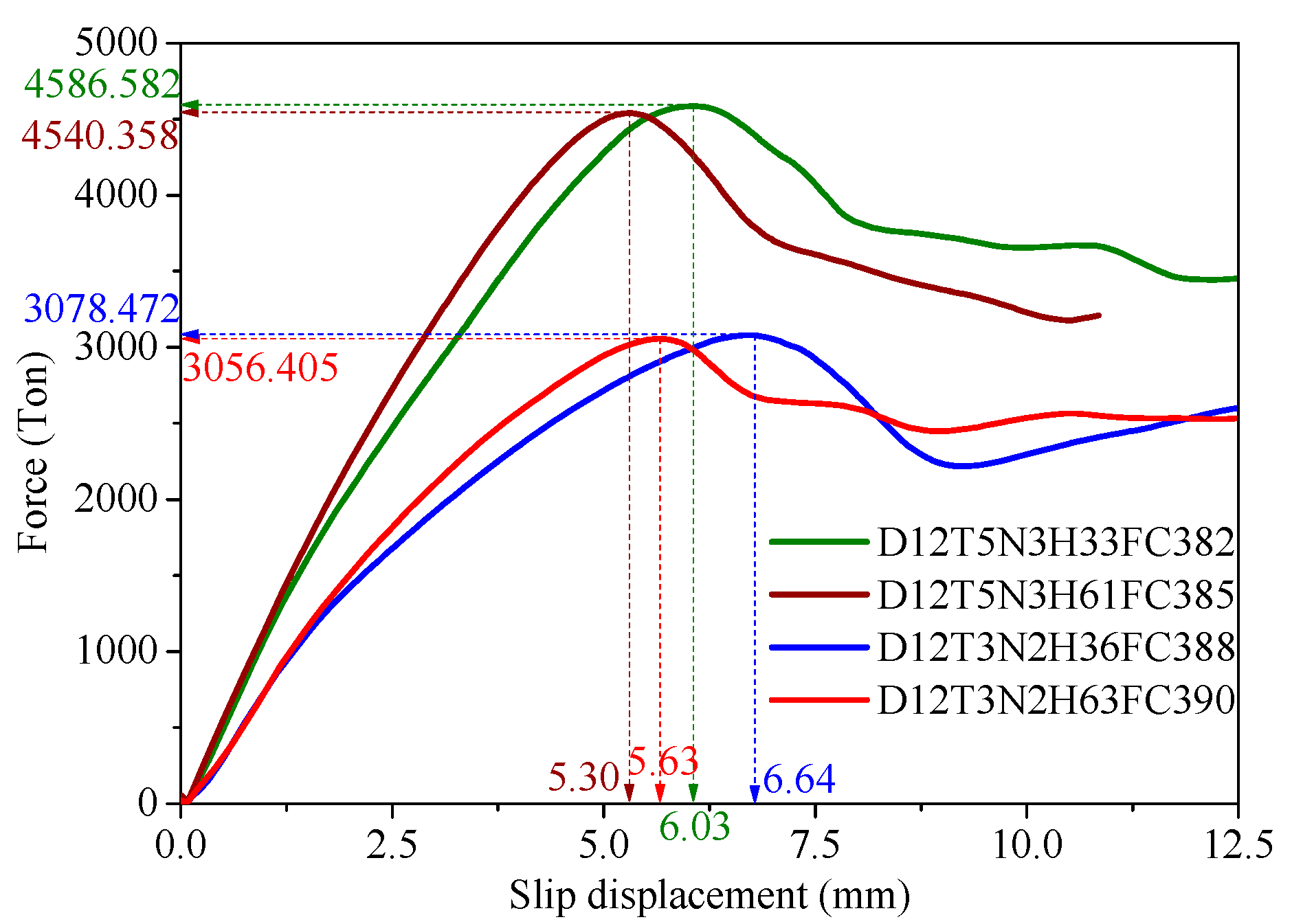
3.1. Influence of Number of Shear Stoppers on Bearing Strength of Infilled Concrete
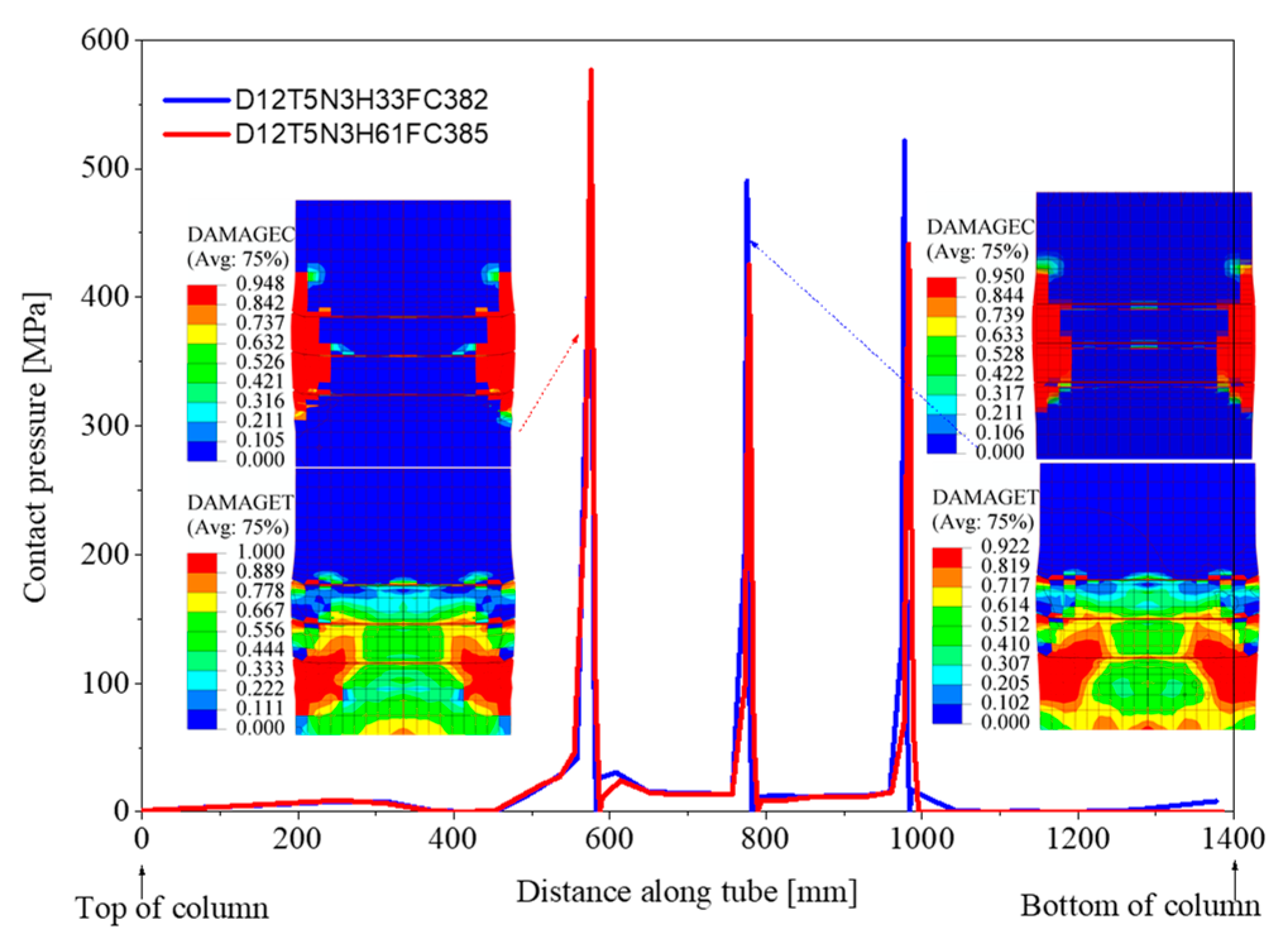
3.2. Influence of Shear Stopper Height on Bearing Strength of Infilled Concrete
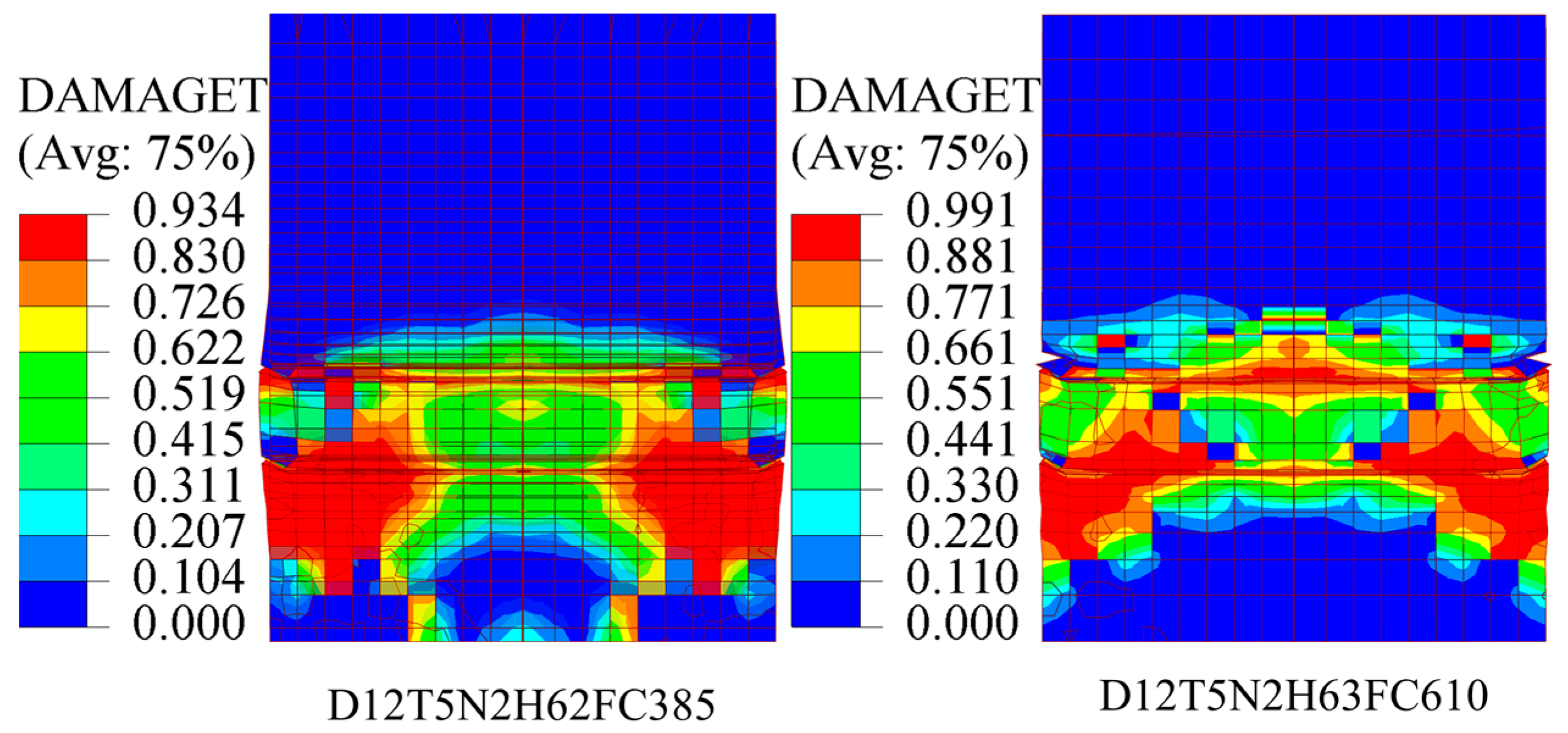
3.3. Influence of Concrete Compressive Strength on Bearing Strength of Infilled Concrete
3.4. Influence of D/t Ratio on Bearing Strength of Infilled Concrete
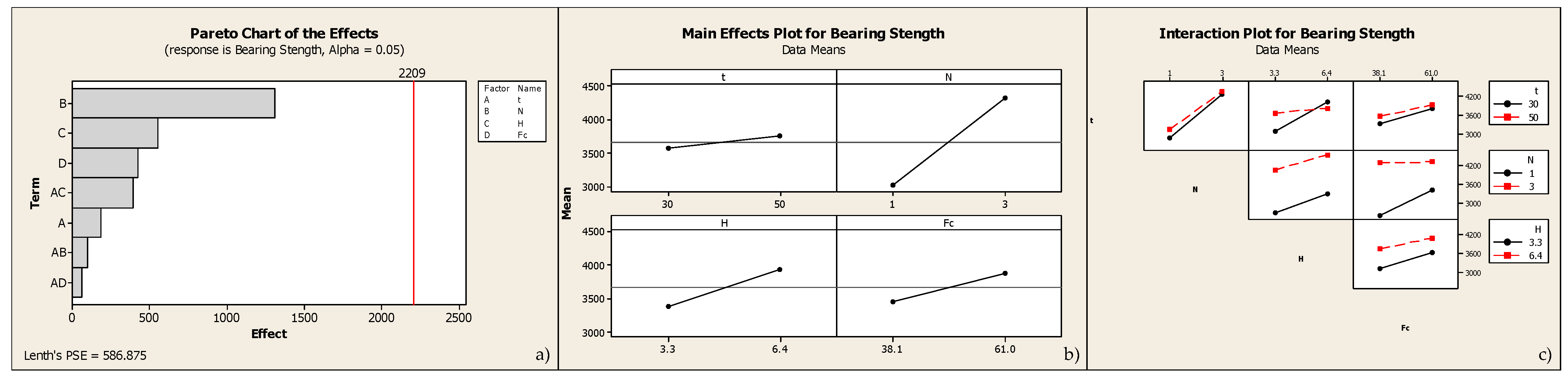
3.5. Investigation of the Impact of Geometric and Mechanical Parameters on Bearing Strength
4. Conclusions
- The number of shear stoppers was among the most critical parameters that significantly impacted the bearing strength of the infilled concrete in circular CFST columns with a large diameter. When the number of shear stoppers was high, the bearing strength of the infilled concrete increased considerably. Firstly, the high number of shear stoppers increased the contact capacity between the infilled concrete and the steel tube, allowing them to work together efficiently. This mutual transmission mechanism enhanced the bearing capacity of the CFST column. Secondly, the shear stoppers served as reinforcing ribs for the steel tube wall, enhancing its ability to resist lateral deformation, preventing local buckling, increasing the confinement effect, and enhancing the concrete strength. Thus, they considerably increased the bearing capacity of the CFST column.
- Although the analysis results indicate that the height of the shear stopper was one of the parameters that affected the bearing strength of the infilled concrete, ranked second only to the number of shear stoppers, increasing the height of the shear stopper did not significantly enhance the bearing strength of the infilled concrete. However, this parameter considerably improved the bearing strength when complemented with an increase in the compressive strength of the concrete. Thus, when seeking to improve the bearing strength of infilled concrete, we must consider adjusting the parameters to collaborate synergistically to achieve maximum efficacy.
- The study confirmed that an increase in concrete strength had only a slight effect on the bearing strength. Additionally, the use of high-strength concrete reduced the lateral expansion of the infilled concrete, decreasing its confinement effect. Furthermore, when the infilled concrete slipped through the shear stoppers, the concrete part interacting with the shear stoppers could have been damaged, leading to the incapacity of the infilled concrete to bear the load. Therefore, it is necessary to carefully consider reinforcing the compressive strength of concrete to achieve maximum efficiency while avoiding unnecessary waste.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tao, Z.; Han, L.-H.; Wang, D.-Y. Strength and ductility of stiffened thin-walled hollow steel structural stub columns filled with concrete. Thin-Walled Struct. 2008, 46, 1113–1128. [Google Scholar] [CrossRef]
- Moon, J.; Kim, J.J.; Lee, T.-H.; Lee, H.-E. Prediction of axial load capacity of stub circular concrete-filled steel tube using fuzzy logic. J. Constr. Steel Res. 2014, 101, 184–191. [Google Scholar] [CrossRef]
- Han, L.-H.; Li, W.; Bjorhovde, R. Developments and advanced applications of concrete-filled steel tubular (CFST) structures: Members. J. Constr. Steel Res. 2014, 100, 211–228. [Google Scholar] [CrossRef]
- Li, G.-C.; Chen, B.-W.; Yang, Z.-J.; Liu, Y.-P.; Feng, Y.-H. Experimental and numerical behavior of eccentrically loaded square concrete-filled steel tubular long columns made of high-strength steel and concrete. Thin-Walled Struct. 2021, 159, 107289. [Google Scholar] [CrossRef]
- Roeder, C.W. Overview of hybrid and composite systems for seismic design in the United States. Eng. Struct. 1998, 20, 355–363. [Google Scholar] [CrossRef]
- Al-Khaleefi, A.M.; Terro, M.J.; Alex, A.P.; Wang, Y. Prediction of fire resistance of concrete filled tubular steel columns using neural networks. Fire Saf. J. 2002, 37, 339–352. [Google Scholar] [CrossRef]
- Chung, K.; Park, S.; Choi, S. Fire resistance of concrete filled square steel tube columns subjected to eccentric axial load. Int. J. Steel Struct. 2009, 9, 69–76. [Google Scholar] [CrossRef]
- Kodur, V.; Franssen, J.-M. Structures in Fire. In Proceedings of the Sixth International Conference, SiF’10: Preface, East Lansing, MI, USA, 2–4 June 2010; Kellogg Hotel & Conference Center Michigan State University. DEStech Publications, Inc.: Lancaster, PA, USA, 2010; p. 1026. [Google Scholar]
- Varma Amit, H.; Ricles James, M.; Sause, R.; Lu, L.-W. Experimental Behavior of High Strength Square Concrete-Filled Steel Tube Beam-Columns. J. Struct. Eng. 2002, 128, 309–318. [Google Scholar] [CrossRef]
- Roeder, C.W.; Cameron, B.; Brown, C.B. Composite Action in Concrete Filled Tubes. J. Struct. Eng. 1999, 125, 477–484. [Google Scholar] [CrossRef]
- Marshall, I.H. Composite Structures. In Proceedings of the 1st. International Conference on Composite Structures, Paisley College of Technology, Paisley, Scotland, 16–18 September 1981; Applied Science Publishers: London, UK; Englewood, NJ, USA, 1981. [Google Scholar]
- British-Standards-Institution. Steel, Concrete and Composite Bridges—Part 5: Code of practice for design of composite bridges. In B.S. (Series); British Standards Institution: London, UK, 1979; p. 57. [Google Scholar]
- Furlong Richard, W. Strength of Steel-Encased Concrete Beam Columns. J. Struct. Div. 1967, 93, 113–124. [Google Scholar] [CrossRef]
- Virdi, K.S.; Dowling, P.J. The Ultimate Strength of Composite Columns in Biaxial Bending. Proc. Inst. Civ. Eng. 1973, 55, 251–272. [Google Scholar] [CrossRef]
- Hunaiti, Y.M.; Shakir-Khalil, H. Behaviour of Battened Composite Columns; University of Manchester: Manchester, UK, 1985; p. 204. [Google Scholar]
- Hunaiti Yasser, M. Bond Strength in Battened Composite Columns. J. Struct. Eng. 1991, 117, 699–714. [Google Scholar] [CrossRef]
- Xu, C.; Chengkui, H.; Decheng, J.; Yuancheng, S. Push-out test of pre-stressing concrete filled circular steel tube columns by means of expansive cement. Constr. Build. Mater. 2009, 23, 491–497. [Google Scholar] [CrossRef]
- Qu, X.; Chen, Z.; Nethercot, D.A.; Gardner, L.; Theofanous, M. Push-out tests and bond strength of rectangular CFST columns. Steel Compos. Struct. 2015, 19, 21–41. [Google Scholar] [CrossRef]
- Virdi, K.S.; Dowling, P.J. Bond strength in concrete filled circular steel tubes. In CESLIC Report CC11; Department of Civil Engineering, Imperial College: London, UK, 1975. [Google Scholar]
- Virdi, K.S.; Dowling, P.J. Bond Strength in Concrete Filled Steel Tubes; IVBH: San Antonio, TX, USA, 1980. [Google Scholar]
- Johansson, M.; Gylltoft, K. Mechanical Behavior of Circular Steel–Concrete Composite Stub Columns. J. Struct. Eng. 2002, 128, 1073–1081. [Google Scholar] [CrossRef]
- Guan, M.; Lai, Z.; Xiao, Q.; Du, H.; Zhang, K. Bond behavior of concrete-filled steel tube columns using manufactured sand (MS-CFT). Eng. Struct. 2019, 187, 199–208. [Google Scholar] [CrossRef]
- Starossek, U.; Falah, N. The interaction of steel tube and concrete core in concrete-filled steel tube columns. In Proceedings of the Tubular Structures XII: Proceedings of Tubular Structures XII, Shanghai, China, 8–10 October 2008; pp. 75–84. [Google Scholar]
- Starossek, U.; Falah, N.; Löhning, T. Numerical Analyses of the Force Transfer in Concrete-Filled Steel Tube. In Proceedings of the 4th International Conference on Advances in Structural Engineering and Mechanics(ASEM’08), Jeju, Republic of Korea, 30 May 2010; Techno-Press: Daejeon, Republic of Korea, 2010; pp. 241–256. [Google Scholar]
- Petrus, C.; Abdul Hamid, H.; Ibrahim, A.; Nyuin, J.D. Bond strength in concrete filled built-up steel tube columns with tab stiffeners. Can. J. Civ. Eng. 2011, 38, 627–637. [Google Scholar] [CrossRef]
- Song, T.; Tao, P.Z.; Uy, B.; Han, L.-H. Bond strength in full-scale concrete-filled steel tubular columns. In Proceedings of the Advances in Structural Engineering and Mechanics (ASEM15), Incheon, Republic of Korea, 25–29 August 2015. [Google Scholar]
- Ferrotto, M.F.; Fenu, L.; Xue, J.-Q.; Briseghella, B.; Chen, B.-C.; Cavaleri, L. Simplified equivalent finite element modelling of concrete-filled steel tubular K-joints with and without studs. Eng. Struct. 2022, 266, 114634. [Google Scholar] [CrossRef]
- Li, N.; Xi, Y.; Li, H.; Zhang, G.; Ren, T.; Mu, X. Bearing Strength of Concrete-Filled Steel Tube Reinforced with Internal Transverse Stiffened Bars under Axial Compression. Scanning 2022, 2022, 1704544. [Google Scholar] [CrossRef]
- Wu, R.-M.; Wang, L.-Q.; Tong, J.-Z.; Tong, G.-S.; Gao, W. Elastic buckling formulas of multi-stiffened corrugated steel plate shear walls. Eng. Struct. 2024, 300, 117218. [Google Scholar] [CrossRef]
- Tong, J.; Wu, R.; Wang, L. Experimental and numerical investigations on seismic behavior of stiffened corrugated steel plate shear walls. Earthq. Eng. Struct. Dyn. 2023, 52, 3551–3574. [Google Scholar] [CrossRef]
- Yu, C.-Q.; Tong, G.-S.; Tong, J.-Z.; Zhang, J.-W.; Li, X.-G.; Xu, S.-L. Experimental and numerical study on seismic performance of L-shaped multi-cellular CFST frames. J. Constr. Steel Res. 2024, 213, 108360. [Google Scholar] [CrossRef]
- Ypma, T.J. Historical Development of the Newton–Raphson Method. SIAM Rev. 1995, 37, 531–551. [Google Scholar] [CrossRef]
- International-Federation-for-Structural-Concrete-(FIB). Fib Model Code 2010. In Structural Concrete; Wiley Subscription Services, Inc.: London, UK, 2010; pp. 74–150. [Google Scholar] [CrossRef]
- Krätzig, W.B.; Pölling, R. An elasto-plastic damage model for reinforced concrete with minimum number of material parameters. Comput. Struct. 2004, 82, 1201–1215. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Liang, Q.Q. High strength circular concrete-filled steel tubular slender beam–columns, Part I: Numerical analysis. J. Constr. Steel Res. 2011, 67, 164–171. [Google Scholar] [CrossRef]
- Liang, Q.Q. Performance-based analysis of concrete-filled steel tubular beam–columns, Part I: Theory and algorithms. J. Constr. Steel Res. 2009, 65, 363–372. [Google Scholar] [CrossRef]
- Gadamchetty, G.; Pandey, A.; Gawture, M. On Practical Implementation of the Ramberg-Osgood Model for FE Simulation. SAE Int. J. Mater. Manuf. 2016, 9, 200–205. [Google Scholar] [CrossRef]
- Rezaeian, A.; Jahanbakhti, E.; Fanaie, N. Numerical Study of Panel Zone in a Moment Connection without Continuity Plates. J. Earthq. Eng. 2022, 26, 930–948. [Google Scholar] [CrossRef]
- Francavilla, A.; Zienkiewicz, O. A note on numerical computation of elastic contact problems. Int. J. Numer. Methods Eng. 1975, 9, 913–924. [Google Scholar] [CrossRef]
- Chan, S.K.; Tuba, I.S. A finite element method for contact problems of solid bodies—Part I. Theory and validation. Int. J. Mech. Sci. 1971, 13, 615–625. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Taylor, R.L.; Sackman, J.L.; Curnier, A.; Kanoknukulchai, W. A finite element method for a class of contact-impact problems. Comput. Methods Appl. Mech. Eng. 1976, 8, 249–276. [Google Scholar] [CrossRef]
- Kikuchi, N.; Oden, J.T. Contact Problems in Elasticity: A Study of Variational Inequalities and Finite Element Methods; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1988. [Google Scholar]
- Han, L.-H.; Yao, G.-H.; Tao, Z. Performance of concrete-filled thin-walled steel tubes under pure torsion. Thin-Walled Struct. 2007, 45, 24–36. [Google Scholar] [CrossRef]
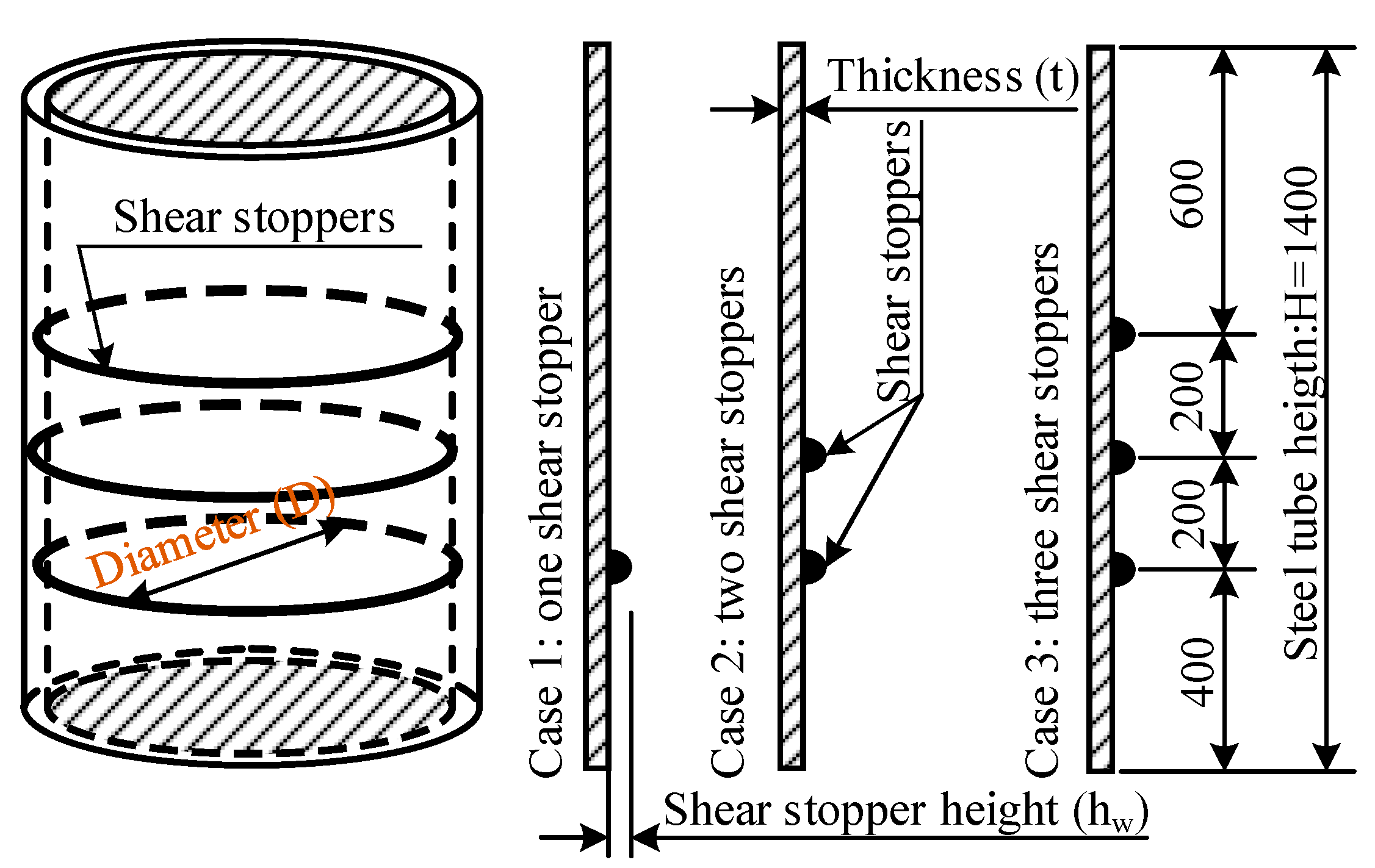
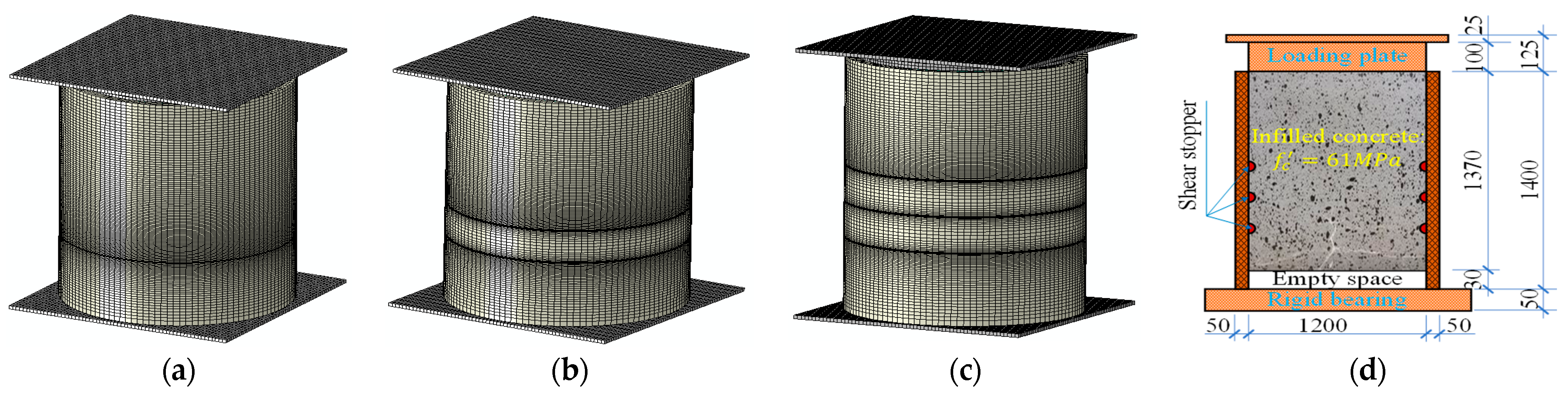




| No. | Mark 1 | D (mm) | t (mm) | D/t | (mm) | Concrete Compressive Strength (MPa) | Pipe Height H (mm) | |
|---|---|---|---|---|---|---|---|---|
| 1 | D12T5N1H40FC382 | 1200 | 50 | 24 | 1 | 4.0 | 38.2 | 1400 |
| 2 | D12T5N2H35FC381 | 1200 | 50 | 24 | 2 | 3.5 | 38.1 | 1400 |
| 3 | D12T5N3H33FC382 | 1200 | 50 | 24 | 3 | 3.3 | 38.2 | 1400 |
| 4 | D12T5N2H62FC385 | 1200 | 50 | 24 | 2 | 6.2 | 38.5 | 1400 |
| 5 | D12T5N3H61FC385 | 1200 | 50 | 24 | 3 | 6.1 | 38.5 | 1400 |
| 6 | D12T5N2H63FC610 | 1200 | 50 | 24 | 2 | 6.3 | 61.0 | 1400 |
| 7 | D12T3N2H36FC388 | 1200 | 30 | 40 | 2 | 3.6 | 38.8 | 1400 |
| 8 | D12T3N3H35FC388 | 1200 | 30 | 40 | 3 | 3.5 | 38.8 | 1400 |
| 9 | D12T3N2H63FC390 | 1200 | 30 | 40 | 2 | 6.3 | 39.0 | 1400 |
| 10 | D12T3N2H35FC610 | 1200 | 30 | 40 | 2 | 3.5 | 61.0 | 1400 |
| 11 | D12T3N2H64FC610 | 1200 | 30 | 40 | 2 | 6.4 | 61.0 | 1400 |
 .
.| StdOrder | RunOrder | CenterPt | Blocks | t | N | hw | Bearing Strength | |
|---|---|---|---|---|---|---|---|---|
| 7 | 1 | 1 | 1 | 30 | 3 | 6.4 | 38.1 | 4505 |
| 4 | 2 | 1 | 1 | 50 | 3 | 3.3 | 38.1 | 4100 |
| 2 | 3 | 1 | 1 | 50 | 1 | 3.3 | 61 | 3250 |
| 6 | 4 | 1 | 1 | 50 | 1 | 6.4 | 38.1 | 3050 |
| 1 | 5 | 1 | 1 | 30 | 1 | 3.3 | 38.1 | 2150 |
| 5 | 6 | 1 | 1 | 30 | 1 | 6.4 | 61 | 3580 |
| 8 | 7 | 1 | 1 | 50 | 3 | 6.4 | 61 | 4620 |
| 3 | 8 | 1 | 1 | 30 | 3 | 3.3 | 61 | 4050 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, M.; Dinh, N.-H.; Dang, C.-T.; Truong, H.-C. Numerical Study of Bearing Strength of Infilled Concrete in Large Diameter CFST Column Reinforced by Shear Stoppers. Designs 2024, 8, 9. https://doi.org/10.3390/designs8010009
Pham M, Dinh N-H, Dang C-T, Truong H-C. Numerical Study of Bearing Strength of Infilled Concrete in Large Diameter CFST Column Reinforced by Shear Stoppers. Designs. 2024; 8(1):9. https://doi.org/10.3390/designs8010009
Chicago/Turabian StylePham, My, Ngoc-Hieu Dinh, Cong-Thuat Dang, and Hoai-Chinh Truong. 2024. "Numerical Study of Bearing Strength of Infilled Concrete in Large Diameter CFST Column Reinforced by Shear Stoppers" Designs 8, no. 1: 9. https://doi.org/10.3390/designs8010009
APA StylePham, M., Dinh, N.-H., Dang, C.-T., & Truong, H.-C. (2024). Numerical Study of Bearing Strength of Infilled Concrete in Large Diameter CFST Column Reinforced by Shear Stoppers. Designs, 8(1), 9. https://doi.org/10.3390/designs8010009








