Whist Game Cards Calibration Strategies-Based Technique for Conceptual Design Morphological Chart Refinement

Abstract

High-quality concept design is a key factor of successful product performance and efficiency. Conventional conceptual design morphological chart serves to combine product concept designs. Nevertheless, the huge number of combined concept designs and how to reduce is an important research point. In this paper, concepts design combined after refinement of possible sub-functions means (M) in the product conceptual design morphological chart to less and most promising means based on calibration proceeded in binary for the means regarding numerical scales applied to a package of quality attributes (QAs). The calibration proceeds in accordance with single suit whist game between two competitors’ strategies. The game tricks number depends on QAs number, and the summation of tricks scored by each means give M numerical value. Means with the high numerical values keep existence while means with the weak numerical values were eliminated from the chart. The case study approved the current technique reliability and flexibility for assessing sub-functions means which accommodates a wide variety of QAs to solve the problem of useless and abundance concepts design through morphological chart refinement. In addition, these capabilities make designers able to specify more QAs to meet different product stakeholders’ requirements. Beside these advantages, the opportunities for further development and limitations are considered in discussion and conclusion.

1. Introduction

Conceptual design morphological chart form by decomposition of product overall function into sub-functions and series of possible means corresponding to each sub-function and use to combine concepts design. The stage of searching sub-functions means requires more abstract and designers must be familiar with some design information and background associate with the problem to facilitate concepts design combination step.

Morphological chart also called morphological table is an important tool for concepts design generation process. It includes two column lifts, and right-side, the functions list in left side column, while the possible solutions principles on the right side to each function [1]. This chart assists in searching sub-functions’ solutions principles, whether existing or customize new solution principle to implement in the concept development stage [2]. In morphological chart, designers can visualize sub-functions and its means, as it formalized due to a decomposition for a design problem into sub-problems, and search for sub-solution that satisfies each sub-problem then the ultimate solution is extracted via some sub-solutions combination [3,4].

The primary purpose of morphological chart usage is to understand the interrelationships between objects (components), and sub-objects (sub-components) that form concepts design in accordance with these relationships. In another word, the morphological chart work as a magnifier tool of artefacts’ features with suitable alternatives for each feature. The solutions principles (i.e., sub-components) in morphological chart, must be compatible geometrically, technically, and economically, because each component performance affects other sub-components performance, with that the overall solution relies on components performance [5].

In general, in conceptual design process, morphological chart lists the required sub-functions and means for design solutions’ compilation which should all be at the same level of detail, and the classical method for listing product’s sub-functions and means on morphological charts is; sub-functions allocate in the left column, and the all-possible means of sub-functions list in rows corresponding to each sub-function cell. The design solutions alternatives generated via morphological chart for any problem are classified into small part as existing solutions, some are new solutions, while other (possibly a large number) are impossible solutions.

It is now understood that morphological chart plays an important role in the conceptual design activities; this essential role recognizes combination of the overall design solutions of a design problem as expose designers to an available information before getting the final design solution [6]. Despite the key role which conventional morphological chart plays in design solutions, too many solutions alternatives generated in accordance with the chart size cause difficulties in selecting the ideal one in some cases [3,7,8]. Since more than only one concepts design for the problem can be generated, improving concept design combination process is possible within a control for the conceptual design morphological chart size through a few and potential sub-functions’ means [9,10].

To solve these difficulties, designers have developed some methods to control and reduce the generated concepts design number to a more manageable level by refinement procedures. For example, mothed of selection only for a limited set of means which can achieve the intended sub-functions, especially those looking more promising and practical or are well-known effective choices. Another methodology identifies the infeasible or incompatible pairs of means to exclude the solution which contain them.

The motivation of this paper is to introduce a simple refinement technique for morphological chart by reducing the sub- functions’ principles solution entries in the chart, in order to improve design space exploration, and solve the problem of the big number of generated concepts design via morphological chart by generating small number of solution alternatives.

The purposes of this technique is to design simply eliminate means with less quality characteristics (i.e., the weakest means) out of the possible sub-functions’ means list in product conceptual design morphological chart. Consequently, the remind sub-functions’ means highly meet the quality characteristics requirements, and the number of the generated concepts design via the chart naturally will be less. In another word, the objective of the current technique is to grasp design difficulties which rise from the big number of solution schemes generated from morphological chart by reducing the chart entries (sub-functions means). Moreover, this technique not only reduces the number of design concepts’ combinations, it also serves to introduce more concrete design solutions alternatives.

This refinement technique is formed in accordance with the solitaire whist game fundamental principles to calibrate between two or more sub-functions means regarding design requirements and constraints satisfaction (i.e., calibration means the act of comparison which excluding any subsequent adjustment), based on a package of product quality attributes.

Product quality attributes (QAs) refer to incorporate features that have the capacity to meet consumer needs and gives customer satisfaction by altering products or services to make it free from deficiencies, this affects the success of the product and helps build its reputation in the customer markets. When the company creates high-quality products which fulfil its customers’ needs, this can reduce production costs, and improve return on investment [11]. When evaluating product quality, enterprises consider several key factors; whether the product can solve the problem and works effectively or satisfies the customers’ purposes and meets industrial standards. Therefore, QAs utilize to represent all product’s quality characteristics such as performance efficacy, materials, and adapted technologies to ensure that the required product quality specified in the early design stage, hence the product conceptual design morphological chart outcome will be high quality solution alternatives. QAs can be assumptions, constraints, or product stakeholders’ requirements such as performance, security, reliability which can be combined with functional requirements [12,13]. In software system design and implementation, four QAs, performance, dependability, security, and safety have used to make objective decisions on design trade-offs and enable designers to make reasonable and accurate predictions on system performance to realize a better overall system [14].

The rest of this article is organized as follows. Section 2 represents a literature review of morphological chart and whist game. Section 3 applies the current research methodology to a case study. Finally, a brief discussion and conclusions are presented in Section 4.

2. Literature Review

Design concept generation occur over two distinct stages: searching features to fulfil functional requirements, and generating concepts design by combining the features. Understanding existing solutions to similar problems and sub-problems make concept design generation smoother, as designer can find a new design solution or customize an existence solution. This means, customizing an existence solution with relevant components’ functions is helpful to find design solution faster and is most cost-effective than starting a new design. There are different design tools such as morphological chart support these two design stages [15]. Morphological chart is a design tool which aids designers to identify consistence design solutions schemes, besides providing significant help by making designers’ ideas more clear before design solution generation. Figure 1 illustrates morphological chart which encompasses possible sub-functions or features (F) and its relevant means that can be combined to form concepts design. Design solutions schemes are created from morphological chart are proportional to the sub-functions number after browsing the chart content, then the designer determines the most promising concepts design, thus in case the number of possible sub-solutions and means are big, the combined systems generated usually quite a lot as these systems include not only existing conventional means, but also various new means [16,17]. The number of concepts design combinations that can be created from the chart calculate regarding the sub-functions and proposed means by multiplying the number of means time sub-functions, Equation (1) [7].

$${\displaystyle \prod _{i=1}^n{\mathrm{M}}_i}\mathrm{for}i=1,2,3,\dots n$$

(1)

Morphological chart work in accordance with morphological thinking principles, which is known as a systematic full combination method of all possible-combinations, and this method utilized to form design concepts form after funding means that possibly fulfil all the require sub-functions based on functional representation. The original morphological charts are developed to contain product specification index with list of relevant components for specification index; the designer selects the required parts and features of the sketches by browsing and integrating it into final design conceptual solution [18]. Lately, morphological chart has become one of the most effective tools for the early design stage [4,17,19].

A considerable work and literature about the morphological chart are presented in [20]. In this literature, morphological chart is identified as a method to construct, and study all the relationships contained in multi-dimensional as well as a tool for listing possible comprehensive conceptual design solutions, and serve to store information succinctly by listing features with the conceptual solutions [21]. Many researches applied morphological charts in design activities to generate conceptual design schemes; the chart consists of the desired product sub-functions in the left side column, and its possible means list in the right side of each sub-functions, these sub-solutions are often arranged in accordance with its detail such as technical characteristics and performance specification [22]. The morphological chart applied in many disciplines from smart furniture production, architecture design, to automotive components and management sciences. In all these applications, morphological chart showed high efficiency and achieved accurate results [8,23].

Although morphological chart provides reliable visualization for product components ideas and identifies features during conceptual design, these ideas visualized the overall design solutions form by matching the individual sub-solutions ideas of each component and combining them together [24,25]. However, an important question related to morphological chart is; “How to select the best sub-function means for a specific feature from the available means options in concept design is?” Based on this question, methods to solve such an essential problem are high required in order to aid products’ designers in selection of the optimal sub-functions means and narrow down the sub-solutions means frame to practical solutions combinations field by reducing morphological charts elements [26]. In systematic approach, the valuation criteria must first be specified by their relative contribution to the overall concept design value to eliminate relatively unimportant criteria before the evaluation begins [27]. A backwards design method is an effective systematic approach for concept design refinement specially for design cases where the features shapes are more important, in this method unworkable sub-function means eliminate or modified after the concept design is produced until the design meets all the functions [28].

Nevertheless, these methods are team-based approaches beside ideas generated and developed gradually [29]. Nevertheless, product designers can visualize more easily morphological chart and enhance the exploration of the design space by refining sub-functions means in the morphological chart [30,31]. Morphological chart refinement provides good help for designers by reducing the huge number of the possible sub-solutions means to select the best concepts design combination, in this regard and for the refinement purpose the design solution selection matrix is developed to aid designers in concepts design evaluation [32].

This paper will make a valuable contribution toward solving the problem of sub-functions means selection beside narrowing down the sub-functions means frame by a refinement technique for product conceptual design’s morphological chart sub-functions means based on QAs in order to generate a few and optimal concepts design.

Qas represent technical, performance, or economic attributes which can be specified by design, marketing, or manufacturing departments and utilize to assess in sub-functions means’ calibration to ensure that the proposed means satisfies the expected and required product’s parameters and maintaining this feasibility in the final solution. In accordance to the principle of possibility to exploit optimization during the conceptual stages and that to arrive at good potential concepts design combinations [17,33].

Unlike previous approach, in the whist game strategies-based technique the sub-functions means’ refinement was made in accordance with a comprehensive QAs, and sub-functions mean which have small numerical values were eliminated while the most promising sub-functions means were kept before generating optimal concepts design. As a result, it enhances the reliability of each sub-function means individually, and increases its quality value based on QAs.

To achieve this objective, a simple whist game with totally ordered single suit of 2n cards playing strategies was applied to calibrate (i.e., calibration means the act of comparison which excluding any subsequent adjustment.) between the conceptual design—morphological chart’s sub-functions’ means (M). In this game, the competitors are represented by M, while QAs are the deck of poker cards used in the real whist, thus the number of QAs assigned the number of the deal tricks, and the cards numbers (i.e., 2, 3, 4, 5, 6, 7, 8, 9) represented by the numerical scales. This deck of cards is selected to achieve the desired purpose of the morphological chart refinement, in addition to making the calibration between two M proceeding as a game of whist playing between two competitors exactly. For this game, numbers 2, 3, 4, 5, 6, 7, 8, and 9 are employed as numerical scale for QAs, and like the other scales the smallest element always represents the worst choice, and vice versa. Conventionally, the solitaire deck cards have four suits (i.e., hearts, diamonds, spades, and clubs), each suit has N = 13 cards which are; A K Q J 10 9 8 7 6 5 4 3 2. There are four participants in two fixed partnerships which organize face-to-face pair, and beginning with player on his left the dealer gives each player one card at every distribution around until the last card. The game was played in the clockwise rotation, where the left player takes the lead and plays any card, every player tries to play a card following the leader card’s suit. In case the player cannot follow the turn suit, then can play any card according to his expectation [34,35].

In general knowledge, the objective of the game is the player tries to maximize the total number of wined points and the whist game not unexpected, thus whist game competitors each try his best to win all the possible tricks as can and trick is won by the player with the highest card, then winner of each trick leads the next one. At the end of the deal, player with the most points wins the game. Although the whist game appears very simple but is quite complex, because it is difficult to find a best strategy for manipulating the cards and determine the trick numerical value [27,36]. For example, in two competitors’ game, the cards are distributed for two opponents M1 and M2, each M given “n” cards. Out of the two, one competitor fixed as having the first card’s drooping right (leader), and the second one reacts to the leader. The leader droop one card, and the opponent plays one card in accordance with the first player card suit. Player with high cards scored this trick, and take the lead of the next trick. The cards that drooped remove from each hand, and the game continues until all the cards are used up [37].

As in morphological chart means, each sub-function is possibly satisfying the concept solution. Nevertheless, the satisfaction degrees differ from means to means. Therefore, the numerical scales (cards’ numbers) give the designers the ability to clarify this variation by calculating the trick values of each means regarding the QAs.

3. Research Methodology

When products meet various standards of consumers, it will describe high-quality products, and product’s quality attributes include; physical criteria or features, durability and lifespan, there are also service and time factors affecting the product’s quality.

In this technique QAs are applied to the product conceptual design sub-functions “features” and principle solutions “means” are allocated in morphological chart, Figure 2. Then, the sub-functions’ means calibrate binary (i.e., each pair of means that relate to one sub-function) regarding the QAs to clear out each means (i.e., shape, or component) numerical value. Based on the numerical values, a refinement processes are made to reduce the number of the possible means, and the conceptual design morphological chart narrows down sequentially. Figure 2 illustrates the proposed technique procedures and application as following:

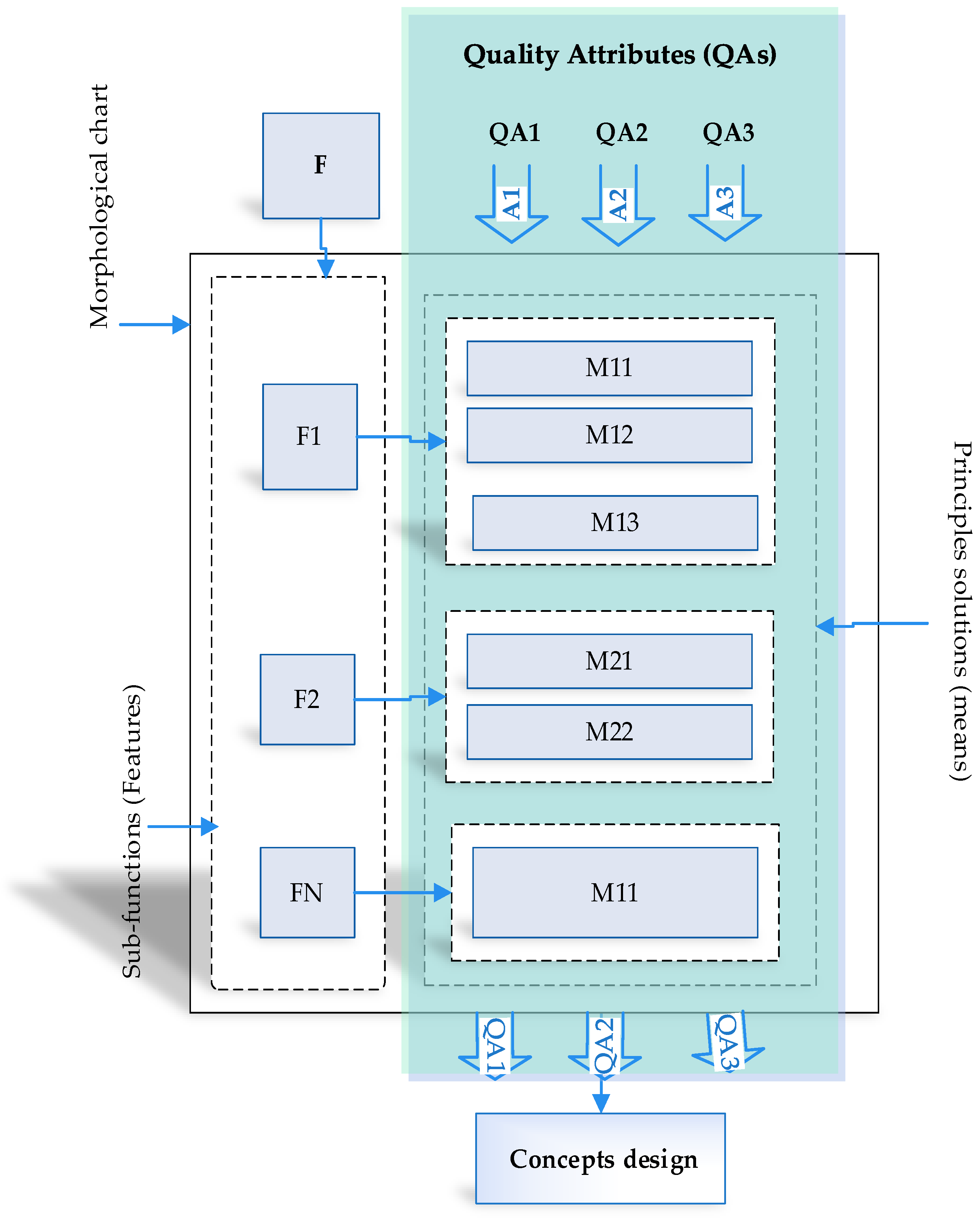
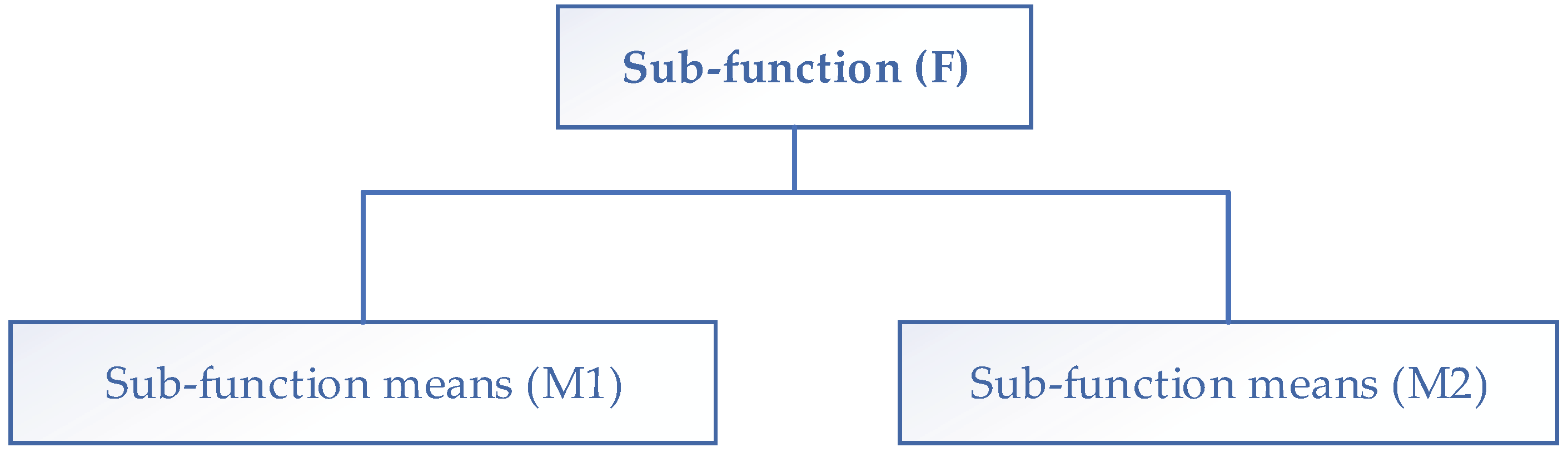
• Set the conceptual design morphological cart; within this step the product overall function decomposes into sub-functions or features (F).
• Obtain the sub-function means (M); searching of possible principle solutions of each sub-function.
• Set the quality attributes (QAs); a package of QAs develops to represent the designers and customers required quality attributes for on product.
• Apply QAs to the sub-function means; to estimate QAs numerical scale on the specific sub-function means.
• Estimate QAs numerical scale “cards” on the sub-function means; the numerical scales are whist game cards suit; 2, 3, 4, 5, 6, 7, 8, 9 distribute to two opponents (means) which relate to specific sub-function.
• Calibrate M regarding QAs numerical scales obtained in the previous step, the calibration process will make to determine every M numerical value.
• Refine M with respect to numerical values; the sub-functions’ means reduce and morphological chart narrow down by the refinement proceeding to M.
• Set the refined morphological chart; the morphological chart reformed with less sub-functions means (i.e., the most promising sub-functions means), and then less concepts design generated as a result of the refinement processes.

With QAs numerical scales distribute to QA of first Mi on one-side, and other different numerical scales also will be given to same QA of the second Mi on other-side. Therefore, the numerical scales number for every “M” depends on the number of QAs, as each card represents a numerical scale of one QA. That means, if two QAs implemented to the sub-functions’ means, then each “M” will have two numerical scales, and if “M” has three QAs, it will have three numerical scales too, and so on.

3.1. Quality Attributes (QAs) Application Reasons

As mentioned in previous sections, the objective of applying QAs is to form comprehensive quality characteristics for sub-function means and concepts design. Therefore, QAs such as performance, weight, shape, abundancy, creativity etc., which are utilized to estimate the comprehensive numerical values of sub-functions means regarding numerical scales; following are some quality attributes’ application reasons:

• Performance attribute; performance defined as the final function or service which product design to provide it exactly as the end users want, thus performance applied to sub-function-means to predict its structural performance and performance values;
• Weight attribute; applied to sub-function means to estimate durability and material characteristics;
• Cost attribute; cost means contribution analysis which use to estimate profitability at the markets segment and consumers level, so it enhances the decision making;
• Shape attribute; applied to sub-function-means to define the instructions for combining means into concepts design, and the shape complexity level;
• Abundancy attribute; applied for sub-function means to evaluate its abundance percentage, sources availability and quality accessibility;
• Novelty attribute; defined as being original or new therefore interesting, and this original usage is derived as the concepts design;

In addition to designers, product’s potential stakeholders (i.e., customers and suppliers) can contribute to QAs specification and numerical scales distribution. Calibration between “M” proceeds regarding QAs numerical scales (cards), so the refinement can be proceeded to all possible sub-functions means comprehensively. Based on the whist game strategies, this gives more simpler process to calculate each means’ numerical value.

3.2. Whist Strategies Based Numerical Scales Calibration

The calibration proceeds individually for every trick, as a deal contents number of tricks (i.e., two, three, or four). A single suit with eight cards (2, 3, 4, 5, 6, 7, 8, 9) represent numerical scales set in up or down arrangement. This can give an advantage to estimate which QA worth specific cards to represents assessing numerical scale for any sub-function means (M). Say, a product conceptual design morphological chart includes sub-function (F1) which has two promising means M1 and M2 as in Figure 3. As M1 and M2 compete based on “Whist game” strategies, the lift player leads the first trick, then both competitors will follow the normal game rules. This advantage maximizes the number of tricks possible to be taken by the leader. However, in the game’s conventional strategies the leader often avoids winning the first trick. This means, the other competitor has a good chance to win the first trick and make a normal lead. Therefore, there is no conflict on whether the player trying to score tricks as play leader’s role, or when reacts later.

As a deal with “N” cards arranged from 2 to 9, the two competitors play with n1 + n2 = 9 8 7 6 5 4 3 2 cards following Equations (2) and (3).

Suppose there are “M” competitors:

$$\mathrm{M}={\displaystyle \sum _{i=1}^2{\mathrm{M}}_i}=\mathrm{M}1+\mathrm{M}2,\to i\in (1,2)$$

(2)

Then each competitor has number of cards (n):

$$\mathrm{n}=\frac{\mathrm{N}}{\mathrm{M}}\to \mathrm{n}\subset N$$

(3)

Two sub-function means M1 and M2 will be assessing according to QAs numerical scales “2, 3, 4, 5, 6, 7, 8 9”, every QA gives two cards to represent QA numerical scales on M. By means, each two cards distribute between one QA located on both M1 and M2.

For instance, QA1 represents the quality attribute “cost”, and as QA1 is allocated on M1 as well as M2. So, based on designer’s perception estimation of QA1 on M1 and QA1 on M2 two cards distribute to M1 and M2; the first card represents the numerical scale of QA1 on M1, while the second card represents the numerical scale of QA1 on M2.

For calibration purpose, M1 and M2 are treated like two players competing in solitaire whist game strategies. Moreover, the game trade-off processes as any one of the players win tricks regarding cards strengthen, with its ability for heuristic against the counterpart or competitor. Considering the game procedures, each one of the two-players has “n” cards which are totally ordered, and both players know the contents and order of both hands. The leader selects one of his cards to drop for trick’s starting, and the opponent plays one card in reaction, then the higher numerical scale wins this trick. The trick adds to the score of the winner, and in the same time the winner qualifies to lead the next trick action. The drooped cards remove from each player hand, then a new position is created for the rest of the cards (n-1) until the game cards finish. For example, say, a design feature (F1) has two possible means which are M1 and M2, thus four quality attributes QA1, QA2, QA3, and QA4 supposed to assess M1 and M2 then QAs numerical scales of M1 and M2 entries are:

M1 = (QA11, QA12, QA13, QA14), & M2 = (QA21, QA22, QA23, QA24)

Which are defined by

QA11, QA12, QA13, QA14, QA21, QA22, QA23, QA24 = QA_ij

For; i = 1, 2 and j = 1, 2, 3, 4.

That “i” represents sub-function means (M), and “j” represents quality attributes (QAs) order. For calibration between M1 and M2, with two quality attributes QA1 and QA2, the QA1 and QA2 allocated on both M1 and M2, thus numerical scales (Ns) will distribute in way like; MQA11 and MQA12 (Ns11 and Ns12), and MQA21 and MQA22 (Ns21 and Ns22). Therefore, trick’s values (Tv) for the two players obtain according to following conditions:

The firth trick’s value (Tv1), for M1;

Tv1 = 1, {if Ns11 > Ns21}. Tv1 = 0, {if Ns11 < Ns21}.

And for M2;

Tv1 = 1, {if Ns21 > Ns11}. Tv1 = 0, {if Ns21 < Ns11}.

The second trick’s value (Tv2), for M1;

Tv2 = 1, {if Ns12 > Ns22}. Tv2 = 0, {if Ns12 < Ns22}.

And for M2;

Tv2 = 1, {if Ns22 > Ns12}. Tv2 = 0, {if Ns22 < Ns12}.

In case of having QA3 and QA4 utilized for M1 with M2 calibration, then tricks’ values (Tv3 and Tv4) will be obtained in accordance with the same conditions. As a result, numerical value for each player (M) is the summation of the tricks’ values scored by the player.

The following sub-sections are examples for calibration between M1 and M2 with two, three, and four QAs numerical scales to obtain numerical values.

3.2.1. Two QAs Numerical Scales Calibration

In this case, F1 has two proposed sub-function means; M1 and M2 are assessed with two quality attributes (QA1, QA2) which represent, performance and novelty attributes respectively. A calibration proceeded between M1 and M2 to determine which one is the best solution for F1, that after QA1 and QA2 numerical scales set on the sub-function means with respect to the designer perspective.

For this case, “9, 8, 7, 6” numerical scales are distributed as; QA1 numerical scale is 8 for M1, and 9 in M2, where QA2 numerical scale is 6 for M1, and 7 in M2.

[8, 6] vs. [9, 7]

Therefore, for this deal M1 leads to the manipulating action and starting the first trick by dropping either 8 or 6, then M2 reacts with dropping 9 or 7. The result of M1 action and M2 reaction make M2 able to win the two tricks. Nevertheless, M2 is able to win one trick in case of M2 plays 7 in reaction. So, this logical understanding of these numerical scales calibration makes the standard numerical values for M1 and M2 can be obtain as following:

M1 numerical value:

Nv1 = 1.000 + 0.500 = 1.500

M2 numerical value:

Nv2 = 1.000 +0.500 = 1.500

3.2.2. Three QAs Numerical Scales Calibration

In this case, the two sub-function means (M1, M2) are assessed with three quality attributes (QA1, QA,2, QA3) which represent performance, novelty, and cost attributes respectively. A calibration proceeded between M1 and M2 to determine which M is an optimal solution for F1, after QA1, QA2, and QA3 numerical scales are estimated.

For this case “9, 8, 7, 6, 5, 4” cards are distributed such as QA1 numerical scales are 7 for M1, and 4 in M2; where QA2 numerical scales are 8 for M1, and 9 in M2; QA3 numerical scales take 5 for M1, and 6 in M2. These six numerical scales for two sub-function means arranged as following:

[8 7 5] vs. [9 6 4]

Calibration processes of these cards can be analyzed as M1 leading the deal right, if M1 droop 7 or 8, then M2 withdraw 9 to win the first rick. Sequency, M2 leads the next trick by 6 or 4, so M1 able to win the second and third trick. However, if M1 dropped 5, M2 can play 6 to win the first trick, also the numerical scale 9 can help M2 to win the trick in any situation. Therefore, the standard numerical values for the two players in this three tricks deal are obtained as following:

M1numerical value;

Nv1 = 2.000 + 0.500 = 2.500

M2 numerical value;

Nv2 = 1.000 + 0.500 = 1.500

3.2.3. Four QAs Numerical Scales Calibration

For this numerical values modelling, the potential sub-function means M1 and M2 are assessed by four quality attributes (QA1, QA2, QA3, QA4) which represent; performance, cost, novelty, and abundancy respectively. The single suit 9, 8, 7, 6, 5, 4, 3, 2 numerical scales are distributed on M1 and M2 as following:

[8 7 3 2] vs. [9 6 5 4]

As M2 has the biggest card (9), thus M2 is able to take this trick in any situation. However, with M1 on lead of cards drooping, M2 could win three of the four tricks simultaneously. Therefore, the standard numerical values of M1 and M2 from this four tricks’ deal are obtained as following:

M1 numerical value;

Nv1 = 1.000

M2 numerical value;

Nv2 = 3.000

4. Case Study

The main objective of this technique is to refine possible sub-functions’ means in conceptual design morphological chart to unenlarged number by eliminating the weakest sub-functions’ means, and leave the most promising sub-functions’ means. Therefore, a product design problem of “transmission device conceptual design morphological chart” is utilized in the current refinement technique’s application to approve its usability and efficiency

Table 1. Original conceptual design morphological chart of the transmission device.

				Means (M)
Sub-Functions (F)		M1	M2	M3	M4
F1	Driving device	Hydraulic drive	Electromagnetic drive	Motor drive
F2	Transfer torque	Gear transmission	V-belt transmission	Bar transmission	Chain wheel transmission
F3	Connecting transmission surface	Square surface	Circular surface
F4	Transmission frame layout	Concatenated	Integrated
F5	Install device	Horizontal installation	Gradient installation
F6	Protect device	Independent motor	Wireless switch	Overload protection
F7	Place cargo	Positioning slot	Positioning cylinder	Positioning board

. This transmission device is designed by design research group in Zhejiang university of technology (ZJUT) Mechanical engineering college [38].

The transmission device conceptual design morphological chart above, contents nineteen sub-functions’ means; (M11, M12, M13), (M21, M22, M23, M24), (M31, M32), (M41, M42), (M51, M52), (M61, M62, M63), and (M71, M72, M73) corresponding to the features F1, F2, F3, F4, F5, F6, and F7 respectively,

Table 2. Original conceptual design morphological chart of the transmission device.

F	M
F1	M11	M12	M13
F2	M21	M22	M23	M24
F3	M31	M32
F4	M41	M42
F5	M51	M52
F6	M61	M62	M63
F7	M71	M72	M73

. According to Equation (1), these 19 means make the designers able to generate 864 concepts design. However, a big part of these combinations is not suitable for manufacturing and form final products. Therefore, sub-functions’ means must be reduced to save designers time, resources, and to introduce a few concepts design with high-quality attributes. Based on this purpose, the current technique is applied to realize the purpose of this product morphological chart refinement, and the application procedures with steps shown in Figure 2.

4.1. Product Quality Attributes (QAs) Specification

For this transmission device design case, product features’; performance, cost, novelty, and abundancy attributes are represented by QA1, QA2, QA3, QA4. In order to refine the conceptual design morphological chart, calibration proceed between the sub-functions’ means regarding a single suit of N = 9 8 7 6 5 4 3 2 numerical scales and that in accordance with whist game strategies.

As the number of selected QAs determine the tricks’ number, thus in this case every calibration deal contents four tricks. Therefore, every two competitors (M) compete in total “4” points in each calibration deal.

4.2. Numerical Scales Calibration and Numerical Values (Nv) Modelling

In order to model the numerical values (Nv) of the sub-functions means (M1, M2, M3) of product feature (F1), calibration proceed in binary between these potential sub-functions’ means. Therefore, the calibration proceeds for M1 vs. M2, and then for M1 vs. M3 as following:

M1 vs. M2

[9 6 5 3] vs. [8 7 4 2]

Obviously, if M1 starts with 9, M2 will react with 2, which means the first trick going to be scored by M1. Then M1 may manipulating with 3, so M2 able to score the second trick with 4, as well as able to score the rest two tricks possibly. In the case M1 droop 6 or 5, then M2 must react with 8 or 7 and score this one, and may manipulate with 4 in the third trick. In this time, M1 can score the third trick with 6 or 5 and lose the fourth trick. As a result, these two sub-functions’ means numerical values obtain as following:

M1 numerical value;

Nv1 = 1.000 + 0.500 = 1.500

M2 numerical value;

Nv2 = 2.000 + 0.500 = 2.500

For M1 and M3 numerical scales calibration as following:

M1 vs. M3;

[9 8 5 4] vs. [7 6 3 2]

In this around, M1 can drop 9 or 8, when in reaction M2 can drop 3 and 2 numerical scale, thus absolutely M1 able to score these two tricks. However, M2 can score the last two tricks with 7 and 6 numerical scales. As a result, these two sub-functions’ means numerical values obtain as following:

M1numerical value;

Nv1 = 2.000

M2 numerical value;

Nv2 = 2.000

Because of limitations on the length of this article, the numerical scales distribution, beside calibration modelling processes for; [(M21 vs. M22), (M21 vs. M23), (M21 vs. M24), (M31 vs. M32), (M41 vs. M42), (M51 vs. M52), (M61 vs. M62), and (M71 vs. M72)] are omitted. Nevertheless, the numerical values of these sub-functions’ means are listed directly on

Table 3. Sub-functions means (M) with QAs numerical scales and M numerical values.

	F	M	Numerical Scales of QAs				Nv
Productconceptual design	F1	M11 M12	9 8	6 7	5 4	3 2	1.500 2.500
		M11 M13	9 7	8 6	5 3	4 2	2.000 2.000
	F2	M21 M22	7 9	4 8	3 6	2 5	1.000 3.000
		M21 M23	8 9	5 7	4 6	2 3	1.500 2.500
		M21 M24	8 9	7 6	4 5	2 3	1.500 2.500
	F3	M31 M32	9 8	7 5	6 4	3 2	2.500 1.500
	F4	M41 M42	8 9	7 6	5 4	2 3	3.000 1.000
	F5	M51 M52	9 8	7 6	4 5	2 3	2.250 1.750
	F6	M61	7	5	4	3	1.000
		M62	9	8	6	2	3.000
	F7	M71	9	8	7	2	3.000
		M72	6	5	4	3	1.000

. Furthermore, numerical values of Mx and My with four QAs numerical scales for 50 cases are listed on

Table 4. Four QAs numerical scales modelling with M numerical values.

Item	X-Numerical Scales of QAs	Y-Numerical Scales of QAs	X-Numerical Values	Y-Numerical Values
01	9 8 7 6	5 4 3 2	4.000	0.000
02	9 8 7 5	6 4 3 2	3.500	1.500
03	9 8 7 4	6 5 3 2	3.000	1.000
04	9 8 7 3	6 5 4 2	3.000	1.000
05	9 8 7 2	6 5 4 3	3.000	1.000
06	9 8 6 5	7 4 3 2	3.000	1.000
07	9 8 6 4	7 5 3 2	2.000	2.000
08	9 8 6 3	7 5 4 2	2.000	2.000
09	9 8 5 4	7 6 3 2	2.000	2.000
10	9 8 5 3	7 6 4 2	2.500	1.500
11	9 8 4 3	7 6 5 2	2.000	2.000
12	9 7 6 4	8 5 3 2	2.500	1.500
13	9 7 6 3	8 5 4 2	2.500	1.500
14	9 7 5 4	8 6 3 2	2.500	1.500
15	9 7 5 3	8 6 4 2	2.500	1.500
16	9 7 4 3	8 6 5 2	1.500	3.500
17	9 6 5 4	8 7 3 2	3.000	1.000
18	9 6 5 3	8 7 4 2	2.500	1.500
19	9 6 4 3	8 7 5 2	1.000	3.000
20	8 7 6 5	9 4 3 2	3.000	1.000
21	8 7 6 4	9 5 3 2	2.500	1.500
22	8 7 6 3	9 5 4 2	2.500	1.500
23	8 7 6 2	9 5 4 3	2.125	1.875
24	8 7 5 4	9 6 3 2	2.000	2.000
25	8 7 5 3	9 6 4 2	2.000	2.000
26	8 7 5 2	9 6 4 3	2.000	2.000
27	8 7 4 3	9 6 5 2	1.875	2.125
28	8 7 4 2	9 6 5 3	1.750	2.250
29	8 7 3 2	9 6 5 4	1.500	2.500
30	8 6 5 3	9 7 4 2	1.750	2.250
31	8 6 5 2	9 7 4 3	1.500	2.500
32	8 6 4 2	9 7 5 3	1.500	2.500
33	8 6 3 2	9 7 5 4	1.500	2.500
34	8 5 4 3	9 7 6 2	1.500	2.500
35	8 5 4 2	9 7 6 3	1.500	2.500
36	8 5 3 2	9 7 6 4	1.500	2.500
37	7 6 5 4	9 8 3 2	2.000	2.000
38	7 6 5 3	9 8 4 2	1.750	2.250
39	7 6 5 2	9 8 4 3	1.500	2.500
40	7 6 4 3	9 8 5 2	1.500	2.500
41	7 6 4 2	9 8 5 3	1.500	2.500
42	7 6 3 2	9 8 5 4	1.250	2.750
43	7 5 4 3	9 8 6 2	1.000	3.000
44	7 5 4 2	9 8 6 3	1.000	3.000
45	7 5 3 2	9 8 6 4	1.000	3.000
46	7 4 3 2	9 8 6 5	1.000	3.000
47	6 5 4 3	9 8 7 2	1.000	3.000
48	6 5 4 2	9 8 7 3	0.875	3.125
49	6 5 3 2	9 8 7 4	0.750	3.250
50	6 4 3 2	9 8 7 5	0.500	3.500

. This table contains the numerical values from calibration between two sub-function means (Mx and My) with four QAs numerical scales. In this table, authors modelled eight (2, 3, 4, 5, 6, 7, 8, 9) numerical scales in different probabilities of these numerical scales’ distribution between Mx and My. Of course, the calibration between Mx and My proceed in accordance with the conventional whist game strategies.

4.3. The Calibration Results and Numerical Values Analyses

From Table 3, sub-functions’ means M11 and M12 numerical values are 1.500 and 2.500 respectively, it is thus clear that M11 can be removed against M12. On the other side, M11 and M13 have 2.000 and 2.000 numerical values. Since M11 and M13 numerical values are the same, therefore M13 can be removed with M11. As a result, M12 is the most promising solution for F1.

For F2, (1.000–3.000), (1.500–2.500), and (1.500–2.500) are the numerical values of (M21 vs. M22), (M21 vs. M23), and (M21 vs. M24) respectively. These show, the necessity of excluding M21 which has the weakest numerical value. Sequentially, the F2 solution can be M22, M23, or M24.

But for farther refinement, a new distribution for numerical scales followed by calibration made for (M22 vs. M23) and (M22 vs. M24) is done, corresponding to; (9 8 5 4 vs. 7 6 3 2) and (8 7 5 4 vs. 9 6 3 2), and produced (2.750–1.250) and (2.000–2.000) numerical values respectively. This pointed out that in compare with M22 numerical value, M23 numerical value is the smaller one, while M24 numerical value is equivalent to M22 numerical value. Given that, M22 and M24 are the best solution for F2.

For F3, the numerical scales on M31 and M32 generated 2.500–1.500 numerical values, this a conclusion that M31 is the optimal solution for F3. The same for F4, M41 is most promising means clearly, when M51 is the best choice for F5.

Likewise, calibration modelling for the sub-functions means (M61 vs. M61) and (M71 vs. M72) produced numerical values as shown in Table 3. Accordingly, the most promising sub-functions means for F6 and F7 are M62 and M71 respectively.

Finally, after these series of calibration between sub-functions means (M) numerical scales with the refinement made for the original conceptual design morphological chart which contains 19 possible solutions for 7 sub-functions (F), the refined morphological chart of the transmission device conceptual design just contains 8 solutions for the 7 sub-functions

Table 5. Conceptual design refined morphological chart of the transmission device.

F	M
1	M12
2	M22	M24
3	M31
4	M41
5	M51
6	M62
7	M71

.

Overall, in comparing with the original morphological chart, it is thus clear that just two concepts designs (i.e., 1* 2* 1* 1* 1* 1* 1 = 2) can be generated via the transmission device conceptual design refined morphological chart. This comparation result indicates that there was significant difference between the number of concepts design which combined the original morphological chart (864) and the refined chart

Table 6. The transmission device conceptual design refined morphological chart.

Sub-Functions (F)		Means (M)
1	Driving device	Electromagnetic drive
2	Transfer torque	V-belt transmission	Chain wheel transmission
3	Connecting transmission surface	Square surface
4	Transmission frame layout	Concatenated
5	Install device	Horizontal installation
6	Protect device	Independent motor
7	Place cargo	Positioning slot

. Interestingly, there were also differences in the quality attributes implicit into concepts design generated through the two charts. No doubt, the concepts design combined via the refined morphological chart are more concreted with high quality and combinations.

5. Discussion and Conclusions

In the product conceptual design and development activities, an initial objective of conventional morphological chart is to improve the quality of concepts design. Nevertheless, several studies have shown that designers often face a problem of selecting the better and high-quality concepts design among a huge number of concepts design combinations which resulted due to the big number of sub-functions means (M).

This paper sets out with the aim of reducing the number of sub-functions’ means in morphological chart by a new refinement technique with respect to whist game card “calibration” strategies in order to solve this problem.

This refinement technique, applying calibration between the numerical scales (cards) distribute in every binary of means related for one sub-function regarding product quality attributes (QAs) to obtain a comprehensive numerical value for each sub-function means. Based on numerical values, a refinement proceeds for the means to exclude the sub-functions’ means with weak numerical values.

The current refinement technique was implemented to conceptual design original morphological chart of transmission device which contains nineteen principles solutions corresponding to seven sub-functions. The results of this technique application approved the capability of this technique to reduce the possible sub-functions means in the morphological chart to more acceptable and small contents number of sub-functions’ means in the chart. There was a significant difference between the two morphological charts sub-functions’ means number, since the refined conceptual design morphological chart of the transmission device just contains eight sub-functions’ means. Therefore, through the refined morphological chart, there are just two concept designs that can be combined instead of generating 864 concepts design combinations from the original morphology. Moreover, the concept designs are generated via the refined chart with high-quality design solutions, that because of precision selection of the sub-functions’ means regarding QAs.

Likewise, the current technique considered an appropriate design tool for satisfying product stakeholders’ different quality attributes (QAs) requirements such as; cost, performance, and highly modular mature technology etc. In addition to product designers, product stakeholders can also participate in the QAs selection and numerical scales distribution.

Therefore, there are two primary contributions of this paper. First, to refine sub-functions’ means and narrow down conceptual design morphological chart frame to reduce the number of generated concepts design from the chart. Second, to introduce a highly quality concepts design combinations which should implicit product designers’ and stakeholders’ quality attributes requirements.

Despite the potential applications and primary contributions listed above, however the current technique face some limitations points which represent a future’s work points. First, since refinement apply to sub-functions’ means within morphological chart that were selected through the previous design stage, designers may ignore to select some means with high quality attributes intentionally or reasonably. Thus, a further study with more focus on integrate this refinement technique with other early conceptual design methods (e.g., QFD) to obtain more information about consumers’ quality attributes requirements and priorities is therefore suggested. Second, the current refinement technique works accurately for simple or small size mechanical product system (e.g., the application design case morphological chart contains just seven sub-function). Therefore, possible extension is to develop the current technique to be useable for complex mechanical design problems morphological chart refinement. In addition, a highly precision method which assists designers and product stakeholders in selection of suitable QAs for each case individually to make potential refinement to its conceptual design morphological chart should be developed in the future.