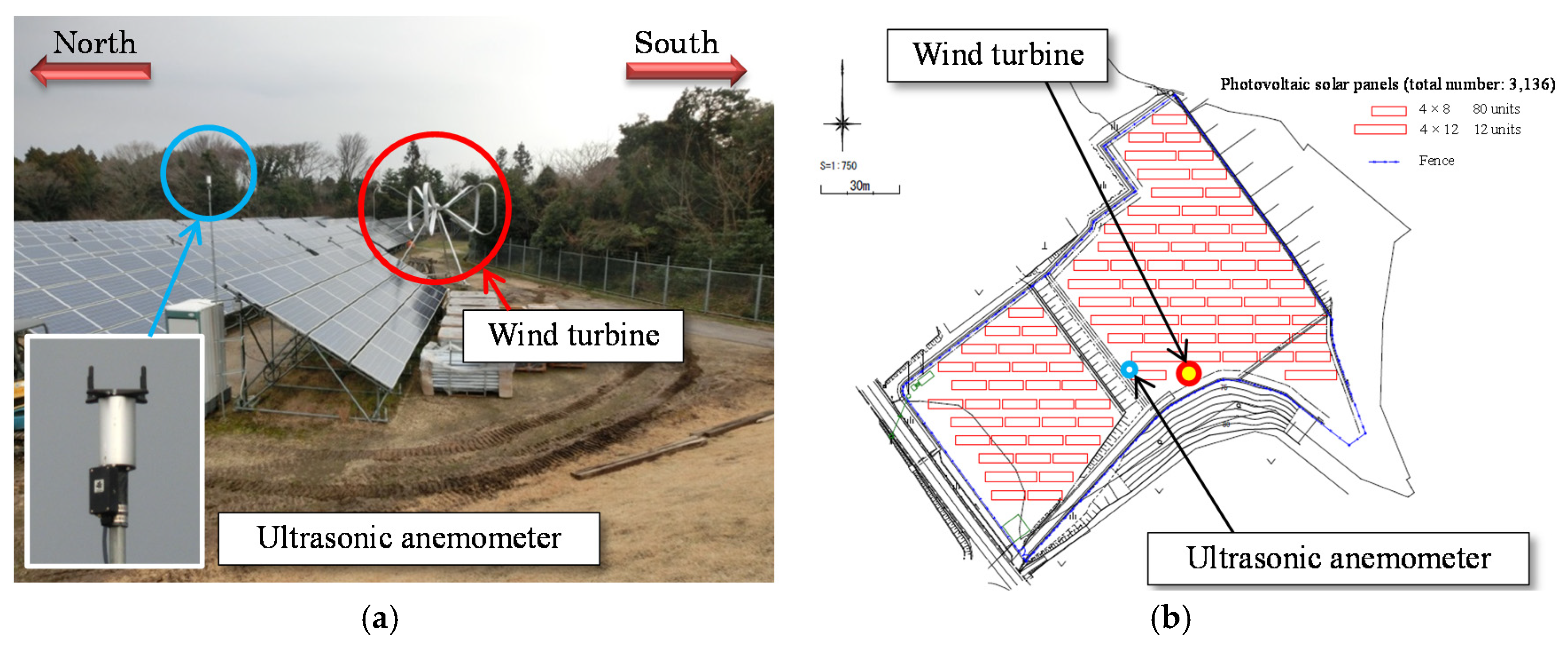
This section includes the following descriptions: the specifications and the characteristics of the wind-turbine rotor (
Section 2.1), the mechanism, final design, and movement prediction of the OCS (
Section 2.2), the geared generator and the performance prediction of the BWT (
Section 2.3), the power-generation control system (
Section 2.4), and the site of the experiments (
Section 2.5). It should be noted that the prediction described in
Section 2.3 about the BWT’s performance is a little different from that reported previously for the first experiment series of forcible rotations (implementation: 22 December 2016) [
8] because of modifications to the parameters used in the prediction code in addition to the alteration of the design of the OCS.
2.1. Wind-Turbine Rotor
Figure 1 shows the prototype of the BWT equipped with an OCS for five looped blades. Two photographs in
Figure 1 were taken in the second experiment series of forcible rotations (implementation: 25 July 2017); the left-hand photograph (a) shows the no-twist state, in which the main straight parts of blades are in the vertical condition, and the right-hand photograph (b) shows the twist state, in which the twist angle
η is 30 degrees. Those photographs are used in
Figure 1 in order to illustrate the main feature of the wind turbine developed in this study, even though the second experiment series of forcible rotations was not successful because a great decrease in rotational speed and large time lag were observed during the process of the twisted blades returning to the original no-twist state. In the forcible rotation experiments, the turbine rotor was equipped with an induction motor instead of a generator. The diameter of the rotor
D was 7.0 m and the height
H was 2.7 m. The specification of the BWT rotor is given in
Table 1.
The OCS was located at the rotor center, or hub position, of the wind turbine and the height from the ground level was 4.3 m. As mentioned before, the concept of development was “cost reduction by large rotor and small generator” and the goal was cost reduction by enlarging the turbine rotor using cost-effective extruded aluminum blades and, on the other hand, by adopting a small-capacity generator and other electric devices with small capacity, which tend to become expensive depending on their capacity. As mentioned, cost reduction could also be contributed by the mechanical OCS, since it can increase the capacity factor by continuing the electric generation during any strong wind conditions without stopping the wind turbine.
The prototype of the BWT was originally planned to be installed on the top of a high-rise building to obtain large wind energy. All the parts of the BWT, including the blades in a disassembled state, can be carried to the highest floor by using the elevators of the buildings. It is one of the features of the prototype that a rope made of high tenacity polyarylate fiber (φ10 mm, breaking load: 53.9 kN) is inserted into each blade and all the five ropes are connected each other at the hub of rotor in order to prevent the scattering of fragments of broken blades in case of damage to the turbine rotor.
Because the BWT structure enables the generator to be installed close to the center of the rotor, the rotational axis of the wind turbine becomes short. The length between the rotor center and the first bearing is 0.158 m in the case of the prototype.
As shown in
Figure 1, the stand consists of three legs which support the stand-top part located just below the hub of the rotor. The tripod structure gives the stand robustness so as not to vibrate against the exciting force of the rotor. Each base plate of the legs was anchored to the ground by three ground screws (length: 1.6 m) instead of an expensive concrete foundation.
2.2. Over-Speed Control System (OCS)
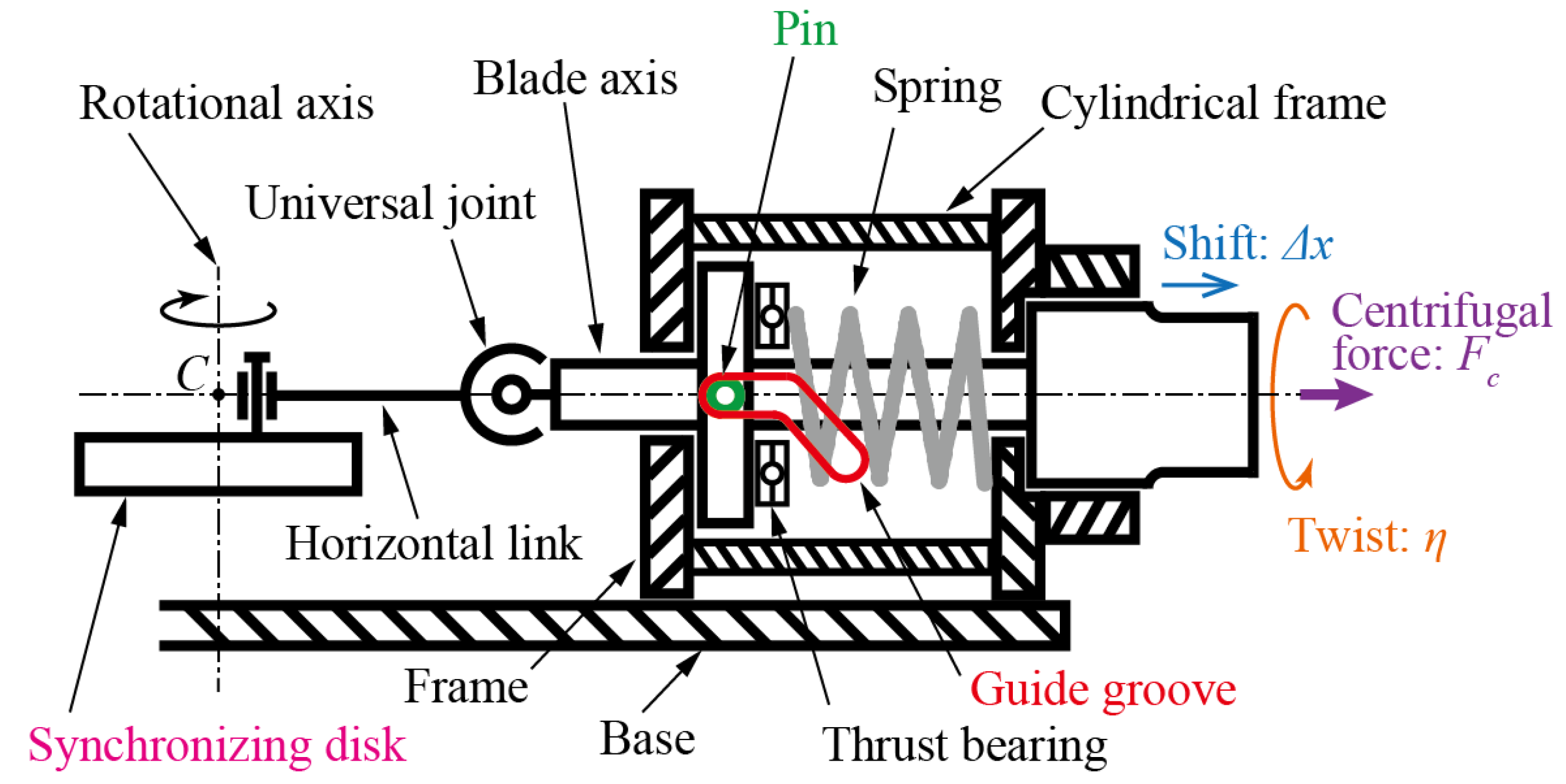
Figure 2 is a photograph of the improved OCS. Five units are connected to a synchronizing disk located at the center of rotor hub by five links to obtain the same movements for all the blades. Universal joints configure the link portion and are important parts for realizing the blades’ twist. The universal joints used in the previous experiments were commercial products and were made of high-strength zinc alloy. However, due to the stress levels and the lack of strength, they were exchanged by trial products (Matsumura Seiki, Inc., Tottori, Japan) made of stainless steel.
The schematic diagram of an OCS unit is illustrated in
Figure 3. Centrifugal force
Fc acting on a blade moves a blade axis (max. diameter: 90 mm, min. diameter: 50 mm) inside a cylindrical frame in the radial direction (
x direction). By this movement, a pin (
φ20 mm) jutting out on both sides from the blade axis moves along a pair of guide grooves, each of which consists of a straight portion and a helical portion.
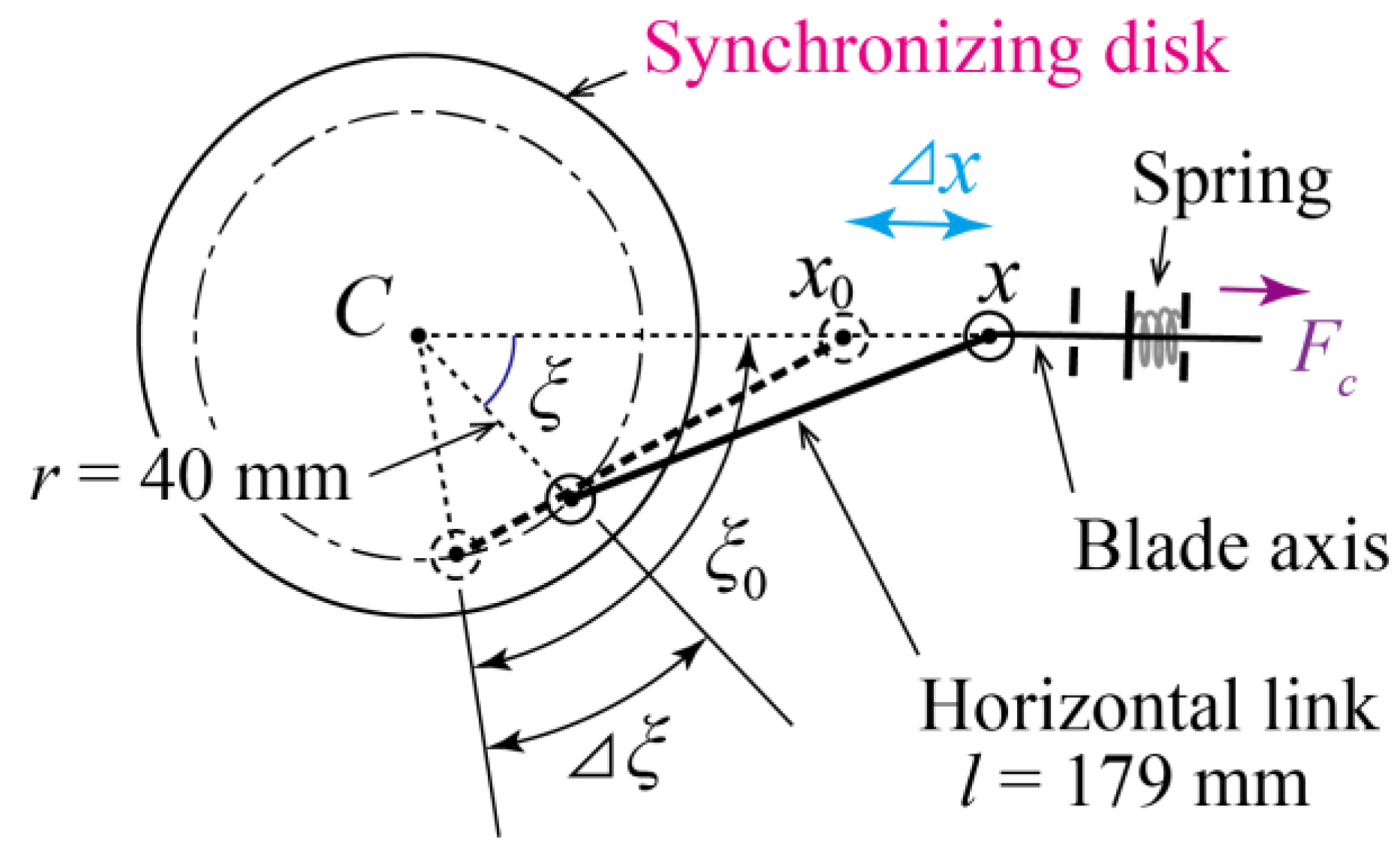
Figure 4 is the schematic diagram to illustrate the relation between the rotational angle Δ
ξ of the synchronizing disk and the displacement Δ
x of the blade axis, which is the same as the shrinkage of a spring from the initial length. In the OCS, the length of each spring is 115 mm under the initial condition, or stationary condition, of the turbine rotor, and the centrifugal force
Fc is equal to zero in that state. In the initial condition, the distance between the pivot of a universal joint and the center
C of the synchronizing disk is
x0 = 184.5 mm; the angle between the line segment (
r = 40 mm), which connects the center
C of the synchronizing disk and one end of the horizontal link (length:
l = 179 mm), and the direction of the blade axis (
x direction) is
ξ0 = 75.89°.
Until the third experiment series of forcible rotations (implementation: 31 August 2017), the natural length of the springs was 115 mm. The natural length of the springs used in the fourth experiment series of forcible rotations (implementation: 15 December 2017) was 125 mm in order to generate an initial restoring force. In advance, the springs were compressed by 10 mm so as to be the initial length of 115 mm in the stationary condition of the rotor. This improvement eliminates the lack of stroke length of blade axes and contributes to diminishing the inclination of the helical portion of guide grooves. The constant of springs used in the final experiment-series was k = 548 N/mm.
The rotational angle Δ
ξ [rad] of the synchronizing disk and the displacement Δ
x [mm] of the blade axis are given by the following Equations, from (1) to (3):
The relation between the displacement (shrinkage) Δ
x [mm] of a spring from the initial length and the restoring force
Fs [N] is expressed by Equation (4):
where
Fp is the initial restoring force by the pre-compression of the spring. Equation (4) means that a pin does not move along the guide grooves until the centrifugal force acting on a blade exceeds 5480 N.
Considering the displacement Δ
x, the centrifugal force
Fc acting on a blade when the turbine rotor revolves at an angular velocity ω is given by the following Equation (5):
where
mb is the total mass of a blade including the blade axis, connection parts, bolts, nuts, and so on.
xb is the
x-coordinate of the center of mass of the blade based on the rotational center
C under stationary condition.
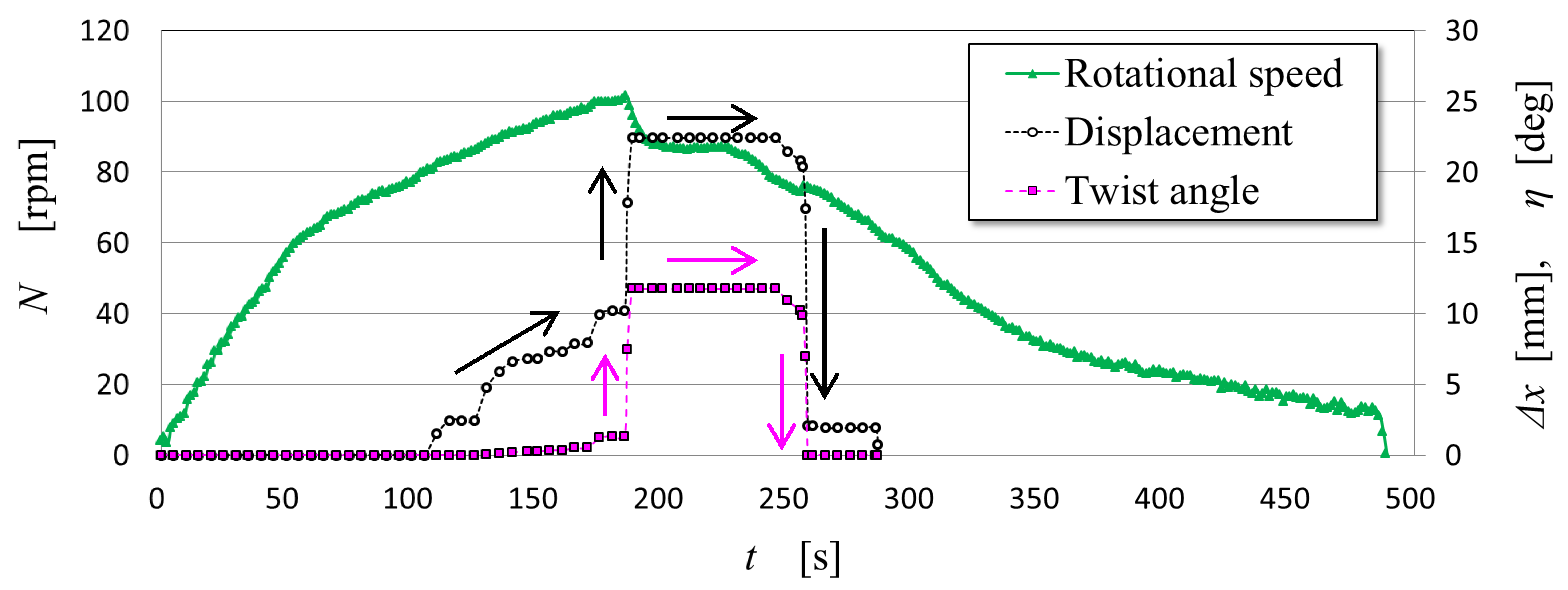
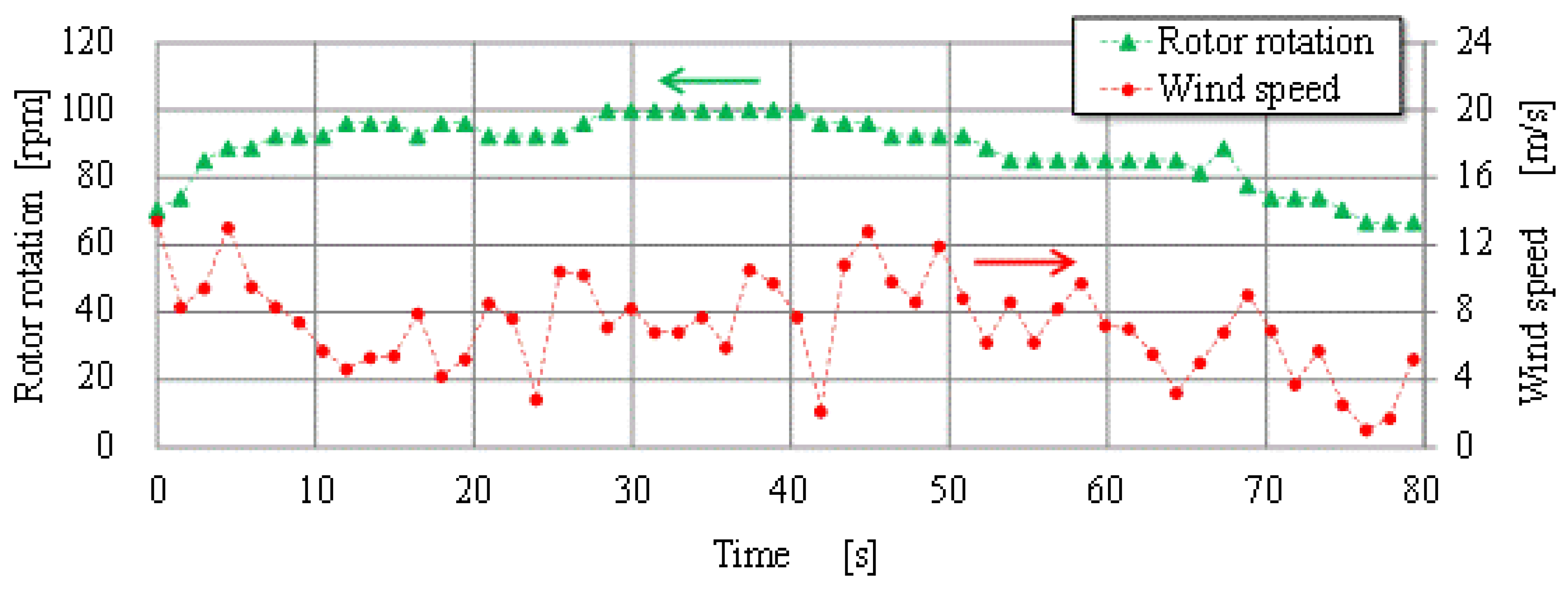
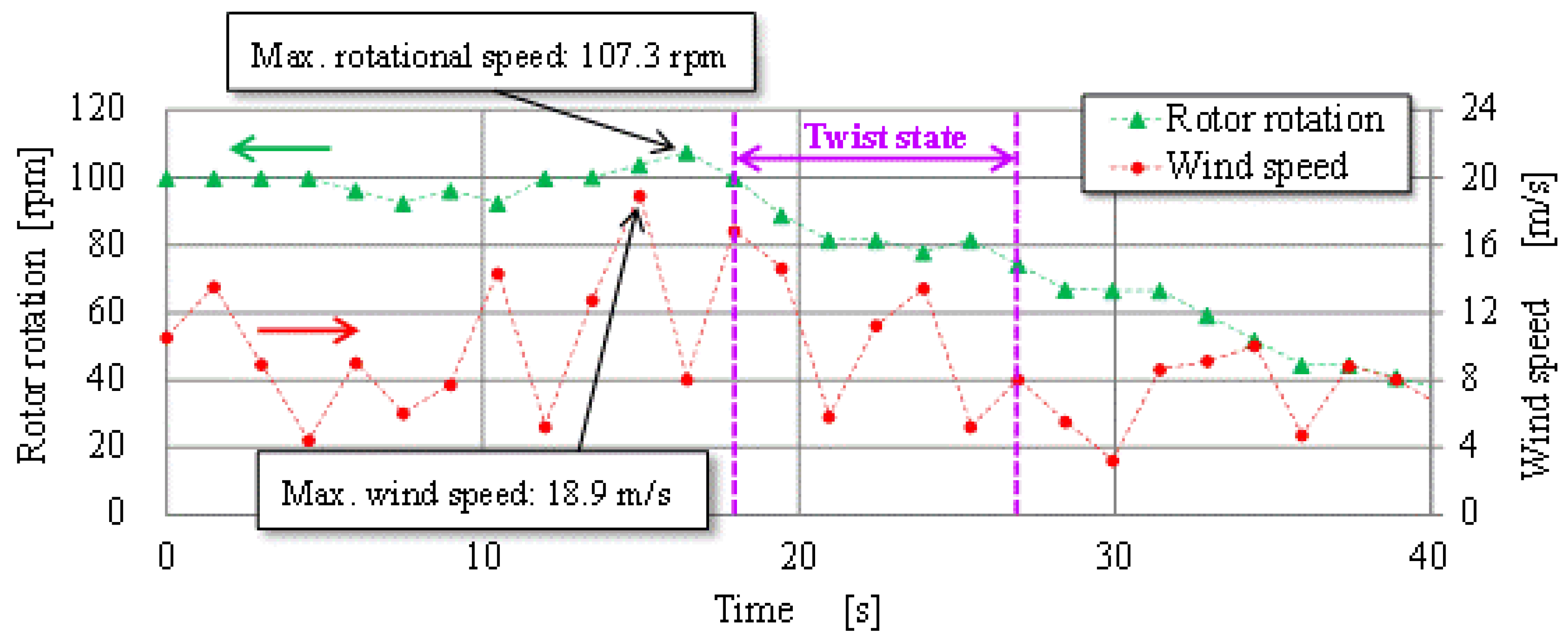
Since the aerodynamic force acting on the blades in the radial direction was predicted to be much smaller than the centrifugal force when wind speed was not very large, the OCS was designed by considering only the centrifugal force until the third experiment series of forcible rotations. However, as shown in
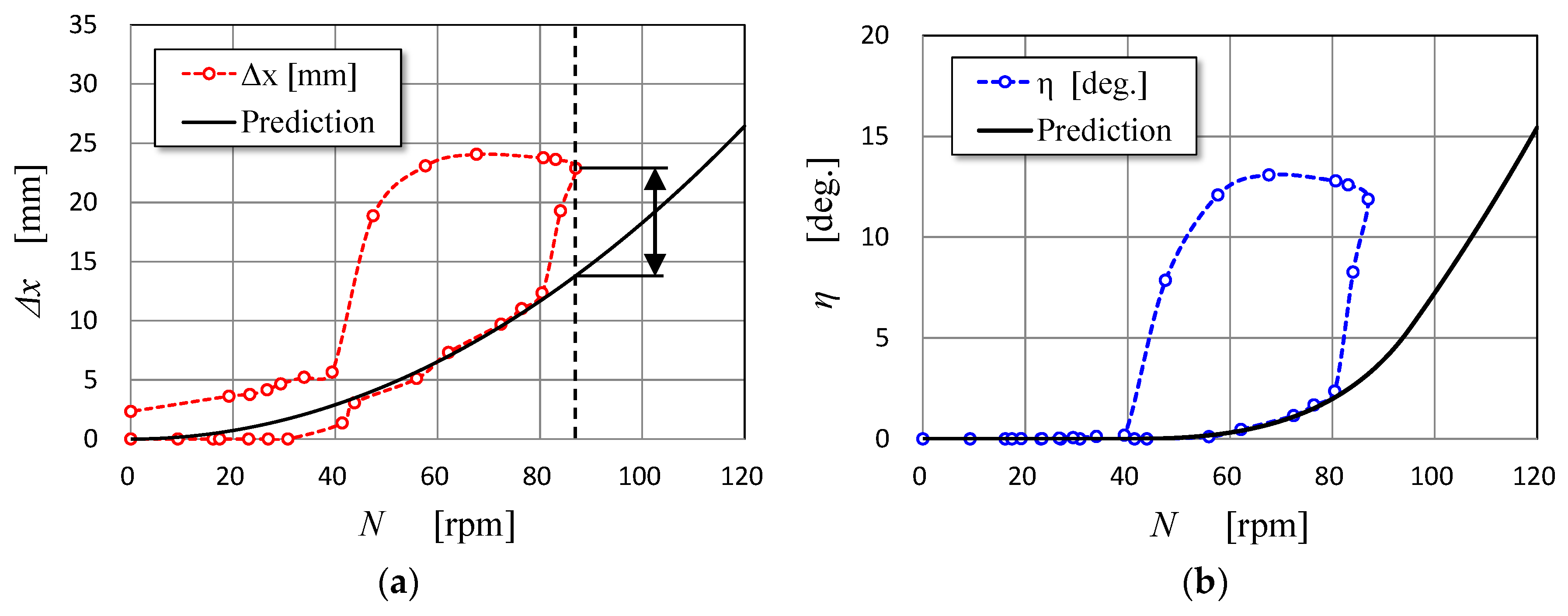
Figure 5, which indicates the observed results of the third forcible rotation experiments, the behavior of the blade-axis displacement Δ
x was different from the prediction obtained by considering only the centrifugal force at the conditions of the rotor rotational speed of 80 rpm or more, when the blades were greatly twisted. This means the existence of large force in radial direction except for the centrifugal force, but the cause of this phenomenon has not been made clear yet. As shown in
Figure 5a,b, it is clear that the force in question is produced in association with the blade twist. Large twist moment might be generated by some causes, such as the deformation of the blades or the unexpectedly large distance between the aerodynamic center and the supporting point of a blade.
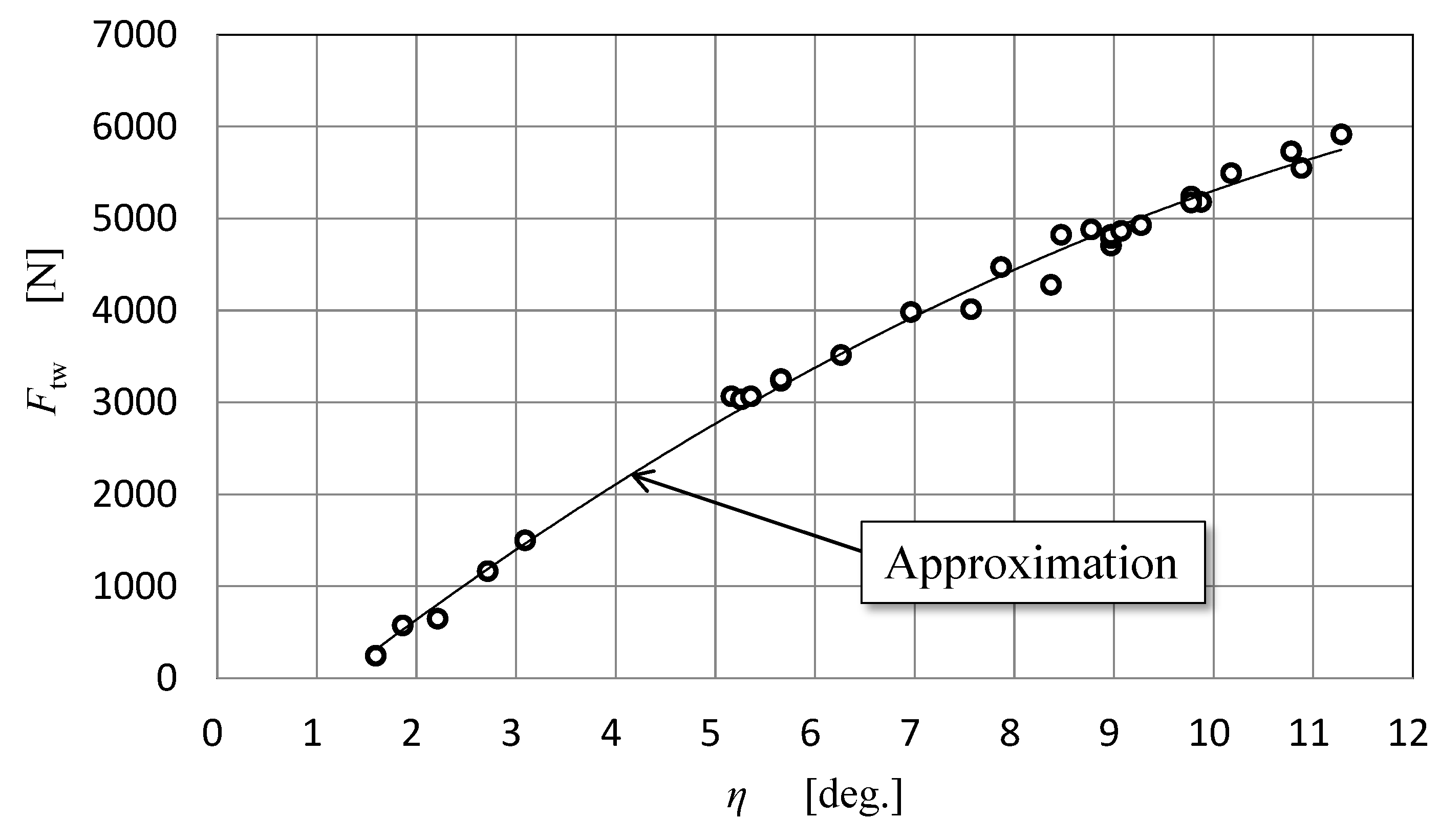
Figure 6 shows the relations, which were obtained from the selected data in the third experiment series of forcible rotations, between the radial force
Ftw deprived of the centrifugal force and the twist angle
η. A line in black in
Figure 6 is the approximation curve, which is expressed by Equation (6):
which is valid at
η > 1.211° and when
η is less than 1.211° the force in question is assumed to be zero (
Ftw = 0).
Under the condition of constant rotor rotation, the equilibrium of forces acting on a blade axis in the radial direction is assumed to be
Fc +
Ftw =
Fs. From this assumption, the displacement Δ
x is given as a result of the following Equation:
By using Equation (7), when the shape of a guide groove is given, the displacement Δx and also the twist angle η can be decided for an arbitrary rotor rotational speed N = 30 ω/π [rpm]. Although the force Ftw is a function of η (see Equation (6)), in the calculation process of Δx and η from the stationary state (N = 0; Ftw = 0) with a small interval of rotational speed ΔN, the value of Ftw obtained from the preceding calculation can be substituted for the value of Ftw in the next step of the calculation.
Figure 7 is an illustration of a cylindrical frame with the guide grooves of the final design, with which the pre-compression of springs is applied. Two guide grooves are formed at the positions of the rotational symmetry with respect to the center line of the cylindrical frame. A guide groove has a straight portion (4 mm) and a helical portion. The angle between the center line of the helical portion and the center line of the cylindrical frame is
ζ = 46.73°, when it is considered with an expansion plan. The inclination angle
ζ of the final design becomes small compared to the previous designs of the guide grooves. In addition, the maximum blade twist angle that can be realized by this final design is
η = 18°.
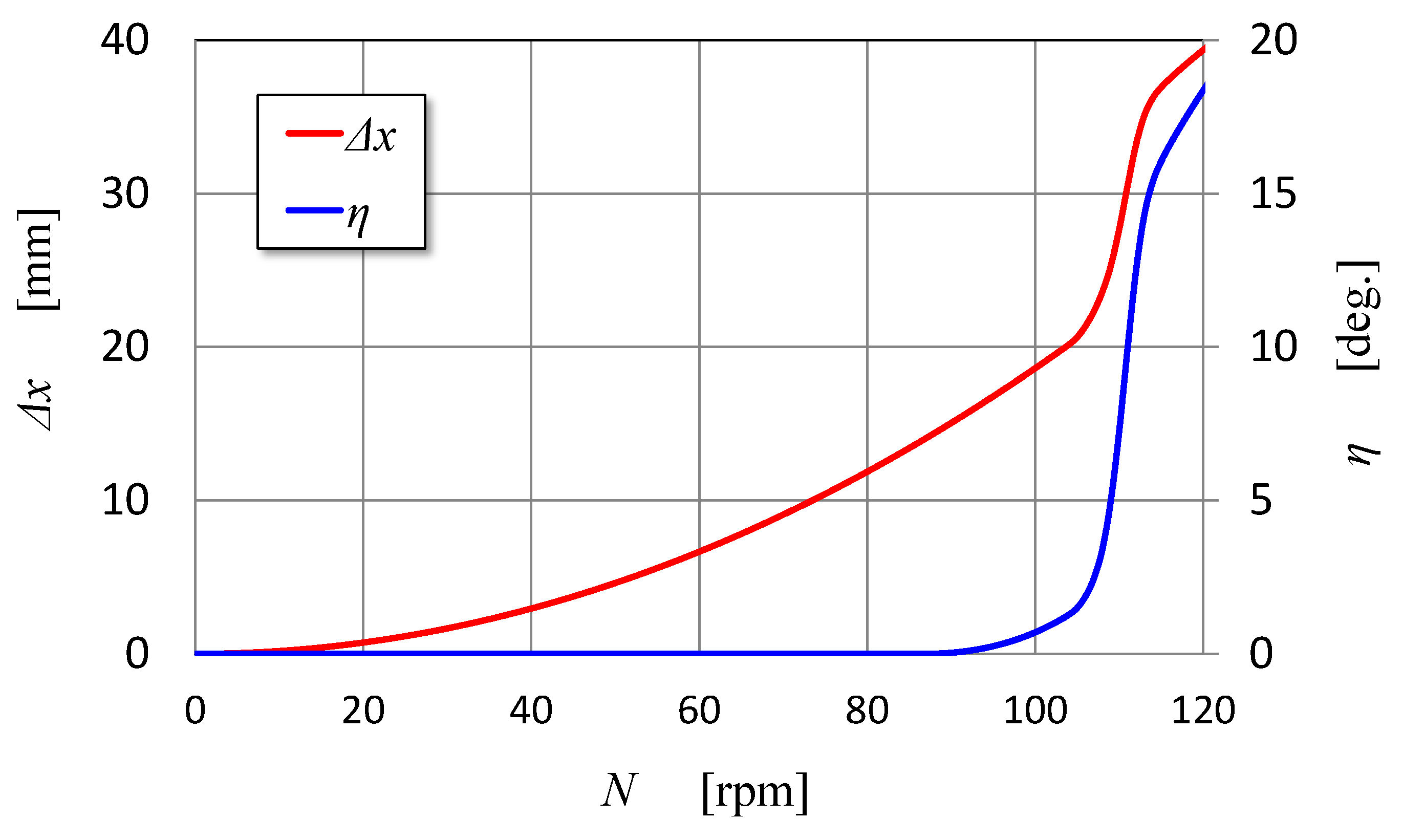
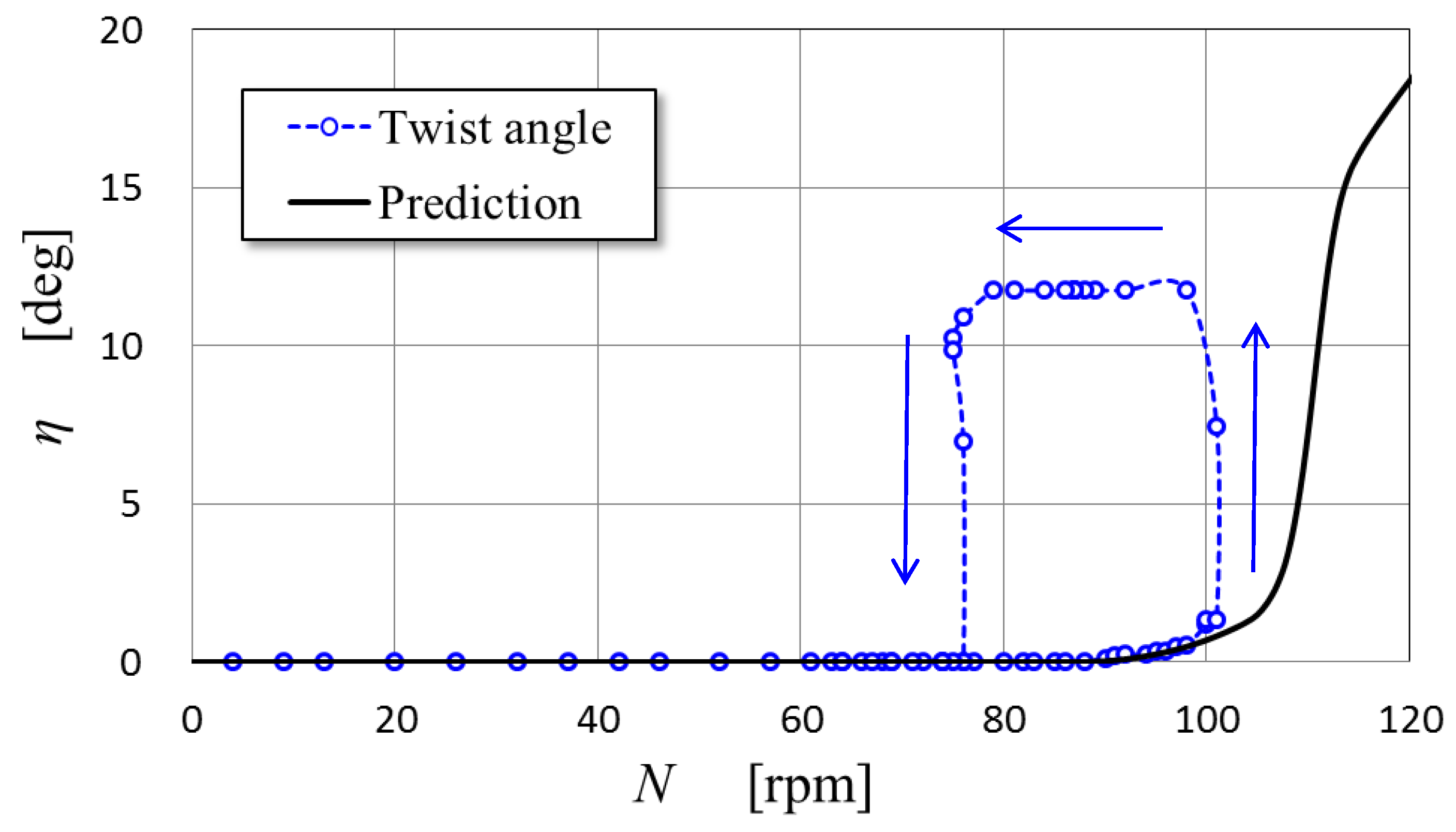
Figure 8 shows the prediction based on the final shape of the guide grooves about the dependence of the displacement and the twist angle on the rotational speed. The prediction shows that the blades begin to be twisted at the rotational speed of around 90 rpm. Since the twist angle becomes large abruptly when the rotational speed exceeds 110 rpm according to
Figure 8, the rated rotational speed of the BWT after this study is assumed to be 110 rpm.
2.3. Generator and Prediction of the Performance of the Butterfly Wind Turbine (BWT)
The generator installed in the BWT is shown in
Figure 9. That is a permanent magnet-type multi-pole generator (SKY Electronics Co., Ltd., Shimanto-cho, Japan, MG450W, 5 kW, 350 rpm, 48 poles) and is coreless and inner rotor type. A speed-increasing planetary gear (Matex Co., Ltd., Yao, Japan, LGU-200, 3:1) is combined with the generator. As shown in
Figure 9, the planetary gear is connected to the bottom of the stand-top part, in which there are three bearings to hold the rotational axis (max. diameter: 90 mm) at the center. The stand-top part has three attachment plates for connection with the tripod legs.
The performance of the wind turbine was predicted by the blade element momentum (BEM) theory [
11] in this study. The rotor of the BWT has a double-blade structure, which means that fluid flowing into the rotor swept area
A has the possibility to intersect the blades four times. Therefore, in the prediction based on the BEM theory, the quadruple-multiple streamtube (QMS) model [
12], which nested the double-multiple streamtube (DMS) model [
13], was used as the flow field model. The flow field was divided into 20 in the height direction and was divided into 180 in the perpendicular direction to the main stream. In the direction of the main stream, the flow is divided into four portions (QMS) or two portions (DMS), depending on the number intersecting the blades. A decrease in rotor output power caused by blade twist was simulated by considering the reduction of the swept area
A and the effective pitch angle
θ [
14]. In the present study, the effective pitch angle caused by blade twist is defined by Equation (8):
where
r is the local radius from a base point in a blade cross section to the rotor rotational axis and
z is the local height of the base point from the equator plane.
The BEM-based prediction needs aerodynamic data of the blade section (NACA 0018). The two-dimensional aerodynamic data of lift and drag coefficients (
CL2d,
CD2d) were prepared from the combination of the data reported by Sheldahl and Klimas [
15] and the data proposed by Kumar et al. [
16] for a low Reynolds number. The data on moment coefficient (
CM2d) around the quarter point of a blade chord was obtained from two-dimensional computational fluid dynamics (CFD) analysis [
17] previously carried out at Tottori University. In order to consider the effects of induced drag, the data correction method reported by Murata et al. [
18] was used in this study. The dynamic stall model proposed by Paraschivoiu based on the modified Gormont model [
12] was also introduced in the prediction.
In the present prediction, from the experiences based on some previous experiments and CFD analyses [
7,
13], the upstream speed of the double-blade structure rotor is corrected by Equation (9):
where
V∞ is the upstream uniform velocity speed and
V∞c is the corrected upstream speed of each streamtube located at an arbitrary local height.
r1 and
r2 are the local radius of outer rotor and the local radius of inner rotor, respectively, at an arbitrary height. The values of
r1 and
r2 vary depending on the height after the blade twist.
σ’in is the local solidity of the inner rotor and is defined by
Bc2/
r2.
B is the number of blades and
c2 is the blade chord length of the inner rotor corresponding to the local radius
r2.
Ff is introduced as a fitting parameter that does not depend on the local height.
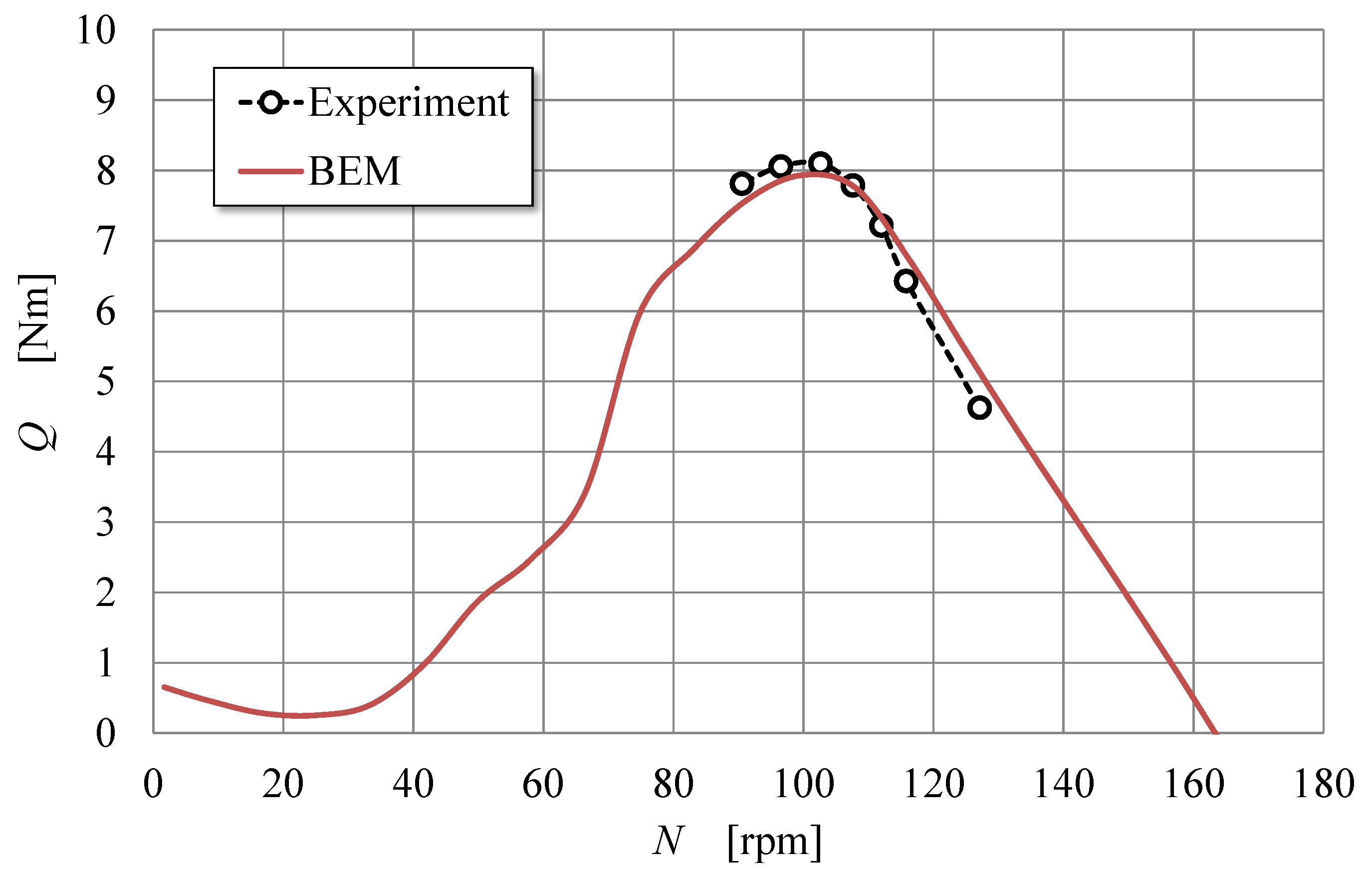
In this study, the tuning of in-house software for the performance prediction was conducted by fitting of the torque curve predicted by the above-mentioned BEM method to the experimental torque curve obtained from the previous generation experiments of a 3 m-diameter BWT with four circular blades (ACBBWT) [
19]. In that process, the experimental power performance was converted to the torque performance by assuming the generator loss of 20%.
Figure 10 is the result of the best fitting, in which the value of the fitting parameter
Ff is 0.4.
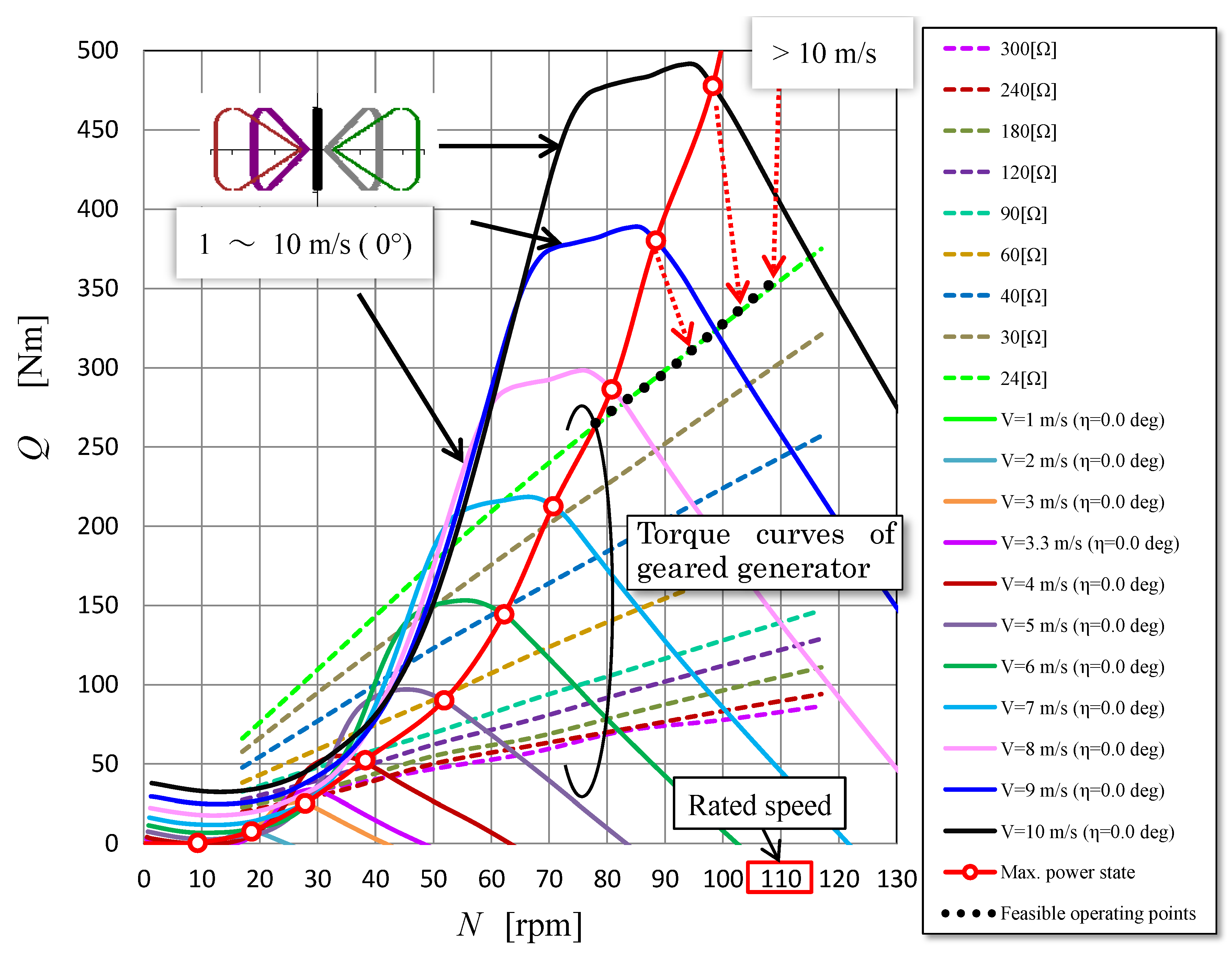
The prediction of torque curves of 7 m-diameter BWT without OCS, i.e., in the no-twist condition, is illustrated at intervals of 1 m/s from 1 m/s to 10 m/s in
Figure 11. The broken lines are the experimentally obtained torque characteristics of the coreless generator (see
Figure 9) combined with the increasing gear (3:1) and they depend on the value of external resistance (24 Ω–300 Ω). Since the horizontal axis of
Figure 11 is indicated by the rotational speed of the turbine rotor, please note that the generator speed increased by the gear is three times as high as the speed indicated by the horizontal axis. A line in red indicates the maximum output conditions at each wind speed. When wind speed is 7 m/s or less, optimum control can be theoretically realized. That is, the output resistance of the generator is controlled so as to reconcile the intersection (operating point) of a rotor torque curve and a generator torque curve to a point on the maximum power curve by changing the pulse width of the output signals of the generator. However, in the case of
Figure 11, the operating point cannot be on the maximum power curve when the wind speed is 8 m/s or more because the maximum current, or torque, of the generator is limited by the allowed smallest external (or output) resistance of 24 Ω. Therefore, in that case, the pulse width modulation (PWM) is performed to get the operating point positioned on the generator torque curve of 24 Ω and to be less than the rated rotor speed of 110 rpm. In general, at the resultant operating point, the output power decreases and the rotational speed increases.
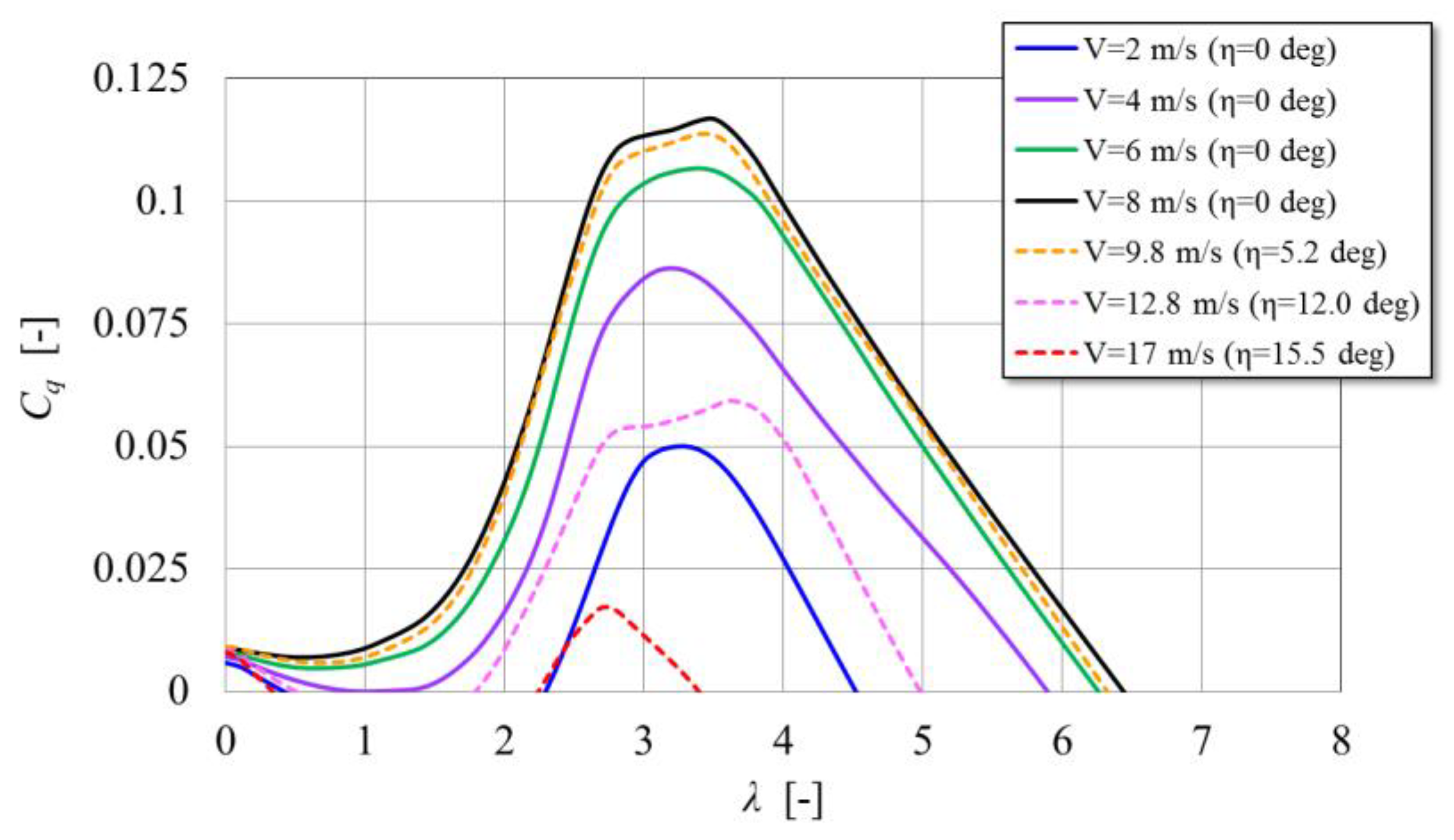
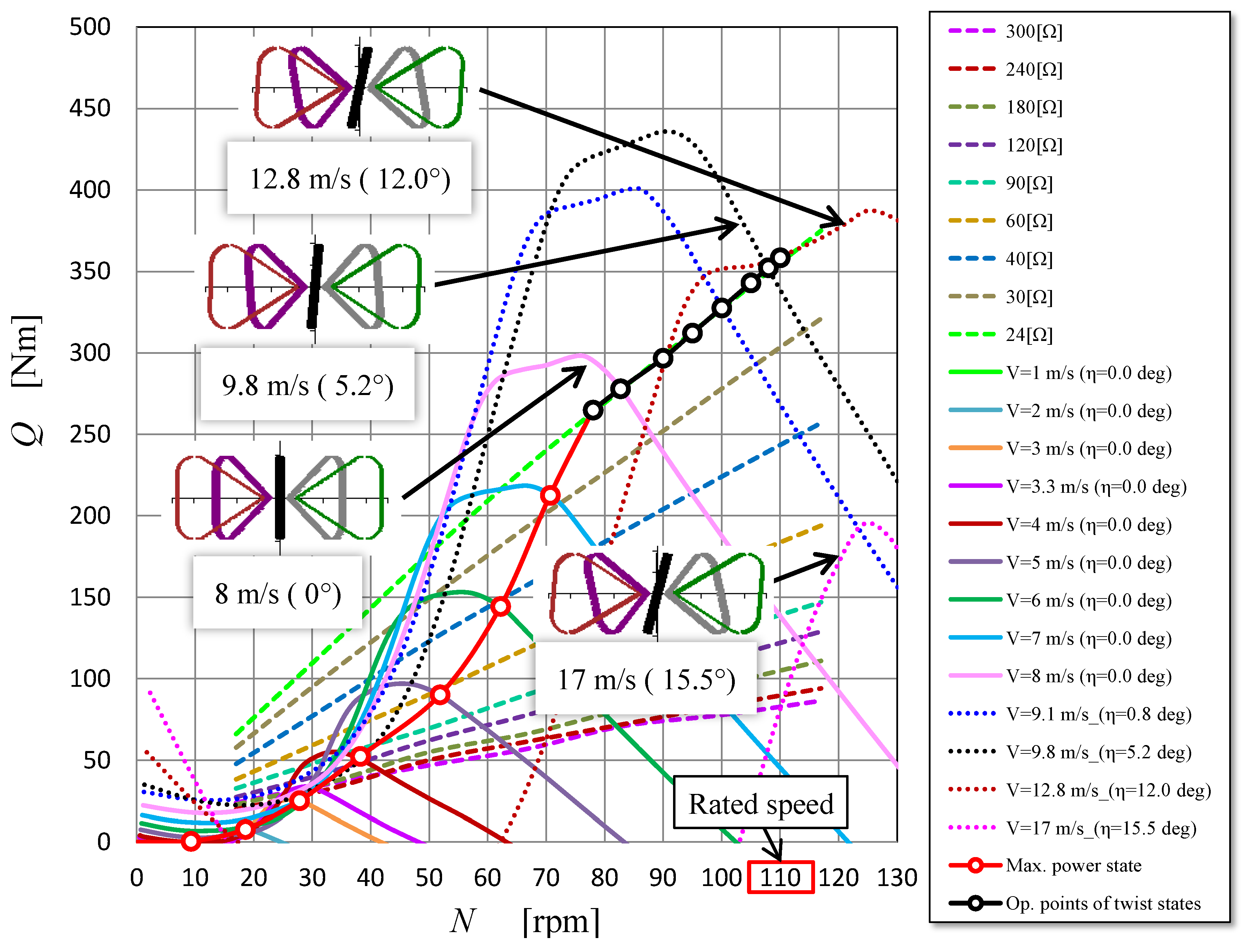
Figure 12 illustrates the predicted torque characteristics of the BWT equipped with the modified OCS. The rotor torque curves when the wind speed is 8 m/s or lower are almost the same as those in
Figure 11, because the blades do not twist at all or the twist angle is very small even if they twist. When the wind speed is 9 m/s or higher, the decrease of maximum torque is predicted because of the blade twist. According to the prediction, in the case of wind speed of 12.8 m/s, the twist angle becomes 12 degrees and the turbine rotor rotates in a condition close to the rated speed. If wind speed is higher than the rated wind speed (about 13 m/s), as in the case of 17 m/s shown in
Figure 12, the rotor torque curve cannot intersect with the generator torque curve of 24 Ω of the control target, because the blades are inclined to a large twist angle (15.5° at 17 m/s) and the maximum rotor torque is greatly reduced. That state means that the turbine rotor cannot rotate the generator due to large aerodynamic resistance and the rotor rotational speed must be reduced. However, if the strong wind over the rated wind speed continues to blow, the turbine rotor is accelerated again after slowing down and obtaining a small twist angle. An increase and decrease of rotor rotation near the rated rotor speed is predicted and an almost constant output power could be continued.
For reference, the non-dimensional torque and power curves of the BWT are shown in
Figure A1 and
Figure A2 of
Appendix A. The maximum power coefficient of 0.415 is predicted in the case of 8 m/s without twist due to less tip loss and arm drag as the features of the BWT.
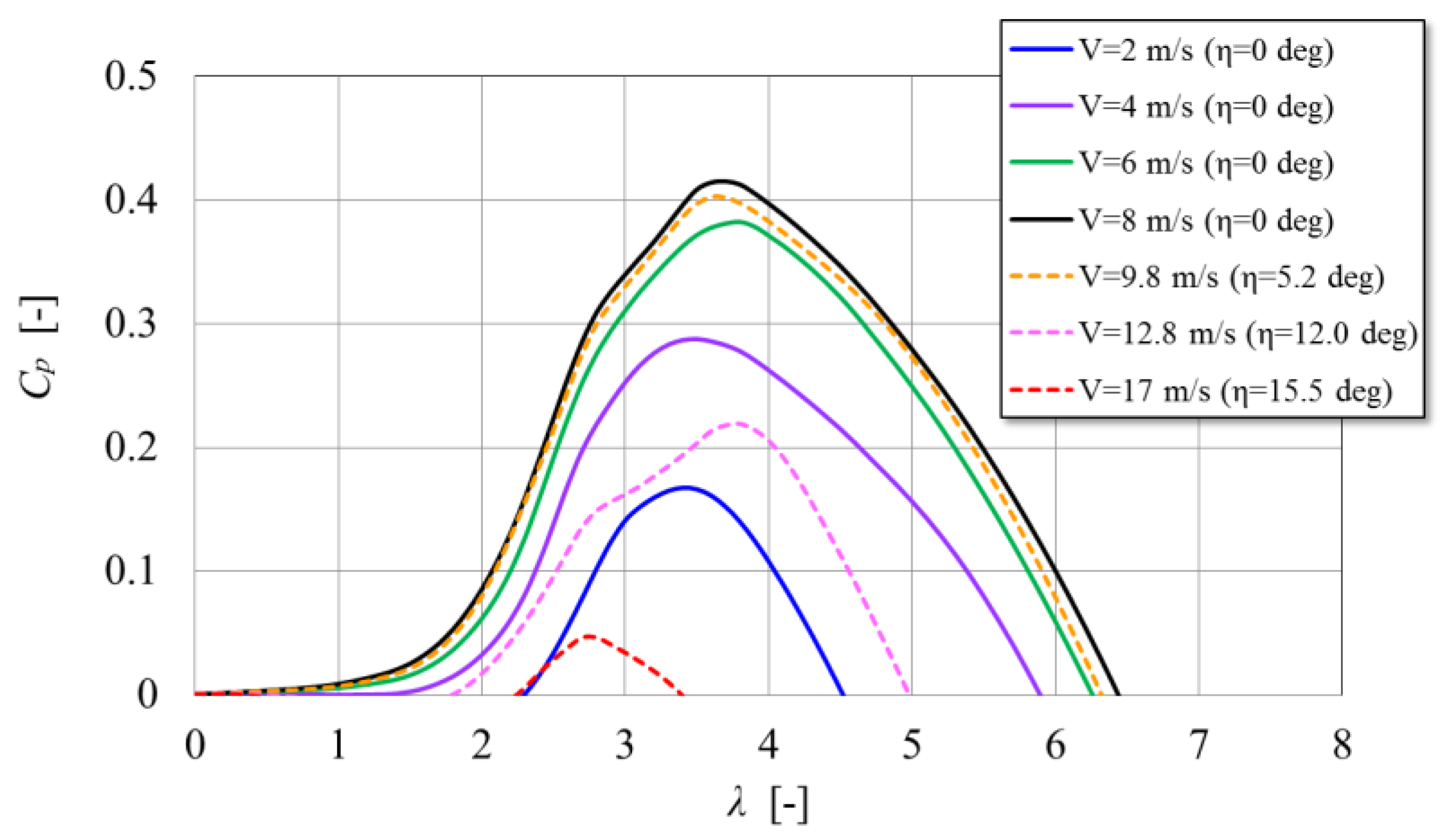
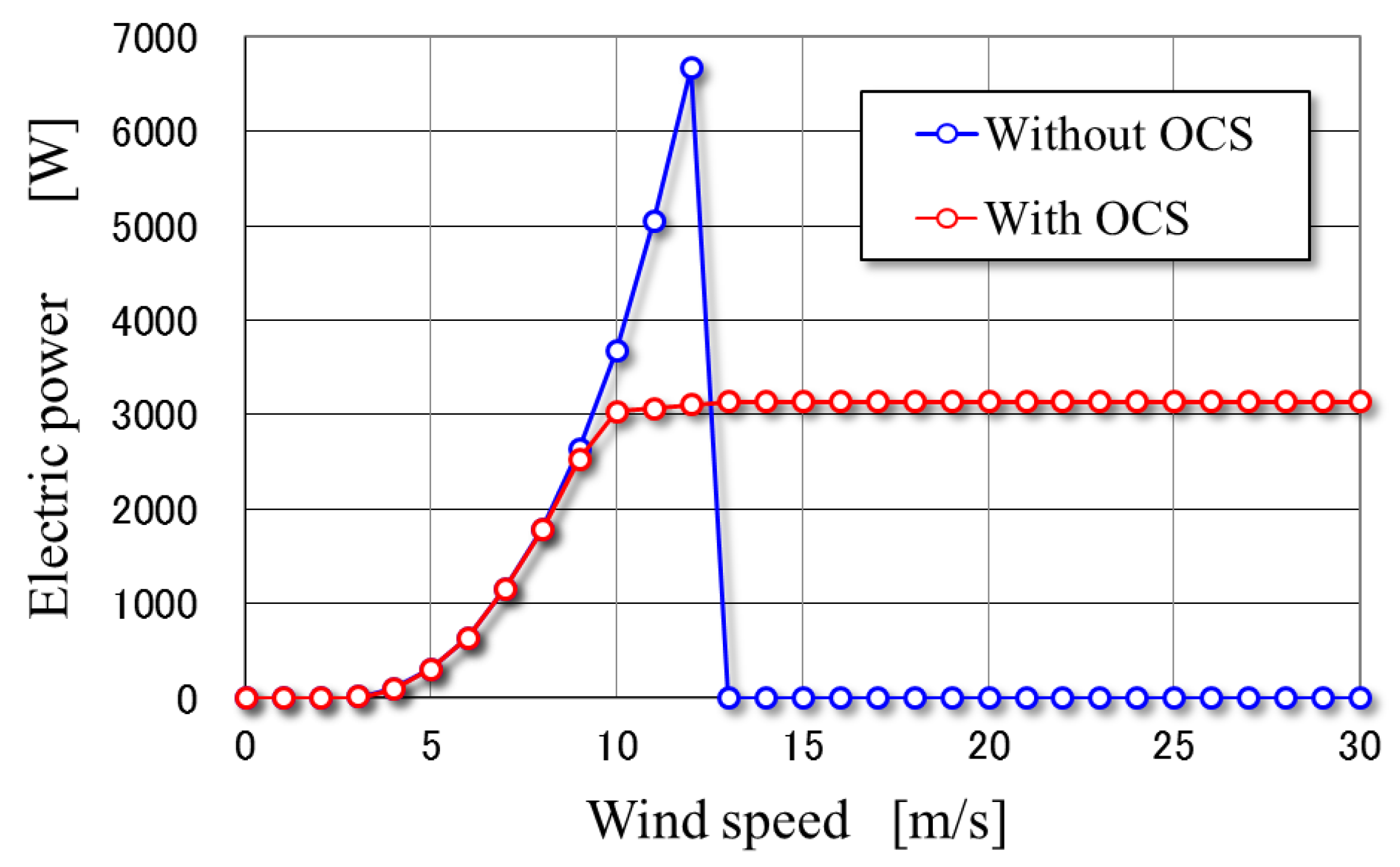
Comparisons between the power curves of the BWT with and without the OCS is shown in
Figure 13, which are calculated based on the torque curves shown in
Figure 11 and
Figure 12. In the case without the OCS, the use of a virtual generator is assumed until the cutout wind speed of 12 m/s (the rated electric power: 6674 W) with a control tracking the maximum power conditions denoted by the line in red shown in
Figure 11. In
Figure 13, the electric power is calculated by considering the total efficiency (e.g., 150 rpm, 60 Ω: 63.6%; 351 rpm, 24 Ω: 76.4%) of the generator and the speed-increasing gear based on the results of preliminary experiments. In the case of the BWT with the OCS, the maximum electric power (the rated electric power: 3145 W) is much smaller than the case of the BWT without the OCS. However, the cutout is not defined theoretically, although the power curve of the BWT with the OCS is not illustrated at the wind condition of 31 m/s or higher in
Figure 13.
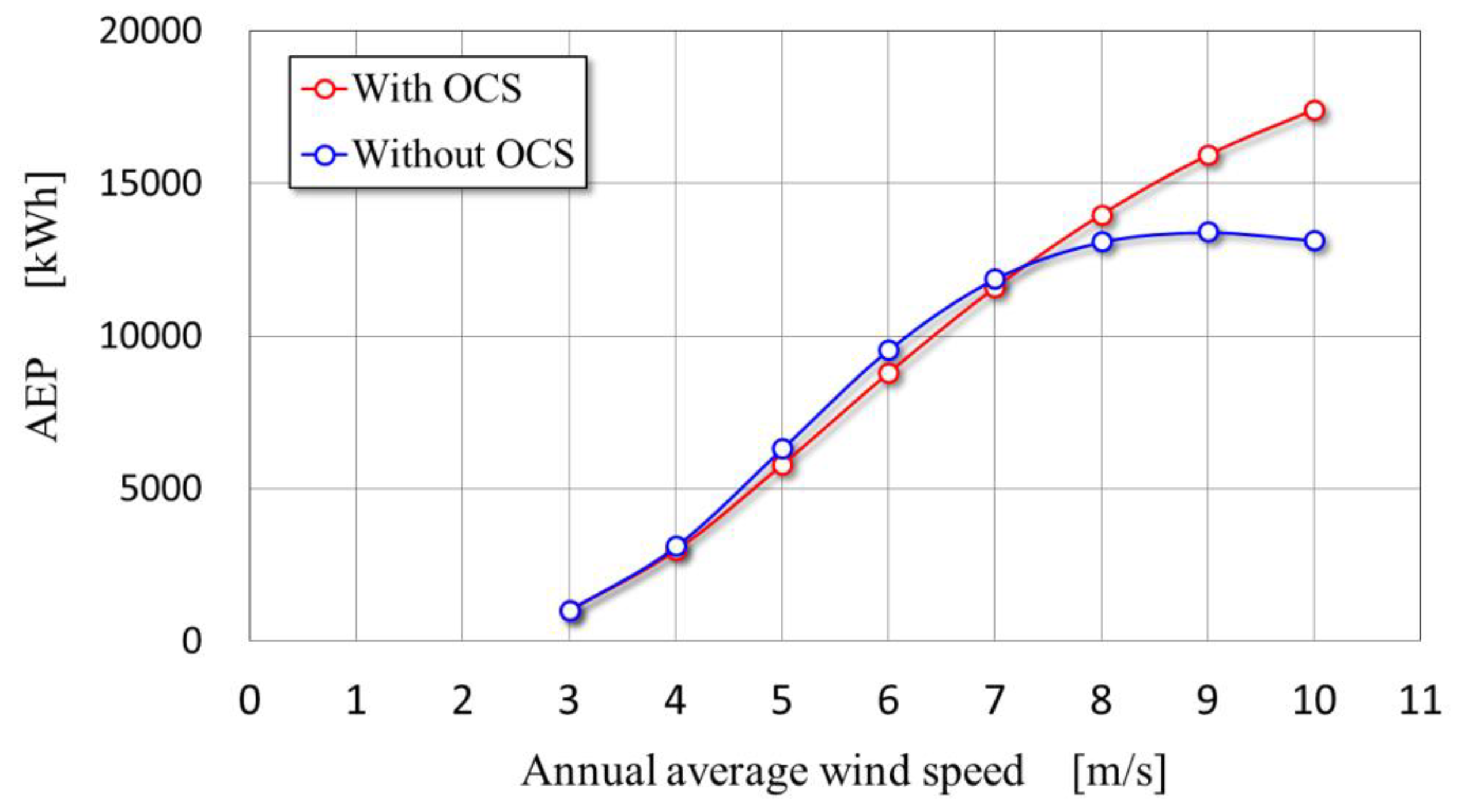
The predictions of the annual energy production (AEP) based on the power curves in
Figure 13 are shown in
Figure 14, in which the Rayleigh distribution [
20] was used to represent the wind speed probability density.
Figure 14 shows that there is little difference in AEP between the BWT without the OCS and the BWT with the OCS at the annual average wind speed of 7 m/s or lower. According to the prediction, the AEP of the BWT with the OCS amounts to 5791 kWh at the site where the annual average wind speed is expected to be 5 m/s.
Although the difference of AEP between both turbines with and without the OCS is little in the case of low annual average wind speed, as mentioned above, the wind power system without the OCS will be expensive because it needs a generator of large capacity and, therefore, other electrical devices of high performance. On the other hand, the total cost of the wind-power system with the OCS will be reduced because the capacities of the electrical devices could be small, although the manufacturing cost of the OCS is added.
In addition, if the turbine rotor is equipped with a simple stopper to hold the rotor for maintenance, the system with the OCS needs no other mechanical brake such as a disk brake. The capacity factor of the BWT with the OCS is improved, as understood from
Figure 13. The effects will be produced at the high wind potential sites as shown in
Figure 14. The wind-power system is controlled electrically by a controller regardless of the presence of the OCS. Although the wind-power system without the OCS might reach an over-speed condition in the case of loss of electrical control, the system with the mechanical OCS could prevent over-speed even when some electrical system problem occurs.
2.4. Power-Generation Control System
In the project, at first, the wind-power generation system was designed for grid connection, in which the generated electricity was supposed to be supplied to the grid through a power conditioning system (PCS). The control of the wind turbine was planned to be carried out by the function of maximum power point tracking (MPPT) of the PCS. However, in resolving the difficulty of getting permission early for grid connection because of the first development of a wind turbine with a special shape, the system was altered to use both the independent operation of the PCS and power-generation controller with a data table in order to give priority to the investigation of the generation performance of the BWT equipped with the OCS.
Figure 15 shows the inside of the first control console planned in the project. The PCS (Diamond Electric Mfg. Co., Ltd., Osaka, Japan, DPC-45B, 4.5 kW) is an inside-installation type for the photovoltaic power-generation system. In the preceding stage, the controller No. 1 (SKY Electronics Co., Ltd., Yonago, Japan, CL302) is installed. The resistor No. 1 (2 kW/10 Ω × 3) is used to consume the generated electric power in case of emergency stop. Apart from this, another resistor (1 kW/2.2 Ω × 1) is equipped for functioning as a short-circuit brake to hold the rotor. The data logger system (sampling interval: about 1.5 s) records generator conditions (voltage, current, electric power, and rotational speed), wind conditions (wind speed and direction), status of the PCS, and so forth, and outputs those data to an SD memory card.
Figure 16 shows the generation controller No. 2 (SKY Electronics Co., Ltd., Yonago, Japan, CL302) and the resistor No. 2 (1 kW/10 Ω × 2), which were installed on the inner door panel of the control console after the alteration of the first plan.
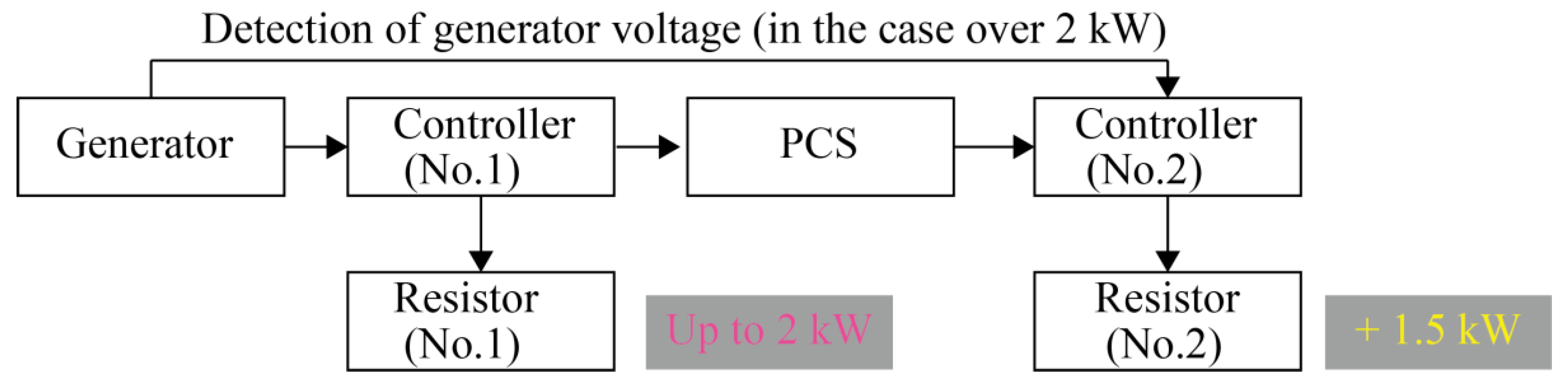
The schematic diagram of the power-generation control system after the plan alteration is illustrated in
Figure 17. When the electric power is 2 kW or less, the controller No. 1 controls the input current to the resistor No. 1 by PWM referring to a data table of target electric power against the generated voltage. Most of the generated electricity is consumed by the resistor No. 1. When the generated power exceeds 2 kW, the excess electric power passing through the PCS of independent operation is consumed at resistor No. 2, in which the controller No. 2 is used to track the target condition.
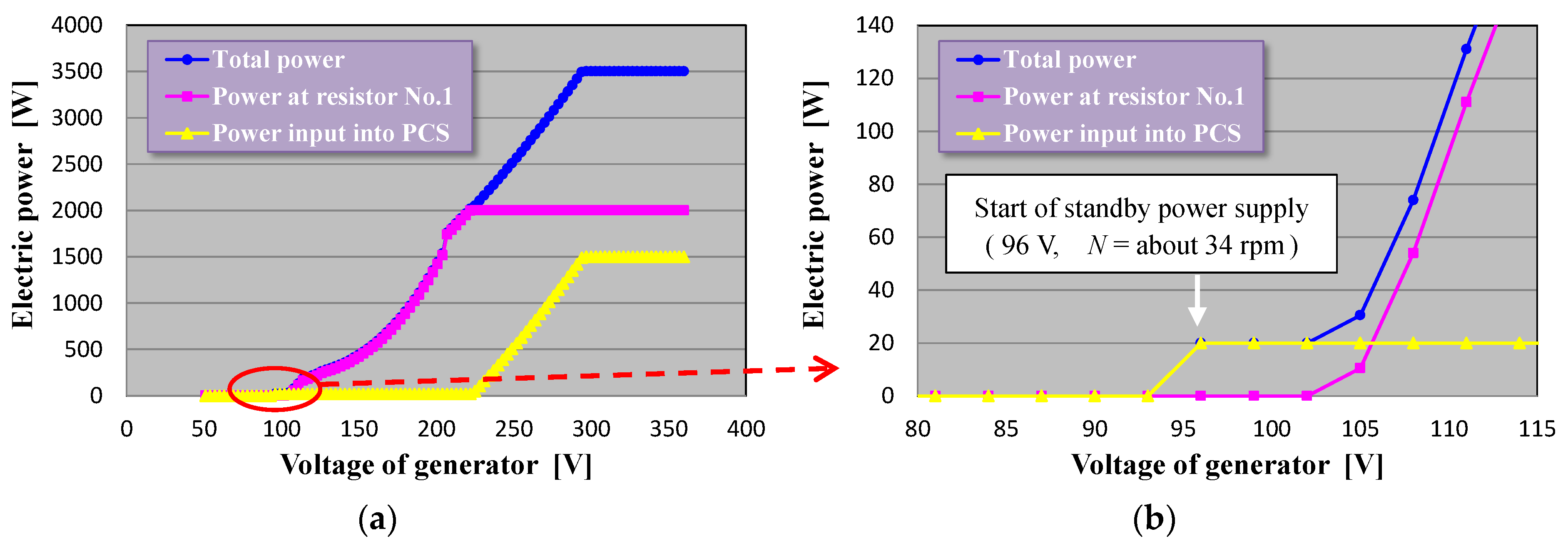
Figure 18a shows the target electric power against the generator voltage. As shown in
Figure 18a, the power-generation control system can deal with the maximum electric power of 3.5 kW. When the rotor rotational speed is low, the control system makes almost unloaded state, or non-electric current state, to improve the starting characteristics of the wind turbine rotor. The graph near the generation start point is magnified in
Figure 18b. The standby power (20 W) is supplied to the PCS when the generator voltage becomes more than 96 V, which corresponds to the rotor rotational speed of about 34 rpm. When the voltage reaches 105 V, the electric current starts to flow into the resistor No.1. Since the PCS is originally for grid connection, the independent mode of the PCS cannot continue by default. Therefore, a part of the control program of the PCS was altered so as to continue the independent mode by the manufacturer of the PCS.