Positive Impulse Phase versus Propulsive Impulse Phase: Correlations between Asymmetry and Countermovement Jump Performance
Abstract
:1. Introduction
2. Materials and Methods
2.1. Testing Protocols
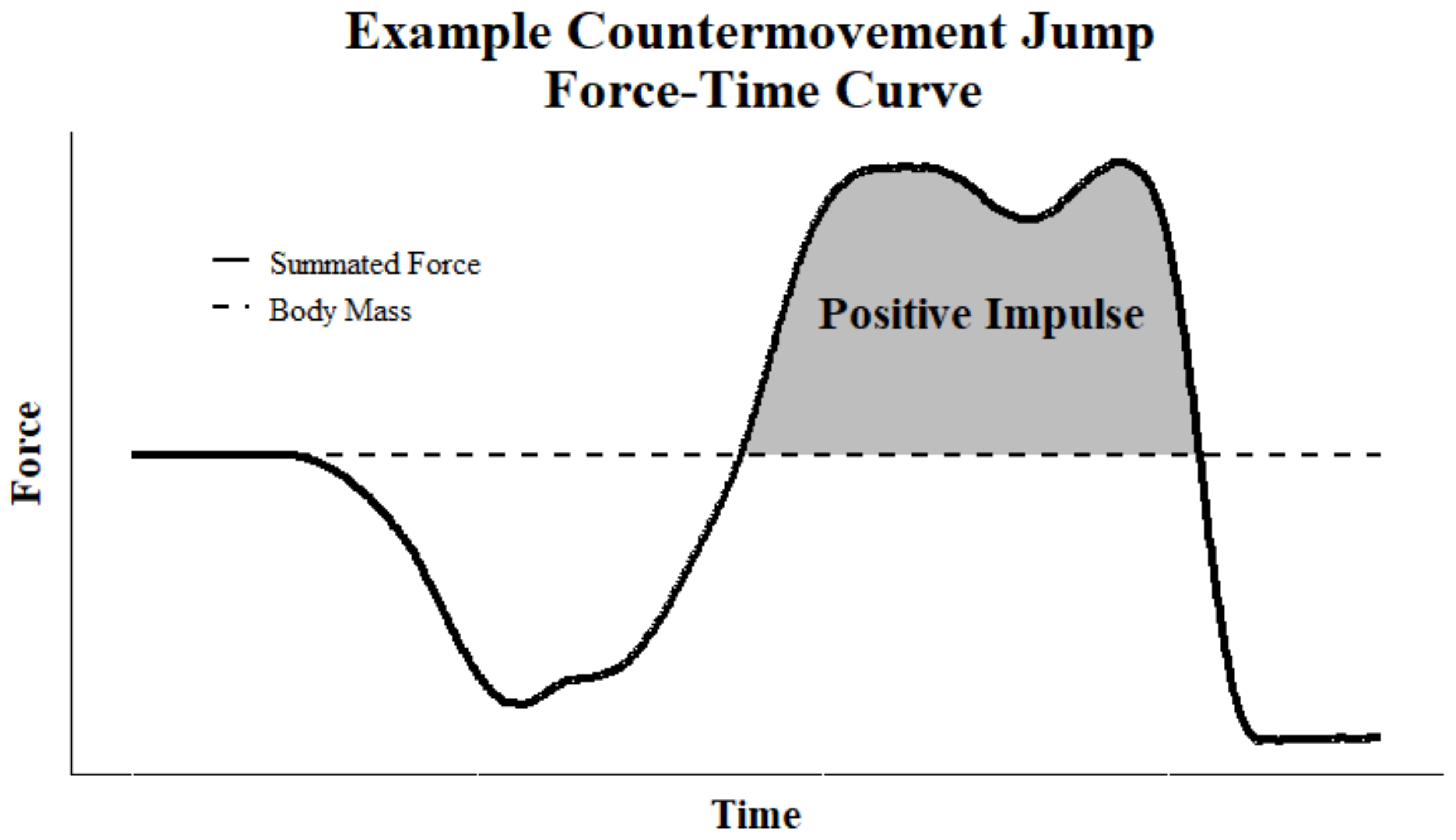
2.2. Data Analysis
2.3. Statistics
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guiard, Y. Asymmetric division of labor in human skilled bimanual action: The kinematic chain as a model. J. Mot. Behav. 1987, 19, 486–517. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.; Turner, A.; Read, P. Effects of inter-limb asymmetries on physical and sports performance: A systematic review. J. Sports Sci. 2018, 36, 1135–1144. [Google Scholar] [CrossRef] [PubMed]
- Maloney, S.J. The relationship between asymmetry and athletic performance: A critical review. J. Strength Cond. Res. 2019, 33, 2579–2593. [Google Scholar] [CrossRef] [PubMed]
- Rouissi, M.; Chtara, M.; Owen, A.; Chaalali, A.; Chaouachi, A.; Gabbett, T.; Chamari, K. Effect of leg dominance on change of direction ability amongst young elite soccer players. J. Sports Sci. 2016, 34, 542–548. [Google Scholar] [CrossRef]
- Bailey, C.; Sato, K.; Burnett, A.; Stone, M. Carry-over of force production symmetry in athletes of differing strength levels. J. Strength Cond. Res. 2015, 29, 3188–3196. [Google Scholar] [CrossRef]
- Bussey, M. Does the demand for asymmetric functional lower body postures in lateral sports relate to structural asymmetry of the pelvis? J. Sci. Med. Sport 2010, 13, 360–364. [Google Scholar] [CrossRef]
- Bell, D.R.; Sanfilippo, J.L.; Binkley, N.; Heiderscheit, B.C. Lean mass asymmetry influences force and power asymmetry during jumping in collegiate athletes. J. Strength Cond. Res. 2014, 28, 884. [Google Scholar] [CrossRef] [Green Version]
- Madruga-Parera, M.; Bishop, C.; Fort-Vanmeerhaeghe, A.; Beltran-Valls, M.; Skok, O.; Romero-Rodríguez, D. Interlimb asymmetries in youth tennis players: Relationships with performance. J. Strength Cond. Res. 2020, 34, 2815–2823. [Google Scholar] [CrossRef]
- Maloney, S.; Richards, J.; Nixon, D.; Harvey, L.; Fletcher, I. Do stiffness and asymmetries predict change of direction performance? J. Sports Sci. 2017, 35, 547–556. [Google Scholar] [CrossRef] [Green Version]
- Maulder, P.; Cronin, J. Horizontal and vertical jump assessment: Reliability, symmetry, discriminative and predictive ability. Phys. Ther. Sport 2005, 6, 74–82. [Google Scholar] [CrossRef]
- Dos’Santos, T.; Thomas, C.; Jones, P.; Comfort, P. Asymmetries in single and triple hop are not detrimental to change of direction speed. J. Trainology 2017, 6, 35–41. [Google Scholar] [CrossRef] [Green Version]
- Hoffman, J.R.; Ratamess, N.A.; Klatt, M.; Faigenbaum, A.; Kang, J. Do bilateral power deficits influence direction-specific movement patterns? Res. Sports Med. 2007, 15, 125–132. [Google Scholar] [CrossRef]
- Benjanuvatra, N.; Lay, B.; Alderson, J.; Blanksby, B. Comparison of ground reaction force asymmetry in one-and two-legged countermovement jumps. J. Strength Cond. Res. 2010, 27, 2700–2707. [Google Scholar] [CrossRef]
- Impellizzeri, F.; Rampinini, E.; Maffiuletti, N.; Marcora, S. A vertical jump force test for assessing bilateral strength asymmetry in athletes. Med. Sci. Sports Exerc. 2007, 39, 2044–2050. [Google Scholar] [CrossRef] [Green Version]
- Carroll, T.J.; Benjamin, B.; Stephan, R.; Carson, R.G. Resistance training enhances the stability of sensorimotor coordination. Proc. R. Soc. London. Ser. B Biol. Sci. 2001, 268, 221–227. [Google Scholar] [CrossRef] [Green Version]
- Sole, C.; Mizuguchi, S.; Sato, K.; Moir, G.; Stone, M. Phase characteristics of the countermovement jump force-time curve: A comparison of athletes by jumping ability. J. Strength Cond. Res. 2018, 32, 1155–1165. [Google Scholar] [CrossRef]
- Linthorne, N.P. Analysis of standing vertical jumps using a force platform. Am. J. Phys. 2001, 69, 1198–1204. [Google Scholar] [CrossRef] [Green Version]
- Kraska, J.; Ramsey, M.; Haff, G.G.; Fethke, N.; Sands, W.; Stone, M.E.; Stone, M.H. Relationship between strength and un-weighted and weighted vertical jump height. Int. J. Sport Physiol. Perform. 2009, 4, 461–473. [Google Scholar] [CrossRef] [Green Version]
- Comfort, P.; Dos’Santos, T.; Jones, P.; McMahon, J.; Suchomel, T.; Bayzler, C.; Stone, M.H. Normalization of early isometric force production as a percentage of peak force during multijoint isometric assessment. Int. J. Sports Physiol. Perform. 2019, 15, 478–482. [Google Scholar] [CrossRef]
- Stone, M.H.; O’Bryant, H.S.; Hornsby, G.; Cunanan, A.; Mizuguchi, S.; Suarez, D.G.; South, M.; Marsh, D.J.; Haff, G.G.; Ramsey, M.W.; et al. The use of the isometric mid-thigh pull in the monitoring of weightlifters: 25+ years of experience. UKSCA J. Prof. Strength Cond. 2019, 54, 10–26. [Google Scholar]
- Chavda, S.; Bromley, T.; Jarvis, P.; Williams, S.; Bishop, C.; Turner, A.; Lake, J.; Mundy, P. Force-time characteristics of the countermovement jump: Analyzing the curve in Excel. Strength Cond. J. 2018, 40, 67–77. [Google Scholar] [CrossRef] [Green Version]
- Sato, K.; Heise, G. Influence of weight distribution asymmetry on the biomechanics of a barbell back squat. J. Strength Cond. Res. 2012, 26, 342–349. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bazyler, C.D.; Bailey, C.A.; Chiang, C.Y.; Sato, K.; Stone, M.H. The effects of strength training on isometric force production symmetry in recreationally trained males. J. Trainol. 2014, 3, 6–10. [Google Scholar] [CrossRef] [Green Version]
- Behringer, M.; Vom Heede, A.; Matthews, M.; Mester, J. Effects of strength training on motor performance skills in children and adolescents: A meta-analysis. Pediatr. Exerc. Sci. 2011, 23, 186–206. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carroll, K.M.; Wagle, J.P.; Sole, C.J.; Stone, M.H. Intrasession and intersession reliability of countermovement jump testing in division-I volleyball athletes. J. Strength Cond. Res. 2019, 33, 2932–2935. [Google Scholar] [CrossRef]
- Hart, L.M.; Cohen, D.; Patterson, S.; Springham, M.; Reynolds, J.; Read, P. Previous injury is associated with heightened countermovement jump force-time asymmetries in professional soccer players. Transl. Sports Med. 2019, 2, 256–262. [Google Scholar] [CrossRef]
- Jones, P.; Bampouras, T. A comparison of isokinetic and functional methods of assessing bilateral strength imbalance. J. Strength Cond. Res. 2010, 24, 1553–1558. [Google Scholar] [CrossRef]
- Aagaard, P.; Simonsen, E.B.; Andersen, J.L.; Magnusson, P.; Dyhre-Poulsen, P. Neural adaptation to resistance training: Changes in evoked V-wave and H-reflex responses. J. Appl. Physiol. 2002, 92, 2309–2318. [Google Scholar] [CrossRef]
- Suarez, D.; Dylan, G.; Wagle, J.; Cunanan, A.; Sausaman, R.; Stone, M.H. Dynamic correspondence of resistance training to sport: A brief review. Strength Cond. J. 2019, 41, 80–88. [Google Scholar] [CrossRef]
- Sannicandro, I.; Piccinno, A.; Rosa, R.; Pascalis, S. Functional asymmetry in the lower limb professional soccer players. Br. J. Sports Med. 2011, 45, 370. [Google Scholar] [CrossRef]
- Bailey, C.; Sato, K.; Burnett, A.; Stone, M. Force-production asymmetry in male and female athletes of differing strength levels. Int. J. Sports Physiol. Perform. 2015, 10, 504–508. [Google Scholar] [CrossRef]
- Kozinc, Z.; Šarabon, N. Inter-limb asymmetries in volleyball players: Differences between testing approaches and association with performance. J. Sports Sci. Med. 2020, 19, 745. [Google Scholar]
| Males | Females | |
|---|---|---|
| Body Mass (kg) | 76.3 ± 7.8 | 68.8 ± 12.0 |
| Height (cm) | 178.3 ± 5.9 | 165.3 ± 19.5 |
| Age | 19.7 ± 1.5 | 19.5 ± 0.8 |
| IPFa | 189.6 ± 27.2 | 153.4 ± 25.4 |
| JH0 (cm) | 30.82 ± 4.25 | 21.44 ± 4.72 |
| JH20 (cm) | 22.19 ± 3.67 | 14.42 ± 3.19 |
| PIAS0 | 7.10 ± 5.45 | 5.96 ± 5.55 |
| PIAS20 | 7.06 ± 4.59 | 5.53 ± 4.25 |
| Description | Pearson Correlation (r) with [CI] | R2 | p Value | |
|---|---|---|---|---|
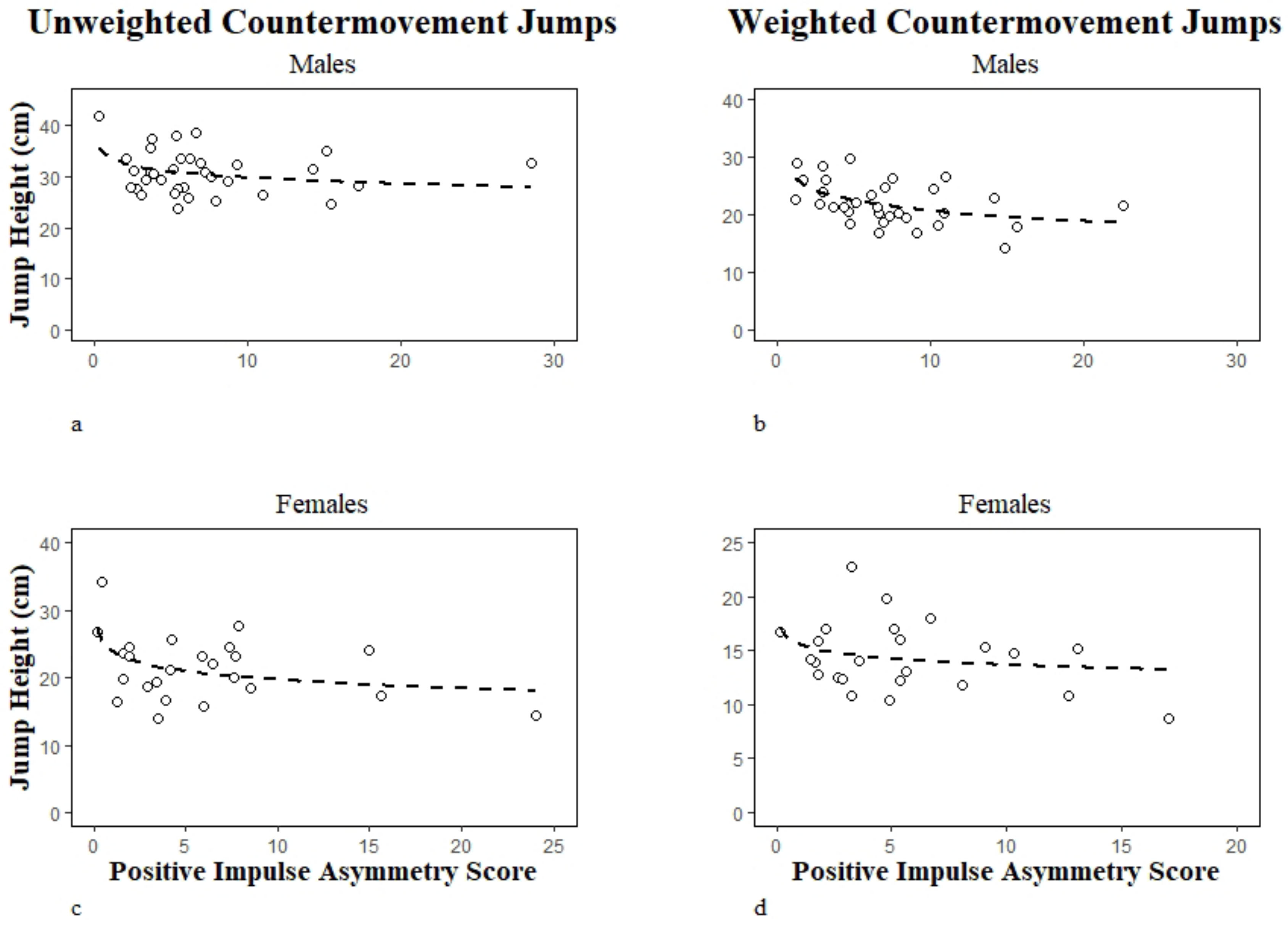
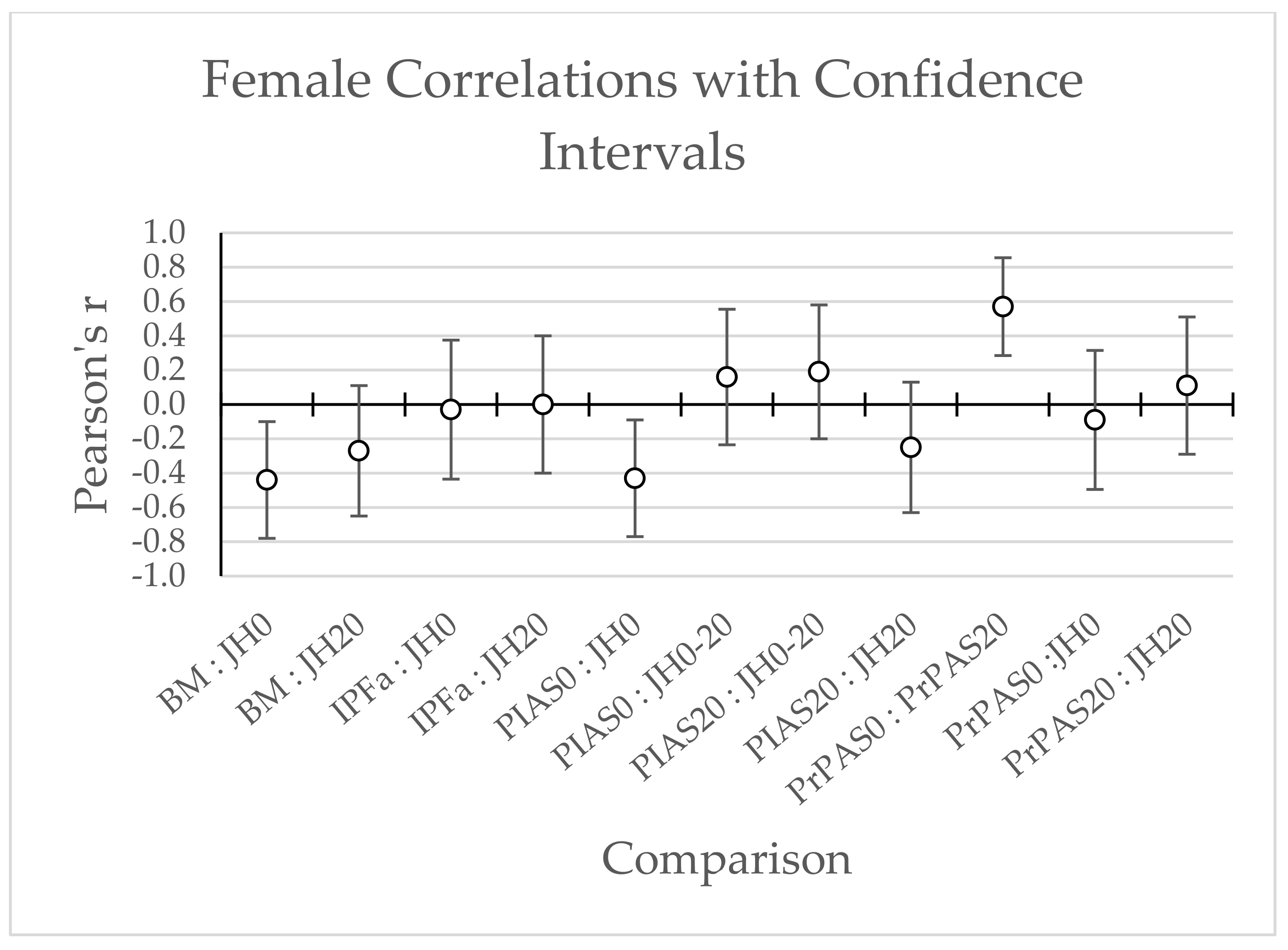
| Females (n = 24) | Jump Height 0 kg: PIAS0 | −0.43 [−0.71, −0.03] | 0.19 | 0.03 * |
| Jump Height 20 kg: PIAS20 | −0.25 [−0.59, 0.17] | 0.06 | 0.23 | |
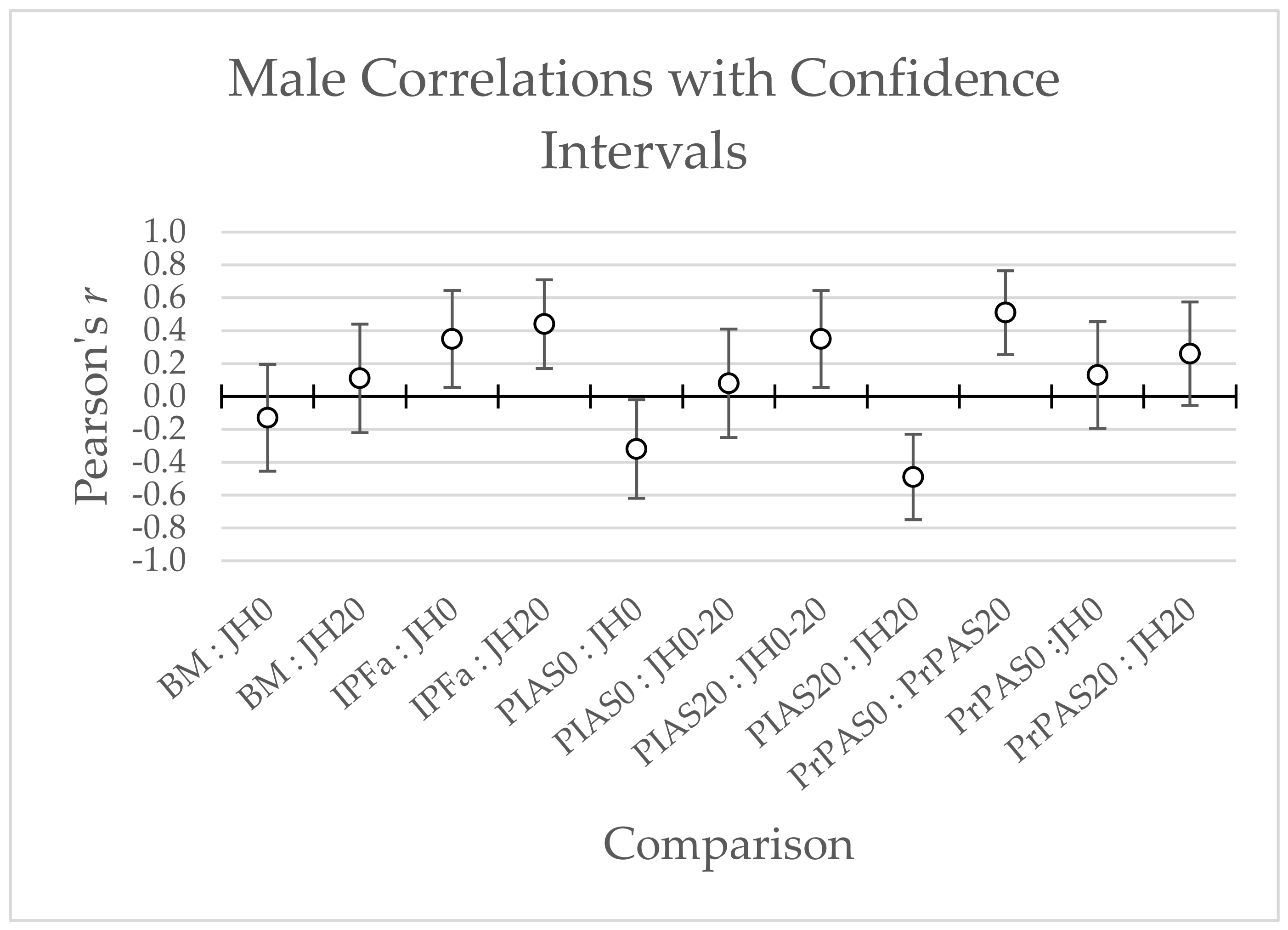
| Males (n = 35) | Jump Height 0 kg: PIAS0 | −0.32 [−0.59, 0.01] | 0.10 | 0.06 |
| Jump Height 20 kg: PIAS20 | −0.49 [−0.71, −0.19] | 0.24 | <0.01 * | |
| Description | Pearson Correlation (r) with [CI] | R2 | p Value | |
|---|---|---|---|---|
| Females (n = 24) | Jump Height 0 kg: PrPAS0 | −0.09 [−0.48, 0.33] | 0.01 | 0.66 |
| Jump Height 20 kg: PrPAS20 | 0.11 [−0.31, 0.49] | 0.01 | 0.60 | |
| Males (n = 35) | Jump Height 0 kg: PrPAS0 | 0.13 [−0.21, 0.44] | 0.02 | 0.46 |
| Jump Height 20 kg: PrPAS20 | 0.26 [−0.08, 0.55] | 0.07 | 0.13 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Painter, K.B.; Hornsby, W.G.; Carroll, K.; Mizuguchi, S.; Stone, M.H. Positive Impulse Phase versus Propulsive Impulse Phase: Correlations between Asymmetry and Countermovement Jump Performance. J. Funct. Morphol. Kinesiol. 2022, 7, 31. https://doi.org/10.3390/jfmk7020031
Painter KB, Hornsby WG, Carroll K, Mizuguchi S, Stone MH. Positive Impulse Phase versus Propulsive Impulse Phase: Correlations between Asymmetry and Countermovement Jump Performance. Journal of Functional Morphology and Kinesiology. 2022; 7(2):31. https://doi.org/10.3390/jfmk7020031
Chicago/Turabian StylePainter, Keith B., William Guy Hornsby, Kevin Carroll, Satoshi Mizuguchi, and Michael H. Stone. 2022. "Positive Impulse Phase versus Propulsive Impulse Phase: Correlations between Asymmetry and Countermovement Jump Performance" Journal of Functional Morphology and Kinesiology 7, no. 2: 31. https://doi.org/10.3390/jfmk7020031
APA StylePainter, K. B., Hornsby, W. G., Carroll, K., Mizuguchi, S., & Stone, M. H. (2022). Positive Impulse Phase versus Propulsive Impulse Phase: Correlations between Asymmetry and Countermovement Jump Performance. Journal of Functional Morphology and Kinesiology, 7(2), 31. https://doi.org/10.3390/jfmk7020031









