Abstract
We present the first Thomson scattering measurements of electron density and temperature in the Large Plasma Device (LAPD), a 22 m long magnetized linear plasma device at the University of California Los Angeles (UCLA). The diagnostic spectrally resolves the Doppler shift imparted on light from a frequency-doubled Nd:YAG laser when scattered by plasma electrons. A fiber array coupled to a triple-grating spectrometer is used to obtain high stray light rejection and discriminate the faint scattering signal from a much larger background. In the center of the plasma column, the measured electron density and temperature are about cm and T 3 eV, respectively, depending on the discharge parameters and in good agreement with Langmuir probe data. Optical design considerations to maximize photon count while minimizing alignment sensitivity are discussed in detail and compared to numerical calculations. Raman scattering off of a quartz crystal probe is used for an absolute irradiance calibration of the system.
1. Introduction
The Large Plasma Device (LAPD) is a 22 m long, magnetized linear plasma device used to study a number of fundamental processes, including the dispersion and damping of kinetic and inertial Alfvén waves, turbulence and transport, and wave-particle interactions [1]. Accurate point measurements of plasma density and temperature are crucial for the interpretation of these experiments.
We have developed a Thomson scattering (TS) [2,3] diagnostic to provide first-principle, non-intrusive point measurements of plasma density and temperature with high spatial and temporal resolution. The instrument has several advantages compared to other available diagnostics such as swept Langmuir probes [4], microwave interferometers [5], or self-emission spectroscopy [6,7], as it overcomes some of their limitations including model dependence, integration over the line-of-sight, or refraction at density gradients. Most importantly, TS allows measurements in transient plasmas with lifetimes of less than a microsecond, such as exploding laser-produced plasmas used in experiments on laboratory-scaled collisionless shocks [8,9], magnetospheres [10], ion-ion beam instabilities [11,12], diamagnetic cavities [13,14], magnetic reconnection [15], or magnetic field generation and amplification [16].
Like similar TS systems on other plasma devices [17,18,19,20,21,22,23,24], the diagnostic employs a triple-grating spectrometer (TGS) with a spatial notch filter to achieve high stray light rejection over a narrow wavelength range. In contrast to other TS diagnostics, the instrument described here is designed to maximize alignment flexibility and stability at the cost of optical extent and total photon count and therefore uses a relatively small solid angle collection lens outside the vacuum vessel. This allows the diagnostic to be readily moved from port to port as needed to support a wide range of user experiments.
The paper is structured as follows: Section 2 describes the experimental configuration. We then discuss optical design considerations and the trade-offs between optical extent and beam pointing sensitivity in Section 3 and compare them to numerical calculations of the overall photon collection efficiency. In Section 4, we present experimental results, including the absolute spectrometer irradiance calibration using Raman scattering off of a quartz crystal probe (Section 4.1), TS measurements of electron density, and temperature (Section 4.2), and a comparison to Langmuir probe data (Section 4.3). Section 5 is a summary.
2. Experimental Setup
The LAPD creates highly magnetized plasmas that are large enough (19 m length, 50 cm diameter) to support Alfvén waves [1]. Quiescent and current-free plasmas are created at up to 1 Hz repetition rate in a steady, axial magnetic field up to 2500 G by pulsing cathodes at either end of the machine negatively with respect to anode grids 30–50 cm away. The plasma reaches a steady state a few ms after the discharge is initiated and has a variable lifetime of around 10 ms. Figure 1a shows a schematic of the LAPD with the two plasma sources on either end. For the work described here, the TS diagnostic was installed in port 32 about 7 m from the north source and about 1.5 m from the longitudinal center of the plasma column.
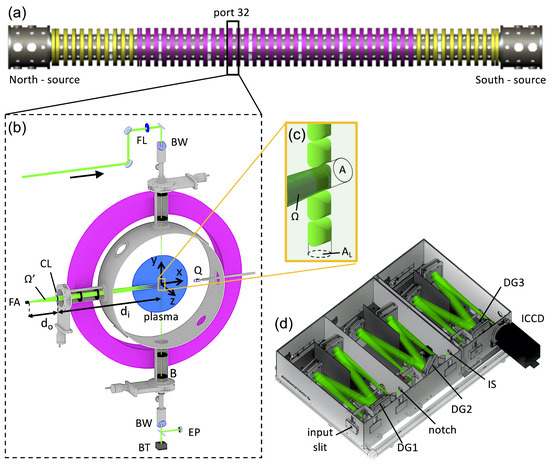
Figure 1.
(a) Schematic layout of the 22 m long LAPD showing the two plasma sources on either end and the magnetic field coils (yellow and pink). The TS diagnostic is installed in port 32 as indicated by the box. (b) Detailed view of the segment around port 32. The TS probe beam is focused by a focusing lens (FL) before it enters the vessel through a Brewster window (BW) on top of the machine and is linearly polarized in the center of the plasma along the z-axis, perpendicular to the direction of the collected light. Scattered light is collected by a collection lens (CL) at a distance of d from the scattering volume. The light collected in a solid angle is then focused into a 40 × 200 m core fiber array (FA) located a distance of d from the lens. Unscattered light exits the chamber through baffles (B) and a Brewster window (BW) and terminates in a beam trap (BT). A fraction of the transmitted light is measured with a pyroelectric energy pickup (EP) to monitor the total laser energy for each shot. A quartz-crystal probe (Q) can be inserted along the axis and into the scattering volume using a motorized probe drive. (c) The scattering volume is defined by the intersection of the waist of the focused probe beam of cross-section A and the projection of the fiber array onto the beam. The projected area of a single fiber at the beam is A. Only the path of the light collected by the central fiber with source solid angle is shown. (d) The triple-grating spectrometer showing the light path from the input slit through the notch filter, the intermediate slit (IS) and onto the image intensified camera (ICCD) guided by internal mirrors and diffraction gratings (DG) along the way.
The setup and scattering schematic are depicted in Figure 1b. A frequency-doubled Nd:YAG laser produces 8 ns pulses of 105 mJ energy at a wavelength of = 532 nm in a 10 mm diameter beam. A slow (f/150) spherical lens with a focal length of 1.5 m on top of the chamber focuses the beam through a Brewster window vertically down to a focus in the center of the plasma column. This configuration produces a cylindrical "pencil" beam with a diameter of around 1 mm that remains constant over several centimeters around the focus. The beam is linearly polarized along the z-axis using a half-waveplate. The Brewster window and a series of baffles minimize stray light entering the collection optics. The probe beam exits the vacuum chamber through baffles and a second Brewster window and terminates in a beam trap. A 10% fraction of the transmitted light is recorded on a pyroelectric energy sensor to measure the beam energy in each pulse.
Scattered light collection is accomplished by a 50 mm diameter and f = 20 cm focal length lens located outside the vacuum chamber at d = 94 cm from the scattering volume. The lens images the probe beam waist onto a vertical fiber array located at d = 25 cm from the lens. The fiber array consists of 40 linearly arranged 200 μm core optical fibers mapped end to end with combined slit dimensions of 8.8 mm × 0.22 mm, considering also the 0.22 mm outer diameter edge cladding. The fiber array is magnified by a factor of and projected onto the probe beam, defining the scattering volume (Figure 1c). Integrating light from all 40 fibers, therefore, results in a 33 mm × 0.74 mm long vertical scattering volume. The spatial resolution of a single fiber is less than 1 mm. The fibers used in the array are 0.22 in the numerical aperture (NA) and 25 m in length, and are coupled directly to the input slit of the spectrometer. Collected light is injected into each fiber in an f/5 beam to match the f-number (f/#) of the spectrometer.
To effectively discriminate the faint Thomson scattering signal from the much brighter unshifted stray light at , either a volume Bragg grating (VBG) or a TGS is typically used. Compared to a VBG [25,26], a TGS provides the advantage of a flexible notch filter configuration at the expense of slightly lower system throughput [19]. Unlike a VBG, the TGS is compatible with both 532 nm and 527 nm probe beams and therefore with experiments that require much higher probe beam energies [27,28,29]. A triple-grating 0.5 m focal length f/4 Czerny–Turner-type imaging spectrometer is used (Figure 1d). The spectrometer is equipped with toroidal, silver-coated mirrors and three 1200 grooves/mm holographic aluminum-coated gratings blazed at 500 nm with a 25% total transmission efficiency. The input and intermediate slit (IS) are kept at 200 m and 1.5 mm, respectively, yielding a spectral resolution of 0.22 nm over a spectral range of 19.4 nm. A notch mask is placed in between the double-subtractive spectrometers to remove light at . A 0.75 mm wide and 50 m thick stainless steel mask blocks a wavelength range of 1.5 nm with an extinction ratio of 2.0 × 10 integrated over the entire spectrum [30,31]. The notch mask also acts to reduce the intensity of the broad Lorentzian wings of the instrument-broadened laser line outside of the 1.5 nm blocking width, since the 532 nm signal is removed before light reaches and scatters off of the second and third gratings (DG2 and DG3). The second spectrometer stage collects the unblocked scattered light and recreates a one-to-one image of the input slit on the intermediate slit. The third grating (DG3) disperses the photons and creates a spectrum that is focused onto the detector.
Spectra are recorded using an image-intensified charge-coupled device (ICCD) camera mounted directly to the output of the third spectrometer stage. The camera is equipped with a generation III photocathode with a quantum efficiency of 50% at 532 nm. The camera operates at a maximum micro-channel plate (MCP) gain and uses a 2 × 2 pixel hardware binning in order to increase the pixel count. Even with binning and full gain, the pixel count is a small fraction of the 16-bit maximum and well within the linear response range. The spectra are further binned horizontally over two pixels into 256 total bins with 0.076 nm/bin. For the spectra presented here, the image is also binned vertically over the entire fiber array and all 512 pixels. The MCP gate width is fixed at 100 ns, with the 8 ns laser pulse centered in the 100 ns window, and so the temporal resolution is determined by the laser pulse duration. An equal number of TS and background shots are recorded back to back. The laser is pulsing at 1/2 Hz while the plasma is produced at 1/4 Hz. Every other spectrum is therefore recorded between two plasma discharges and serves as background. To increase the signal-to-noise ratio (SNR) several hundred shots are averaged to obtain one spectrum. The 20 e pixel readout noise with the ICCD cooled to −20 °C is insignificant (<1 count) when averaging multiple shots. Due to the short exposure time, the plasma self-emission is negligible and the total noise is determined only by the shot noise of the laser. Assuming Poisson statistics, the SNR increases as SNR , where S is the number of laser shots.
3. Design Considerations
Only a small number of photons are Thomson scattered off of the tenuous LAPD plasma, and the optical system must be carefully designed to maximize the light collection efficiency. Simultaneously, the probe beam and collection optics must be flexible enough so that they can be easily moved from port to port to support various user experiments in different geometries. This requires a robust optical system that is insensitive to alignment changes. Furthermore, the focusing and collection lenses must be placed outside the plasma chamber to avoid contamination via film coating deposition, which limits the solid angles. In the following we will discuss how to optimize the trade-offs between photon collection efficiency and alignment sensitivity to elucidate why we opted for a collection geometry with a relatively small (f/19) collection lens, and to help guide the design of similar diagnostics elsewhere.
For laser scattering off of microscopic particles the scattered power is
where is the incident laser power, n is the density of scattering particles, is the length of the scattering volume, and is the scattering cross-section [3]. The total number of scattering particles in the scattering volume is , where is the cross-section of the focused laser beam. Therefore, the unitless scattering probability in Equation (1) represents the fraction of the laser beam cross-section that is occupied by particles [32]. In the case of TS, the scattering cross-section depends on the direction of scattering, and is replaced by the differential cross-section times the solid angle of detection , which is defined by the f-number of the collection lens. Since , where is the laser energy per pulse and is the pulse length, the total number of photons scattered into the solid angle of the collection lens is [33]
where is the focused laser intensity, is the energy of one photon of frequency , is the scattering volume, and n is the electron density. For scattering perpendicular to the probe beam (), as in this case, the differential scattering cross-section is , where m is the classical electron radius. Only a fraction of the photons scattered into the collection lens make it to the detector. The optical transmission through the optical fiber and spectrometer is only around , determined mostly by the reflectivity of the three diffraction gratings. Photons are converted to photo-electrons with quantum efficiency , which are multiplied by the MCP of gain g = 233 before being recorded on the ICCD. The total number of photo-electrons (counts) on the detector area is then
where k is the experimental throughput parameter that is exactly the same for all types of scattering, and can be determined in situ using Rayleigh [34] or Raman [35] scattering off of a known gas or solid target [30]. Maximizing the photon collection efficiency requires maximizing k.
At first glance, it would seem that a slow (f/19) collection lens would result in more than an order of magnitude loss in light collection, compared to a much faster lens (f/4). However, it must be considered that and are dependent variables, and increasing one decreases the other [31]. The effect of the collection lens and beam focus parameters on k is best evaluated using the optical extent , which is the same for the source and the detector [36]. Here, is the spectrometer entrance area defined by the slit or the fiber array, and is the solid angle of light entering the spectrometer, while A is the source area and is the solid angle over which scattered light is collected. The system throughput is set by whatever limits G, either at the source (i.e., the scattering volume) or the detector. Since the solid angle injected into the spectrometer and the fiber array cross-section are fixed, the maximum possible throughput is the spectrometer optical extent, which is sr·mm in this setup. When the source is an infinite sheet of light, the source area is determined by the projection of the detector area onto the source with magnification M. The source optical extent is then identical to the spectrometer extent since , and = . Increasing the solid angle of the collection lens by using a larger diameter lens or by placing the lens closer to the source results in a proportionally smaller projection A, and the photon count remains the same. By contrast, in the case of TS, the effective source area is defined by the intersection of the focused laser beam and the projection of the detector area. The beam waist w is fixed by the f-number of the focusing lens and also depends on the laser beam quality. In the simplified one-dimensional case and a homogeneous beam of diameter w there are two distinct cases: I) when the width d of the fiber projection is , the beam acts like a sheet of light and the photon collection efficiency is independent of the collection lens f-number (); II) when , then the source area is , and the effective optical extent is limited by the scattering volume (). Since the f-number injected into the fibers and spectrometer is fixed, f/#, the optical extent in this regime, scales inversely proportional to the f-number of the collection lens
In order to evaluate the effective throughput in the more realistic case of a Gaussian beam waist projected onto circular fibers, a simple numerical integration on a discrete two-dimensional grid with 1 m × 1 m pixel resolution is used.
Figure 2 compares the optical extent as a function of for several different conditions: the blue curve shows the simple one-dimensional case of a square fiber and a homogeneous beam of width w = 1.1 mm, equivalent to the spectral () full-width of the beam used in the experiment. Consistent with Equation (4), the extent increases linearly until when . This point separates the two regimes I and II. For small equivalent to large f-numbers, the fiber projection is much larger than the beam, and the effective optical extent is only a fraction of the spectrometer extent. The photon count is reduced since the demagnified image of the beam underfills each fiber. The black curve shows G for a Gaussian beam consistent with the actual experimental conditions (s = 0.4 mm) projected onto circular fibers. For large f-numbers, G still increases linearly with . However, the transition between the two regimes occurs more smoothly. The point design used in the experiment at f/19 results in an optical extent of . Increasing the solid angle of collection past this point by using a larger lens or placing the lens closer to the beam does not significantly increase the signal count.
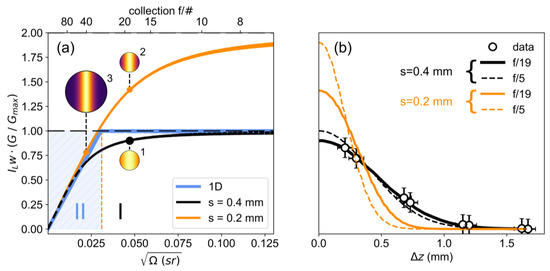
Figure 2.
(a) Numerical simulation of the effective optical extent as a function of collection lens solid angle and f-number for a simple one-dimensional case (blue), the Gaussian beam used in the experiment (black), and a hypothetical higher-quality beam with a smaller beam waist (orange). The insets show the simulated intensity distribution on the fiber in three representative cases. The point design used here (case 1) is indicated by the black dot. (b) The measured alignment sensitivity (circles) is best reproduced using a Gaussian beam waist of standard deviation s = 0.41 mm (black solid line). The data were obtained by measuring the intensity of the 127 cm Stokes–Raman scattering line off of the quartz probe as the fibers are translated by across the beam, where is the magnification of the collection branch. A much faster (f/5) collection cone (black segmented line) has only a minor effect on the collection efficiency since the beam is larger than the fiber projection in both cases and the optical extent is already close to . Overall system throughput could only be increased by reducing the focused beam waist size, although this would occur at the expense of alignment sensitivity (orange lines).
When the fiber projection is smaller than the beam waist (regime I), the effective optical extent is the spectrometer extent , independent of the beam size. However, a more tightly focused and higher intensity beam still results in a higher collection efficiency, because more energy is concentrated in the scattering volume. Equation (3) shows that . Although the intensity decreases inversely proportional to the square of the beam waist , the light throughput increases only linearly . The vertical axis used in Figure 2a is therefore , with normalized to the point design ( mm). The orange curve in Figure 2a shows a hypothetical case of a higher quality laser beam that can be focused to a smaller waist ( mm). The optical extent at large-collection solid angles is still ; however, the maximum k is now twice as large. In regime II, the light collection efficiency is independent of the beam waist, since the full beam is collected in either case over the same , as indicated by the insert for an f/40 collection lens (case 3 in Figure 2).
Figure 2b illustrates the alignment sensitivity and variation of k with a mismatch between the beam and fiber. Numerical calculations are compared to data obtained by measuring the Raman scattering intensity off of a quartz calibration probe as the fiber array is translated transversely to the beam. Raman scattering off of a crystal is described in more detail below in Section 4.1. In the figure, is the transverse displacement of the magnified projection at the beam waist and not the translation of the fibers (). The numerical model fits the data best for a Gaussian beam profile with a width of s = 0.41 mm, which is ten times the diffraction limit. Mismatching the fiber projection and the beam by ±0.5 mm reduces k by 40%. Using a much faster f/5 collection lens does only have a minor effect on the collection efficiency (black dashed line) since the beam is larger than the fiber projection in both cases. In the experiments, we found the alignment and k to be stable within a few percent over the course of several days. Figure 2b compares calculations for the beam used in the experiment (black) and a hypothetical higher quality or more tightly focused beam ( mm, orange) both for the f/19 collection lens used in the experiment (solid lines) and a faster f/5 lens (dashed lines). While this more narrow beam in combination with a fast collection lens increases the peak k by a factor of two, a mismatch of ±0.5 mm also results in a drop of k by more than 95%. There is only a 30% gain when switching from f/19 to f/5. Replacing the 50 mm collection lens with a larger 75 mm lens (f/12) would only lead to a modest 20% increase in photon count with this more narrow beam, and to less than a 5% increase with the existing beam m ( mm).
4. Results and Discussion
Thomson scattering can be collective or non-collective, depending on the scattering parameter , where is the scattering vector, is the electron screening length, and is the Boltzmann constant. When the scattering scale length is short compared to , then and the scattering is non-collective (incoherent) [2,3]. If the energy distribution is Maxwellian, the TS spectrum then has a Gaussian profile, where the width is dependent on the electron temperature, while the electron density can be derived from the integrated area under the curve after an intensity calibration.
4.1. Absolute Irradiance Calibration
Per Equation (3), the electron density can be determined from the integrated area under the TS spectrum (total counts) when the experimental throughput parameter k is known.
Since k is difficult to calculate accurately a priori, it is best determined experimentally in situ. In this experiment, Raman scattering off of a 19 mm quartz cuboid probe is used to absolutely calibrate the throughput of the optical system and spectrometer (Figure 3). A detailed description of this technique is given in [30] and is not repeated here. The probe can be inserted into the beam and scattering volume using a motorized probe drive (Figure 1). This technique allows alignment and absolute calibration of the system without breaking vacuum and while the plasma is operational. Raman scattering off of the quartz can also be used to align the collection branch by centering the beam waist image onto the fiber array (Figure 2b). Quartz has a high optical damage threshold in excess of 100 J/cm [37] and can be fielded in the focused beam as long as the energy does not exceed about 100 mJ. The Raman scattering response of quartz has been absolutely calibrated previously using Raman and Rayleigh scattering in nitrogen [30], where it has been shown that, for the bright 127 cm Stokes–Raman line, cm. Figure 3 shows the Raman spectrum from the quartz crystal probe obtained with a probe beam energy of 8 mJ. The measured area under the bright 127 cm line of counts corresponds to cm, accounting also for the different laser energies used for calibration and TS shots.
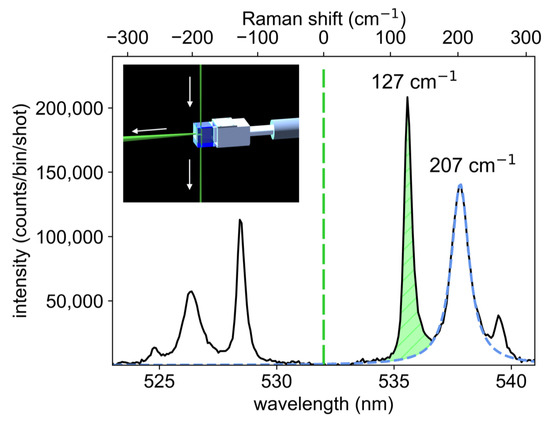
Figure 3.
Raman scattering spectrum from the quartz crystal probe. The much brighter Rayleigh signal at 532 nm is effectively blocked by the notch. The area under the 127 cm Stokes–Raman line (shaded green) is used to absolutely calibrate the spectrometer. It overlaps with the broad Lorentzian wings of the adjacent 207 cm line (dashed blue), which must be subtracted from the signal. The inset illustrates the beam intersecting the quartz probe from the top to bottom and the scattered light collected by the central fiber.
4.2. Thomson Scattering Measurements
The electron temperature is related to the width of the Gaussian profile by the following formula [19]
where c is the speed of light, is the electron mass, and is the spectral (e) half-width, which is proportional to the standard deviation . For and nm, the formula can be simplified to
Figure 4 shows the TS spectrum measured at t = 4.5 ms after the breakdown and averaged over 7000 discharges.
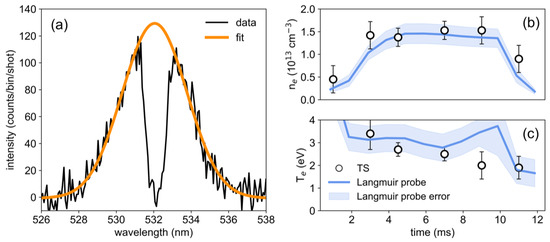
Figure 4.
(a) Measured TS spectrum at t = 4.5 ms obtained by averaging 7000 shots. The central 1.5 nm region of the spectrum is suppressed by the notch. The Gauss-fit (orange) has a standard deviation of s = 1.7 ± 0.1 nm, corresponding to a temperature of 2.7 ± 0.3 eV. (b,c) Comparison of the electron density and temperature derived from Langmuir probe measurements (solid lines) and from the TS spectra (circles).
Plasmas were created in helium at 2.8·10 torr with both plasma sources operating and a main discharge current of 9.9 kA pulsed on for 10 ms. The central 1.5 nm section around is suppressed by the notch. A Gaussian fit to the data excluding the notch has a width of s = 1.7 ± 0.1 nm, consistent with 2.7 ± 0.3 eV. The area under the spectrum of counts corresponds to an electron density of (1.4 ± 0.2) cm. With a scattering parameter , the scattering is non-collective. Figure 4b shows the evolution of the density and temperature as measured by TS. The measurements at 4.5 ms and 7 ms were averaged over 7000 discharges and have a higher accuracy. All other spectra were averaged only over 500 discharges. Measured temperatures decrease from 3.4 eV at 3 ms to 1.9 eV at 11 ms. The measured density remains relatively flat at around 1.5 × 10 cm for most of the discharge. When the probe beam is polarized along the -axis, the signal goes away (not shown), confirming that the signal is indeed TS. These first scattering measurements presented here were obtained without the final laser amplifier stage and at a reduced probe beam energy of 105 mJ. Furthermore, only 20 of the 40 collection fibers were operational. This limitation resulted in a photon count almost an order of magnitude lower than the point design. Integration of the scattering signal over 500–1000 shots was required to produce a high-fidelity TS spectrum.
Without the notch mask installed and without a plasma, we measure a stray light amplitude more than two orders of magnitude that of the TS signal. This is sufficiently bright for the faint wings of the instrument-broadened laser line [30,31] to exceed the measured TS signal. While a constant stray light can be subtracted with each background shot, its noise cannot. This confirms that a notch filter with an extinction ratio of at least 10 is required in the LAPD to discriminate the faint scattering signal from the stray light.
4.3. Comparison with Langmuir Probe Measurements
Figure 4b,c compare Thomson scattering data and Langmuir probe [38,39,40,41] measurements. Electron density and temperature were derived from the current–voltage (I–V) trace obtained in bias voltage sweeps [4,42,43]. The traces from ten discharges were averaged for each measurement. The maximum error in estimates from the Langmuir probe was 1.3 eV, based on the shot-to-shot variation. Relative Langmuir probe measurements of the electron density profile across the plasma column were calibrated with measurements of the line-integrated density obtained by a 100 GHz microwave interferometer based on a Gunn diode and horn [5]. Temperatures derived from the Langmuir sweeps are on average around 10% higher than the TS measurements, while the densities are slightly lower. However, the overall trend is the same for both diagnostics. This discrepancy might be caused in part by longitudinal density and temperature gradients as the Langmuir probe and the TS-sampled plasma are from different axial locations. The Langmuir probe was installed two ports from the TS diagnostic and 0.64 m closer to the main plasma source. Longitudinal gradients due to the high-fill pressure could also be responsible for the relatively low temperatures observed in this experiment. It is worth noting that a major upgrade to the plasma source has recently been completed to provide a significant increase in the discharge power density and allow access to higher density and temperature operating regimes. Langmuir probe measurements that observed electron temperatures in excess of 10 eV will be validated with future TS measurements.
5. Conclusions
The total TS photon count is proportional to the optical extent of the scattering volume or spectrometer, whichever is smaller. When the laser beam waist exceeds the fiber projection, then , independent of beam size and collection lens solid angle. The total system throughput then increases inversely proportional to the beam waist as beam intensity increases. This is the regime of most TS setups, including the one described here. In this regime, the photon count can only be increased significantly by either reducing the probe beam waist or increasing the total fiber area. When the fiber projection exceeds the beam waist, the optical extent increases proportionally to . The total system throughput is then independent of both the beam waist size and beam intensity. Preliminary TS spectra produced with only half of the fibers operational and using only 20% of the nominal laser energy yield electron densities around 1.5 × 10 cm and temperatures around 3 eV, in good agreement with Langmuir probe measurements. The scattering signal from at least 500 shots had to be averaged to obtain spectra with sufficiently SNR to extract the density and temperature. The next iteration of this diagnostic will double the number of fibers and increase the beam energy by a factor of five. Spectra with similar SNR can then be collected in as little as 10–100 discharges, while averaging a thousand shots will significantly improve the accuracy of the fits.
Author Contributions
Conceptualization, M.K., S.G., B.S. and C.N.; investigation, M.K., S.G., S.P.T., W.G. and C.N.; validation, M.K., S.G., M.J.V., S.P.T., W.G. and C.N.; writing—original draft preparation, S.G., M.K. and C.N.; writing—review and editing, S.G., M.K., S.P.T., W.G., M.J.V., B.S. and C.N.; supervision, C.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the U.S. DOE Office of Science, Fusion Energy Sciences under contract numbers DE-SC0019011 and DE-SC0021133, and by the Defense Threat Reduction Agency and Lawrence Livermore National Security LLC under contract numbers B643014 and B649519. The Basic Plasma Science Facility (BaPSF) is supported by grants through the National Science Foundation (PHY-1561912) and the Department of Energy (DE-FC02-07ER54918). One of the authors (M.J.V.) was supported by the APS Bridge Program and the UCLA Competitive Edge Program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
We would like to thank Zoltan Lucky, Marvin Drandell, and Tai Ly for their expert technical support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gekelman, W.; Pribyl, P.; Lucky, Z.; Drandell, M.; Leeneman, D.; Maggs, J.; Vincena, S.; Compernolle, B.V.; Tripathi, S.; Morales, G.; et al. The upgraded Large Plasma Device, a machine for studying frontier basic plasma physics. Rev. Sci. Instrum. 2016, 87, 025105. [Google Scholar] [CrossRef] [PubMed]
- Froula, D.; Glenzer, S.; Luhmann, N.C., Jr.; Sheffield, J. Plasma Scattering of Electromagnetic Radiation: Theory and Measurement Techniques. Fusion Sci. Technol. 2012, 61, 104–105. [Google Scholar] [CrossRef]
- Evans, D.; Katzenstein, J. Laser light scattering in laboratory plasmas. Rep. Prog. Phys. 1969, 32, 207–271. [Google Scholar] [CrossRef]
- Chen, F. Lecture Notes on Langmuir Probe Diagnostics; IEEE-ICOPS Meeting: Jeju, Korea, 2003. [Google Scholar]
- Gilmore, M.; Gekelman, W.; Reiling, K.; Peebles, W. A reliable millimeter-wave quadrature interferometer. arXiv 2020, arXiv:2002.11190. [Google Scholar]
- Boivin, R.F.; Kline, J.L.; Scime, E.E. Electron temperature measurement by a helium line intensity ratio method in helicon plasmas. Phys. Plasmas 2001, 8, 5303–5314. [Google Scholar] [CrossRef]
- Bondarenko, A.S.; Schaeffer, D.B.; Everson, E.T.; Clark, S.E.; Constantin, C.G.; Niemann, C. Spectroscopic measurement of high-frequency electric fields in the interaction of explosive debris plasma with magnetized background plasma. Phys. Plasmas 2014, 21, 122112. [Google Scholar] [CrossRef]
- Niemann, C.; Gekelman, W.; Constantin, C.G.; Everson, E.T.; Schaeffer, D.B.; Bondarenko, A.S.; Clark, S.E.; Winske, D.; Vincena, S.; Van Compernolle, B.; et al. Observation of collisionless shocks in a large current-free laboratory plasma. Geophys. Res. Lett. 2014, 41, 7413–7418. [Google Scholar] [CrossRef]
- Schaeffer, D.B.; Winske, D.; Larson, D.J.; Cowee, M.M.; Constantin, C.G.; Bondarenko, A.S.; Clark, S.E.; Niemann, C. On the generation of magnetized collisionless shocks in the large plasma device. Phys. Plasmas 2017, 24, 041405. [Google Scholar] [CrossRef]
- Schaeffer, D.; Cruz, F.; Dorst, R.; Cruz, F.; Heuer, P.; Constantin, C.; Pribyl, P.; Niemann, C.; Silva, L.; Bhattacharjee, A. Laser-Driven, Ion-Sale Magnetospheres in Laboratory Plasmas. I. Experimental Platform and First Results. arXiv 2022, arXiv:2201.02176. [Google Scholar]
- Heuer, P.; Weidl, M.; Dorst, R.; Schaeffer, D.; Tripathi, S.; Vincena, S.; Constantin, C.; Niemann, C.; Wilson, L.B., III; Winske, D. Laboratory Observations of Ultra-low-frequency Analog Waves Driven by the Right-hand Resonant Ion Beam Instability. Astrophys. J. 2020, 891, L11. [Google Scholar] [CrossRef]
- Keenan, B.D.; Le, A.; Winske, D.; Stanier, A.; Wetherton, B.; Cowee, M.; Guo, F. Hybrid particle-in-cell simulations of electromagnetic coupling and waves from streaming burst debris. Phys. Plasmas 2022, 29, 012107. [Google Scholar] [CrossRef]
- Collette, A.; Gekelman, W. Structure of an Exploding Laser-Produced Plasma. Phys. Rev. Lett. 2010, 105, 195003. [Google Scholar] [CrossRef] [PubMed]
- Niemann, C.; Gekelman, W.; Constantin, C.G.; Everson, E.T.; Schaeffer, D.B.; Clark, S.E.; Winske, D.; Zylstra, A.B.; Pribyl, P.; Tripathi, S.K.P.; et al. Dynamics of exploding plasmas in a large magnetized plasma. Phys. Plasmas 2013, 20, 012108. [Google Scholar] [CrossRef]
- Gekelman, W.; Collette, A.; Vincena, S. Three-dimensional current systems generated by plasmas colliding in a background magnetoplasma. Phys. Plasmas 2007, 14, 062109. [Google Scholar] [CrossRef]
- Pilgram, J.; Adams, M.; Constantin, C.; Heuer, P.; Ghazaryan, S.; Kaloyan, M.; Dorst, R.; Schaeffer, D.; Tzeferacos, P.; Niemann, C. High Repetition Rate Exploration of the Biermann Battery Effect in Laser Produced Plasmas over Large Spatial Regions. High Power Laser Sci. Eng. 2022, 2, 1–11. [Google Scholar] [CrossRef]
- Muraoka, K.; Uchino, K.; Bowden, M.D. Diagnostics of low-density glow discharge plasmas using Thomson scattering. Plasma Phys. Control. Fusion 1998, 40, 1221–1239. [Google Scholar] [CrossRef]
- Kono, A.; Nakatani, K. Efficient multichannel Thomson scattering measurement system for diagnostics of low-temperature plasmas. Rev. Sci. Instrum. 2000, 71, 2716–2721. [Google Scholar] [CrossRef]
- Van de Sande, M.J.; Van der Mullen, J.J.A.M. Thomson scattering on a low-pressure, inductively-coupled gas discharge lamp. J. Phys. Appl. Phys. 2002, 35, 1381–1391. [Google Scholar] [CrossRef]
- Belostotskiy, S.G.; Khandelwal, R.; Wang, Q.; Donnelly, V.M.; Economou, D.J.; Sadeghi, N. Measurement of electron temperature and density in an argon microdischarge by laser Thomson scattering. Appl. Phys. Lett. 2008, 92, 221507. [Google Scholar] [CrossRef]
- Yamamoto, N.; Tomita, K.; Sugita, K.; Kurita, T.; Nakashima, H.; Uchino, K. Measurement of xenon plasma properties in an ion thruster using laser Thomson scattering technique. Rev. Sci. Instrum. 2012, 83, 073106. [Google Scholar] [CrossRef]
- Lee, K.Y.; Lee, K.I.; Kim, J.H.; Lho, T. High resolution Thomson scattering system for steady-state linear plasma sources. Rev. Sci. Instrum. 2018, 89, 013508. [Google Scholar] [CrossRef] [PubMed]
- Seo, B.; Bellan, P.M. Experimental investigation of the compression and heating of an MHD-driven jet impacting a target cloud. Phys. Plasmas 2018, 25, 112703. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Shi, J.; Wu, D.; Feng, C.; Wu, G.; Yuan, K.; Ding, H. Comparison of Terahertz time domain spectroscopy and laser Thomson scattering for electron density measurements in inductively coupled plasma discharges. J. Instrum. 2019, 14, C12019. [Google Scholar] [CrossRef]
- Vincent, B.; Tsikata, S.; Mazouffre, S.; Minea, T.; Fils, J. A compact new incoherent Thomson scattering diagnostic for low-temperature plasma studies. Plasma Sources Sci. Technol. 2018, 27, 055002. [Google Scholar] [CrossRef]
- Shi, P.; Srivastav, P.; Beatty, C.; Nirwan, R.S.; Scime, E.E. Incoherent Thomson scattering system for PHAse space MApping (PHASMA) experiment. Rev. Sci. Instrum. 2021, 92, 033102. [Google Scholar] [CrossRef]
- Zweben, S.J.; Caird, J.; Davis, W.; Johnson, D.W.; Le Blanc, B.P. Plasma turbulence imaging using high-power laser Thomson scattering. Rev. Sci. Instrum. 2001, 72, 1151–1154. [Google Scholar] [CrossRef][Green Version]
- Niemann, C.; Constantin, C.; Schaeffer, D.; Tauschwitz, A.; Weiland, T.; Lucky, Z.; Gekelman, W.; Everson, E.; Winske, D. High-energy Nd:glass laser facility for collisionless laboratory astrophysics. J. Instrum. 2012, 7, P03010. [Google Scholar] [CrossRef]
- Schaeffer, D.; Constantin, C.; Bondarenko, A.; Everson, E.; Niemann, C. Spatially resolved Thomson scattering measurements of the transition from the collective to the non-collective regime in a laser-produced plasma. Rev. Sci. Instrum. 2016, 87, 11E701. [Google Scholar] [CrossRef]
- Ghazaryan, S.; Kaloyan, M.; Niemann, C. Silica Raman scattering probe for absolute calibration of Thomson scattering spectrometers. J. Instrum. 2021, 16, P08045. [Google Scholar] [CrossRef]
- Kaloyan, M.; Ghazaryan, S.; Constantin, C.G.; Dorst, R.S.; Heuer, P.V.; Pilgram, J.J.; Schaeffer, D.B.; Niemann, C. Raster Thomson scattering in large-scale laser plasmas produced at high repetition rate. Rev. Sci. Instrum. 2021, 92, 093102. [Google Scholar] [CrossRef]
- Van de Sande, M. Laser Scattering on Low Temperature Plasmas: HIGH Resolution and Stray Light Rejection. Ph.D. Thesis, Technical University Eindhoven, Eindhoven, The Netherlands, 2002. [Google Scholar] [CrossRef]
- Schaeffer, D.B.; Kugland, N.L.; Constantin, C.G.; Everson, E.; Compernolle, B.V.; Ebbers, C.; Glenzer, S.; Niemann, C. A scalable multipass laser cavity based on injection by frequency conversion for noncollective Thomson scattering. Rev. Sci. Instrum. 2010, 81, 10D518. [Google Scholar] [CrossRef] [PubMed]
- Berni, L.; Campos, D.; Machida, M.; Moshkalyov, S.; Lebedev, S. Molecular Rayleigh scattering as calibration method for Thomson scattering experiments. Braz. J. Phys. 1996, 26, 755. [Google Scholar]
- Flora, F.; Giudicotti, L. Complete calibration of a Thomson scattering spectrometer system by rotational Raman scattering in H2. Appl. Opt. 1987, 26, 4001. [Google Scholar] [CrossRef] [PubMed]
- Ridl, M.J. Optical Design Fundamentals for Infrared Systems, 2nd ed.; SPIE Tutorial Texts in Optical Engineering: Bellingham, WA, USA, 2001; ISBN-13: 978-0819440518. [Google Scholar] [CrossRef]
- Said, A.; Xia, T.; Dogariu, A.; Hagan, D.; Soileau, M.; Stryland, E.V.; Mohebi, M. Measurement of the optical damage threshold in fused quartz. Appl. Opt. 1995, 34, 3374. [Google Scholar] [CrossRef]
- Irisawa, J.; John, P.K. Comparison of Langmuir Double Probe and Laser Scattering Measurements of Plasma Parameters. Rev. Sci. Instrum. 1973, 44, 1021–1023. [Google Scholar] [CrossRef]
- Jones, L.A. Comparison of Langmuir probe and Thomson scattering measurements of electron temperature and density. J. Appl. Phys. 1974, 45, 5206–5208. [Google Scholar] [CrossRef]
- Godyak, V.A.; Alexandrovich, B.M. Comparative analyses of plasma probe diagnostics techniques. J. Appl. Phys. 2015, 118, 233302. [Google Scholar] [CrossRef]
- Ryan, P.J.; Bradley, J.W.; Bowden, M.D. Comparison of Langmuir probe and laser Thomson scattering for electron property measurements in magnetron discharges. Phys. Plasmas 2019, 26, 073515. [Google Scholar] [CrossRef]
- Mott-Smith, H.M.; Langmuir, I. The Theory of Collectors in Gaseous Discharges. Phys. Rev. 1926, 28, 727–763. [Google Scholar] [CrossRef]
- Chen, F.F.; Etievant, C.; Mosher, D. Measurement of Low Plasma Densities in a Magnetic Field. Phys. Fluids 1968, 11, 811–821. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).