High-Brightness Beam Technology Development for a Future Dynamic Mesoscale Materials Science Capability
Abstract
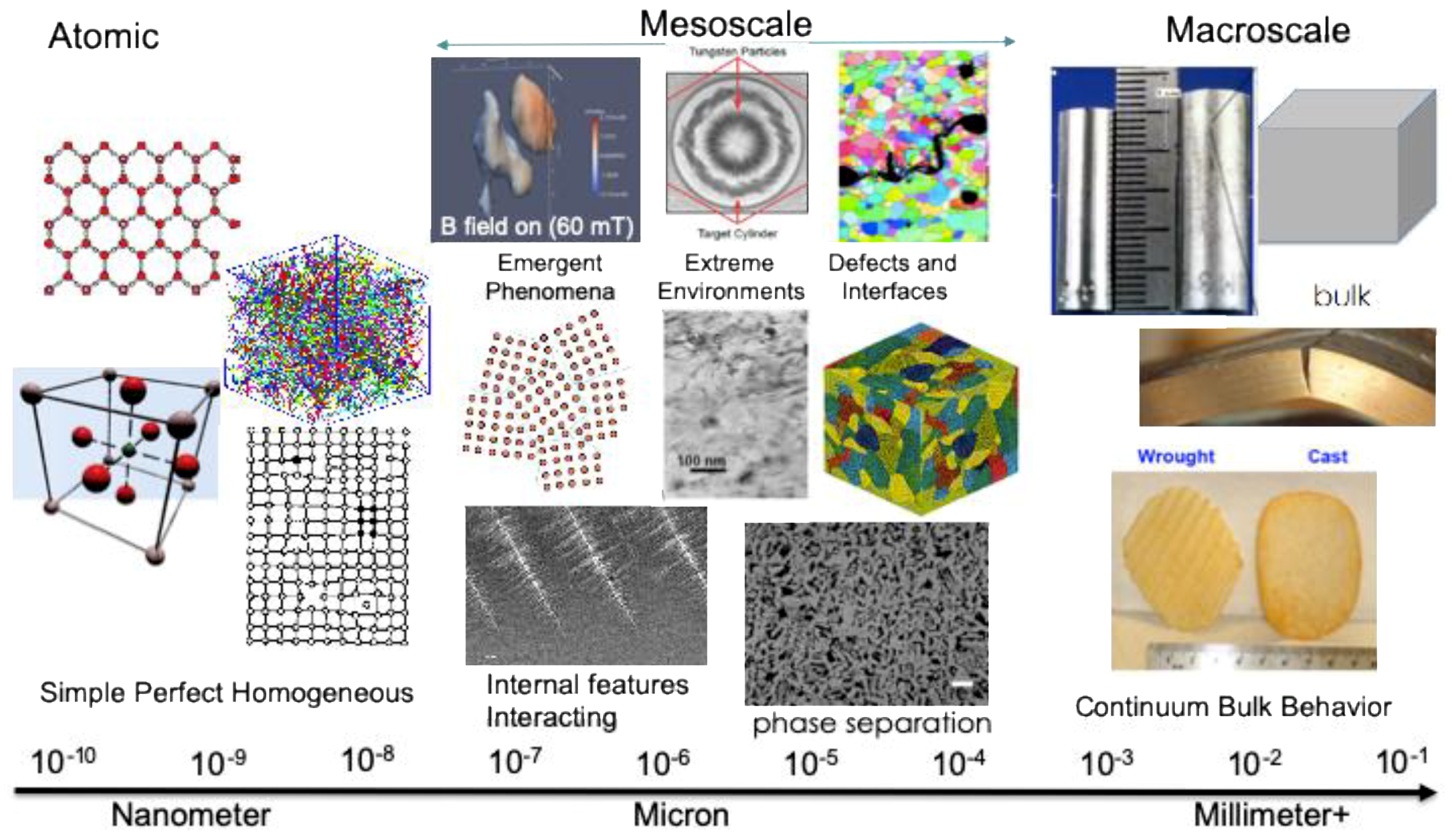
1. Introduction
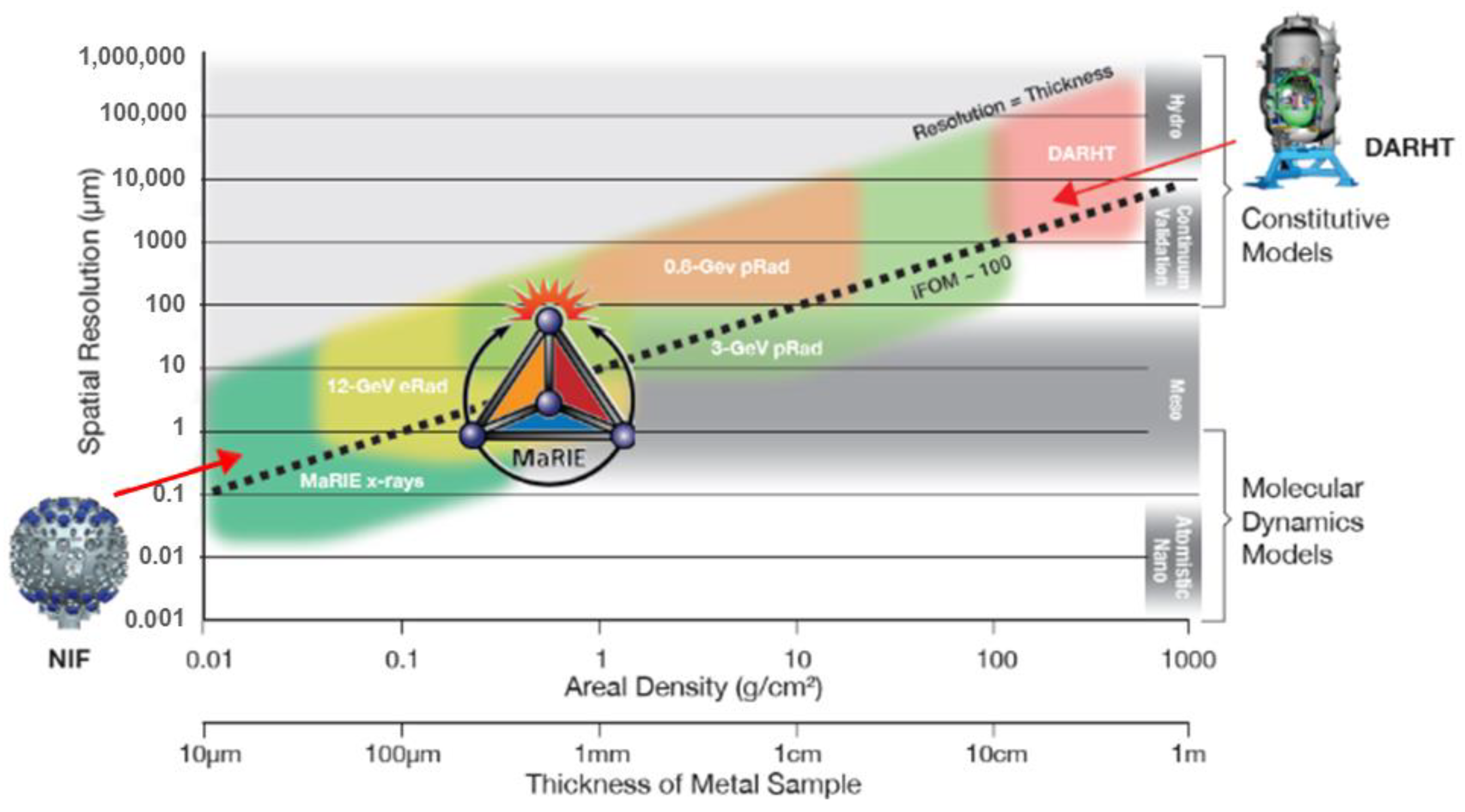
2. The MaRIE XFEL Concept
- 42 keV X-ray energy;
- 5 × 1010 photons per X-ray pulse;
- 0.02% spectral bandwidth of the X-rays.
3. Comparison of XFEL Accelerator Architectures
3.1. Conventional XFEL Architecture
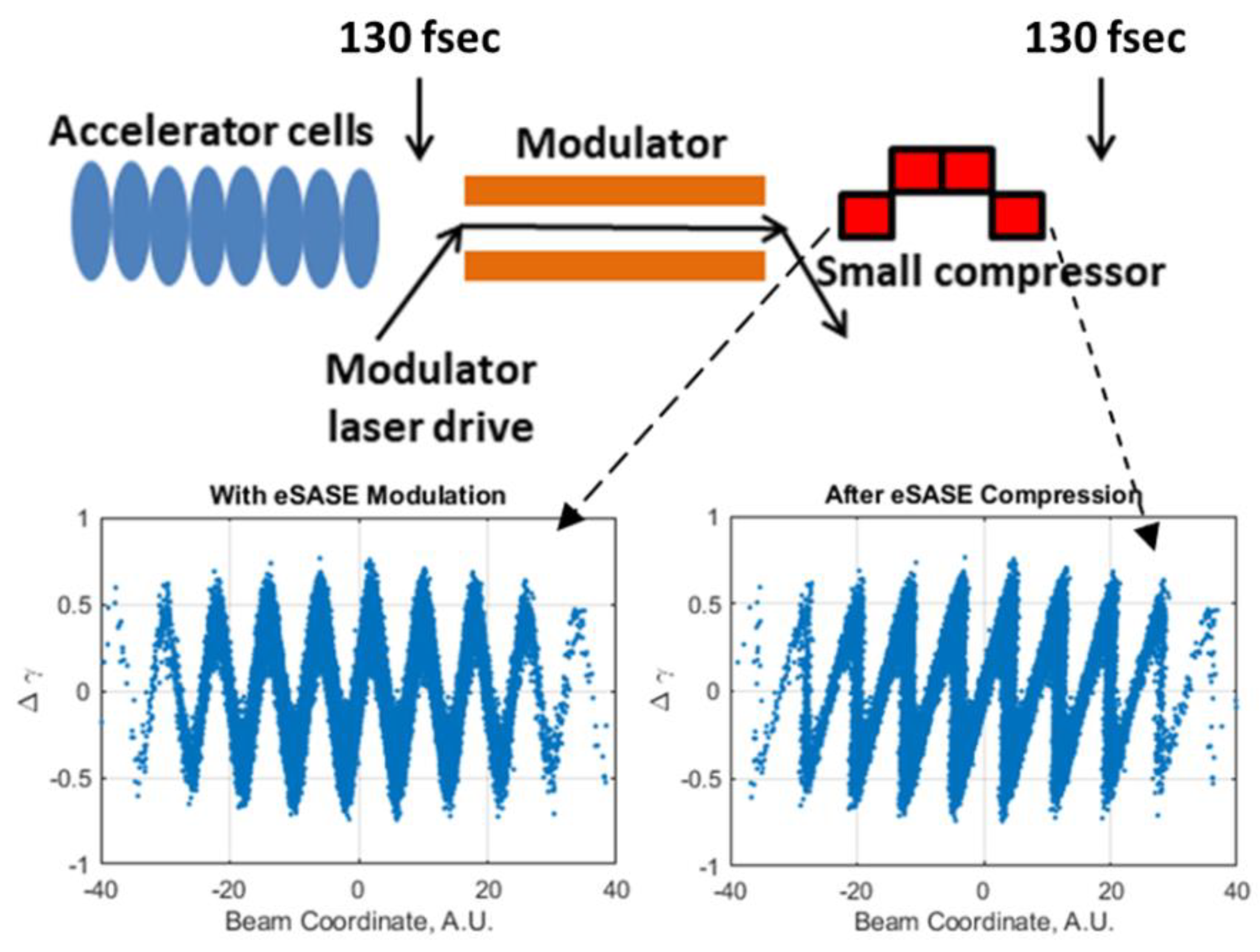
3.2. Microbunched XFEL Architecture
4. Background Theory and Application
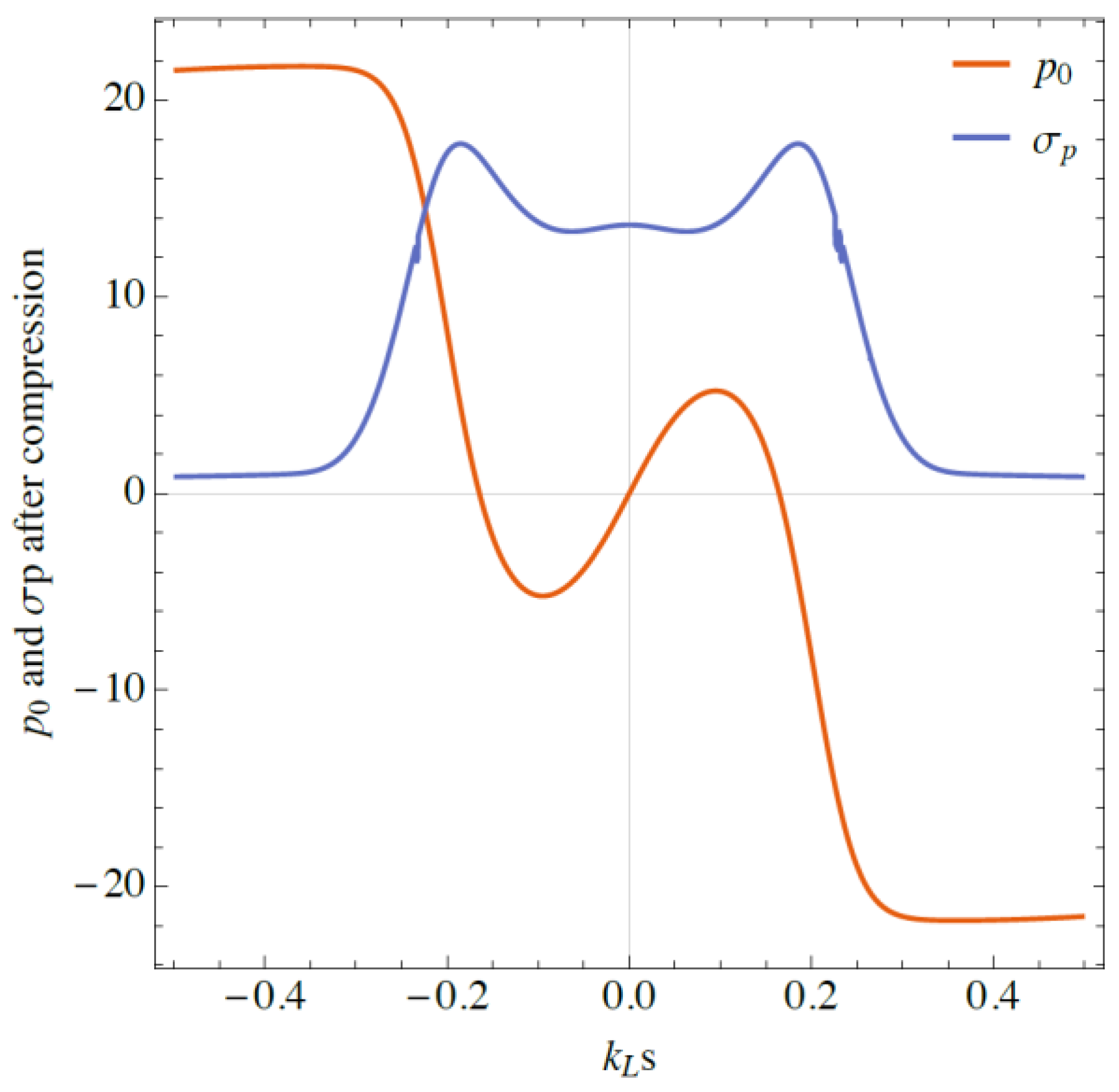
4.1. Idealized Background Theory for a Single Modulation Wavelength
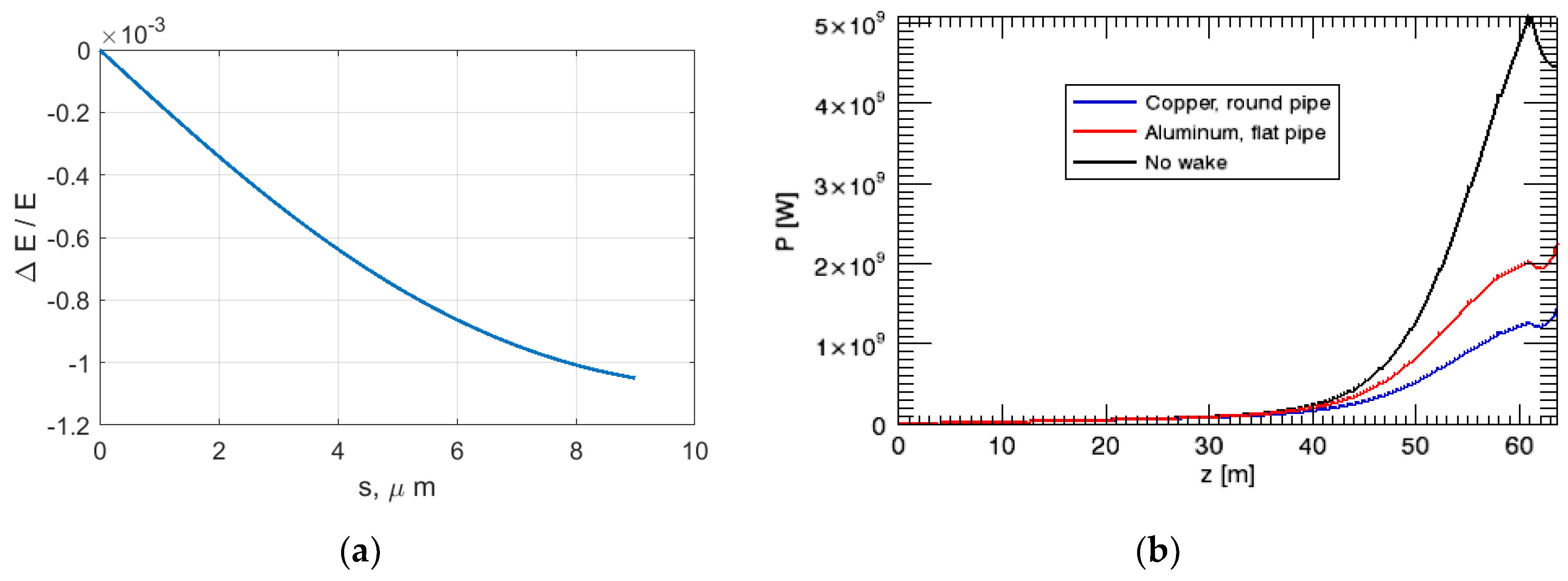
4.2. Other LABC Considerations
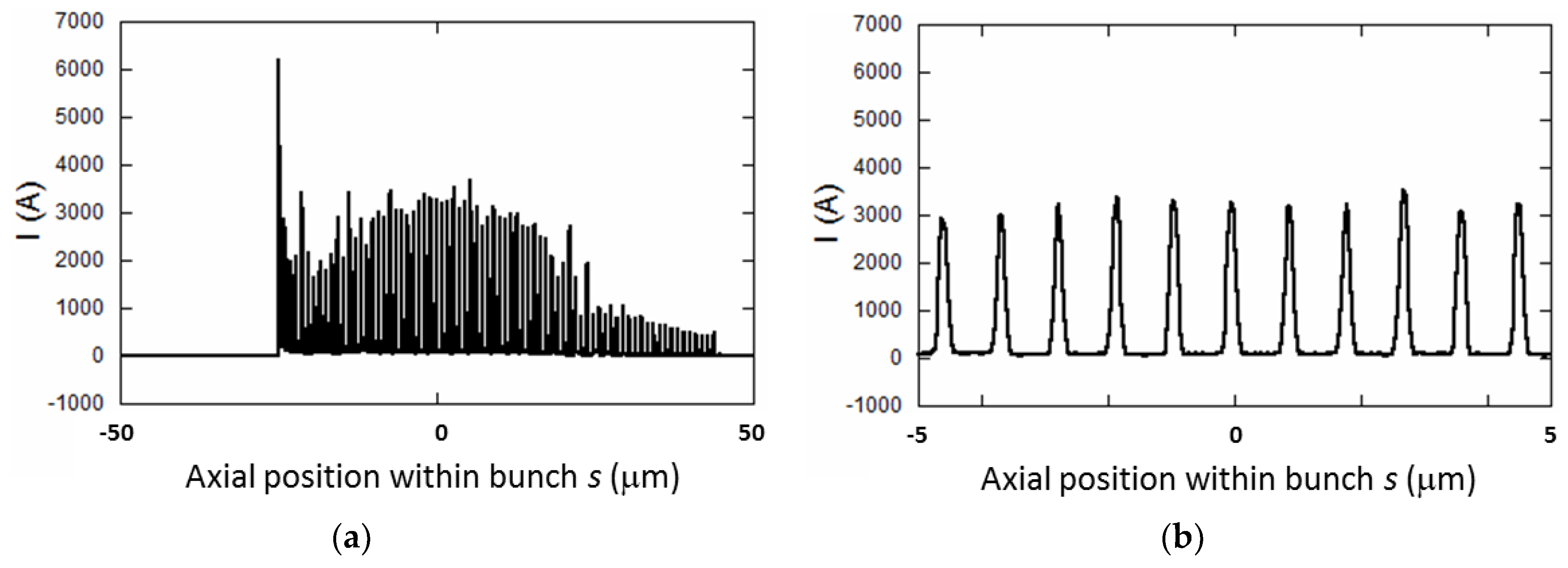
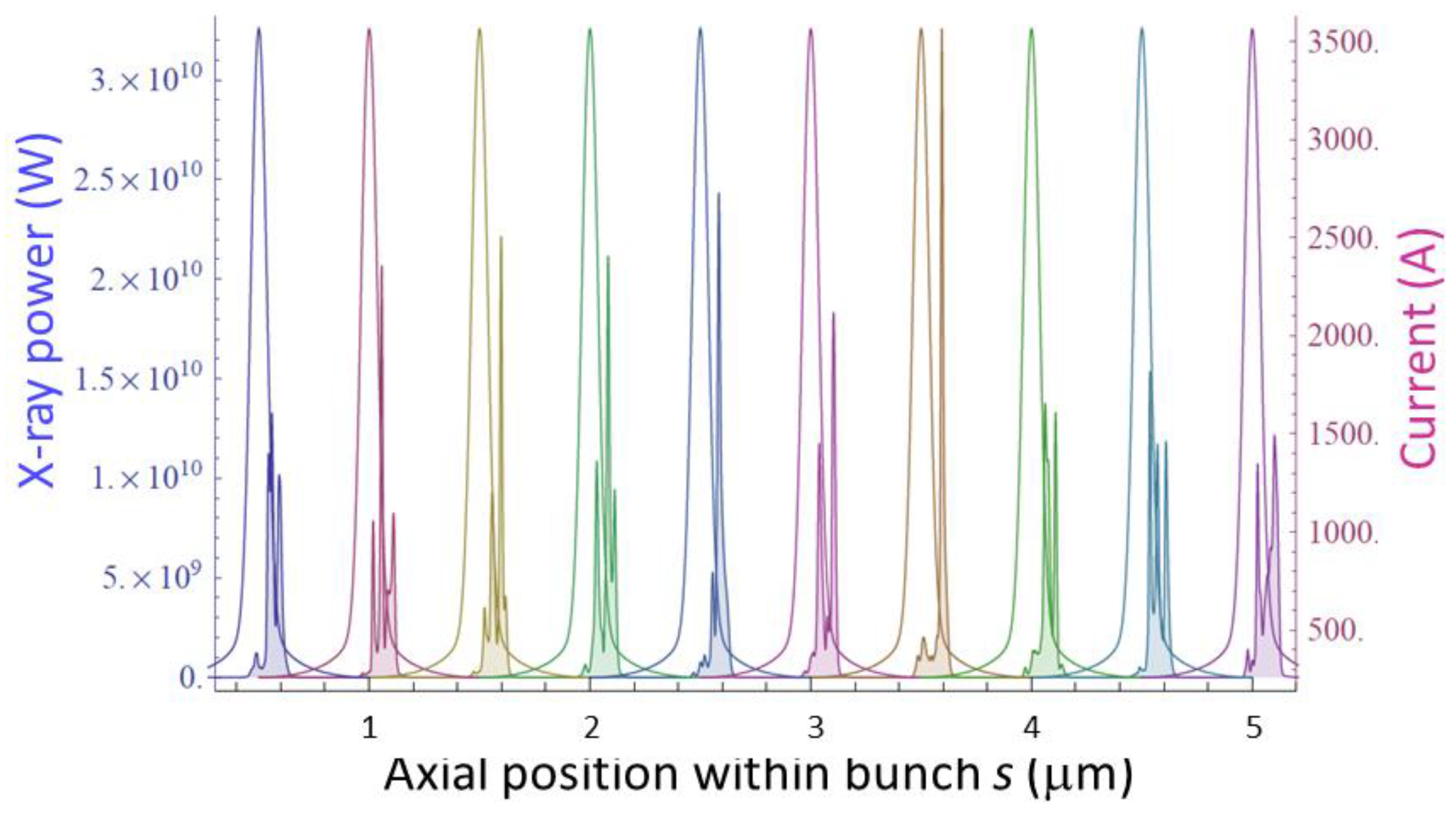
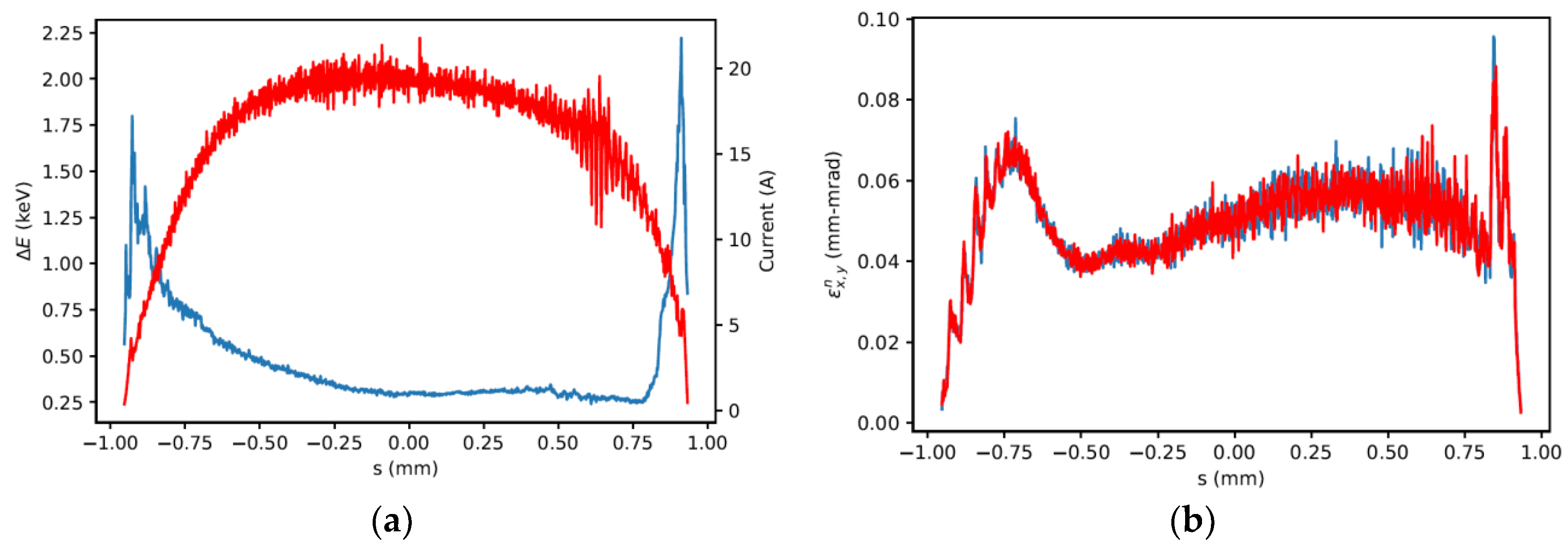
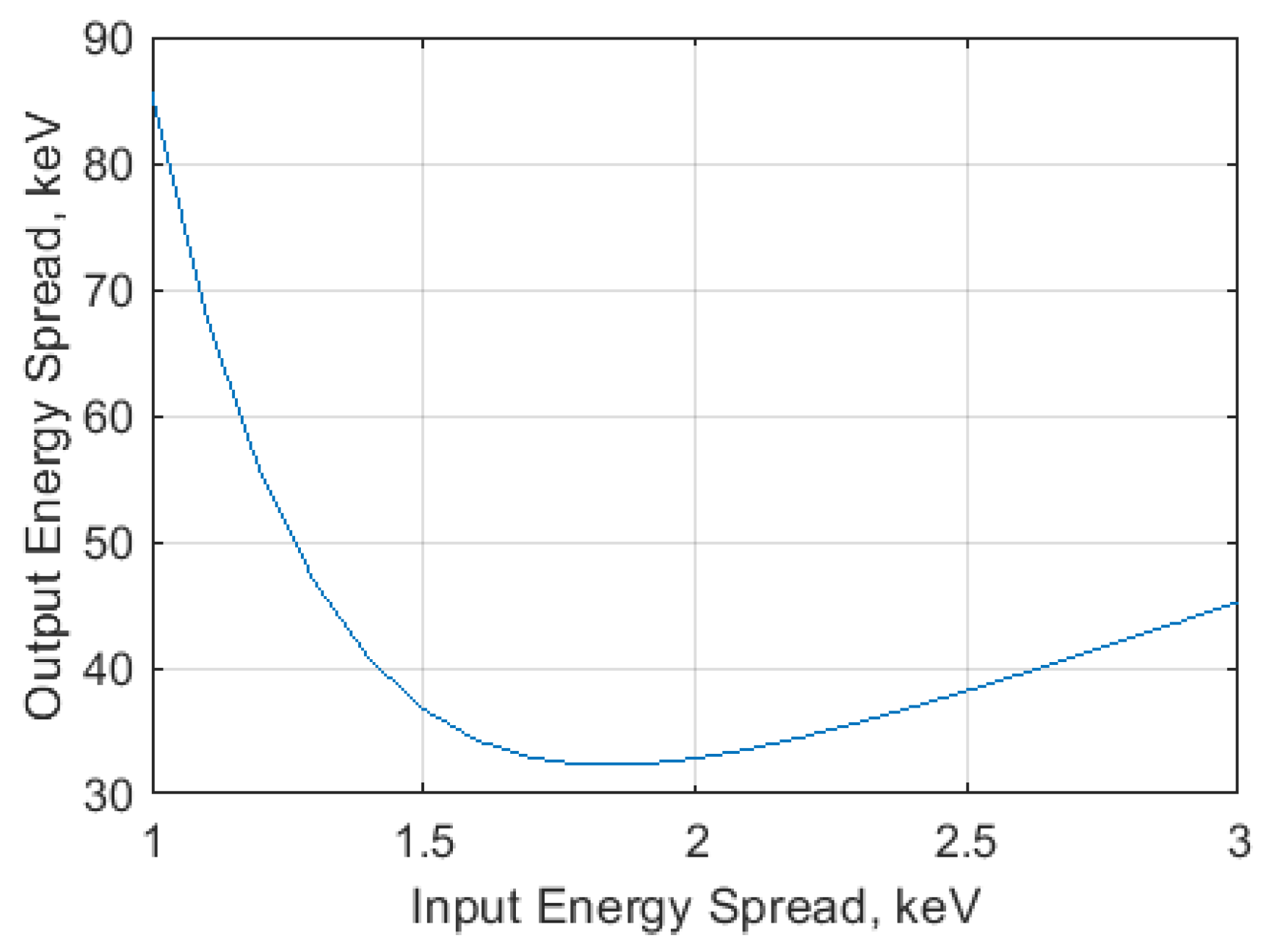
4.3. Application of Theory to a Point Design
5. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Juno—Mission to Jupiter. Available online: https://www.nasa.gov/mission_pages/juno/main/index.html (accessed on 22 September 2019).
- ITER—The Way to New Energy. Available online: https://www.iter.org/ (accessed on 22 September 2019).
- Wilson, L.A.; Rao, G.R. Frontiers of Materials Research, a Decadal Survey; National Academies Press: Washington, DC, USA, 2019. [Google Scholar]
- Dual Axis Radiographic Hydrodynamic Test Facility. Available online: https://www.lanl.gov/science-innovation/science-facilities/DARHT (accessed on 22 September 2019).
- Laser, Photonics, and Fusion Science: Science and Technology on a Mission. Available online: https://lasers.llnl.gov/ (accessed on 22 September 2019).
- Sheffield, R.L.; Barnes, C.W.; Tapia, J.P. Matter-radiation interactions in extremes (MaRIE) project overview. In Proceedings of the 38th International Free Electron Laser Conference, Santa Fe, NM, USA, 20–25 August 2017; pp. 24–28. [Google Scholar]
- Los Alamos Neutron Science Center. Available online: https://lansce.lanl.gov/ (accessed on 22 September 2019).
- National Nuclear Security Administration. Matter-Radiation Interactions in Extremes (MaRIE) Enterprise Requirements Validation Report. In Proceedings of the 38th International Free Electron Laser Conference, Santa Fe, NM, USA, 20–25 August 2017. [Google Scholar]
- Linac Coherent Light Source. Available online: https://lcls.slac.stanford.edu/ (accessed on 22 September 2019).
- Xie, M. Design optimization for an X-ray free electron laser driven by the SLAC linac. In Proceedings of the IEEE 1995 Particle Accelerator Conference, Dallas, TX, USA, 1–5 May 1995; IEEE Cat. No. 95CH35843. Volume 3, pp. 183–185. [Google Scholar]
- Russell, S.J.; Carlsten, B.E.; Duffy, L.D.; Krawczyk, F.L.; Lewellen, J.W., IV; Sheffield, R.L. MaRIE XFEL pre-conceptual reference design injector. In Los Alamos National Laboratory, Technical Report LA-UR-15-21963; Los Alamos National Laboratory: Los Alamos, NM, USA, 2010. [Google Scholar]
- Krasilnikov, M.; Stéphan, F.; Asova, G.; Grabosch, H.-J.; Gros, M.; Hakobyan, L.; Isaev, I.; Ivanisenko, Y.; Jachmann, L.; Khojoyan, M.; et al. Experimentally minimized beam emittance from anL-band photoinjector. Phys. Rev. Spéc. Top. Accel. Beams 2012, 15, 100701. [Google Scholar] [CrossRef]
- Lewellen, J.; Bishofberger, K.; Yampolsky, N.; Krawczyk, F.; Duffy, L.; Russell, S.; Sheffield, R.; Yampolsky, N. Status of the MaRIE X-FEL accelerator design. In Proceedings of the 6nd International Particle Accelerator Conference IPAC2015, Richmond, VA, USA, 3–8 May 2015; pp. 1894–1896. [Google Scholar]
- Saldin, E.L.; Schneidmiller, E.A.; Yurkov, M.V. Klystron instability of a relativistic electron beam in abunch compressor. Nucl. Instrum. Methods Phys. Res. A. 2002, 490, 1–8. [Google Scholar] [CrossRef]
- Lumpkin, A.H.; Thurman-Keup, R.; Edstrom, D.; Ruan, J.; Eddy, N.; Prieto, P.; Napoly, O.; Carlsten, B.E.; Bishofberger, K. Submacropulse electron-beam dynamics correlated with higher-order modes in Tesla-type superconducting rf cavities. Phys. Rev. Accel. Beams 2018, 21, 064401. [Google Scholar] [CrossRef]
- Carlsten, B.E. Tutorial on X-Ray Free-Electron Lasers. IEEE Trans. Plasma Sci. 2018, 46, 1900–1912. [Google Scholar] [CrossRef]
- Saldin, E.; Schneidmiller, E.; Yurkov, M. Calculation of energy diffusion in an electron beam due to quantum fluctuations of undulator radiation. Nucl. Instrum. Methods Phys. Res. Sect. A 1996, 381, 545–547. [Google Scholar] [CrossRef][Green Version]
- Cahill, A.D.; Rosenzweig, J.B.; Dolgashev, V.A.; Tantawi, S.G.; Weathersby, S. High gradient experiments with X-band cryogenic copper accelerating cavities. Phys. Rev. Accel. Beams 2018, 21, 102002. [Google Scholar] [CrossRef]
- Rosenzweig, J.; Cahill, A.; Carlsten, B.; Castorina, G.; Croia, M.; Emma, C.; Fukusawa, A.; Spataro, B.; Alesini, D.; Dolgashev, V.; et al. Ultra-high brightness electron beams from very-high field cryogenic radiofrequency photocathode sources. Nucl. Instrum. Methods Phys. Res. Sect. A 2018, 909, 224–228. [Google Scholar] [CrossRef]
- Carlsten, B.E.; Raubenheimer, T.O. Emittance growth of bunched beams in bends. Phys. Rev. E 1995, 51, 1453–1470. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, C.E.; Ryne, R.D.; Yampolsky, N.A.; Qiang, J.; Carlsten, B.E. Large scale simulation of synchrotron radiation using a Lienard-Wiechert approach. In Proceedings of the 3rd International Particle Accelerator Conference IPAC2012, New Orleans, LA, USA, 2–25 May 2012; pp. 1689–1691. [Google Scholar]
- Bane, K.L.F.; Stupakov, G. Resistive wall wakefield in the LCLS undulator. In Proceedings of the 2005 Particle Accelerator Conference, Knoxville, TN, USA, 16–20 May 2005; pp. 3390–3392. [Google Scholar]
- Huang, Z.; Wu, J. Microbunching instability due to bunch compression. In SLAC National Accelerator Laboratory Technical Report SLAC-PUB-11597; SLAC National Accelerator Laboratory: Stanford, CA, USA, 2005. [Google Scholar]
- Borland, M.; Chae, Y.; Emma, P.; Lewellen, J.; Bharadwaj, V.; Fawley, W.; Krejcik, P.; Limborg, C.; Milton, S.; Nuhn, H.-D.; et al. Start-to-end simulation of self-amplified spontaneous emission free electron lasers from the gun through the undulator. Nucl. Instrum. Methods Phys. Res. Sect. A 2002, 483, 268–272. [Google Scholar] [CrossRef]
- Wu, J. (Undulator) wakefield measurements at LCLS. In Proceedings of the Compact X-ray FELs Using High-Brightness Beams, Berkeley, CA, USA, 5–6 August 2010. [Google Scholar]
- Huang, Z.; Brachmann, A.; Decker, F.-J.; Ding, Y.; Dowell, D.; Emma, P.; Frisch, J.; Gilevich, S.; Hays, G.; Hering, P.; et al. Measurements of the linac coherent light source laser heater and its impact on the x-ray free-electron laser performance. Phys. Rev. Spéc. Top. Accel. Beams 2010, 13, 020703. [Google Scholar] [CrossRef]
- Borland, M. Elegant: A flexible SDDS-compliant code for accelator simulation. In Argonne National Laboratory Technical Report Advanced Photon Source LS-287; Argonne National Laboratory: Lemont, IL, USA, 2000. [Google Scholar]
- Lewellen, J.W. (Los Alamos National Laboratory, Los Alamos, NM, USA). Private communication, 2019.
- Marksteiner, Q.R.; Anisimov, P.M.; Lewellen, J.W.; Yampolsky, N.A.; Carlsten, B. Using Laser Compression to Enhance Hard X-Ray FEL Performance; LA-UR-13-23470; Los Alamos National Laboratory: Los Alamos, NM, USA, 2013.
- Zholents, A.A. Method of an enhanced self-amplified spontaneous emission for x-ray free electron lasers. Phys. Rev. Spéc. Top. Accel. Beams 2005, 8, 040701. [Google Scholar] [CrossRef]
- Hemsing, E.; Stupakov, G.; Xiang, D.; Zholents, A. Beam by design: Laser manipulation of electrons in modern accelerators. Rev. Mod. Phys. 2014, 86, 897–941. [Google Scholar] [CrossRef]
- Reiche, S. GENESIS 1.3: A fully time-dependent FEL simulation code. Nucl. Instrum. Methods Phys. Res. A 1999, 429, 243–248. [Google Scholar] [CrossRef]
- Sudar, N.; Musumeci, P.; Gadjev, I.; Sakai, Y.; Fabbri, S.; Polyanskiy, M.; Pogorelsky, I.; Fedurin, M.; Swinson, C.; Kusche, K.; et al. Demonstration of Cascaded Modulator-Chicane Microbunching of a Relativistic Electron Beam. Phys. Rev. Lett. 2018, 120, 114802. [Google Scholar] [CrossRef] [PubMed]
- Derbenev, Y.S.; Rossbach, J.; Saldin, E.L.; Shiltsev, V.D. Microbunch radiative tail-head interaction. In DESY Technical Report TESLA-FEL 95-05; Deutsches Elektronben-Synchrotron: Hamburg, Germany, 1995. [Google Scholar]
- Robles, R. Bunch compression studies for a compact X-ray free electron laser. In Proceedings of the High Energy X-ray FELs Workshop, Santa Fe, NM, USA, 9–11 July 2019. [Google Scholar]
- Robles, R. (UCLA, Los Angeles, CA, USA). Private communication, 2019.












© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carlsten, B.E.; Anisimov, P.M.; Barnes, C.W.; Marksteiner, Q.R.; Robles, R.R.; Yampolsky, N. High-Brightness Beam Technology Development for a Future Dynamic Mesoscale Materials Science Capability. Instruments 2019, 3, 52. https://doi.org/10.3390/instruments3040052
Carlsten BE, Anisimov PM, Barnes CW, Marksteiner QR, Robles RR, Yampolsky N. High-Brightness Beam Technology Development for a Future Dynamic Mesoscale Materials Science Capability. Instruments. 2019; 3(4):52. https://doi.org/10.3390/instruments3040052
Chicago/Turabian StyleCarlsten, Bruce E., Petr M. Anisimov, Cris W. Barnes, Quinn R. Marksteiner, River R. Robles, and Nikolai Yampolsky. 2019. "High-Brightness Beam Technology Development for a Future Dynamic Mesoscale Materials Science Capability" Instruments 3, no. 4: 52. https://doi.org/10.3390/instruments3040052
APA StyleCarlsten, B. E., Anisimov, P. M., Barnes, C. W., Marksteiner, Q. R., Robles, R. R., & Yampolsky, N. (2019). High-Brightness Beam Technology Development for a Future Dynamic Mesoscale Materials Science Capability. Instruments, 3(4), 52. https://doi.org/10.3390/instruments3040052





