Output Power Limit in Energy Harvesting Systems Based on Magnetic Induction Incorporating High-Frequency Effects
Abstract
:1. Introduction
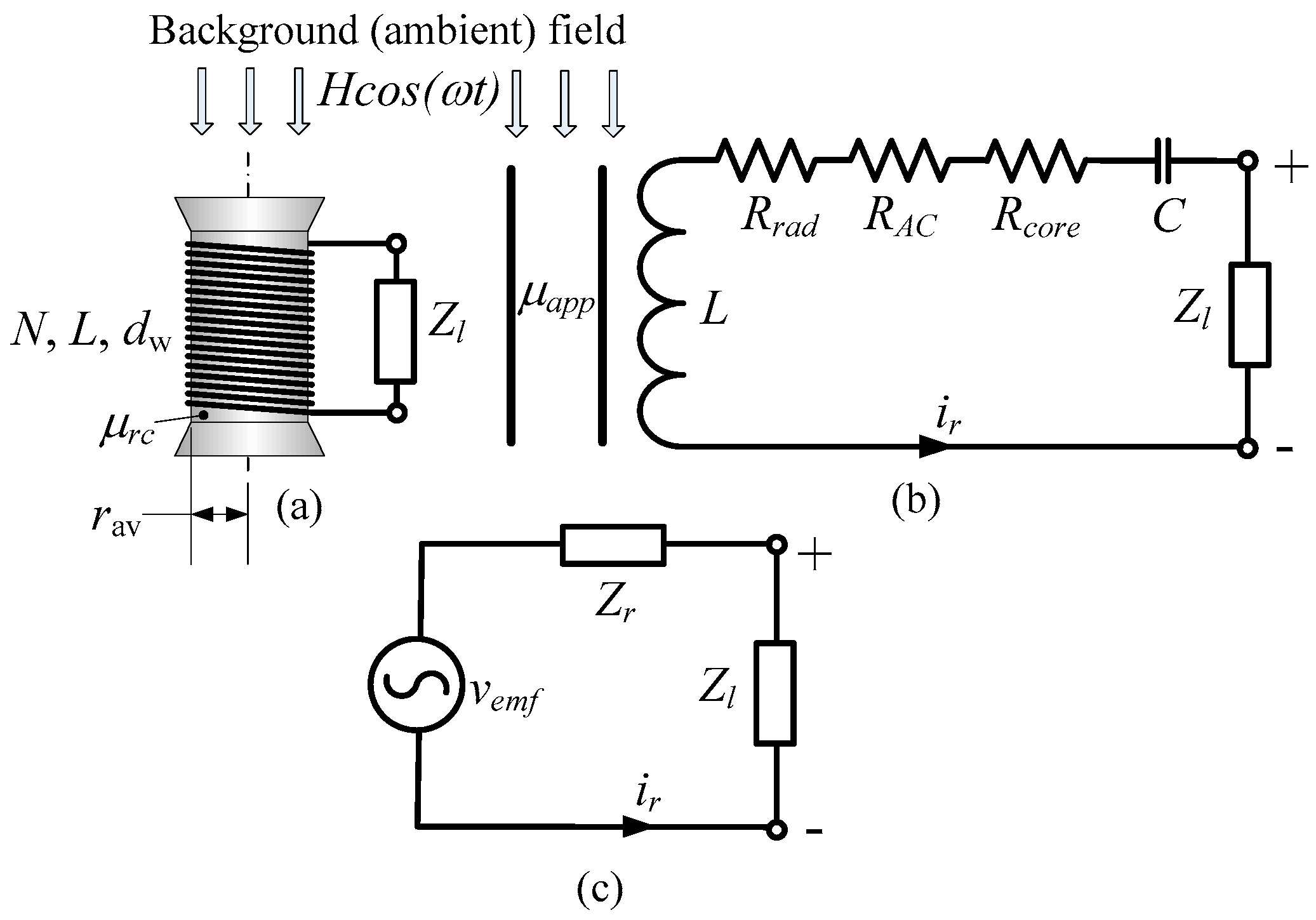
2. Maximal Received Power in Receiver Coil Subjected to a Given Ambient Magnetic Field
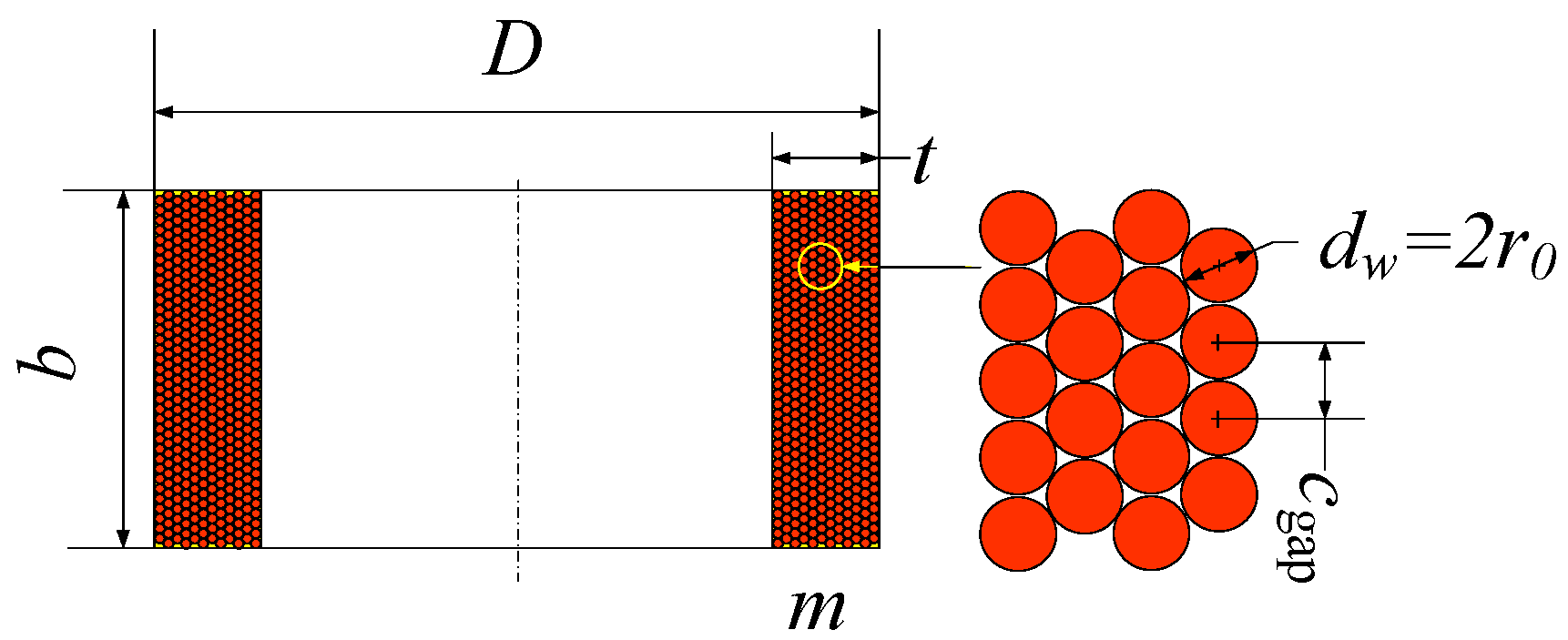
3. Resistance Terms of the Equivalent Circuit
4. Explicit Power Expressions
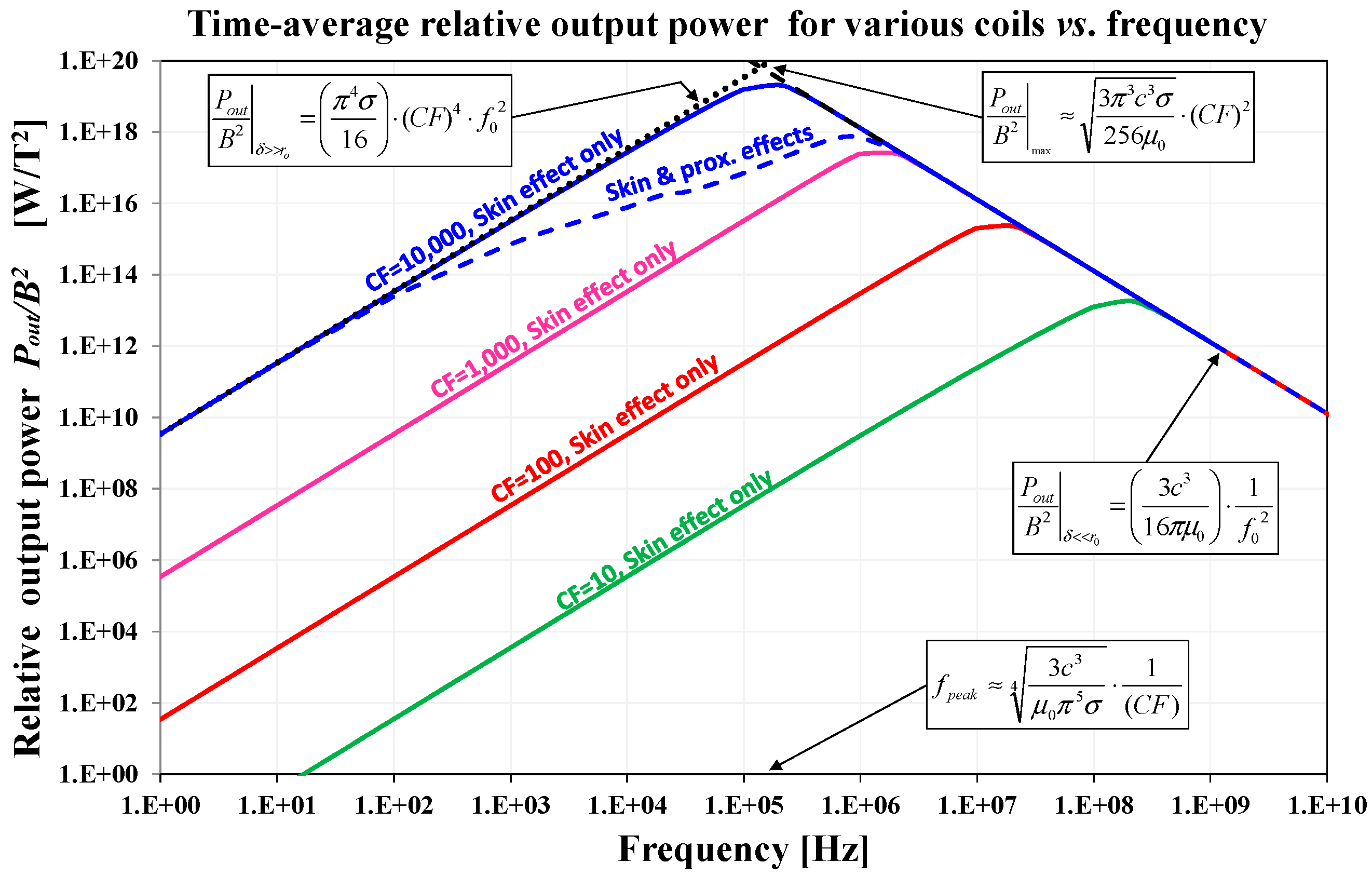
5. Results
6. Discussion
7. Comparison with Existing Literature
8. Summary and Conclusions
Author Contributions
Conflicts of Interest
References
- Shashank Priya, E.; Inman, D.J. Energy Harvesting Technologies; Springer Science+Business Media: New York, NY, USA, 2009. [Google Scholar]
- Olivo, J.; Carrara, S.; de Micheli, G.; de Micheli, G. Energy Harvesting and Remote Powering for Implantable Biosensors. IEEE Sens. J. 2011, 11, 1573–1586. [Google Scholar] [CrossRef]
- Roscoe, N.; Judd, M.D.; Fitch, J. Development of magnetic induction energy harvesting for condition monitoring. In Proceedings of the 44th International Universities Power Engineering Conference (UPEC), Glasgow, UK, 1–4 September 2009; pp. 1–5. [Google Scholar]
- Chen, Y.-C.; Yu, S.-C.; Cheng, S.-H.; Cheng, Y.-T. A Flexible Inductive Coil Tag for Household Two-Wire Current Sensing Applications. IEEE Sens. J. 2012, 12, 2129–2134. [Google Scholar] [CrossRef]
- Roscoe, N.M.; Judd, M.D. Harvesting Energy from Magnetic Fields to Power Condition Monitoring Sensors. IEEE Sens. J. 2013, 13, 2263–2270. [Google Scholar] [CrossRef]
- Santos, M.P.D.; Vieira, D.A.; Rodriguez, Y.P.M.; de Souza, C.P.; de Moraes, T.O.; Freire, R.C.S. Energy harvesting using magnetic induction considering different core materials. In Proceedings of the 2014 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Montevideo, Uruguay, 12–15 May 2014; pp. 942–944. [Google Scholar]
- Yuan, S.; Huang, Y.; Zhou, J.; Xu, Q.; Song, C.; Thompson, P. Magnetic Field Energy Harvesting Under Overhead Power Lines. IEEE Trans. Power Electron. 2015, 30, 6191–6202. [Google Scholar] [CrossRef]
- Vieira, D.A.; Santos, M.P.; Costa, A.C.F.M.; Souza, C.P. Ni-Zn Ferrite Core Characterization for Magnetic-based Energy Harvesting Application. IEEE Lat. Am. Trans. 2016, 14, 4070–4075. [Google Scholar] [CrossRef]
- Tsunoda, Y.; Tsuchiya, C.; Segawa, Y.; Sawaya, H.; Hasegawa, M.; Ishigaki, S.; Ishibashi, K. A small-size energy-harvesting electric power sensor for implementing existing electrical Appliances into HEMS. IEEE Sens. J. 2016, 16, 457–463. [Google Scholar] [CrossRef]
- Jiang, W.; Lu, J.; Li, F.; Hashimoto, S.; Lin, Z. A non-intrusive magnetic energy scavanger for renewable power generation state monitoring. In Proceedings of the 2016 IEEE International Conference on Renewable Energy Research and Applications (ICRERA), Birmingham, UK, 20–23 November 2016; Volume 5, pp. 562–566. [Google Scholar]
- Arnold, D.P. Review of microscale magnetic power generation. IEEE Trans. Magn. 2007, 43, 3940–3951. [Google Scholar] [CrossRef]
- Priya, S.; Inman, D.J. Electromagnetic energy harvesting. In Proceedings of the International Conference on Robotics and Mechatronics (IcRoM 2018), Tehran, Iran, 23–25 October 2018; pp. 322–325. [Google Scholar]
- Mallick, D.; Paul, K.; Roy, S. Design Optimization of Fully Integrated, MEMS Electromagnetic Energy Harvesting Devices using Patterned Micro-magnet Arrays. In Proceedings of the 2018 IEEE 18th International Conference on Nanotechnology (IEEE-NANO), Cork, Ireland, 23–26 July 2018; pp. 1–3. [Google Scholar]
- Gulbahar, B. Energy Harvesting and Magneto-Inductive Communications With Molecular Magnets on Vibrating Graphene and Biomedical Applications in the Kilohertz to Terahertz Band. IEEE Trans. Mol. Biol. Multi-Scale Commun. 2018, 3, 194–206. [Google Scholar] [CrossRef]
- Li, C.; Shuai, W.; Luk, P.; Gu, M.; Jiao, Z. Enhanced Bandwidth Nonlinear Resonance Electromagnetic Human Motion Energy Harvester Using Magnetic-Springs and Ferrofluid. IEEE/ASME Trans. Mechatronics 2019, 24, 710–717. [Google Scholar] [CrossRef]
- Roy, S.; Mallick, D.; Paul, K. MEMS-Based Vibrational Energy Harvesting and Conversion Employing Micro-/Nano-Magnetics. IEEE Trans. Magn. 2019, PP, 1–15. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, J.; Lan, D.; Chao, K.K.; Liou, S.; Shahnasser, H.; Fechter, R.; Hirose, S.; Harrison, M.; Roy, S. A low-frequency versatile wireless power transfer technology for biomedical implants. IEEE Trans. Biomed. Circuits Syst. 2013, 7, 526–535. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Kim, E.S. Vibration energy harvesting based on magnet and coil arrays for watt-level handheld power source. Proc. IEEE 2014, 102, 1747–1761. [Google Scholar] [CrossRef]
- Zhang, Q.; Kim, E.S. Micromachined energy-harvester stack with enhanced electromagnetic induction through vertical integration of magnets. J. Microelectromech. Syst. 2015, 24, 384–394. [Google Scholar] [CrossRef]
- Khan, F.U.; Iqbal, M. Electromagnetic-based bridge energy harvester using traffic-induced bridge’s vibrations and ambient wind. In Proceedings of the 2016 International Conference on Intelligent Systems Engineering (ICISE), Islamabad, Pakistan, 15–17 January 2016; pp. 380–385. [Google Scholar]
- Gatti, R.R.; Howard, I.M.; Lumentut, M.F. Design and simulation of core-ring magnet configurations for maximising energy transduction in linear actuators and micro-energy generators. In Proceedings of the 2016 International Conference on Energy Efficient Technologies for Sustainability (ICEETS), Nagercoil, India, 7–8 April 2016; pp. 796–801. [Google Scholar]
- Lee, B.-C.; Chung, G.-S. Design and analysis of a pendulum-based electromagnetic energy harvester using anti-phase motion. IET Renew. Power Gener. 2016, 10, 1625–1630. [Google Scholar] [CrossRef]
- Torres, E.; Ponce, P.; Molina, A. Electromagnetic induction generator toward energy harvesting for dynamic systems. In Proceedings of the 2017 IEEE International Conference on Industrial Technology (ICIT), Toronto, ON, Canada, 22–25 March 2017; pp. 418–422. [Google Scholar]
- Buccolini, L.; Conti, M. An Energy Harvester Interface for Self-Powered Wireless Speed Sensor. IEEE Sens. J. 2017, 17, 1097–1104. [Google Scholar] [CrossRef]
- Xu, Y.; Bader, S.; Oelmann, B. A Survey on Variable Reluctance Energy Harvesters in Low-Speed Rotating Applications. IEEE Sens. J. 2018, 18, 3426–3435. [Google Scholar] [CrossRef]
- Silva, M.T.P.; Vasconcelos, F.X.E.V.H. Temperature sensing system with short-range wireless sensor based on inductive coupling. IEEE Sens. J. 2011, 11, 2469–2478. [Google Scholar] [CrossRef]
- Leon-salas, W.D.; Halmen, C. A RFID sensor for corrosion monitoring in concrete. IEEE Sens. J. 2016, 16, 32–42. [Google Scholar] [CrossRef]
- Salas, M.; Focke, O. Wireless power transmission for structural health monitoring of fiber-reinforced-composite materials. IEEE Sens. J. 2014, 14, 2171–2176. [Google Scholar] [CrossRef]
- Chen, W.; Yan, G.; He, S.; Ke, Q.; Wang, Z.; Liu, H. Wireless powered capsule endoscopy for colon diagnosis and treatment. Physiol. Meas. 2013, 34, 1545–1651. [Google Scholar] [CrossRef]
- Poon, A.S.Y.; O’Driscoll, S.; Meng, T.H. Optimal operating frequency in wireless power transmission for implantable devices. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; pp. 5673–5678. [Google Scholar]
- Poon, A.S.Y.; O’driscoll, S.; Meng, T.H. Optimal frequency for wireless power transmission into dispersive tissue. IEEE Trans. Antennas Propag. 2010, 58, 1739–1750. [Google Scholar] [CrossRef]
- Sun, T.; Xie, X.; Wang, Z. Wireless Power Transfer for Medical Microsystems, 1st ed.; Springer: New York, NY, USA; Heidelberg, Germany; Dordrecht, The Netherlands; London, UK, 2013. [Google Scholar]
- Kong, S.; Kim, M.; Koo, K.; Ahn, S.; Bae, B.; Kim, J. Analytical expressions for maximum transferred power in wireless power transfer systems. In Proceedings of the 2011 IEEE International Symposium on Electromagnetic Compatibility, Long Beach, CA, USA, 14–19 August 2011; pp. 379–383. [Google Scholar]
- Qusba, A.; RamRakhyani, A.K.; So, J.-H.; Hayes, G.J.; Dickey, M.D.; Lazzi, G. On the design of microfluidic implant coil for flexible telemetry system. IEEE Sens. J. 2014, 14, 1074–1080. [Google Scholar] [CrossRef]
- Lu, C.; Raghunathan, V.; Roy, K. Efficient design of micro-scale energy harvesting systems. IEEE J. Emerg. Sel. Top. Circuits Syst. 2011, 1, 254–266. [Google Scholar] [CrossRef]
- Cepnik, C.; Wallrabe, U.; Radler, O.; Rosenbaum, S.; Strohla, T. On a novel optimization approach of electromagnetic energy harvesters. In Proceedings of the 2011 Fourth International Conference on Modeling, Simulation and Applied Optimization, Kuala Lumpur, Malaysia, 19–21 April 2011; Volume 1, pp. 1–6. [Google Scholar]
- Silay, K.M.; Dehollain, C.; Declercq, M. A closed-loop remote powering link for wireless cortical implants. IEEE Sens. J. 2013, 13, 3226–3235. [Google Scholar] [CrossRef]
- Ramrakhyani, A.K.; Mirabbasi, S.; Chiao, M. Design and optimization of resonance-based efficient wireless power delivery systems for biomedical implants. IEEE Trans. Biomed. Circuits Syst. 2011, 5, 48–63. [Google Scholar] [CrossRef]
- Morag, Y.; Tal, N.; Nazarathy, M.; Levron, Y. Thermodynamic Signal to Noise and Channel Capacity Limits of Magnetic Induction Sensors and Communication Systems. IEEE Sens. J. 2016, 16, 1575–1585. [Google Scholar] [CrossRef]
- Morag, Y.; Tal, N.; Levron, Y. Power Transfer Limits and optimal operation frequency in Induction Power Transfer Systems Incorporating High-frequency effects. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Anacapri, Italy, 22–24 June 2016; pp. 79–84. [Google Scholar]
- Śran, H.C.; Fergeau, P. An optimized low-frequency three-axis search coil magnetometer for space research. Rev. Sci. Instrum. 2005, 76, 1–10. [Google Scholar]
- Slawomir, T. Induction coil sensors—A review. Meas. Sci. Technol. 2007, 18, R31. [Google Scholar]
- Coillot, C.; Leroy, P. Induction Magnetometers Principle, Modeling and Ways of Improvement. In Magnetic Sensors Principles and Applications; Kuang, K., Ed.; InTechOpen: Rijeka, Croatia, 2012. [Google Scholar]
- Lehner, G. Time-dependent problems I (Quasi-stationary approximation). In Electromagnetic Field Theory for Engineers and Physicists; Springer: Berlin/Heidelberg, Germany, 2010; pp. 369–404. [Google Scholar]
- Terman, F.E. Inductance and mutual inductance. In Radio Engineer’s Handbook; McGraw-Hill Book Company: New York, NY, USA, 1943; Volume 28, pp. 60–62. [Google Scholar]
- Balanis, C.A. Loop antenna. In Antenna Theory-Analysis and Design; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005; pp. 231–260. [Google Scholar]
- Kraus, J.D.; Marhefka, R.J. The loop antenna. In Antennas for All Applications, 3rd ed.; McGraw-Hill Book Company: New York, NY, USA, 2002; pp. 217–219. [Google Scholar]
- Kraus, J.D.; Marhefka, R.J. Self and mutual impedances. In Antennas for All Application; McGraw-Hill Book Company: New York, NY, USA, 2002; pp. 438–440. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morag, Y.; Levron, Y. Output Power Limit in Energy Harvesting Systems Based on Magnetic Induction Incorporating High-Frequency Effects. Instruments 2019, 3, 26. https://doi.org/10.3390/instruments3020026
Morag Y, Levron Y. Output Power Limit in Energy Harvesting Systems Based on Magnetic Induction Incorporating High-Frequency Effects. Instruments. 2019; 3(2):26. https://doi.org/10.3390/instruments3020026
Chicago/Turabian StyleMorag, Yahav, and Yoash Levron. 2019. "Output Power Limit in Energy Harvesting Systems Based on Magnetic Induction Incorporating High-Frequency Effects" Instruments 3, no. 2: 26. https://doi.org/10.3390/instruments3020026
APA StyleMorag, Y., & Levron, Y. (2019). Output Power Limit in Energy Harvesting Systems Based on Magnetic Induction Incorporating High-Frequency Effects. Instruments, 3(2), 26. https://doi.org/10.3390/instruments3020026




