1. Introduction
On 9 January 2023, K. Alex Müller (Alex), Nobel Prize Winner, Fellow of IBM, Professor of Physics at the University of Zurich and multiple Honorary Doctor of Physics, passed away peacefully in his 95th year (Figure 1). During his long life, he devoted many years to solid-state physics, with an emphasis on perovskites, their characterization and their peculiar and unique properties, which led to breakthrough discoveries and culminated in his Nobel prize-winning detection of high-temperature superconductivity in cuprate ceramics. This latter achievement caused a world-wide turn in physics with promising expectations for new applications, novel device techniques, unique power supplies, etc.

Figure 1.
K. Alex Müller (Alex), Tertianum Zollikerberg (Zurich), 2022. (Photo ABH).
A side effect of being awarded this highest prize in physics was that Alex became famous worldwide, and his life story became known to almost every interested researcher in the field. This raises the question of what else can be said about him. Hugo Keller (HK) met Alex for the first time in the early 1970s, and Annette Bussmann-Holder (ABH) later that same decade (see Figure 2). By this time, Alex was already famous and internationally known. Both of us were just postdocs and at the beginning of our scientific career. These first encounters were therefore experienced with reverence, admiration and respect. Amazingly, from then on, years of collaborations ensured, followed by years of friendship, which lasted until he passed away. Since our first meetings differed substantially, we will tell each of these stories individually. Both narrations converge with the authors’ first meeting with each other, since, from that point on, Alex brought us together through bout science and friendship. Below are some of Alex’s many guiding principles:
“In order to be an irreproachable member of a flock of sheep, most notably one has to be a sheep”(Albert Einstein)
“People with courage and character always seem sinister to the rest”(Hermann Hesse)
“To achieve the possible, we must attempt the impossible again and again”(Hermann Hesse)

Figure 2.
Left side: Alex and ABH, Tertianum Zollikerberg (Zurich), 6 May 2019. (Photo HK). Right side: Alex and HK, Tertianum Zollikerberg, 14 September 2022. (Photo ABH).
2. First Encounters and Scientific Interactions with HK
As a teenager, I devoured books on scientific subjects, and I was particularly fascinated by physics. I set up a small laboratory in the basement of our house where I carried out physics experiments, made simple electronic devices and built airplane models. When I was 14 years old, I already knew that I wanted to study physics, and this wish came true. As a physics student at ETH Zurich, I attended a special lecture by Prof. Werner Känzig in the winter semester of 1971/72 entitled “Phasenumwandlungen und kritische Phänomene” (“Phase transitions and critical phenomena”), a research topic that was very prevalent at the time and which I was enthusiastic about. It was in this lecture that I first heard about the groundbreaking work of K. Alex Müller and Walter Berlinger on strontium titanate (STO) performed at the IBM Research Laboratory in Rüschlikon (see Figure 3) [1]. The two authors studied the temperature dependence of the order parameter (rotation angle of the octahedra in STO) at the structural phase transition temperature in STO and showed that this deviates from the classical mean-field Landau theory in the immediate vicinity below . The critical exponent was found to be and not as predicted by mean-field theory, demonstrating for the first time that the critical behavior of the order parameter in a second-order structural phase transformation is universal (see Figure 4) [1]. As a young student, I was very impressed by this brilliant work.

Figure 3.
Excerpt from the lecture notes “Phasenumwandlungen und kritische Phänomene” by Prof. W. Känzig (ETH Zurich). The picture shows the twisting of the octahedra below the critical temperature of STO as described by Müller and Berlinger in Ref. [1].
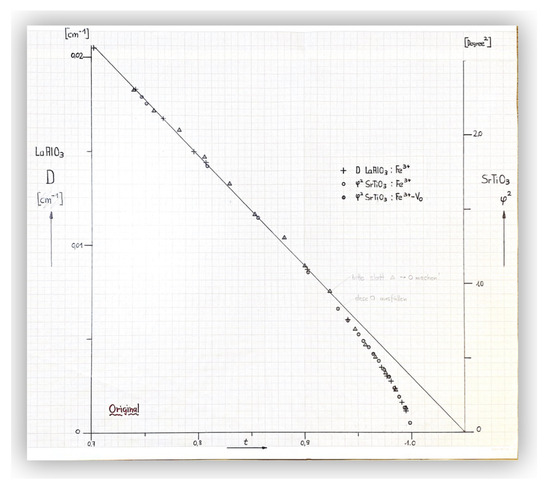
Figure 4.
of STO and crystal field parameter D of versus reduced temperature in the range , showing the crossover from mean-field Landau to critical behavior at . This is the original hand drawn figure by K. Alex Müller and Walter Berlinger published in Ref. [1]. (Photo HK).
STO remained Alex’s “favorite child” throughout his scientific career from his PhD thesis (see Figure 5) [2] in 1958 until old age [3,4]. In a recent highlight of Physical Review B [5] it was even argued that the Müller–Burkard paper [6] initiated the discovery of high-temperature superconductivity in cuprates [7]. The Editors of Physical Review made the following statement [5]: “Müller’s deep understanding of the promise of perovskites such as led to the discovery with J.G. Bednorz in 1986 of a new class of superconductors, which earned them the Nobel Prize for Physics in the year 1987”.
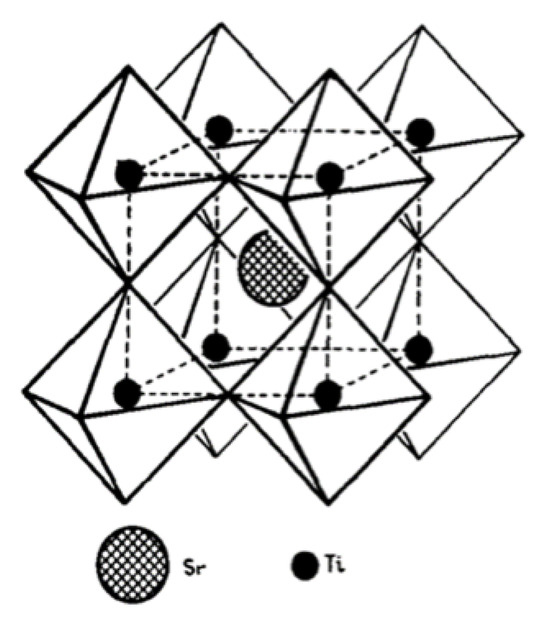
Figure 5.
Crystal structure of (STO). Figure taken from Alex’s PhD thesis [2].
After my studies at the ETH, I moved to the University of Zurich at the end of 1973 to work on a doctoral thesis in Prof. Walter Kündig’s group. Alex was a private lecturer at the University of Zurich at that time. One day in 1974, Alex stood at the door of my laboratory and briefly introduced himself (of course, I already knew who he was!). He told me: “I am going to give a special lecture on Group Theory and Quantum Mechanics the next semester. Would you be interested in taking part?” I enthusiastically agreed. That was my first personal encounter with Alex—my last meeting with Alex was just before Christmas 2022. There are almost 50 years in between.
We were just a few students in the “Group Theory and Quantum Mechanics” lecture, which was very demanding, but thanks to his profound knowledge, his charming manner and his proverbial humor, Alex guided us safely through the course and established a fatherly relationship with us students (see Figure 6). At the end of the semester, he invited us all to a cozy meal in a fine restaurant.

Figure 6.
Excerpt from Alex’s copy of Group Theory and Quantum Mechanics by Michael Tinkham, which he used for the lecture. The book is littered with his personal handwritten notes. (Photo HK).
Was it coincidence or providence that the subject of my doctoral thesis was in the field of phase transitions and critical phenomena, an area in which Alex was doing intensive research at the IBM Research Laboratory? Using the Mössbauer effect, I investigated the critical behavior of the order parameter of the antiferromagnetic layer structure (CH3NH3)2FeCl4 [8,9]. When I showed Alex my first results, he was very enthusiastic and invited me to give a talk at IBM to present my work (Alex was the first to recognize the importance of my findings). As a young PhD student, I felt very honored and proud to give a talk at this prestigious laboratory—Alex was then already a world-renowned expert in the field of structural phase transitions, critical phenomena and ferroelectricity.
After my doctorate, I took up a postdoctoral position at the University of Illinois at Urbana-Champaign (USA), where I turned to a completely new field of research, namely, biomolecular physics. In 1980, I presented my work on oxymyoglobin [10] at the APS March Meeting in New York, where I met Alex again after almost two years. He told me that he was on sabbatical at the IBM Research Center in Yorktown Heights (USA) and now working on superconductivity in granular materials.
After my return to the Physics Institute at the University of Zurich in 1980, I resumed my earlier research work in the field of phase transformations and critical phenomena and wrote a habilitation thesis on this subject [11]. Alex, who regularly attended the weekly solid-state physics seminar at the Physics Institute, was very interested in my work. Therefore, at that time, I often visited the IBM Research Laboratory in Rüschlikon to discuss with Alex and his colleagues and to attend lectures and conferences. It was always a great and enriching pleasure for me to discuss science and other topics with Alex. Despite his profound expertise and acumen, he always made me feel like an equal interlocutor thanks to his warm-hearted charisma, which I appreciated a lot.
Between the years 1983 and 1986, Alex came to the Physics Institute very rarely (I refer to this period as the “Dark Age with Alex”). I was worried that he had lost interest in the Physics Institute or was even ill. Every year at the beginning of December, there was a small Christmas party for all the staff at the Physics Institute. On 5 December 1986, there was another Christmas party, and I was very pleased that Alex was also present and in good health. After the meal, Alex invited me to his table. Over a glass of wine, he confided to me: “Next Wednesday I will be reporting on a new type of compound, a perovskite, which is superconducting. That might interest you, since you have also worked with perovskites.” In this seminar (see Figure 7), he announced his groundbreaking discovery, which he made together with J.G. Bednorz (see Figure 8) [7], in public—and I was there as a witness. I don’t think everyone present in the lecture hall recognized the significance of this great discovery—but I was very surprised and deeply impressed! After his lecture Alex, Georg Bednorz (Georg), Walter Kündig and I celebrated the great discovery in an Italian restaurant with an excellent meal and a good glass of wine. Afterwards, I gave a physics lecture for prospective secondary school teachers. I think it was one of the “best” lectures I have ever given.

Figure 7.
Announcement of the seminar by Alex on 10 December 1986 at the Physics Institute of the University of Zurich. (University of Zurich (UZH) Archive).

Figure 8.
Excerpt (“Discussion”) from a handwritten draft of the 1986 Nobel Prize paper of J.G. Bednorz and K.A Müller [7] by Alex. (UZH Archive).
Soon after Alex’s seminar presentation, we received the first samples of these novel cuprate high-temperature superconductors (HTSs) from Georg for muon spin-rotation (SR) experiments. At that time, we were one of the world’s leading groups conducting SR studies in magnetic solids at the Paul Scherrer Institute (PSI) in Villigen (Switzerland). The PSI had, and still has today, the best accelerator facility for the production of high-intensity spin-ploarized muon beams. In the SR technique, the spin-polarized positive muon () serves as a very sensitive microscopic magnetic probe of the local magnetic field at the muon stopping site in a magnetic solid, such as a magnetically ordered system or a superconductor. Alex immediately recognized the power and uniqueness of SR for investigating the microscopic magnetic and electronic properties of the newly discovered cuprate HTSs. Indeed, over the years SR experiments have made many important contributions to the understanding of the complex properties of cuprate HTSs which may not directly be achieved by other experimental techniques (some prominent examples are presented here). In 1987, my first joint paper with Alex and Georg dealing with a SR study of cuprate HTSs was published [12].
At the beginning of 1988, the first major international conference High Temperature Superconductors, Materials and Mechanisms of Superconductivity, HTSC-M2S was held in Interlaken (Switzerland), which was triggered by the groundbreaking discovery of Georg and Alex [7] and attended by numerous renowned scientists from all over the world. It was a great honor for me to present our latest SR results at this conference [13]. In this work, we investigated the internal magnetic fields in sintered YBa2Cu3O7−δ samples: hysteresis (field-cooling vs. zero-field cooling) and flux trapping effects, which were interpreted in terms of models of weakly coupled superconducting grains (granular superconductivity, glasslike superconducting states) [13,14], a research topic Alex was very interested in since he had started working on superconductivity [15].
SR is a very elegant and unique experimental tool used to determine the local magnetic field distribution in type 2 superconductors, from which the magnetic penetration depth —a fundamental quantity of a superconductor—can be determined directly [16]. Over the years, we performed a number of systematic SR studies of in YBa2Cu3O7−δ and other cuprate high-temperature superconductors (HTSs) (see, e.g., [16,17,18]). Somewhat later, using SR, we also succeeded for the first time in detecting flux-lattice melting (similar to the melting of ice into water) in the vortex phase in single-crystal Bi2.15Sr1.85CaCu2O8+δ at a microscopic level [19]. This first-order phase transition manifests itself in an abrupt change in the local magnetic field distribution at the melting temperature . Further important pioneering applications of the SR method for the investigation of fundamental properties of cuprate HTSs are presented below.
In 1988, the IBM Workshop on High-Temperature Superconductity took place in Oberlech (Austria), and many well-known and leading experts in the field took part. I was proud to be able to present our SR results to such a prestigious audience [20]. Two years later, Georg and Alex organized a two-week conference in the legendary Erice (Sicily) with the title Earlier and Recent Aspects of Superconductivity, where I introduced our work [21]—this conference has remained a particularly good memory for me, not least because Alex developed the idea of searching for superconductivity in systems with Jahn–Teller centers at a workshop entitled Statics and Dynamics of Nonlinear Systems in Erice in 1983, inspired by a theoretical model proposed by Harry Thomas and coworkers [22] at this workshop. It was a very eventful time for me in Erice.
After winning the Nobel Prize, Alex was a very sought-after person. He traveled a lot to give lectures, accept honors and take part in conferences. Our director of the Physics Institute at the time, Prof. Ernst Brun, provided Alex with a large office with a wonderful view of Zurich—it was a great honor for all of us to have a Nobel Prize winner at the Physics Institute. Unfortunately, Alex didn’t have much time to make extensive use of his office, because he was very busy and on the move a lot. I was a private lecturer at the University of Zurich at the time and had my office space in my lab surrounded by noisy vacuum pumps. One day, Alex came into my “office”. He said: “How can you work here in peace with all this noise! You should use my office, I am rarely here.” I didn’t quite dare to accept his generous offer. Some time later, he asked me if I had used his office. I said no. But he insisted that I do so in the future. So I was the only one at the Physics Institute who was allowed to work in the office of our Nobel Prize winner Alex Müller—and I did it with joy and pride!
I went to the IBM Research Laboratory almost every week to listen to lectures on current topics or to discuss new findings with Alex or Toni Schneider. At Alex’s suggestion, we—Alex, Emmanuel Kaldis (ETH Zurich) and I—organized a special “High- Seminar”, which took place alternately at the University of Zurich and at ETH Zurich with renowned speakers from all over the world. The so-called “Green Seminar” (the announcement was on green paper) was a great success in the Zurich area at the time.
In 1993, the Physics Institute moved from the University Center to the Campus Irchel into a newly constructed building with plenty of space. Alex was assigned a spacious office on the third floor, and I was given an office on the first floor. One day Alex stood in front of my office and said: “I feel very lost in my office. I would like to have the office next to yours, if it is possible, so we may have discussions when I am at the Institute.” I put Alex’s request to the head of the Institute and he immediately agreed. The only problem was that the office next to mine was much smaller. I suggested to Alex that we swap offices—as a Nobel laureate, he should have the larger office. But Alex insisted that he moves into the smaller office, saying: “Hugo, you have a research group with students, PhD students, and postdocs—you need a big office”. That’s Alex! That was a great honor and a stroke of luck for me: for more than twenty years, our offices were door-to-door (see Figure 9). Alex came to the Institute regularly, especially every Wednesday for the solid-state physics seminar (see Figure 7); it made no difference whether the speaker was a master’s student, a Ph.D. student or a well-known professor. The seminar was always very well attended with a very special atmosphere in the seminar room, mainly because of Alex’s presence—his informative comments and pointed questions testifying his broad and well-founded expertise.

Figure 9.
Alex’s “small” office at the Physics Institute at the University of Zurich, Campus Irchel, 10 April 2007. (Photo HK).
I have very fond memories of the many discussions I had with Alex over a cup of tea in his office. We discussed a wide range of topics, from physics to politics, history, literature and art, technology (especially cars) and C.G. Jung’s depth psychology, which he was particularly interested in (for more details, see Section 7). When Alex felt in his element, he would light up his tobacco pipe and smile—smoking was strictly forbidden in the university rooms! Alex was also a very gifted and accomplished storyteller, and it was always very exciting and thrilling for me to listen to him telling stories and anecdotes from his youth at the boarding school in Schiers (located in the Swiss Alps), from his student days at ETH Zurich, from his military service or from his private life with his black humor and a smile on his face. Of course, we also had many interesting discussions about our joint research projects and publications. Alex was my scientific role model and mentor and played a decisive role in shaping my scientific career—I am very grateful to him for that.
Back to science—In 1990, the Congress Ampere took place at the University of Stuttgart (Germany). Alex and I were accommodated in the same hotel, the “Dachswald”, which was located in a forest a little outside the campus in a beautiful area. Every morning, Alex and I walked to the conference together. One morning, Alex asked me if I would be interested in working with him on a new project. Of course, I agreed enthusiastically—it was the birth of our joint research enterprise on “Isotope Effects in Cuprate Superconductors” at the University of Zurich. At that time, the conventional wisdom was that the cuprate HTSs show no or only a negligibly small degree of oxygen (16O/18O) isotope effect (OIE) on the superconducting transition temperature [23]. Therefore, the majority of the community working in the field assumed that lattice effects play no or a minor role in the occurence of high-temperature superconducivity, and alternative pairing mechanisms of a purely electronic nature were proposed (see, e.g., [24]). Unfortunately, this assumption steered the whole field in the “wrong” direction! As a matter of fact, it was already well established in 1990 that although the OIE is small at optimal doping, it increases strongly with decreasing doping (see, e.g., [25,26,27]). This important experimental fact was overlooked or even ignored by many researchers at the time—but not by Alex. From the beginning, Alex was firmly convinced that the Jahn–Teller (JT) effect must play a decisive role in superconductivity in the cuprates and that the superconducting charge carriers should have a polaronic character, being reflected in a pronounced isotope effect on [28]. The goal of the isotope effect project that Alex envisioned was very ambitious: to investigate how the different oxygen atoms on the different lattice positions (plane (p), apex (a), and chain (c)) in optimally doped YBa2Cu3O6+x contribute to the total OIE on (site-selective oxygen isotope effect (SOIE)). Alex was convinced that the major contribution to the OIE on must come from the apex oxygen due a large anharmonicity associated with it [28].
First attempts to perform isotope effect studies of cuprate HTSs on partially and selectively oxygen-isotope-exchanged samples are described in the review article of Franck [27]. As a prominent example, we mention the early work of Cardona et al. [29], who investigated the Raman and infrared spectra of YBa2 and for various concentrations y of 16O substituted by 18O. No OIE on is observed if only one out of seven 16O is substituted by 18O. For a substitution of 85%, however, an isotope shift of is found, in agreement with previous results [27]. This clearly indicates that not all oxygen sites contribute equally to the isotope shift.
The preparation of the required partially substituted 16O/18O YBa2Cu3O6+x samples turned out to be extremely difficult. We used a new two-step exchange process which allowed us to prepare fully and site-selectively 16O/18O-exchanged YBa2Cu3Ox samples simultaneously [30,31]. After almost three years of hard and patient work, we finally succeeded in preparing and reproducing reliable samples. But shortly before reaching our goal, we became aware of a paper by Nickel et al. [32] presenting new results on the site-selective OIE on in . In this work, a reversed OIE of = +(0.10–0.14) was observed in samples where ≈95% of the CuO2 planes were occupied by 18O and the apex and chain sites by 16O. This means that a substantial contribution of the total OIE must arise from the apex/chain oxygens. This was an exciting result and exactly what Alex expected. But of course, we were also a little bit dejected, as we were overtaken by another research group shortly before the finish line. However, as this project was linked to Damian Zech’s doctoral thesis and we wanted to confirm the results of Nickel et al. [32], we continued. A few months later, we had the first revealing results [30,31]. To our great surprise, our results were in contrast to those of Ref. [32]: more than 80% of the total OIE on comes from oxygen atoms in the planes (see Figure 10) [31]. Did we perhaps make a mistake or even accidentally mix up the samples? A careful check confirmed the accuracy of our results. But the result was not as Alex had expected. I absolutely had to tell him this. I called Alex at home with a gloomy feeling: “Alex, we have the first meaningful results on the site-selective isotope effect—the main contribution comes from the oxygen atoms in planes, not from the apex oxygen.” There was silence on the phone for a while. Then Alex said: “Great, I would like to have a look at the results. I will be at the Physics Institute in the afternoon.” Alex didn’t doubt our results for a moment, but accepted them straight away. To complete the story, we were able to show that the results of Nickel et al. [32], which were performed on highly doped samples, make a reliable determination of a small isotope shift of by means of magnetization measurements very difficult and this is very likely the reason for the controversial results [30].
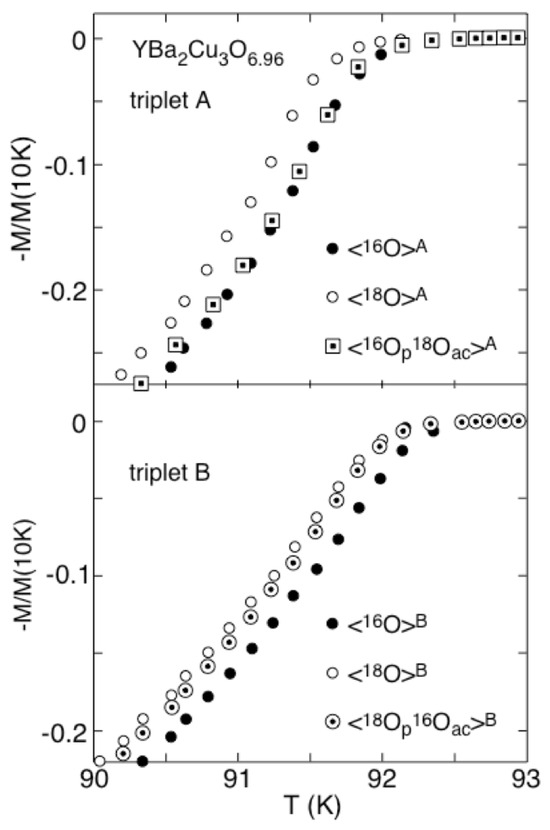
Figure 10.
Magnetization curves near , showing the SOIE in optimally doped for (triplet A) and (triplet B). The meaning of the symbols are as follows: triplet A: (16O at all oxygen sites), (18O at all oxygen sites), (16O at planar sites p, 18O at apex and chain sites ac); triplet B: (16O at all oxygen sites), (18O at all oxygen sites), (18O at planar sites p, 16O at apex and chain sites ac). It is evident from the figure that the planar oxygen mainly contributes to the total OIE on (after Ref. [31]).
The SOIE results of optimally doped YBa2Cu3O7−δ shown in Figure 10 [31] were complemented by further SOIE studies of () [33,34]. In Figure 11 the OIE exponent (where is the oxygen isotope mass) for is plotted as function of . It is obvious that the major contribution to the total OIE on arises from the planar oxygens at all doping levels x. Over the years, we have performed a number of OIE studies on in different families of cuprate HTSs (see, e.g., [35,36,37,38]). All families clearly show a generic behavior: the OIE exponent increases rapidly with decreasing doping (see Figure 11 and 18) and becomes substantially larger than even the BCS value . This exciting and important finding has, however, not been properly appreciated by the community, since many were convinced that a purely electronic mechanism is behind the electron pairing.
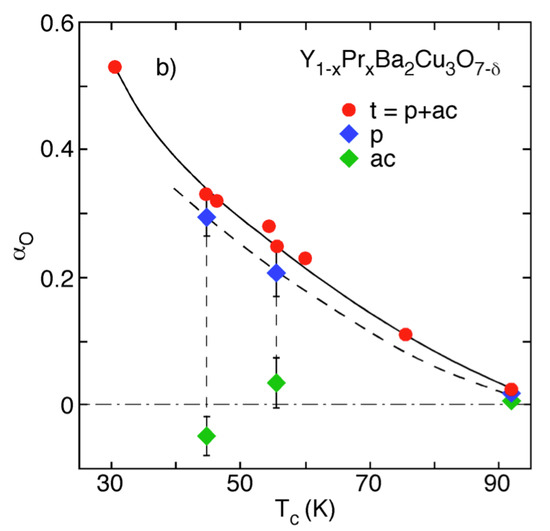
Figure 11.
Total (t) and partial (p, ac) OIE exponent as a function of for (t = total: all oxygen sites; p: planar oxygen sites; ac: apex and chain oxygen sites). Solid and dashed lines are guides to the eye (after Ref. [37]).
Here, it is interesting to note that for the giant magnetoresistance compound , we observed a huge OIE on the ferromagnetic transition temperature of [39]. The compound contains and ions. The ground state of the is degenerate, leading to a spontaneous localized distortion of the lattice around the ion (JT effect). It is argued that the large OIE on is due to the coupling of the charge carriers to the localized JT lattice distortions and also determines the magnetoresistive properties of [39]. Obviously, there are certain similarities between the manganates and the cuprates, and it is reasonable to assume that similar mechanisms based on the JT effect determine the physical properties of these two substance classes (magnetoresistive properties of the manganates, superconducting properties of the cuprates).
To further test the JT polaron concept, we have carried out detailed investigations of the OIE on the magnetic penetration depth in cuprate HTSs. The zero-temperature in-plane magnetic penetration depth is given by [37]:
where denotes the superconducting carrier density and the in-plane effective mass of the carriers. This means that a possible OIE shift of must originate from either or or both. By using various types of experimental techniques such as magnetization measurements [40], magnetic torque [41], SR [34], and low-energy SR [42] and different types of samples (powder, single crystal, thin film), we succeeded to detect a pronounced and consistent doping-dependent OIE on in CuO4 and [35,36,37,38].
In order to evaluate the magnetic properties of tiny crystals of superconductors (microcrystals with a mass ≤ 1 g), we developed new types of highly sensitive piezoresistive cantilevers specially designed for torque magnetometry with a torque resolution of ≃ [43,44,45]. We applied this novel technique to investigate the OIE on of underdoped microcystals of CuO4 (mass g) [41]. It should be emphasized that for reliable OIE studies on single-crystal samples, tiny microcrystals are absolutely necessary in order to ensure a complete oxygen (16O/18O) exchange and back exchange [41]. The main results of this study are displayed in Figure 12. A substantial OIE on the superfluid density is apparent, which increases with increasing doping x. Note that and the superfluid density decrease with increasing oxygen mass (16O →18O). It should be pointed out that for a conventional phonon-mediated superconductor, no isotope effect on the superfluid density (magnetic penetration depth) should occur as demonstrated for instance for the layered two-band superconductor MgB2 by our group [46].
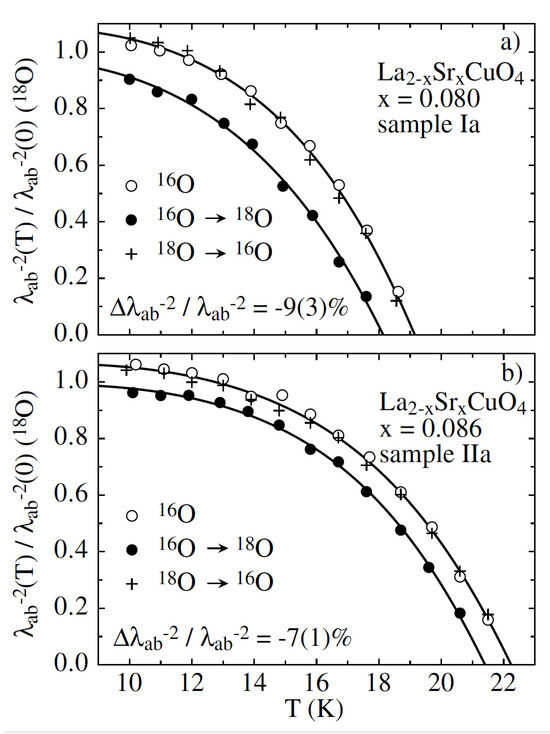
Figure 12.
Normalized in-plane superfluid density for microcrystals determined by torque magnetometry: (a) ; (b) . The oxygen-isotope-exchange procedure is reproducible, as indicated by the cross symbols (+) (from Ref. [41]).
To further substantiate the JT polaron concept, we also carried out a SOIE investigation of the magnetic penetration depth in using SR [34]. The result is as expected: the main contribution to the total OIE of the superfluid density () stems from the oxygen atoms in the planes (see Figure 13) analogous to the superconducting transition temperature (see Figure 11).
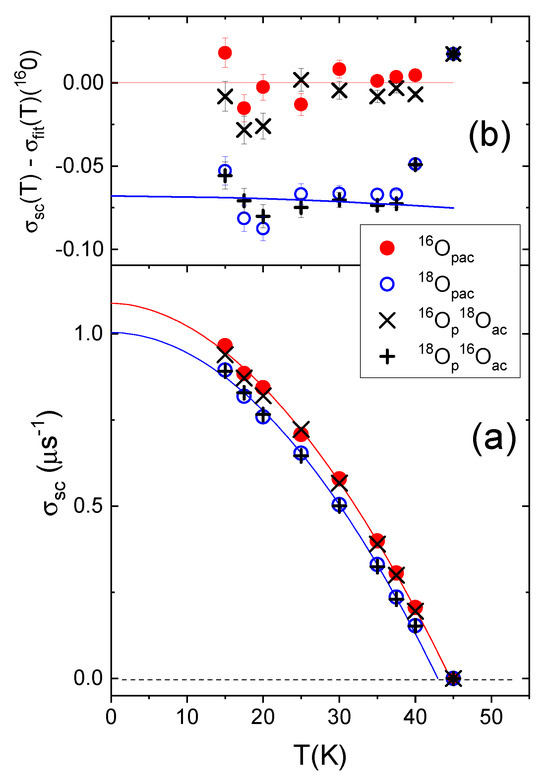
Figure 13.
(a) Temperature dependence of the depolarization rate in site-selective samples (200 mT, field-cooled). The notations of the oxygen-substituted samples are the same as in Figure 10. Here, 16,18Opac means fully exchanged 16,18O samples. The dashed lines correspond to fits to power laws as described in [34]. (b) The same data as in (a) after subtracting the fitted power law curve for the 16 Opac sample. It is evident that the main contribution to the total OIE on the superfluid density comes from the planar oxygens (after Ref. [34]).
To conclude, concerning the OIEs on the critical temperature and the the superfluid density , in a review article, P.W. Anderson made the following statement [47]: “But, experiment is the best teacher. The isotope effect measurements of Keller [42] find a reasonably-sized isotope effect on , apparently confirming the phonon hypothesis; but Keller was thorough enough to also measure the isotope shift of , the superfluid density, ; and he finds that this shifts by the same fractional amount.”
The origin of the so-called pseudogap temperature is considered to be important to understand the physics of cuprate HTSs. However, the physical meaning of is not well defined. It depends on the experimental technique (length and time scale, magnetic- or charge-sensitive method, etc.) how is determined, and it is more a “crossover temperature” than a real phase transition temperature (see, e.g., [48,49]). Here, is defined as the temperature where deviations from the average local structure occur (charge ordering or charge-stripe ordering temperature), and consequently, lattice—but not magnetic—effects should be directly involved. Therefore, Alex was convinced that one should observe a substantial OIE on . The first OIE study on in was carried out in collaboration with Bianconi’s group in Rome using the X-ray absorption near edge structure (XANES) technique (see Figure 14) [48]. A huge negative OIE on of was determined for . Additional XANES studies of [49] as well as neutron crystal-field spectroscopy (NCFS) studies of [50,51] also confirmed a large doping-dependent negative OIE on . Similar results were also obtained for by means of NCFS experiments [52]. It is interesting to note that the OIEs on and are sign-reversed: both are strongly doping dependent, but the OIE on is much larger.
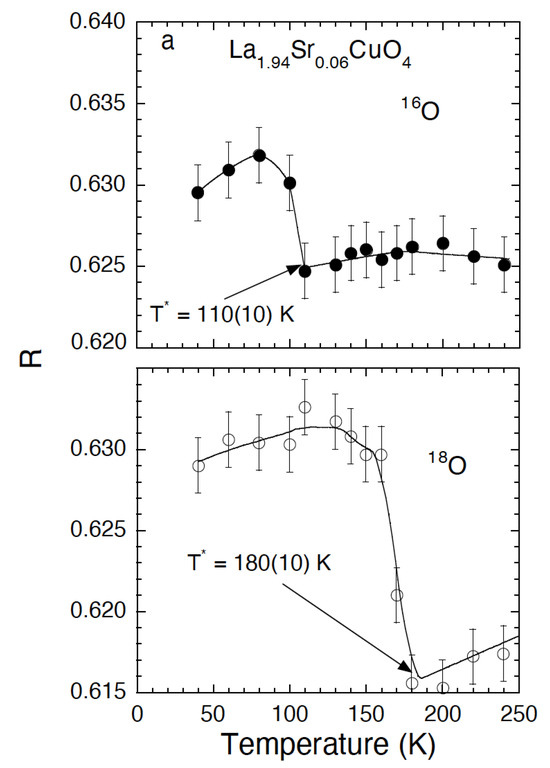
Figure 14.
Temperature dependence of the XANES peak intensity ratio R for the 16O and 18O samples of . A huge negative OIE shift of is observed (from Ref. [48]).
In addition to the OIEs on the superconducting transition temperature , the magnetic penetration depth (superfluid density) and the “pseudogap” temperature (charge-stripe ordering temperature) discussed above, we have also observed OIE’s on several other physical quantities of cuprates such as the spin glass temperature [53,54], the Néel temperature [54], the spin-stripe ordering temperature [55] and the superconducting gap [56]. All these studies give a consistent picture that the superconducting charge carriers in the cuprates have a polaronic character and that local lattice deformations play an important role in understanding these materials, as outlined in several review papers (see, e.g., [4,35,36,37,38,57]).
From the very beginning of the discovery of high-temperature superconductivity, Alex has pointed out that the cuprates exhibit microscopic inhomogeneities that are not due to poor sample preparation, but are an intrinsic property of the cuprates that is central to understanding the physical properties of these materials. In contrast to the generally accepted assumption that the cuprate HTSs are pure d-wave superconductors, Alex proposed in 1995 that the cuprates have a mixed s- and d-wave order parameter [58]. He came to this conclusion on the basis of various experimental results that he presented at a conference “High-Tc Superconductivity 1996: Ten Years after the Discovery” in Delphi (Greece) in 1996 on the occasion of the 10th anniversary of the discovery of high-temperature superconductivity [59]. Participating in this conference was a great enrichment for me in many ways: (1) I had the pleasure of giving an introductory lecture on superconductivity to the students and non-experts at this conference; (2) I benefited a lot from the contributions, broadened my horizon in the field of superconductivity and met many scientists from all over the world; and finally, (3) I was very lucky to meet Annette Bussmann-Holder (ABH) in Delphi. During the conference, we often went to dinner together with Georg, having interesting discussions. This meeting led to many years of close and very fruitful cooperation and deep friendship with Annette, which continues to this day—almost 30 years now.
Back in Zurich, Alex invited me to co-author the manuscript of his contribution at the Delphi conference [59]. The manuscript went back and forth between us—by fax, by post, on the phone or in his office at the Physics Institute. Alex also kept sending me letters (by post or fax) (at that time Alex was not familiar with sending e-mail messages). A typical letter from Alex to me concerning our “Delphi Paper” [59] is displayed in Figure 15—his handwriting and style are his “trademark”. Almost 10 years later, using the SR method, we succeeded in proving that a two-component s- and d-wave order parameter is indeed present in the cuprate HTSs [60,61,62,63].

Figure 15.
Letter from Alex to HK dated 23 February 1997 regarding the publication of the “Delphi Paper” [59]. (Photo HK).
SR is a powerful tool to investigate the pairing symmetry (s, d, ) of cuprate HTSs in the bulk of a sample by measuring the temperature dependence of the magnetic penetration depth. As an example, in Figure 16a, the temperature dependence of the SR relaxation rate ( is the in-plane magnetic penetration depth) of a single-crystal sample of is shown, determined for different applied magnetic fields H perpendicular to the plane [60]. An analysis of the SR data with a phenomenological two-component model with uncoupled -wave order parameters reveals a good agreement between experiment and theory (see Figure 16b). A more detailed theoretical description of the two-component model with coupled -wave order parameters is given in Section 4. As expected, the large d-wave gap contributes more strongly to the superfluid density (≈70%) than the much smaller s-wave gap (≈30%), but the s-wave component is relevant to describing the SR data consistently. In further experiments, we investigated the temperature dependence of the magnetic penetrations depths , and along the three principal crystallographic axes a, b and c in single-crystal YBa2Cu3O7−δ [61] and [62]. A careful analysis of the SR data with the same two-component model yields again the coexistence of large d-wave gaps with a small s-wave gaps. In the plane, however, the d-wave component is dominant, similar to (see Figure 16) and along the c-axis the superfluid density exhibits an almost pure s-wave character (the d-wave component—although present—must be negligibly small) [61,62]. Recently, the OIE on the in-plane superfluid density within the d-wave and s-wave pairing channels of was measured by means of SR [63], exhibiting that the dominant contribution to the OIE stems from the d-wave component while the contribution from the s-wave component is almost zero.
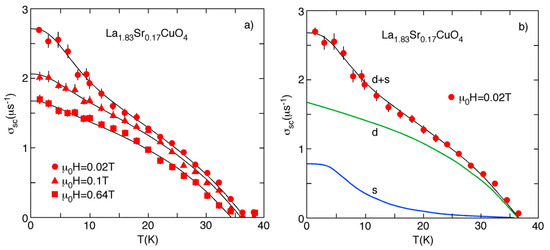
Figure 16.
(a) Temperature dependence of the SR relaxation rate of a single-crystal sample of measured at different applied magnetic fields H perpendicular to the plane. The solid lines represent fits to the SR data using a two-component (two-gap) model. (b) The green and blue lines correspond to the contributions of d- and s-wave gap, respectively (after Ref. [60]).
From all these experiments [60,61,62,63], we conclude that a mixed order parameter is a generic feature of cuprate HTSs, as originally predicted by Alex [58,59].
3. First Encounters and Scientific Interactions with ABH
In 1978 I started my first professional position as a postdoc at the Max Planck Institute for Solid-State Research in Stuttgart (MPI) in the group of Prof. Heinz Bilz. During my PhD, I was mostly involved in experimental work in the field of multiferroic materials and the characterization of their properties. In contrast to that work, I collaborated with the group of Heinz Bilz, which concentrated on theoretical solid-state research, where I was supposed to focus on ferroelectric phase transitions. During lengthy literature research in this field, I frequently came across Alex’s name, and I became aware that he was very influential and dominant in this field. He was also a good friend of Heinz Bilz and often mentioned by him. Many times he visited the MPI, having long discussions with Heinz. When I became more involved in Heinz’s work, I was asked to join their discussions. My first participation in an international conference was in the summer of 1979 in Portoroc in former Yugoslavia on the occasion of the European Meeting of Ferroelectricity (EMF). Here, it became clear to me how important Alex was in the ferroelectric community. He was not only a member of the organizing committee, but also the plenary speaker, chairman and moderator of several discussion rounds. But, at the same time, I became aware of the fact that he was rigorously defending his ideas and rather rudely, undermining his own opinion—a feature of his character which vanished with increasing age. Since I accompanied Heinz—also a plenary speaker—I joined him for dinners, which were also typically held together with Alex. Here, I found out that Alex liked good food and good wines and that he was an excellent entertainer with a lot of humor.
After this first meeting, I encountered Alex frequently at the MPI, since he continued his discussions with Heinz and later became a member of the institute’s advisory board. Almost every time, he visited me in my office even though Heinz had died in 1986, and if I was not present, he left notes on my desk. After having received the Nobel prize in 1987, Alex was very often invited all over the world, and his visits at the MPI occurred less frequently. Nevertheless, he took his role as advisory board member of the MPI seriously and always took part in these meetings. He continued to see me on these occasions, and we continued our discussions on ferroelectricity and possible connections to superconductivity. In 1989, he came again to my office and told me that his friend Prof. Harry Thomas of the University of Basel had asked him to be referee to my habilitation work. He was very much against my wish to become habilitated, giving the argument that I would eventually be unable to care for my three children as well as he had in mind. He even came to our house for dinner so I could convince him that neither my children nor my husband were suffering from me frequently traveling and intensively pursuing my career. Consequently, he accepted the referee role and discussed the habilitation work in great detail with me. From then on, he was often in our house, and our children were surprised how friendly and humorous he was when talking with them. This continued for the rest of his life, and each time we met he asked for them and also for my husband. He also visited us in our home at the Lago di Garda (Italy), where he arrived with his light blue antique Alfa Romeo. Unfortunately, the starting motor had a defect, which meant that the car had to be pushed to get started, unless it was parked on a declined slope. This was a very memorable encounter, where we had intense philosophical conversations. In addition to our personal interactions, Alex and I tried to arrive at conclusions on the pairing glue in superconducting cuprates. Here, our common background on ferroelectricity was centered, since cuprates and ferroelectric perovskites have many common features, i.e., related structural units, structural instabilities, unusual dielectric properties, anharmonic lattice dynamics, and the fact that both are oxides. The latter is special, since the oxygen ion is unstable as a free ion [64] and consequently tries to stabilize itself by transferring one of its outer electrons to neighboring ions in a solid. This results in dynamic charge transfer and covalency. In addition, anharmonic higher-order electron–phonon interactions are activated, which have been shown to be responsible for ferroelectricity in perovskites [65,66,67]. After having written a couple of papers on the interrelation between ferroelectricity and superconductivity (see, e.g., [68]), Alex started to like this approach, which led to our first co-authored paper, namely "Theory of dynamic stripe induced superconductivity" [69]. Collaboration with Alex turned out to not be easy, since he often changed his mind on the style and wording and could become very upset with me, typically ending in a late night phone call which worried me a lot. In particular in this first paper, a mistake in some equations had occurred to me which only he noticed, not any of the other theoretically involved coauthors. Shortly after the publication of this paper, I was contacted by Springer, asking me whether I would like to edit a book on superconductivity in the Springer Series Structure and Bonding [70].
I talked to Alex about this project and whether he would be willing to be co-editor. After a while, he agreed to this proposal, and together we started contacting possible coauthors. Actually, a number of well-known people in the field accepted our invitation, and a comprehensive review was edited in 2004 with the prestigious title Superconductivity in Complex Systems (see Figure 17). The first chapter of the book was written by Alex, entitled "Essential Heterogeneities in Hole-Doped Cuprate Superconductors”. The following chapter was by R. Micnas, S. Robaszkiewicz, A. Bussmann-Holder on “Two-Component Scenarios for Non-Conventional (Exotic) Superconductors”; chapter 5 was by H. Keller, titled “Unconventional Isotope Effects in Cuprate Superconductors”; and the last chapter marks a mile stone in our joint careers, namely “Evidences for Polaron Formation in Cuprates” by A. Bussmann-Holder, H. Keller and K. A. Müller. This paper heralded our long-lasting collaboration and friendship.

Figure 17.
Draft preface to the Springer book Superconductivity in Complex Systems [70] edited by Alex and ABH. (Photo ABH).
4. Scientific Interactions with Alex
While HK had scientific exchanges and common research projects with Georg and Alex almost directly after their breakthrough discovery (see Section 2). HK, Alex and I started our collaborations only after 2004, as mentioned above. The emphasis in these interactions was specifically on the identification of the pairing mechanism in cuprates. Our starting ansatz was Alex’s original concept, namely polaron formation, the Jahn–Teller effect and its experimental evidences. In addition, we concentrated on heterogeneity as an essential ingredient for superconductivity in cuprate HTSs. The background for this interest was Alex’s enormous knowledge on perovskites [3], and especially [4], both of which are known for exhibiting locally different properties as compared to global ones. The similarity between them and cuprate HTSs correspondingly suggests that this material class is also dominated by differing spatial- and time-dependent responses, as experimental results by the group of A. Bianconi et al. confirmed early on in 1996 [71]. In addition, one has to be reminded that the Nobel prize devoted to Georg and Alex was entitled “For the discovery of superconductivity in ceramic oxides” [72], often unknown to many researchers. Only a year after the discovery, Alex’s starting point, polarons and bipolarons, was heavily questioned to be the origin of the pairing mechanism, mainly due to the discovery of an almost vanishing isotope effect on [23] (see Section 2). Even though more elaborate and extended isotope studies were performed immediately after this one (see, e.g., [25,26,27]), which showed that these first results do not hold for any doping level as shown in Figure 18, first doubts on any involvement of the lattice were raised related to the fact that the undoped parent compounds are antiferromagnetic. Soon, the origin of the pairing mechanism in cuprate HTSs had become a controversial issue and a question of belief. Different sects had evolved from 1987 on, and their members were fighting against each other, thereby frequently ignoring scientific facts and issues. On the one hand, purely electronic mechanisms were favored, including spin fluctuations, on the other hand, electron–phonon interactions à la BCS were discussed by other groups. The central origin of the pairing mechanism as originally proposed by Alex [72], namely polaron or bipolaron formation, was, however, mostly ignored. That was the reason why we followed—as discussed above—this approach. Experimentally, the observations of unconventional isotope effects was the starting point to bring polarons into the game, as outlined in detail by HK (see Section 2), since these observations are beyond BCS theory and find no explanations within purely electronic approaches.
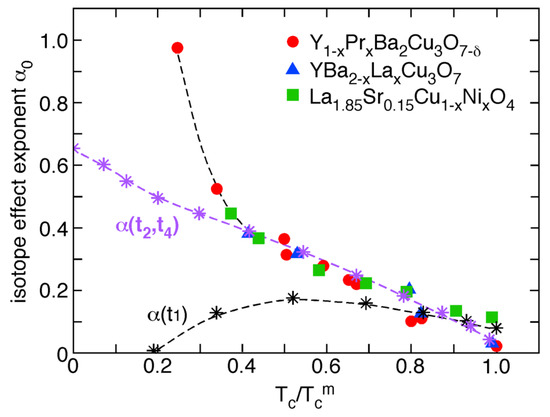
Figure 18.
Measured OIE exponent for various families of cuprate HTSs as a function of reduced temperature , where is the maximum for the corresponding family. The behavior of vs. is a generic feature for all cuprate families. The black stars represent the theoretical when only the nearest neighbor hopping integral () is renormalized. The purple stars denote the calculated when both the second nearest neighbor () and the interplanar () hopping integrals are renormalized. It is evident that in order to describe the measured the interplanar hopping is crucial, demonstrating the three-dimensionality of superconductivity in cuprates (from Ref. [38]).
The concept of polarons was introduced by Lev Landau in 1933 [73] and Solomon Pekar in 1946 [74,75] to describe an electron moving in a dielectric crystal, where the atoms displace from their equilibrium positions to effectively screen the charge of an electron, known as a phonon cloud. The essential ingredient—important to cuprate HTSs—is the lowering of the electron mobility and increasing the electron’s effective mass. The general concept of a polaron has later been extended to describe other interactions between the electrons and ions in metals that result in a bound state, or a lowering of energy compared to the non-interacting system. Major theoretical work has focused on solving Fröhlich [76,77] and Holstein [78,79] Hamiltonians. Finding exact numerical solutions for the case of one or two electrons in a large crystal lattice is still an active field of research, as is the study of cases with many interacting electrons [80]. The coupling of two polarons to a bipolaron may cause Bose–Einstein condensation and induce superconductivity with very different properties as compared to the BCS mechanism. A review has been published by A.S. Alexandrov [81] and by S. Aubry [82] with possible implications to high-temperature superconductivity.
These concepts were the motivation behind Alex’s search for superconductivity in oxides, since these have small carrier densities in combination with strong electron–phonon (lattice) interaction. In addition, he was inspired by his friend Harry Thomas, Professor at the University of Basel, who introduced the Jahn–Teller (JT) polaron [22].
The Jahn–Teller (JT) effect was postulated in 1937 by Hermann Jahn and Edward Teller, stating that “stability and degeneracy of a molecule are not possible simultaneously unless the molecule is a linear one”, in regards to its electronic state [83]. This leads to a break in degeneracy, which stabilizes the molecule and, in consequence, reduces its symmetry. Since 1937, the theorem has been revised by Housecroft and Sharpe [84], who elegantly eloquently phrased their theorem as “any non-linear molecular system in a degenerate electronic state will be unstable and will undergo distortion to form a system of lower symmetry and lower energy, thereby removing the degeneracy”. This is most commonly observed with transition-metal octahedral complexes; however, it can be observed in tetrahedral compounds as well. Höck et al. [22] extended this picture to a band type description where the JT center can move through the lattice like a polaron.
The consequences of such an approach are manifold; namely, the electrons are dressed by a lattice cloud and have a heavy effective mass. Furthermore, their velocity is considerably reduced as compared to free electrons. The involved phonon modes on the other hand are modified and shifted in energy. These effects should be visible experimentally, since the phonon dressing causes an isotope effect on various properties, and the lattice modes experience the opening of the superconducting and the pseudogap and strong deviations from typical Debye–Waller behavior.
Applying the above approach to cuprate HTSs requires the inclusion of an additional complication, namely, its inherent heterogeneity. This is clearly visible—as early on suggested by Alex [58]—in a two-component behavior. For the superconducting properties, this implies that two components coexist, namely . This shows up in there being two superconducting gaps, two length scales for the penetration depth, two different isotope coefficients, etc. However, these are not independent of each other, but are coupled, as suggested very early by Suhl, Matthias and Walker [85] and Moskalenko [86]. While in Refs. [85,86], the coupled gaps are assumed to be isotropic, in the case of cuprate HTSs, they must consist of a d-wave gap and an s-wave one in order to account for experimental findings. This greatly impedes the calculations of the mentioned properties, since it implies that coupled equations with different symmetries have to be solved simultaneously in a self-consistent manner. In addition, new parameters enter this procedure which cannot be uniquely derived experimentally. The advantage of the coupled system is that the limits of the superconducting transition temperature as given by BCS or Eliashberg theory can easily be considerably exceeded and thus explain the observed ’s of cuprate HTSs. Upon starting with measured superconducting gap values and the corresponding , all involved parameters can unambiguously be determined by theory from which conclusions about the role of the individual quantities can be drawn. Thus, we figured out that, typically, the interband interactions are rather small, whereas the two intra-band ones have distinctly different values, the one assigned to the d-wave channel being dominant while the s-band channel represents a minority. It is important to note that each channel always carries a component of the other such that their individual characters are lost. In addition to these very involved solutions of the coupled system, the isotope effect represents an additional challenge. Based on a BCS-type approach, the experimentally derived isotope effect exponent cannot be reproduced theoretically, since its maximum value cannot exceed , even in a coupled band approach. Alternatively, the polaron picture has been tested. As said above, the considered quasi-particle, electron (hole) plus phonon cloud dresses the electron (hole) and makes it heavier. The phonon mass, i.e., the ions, enters this cloud exponentially in the kinetic energy. This causes an isotope effect on this energy, which manifests in a variety of characteristics. However, not all parts of the kinetic energy are affected in the same way, only very specific bands, which are the nearest neighbor hopping band , the next nearest neighbor band and the interplanar hopping band , thereby clearly demonstrating that a single-band approach is insufficient, despite being promoted by various groups (see, e.g., [87]).
Amazingly, the nearest neighbor renormalized band yields the wrong sign of the isotope effect, whereas the combined effect of the next nearest and interband polaron renormalization effects predict the correct isotope effect, as determined experimentally (see Figure 18). This observation allows us to conclude that the specific lattice distortion is responsible for the observed isotope effects, namely a JT distortion, thereby closing the circle back to Alex’s starting point. The nearest neighbor hopping band couples to a half breathing mode, as shown in the left Figure 19. This has, however, the wrong sign with respect to the OIE. The second nearest neighbor hopping integral is triggered by the -type mode, which is a JT active displacement pattern, as shown on the right side of Figure 19. This mode contributes distinctively to the OIE on (see Figure 18). In addition to isotope effects on , others have been calculated, namely, the effect on the superfluid density (penetration depth) (see Section 2) and on the superconducting energy gaps, the latter being predicted by theory [56,88] and afterwards verified experimentally [56]. This rarely happens in the field of high-temperature superconductivity, and is definitely an example where theory comes prior to the experiment.
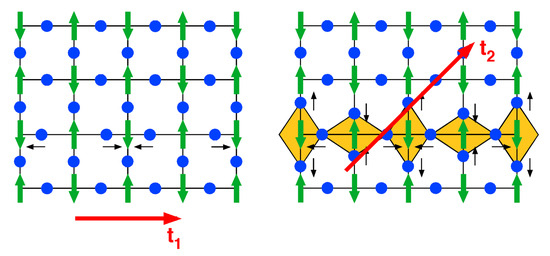
Figure 19.
The relevant ionic displacements in the plane of a cuprate HTS dominated by the nearest (left panel) or second nearest (right panel) hopping integrals, giving rise to a -type phonon mode (yellow areas). The interplanar hopping integral is not shown in this two-dimensional schematic representation. Note, however, that is relevant to describe the OIE on as demonstrated in Figure 18 (from Ref. [38]).
Another experimental miracle could also be solved using the above-described theoretical approach, namely the observation of substantial deviations in the Debye–Waller factor from expectations. Typically, the Debye–Waller factor is fully determined by the displacement–displacement correlation function, which increases smoothly with the increasing temperature and becomes saturated at the high-temperature limit. The behavior of cuprate HTSs is distinctly different since divergences at two temperatures are observed [89,90,91] in X-ray absorption spectroscopic experiments and by Cu K-edge EXAFS and XANES. These divergences occur around the pseudogap temperature and in the vicinity of . Since the consequences of polaron formation on the electronic properties including isotope effects have been shown to reproduce experimental data well, their influence on the lattice was tested in a next step. Since the lattice experiences a renormalization due to the coupling to the electronic bands, changes in the electronic structure are directly mirrored in the lattice response. Indeed, two anomalies were observed there around and , which we identified as the onset temperature of polaron formation and coherence. Importantly, at , this appeared only as long as the superconducting gap has a d-wave contribution, which causes its vanishing along the diagonal in the CuO plane. A kind of summary of all achievements resulting from our combined work, namely that of Alex, HK and myself, has been given in [38].
Very rarely, Alex would not coauthor our collaborative papers, since he felt he had not sufficiently taken part in the work. This was quite typical for him and very different from other well-known scientists. Typically, PhD students list their supervisors as coauthors, even if there was no real contribution from them. Alex only agreed to coauthor a paper when he had actively been instrumental to it. He was very rigorous in this respect and would carefully read not only the list of authors but also the acknowledgments. As stated above, it was not easy to have him as a coauthor, since again, unlike others, he carefully read each word and phrase and would inevitably complain heavily about the wording. Nevertheless, his criticism was always correct, and his corrections well-founded. We benefited a lot from his contributions and each time were inspired by him.
5. Conferences Dedicated to the Work of Alex
After Georg and Alex had been honored with the Nobel prize in 1987 for their breakthrough discovery of superconductivity in ceramic oxides, many conferences and books were devoted to this new class of materials. ABH and HK had the privilege of participating with Alex in numerous conferences, meetings and workshops around the world. Naturally, it is impossible to mention all the conferences Alex influenced, but some deserve to be highlighted. In early 2000, ABH and HK organized an international conference on high-temperature superconductivity in the Swiss Mountains in Klosters, a place near where Alex had spent many years of his early childhood and youth. The conference covered many topics related to high-temperature superconductivity, featuring controversial aspects of the field. The invited speakers were renowned scientists from all over the world, ranging from Russia and China to the US and Europe. Two scientists need to be highlighted, Vitaly Ginsburg (VG) and John Goodenough (JG), who both later received the Nobel prize in physics (VG, 2003) and in chemistry (JG, 2019), respectively.
VG gave an impressive introductory talk on the Landau–Ginzburg theory for superconductivity developed in 1950. At that time, Lev Landau was the leading scientist at the Russian Academy of Sciences in Moscow, Ginzburg was his student. The basic ingredient of the Landau-Ginzburg theory was that phase transitions can be described in terms of an order-parameter, which in the case of a superconducting transition was represented by the electron. Ginzburg tried to correct this ansatz by attributing an asterix to the electronic charge e, namely , which, however, was heavily criticized by Landau, who in response told him: “In my theories there is no space for an asterix”. In Klosters, he presented this story and further theoretical developments.
JG’s career started with his work on random access memories (RAMs), which led him to the development of cooperative orbital ordering, also known as a cooperative Jahn–Teller distortion in oxide materials, and subsequently to the rules for the sign of the magnetic superexchange in magnetic materials, now known as the Goodenough–Kanamori rules (with Junjiro Kanamori) [92,93]. JG was the eminent expert in transition metal perovskite oxides and had a deep understanding of this material class. During his time at Oxford University, JG discovered in 1980 that by using as a lightweight, high-energy-density cathode material, he could double the capacity of lithium-ion batteries. In Klosters, he was talking about the similarity between cuprate HTSs and perovskite oxides and how superconductivity could be enabled in the former through charge transfer. JG was well-known for his very loud, polarizing laughter. Being asked questions by him after a talk was dreadful, since he always addressed the weak points of a talk. ABH met him for the last time in the US when he was well in his ninties, still having his characteristic laughter and his sharp mind.
In addition to these two personalities, many other famous colleagues took part in the Klosters conference, presenting many different aspects of high-temperature superconductivity and initiating controversial discussions. It has to be mentioned that even though ABH and HK organized the event, the invited selection of speakers was greatly influenced by Alex.
Another event, organized by HK, ABH and Davor Pavuna (EPFL Lausanne, Switzerland) took place in 2006 at the University of Zurich on the occasion of 20 years of cuprate HTSs. The diversity of speakers was very similar to the 2000 Klosters conference, although with different speakers and new topics, concentrating on lattice effects and inhomogeneity. The speakers of the symposium were proposed by Alex and Georg. A photo from this symposium is shown in Figure 20.

Figure 20.
International Symposium in Honor of J.G. Bednorz and K.A. Müller—20 years after the discovery of cuprate superconductors, University of Zurich, Campus Irchel, 2006. Group photo of the participants of the symposium. (Photo UZH).
A number of other workshops and conferences were organized by both of us or one of us, but the most prominent ones are given above.
6. Books and Special Issues Dedicated to the Work of Alex
In 2007, ABH and HK decided to edit a book to honor Alex on the occasion of his 80th birthday. The book was edited by Springer and entitled High Superconductors and Related Transition Metal Oxides [94]. We invited a large number of well-known scientists to contribute to this issue and indeed received 30 articles, all of which were published. While most of the authors dealt with their own research field and focused on their results related to high-temperature superconductivity, some emphasized their personal connections with Alex, including anecdotes related to and collaborations with him. We presented the book to Alex at his birthday celebration. A short time later when we met Alex again, he had read each article and commented on it to us. In addition, he contacted each author thanked them for the contribution and added comments regarding the contents of the article. We found this quite amazing, since it took him some time and effort to go through this volume article by article.
Ten years later, we started a similar effort, now with Antonio Bianconi as additional editor, to honor his 90th birthday. Again, Springer edited the volume entitled “High Copper Oxide Superconductors and Related Novel Materials” in the Springer Series in Material Sciences 255 [95]. At that time, some of the authors who contributed to the last volume had passed away, and new ones contributed instead. Altogether, we received 26 papers which were published. These papers, like before, mainly dealt with the authors’ own results on high-temperature superconductivity, but a larger proportion of them described their personal interactions with Alex compared to the 2007 editing. Also, the individual focus of the papers had somewhat changed to heterogeneity in contrast to the homogeneous aspect emphasized ten years before. We presented the book to Alex at his 90th birthday. Despite his advanced age, he discussed the articles with us, their role in the field of high-temperature superconductivity, as well as aspects which were not in line with his opinion. This time, however. he did not get back to each contributor, only to a few selected ones.
Since we got the impression that Alex’s focus had moved away from science, we edited a third and “final” book in 2021 to honor his life work, not on his 95th birthday, but a year before, again in collaboration with Antonio Bianconi. The book was issued in the open access journal Condensed Matter of MDPI and was published online and as a hardback version and consisted of 20 contributions. Since only 4 years have passed between the last book and this one, many invited contributors from the former issue declined to contribute, reasoning that nothing new was to be added. Nevertheless, new authors agreed to contribute, focusing more on Alex’s role in the study of ferroelectricity and structural phase transitions, his first topic before turning to high-temperature superconductivity. This book is entitled From Quantum Paraelectric/Ferroelectric Perovskite Oxides to High Temperature Superconducting Copper Oxides [96] indicating the preference of honoring Alex for his enormous research successes achieved on his favorite material, namely . When presenting the book to him one day after his 94th birthday on 21 April 2021, he was very pleased and scanned through the volume, but it was almost immediately clear to us that his mind had moved away from physics (see Figure 21). We believed that this was the last point in time we were able to catch his interest in his former research.

Figure 21.
Alex scanning through the special volume From Quantum Paraelectric/Ferroelectric Perovskite Oxides to High Temperature Superconducting Copper Oxides [96], Tertianum Zollikerberg (Zurich), 21 April 2021. (Photo HK).
After he had passed away in early 2023, we were asked by many journals and societies to edit an obituary for Alex, which we did indeed. The editor of Physica C: Superconductivity and its Applications Dirk van der Marel approached HK to edit a Special Issue titled “Oxide superconductors and beyond—In memoriam of Professor Karl Alex Müller” to honor Alex posthumously. Many researchers agreed to our invitation, and we received 46 contributions reflecting different aspects of Alex’s enormous influence on new developments in condensed matter physics [97].
7. Personal Encounters, Anecdotes and Curiosities with Alex
While in the above chapters, mainly scientific interactions with Alex have been addressed, in the following, we give some insight into his interests outside of physics, followed by anecdotes of him.
After the early death of his mother, Alex was sent to the Evangelical College in Schiers (Evangelische Lehranstalt in Schiers) located in the Swiss Alps at the age of eleven. This boarding school became like a new home for him for the next seven years. He devoted his free time there to numerous activities. He was a member of the local scout group and the model airplane construction group. Probably initiated by his mother, who gave him a kit to make a single-tube radio, Alex became an accomplished radio hobbyist and built sophisticated tube radio receivers as a teenager (see Figure 22) [98]. The alpine landscape of Schiers had a decisive influence on his life. In his free time, he went on mountain tours, and he learned to ski as a young boy—the area around Schiers was ideal for pursuing this passion. Over the years, Alex became an accomplished and passionate skier, even becoming “Schiers Alpine Ski Champion (downhill and slalom)” at the age of 18. Alex was a very active skier until the ripe old age of 85. Alex’s interest in technology and natural sciences was also awakened at the boarding school in Schiers. It is therefore not surprising that Alex originally wanted to study electrical engineering at ETH Zurich. However, his chemistry teacher, Dr. Sauer, who had a great influence on him, advised him to study physics. As we all know, this was wise advice.

Figure 22.
Alex as a young radio hobbyist (ca. 1940). (Photo from Ref. [98]).
As a physics student at ETH Zurich, Alex attended lectures in theoretical physics by Prof. Wolfgang Pauli. Pauli left a deep impression on Alex, and he had a heartfelt admiration for the professor. Even in his old age, Alex still recounted his experiences with Pauli from his student and doctoral student days at ETH. He told us one particular story again and again: At his oral diploma examination in 1952, Pauli gave him the topic of “skin effect”. Alex went to the blackboard and started to derive the equations for the skin effect. He made rapid progress. Pauli watched him attentively. Suddenly, Pauli stood up, picked up a piece of chalk and finished the derivation with the comment: “You can also do it like this, you’ve done well, Mr. Müller!” As a reward, Alex received a good grade for Pauli’s exam. In 1958, Alex completed his doctoral thesis and decided to take up a position at the Battelle Memorial Institute in Geneva (Switzerland). On 14 December 1958, Alex wrote a letter of thanks to Prof. Pauli and to say goodbye (see Figure 23), since Pauli was seriously ill at the time. Pauli was in the Rotkreuzspital in Zurich lying in room no. 137 ( is the fine structure constant!). He died on 15 December 1958—just one day after Alex had written the letter to him.

Figure 23.
Letter from Alex to Prof. Dr. Wolfgang Pauli from 14 December 1958. Pauli was then a patient in the Rotkreuzspital in Zurich. (Copy of the original letter).
Pauli maintained a close relationship with the famous Swiss depth psychologist Carl Gustav Jung for many years. In a lively exchange of letters, the two discussed the common foundations of physics and Jungian psychology. The discussion between the two luminaries in their respective fields was conducted at a very high scientific level. Significant scientific–theoretical insights were developed between them, focusing on concepts such as symmetry, complementarity and synchronicity.
Inspired by his highly respected teacher Wolfgang Pauli, Alex became interested early on (1952) in the joint scientific–theoretical work of W. Pauli and C.G. Jung and the closely related Jungian depth psychology. Depth psychology was initially a difficult new territory for him, but over the years, he immersed himself more and more in this complex field and dealt with it until the end of his life [98]. In particular, he studied the meaning of dreams, the symbolism of symmetry and numbers, synchronicity and archetypal forms [98]. Alex repeatedly emphasized: “There are no coincidences in life—everything is linked in time and space.” In his view, his discovery of high-temperature superconductivity with Georg was not accidental.
Alex was a man of many interests. In addition to physics, the natural sciences, philosophy and depth psychology, he also had a profound knowledge of world history, politics, art, literature and music. He was particularly fascinated by the German poets Johann Wolfgang Goethe and Thomas Mann, as well as by the German composer Felix Mendelsohn Bartholdy. Alex’s wife, Inge, was an opera singer, and they loved to visit operas all over the world. Alex deeply enjoyed accompanying her and thereby became a true aficionado of the opera scene. It was always a great pleasure to listen to him when he spoke on one of these topics with expertise, enthusiasm and dark humor. Frequently, Alex would talk to HK and ABH about the First and Second World Wars, of which he possessed an amazingly broad knowledge. He knew almost all the important strategic battles and the names of the commanding officers. He was also knowledgeable of the reasons behind these battles.
Alex told us (ABH and HK) several times that he has always been lucky in life; everything has just fallen into his lap—including the discovery of high-temperature superconductivity!
Alex also had an extraordinary flair for talented young scientists. He “discovered” both Gerd Binnig and Georg Bednorz and brought them to the IBM Research Laboratory in Rüschlikon, with permanent positions. Both later received the Nobel Prize in Physics: Gerd Binnig in 1986 with Heinrich Rohrer and Ernst Ruska (1986) and Georg Bednorz with Alex himself in 1987. He encouraged many young scientists and actively supported them in their scientific careers. It was mainly thanks to Alex that HK was appointed as Professor at the University of Zurich. Alex not only supported young scientists in their research work, but also provided generous financial support out of his own pocket. For this reason, he set up the K. Alex Müller Stiftung (K. Alex Müller Foundation) at the University of Zurich, where HK had the honor of being a member of the Board of Trustees.
In light of the discovery of high-temperature superconductivity by Georg and Alex, several national research programs were launched in Switzerland between 1987 and 2013, which were funded by the Swiss National Science Foundation. All interested institutions such as Swiss universities, ETH Zurich, EPFL Lausanne, Paul Scherrer Institute (PSI), private research institutes and industrial laboratories were involved in these programs with the common aim of studying new cuprate HTSs and similar novel materials and bringing them to technical application. Alex was instrumental in the realization of these programs. This not only created additional positions for young scientists, but also provided considerable funding for laboratory facilities, joint meetings and conferences.
In the 1990s, Alex, together with Prof. Walter Kündig (University of Zurich), played a key political role in the realization of the Swiss Light Source (SLS), a third-generation synchrotron light source, at PSI, despite much resistance from the physics community. He recognized early on the importance of such a facility for Switzerland as a research and industrial hub.
Alex was also a passionate car enthusiast (see Figure 24). For several years, he was the proud owner of a burgundy and a dark blue Jaguar as well as a historic oldtimer, a light blue Alfa Romeo sports car (without a synchronized gearbox). He modified the garage in his house so that he had access to his cars from below and above in order to be able to carry out repairs and service work himself, which he indeed did with professional care and passion. Alex loved driving. In 1996, for example, at the age of 69, he drove from Zurich to Delphi (Greece) to a conference and back, accompanied by his wife Inge. As Inge told us, the journey was very adventurous. Alex kept his drivers license until he was more than 90 years old. His most recent car was a “British green” Jaguar, which he proudly showed us in the underground garage of the Tertianum (his retirement home near Zurich).

Figure 24.
Alex and his “rented” car, Santa Fe (USA), 2006. (Photo HK).
As outlined above, Alex was not always easy to get along with in his social and scientific life and used to describe people sometimes by their prominent characteristic features. ABH once mentioned a colleague whom Alex could not remember the name of, so he asked whether ABH had this little heavy lady in mind. Another colleague of ours was characterized as the one with the horse teeth. Similarly, he mentioned another colleague as the person giving the worst talks he had ever heard. On the other hand, he also described someone else as really elegant and very good looking. When I could not identify a person he was talking about, he answered that they are slippery like an eel. Eventually, we stopped using true names altogether, using our personal impressions and characterizations instead—a really bad habit which I unfortunately did not lose.
A notable anecdote about Alex happened to ABH in 2001 during the international meeting on ferroelectricity in Madrid, Spain: Alex was the star at the meeting and almost always surrounded by journalists and/or scientists who wanted to talk to the Nobel prize winner. He did not feel comfortable with the situation and tried to escape this environment by vanishing in various bodegas with close friends. One evening, he apologized for not joining the “gang” because he had been invited to a reception by the Spanish king. Nevertheless, he promised to meet up with us later on in the evening in a cozy bar. Completely unexpectedly, he arrived there only shortly after us, explaining that the king was delayed and he was not in the mood to wait for him. Actually, this was very typical for him, since it showed that whatever authority he was supposed to meet, he had his own rules and applied those independent of one’s status.
Another memorable encounter with him happened in the Swiss Alps on the occasion of the conference on superconductivity in Klosters. Since we, ABH and HK, had organized this event, we had planned for extended lunch breaks to give the participants the opportunity for skiing in this fantastic environment. I (ABH) was accompanied by my husband and children, and we used these breaks for skiing almost every day. On one occasion, we had just left the ski lift when Alex also arrived on the top of the mountain. We were surprised, and I mentioned what a strange accident this was. Alex replied that there are no “accidents”, but everything is predestinated. We decided to take the rope downhill together with a lunch break in a small lodge. My children, being very good skiers, wanted to impress Alex and took the fastest possible rope to the lodge. But Alex arrived there before them despite being already in his eighties.
In 2015, I (ABH) was asked by the IEEE History Center, The Institute of Electrical and Electronics Engineers Inc. to conduct an interview with Alex which was published in the same year by IEEE [99]. Alex agreed to it, and in view of his scarce time, we held the interview in my car on the way from Zollikerberg (near Zurich) to Geneva, where he gave his last talk at The International Conference M2S 2015. Despite a couple of unfortunate incidents, it was his best talk and highly appreciated by the audience. During our journey, we had plenty of time to talk, and this was summarized later in the above-mentioned article which Alex had agreed to publish. Since the Swiss police is very concerned that the speed limit on the roads and the “Autobahnen” (highways) is taken seriously, I strictly obeyed the traffic regulations. At one point during the trip a car in front of us was driving extremely slowly such that ABH decided to pass the car. Alex looked out of the window and remarked: “A typical female driver!!”. I looked at him and said: “I am also female”. More such remarks happened during this memorable ride which remain very vivid.
On the occasion of a conference in Stuttgart in 1990 Alex and I (HK) were invited by the conference organizer to a private party near Stuttgart. Alex had his Jaguar with him and invited me to drive to the party with him. We met in the lobby of the hotel to leave. Alex looked at my name badge from the conference. “Oh, I forgot my name badge in the room, I’ll get it”. “But you don’t need it, Alex”, I said, “everyone at the party knows you”. But Alex went back to his room and got his name badge.
In 2006, at a conference in Santa Fe (USA) I was traveling with Alex by car from Los Alamos to Santa Fe. It was night, bad weather (rain, light snowfall), poor visibility and a winding pass road. Alex being at the wheel said: “Hugo, can you see anything? I can’t see anything!” Alex pressed on the accelerator and drove on happily—we arrived safely back in Santa Fe (the car Alex was driving is shown in Figure 24).
During a break of a conference in Les Diablerets in the Swiss Alps (around 2000), Alex and I were sitting together at a table. A well-known physicist from the USA sat down with us. He asked Alex if he was still working at IBM. “No”, said Alex, “I’m now working in Hugo Keller’s group at the University of Zurich.” The physicist from the USA made an astonished face and Alex smiled mischievously.
Alex and ABH shared the same bad habit of smoking. Mostly, Alex would smoke a pipe, but when he was with ABH, he preferred a cigarette. Numerous photos exist of the two sharing a bench and smoking happily together (see Figure 25). In one of his private letters to ABH, Alex told her his thoughts about smokers and the consequences arising from it. The original letter (see Figure 26) and its translation are given below:
- -
- Sigmund Freud was a cigar smoker what he highly esteemed. However he was such a heavy smoker that he developed mouth cancer. After its surgery he continued smoking and the cancer was inoperable →+
- -
- C.G. Jung smoked with devotion pipe. He was suffering from renal failure at high age, yet he continued smoking even during dialysis. Whenever I was smoking too much pipe I got renal pain. Ergo one may speculate that C.G. Jung damaged his renal further by smoking deliberately →+
- -
- Wolfgang Pauli was frequently smoking pipe. He fell sick of liver cancer without a chance of healing →+
Do these examples of famous people show that one should stop smoking? My answer is NO! Why? Smoking enabled these celebrities to achieve spectacular results besides of their knowledge. A related case happened with the famous symphonians. …

Figure 25.
Alex and ABH “smoking with pleasure”. Left side: at a conference in Erice (Sicily), 2003. (Source of photo unknown). Right side: in front of the Tertianum in Zollikerberg (Zurich), 2018. (Photo HK).

Figure 26.
Letter from Alex to ABH, describing the “importance of smoking”, 5 January 2012. (Photo ABH).
On the occasion of the 22nd Condensed Matter Conference of the European Physical Society (CMD EPS) 2008 in Rome, Alex was a plenary speaker and, like always, surrounded by a huge crowd of participants. During a break, he came to me (ABH) to propose an escape and instead visit a special small church in the center of Rome. This church is known for its beautiful paintings by Michelangelo. It has to be mentioned that the University of Rome, La Sapienza and the center of Rome are quite a distance apart, and it was August, the hottest month in Rome. Alex went shortly to his hotel to drop the conference booklet, and I waited in front of the hotel. We took the shortest route to the church which we, however, did not find, since it is small and squeezed between the city houses of downtown Rome. Having had a small lunch, we decided to go back to the hotel so that Alex could have break. I had not paid any attention to the hotel location or its name, but had simply followed Alex. This turned out to be a major mistake, since Alex neither knew its name nor its address. Alex suggested possible names of the hotel, so that it could have been looked up in a phone book or we could ask a taxi driver. None of the names existed, and we continued walking in the summer heat, hoping to accidentally find the right place. After a long long walk, I suggested phoning the chair of Alex’s session, Antonio Bianconi. Unfortunately, he was in a session and did not answer the call. Another hour passed with us both getting rather desperate and tired, since we continued walking. Then, finally, Antonio phoned us and provided us with the information we needed. We were already pretty close to the hotel. Alex did not show up at the conference for the rest of the day.
In the above, we (ABH and HK) have summarized our professional and personal interactions with Alex. Our experiences are beyond what is broadly known of him and are hoped to give insights into his life and characteristic attitudes. We finish our story about Alex with the typical words he used in his many letters to ABH (right side of Figure 27): “Machts gut! Euer Alex.”

Figure 27.
Left side: Alex, Santa Fe (USA), 2006. (Photo HK). Right side: From a letter from Alex to ABH: “Machts gut! Euer Alex” (“Take care! Your Alex”). (Photo ABH).
Author Contributions
Both authors (A.B.-H. and H.K.) have contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data and figures are available from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Müller, K.A.; Berlinger, W. Static critical exponents at structural phase transitions. Phys. Rev. Lett. 1971, 26, 13–16. [Google Scholar] [CrossRef]
- Müller, K.A. Paramagnetic Resonance of Fe3+ in SrTiO3 single crystals. Helv. Phys. Acta 1958, 31, 173–204. [Google Scholar]
- Müller, K.A.; Kool, T.W. Properties of Perovskites and Other Oxides; World Scientific Publishing: Singapore, 2010. [Google Scholar]
- Bussmann-Holder, A.; Keller, H. From SrTiO3 to Cuprates and Back to SrTiO3: A Way Along Alex Müller’s Scientific Career. Condens. Matter 2021, 6, 2. [Google Scholar] [CrossRef]
- Physical Review B; 50th Anniversary Milestones, Collections. 2020. Available online: https://journals.aps.org/prb/50th (accessed on 25 April 2024).
- Müller, K.A.; Burkard, H. SrTiO3: An intrinsic quantum paraelectric below 4 K. Phys. Rev. B 1979, 19, 3593–3602. [Google Scholar] [CrossRef]
- Bednorz, J.G.; Müller, K.A. Possible High Tc Superconductivity in the Ba-La-Cu-O System. Z. Phys. B-Condens. Matter 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Keller, H.; Kündig, W.; Arend, H. Critical exponent β of the two-dimensional antiferromagnet (CH3NH3)2FeCl4. J. Phys. 1976, 37, 629–632. [Google Scholar] [CrossRef]
- Keller, H. Mössbauer-Untersuchungen an der zweidimensionalen magnetischen Schichtstruktur (CH3NH3)2FeCl4. Ph.D. Thesis, University of Zurich, Zurich, Switzerland, 1977. [Google Scholar]
- Keller, H.; Debrunner, P.G. Evidence for conformational and diffusional mean square displacements in frozen aqueous solution of oxymyoglobin. Phys. Rev. Lett. 1980, 45, 68–71. [Google Scholar] [CrossRef]
- Keller, H.; Savić, I.M. Mössbauer studies of the static and dynamic critical behavior of the layered antiferromagnets RbFeF4 and KFeF4. Phys. Rev. B 1983, 28, 2638–2652. [Google Scholar] [CrossRef]
- Schneider, J.W.; Baumeler, H.; Keller, H.; Odermatt, W.; Patterson, B.D.; Müller, K.A.; Bednorz, J.G.; Blazey, K.W.; Morgenstern, I.; Savić, I.M. Internal magnetic fields in the high-Tc superconductors La1.8Sr0.2CuO4 and YBa2Cu3O7−δ from muon spin rotation experiments. Phys. Lett. 1987, 124A, 107–111. [Google Scholar] [CrossRef]
- Keller, H.; Pümpin, B.; Kündig, W.; Odermatt, W.; Patterson, B.D.; Schneider, J.W.; Simmler, H.; Connell, S.; Müller, K.A.; Bednorz, J.G.; et al. Internal magnetic fields in YBa2Cu3O7−δ from muon spin rotation experiments: Discussion in terms of a glasslike superconducting state. Physica C 1988, 153–155, 71–74. [Google Scholar] [CrossRef]
- Pümpin, B.; Keller, H.; Kündig, W.; Odermatt, W.; Patterson, B.D.; Schneider, J.W.; Simmler, H.; Connell, S.; Müller, K.A.; Bednorz, J.G.; et al. Internal magnetic fields in the high-temperature superconductor YBa2Cu3O7−δ from muon spin rotation experiments. Z. Phys. B-Condens. Matter 1988, 72, 175–180. [Google Scholar] [CrossRef]
- Müller, K.A.; Pomerantz, M.; Knoedler, C.M.; Abraham, D. Inhomogeneous Superconducting Transitions in Granular Al. Phys. Rev. Lett. 1980, 45, 832–835. [Google Scholar] [CrossRef]
- Pümpin, B.; Keller, H.; Kündig, W.; Odermatt, W.; Savić, I.M.; Schneider, J.W.; Simmler, H.; Zimmermann, P.; Kaldis, E.; Rusiecki, S.; et al. Muon-spin-rotation measurements of the London penetration depths in YBa2Cu3O6.97. Phys. Rev. B 1990, 42, 8019–8029. [Google Scholar] [CrossRef] [PubMed]
- Pümpin, B.; Keller, H.; Kündig, W.; Odermatt, W.; Savić, I.M.; Schneider, J.W.; Simmler, H.; Zimmermann, P.; Bednorz, J.G.; Maeno, Y.; et al. Measurement of the London penetration depths in YBa2Cu3Ox by means of muon spin rotation (μSR) experiments. Physica C 1989, 162–164, 151–152. [Google Scholar] [CrossRef]
- Zimmermann, P.; Keller, H.; Lee, S.L.; Savić, I.M.; Warden, M.; Zech, D.; Cubitt, R.; Forgan, E.M.; Kaldis, E.; Karpinski, J.; et al. Muon-spin rotation studies of the temperature dependence of the magnetic penetration depth in the YBa2Cu3Ox family and related compounds. Phys. Rev. B 1995, 52, 541–552. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.L.; Zimmermann, P.; Keller, H.; Warden, M.; Savić, I.M.; Schauwecker, R.; Zech, D.; Cubitt, R.; Forgan, E.M.; Kes, P.H.; et al. Evidence for flux-lattice melting and a dimensional crossover in single-crystal Bi2.15Sr1.85CaCu2O8+δ from muon spin rotation studies. Phys. Rev. Lett. 1993, 71, 3862–3865. [Google Scholar] [CrossRef]
- Keller, H. Muon-spin rotation experiments in high-Tc superconductors and related materials. IBM J. Res. Develop. 1989, 33, 314–323. [Google Scholar] [CrossRef]
- Keller, H. Muon spin rotation experiments in high-Tc superconductors. In Earlier and Recent Aspects of Superconductivity; Bednorz, J.G., Müller, K.A., Eds.; Springer Series in Solid-State Sciences 90; Springer: Berlin/Heidelberg, Germany, 1990; pp. 222–239. [Google Scholar]
- Höck, K.-H.; Nickisch, H.; Thomas, H. Jahn-Teller effect in itinerant electron systems: The Jahn-Teller polaron. Helv. Phys. Acta 1983, 56, 237–243. [Google Scholar]
- Batlogg, B.; Cava, R.J.; Jayaraman, A.; van Dover, R.B.; Kourouklis, G.A.; Sunshine, S.; Murphy, D.W.; Rupp, L.W.; Chen, H.S.; White, A.; et al. Isotope Effect in the High-Tc Superconductors Ba2YCu3O7 and Ba2EuCu3O7. Phys. Rev. Lett. 1987, 58, 2333–2336. [Google Scholar] [CrossRef]
- Anderson, P.W. The Resonating Valence Bond State in La2CuO4 and Superconductivity. Science 1987, 235, 1196–1198. [Google Scholar] [CrossRef]
- Crawford, M.K.; Farneth, W.E.; McCarron, E.M.; Harlow, R.L.; Moudden, A.H. Oxygen Isotope Effect and Structural Phase Transitions in La2CuO4-Based Superconductors. Science 1990, 250, 1390–1394. [Google Scholar] [CrossRef]
- Franck, J.P.; Jung, J.; Mohamed, A.K.; Gygax, S.; Sproule, G.I. Observation of an oxygen isotope effect in superconducting (Y1−xPrx)Ba2Cu3O7−δ. Phys. Rev. B 1991, 44, 5318–5321. [Google Scholar] [CrossRef] [PubMed]
- Franck, J.P. Experimental studies of the isotope effect in high temperature superconductors. In Physical Properties of High Temperature Superconductors IV; Ginsberg, D.M., Ed.; World Scientific: Singapore, 1994; pp. 189–293. [Google Scholar]
- Müller, K.A. On the oxygen isotope effect and apex anharmonicity in high-Tc cuprates. Z. Phys. B-Condens. Matter 1990, 80, 193–201. [Google Scholar] [CrossRef]
- Cardona, M.; Liu, R.; Thomsen, C.; Kress, W.; Schönherr, E.; Bauer, M.; Genzel, L.; König, W. Effect of isotopic substitution of oxygen on Tc and the phonon frequencies of high Tc superconductors. Solid State Commun. 1988, 76, 789–793. [Google Scholar] [CrossRef]
- Zech, D.; Keller, H.; Müller, K.A.; Conder, K.; Kaldis, E. Site-selective Oxygen Isotope Effect in Highly Doped YBa2Cu3Ox. Physica C 1994, 235–240, 1221–1222. [Google Scholar] [CrossRef]
- Zech, D.; Keller, H.; Conder, K.; Kaldis, E.; Liarokapis, E.; Poulakis, N.; Müller, K.A. Site-selective oxygen isotope effect in optimally doped YBa2Cu3O6+x. Nature 1994, 371, 681–683. [Google Scholar] [CrossRef]
- Nickel, J.H.; Morris, D.E.; Ager, J.W. Locus of Pairing Interaction in YBa2Cu3O7 by Site-Selective Oxygen Isotope Shift: 18O in CuO2 Plane Layers. Phys. Rev. Lett. 1993, 70, 81–84. [Google Scholar] [CrossRef]
- Zhao, G.M.; Ager, J.W., III; Morris, D.E. Site dependence of large oxygen isotope effect in Y0.7Pr0.3Ba2Cu3O6.97. Phys. Rev. B 1996, 54, 14982–14985. [Google Scholar] [CrossRef]
- Khasanov, R.; Shengelaya, A.; Morenzoni, E.; Angst, M.; Conder, K.; Savić, I.M.; Lampakis, D.; Liarokapis, E.; Tatsi, A.; Keller, H. Site-selective oxygen isotope effect on the magnetic field penetration depth in underdoped Y0.6Pr0.4Ba2Cu3O7-δ. Phys. Rev. B 2003, 68, 220506(R). [Google Scholar] [CrossRef]
- Zhao, G.M.; Conder, K.; Keller, H.; Müller, K.A. Oxygen isotope effects in La2−xSrxCuO4: Evidence for polaronic charge carriers and their condensation. J. Phys. Condens. Matter 1998, 10, 9055–9066. [Google Scholar] [CrossRef]
- Zhao, G.M.; Keller, H.; Conder, K. Unconventional isotope effects in the high-temperature cuprate superconductors. J. Phys. Condens. Matter 2001, 13, R569–R587. [Google Scholar] [CrossRef]
- Keller, H. Unconventional Isotope Effects in Cuprate Superconductors. In Superconductivity in Complex Systems; Müller, K.A., Bussmann-Holder, A., Eds.; Structure and Bonding 114; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2005; pp. 143–169. [Google Scholar]
- Keller, H.; Bussmann-Holder, A.; Müller, K.A. Jahn-Teller physics and high-Tc superconductivity. Mater. Today 2008, 11, 38–46. [Google Scholar] [CrossRef]
- Zhao, G.-M.; Conder, K.; Keller, H.; Müller, K.A. Giant oxygen isotope shift in the magnetoresistive perovskite La1−xCaxMnO3+y. Nature 1996, 381, 676–678. [Google Scholar] [CrossRef]
- Zhao, G.-M.; Hunt, M.B.; Keller, H.; Müller, K.A. Evidence for polaronic supercarriers in the copper oxide superconductors La2−xSrxCuO4. Nature 1997, 385, 236–239. [Google Scholar] [CrossRef]
- Hofer, J.; Conder, K.; Sasagawa, T.; Zhao, G.M.; Willemin, M.; Keller, H.; Kishio, K. Oxygen-isotope effect on the in-plane penetration depth in underdoped La2−xSrxCuO4 single crystals. Phys. Rev. Lett. 2000, 84, 4192–4195. [Google Scholar] [CrossRef] [PubMed]
- Khasanov, R.; Eshchenko, D.G.; Luetkens, H.; Morenzoni, E.; Prokscha, T.; Suter, A.; Garifinov, N.; Mali, M.; Roos, J.; Conder, K.; et al. Direct observation of the oxygen isotope effect on the in-plane magnetic field penetration depth in optimally doped YBa2Cu3O7−δ. Phys. Rev. Lett. 2004, 92, 057602. [Google Scholar] [CrossRef] [PubMed]
- Zech, D.; Hofer, J.; Rossel, C.; Bauer, P.; Keller, H.; Karpinski, J. Effective mass anisotropy of HgBa2Ca3Cu4O10 measured on a microcrystal by means of miniaturized torque magnetometry. Phys. Rev. B 1996, 53, R6026–R6029. [Google Scholar] [CrossRef]
- Rossel, C.; Bauer, P.; Zech, D.; Hofer, J.; Willemin, M.; Keller, H. Active microlevers as miniature torque magnetometers. J. Appl. Phys. 1996, 79, 8166–8173. [Google Scholar] [CrossRef]
- Willemin, M.; Rossel, C.; Brugger, J.; Despont, M.; Rothuizen, H.; Vettiger, P.; Hofer, J.; Keller, H. Piezoresistive cantilever designed for torque magnetometry. J. Appl. Phys. 1998, 83, 1163–1170. [Google Scholar] [CrossRef]
- Di Castro, D.; Angst, M.; Eshchenko, D.G.; Khasanov, R.; Roos, J.; Savić, I.M.; Shengelaya, A.; Budko, S.L.; Canfield, P.C.; Conder, K.; et al. Absence of a boron isotope effect in the magnetic penetration depth of MgB2. Phys. Rev. B 2004, 70, 014519. [Google Scholar] [CrossRef]
- Anderson, P.W. Present status of the theory of the high-Tc cuprates. Low Temp. Phys. 2006, 32, 282–289. [Google Scholar] [CrossRef]
- Lanzara, A.; Zhao, G.-M.; Saini, N.L.; Bianconi, A.; Conder, K.; Keller, H.; Müller, K.A. Oxygen-isotope effect of the charge-stripe ordering temperature in La2−xSrxCuO4 from X-ray absorption spectroscopy. J. Phys. Condens. Matter 1999, 11, L541–L546. [Google Scholar] [CrossRef]
- Bendele, M.; von Rohr, F.; Guguchia, Z.; Pomjakushina, E.; Conder, K.; Bianconi, A.; Simon, A.; Bussmann-Holder, A.; Keller, H. Evidence for strong lattice effects as revealed from huge unconventional oxygen isotope effects on the pseudogap temperature in La2−xSrxCuO4. Phys. Rev. B 2017, 95, 014514. [Google Scholar] [CrossRef]
- Rubio Temprano, D.; Conder, K.; Furrer, A.; Mutka, H.; Trounov, V.; Müller, K.A. Oxygen and copper isotope effects on the pseudogap in the high-temperature superconductor La1.81Ho0.04Sr0.15CuO4 studied by neutron crystal-field spectroscopy. Phys. Rev. B 2002, 66, 184506. [Google Scholar] [CrossRef]
- Häfliger, P.S.; Podlesnyak, A.; Conder, K.; Pomjakushina, E.; Furrer, A. Pseudogap of the high-temperature superconductor La1.96−xSrxHo0.04CuO4 as observed by neutron crystal-field spectroscopy. Phys. Rev. B 2006, 74, 184520. [Google Scholar] [CrossRef]
- Rubio Temprano, D.; Mesot, J.; Janssen, S.; Conder, K.; Furrer, A.; Mutka, H.; Müller, K.A. Large Isotope Effect on the Pseudogap in the High-Temperature Superconductor HoBa2Cu4O8. Phys. Rev. Lett. 2000, 84, 1990–1993. [Google Scholar] [CrossRef]
- Shengelaya, A.; Zhao, G.-M.; Aegerter, C.; Conder, K.; Savić, I.M.; Keller, H. Giant oxygen isotope effect on the spin glass transition in La2−xSrxCu1−zMnzO4 as revealed by muon spin rotation. Phys. Rev. Lett. 1999, 83, 5142–5146. [Google Scholar] [CrossRef]
- Khasanov, R.; Shengelaya, A.; Di Castro, D.; Morenzoni, E.; Maisuradze, A.; Savić, I.M.; Conder, K.; Pomjakushina, E.; Bussmann-Holder, A.; Keller, H. Oxygen isotope effect on the superconducting transition and magnetic states within the phase diagram of Y1−xPrxBa2Cu3O7−δ. Phys. Rev. Lett. 2008, 101, 077001. [Google Scholar] [CrossRef]
- Guguchia, Z.; Khasanov, R.; Bendele, M.; Pomjakushina, E.; Conder, K.; Shengelaya, A.; Keller, H. Negative Oxygen Isotope Effect on the Static Spin Stripe Order in Superconducting La2−xBaxCuO4 (x=1/8) Observed by Muon-Spin Rotation. Phys. Rev. Lett. 2014, 113, 057002. [Google Scholar] [CrossRef]
- Khasanov, R.; Strässle, S.; Conder, K.; Pomjakushina, E.; Bussmann-Holder, A.; Keller, H. Universal correlations of isotope effects in Y1−xPrxBa2Cu3O7−δ. Phys. Rev. B 2008, 77, 104530. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Keller, H. Superconductivity and the Jahn-Teller Polaron. Condens. Matter 2022, 7, 10. [Google Scholar] [CrossRef]
- Müller, K.A. Possible coexistence of s- and d-wave condensates in copper oxide superconductors. Nature 1995, 377, 133–135. [Google Scholar] [CrossRef]
- Müller, K.A.; Keller, H. s and d Wave Symmetry Components in High-Temperature Cuprate Superconductors. In High-Tc Superconductivity 1996: Ten Years after the Discovery; Kaldis, E., Liarokapis, E., Müller, K.A., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA; London, UK, 1997; pp. 7–29. [Google Scholar]
- Khasanov, R.; Shengelaya, A.; Maisuradze, A.; La Mattina, F.; Bussmann-Holder, A.; Keller, H.; Müller, K.A. Experimental evidence for two gaps in the high-temperature La1.83Sr0.17CuO4 superconductor. Phys. Rev. Lett. 2007, 98, 057007-1. [Google Scholar] [CrossRef] [PubMed]
- Khasanov, R.; Strässle, S.; Di Castro, D.; Masui, T.; Miyasaka, S.; Tajima, S.; Bussmann-Holder, A.; Keller, H. Multiple gap symmetries for the order parameter of cuprate superconductors from penetration depth measurements. Phys. Rev. Lett. 2007, 99, 237601-1. [Google Scholar] [CrossRef] [PubMed]
- Khasanov, R.; Shengelaya, A.; Karpinski, J.; Bussmann-Holder, A.; Keller, H.; Müller, K.A. s-wave symmetry along the c-axis and s+d in-plane superconductivity in bulk YBa2Cu4O8. J. Supercond. Nov. Magn. 2008, 21, 81–85. [Google Scholar] [CrossRef]
- Khasanov, R.; Shengelaya, A.; Conder, K.; Karpinski, J.; Bussmann-Holder, A.; Keller, H. Oxygen isotope effect on the superfluid density within the d-wave and s-wave pairing channels of YBa2Cu4O8. Physica C 2023, 613, 1354332. [Google Scholar] [CrossRef]
- Bussmann, A.; Bilz, H.; Roenspiess, R.; Schwarz, K. Oxygen polarizability in ferroelectric phase transitions. Ferroelectrics 1980, 25, 343–346. [Google Scholar] [CrossRef]
- Migoni, R.L.; Bilz, H.; Baeuerle, D. Origin of Raman Scattering and Ferroelectricity in Oxidic Perovskites. Phys. Rev. Lett. 1976, 37, 1155–1158. [Google Scholar] [CrossRef]
- Bilz, H.; Benedek, G.; Bussmann-Holder, A. Theory of ferroelectricity: The polarizability model. Phys. Rev. B 1987, 35, 4840–4849. [Google Scholar] [CrossRef]
- Bussmann-Holder, A. The polarizability model for ferroelectricity in perovskite oxides. J. Phys. Condens. Matter 2012, 24, 273202. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Simon, A.; Büttner, H. Possibility of a common origin to ferroelectricity and superconductivity in oxides. Phys. Rev. B 1987, 39, 207–214. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Müller, K.A.; Micnas, R.; Büttner, H.; Simon, A.; Bishop, A.R.; Egami, T. Theory of dynamic stripe induced superconductivity. J. Phys. Condens. Matter 2001, 13, L169. [Google Scholar] [CrossRef]
- Müller, K.A.; Bussmann-Holder, A. (Eds.) Superconductivity in Complex Systems; Structure and Bonding 114; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2005. [Google Scholar]
- Bianconi, A.; Saini, N.L.; Lanzara, A.; Missori, M.; Rossetti, T.; Oyanagi, H.; Yamaguchi, H.; Oka, K.; Ito, T. Determination of the Local Lattice Distortions in the CuO2 Plane of La1.85Sr0.15CuO4. Phys. Rev. Lett. 1996, 76, 3412–3415. [Google Scholar] [CrossRef] [PubMed]
- Bednorz, J.G.; Müller, K.A. Perovskite-Type Oxides—The New Approach to High-Tc Superconductivity. Nobel Lect. 1987, 60, 424–457. [Google Scholar] [CrossRef]
- Landau, L.D. Electron motion in crystal lattices. Phys. Z. Sowjetunion 1933, 3, 67–68. [Google Scholar]
- Pekar, S.I. Quantum states and optical transitions of electron in a polaron and at a color center of a crystal. J. Phys. USSR 1946, 10, 341–346. [Google Scholar]
- Landau, L.D.; Pekar, S.I. Effective mass of a polaron. Zh. Eksp. Teor. Fiz. 1948, 18, 419–423. [Google Scholar]
- Fröhlich, H.; Pelzer, H.; Zienau, S. Properties of slow electrons in polar materials. Phil. Mag. 1950, 41, 221–242. [Google Scholar] [CrossRef]
- Fröhlich, H. Electrons in lattice fields. Adv. Phys. 1954, 3, 325–362. [Google Scholar] [CrossRef]
- Holstein, T. Studies of polaron motion: Part I. The molecular-crystal model. Ann. Phys. 1959, 8, 325–342. [Google Scholar] [CrossRef]
- Holstein, T. Studies of polaron motion: Part II. The “small” polaron. Ann. Phys. 1959, 8, 343–389. [Google Scholar] [CrossRef]
- Devreese, J.T.; Alexandrov, A.S. Fröhlich polaron and bipolaron: Recent developments. Rep. Prog. Phys. 2009, 72, 66501–66564. [Google Scholar] [CrossRef]
- Alexandrov, A.S. Superconducting Polarons and Bipolarons. In Polarons in Advanced Materials; Springer Series in Materials Science 103; Alexandrov, A.S., Ed.; Springer: Dordrecht, The Netherlands, 2007; pp. 257–310. [Google Scholar]
- Aubry, S. Small Adiabatic Polarons and Bipolarons. In Polarons in Advanced Materials; Springer Series in Materials Science 103; Alexandrov, A.S., Ed.; Springer: Dordrecht, The Netherlands, 2007; pp. 311–372. [Google Scholar]
- Jahn, H.A.; Teller, E. Stability of Polyatomic Molecules in Degenerate Electronic States I—Orbital Degeneracy. Proc. Roy. Soc. A 1937, 161, 220–235. [Google Scholar]
- Housecroft, C.; Sharpe, A.G. Inorganic Chemistry, 3rd ed.; Prentice Hall: Hoboken, NJ, USA, 2008; p. 644. [Google Scholar]
- Suhl, H.; Matthias, B.T.; Walker, L.R. Bardeen-Cooper-Schrieffer Theory of Superconductivity in the Case of Overlapping Bands. Phys. Rev. Lett. 1959, 3, 552–555. [Google Scholar] [CrossRef]
- Moskalenko, V. Superconductivity in metals with overlapping energy bands. Fiz. Met. Metalloved. 1959, 8, 2518–2529. [Google Scholar]
- Zhang, F.C.; Rice, T.M. Effective Hamiltonian for the superconducting Cu oxides. Phys. Rev. B 1988, 37, 3759(R)–3763(R). [Google Scholar] [CrossRef] [PubMed]
- Bussmann-Holder, A.; Keller, H. Polaron formation as origin of unconventional isotope effects in cuprate superconductors. Eur. Phys. J. B 2005, 44, 487–490. [Google Scholar] [CrossRef]
- Oyanagi, H. Lattice effects in high-temperature superconducting cuprates revealed by X-ray absorption spectroscopy. In High Tc Superconductors and Related Transition Metal Oxides; Bussmann-Holder, A., Keller, H., Bianconi, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 253–258. [Google Scholar]
- Mustre de Leon, J.; Conradson, S.D.; Batistić, I.; Bishop, A.R. Evidence for an axial oxygen-centered lattice fluctuation associated with the superconducting transition in YBa2Cu3O7. Phys. Rev. Lett. 1990, 65, 1675–1678. [Google Scholar] [CrossRef] [PubMed]
- Mustre de Leon, J.; Acosta-Alejandro, M.; Conradson, S.D.; Bishop, A.R. Local structure fluctuations as a signature of an inhomogeneous ground state in high-Tc superconductors. J. Synchrotron Rad. 2005, 12, 193–196. [Google Scholar] [CrossRef]
- Goodenough, J.B. Theory of the Role of Covalence in the Perovskite-Type Manganites [La, M(II)]MnO3. Phys. Rev. 1955, 100, 564–573. [Google Scholar] [CrossRef]
- Kanamori, J. Superexchange interaction and symmetry properties of electron orbitals. J. Phys. Chem. Solids 1959, 10, 87–98. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Keller, H. (Eds.) High Tc Superconductors and Related Transition Metal Oxides; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Bussmann-Holder, A.; Keller, H.; Bianconi, A. (Eds.) High Tc Copper Oxide Superconductors and Related Novel Materials; Springer Series in Materials Science 255; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Bussmann-Holder, A.; Keller, H.; Bianconi, A. (Eds.) From Quantum Paraelectric/Ferroelectric Perovskite Oxides to High Temperature Superconducting Oxides; MDPI Condensed Matter: Basel, Switzerland, 2021. [Google Scholar]
- Available online: https://www.sciencedirect.com/journal/physica-c-superconductivity-and-its-applications/special-issues (accessed on 25 April 2024).
- Müller, K.A. Erinnerungen, Einsichten und Tagebuchnotitzen. Personal communication, 2007. [Google Scholar]
- IEEE Interview: K. Alex Müller (interviewee), Annette Bussmann-Holder (interviewer), Geneva, Switzerland, 24–26 August 2015.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).