Systematic Trends in Hybrid-DFT Computations of BaTiO₃/SrTiO₃, PbTiO₃/SrTiO₃ and PbZrO₃/SrZrO₃ (001) Hetero Structures

Abstract

We performed predictive hybrid-DFT computations for PbTiO₃, BaTiO₃, SrTiO₃, PbZrO₃ and SrZrO₃ (001) surfaces, as well as their BaTiO₃/SrTiO₃, PbTiO₃/SrTiO₃ and PbZrO₃/SrZrO₃ (001) heterostructures. According to our hybrid-DFT computations for BO₂ and AO-terminated ABO₃ solid (001) surfaces, in most cases, the upper layer ions relax inwards, whereas the second layer ions shift upwards. Our hybrid-DFT computed surface rumpling s for the BO₂-terminated ABO₃ perovskite (001) surfaces almost always is positive and is in a fair agreement with the available LEED and RHEED experiments. Computed B-O atom chemical bond population values in the ABO₃ perovskite bulk are enhanced on its BO₂-terminated (001) surfaces. Computed surface energies for BO₂ and AO-terminated ABO₃ perovskite (001) surfaces are comparable; thus, both (001) surface terminations may co-exist. Our computed ABO₃ perovskite bulk Γ-Γ band gaps are in fair agreement with available experimental data. BO₂ and AO-terminated (001) surface Γ-Γ band gaps are always reduced with regard to the respective bulk band gaps. For our computed BTO/STO and PTO/STO (001) interfaces, the average augmented upper-layer atom relaxation magnitudes increased by the number of augmented BTO or PTO (001) layers and always were stronger for TiO₂-terminated than for BaO or PbO-terminated upper layers. Our B3PW concluded that BTO/STO, as well as SZO/PZO (001) interface Γ-Γ band gaps, very strongly depends on the upper augmented layer BO₂ or AO-termination but considerably less so on the number of augmented (001) layers.

1. Introduction

Different aspects of (001) surface as well as (001) interface phenomena in ABO₃ perovskites are topics of paramount importance in modern solid state physics [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. All of our hybrid-DFT computed SrZrO₃, PbZrO₃, PbTiO₃, BaTiO₃ and SrTiO₃ solids belong to the group of so-called ABO₃ perovskite compounds [17,18,19]. Strontium zirconate (SrZrO₃) is an extremely interesting material due to its high-temperature electronic properties [20]. The SrZrO₃ phase transitions have been very carefully examined by Kennedy et al. [21] by means of powder neutron diffraction, as well as the Rietveld method [21]. Maniwa et al. [22] and Shirane et al. [23] described PbZrO₃ as antiferroelectric due to its dielectric behaviour. Since then, materials that revealed a structural phase transition between two non-polar phases with a large dielectric anomaly at the high-temperature region of the transition were called antiferroelectrics [22,23]. Antiferroelectric oxides, for example PbZrO₃, become highly promising candidate materials for dielectric energy storage capacitors [24,25]. PbTiO₃ is a crucial component in a wide range of industrially important applications, including sensors, ultrasonic transducers and actuators [26]. Polymer ceramic hybrid composites (PVA/PbTiO₃) are highly promising functional materials in a wide variety of research disciplines, demonstrating useful electrical, optical, mechanical, thermal and antibacterial properties [27]. Ferroelectric materials, for example BaTiO₃, have been mentioned in connection to bacterial degradation [28]. It is demonstrated that the remnant polarization can induce antibacterial activities [29] in ferroelectric materials like BaTiO₃. Lead zirconate titanate Pb(Zr,Ti)O₃ is the most widely used worldwide piezoceramic material for electromechanical device applications [30]. Strontium titanate exhibits photocatalytic activity [31,32]. The identification of highly promising thermoelectric materials, like SrTiO₃, is accelerated by theoretical predictions from ab initio calculations [33,34,35,36]. In general, there is a lot of interest in the science and technology of transition metal oxides, like ABO₃ perovskites, due to their large variety of specific electronic, optical and magnetic properties [37,38,39,40,41,42,43,44,45,46,47,48]. For that reason, during the last 25 years, a lot of theoretical and experimental studies have been performed for PbTiO₃, BaTiO₃, SrTiO₃, SrZrO₃ and PbZrO₃ perovskite (001) surfaces [49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72]. At the same time, it is very difficult to understand why a smaller number of first-principles computations, as well as experimental studies, were devoted to BTO/STO and PTO/STO, as well as SZO/PZO (001) heterostructures [73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88].

SrTiO₃ (STO) perovskite is paraelectric and maintains its cubic centrosymmetric structure at all observed temperatures [89]. BaTiO₃ (BTO), as a function of temperature, undergoes three phase transitions. Namely, the BTO crystal structure changes at 183 K from rhombohedral (R3m) to orthorhombic (Amm2), then at 278 K to tetragonal (P4mm), and finally at 403 K to a high-temperature cubic structure ($P\mathrm{m}\overline{3}\mathrm{m}$) [90]. PbTiO₃ (PTO) undergoes only one phase transition at 766 K from a tetragonal ferroelectric phase, stable at room temperature, with the space group P4mm to the high-symmetry cubic structure with the space group $P\mathrm{m}\overline{3}\mathrm{m}$ [91]. It is well-known that the classical PbZrO₃ (PZO) perovskite exhibits three different phases. Namely, at low temperatures, PZO has an orthorhombic antiferroelectric phase stable at the temperature region up to 230 °C. The PZO rhombohedral ferroelectric phase is stable at the temperature region from 230 °C to 233 °C. Finally, PZO perovskite possesses a cubic paraelectric phase at temperatures above 233 °C [69]. Lastly, for the SrZrO₃ (SZO) perovskite, Ligny et al. [92] discovered the following three phase transitions from enthalphy measurements: orthorhombic (Pnma) → orthorhombic (Cmcm) → tetragonal (I4/mcm) → cubic ($P\mathrm{m}\overline{3}\mathrm{m}$) at temperatures equal to 995 K and 1105 K, as well as 1140 K, respectively [92].

For our hybrid-DFT computations, we adopted the classical cubic unit cells of SrZrO₃, PbZrO₃, PbTiO₃, BaTiO₃ and SrTiO₃ perovskites. The cubic unit cells of all five of our ab initio computed ABO₃ perovskites contain five atoms [93,94,95,96]. They all have exactly the same space group $P\mathrm{m}\overline{3}\mathrm{m}$, as well as the same space group number, 221. In the cubic ABO₃ perovskite matrix, the A-type atom (Sr, Pb or Ba) was located at the cube corner position. Thereby, the ABO₃ perovskite A atom, in our computations, is located at the coordinate system origin and has the following coordinates (0, 0, 0). The B-type ABO₃ perovskite atom (Ti or Zr) is located at the body center location of the cube. The coordinates of the B atom are equal to (½, ½, ½). Finally, the ABO₃ perovskite unit cell’s three oxygen atoms are located at the cube face center positions with the following coordinates (½, ½, 0), (½, 0, ½), (0, ½, ½).

The aim of our research reported herein was to perform necessary additional hybrid-DFT computations for SrZrO₃, PbZrO₃, PbTiO₃, BaTiO₃ and SrTiO₃ perovskite (001) surfaces, as well as their (001) heterostructures, in order to complete our many years of lasting work in this direction, and to create a theory that explains systematic trends in ABO₃ perovskite (001) surface and interface computations. In the first part of our contribution, we present comparative hybrid-DFT computation results dealing with the pristine SrZrO₃, PbZrO₃, PbTiO₃, BaTiO₃ and SrTiO₃ (001) surfaces. We computed the SrZrO₃, PbZrO₃, PbTiO₃, BaTiO₃ and SrTiO₃ (001) surface atom relaxations for both possible BO₂ and AO (001) surface terminations and compared the calculated surface rumplings s and interlayer distances Δd_ij with the available experimental data. As a next step, we computed the SrZrO₃, PbZrO₃, PbTiO₃, BaTiO₃ and SrTiO₃ (001) surface energies, as well as B-O chemical band populations near the BO₂-terminated (001) surfaces. Finally, we computed the band gaps for bulk PbTiO₃, BaTiO₃ and SrTiO₃ and their (001) surfaces by means of different exchange-correlation functionals. As a logical next step, we extended our (001) surface calculations to hybrid-DFT computations of considerably less-studied SrTiO₃/BaTiO₃, SrZrO₃/PbZrO₃ and PbTiO₃/SrTiO₃ (001) heterostructures.

The present paper is structured in the following way. Our hybrid-DFT calculations details, dealing with ABO₃ perovskite (001) surfaces and heterostructures, are described in Section 2. Section 3.1 presents our computation results dealing with SrZrO₃, PbZrO₃, PbTiO₃, BaTiO₃ and SrTiO₃ (001) surfaces, whereas Section 3.2 addresses their SrTiO₃/BaTiO₃, SrZrO₃/PbZrO₃ and PbTiO₃/SrTiO₃ (001) heterostructures. In particular, our novel hybrid-DFT computations are devoted to charge density redistribution and changes in the band structure in stoichiometric, as well as non-stoichiometric (001), heterostructures, consisting of BTO, PTO and PZO (001) thin films, with different thicknesses deposited on the TiO₂-, TiO₂- and ZrO₂-terminated STO and SZO (001) substrate. We analyzed our hybrid-DFT calculation results and detected systematic trends common for all STO/BTO and STO/PTO, as well as SZO/PZO (001), heterostructures.

2. Hybrid-DFT Calculation Details

We carried out our hybrid-DFT computations for the PbTiO₃ (PTO), BaTiO₃ (BTO), SrTiO₃ (STO), PbZrO₃ (PZO) and SrZrO₃ (001) bulk, as well as their BO₂- and AO-terminated (001) surfaces, and their different (001) heterostructures, employing the computer code CRYSTAL [97]. For our hybrid-DFT computations, we employed the nowadays very popular hybrid exchange-correlation functionals B3LYP [98] or B3PW [99,100]. It is worthwhile to note that the hybrid exchange-correlation functionals, for example, B3LYP or B3PW allows achieving an outstanding agreement with the experiment for the band gaps of ABO₃ perovskites as well as related materials, like CaF₂ [101] and MgF₂ [102]. In contrast, density functional theory (DFT) strongly underestimates, while the Hartree–Fock (HF) method, as a rule, very strongly overestimates the ab initio calculated band gaps of solids. For example, the experimental CaF₂ direct band gap value at the Γ-point is equal to 12.1 eV [103]. Our, by means of Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional [104,105], extensively used in DFT, ab initio computed CaF₂ Γ-Γ band gap is very strongly underestimated with respect to the experimental value (12.1 eV) and is equal to 8.45 eV. From another side, our ab initio HF [106] computed CaF₂ Γ-Γ band gap (20.77 eV) is 1.72 times overestimated compared to the experimental CaF₂ band gap value (12.1 eV [105]). According to our hybrid-DFT computations, the hybrid exchange correlation functionals, like B3LYP (10.85 eV) and B3PW (10.96 eV) allows the achievement of the best possible agreement with the experimental CaF₂ Γ-Γ band gap equal to 12.1 eV. The experimentally measured MgF₂ Γ-Γ band gap is equal to 13.0 eV [107]. Again, our PBE exchange-correlation functional computed MgF₂ Γ-Γ band gap is considerably underestimated regarding the experimental value of (13.0 eV) and is equal to 6.9 eV. In contrast, our ab initio HF computed MgF₂ Γ-Γ band gap (19.65 eV) very strongly, namely 1.65 times, overestimates the experimentally measured MgF₂ band gap at Γ-point (13.0 eV). The best possible results, according to our hybrid-DFT computations, are possible to achieve by means of the hybrid exchange-correlation functionals B3LYP (9.42 eV) and B3PW (9.48 eV). Since, as it is possible to see from our computation results for CaF₂ and MgF₂ solids, the hybrid exchange-correlation functionals B3LYP and B3PW allows achieving the best possible results for CaF₂ and MgF₂ Γ-Γ band gaps, we performed all of our coming ABO₃ perovskite (001) surface and interface computations using the B3LYP or B3PW functionals. The B3LYP and B3PW hybrid exchange-correlation functionals make use of 20% of the Hartree–Fock method as well as 80% of the density functional Hamiltonian, when incorporated in the CRYSTAL computer code [97].

The major advantage of the CRYSTAL computer software package, which is of key importance for our hybrid-DFT computations of neutral SrZrO₃, PbZrO₃, PbTiO₃, BaTiO₃ and SrTiO₃ (001) surfaces and interfaces, is the implementation of the isolated 2-dimensional (2D) slab model. In our hybrid-DFT computations, the reciprocal space integration was carried out by examining the Brillouin zone with the 8 × 8 × 8 times expanded Pack–Monkhorst net for the bulk of SrZrO₃, PbZrO₃, PbTiO₃, BaTiO₃ and SrTiO₃ solids, as well as by 8 × 8 × 1 net for their (001) surfaces and interfaces. With a goal of reaching a high accuracy in our ab initio computations, we employed sufficiently large tolerances equal to 7, 8, 7, 7, 14 for the Coulomb overlap, Coulomb penetration and exchange overlap, as well as first exchange pseudo-overlap and the second exchange pseudo-overlap [97].

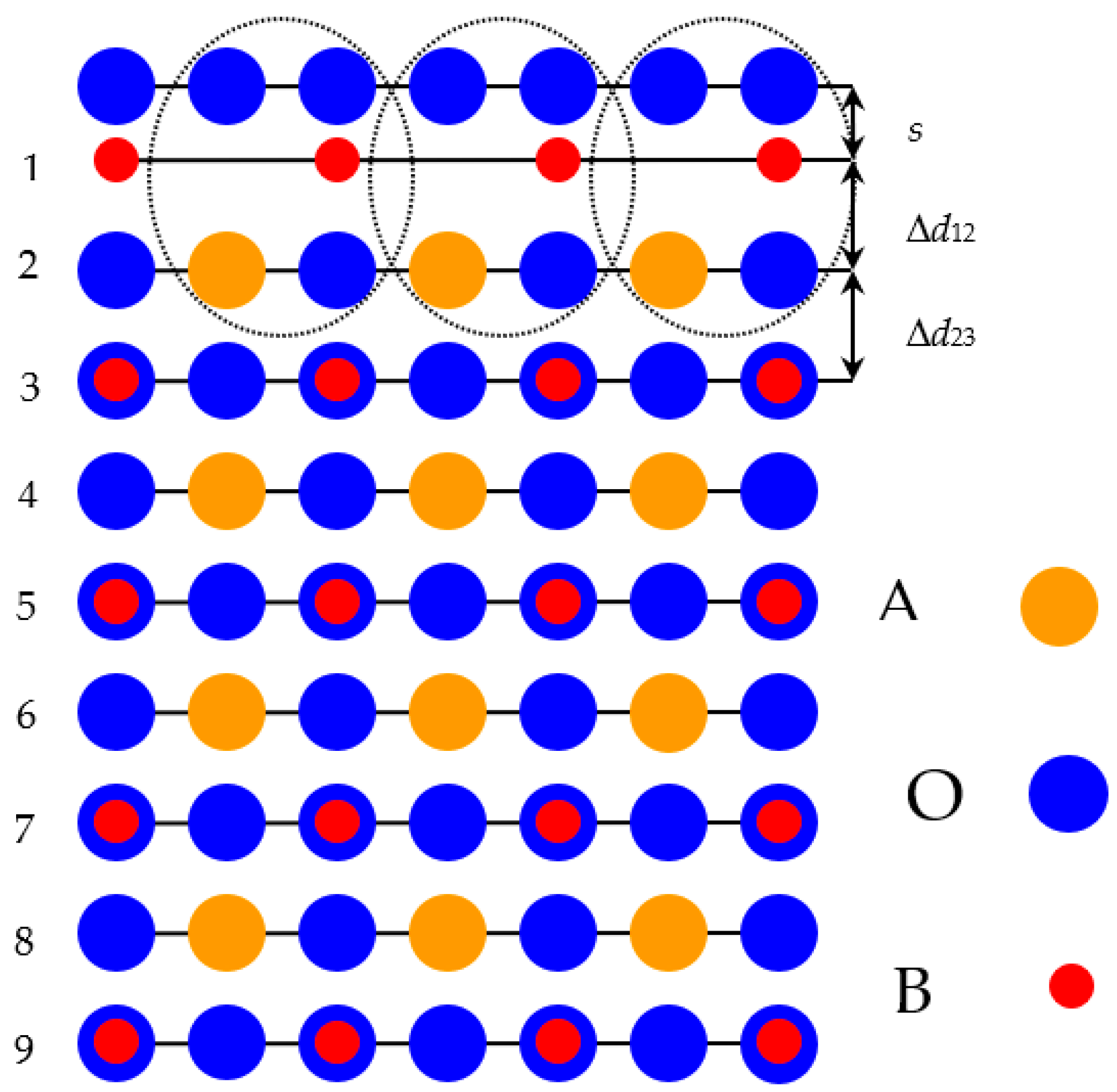
With the aim of computing the neutral BO₂-terminated (001) surfaces of ABO₃ solids, we customized symmetrical slabs. They involved nine neutral as well as alternating BO₂ and AO layers (Figure 1). All of these nine layers were perpendicular to the [001] crystal direction [108,109,110,111]. Taking into consideration the standard ionic charges equal to (+2e) for the A atom and (+4e) for the B atom, as well as (−2e) for the O atom, both alternating BO₂ and AO layers are neutral, since they have a summary slab charge equal to zero. The slab, containing nine layers, used by us for the BO₂-terminated ABO₃ perovskite (001) surface computations (Figure 1) consisted of a supercell containing 23 atoms. Our hybrid-DFT computed BO₂-terminated (001) slabs (Figure 1) of ABO₃ perovskite were non-stoichiometric. They have a unit cell, used in our hybrid-DFT computations, described by the following chemical formula—A₄B₅O₁₄ [112,113,114].

The second slab in our hybdid-DFT computations was terminated from both sides by the AO planes (Figure 2). It also contained nine alternating layers (Figure 2) but consisted of a supercell that incorporated only 22 atoms. Furthermore, the AO-terminated nine-layer slab, used in our hybrid-DFT computations, was non-stoichiometric and has the following chemical formula—A₅B₄O₁₃. For Sr, Ba, Pb, Ti and O atoms [115], we used the basis sets developed in [117]. The inner-core electrons for Sr, Ba, Pb, Ti and Zr atoms were described by a small core Hay–Wadt effective pseudopotentials [97,116]. We computed the number of light oxygen atoms using the all-electron basis sets [97,115]. In order to correctly define the chemical bonding in ABO₃ perovskites, as well as covalency effects, we employed a widely accepted Mulliken population [117,118,119] analysis. The Mulliken population analysis is incorporated in the CRYSTAL computer code [97], used in all of our hybrid-DFT computations for the ABO₃ solid (001) surfaces and their respective heterostructures (Figure 3).

With ambition to compute the ABO₃ solid (001) surface energies, we opened our hybid-DFT computations with cleavage energies for unrelaxed AO- as well as BO₂-terminated (001) surfaces. In our hybrid-DFT computations, the two nine-layer AO- as well as BO₂-terminated slabs contained 22 and 23 atoms of each of them. These two AO- and BO₂-terminated slabs represented together nine ABO₃ perovskite bulk unit cells. Each ABO₃ perovskite bulk unit cell contained five atoms. AO as well as BO₂-terminated ABO₃ perovskite (001) surfaces arose at the same time moment under crystal cleavage. Therefore, the relevant cleavage energy is shared uniformly among created surfaces. Thereby, our ab initio computed ABO₃ perovskite (001) surface cleavage energy is equal for both AO- as well as BO₂-terminations:

E_surf^unrel = ¼ [E_slab^unrel (AO) + E_slab^unrel (BO₂) − 9 E_bulk]

(1)

where E_slab^unrel (AO) and E_slab^unrel (BO₂) are our hybrid-DFT computed total energies for unrelaxed AO- and BO₂-terminated ABO₃ perovskite nine-layer slabs. E_bulk is our hybrid-DFT computed total bulk unit cell energy containing five atoms. Factor 4 in Equation (1) arises from the fact that we created four surfaces during the ABO₃ perovskite cleavage event. As a next step, we computed the relaxation energies for AO- and BO₂-terminated ABO₃ solid (001) surfaces. We relaxed both sides of our nine-layer AO- and BO₂-terminated slabs.

E_rel(Ψ) = ½ [E_slab (Ψ) − E_slab^unrel (Ψ)]

(2)

E_slab(Ψ) is our hybrid-DFT computed slab total energy after the geometry relaxation. In our case the symbol Ψ denotes AO- or BO₂-terminated ABO₃ perovskite (001) surface. After all of our hybrid-DFT computed ABO₃ perovskite AO- or BO₂-terminated (001) surface energy is defined as a sum of the cleavage as well as relaxation energies:

E_surf(Ψ) = E_surf^unrel + E_rel(Ψ)

(3)

As a next step, we will discuss our calculation details for the ABO₃ perovskite (001) heterostructures, using as an example the BaTiO₃/SrTiO₃ (001) interface. At room temperature, the SrTiO₃ substrate has a high-symmetry cubic structure. In our hybrid-DFT computations, we computed both SrTiO₃ and BaTiO₃ perovskites at their cubic, high-symmetry phase with the space group number $P\mathrm{m}\overline{3}\mathrm{m}$. In our hybrid-DFT computations, we modelled the BaTiO₃/SrTiO₃ (001) interface employing the single-slab model. In order to maximally apply the advantages of symmetry, our slabs were symmetrically terminated. In our hybrid-DFT computations, the SrTiO₃ (001) substrate always contained 11 alternating SrO as well as TiO₂ layers. From 1 to 10 BaO and TiO₂ alternating layers were augmented on both sides of the 11-layer TiO₂-terminated SrTiO₃ (001) substrate (Figure 3).

We allowed all coordinated of atoms to relax in our hybrid-DFT computed BaTiO₃/SrTiO₃ (001) heterostructure. In our hybrid-DFT computations, due to restrictions imposed by the cubic symmetry of the system, atomic displacements are possible only along axis z. It is worthwhile to note that the mismatch equal to approximately 2.5 percent among BaTiO₃ and SrTiO₃ bulk lattice constants happens at the time of BaTiO₃ epitaxial growth. The joint equilibrium average lattice constant employed in all of our future hybrid-DFT computations for BaTiO₃/SrTiO₃ (001) interfaces is equal to 3.958 Å. The joint lattice constant for the BaTiO₃/SrTiO₃ (001) interface was hybrid-DFT computed by us for the thickest (001) interface, which consisted of the 11-layer SrTiO₃ substrate as well as, from both sides of this substrate, augmented 10 BaTiO₃ layers. In our hybrid-DFT calculations of the shift (Δz) for each layer of the BaTiO₃/SrTiO₃ (001) heterostructure, we take into consideration the shift of the previous atomic layer. Therefore, the reference z coordinate for each mono-layer N is described by the following equation:

z_N^ref = ½ [z_N-1^Me + z_N-1^O)

(4)

where, in Equation (4), z_N-1^Me as well as z_N-1^O defines the z coordinates for the cation and anion from the previous atomic monolayer.

3. Hybrid-DFT Computation Results

3.1. Pristine SrTiO₃, BaTiO₃, PbTiO₃, SrZrO₃ and PbZrO₃ (001) Surfaces

As an opening to our hybrid-DFT computations, we computed the bulk lattice constants for five ABO₃ perovskites. Our hybrid-DFT computed bulk lattice constants for PbTiO₃ (3.936 Å), BaTiO₃ (4.008 Å), SrTiO₃ (3.904 Å), PbZrO₃ (4.220 Å) and SrZrO₃ (4.195 Å) are in fair agreement with the experimentally detected bulk lattice constants for PbTiO₃ (3.97 Å [120]), BaTiO₃ (4.004 Å [121]), SrTiO₃ (3.898 Å [122]), PbZrO₃ (4.1614 Å [123]) and SrZrO₃ (4.154 Å [21]). Our hybrid-DFT computed effective atomic charges, as well as chemical bond populations for the PbTiO₃, BaTiO₃, SrTiO₃, PbZrO₃ and SrZrO₃ perovskite bulk, are collected in

Table 1. Our hybrid-DFT computed effective atomic charges Q (in e) as well as bond populations P (in e) for atoms in PbTiO₃, BaTiO₃, SrTiO₃, PbZrO₃ and SrZrO₃ bulk matrices.

Bulk Properties		PbTiO3	BaTiO3	SrTiO3	PbZrO3	SrZrO3
Ion	Property	B3PW	B3PW	B3PW	B3LYP	B3LYP
A	Q	+1.354	+1.797	+1.871	+1.368	+1.880
	P	+0.016	−0.034	−0.010	+0.030	+0.002
O	Q	−1.232	−1.388	−1.407	−1.160	−1.351
	P	+0.098	+0.098	+0.088	+0.106	+0.092
B	Q	+2.341	+2.367	+2.351	+2.111	+2.174

.

As we can see from Table 1, our hybrid-DFT computed atomic charges for all five perovskites are considerably smaller than those expected in an ionic model for the A atom (+2e), for the B atom (+4e) and also for the O atom (−2e). For example, our hybrid-DFT computed effective atomic charges for the Pb atom, in the different compounds PbTiO₃ (+1.354e) and PbZrO₃ (+1.368e), are almost equal. The same is also true for the Sr atom. Furthermore, the Sr atom atomic charges in different perovskites, such as SrTiO₃ (+1.871e) and SrZrO₃ (+1.880e), are almost equal (Table 1). The Zr atom effective charges in the PbZrO₃ (+2.111e) and SrZrO₃ (+2.174e) perovskites are almost equal and are always considerably smaller than the Ti atom effective charges in the PbTiO₃ (+2.341e), BaTiO₃ (+2.367e) and SrTiO₃ (+2.351e) crystals. It is worthwhile to note that the Ti atom effective charges in PbTiO₃, BaTiO₃ and SrTiO₃ perovskites (+2.341e, +2.367e and +2.351e, respectively) almost coincide (Table 1). The chemical bond covalency between the B and O atoms are in the range from (+0.088e) between Ti-O atoms in the SrTiO₃ perovskite to (+0.106e) between Zr-O atoms in the PbZrO₃ crystal. The bond populations between Ti-O atoms are equal to (0.098e) in both PbTiO₃ and BaTiO₃ perovskites.

As a next step, we computed the bulk band gaps at the Γ-point for PbTiO₃, BaTiO₃ and SrTiO₃ perovskites and plotted the band structure for BaTiO₃ and PbTiO₃ crystals. We compared our hybrid-DFT computation results for Γ-Γ band gaps with available experimental results. Our B3PW computed SrTiO₃ bulk Γ-Γ band gap is equal to 3.96 eV, which is in fair agreement with the available experimental data for SrTiO₃ direct Γ-Γ bulk band gap equal to 3.75 eV [124] (

Table 2. Our B3PW computation results as well as the experimental data for SrTiO₃, BaTiO₃ and PbTiO₃ bulk Γ-Γ band gaps (in eV) and their structure at room temperature (RT).

Solid	Structure at RT	Exp. Γ-Γ Band Gap (eV)	Ab initio Γ-Γ Band Gap
SrTiO3	Cubic phase	3.75 eV [124]	3.96 eV
BaTiO3	Tetragonal ↔ orthorhombic phase at 278 K	3.38 eV (//c); 3.27 eV (⊥ c) [125]	3.55 eV
PbTiO3	Tetragonal phase	3.4 eV [126]	4.32 eV

). The direct Γ-Γ bulk band gap in the BaTiO₃ perovskite is measured experimentally (Table 2) at the tetragonal to orthorhombic phase transition temperature equal to 278 K. The BaTiO₃ direct bulk Γ-Γ band gap in different experimental conditions is slightly different and is equal to 3.27 eV or 3.38 eV, respectively [125]. Our B3PW computed BaTiO₃ direct bulk Γ-Γ band gap (3.55 eV) (Table 2) is in almost perfect agreement with these experiments (Figure 4a). Finally, our B3PW computed PbTiO₃ bulk band gap at Γ-point (4.32 eV) (Figure 4b) (Table 2) is in satisfactory agreement with the experimentally detected direct PbTiO₃ bulk Γ-Γ band gap (3.4 eV) [126] at the PbTiO₃ perovskite tetragonal phase.

As we can see from

Table 3. Atomic relaxation magnitudes (in % of the a₀) for the BO₂-terminated PbTiO₃, BaTiO₃, SrTiO₃, PbZrO₃ and SrZrO₃ (001) surfaces.

Solid		PbTiO3	BaTiO3	SrTiO3	PbZrO3	SrZrO3
Layer	Ion	TiO2-t.	TiO2-t.	TiO2-t.	ZrO2-t.	ZrO2-t.
1	B	−2.81	−3.08	−2.25	−2.37	−1.38
	O	+0.31	−0.35	−0.13	−1.99	−2.10
2	A	+5.32	+2.51	+3.55	+4.36	+2.81
	O	+1.28	+0.38	+0.57	+1.04	+0.91
3	B	-	-	-	−0.47	−0.04
	O	-	-	-	−0.28	−0.05

, according to our hybrid-DFT computations, all upper-layer atoms for all five perovskites relax inwards in the direction towards the perovskite bulk. The only exception from this systematic trend is the upward relaxation of the TiO₂-terminated PbTiO₃ (001) surface upper-layer O atom by 0.31 % of a₀. Just opposite, all second-layer atoms relax upwards. For both upper layers, the metal atom relaxation magnitudes are always larger than the respective oxygen atom relaxation magnitude [127,128,129,130]. The only exception to this systematic trend is the ZrO₂-terminated SrZrO₃ (001) surface upper-layer oxygen atom relaxation magnitude (−2.10% of a₀), which is slightly larger than the same-layer Sr atom relaxation magnitude (−1.38% of a₀) (Table 3).

In most cases, as it is possible to see from our hybrid-DFT computation results collected in

Table 4. Atomic relaxation magnitudes (in % of the a₀) for the AO-terminated PbTiO₃, BaTiO₃, SrTiO₃, PbZrO₃ and SrZrO₃ (001) surfaces.

Solid		PbTiO3	BaTiO3	SrTiO3	PbZrO3	SrZrO3
Layer	Ion	PbO-t.	BaO-t.	SrO-t.	PbO-t.	SrO-t.
1	A	−3.82	−1.99	−4.84	−5.69	−7.63
	O	−0.31	−0.63	+0.84	−2.37	−0.86
2	B	+3.07	+1.74	+1.75	+0.57	+0.86
	O	+2.30	+1.40	+0.77	+0.09	−0.05
3	A	-	-	-	−0.47	−1.53
	O	-	-	-	−0.47	−0.45

for AO-terminated PbTiO₃, BaTiO₃, SrTiO₃, PbZrO₃ and SrZrO₃ (001) surfaces, all upper-layer atoms relax inwards (Table 4), whereas all second-layer atoms relax upwards. The only two exceptions from this systematic trend are the upward relaxation of O atom on the upper layer of SrO-terminated SrTiO₃ (001) surface by (+0.84% of a₀), as well as the inward relaxation of the second-layer O atom on the SrO-terminated SrZrO₃ (001) surface by a very small relaxation magnitude of only (−0.05 of a₀) (Table 4). It is interesting to notice that for the AO-terminated PbTiO₃, BaTiO₃, SrTiO₃, PbZrO₃ and SrZrO₃ (001) surfaces, the relaxation magnitudes of metal atoms in the upper, as well as the second, surface layers are always larger than the relaxation magnitudes of the respective oxygen atoms (Table 4).

As we can see from

Table 5. Our hybrid-DFT computed surface rumpling s as well as relative displacements Δd_ij for BO₂-terminated PbTiO₃, BaTiO₃, SrTiO₃, PbZrO₃ and SrZrO₃ (001) surfaces in (% of a₀). Relevant experimental data are listed in Table 5 for comparison purposes.

Solid	Functional	Termination	s	Δd12	Δd23
PbZrO3	B3LYP	ZrO2	+0.38	−6.73	+4.83
SrZrO3	B3LYP	ZrO2	−0.72	−4.19	+2.85
	LDA [131]	ZrO2	−0.7	−6.1	+4.2
PbTiO3	B3PW	TiO2-term.	+3.12	−8.13	+5.32
BaTiO3	B3PW	TiO2-term.	+2.73	−5.59	+2.51
SrTiO3	B3PW	TiO2-term.	+2.12	−5.79	+3.55
	LEED [132]	TiO2-term.	+2.1 ± 2	+1 ± 1	−1 ± 1
	RHEED [133]	TiO2-term.	+2.6	+1.8	+1.3

, our hybrid-DFT computed surface rumpling s (Figure 1) is always positive for BO₂-terminated ABO₃ perovskite (001) surfaces. The definitions of surface rumpling s, as well as the near-surface interplanar separations Δd₁₂ and Δd₂₃, are explained in Figure 1. The only exception to this systematic trend is our hybrid-DFT computed negative surface rumpling s for the ZrO₂-terminated SrZrO₃ (001) surface (−0.72) (Table 5). Moreover, the surface rumpling s computed by Wang et al. [131] for the ZrO₂-terminated SrZrO₃ (001) surface is negative (Table 5) (−0.70) and almost coincides with our result (−0.72). The experimental data for the surface rumpling s are available, for example, for the SrTiO₃ crystal. Our B3PW computed surface rumpling s for SrTiO₃ perovskite (+2.12) is in fair agreement with the available LEED [132] (+2.1 ± 2), as well as RHEED [133] (+2.6), experiments (Table 5). It is worthwhile to note that all of our hybrid-DFT computed interlayer distances for all materials (Figure 1) Δd₁₂ are negative. This means that, according to our hybrid-DFT computations, the contraction always happens between the first and second surface layer for all BO₂-terminated ABO₃ perovskite (001) surfaces (Table 5). Oppositely, according to our hybrid-DFT computations, there is always expansion between the second and third surface layer Δd₂₃ (Figure 1) for all of our hybrid-DFT computed BO₂-terminated ABO₃ perovskite (001) surfaces (Table 5).

As we can see from our hybrid-DFT computation results, collected in

Table 6. Our hybrid-DFT computed atomic displacement absolute magnitudes D (in Å) and the effective charges Q (in e), as well as the chemical bond populations P (in e), for BO₂-terminated PbZrO₃, SrZrO₃, PbTiO₃, BaTiO₃ and SrTiO₃ (001) surfaces.

			PbZrO3	SrZrO3	PbTiO3	BaTiO3	SrTiO3
Layer	Prop.	Ion	ZrO2-t.	ZrO2-t.	TiO2-t.	TiO2-t.	TiO2-t.
1	D	B	−0.100	−0.058	−0.111	−0.123	−0.088
	Q		+2.165	+2.196	+2.279	+2.307	+2.291
	P		+0.116	+0.114	+0.114	+0.126	+0.118
	D	O	−0.084	−0.088	+0.012	−0.014	−0.005
	Q		−1.171	−1.277	−1.184	−1.280	−1.296
	P		+0.046	−0.002	+0.044	−0.038	−0.014
2	D	A	+0.184	+0.118	+0.209	+0.101	+0.139
	Q		+1.357	+1.869	+1.275	+1.767	+1.850
	P		+0.022	+0.002	+0.008	−0.030	−0.008
	D	O	+0.044	+0.038	+0.050	+0.015	+0.022
	Q		−1.103	−1.287	−1.167	−1.343	−1.365
	P		+0.098	+0.094	+0.080	+0.090	+0.080
3	D	B	−0.020	−0.001	-	-	-
	Q		+2.116	+2.172	+2.335	+2.365	+2.348
	P		+0.124	+0.102	+0.108	+0.104	+0.096
	D	O	−0.012	−0.002	-	-	-
	Q		−1.148	−1.331	−1.207	−1.371	−1.384
	P		+0.036	+0.002	+0.018	−0.034	−0.010

, the B-O atom chemical bond populations on the BO₂-terminated PbZrO₃, SrZrO₃, PbTiO₃, BaTiO₃ and SrTiO₃ perovskite (001) surfaces (+0.116e, +0.114e, +0.114e, +0.126e, +0.118e, respectively) are always larger than the B-O chemical bond population at the same perovskite bulk (+0.106e, +0.092e, +0.098e, +0.098e, +0.088e, respectively). As we can see from Table 6, the largest chemical bond population is between the Ti-O atoms (+0.126e) on the TiO₂-terminated BaTiO₃ (001) surface, whereas the smallest chemical bond population (+0.114e) is between the Zr-O and Ti-O atoms on the SrZrO₃, as well as the BaTiO₃, ZrO₂ and TiO₂-terminated (001), surfaces. It is worthwhile to note that the Ti atom’s effective charges on the TiO₂-terminated PbTiO₃, BaTiO₃ and SrTiO₃ (001) surfaces (+2.279e, +2.307e and +2.291e, respectively) are reduced with regard to the Ti atom’s effective charges in the PbTiO₃, BaTiO₃ and SrTiO₃ bulk (+2.341e, +2.367e and +2.351e, respectively). Just the opposite situation occurs for the PbZrO₃ and SrZrO₃ perovskites, wherein the Zr atom’s effective charge on the ZrO₂-terminated PbZrO₃ and SrZrO₃ (001) surfaces (+2.165e and +2.196e, respectively) is larger than in the PbZrO₃ and SrZrO₃ bulk matrixes (+2.111e and +2.174e, respectively) (Table 6).

Our hybrid-DFT computed (001) surface cleavage and relaxation, as well as surface energies, for PbTiO₃, BaTiO₃, SrTiO₃, PbZrO₃ and SrZrO₃ perovskites are collected in

Table 7. Our hybrid-DFT computed cleavage and relaxation, as well as surface energies, for PbTiO₃, BaTiO₃, SrTiO₃, PbZrO₃ and SrTiO₃ (001) surfaces (in eV per surface cell).

Surface	Termination	Ecleavage	Erelaxation	Esurface
PbTiO3 (001)	TiO2	1.02	−0.28	0.74
	PbO		−0.19	0.83
BaTiO3 (001)	TiO2	1.30	−0.23	1.07
	BaO		−0.11	1.19
SrTiO3 (001)	TiO2	1.39	−0.16	1.23
	SrO		−0.24	1.15
PbZrO3 (001)	ZrO2	1.20	−0.27	0.93
	PbO		−0.20	1.00
SrZrO3 (001)	ZrO2	1.56	−0.32	1.24
	SrO		−0.43	1.13

. As we can see from Table 7, the largest cleavage energy is for the SrZrO₃ perovskite (001) surface (1.56 eV), whereas the smallest cleavage energy is for the PbTiO₃ perovskite (001) surface (1.02 eV) (Table 7). The largest surface relaxation energy is for the SrO-terminated SrZrO₃ perovskite (001) surface (−0.43), but the smallest surface relaxation energy is for the BaO-terminated BaTiO₃ (001) surface and is only (−0.11 eV) (Table 7). Finally, our hybrid-DTT computed surface energy is largest for the ZrO₂-terminated SrZrO₃ (001) surface (1.24 eV). Oppositely, our hybrid-DFT computed surface energy is the smallest for the TiO₂-terminated PbTiO₃ (001) surface and is only (0.74 eV). The largest energy difference (0.12 eV) for single perovskite (001) surfaces with different terminations is between the TiO₂-terminated BaTiO₃ (001) surface (1.07 eV) and the BaO-terminated BaTiO₃ (001) surface (1.19 eV). This means, that, for all of our hybrid-DFT computed PbTiO₃, BaTiO₃, SrTiO₃, PbZrO₃ and SrZrO₃ (001) surfaces, the surface energies for one perovskite’s both surface terminations are rather close, and thereby both BO₂ and AO (001) surface terminations may exist simultaneously for all our hybrid-DFT computed ABO₃ perovskites (Table 7).

Our B3PW computed bulk band gaps (Figure 4) for PbTiO₃, BaTiO₃ and SrTiO₃ perovskite bulk (4.32 eV, 3.55 eV and 3.96 eV, respectively) are in fair agreement with the available experimental data [124,125,134] (

Table 8. Our hybrid-DFT computed direct Γ-Γ band gaps (in eV) for PbTiO₃, BaTiO₃ and SrTiO₃ perovskite bulk, as well as their BO₂ and AO-terminated (001) surfaces. The experimental PbTiO₃, BaTiO₃ and SrTiO₃ bulk Γ-Γ band gaps are listed for comparison purposes.

Termination	PbTiO3 (Γ-Γ) Gap	BaTiO3 (Γ-Γ) Gap	SrTiO3 (Γ-Γ) Gap
Bulk	4.32 eV	3.55 eV	3.96 eV
TiO2-term. (001)	3.18 eV	2.96 eV	3.95 eV
AO-term. (001)	3.58 eV	3.49 eV	3.72 eV
Experiment	3.4 eV [134]	3.2 eV [125]	3.75 eV [124]

). As we can see from Table 8 and Figure 5 and Figure 6, our B3PW computed (001) surface band gaps for all three perovskites and both (001) surface terminations are always reduced with respect to the PbTiO₃, BaTiO₃ and SrTiO₃ bulk. Namely, our hybrid-DFT computed TiO₂-terminated PbTiO₃, BaTiO₃ and SrTiO₃ (001) surface band gaps are equal to 3.18 eV, 2.96 eV (Figure 5) and 3.95 eV, respectively. At the same time, our hybrid-DFT computed AO-terminated PbTiO₃, BaTiO₃ and SrTiO₃ (001) surface band gaps are equal to 3.58 eV, 3.49 eV (Figure 6) and 3.72 eV, respectively, and are also smaller than the respective bulk band gap values at Γ-point (Table 8).

3.2. BaTiO₃/SrTiO₃, PbTiO₃/SrTiO₃ and SrZrO₃/PbZrO₃ (001) Interfaces

In order to start our hybrid-DFT computations for BTO/STO, PTO/STO and SZO/PZO (001) heterostructures, we computed their joint lattice constants. Our hybrid-DFT computed joint lattice constant for BTO/STO (001) interface is equal to 3.958 Å. This joint BTO/STO (001) interface joint lattice constant was computed for the system containing an 11-layer thick STO substrate, as well as 10 BTO monolayers augmented on both sides of the STO substrate (Figure 3). Thereby, our B3PW computed thickest BTO/STO (001) interface contained 31 monolayers, as well as 78 atoms (Figure 3) [135]. Using a similar model for the PTO/STO (001) thickest interface, our B3PW computed joint lattice constant for this system is equal to 3.91 Å. Finally, our hybrid-DFT computed SZO/PZO (001) interface joint lattice constant for the system containing an 11-layer thick SZO substrate, as well as 10 PZO monolayers augmented symmetrically on both sides of the substrate, is equal to 4.167 Å.

In our hybrid-DFT (001) heterostructure computations, we relaxed all atomic positions only alongside the z-axis, due to the symmetry constraints for the cubic ABO₃ perovskite matrixes. We computed the atomic shifts Δz regarding the averaged coordinate z of the former atomic layer as described in Equation (4). As we can see from Figure 7, our B3PW computed upper SrTiO₃ substrate (001) layer, which contains Ti and O atoms (x = 0) in (Figure 7), relaxes very strongly inside (−5.95% of a₀). According to our B3PW computations, upper BTO (001) layer atoms, augmented on the STO 11-layer (001) substrate, always very strongly shifts (Δz) inwards (x = 1–10 in Figure 7). It is worthwhile to note that the BTO upper-layer atoms inwards-relaxation numerical value Δz considerably depends on the number of the STO (001) 11-layer substrate augmented BTO (001) layers.

In the case of one augmented BTO (001) layer, consisting of the BaO atoms, the atom relaxation magnitude Δz is equal to −1.54% of the joint lattice constant a₀ (Figure 3 and Figure 7). For two augmented BTO (001) layers, where the upper layer contains TiO₂ atoms, the upper-layer atom relaxation magnitude Δz is equal to (−3.20% of a₀) (Figure 7). For three augmented BTO (001) layers, the upper BaO layer atom relaxation magnitude Δz is equal to (−1.84% of a₀), for 4 layers (−3.55% of a₀), for five layers (−2.07% of a₀), for six layers (−3.70% of a₀), for seven layers (−2.21% of a₀), for eight layers (−3.84% of a₀), for nine layers (−2.32% of a₀) and finally, for ten augmented BTO (001) layers, the upper TiO₂ layer atom relaxation magnitude Δz is equal to (−3.92% of a₀) (Figure 7).

As we can see from Figure 8, for one augmented PTO (001) layer (x = 1), consisting of the PbO atoms, on the 11-layer STO (001) substrate (x = 0 for the substrate upper layer TiO₂ atoms relaxation magnitude Δz), the upper layer PbO atoms’ relaxation magnitude Δz is equal to (−6.01% of a₀). For two augmented PTO (001) layers, the upper layer consists of TiO₂ atoms (x = 2), and their relaxation magnitude Δz is equal to (−7.76% of a₀). For three augmented PTO (001) layers (x = 3), the upper layer consists of PbO atoms, and their relaxation magnitude Δz is equal to (−6.97% of a₀). As we can see from Figure 8, for four augmented PTO (001) layers (x = 4), the upper TiO₂ atoms containing layer atoms’ relaxation magnitude Δz is equal to (−8.25% of a₀). For (x = 5), the upper augmented PTO (001) layer atom relaxation magnitude Δz is equal to (−7.26% of a₀), for (x = 6) (−8.38% of a₀), for (x = 7) (−7.34% of a₀), for (x = 8) (−8.54% of a₀), for (x = 9) (−7.42% of a₀) and for (x = 10) (−8.54% of a₀) (Figure 8).

As we can see from Figure 9, our hybrid-DFT computed Γ-Γ band gap for the PTO/STO (001) interface, containing an 11-layer STO (001) substrate as well as a PbO (001) layer (x = 1), augmented on both sides of this substrate, is equivalent to 3.45 eV. For two PTO (001) layers, augmented from both sides on the 11-layer STO (001) substrate, the whole PTO/STO (001) interface system is terminated by the TiO₂ (001) layers from both sides and has a Γ-Γ band gap equal to 3.18 eV (Figure 9). For three PTO (001) layers, augmented on the STO (001) substrate, the whole PTO/STO (001) interface is terminated by the PbO-terminated (001) layer from both sides and has a Γ-Γ band gap equal to 3.25 eV. As we can see from Figure 9, for four augmented PTO (001) layers (x = 4), the Γ-Γ band gap of PTO/STO (001) interface is equal to 3.17 eV, for 5 augmented layers (3.08 eV), for 6 layers (3.05 eV), for 7 layers (2.99 eV), for 8 layers (2.99 eV), for 9 layers (2.94 eV) and, finally, for 10 augmented PTO (001) layers, the Γ-Γ band gap of PTO/STO (001) interface is equal to (2.93 eV).

As we can see from Figure 10a,b, our hybrid-DFT computed Γ-Γ band gap for BTO/STO, as well as SZO/PZO (001) interface Γ-Γ band gap, very strongly depends on the upper augmented layer BO₂- or AO-termination but considerably less so on the number of augmented (001) layers.

4. Conclusions

According to our hybrid-DFT computations for BO₂- and AO-terminated PbTiO₃, BaTiO₃, SrTiO₃, PbZrO₃ and SrZrO₃ (001) surfaces, in most cases, the upper-layer ions relax inwards, towards the bulk, whereas the second-layer ions shift upwards. It is worthwhile to also note that independent calculation results of other authors for ABO₃ perovskite material’s neutral (001) surfaces confirm this systematic trend, that the upper layer ions, in most cases, relax inwards, whereas the second layer ions, again, in most cases, relax upwards [4,9,20,49,50,54,66,67,135,136,137,138].

Our hybrid-DFT computed surface rumpling s for the BO₂-terminated ABO₃ perovskite (001) surfaces (Table 5) is positive for most computed ABO₃ perovskites, such as PbZrO₃, PbTiO₃, BaTiO₃ and SrTiO₃ (+0.38, +3.12, +2.73 and +2.12, respectively). Furthermore, the experimentally detected surface rumpling s for the TiO₂-terminated SrTiO₃ (001) surface matrix by two different experimental methods (LEED [132] and RHEED [133]) is positive (Table 5). Moreover, the agreement between our B3PW computed surface rumpling s for the TiO₂-terminated SrTiO₃ (001) surface (+2.12) and LEED [131] experimentally detected respective SrTiO₃ (001) surface rumpling s (+2.1 ± 2) is almost perfect (Table 5). Nevertheless, there is a single exception to this systematic trend. Namely, our hybrid-DFT computed surface rumpling s for the ZrO₂-terminated SrZrO₃ (001) surface is negative (−0.72) and is in line with another ab initio calculation result performed by Wang et al. [131] (−0.70).

Our hybrid-DFT computed B-O atom chemical bond population values in the bulk of PbTiO₃ (+0.098e), BaTiO₃ (+0.098e), SrTiO₃ (+0.088e), PbZrO₃ (+0.106e) and SrZrO₃ (+0.092e) perovskites are considerably enhanced on their BO₂-terminated PbTiO₃ (+0.114e), BaTiO₃ (+0.126e), SrTiO₃ (+0.118e), PbZrO₃ (+0.116e) and SrZrO₃ (+0.114e) (001) surfaces (Table 6). Our hybrid-DFT computed BO₂- and AO-terminated (001) surface energies for PbTiO₃ (0.74 and 0.83 eV), BaTiO₃ (1.07 and 1.19 eV), SrTiO₃ (1.23 and 1.15 eV), PbZrO₃ (0.93 and 1.00 eV) and SrZrO₃ (1.24 and 1.13 eV) are comparable for both (001) surface terminations (Table 7). Thereby, both BO₂- and AO-terminated (001) surfaces may co-exist in ABO₃ perovskite matrices. It is worthwhile to note that our hybrid-DFT computed ABO₃ perovskite (001) surface energies are always smaller than the (011) [1,2] and especially the (111) [128] surface energies. This means, that, according to our hybrid-DFT computations, the ABO₃ perovskite (001) surfaces are always the most stable, whereas the (011) and especially the (111) ABO₃ perovskite surfaces are considerably less stable. Finally, our hybrid-DFT computed bulk Γ-Γ band gaps for PbTiO₃, BaTiO₃ and SrTiO₃ perovskites are in fair agreement with the experimentally available data. For BO2- and AO-terminated PbTiO₃, BaTiO₃ and SrTiO₃ (001) surfaces (Table 8), the band gaps are always reduced with regard to the respective bulk Γ-Γ band gaps.

For our B3PW computed BTO/STO as well as PTO/STO (001) interfaces, the average augmented upper-layer atom relaxation magnitudes increased by the number of augmented BTO or PTO (001) layers but always independently from the number of augmented layers, which were stronger for TiO₂-terminated than BaO- or PbO-terminated upper augmented layers. All of our B3PW computed PTO/STO (001) interface upper augmented layer average atom displacement magnitudes Δz are between (−6.01% of a₀) for the first augmented layer and (−8.54% of a₀) for 10 augmented layers. In contrast to the PTO/STO (001) interfaces, for our hybrid-DFT computed BTO/STO (001) interfaces, the upper augmented layer average atom displacement magnitudes Δz are considerably smaller, and they are in the range between the (−1.54% of a₀ (1 layer) to −3.92% of a₀ (10 layers), respectively). Our B3PW computed BTO/STO, as well as SZO/PZO (001) interface Γ-Γ band gaps, very strongly depends on the upper augmented layer BO₂- or AO-termination but considerably less so on the number of augmented (001) layers [135,139].

Summing up, all of our hybrid-DFT computed BTO/STO and PTO/STO, as well as PZO/SZO (001) heterostructures, are semiconducting. In general agreement with available experimental data [84], according to our hybrid-DFT computations, the (001) interface layer does not considerably influence the electronic structure of our studied heterostructures. At the same time, the termination of the deposited BTO and PTO, as well as PZO (001), thin films atop STO or SZO (001) substrates, respectively, may shift the band edges regarding the vacuum level and thereby reduce the (001) heterostructure band gap [84].