Weak Ferromagnetism in a One-Orbital Double-Exchange Model with Ising Spins for Cerium Oxides

Abstract

Cerium oxides (ceria) are materials that exhibit weak, room-temperature ferromagnetism without d-electrons. The latter are usually responsible for magnetism in a variety of other oxide compounds, but the underlying mechanism for such a magnetic response in ceria without the d-electrons ($d^0$-magnetism) is still under debate. A possible explanation is Zener double-exchange, where itinerant electrons polarize the localized spins via Hund-coupling as they hop from site to site. Here, we report magnetization and spin-spin correlation results using various values of the Hund-coupling in a one-orbital double-exchange model with Ising spins. In the real material with formula CeO${}_{2-x}$, the oxygen-deficient sites are denoted by x. These sites are related to the density of tetravalent cerium spins (the Ising spin background in our model), which we denoted as and set at $N=0.50$ in our simulations. Our results at this value of localized spin concentration show ferromagnetic tendencies at low carrier densities ($n=0.25$). However, ferromagnetism is lost at intermediate carrier concentrations ($n=0.50)$ due to charge localization at high temperatures, as evident from density of states calculations and Monte Carlo snapshots. To our knowledge, our study based on a realistic Zener-type double exchange mechanism is a first in the study of magnetism in cerium oxides. Our results are also consistent with previous studies using similar Hamiltonians in the context of diluted magnetic semiconductors, where Heisenberg spins were used.

1. Introduction

The focus on the study of strongly correlated electrons is the smallest appropriate length scale that is required to yield fundamental insight into material properties, processes, and behavior. With this in mind, the aim is to predict new materials and states of matter, and to reveal new materials phenomena. The inherent complexity of these systems results in a variety of interesting physics, which makes them ideal candidates for technological applications. Among the best known examples are high-temperature superconductors [1], colossal magnetoresistive manganites (CMR) (see [2] and references therein), and diluted magnetic semiconductors [3]. Another example, cerium oxides, are rare earth materials with applications ranging from the automotive industry (used in catalytic converters [4,5], oxygen sensors [6,7], and as solid oxide fuel cells [8,9]) to medicine (as an antioxidant agent [10,11]). The anti-oxidative properties of cerium oxides are attributed to the coexistence of Ce${}^{3+}$ and Ce${}^{4+}$ oxidative states of the cerium atom, which is is controlled by oxygen deficiencies. Even though the electronic structure of cerium oxides is relatively poor in electrons (compared to other rare and transition metal oxides), there have been reports of room temperature magnetism in these materials [12,13,14,15,16,17,18,19]. For a more comprehensive list, please see [20] and references therein. In this article, we would like to shed light on a possible explanation of this phenomena from a theoretical perspective by considering the basic ingredients of a realistic model for these materials.

The magnetic properties of many transition metal oxides, such as iron oxides and manganese oxides, are well understood: rich 3d-electrons give rise to large magnetic moments that localize in the vicinity of atomic sites which then couple with nearby sites through an exchange interaction and/or double exchange mechanism. Depending on the lattice type and the sign of the exchange coupling, the resulting magnetic order can be antiferromagnetic, ferrimagnetic, or ferromagnetic. An overwhelming majority of the oxides show the first two, rather than ferromagnetism, which points to the fact that the exchange coupling is more often negative rather than positive, where applicable.

In recent studies, reports of weak, high-temperature magnetic responses have started to emerge in a variety of materials with no unpaired 3d-electrons. Some examples include zinc oxide nanoparticles [12,21,22], graphene [23,24], and semiconducting and insulating oxide thin films [25]. In this paper, we focus on cerium oxides, a rare-earth oxide, with chemical formula CeO${}_{2-x}$, where x signifies the amount of oxygen-deficient sites. There are many reports of weak room-temperature ferromagnetic responses in cerium oxides for different values of x as noted in the above references and in further detail in Ref. [20]. One also needs to mention here that the oxygen deficient sites and their contribution to ferromagnetism is not specific to ceria, but exists in other materials as well [26,27]. In ceria, however, oxygen deficiency is achieved by the substitution of lower valent elements on the cation sub-lattice. When $x=0$, each Ce cation in the cerium oxide CeO${}_2$ is in a $4f^0$ state (Ce${}^{4+}$). Upon creation of oxygen deficient sites, the Ce cation grabs an electron, which puts it in a $4f^1$ state (Ce${}^{3+}$). Hence, the process of creation of oxygen deficient sites is manifested in and related to the density of localized spin background of trivalent cerium atoms as we consider below.

To this end, we study the possibility of room temperature ferromagnetism in a one-orbital double exchange based microscopic model Hamiltonian suitable for cerium oxides using Monte Carlo simulations with fermionic exact diagonalization. In our model, we consider the inter-ionic hoppings of $4f$ electrons of Ce ions, in addition to the interaction between itinerant and localized trivalent cerium spins, where the latter is to be modeled by a Hund coupling term. We use classical Ising spin variables as the localized cerium spins occupying the $4f_{y(3x^2-y^2)}$ orbital. The justification for these considerations is discussed in detail in the paper. The nearest-neighbor exchange and superexchange couplings are not considered in the model, because the energy scales associated with these couplings are much smaller than other energy scales in rare-earth oxides, due to the average radius of the $4f$ orbital being much smaller than the atomic radius. As a consequence, any resulting magnetism will be due to the on-site interactions propagated throughout the lattice by the double-exchange physics.

While a more realistic microscopic Hamiltonian for cerium oxides is still being actively researched, the double-exchange based model summarized above is expected to capture the basics of ferromagnetism in these materials. In general, in a realistic model, all hopping matrix elements between O $2p$ and Ce $4f$, $5d$, and $6s$ orbitals should be considered in the Hamiltonian matrix. This in itself is a very difficult problem even in a tight-binding band structure calculation of the unit cell (which consists of 8 O and 4 Ce atoms) due to the shear size of the basis set that needs to be used. However, the $5d$ and $6s$ states are much higher in energy than other states, so it is a good approximation to assume that they do not significantly couple to the lower energy states in the basis set. Thus, we are only interested in electron hopping between the two O $2p$ orbitals, as well as between an O $2p$ and a neighboring Ce $4f$ orbital, giving us a double-exchange type model Hamiltonian. Additional simplifications in these hopping parameters are also possible as explained later in this paper. Furthermore, the occupancy of the $4f$ electrons in the Ce atom can either be 0 or 1, depending on whether there is a Ce${}^{4+}$ or Ce${}^{3+}$ ion at that particular atomic site, respectively. This will restrict the Hund coupling only to the sites where we have a localized spin. Our choice for using a classical Ising variable in order to model this $4f^1$ electron spin is purely technical: to avoid the otherwise notorious sign problem in the Monte Carlo update algorithm [28,29]. Also, the $4f^1$ configuration is a doublet, (${}^2$F${}_{5/2}$ in spectroscopic notation), and Ising spins are expected to be a more efficient way to generate ferromagnetic ordering compared to Heisenberg spins.

The organization of the paper is as follows. In Section 2, we look into the magnetic properties of the free Ce${}^{3+}$ and Ce${}^{4+}$ ions and show how magnetism could arise in the former. We also discuss crystal and electronic structure of cerium oxides in this section. Furthermore in Section 2, we introduce our model, and provide further justification of our assumptions and simplifications. We present our results in Section 3. In Section 4 we discuss our results and highlight future outlook. We conclude in Section 5.

2. Materials and Methods

2.1. Magnetic Properties of Free Ce${}^{4+}$ or Ce${}^{3+}$ Ions

The total angular momentum (J) of the charged particles, specifically electrons, is responsible for the magnetism of solids. There are two contributions to the total angular momentum: 1. Orbital angular momentum (L), which originates from the consideration that an electron orbits around the nucleus (according to the Bohr model), and 2. Spin angular momentum (S), which is a result of an intrinsic property of the electron. In a multi-electron atom or an ion, the total angular momentum of any filled shell ($1s^2$, $2s^2$, $2p^6$, etc.) is zero, because the spin angular momentum and orbital angular momentum cancel each other out. In a partially filled shell, the magnetic moment of the ion can be written as $g{\mu }_{B}J$, where ${\mu }_B=e\hslash /2m_e$ is the Bohr magneton and g is the g-factor [30]:

$$g=\frac{3}{2}+\frac{S(S+1)-L(L+1)}{2J(J+1)}$$

(1)

Given an electron configuration of a partially filled shell, the values of $S,L$, and J can be inferred from Hund’s rules:

• Rule 1: Maximize $S={\sum }_i{m}_{si}$, where $m_s=\pm 1/2$ is the spin quantum number of a single electron.
• Rule 2: Maximize $L={\sum }_i{m}_{li}$ consistent with electron occupancy of the orbitals, where $m_l=0,\pm 1,\pm 2\dots$ etc. is the orbital quantum number.
• Rule 3: Use $J=L-S$ (if the shell is less than half full) or $J=L+S$ (if the shell is more than half full) to calculate the total angular momentum.

The electron configuration of free Ce${}^{4+}$ ion is [Xe], i.e., all shells are filled, and there is no net magnetic moment. This is consistent with experiments where a single crystal CeO${}_2$ was found to be paramagnetic [14]. However, Ce${}^{3+}$ electron configuration ends with $4f^1$, which gives $S=1/2,L=3$, and $J=5/2$, corresponding to an atomic term symbol ${}^2$F${}_{5/2}$. Using these values, the g-factor for the Ce${}^{3+}$ ion is calculated as $g=6/7$. Even though this is small compared to other transition and rare earth metals that exhibit strong magnetism, (e.g., $g=3/2$ and $4/3$ for Fe${}^{2+}$ and Nd${}^{3+}$, respectively), it still shows that the free Ce${}^{3+}$ ions could be magnetic.

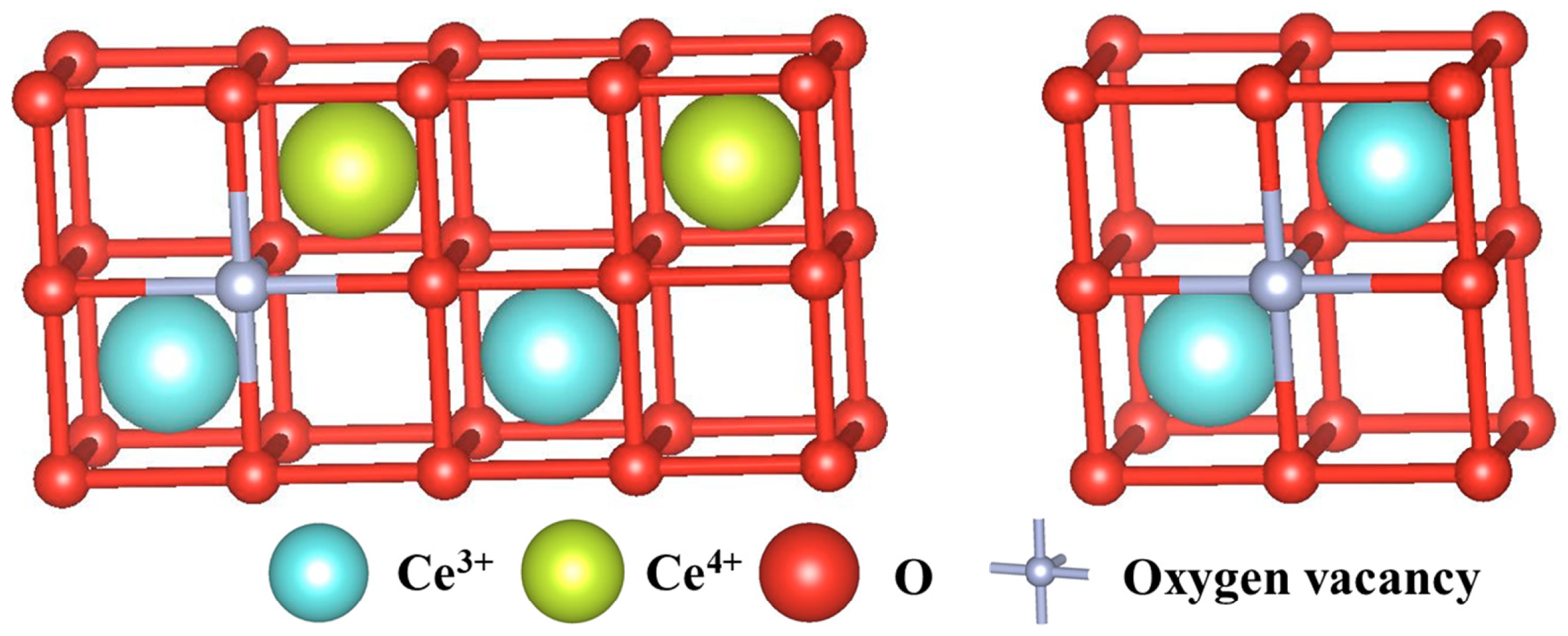
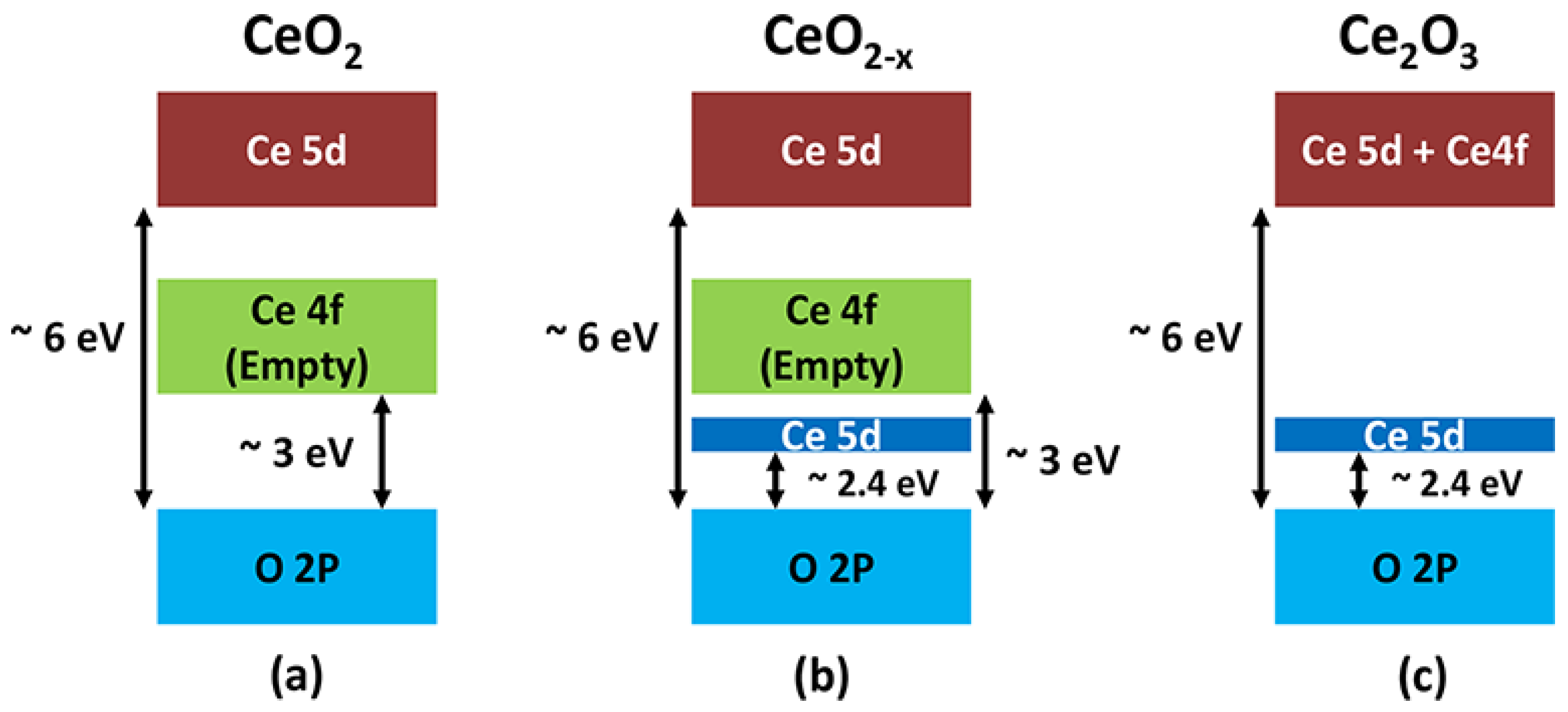
2.2. Crystal and Electronic Structure of Cerium Oxides

The crystal structure of pure stochiometric cerium oxide (CeO${}_2$, or ceria for short, corresponding to $x=0$) is cubic fluorite, with each Ce${}^{4+}$ cation neighboring eight O${}^{2-}$ anions at the corners of a cube, and each O${}^{2-}$ is in turn coordinated by a tetrahedron of Ce${}^{4+}$ ions [31]. The cubic structure is preserved up to an oxygen vacancy of $x=0.28$ [32]. Between $x=0.28$ and $0.5$, a series of ordered oxygen vacancy superstructures are found. At $x=0.5$, a sesquioxide is found that crystallizes in the related hexagonal bixbyite structure, with a chemical formula Ce${}_2$O${}_3$ [33]. A schematic representation of two models indicating the local structure around oxygen vacancies in tetravalent cerium oxide is shown in Figure 1. In our lattice model, we consider a mixture of these two models where the trivalent cerium atoms are distributed randomly over the entire lattice.

In general, when free ions are placed in a crystalline environment to form oxides, drastic changes are expected due to the interaction between the neighboring oxygen ions through crystal-field and ligand-field splitting. These two go hand-in-hand, and are especially large in the case of partially filled d-shells. In addition, the Jahn-Teller effect [35], in which the ions deform spontaneously to lower their crystal-field energy, plays an important role in some partially filled d-shell oxides, leading to interesting charge and orbital ordering [36].

In the case of cerium oxides and other lanthanides, where $4f$ electrons are at play, the crystal-field splitting is about 2 orders of magnitude smaller than those of d-shell electrons, due to the shielding of $4f$ electrons by the $5s,5p,5d$, and $6s$ shells [37,38]. Hence, it is a good approximation to omit the crystal-field and ligand-field splitting in the model Hamiltonian for cerium oxides.

Figure 2 shows the schematic electronic structure of cerium oxides. For $x=0$, namely CeO${}_2$, the material is a wide-bandgap insulator with a bandgap of about 6 eV. There is an empty $4f$ band that lies in the gap about 3 eV above the O $2p$ band. Upon introducing oxygen vacancies, Ce${}^{3+}$ starts to act as a donor and a $5d$ band is created ∼2.4 eV above the O $2p$ band. For $x=0.5$, empty Ce $4f$ and $5d$ bands merge in the conduction band as shown in the figure.

In this paper, when considering the hopping of an electron between Ce sites (labeled by “t” in the next section), we employ the Goodenough-Kanamori rule [40,41], which states that the spin-spin interaction between the cations (Ce in our case) is mediated by a virtual electron transfer from a shared anion (O $2p$ orbitals in this case). This rule is especially valid when the crystal structure is cubic, which is certainly true in the case of CeO${}_{2-x}$ for $x<0.28$. As shown by Anderson later on [42,43], this makes it unnecessary to consider the oxygen sites in a model Hamiltonian.

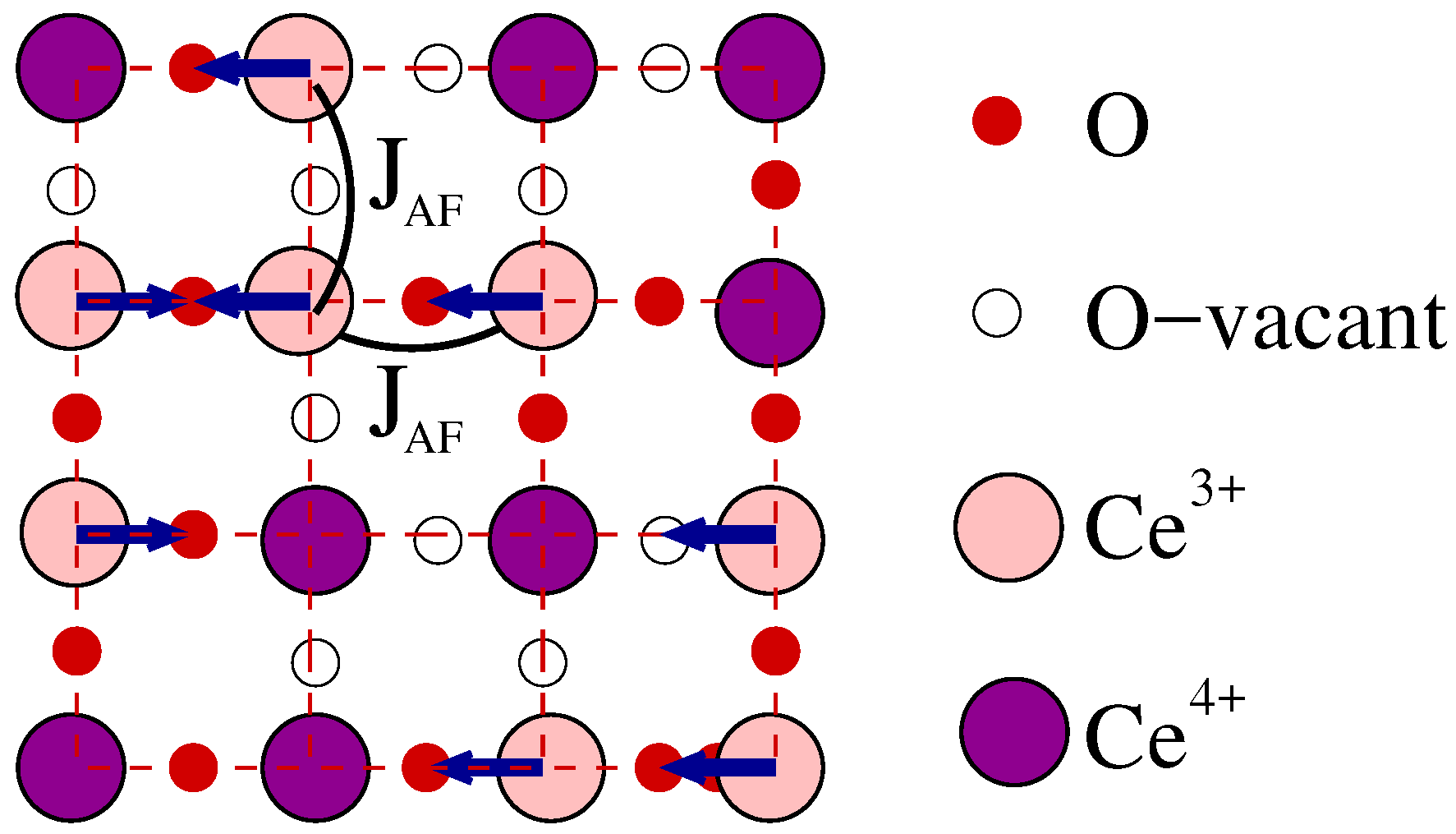
2.3. One-Orbital Model

Above considerations lead us to employ the following lattice Hamiltonian suitable for cerium oxides in our simulations on $8\times 8$ clusters. The model is explicitly defined as:

$$\begin{array}{ccc}\hfill \widehat{H}& =& \sum _{\mathbf{ia}\sigma }{t}^{\mathbf{a}}(d_{\mathbf{i}\sigma }^{†}{d}_{\mathbf{i}+\mathbf{a}\sigma }+\mathrm{h}.\mathrm{c}.)-J_{\mathrm{H}}\sum _{\left\{\mathbf{I}\right\}}{\mathbf{s}}_{\mathbf{i}}·{\mathbf{S}}_{\mathbf{i}}+J_{\mathrm{AF}}\sum _{\langle \mathbf{i},\mathbf{j}\rangle }{\mathbf{S}}_{\mathbf{i}}·{\mathbf{S}}_{\mathbf{j}}\hfill \end{array}$$

(2)

where $\mathbf{a}=\mathbf{x},\mathbf{y},\mathbf{z}$ represents the direction an electron can hop with hopping amplitude $t^{\mathbf{a}}=t^{\mathbf{x}}=t^{\mathbf{y}}=t^{\mathbf{z}}=1$ due to rotational symmetry, which also sets the energy scale used throughout the paper.

The Hund coupling $J_{\mathrm{H}}$ > 0 (i.e., intraionic exchange) represents the interaction between the itinerant electron spin ${\mathbf{s}}_{\mathbf{i}}={\sum }_{\alpha \beta }{d}_{\mathbf{i}\alpha }^{†}{\sigma }_{\alpha \beta }{d}_{\mathbf{i}\beta }$ ($\sigma$ = Pauli matrices) in the conduction band and the localized spin ${\mathbf{S}}_{\mathbf{i}}$ at an ionic site. Comparison of Figure 3 with Figure 1 should give the reader a visual guide regarding how our model is related to the actual material.

In the second term, the Hund coupling $J_{\mathrm{H}}$ (i.e., intraionic exchange) is taken to be positive and represents the interaction between the itinerant electron spin ${\mathbf{s}}_{\mathbf{i}}={\sum }_{\alpha \beta }{d}_{\mathbf{i}\alpha }^{†}{\sigma }_{\alpha \beta }{d}_{\mathbf{i}\beta }$ ($\sigma$ = Pauli matrices) in the conduction band and the localized Ce spin ${\mathbf{S}}_{\mathbf{i}}$ at an ionic site i. $J_{\mathrm{AF}}$ is the superexchange coupling. In the present study, we set $J_{\mathrm{AF}}=0$ because the energy scale associated with this term is smaller than other energy scales. It is expected that for the nearest-neighbor interactions this term will lower the $T_{\mathrm{C}}$ for small values of $J_{\mathrm{AF}}$ as in RbO${}_2$ [44], but an antiferromagnetic (AF) state with small Neél temperature $T_{\mathrm{N}}$ may stabilize at larger values, as in CsO${}_2$ [45]. Results with finite values of the superexchange coupling will be published elsewhere.

Note that the Ce spin is assumed classical with $|{\mathbf{S}}_{\mathbf{i}}|=1$ to avoid the sign problem, an approximation widely used in previous efforts [46]. While the use of a classical spin when dealing with a 1/2 quantum spin is not an ideal approximation, this is needed in order avoid the sign problem associated with Monte Carlo simulations of quantum systems as discussed before.

The interaction term is restricted to randomly selected sites, denoted by the summation index $\mathbf{I}$ in the Hamiltonian above, as is done in simulations of diluted magnetic semiconductor systems [47,48,49]. The density of these randomly selected sites is related to the density of oxygen vacancies present in cerium oxides. For example, when $x=0$ (i.e., pure stoichiometric CeO${}_2$), all Ce ions are in a Ce${}^{4+}$ state, i.e., the $4f$-shell is empty. When an oxygen vacancy is introduced by the substitution of lower valent elements on the cation sub-lattice, the $4f$-shell picks up an electron and we have a Ce${}^{3+}$ ion at an atomic site. In our study, the letter N will refer to the spin concentration, which is set at $N=0.5$. The carrier concentration on the other hand, which corresponds to the density of electrons hopping between sites will be denoted by n.

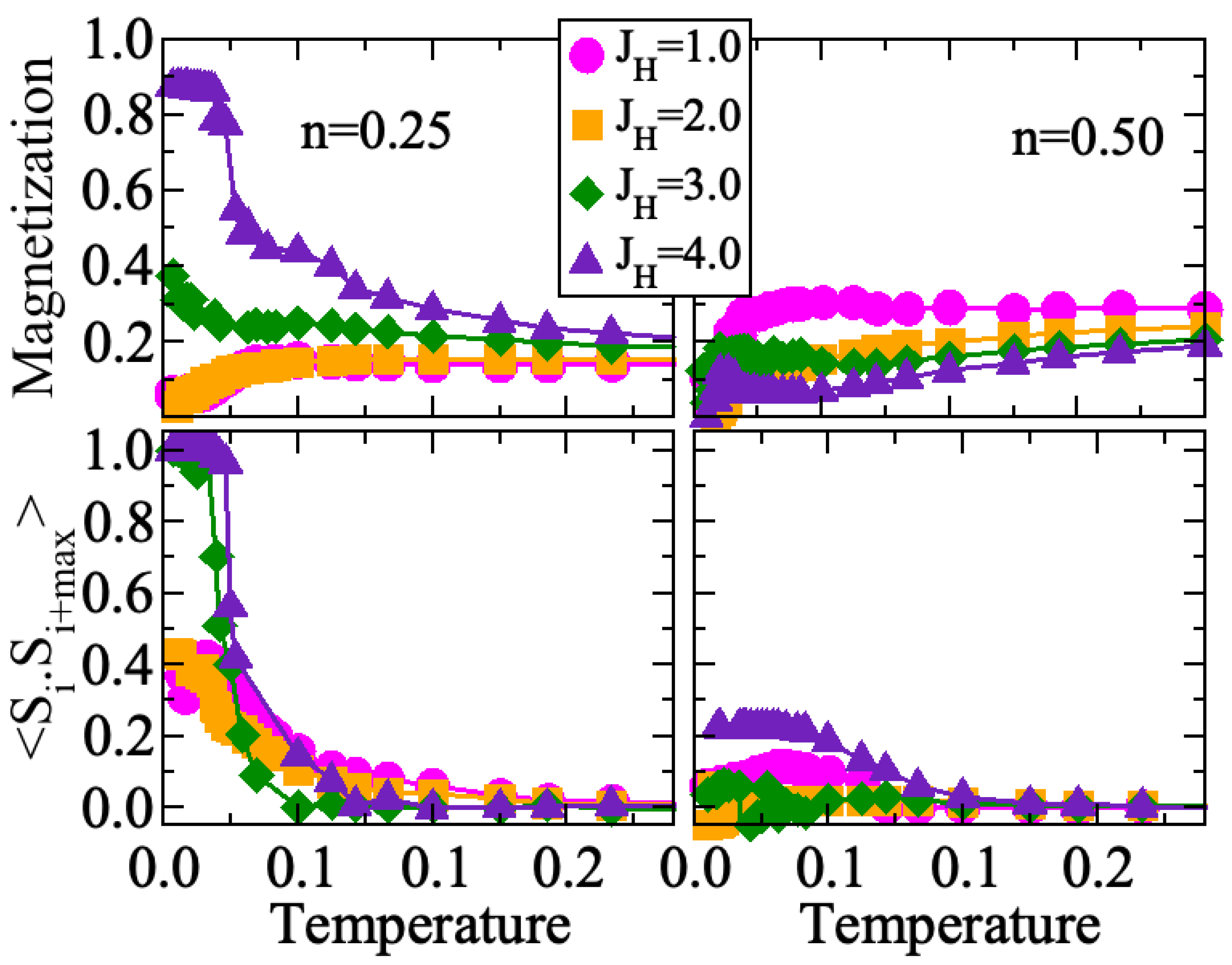
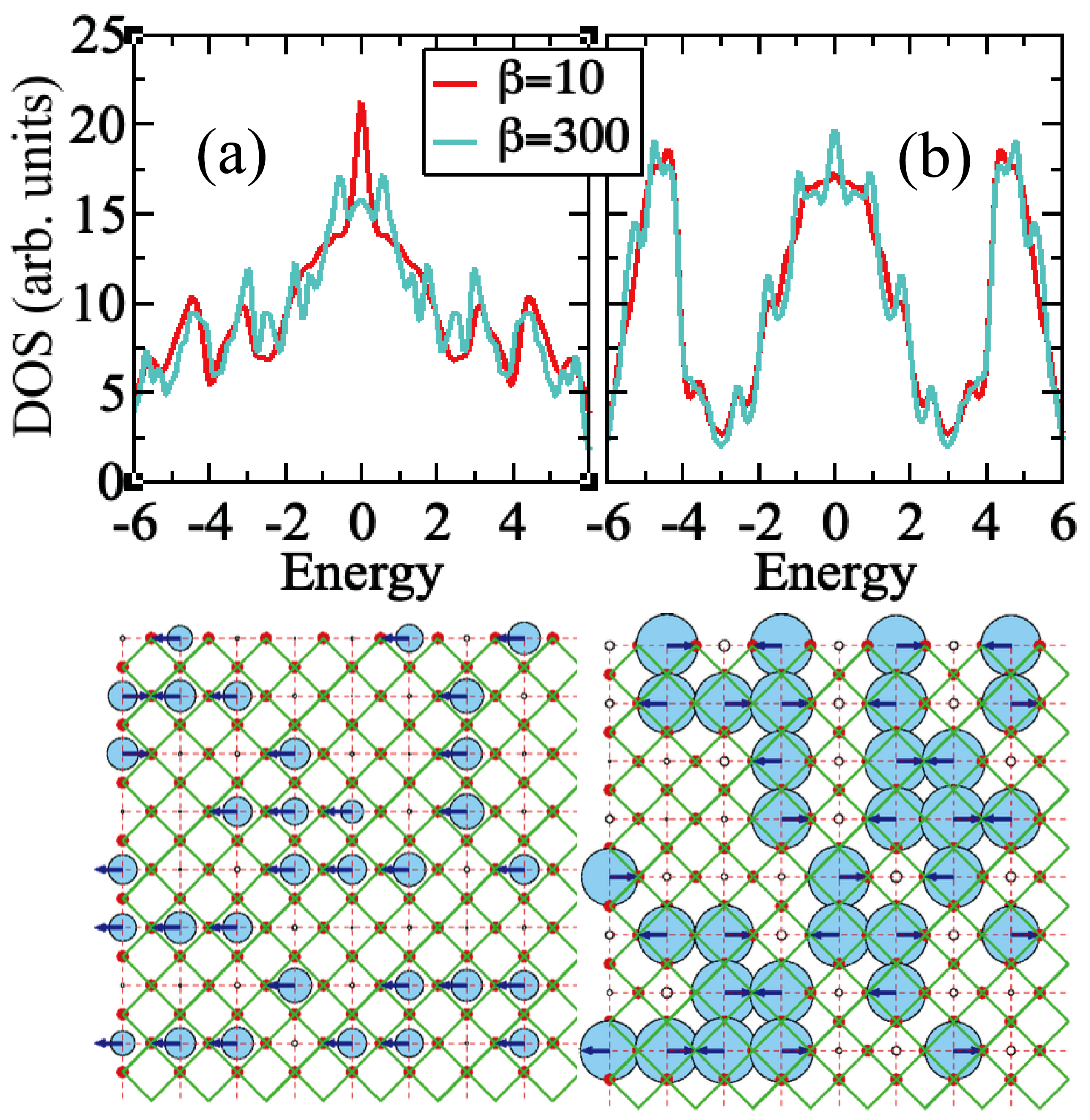
3. Results

In this section we discuss our results obtained using the Hamiltonian described in Equation (2) using exact diagonalization Monte Carlo (EDMC) algorithm [2,46]. We used the spin-phonon-fermion (SPF) code on an $8\times 8$ cluster with periodic boundary conditions, starting with a random configuration of the $N=32$ Ising spins distributed over the 64-site lattice. We then slowly annealed temperature from $T=0.2$ down to as low as $T=0.003$. For each temperature, we used 20,000 thermalization steps followed by another 20,000 measurements steps taken every 5 steps. The latter is to minimize the auto-correlation errors in the Monte Carlo update algorithm. The calculations are done at the Infrastructure for Scientific Applications and Advanced Computing (ISAAC) Facility at the National Institute for Computational Sciences (NICS) at the University of Tennessee, Knoxville.

Figure 4 summarizes our initial results for magnetization (upper two panels) and spin-spin correlations at the maximum distance allowed (lower two panels). The two panels on the left show our results using 16 electrons (n = $0.25$) and the right two panels show using 32 electrons (n = $0.50$). Both magnetization and spin-spin correlation calculations indicate that for n = $0.25$, and as the Hund-coupling $J_{\mathrm{H}}$ increased, a FM state is stabilized at lower temperatures. The FM state is non-existent at the higher carrier density studied, n = $0.50$. This is most likely due to the localization of charge at higher temperatures for larger carrier densities, which seems to take place at higher temperatures. This is apparent from the density of state calculations as well as MC snapshots (see Figure 5). Our results agree with studies done using a similar Hamiltonian but with Heisenberg spins relevant to the DMS materials [47].

4. Discussion

Using our simplistic but realistic model, where itinerant electrons interact with localized Ising spin variables, we investigated the ferromagnetic response using $8\times 8$ lattices via calculations of magnetism and spin structure factors. We did not study larger lattices because the finite size effects are small enough for our purposes. This is because (1) we are only interested in the whether a ferromagnetic response exists at low temperatures, and (2) we are not interested in pinpointing the accurate value of the Curie temperature. We showed that for a carrier concentration of $n=0.25$ and localized spin concentration of $N=32$, a small but robust ferromagnetic response is observed as the Hund coupling strength is increased. A large Hund-coupling is necessary for the itinerant spins to polarize the localized spins as they hop from site to site. Both the magnetism and the spin structure factor at maximum distance with a wave vector $q=(0,0)$ indicate a Curie temperature of about $T_C=0.05-0.10$ depending on the value of the Hund coupling (in units of hopping).

When the carrier density increased to $n=0.50$, the ferromagnetism is lost for all values of the Hund coupling studied in this paper. This is due to the localization of the charge at high temperatures, as seen from the MC snapshots as well as by a gap formation shown in the density of states.

5. Conclusions

The mechanism of small magnetic response in cerium oxides is currently under critical investigation. Zener-type double exchange is among possible explanations, despite the small g-factor $(6/7)$ of the $C{e}^{3+}$ ion (see Section 2). In this study, we used a lattice model with localized Ising spins that interact with itinerant electrons. Our model is similar to models previously studied in the context of diluted magnetic oxides, where Heisenberg spins were used due to large spin values (for example, $S=5/2$ for the d-electrons of the Mn ion). We observed that a ferromagnetic response is possible even with Ising variables using a carrier density of $n=0.25$ and a localized spin density of $N=0.50$. This response dies as the carrier density is increased to $n=0.50$. The latter is due to the localization of charge at higher temperatures.The use of Ising spins in our study better simulates the low spin value of the $C{e}^{3+}$ ion in cerium oxides. The phase space of the current model is vast, and a full study of this and more realistic models is beyond the scope of the current investigation. However, they will be studied in future publications.

In conclusion, we have shown that a simple but realistic double exchange model with Ising spins for cerium oxides exhibit ferromagnetism via a double exchange mechanism. This could be the underlying mechanism of the weak ferromagnetic response that has been experimentally observed in these materials. However, additional studies with more realistic models are needed in order to pinpoint the underlying physics of these materials.